Sequence effect of p(1/3) spectrum loading on service fatigue strength of as-welded and high-frequency mechanical impact (HFMI)-treated transverse stiffeners of mild steel

Abstract

In the meantime, it’s well known that post-weld fatigue strength improvement techniques for welded structures like high-frequency mechanical impact (HFMI) treatment increase the fatigue live of welded joints. Although the current design recommendations for HFMI-treated welded joints give first design proposals for the HFMI-treated welds, in practice the application of HFMI treatment and the associated increase in fatigue resistance are still being discussed. There are, for example, reservations regarding the efficiency of HFMI-treated welded joints under variable amplitude loading (VAL). This paper analyses first results for the sequence effect of VAL of a p (1/3) spectrum on the service fatigue strength of HFMI-treated transverse stiffeners (TS) of mild steel (S355). Fatigue test results with random and high-low loading for the two states as-welded (AW) and HFMI-treated joints will be presented. The modified linear damage accumulation and the failure locations will be discussed. The experimental results show a clear change in the slope of the S-N curve from the as-welded (AW) state to the HFMI state and additionally in the HFMI state from constant amplitude loading (CAL) to variable amplitude loading (VAL). It was particularly noticeable in the experimental results of all tested HFMI series that the specimens failed exclusively in the base material 2–4mm before the HFMI-treated welds. The presented results of the investigations show that with application of the nominal stress concept, no sequence effect was recognizable.

1 Introduction

For the fatigue strength of welded structural steel constructions, the geometrical conditions and local boundary layer conditions at the weld seams are decisive. Many studies, e.g., [1,2,3,4,5,6,7,8,9,10,11,12,13], have shown that mechanical surface treatment of welded joints like high-frequency mechanical impact (HFMI) treatment is particularly suitable to improve the fatigue strength of welded steel constructions and can result in an additional weight reduction of steel structures.

In order to present a safe, economical and resource-saving design proposal for steel structures, a reliable and realistic estimation of the influence of operating service loads as well as of the influences of notch sharpness and the condition of the surface layer after the mechanical treatment on the fatigue behaviour of welded constructions is necessary.

The increase of the fatigue strength of HFMI-treated welded joints under constant loads was determined by comparison of test results of as-welded (AW) and HFMI-treated welds and is accepted by experts and respected in design codes [14, 15]. However, the efficiency of HFMI treatment under real operating conditions is currently questioned. Primarily, this reservation is based on the assumption that the residual compressive stresses generated during operation can be reduced and therefore lose their initial effect, i.e. in [16]. Moreover, it has not yet been clarified how the effect of such postweld treatment can be taken into account in a reliable service fatigue strength analysis. First studies analysed the effect of VAL [11, 17,18,19,20] and came out with first statements. However, no studies are available focussing on sequence effects for single load spectra.

The aim of the research project “HFH-Betriebsfestigkeit” [21] is to investigate the effectiveness of HFMI for welded joints under operating loads. In particular, the sequence effect of different load spectra is analysed. Since the effectiveness of the HFMI process is based on beneficial compressive residual stresses and (strain) hardening of weld toe (WT), extensive investigations of fatigue tests, X-ray diffraction measurements and macro-hardness analyses are carried out to evaluate the behaviour of these parameters under operational loads. The aim is to provide an economical and safe damage accumulation hypothesis for post-treated welded joints, which enables a realistic estimation of the service life of post-treated welded structures under operating loads.

In order to consider the sequence effect in terms of crack initiation and crack propagation, local considerations are necessary, and the physical phenomena behind the damaging behaviour has to be taken into account. Fatigue damage of welded joints is influenced by the complex interactions between the mechanisms of crack closure, plastic flow at the notch (crack) tip and residual stresses. While the effect of single overloads on crack propagation may be explained by induced residual stresses, this is not the case for more complex load spectra [22]. Several predictive models based on fracture mechanics approach have been developed and derivated to analyse and manage the different effects and their impact on the service fatigue strength of welded joints. Anyhow, the complex issue of fatigue crack growth is still subject of research [23]. Interested readers are recommended to study the explanations in, e.g. [22,23,24,25], as well as the sources listed therein. Fracture mechanics approach on HFMI-treated welded joints has been applied, e.g. in [26, 27]. In the study presented in this paper, the sequence influence is considered globally by applying the nominal stress concept. A local analysis of this topic will be presented in further publications.

This paper presents results of the research project “HFH-Betriebsfestigkeit” [21] concerning the sequence effect of variable amplitude loading (VAL) of a p (1/3) spectrum on the service fatigue strength of HFMI-treated transverse stiffeners of mild steel (S355).

2 State of the art – service fatigue strength of HFMI-treated welded joints under variable amplitude loading

2.1 Fatigue test under constant amplitude loading

The increase of fatigue strength of welded joints by HFMI and thus the efficacy of the mechanically post-treatment have already been demonstrated in some studies [4,5,6,7,8,9]. Based on fundamental and diverse studies on the effectiveness of mechanical post-treatment methods for an increase of the fatigue strength of welded joints, first design proposals have been developed [4, 14]. In [14], the allowable stress level is limited to 80% of the nominal yield strength f_y of the steel grade. The investigations in [4] show a significant influence of the mean stress as a function of the steel grade and the post-treatment conditions. In addition, it is suggested to consider the sensitivity of the individual welded details [15]. The currently proposed approach of classifying HFMI-treated welds [14] is based on experimental investigations. A HFMI-treated transverse stiffeners with nominal yield strength of 355≤ f_y <550 MPa is classified to a fatigue class (FATx) of FAT140 at slope of m = 5 [14]. The fatigue class values FATx are the fatigue resistance values for structural details in steel, assessed based on nominal stress [28]. The classification value FATx of the structural details reference to the S-N curve, in which x is the stress range in MPa at N_C=2E+6 cycles [28]. Transverse stiffeners made of high-strength steel with a nominal yield strength of 550 ≤ fy < 750 MPa are classified in a FAT class of FAT160 after the improvement factor from AW to HFMI state according to [14].

2.2 Fatigue test under variable amplitude loading

Compared to the available experiential data of HFMI-treated welded joints under constant amplitude loading (CAL), the number of experimental data under VAL is clearly lower. In addition, the variation of the fatigue test parameters is very wide. Amongst others, the following parameters particularly affect the fatigue resistance of HFMI-treated welds: the type of welded detail with different parameters of geometrical dimensions and notch effects, the quality of the HFMI manufacturing process, the steel grade and the loading conditions under VAL with different stress spectra, stress ratios, irregularity factors and the order of load sequences.

Experiments on longitudinal stiffeners made of high-strength steel (S700) under VAL (straight-line spectra, random, R=−1) show that the residual compressive stresses introduced by the mechanical post-treatment process are significantly reduced during the service loading [29]. According to an analysis of fatigue tests on transverse stiffeners with plate thickness t=5 mm of different steel grades (S355, S690, S960) with a stress ratio of R=0.1 under blocked VAL with high solidity value of the spectrum, damage sums of D=0.3 to D=0.5 respecting the experimental derived service fatigue strength are determined [18]. Investigations on HFMI-treated longitudinal stiffeners (S355) under VAL (straight-line spectra, random, R=0.1, I=0.99) [16] indicate the effectiveness of the post-treatment decreases for a welded detail with a high notch effect and normal strength material under service loading. Deviations occur for the damage accumulation calculation. In [19] existing studies as [16, 17, 29] have been evaluated in view of the design recommendation with D=0.5 or D=1.0. Both values of miner sums have been proved to be conservative respecting the FAT class for HFMI in [14]. As mentioned above, the fatigue resistance of a structural detail with HFMI-treated welded joints is affected by a wide range of parameters. Even if the studies have different test parameters, they already show that the results may also be related to the notch effect of the welded detail. A systematic study with identically test parameters but different structural welded details under VAL is still pending.

2.3 IIW recommendations and damage accumulation

In the recommendations for HFMI-treated welded joints [14], restrictions are given for fatigue design assessment. Because of limited systematic studies for the HFMI-treated state, some of the restrictions were adopted from the recommendations of AW joints and the recommendations for improved welded structures by needle peening or hammer peeing [30].

The restrictions should account for possible uncertainties and possibly legitimate considerations that the beneficial improvement of the HFMI treatment, especially the applied compressive residual stress state, may not be stable [14].

Even though individual studies show that the application of the design recommendations leads in some cases to conservative results, these restrictions are mandatory for a safe and reliable fatigue design. The recommendations are continually adapted to the current state of research and practical experience. The recommendations thus also pursue the aim of obtaining an economic design of the construction.

For a better estimation, evaluation and possibly adaptation of the restrictions, a better understanding of the behaviour of treated structures is necessary, which requires further systematic studies and research.

2.3.1 Restrictions for fatigue design of HFMI-treated welded joints

First and foremost, the recommendations allow an improvement of the FAT classes for the HFMI-treated welded joints of steel structures with a plate thicknesses of t=5 to 50 mm and for nominal yield strength ranging from f_y=235 to 960 MPa. Further, the maximum benefit depends on conditions like the thickness effect, the influence of steel strength, loading effects, stress ratio and constant and variable amplitude loading conditions [14].

To stay with the topic of the paper, the following design proposals and restrictions are given for a mild steel with a nominal yield stress of f_y=355 MPa, a stress ratio of R=-1, a plate thickness of t₁=16 mm, an attachment thickness of t₂=8 mm and the loading effects due to CAL and VAL:

First, a FAT class for the transverse stiffeners has to be chosen. As already mentioned above, the recommendations of HFMI treatment [14] give a proposal for an increase in numbers of FAT classes depending on the nominal yield strength. For transverse stiffeners of mild steel S355, the maximum possible improvement contains 5 classes, from a FAT80 in the AW condition to a FAT140 in the HFMI condition.

Due to the two different FAT classes and the change in the slope of the S-N curve in the AW- and HFMI-treated condition from m_AW=3 to m_HFMI=5, the original and the improved curves intersect in the region of high stress ranges. This results in the restriction of a cycle limit below which HFMI treatment provides no benefit. The intersection point can be determined by Eq. (1).

$$ {\mathrm{N}}_{\mathrm{i},\mathrm{AW},\mathrm{HFMI}}={\mathrm{N}}_{\mathrm{C}}{\frac{\Delta {\upsigma}_{\mathrm{C},\mathrm{AW}}}{\Delta {\upsigma}_{\mathrm{C},\mathrm{HFMI}}}}^{\frac{{\mathrm{m}}_{\mathrm{AW}}\cdotp {\mathrm{m}}_{\mathrm{HFMI}}}{{\mathrm{m}}_{\mathrm{HFMI}}-{\mathrm{m}}_{\mathrm{AW}}}} $$

(1)

For FAT80 and FAT140, a cycle limit of approximately N_i,AW,HFMI≈30,000 cycles can be computed, which gives the associated stress range of approximately Δσ_i,AW,HFMI ≈324 MPa which is determined by Eq. (2).

$$ {\Delta \upsigma}_{\mathrm{i},\mathrm{AW},\mathrm{HFMI}}={{\Delta \upsigma}_{\mathrm{C},\mathrm{AW}}}^{\frac{-{\mathrm{m}}_{\mathrm{AW}}}{{\mathrm{m}}_{\mathrm{HFMI}}-{\mathrm{m}}_{\mathrm{AW}}}}\cdotp {{\Delta \upsigma}_{\mathrm{C},\mathrm{HFMI}}}^{\frac{{\mathrm{m}}_{\mathrm{HFMI}}}{{\mathrm{m}}_{\mathrm{HFMI}}-{\mathrm{m}}_{\mathrm{AW}}}} $$

(2)

From a sheet thickness of t>25mm, a thickness reduction factor has to be taken into account. This restriction is also depending on the size effect of the welded attachment. For details, see the explanations in [14, 28]. No thickness and size effect has to be considered for the details investigated in this paper.

Since the benefit of the HFMI treatment as a weld improvement method is attributed to strain hardening and introduction of compressive residual stresses, the maximum stress level is limited to 80% of the nominal yield strength. Here, the loading effect restriction of rest. σ_max = 0.8·f_y is given, which should ensure that the residual stresses introduced remain stable [14, 30]. Secondly, the maximum allowable stress range for CAL is limited to rest. Δσ ≤ 0.9·f_y. For the values associated to the presented weld detail, see Table 1.

Table 1 Restrictions for the experimental parameters of the transverse stiffeners of mild steel (S355) analysed in this study

Generally, the decisive loading restriction depends on the loading condition. For the CAL series, the stress range restriction rest. Δσ has to be considered, and for the VAL series, the maximum stress restriction rest. σ_max is decisive. In addition, it must be checked whether the equivalent stress range Δσ_eq of the VAL series, Eq. (3), complies with the restriction of the stress range rest. Δσ of CAL.

The influence of the stress ratio R is taken into account in another restriction. For fatigue design, the maximum allowable constant amplitude stress range is given by a bilinear function. An increasing reduction has to be considered for stress ratios R in the region of −0.125≤R<0.5, while for smaller stress ratios, R<−0.125, the reduction remains constant. In order to simplify this situation for the purpose of fatigue design, the above-mentioned benefit in the form of an increase in number of FAT classes depending on the nominal yield strength is now partially reversed as a function of the stress ratio R. A reduction in number of FAT classes depending of the stress ratio between 0.15≤R<0.5 has to be considered. For R ≤ 0.15, no reduction due to stress ratio is necessary.

In conjunction with the mentioned restrictions, the permissible parameter regions of the S-N curve for a mild steel (S355) with the nominal yield strength f_y=355MPa and a stress ratio of R=−1, for the CAL and VAL series, are shown in Fig. 1. Table 1 summarizes the restrictions for the parameters of the investigated transverse stiffness. For comparison, the nominal yield strength f_y=355 MPa and the actual yield strength of the specimen material f_y=420 MPa (see Table 3) were used as reference values.

Fig. 1

Restrictions according to the HFMI IIW recommendations [14], applied to the test specimen

Most fatigue tests in the project [21] described in this paper were performed outside the recommended loading restrictions of the recommendations for HFMI-treated welded joints [14]. This was done in order to explore the influence of high stress levels on the effectiveness of the HFMI treatment. During the HFMI, series fatigue tests, under CAL maximum stress ranges of Δσ_n,max=504 MPa and under VAL of Δσ_n,max=669 MPa, have been applied.

2.3.2 Damage accumulation and damage sums

With the IIW recommendations for HFMI-treated welded joints [14], design methods for service loads of variable amplitudes are now available for AW and for HFMI-treated welded joints. The known formula of the equivalent constant amplitude stress range Δσ_eq is used, as stated in the IIW recommendations for AW joints [28]. The value of Δσ_eq is based on rainflow counting and the modified Palmgren-Miner rule [31]. For HFMI-treated welded joints, the change of the slopes of S-N curve was observed [5] so that Eq. (3) has to be used with the slope parameters m_HFMI=5 and m’_HFMI=9 [14] instead of m_AW=3 and m’_AW=5 [28].

$$ \Delta {\upsigma}_{\mathrm{eq}}={\left(\frac{1}{\mathrm{D}}\cdotp \frac{\sum \Delta {\upsigma}_{\mathrm{i}}^{\mathrm{m}}{\mathrm{N}}_{\mathrm{i}}+\Delta {\upsigma}_{\mathrm{k}}^{\left(\mathrm{m}-{\mathrm{m}}^{\hbox{'}}\right)}\cdotp \sum \Delta {\upsigma}_{\mathrm{j}}^{{\mathrm{m}}^{\hbox{'}}}{\mathrm{N}}_{\mathrm{j}}}{\sum {\mathrm{N}}_{\mathrm{i}}+\sum {\mathrm{N}}_{\mathrm{j}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{m}$}\right.} $$

(3)

While the general applicability of Eq. (3) was shown in [17], the allowable amount of damage sum, e.g. D=0.5, is still under discussion [18]. The calculated real damage sum D_real depends on the base material strength of the different steel grade [18]. For variable block loading with a stress ratio of R=0.1, the real damage sum for a transverse stiffener of mild steel (S355) of D_real=1.6 was presented. For high-strength steels (S690 and S960), the real damage sum had values of D_real=0.63 and D_real=0.74 in the finite life regime [18], which is close to the recommended value of D=0.5 for AW joints [14]. For a more direct comparison of CAL and VAL fatigue test results, the equivalent constant amplitude stress range Δσ_eq was used. One of the problems comparing the results of CAL and VAL fatigue tests is the change of the slope in the high-cycle fatigue region. Because of the limited numbers of studies of VAL fatigue results, a constant damage sum over the whole region results in conservative statements.

Further fatigue test under VAL was carried out on longitudinal stiffeners [5], where the notch effect is higher which leads to a lower benefit and results in suggested damage sums of, e.g. D=0.2 [16]. Additionally, the variation of statements regarding to damage sums depends on the yield strength [16, 29], the stress ratio R [16, 32] and the type of VAL, e.g. load spectrum and sequence of load amplitudes, meaning randomly [17] or blocked [18] loading state. A final assessment based on the results of the existing studies with this wide variation of test parameters would not be serious.

3 Fatigue tests under constant and variable amplitude loadings for as-welded and HFMI-treated transverse stiffeners

3.1 Load sequences and testing procedure

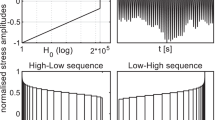
Load sequences under real operating conditions are often randomly distributed. In contrast to AW conditions, for which studies are available, a much smaller number of test results exist for HFMI-treated welded joints under VAL. Speaking of variable loading, one has to distinguish between block loading and random loading. In the research project [21], fatigue tests under CAL and VAL random loading as well as VAL blocked loading in the form of high-low and low-high sorted loading have been performed. The different sequences are qualitatively explained in Fig. 2.

Fig. 2

Studied sequences and stress spectrum

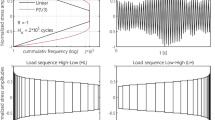
To generate the random load sequence, a combination of standardized load spectra with the matrix method and a scaling function has been chosen. First, a standard random load sequence of Gaussian type has been generated, so that with the level crossing counting method, the generated load sequence leads to a cumulative normal distribution, Eq. (4), with shape parameter ν=2.

$$ \mathrm{H}={\mathrm{H}}_0\cdotp \exp \left(-\ln \left({\mathrm{H}}_0\right)\cdotp {\left(\frac{\upsigma_{\mathrm{a}}}{{\overline{\upsigma}}_{\mathrm{a}}}\right)}^{\upnu}\right) $$

(4)

The generated amplitudes have then been scaled by a scaling function with a p value of p=1/3, Eq. (5).

$$ {\left(\frac{\upsigma_{\mathrm{a}}}{{\overline{\upsigma}}_{\mathrm{a}}}\right)}_{\mathrm{p}}={\left(\frac{\upsigma_{\mathrm{a}}}{{\overline{\upsigma}}_{\mathrm{a}}}\right)}_{\mathrm{p}=0}\cdotp \left(1-\mathrm{p}\right)+\mathrm{p} $$

(5)

With this procedure, the applied load sequences follow an approximated p (1/3) spectrum, which is a typical convex distribution for crane and bridge construction. The spectrum had a sequence length of H₀=2E+5 and an irregularity factor of I=0.99.

Background information and further details on the method used to generate the random load sequence can be found in [33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50] and will be described and discussed in detail in the near future. This section describes the testing procedure and the realization of the different load sequences of a p (1/3) spectrum in relation to the sequence effect.

3.1.1 Methodical approach, statistical evaluation of random fatigue tests and generation of high-low and low-high block loading

To evaluate the influence of the sequence effect, variable amplitude fatigue tests with random loading and ordered high-low and low-high loading for the two states AW and HFMI-treated joints will be carried out in the project “HFH-Betriebsfestigkeit” [21]. In order to be able to assess the influence of load sequence effect as realistically as possible with regard to the result of the fatigue tests, a methodical procedure for generating the load sequences and execution of the experiments is necessary. The chosen methodical procedure for load sequences will be described below and is shown in Figs. 3 and 4.

Fig. 3

Statistical evaluation of the VAL-random-AW series and selection of stress levels associated to factorized spectrum length for the VAL-high-low-AW series

Fig. 4

Target stress level of factorised spectrum length, expected scatter and expected failure scenarios of the VAL-high-low-AW series

With regard to the discussion of the effectiveness of HFMI-treated welded joints and the stability of beneficial residual stresses under VAL, it was analysed whether the order of high and low load levels influences the effectiveness of the HFMI treatment.

In order to be able to estimate the sequence effect as realistically as possible, the stress levels of the high-low and low-high block loading sequences were chosen on the basis of the evaluated random series. This implicitly considers the dispersion of the resulted fatigue tests.

The first series of experiments was tested with random loading. Due to the test accuracies, the machine control and different tolerances, there is a small but measurable deviation between the positive and negative amplitudes of the loading sequence. This means that there is a small deviation of the R ratio which leads to different calculated slopes of the lifetime curves if the fatigue tests are presented in the manner of maximum stress amplitudes ${\overline{\upsigma}}_{\mathrm{a}}$ or the maximum stress ranges Δσ_n,max. As for the general description of fatigue tests and in particular for welded joints in conjunction with high tensile residual stresses (Δσ concept), the stress range Δσ is recommended, and the maximum stress range Δσ_n,max was used for the evaluation.

For the random fatigue tests, all test specimens were tested until total rupture and lay in the finite life region of high cycle fatigue (HCF), so that the S-N curve could be estimated by linear regression as described in [51], for example.

With respect to the given load spectrum length of the random fatigue tests (H₀ = 200,000 cycles), the newly selected spectrum length results from multiplying the original load spectrum length by an integer factor, Eq. (6).

$$ {\mathrm{H}}_{0,\mathrm{new}}=\mathrm{f}\cdotp {\mathrm{H}}_{0,\mathrm{origin}}\kern0.5em ;\mathrm{f}\in {\mathbb{N}}^{\ast}\kern0.5em ;{\mathbb{N}}^{\ast }=\left\{1,2,3,\dots \right\} $$

(6)

Finally, the load level is obtained by applying the well-known formula of the S-N curve, Eq. (7) or Eq. (8), with the identified parameters from the linear regression calculation.

$$ \log \left(\mathrm{N}\right)=\log \left(\mathrm{C}\right)-\mathrm{m}\cdotp \log \left(\Delta \upsigma \right) $$

(7)

$$ \log \left(\Delta \upsigma \right)=\frac{\log \left(\mathrm{N}\right)-\log \left(\mathrm{C}\right)}{-\mathrm{m}} $$

(8)

The target sequences of the high-low and low-high block loading spectra should have the same length and the same amplitudes as a fictitious performed fatigue test of random loading on this load level. It means that the load spectrum of the random, high-low and low-high sequences is equal. The difference is only the unsorted or sorted order and the time of occurrence of stress amplitudes, meaning the characteristic of the sequence effect.

In fatigue tests, generally the target spectrum and the actual spectrum differ from each other. With regard to the evaluation of these fatigue tests carried out in this described way, it should be pointed out that a small deviation of target and actual values of load amplitude varying has to be expected. Further in the case that the target number of load cycle differs from the number of cycles to failure in the high-low or low-high tests, either not the complete series has been tested, or the test sequence has been started from the beginning (see Fig. 4). If there is no sequence effect, the test results of the ordered block loading sequences will be found in the scatter band of the evaluated S-N curve of the random series.

3.2 Fatigue test results and evaluation

The fatigue tests have been carried out at the two involved research institutes of the project [21], at the Laboratory for Steel and Lightweight Structures of the University of Applied Science Munich (LSL) and at the Institute of Joining and Welding of the Technische Universität Braunschweig (IFS). Two types of test facilities were available: a from DOLI reconditioned 400 kN Schenk hydropuls cylinder with a INOVA control system, an INSTRON clamping device and a DOLI hydraulic control system at the LSL institute, and a 580 kN MFL servo-hydraulic testing machine with a WALTER+BAI cylinder control system at the IFS Institute. The fatigue tests were performed under alternating (R=-1, $\overline{\mathrm{R}}$=-1) uniaxial loading with a cyclic frequency of round about 4 Hz.

In the project [21] presented in this paper, extensive investigations of fatigue tests, X-ray diffraction measurements and macro-hardness analyses are carried out. In total, 240 fatigue tests of transverse stiffeners of different steel grades (mild steel (S355) and high-strength steel (S700)) have to be performed with two types of spectrum loading (p (1/3) and straight-line spectra) and different load sequences (random, high-low and low-high). The first results presented below are given for a mild steel (S355), a p (1/3) spectrum and for constant, random (R) and high-low (HL) sequences.

To approximate the detail category of fillet-welded transverse stiffeners, a one-side transverse stiffener with a plate thickness of t₁=16 mm, a stiffener thickness of t₂=8 mm and a fillet weld throat thickness of a=4 mm was chosen. For specimen dimensions, see Fig. 5. In Fig. 6, a typical macro-sections and macro-hardness analyses of the AW (left) and HFMI-treated (right) welded T-joint can be seen. The specimens have been made of a mild steel (S355). The chemical composition, the mechanical properties and the welding parameter are given in Tables 2, 3 and 4.

Fig. 5

T-joint specimen dimensions

Fig. 6

Typical macro-sections and macro-hardness analyses of as-welded (left) and HFMI-treated (right) welded T-joint

Table 2 Chemical composition of mild steel (S355)

Table 3 Mechanical properties of mild steel (S355)

Table 4 Welding process parameters of T-joint of mild steel (S355)

A HiFIT device was used for the HFMI treatment [52]. Figure 7 shows the performed HFMI treatment of the welds of the transverse stiffener, and Fig. 8 show the edge finishing of the specimen.

Fig. 7

Weld toe before (top) and after (bottom) HFMI treatment

Fig. 8

Test specimen, HFMI treatment with and without finishing of the edges

The HFMI treatment track and the two states of specimen edges can be seen. The finishing of the edges was necessary because pre-tests had shown that the failure of the specimen occurred in the base material with crack initiation at the edges and not in the HFMI-treated zone, as expected. The aim of edge finishing was therefore to shift the failure location from the base material to the HFMI-treated zone. In this case, the failure location was no longer on the edge, but anyhow all fatigue-tested HFMI specimen failed in the base material.

With knowledge that a component test cannot be substituted by a small-scale specimen due to the reason of residual stress state, the one-side transverse stiffener was chosen. This had the benefit that crack occurrence can be detected with optical measurement technique and possible failure locations are reduced. The possible secondary bending effects, which affect the fatigue strength, have to be kept in mind and will be evaluated separately.

Due to the one-side weldment, angular misalignment is unavoidable. To compare the residual stress state of the AW and HFMI-treated welded joints, the original residual stress state should be maintained. In order to avoid introducing additional residual stresses during the manufacturing process, the specimens were manufactured by water jet cutting. Additionally the specimens were not flame straightening in order not to influence the residual stress state. Because angular misalignment leads during the clamping process to a mean stress level before the actual fatigue test starts, the clamping areas were straightened. When straightening the clamping areas, care was taken to ensure that no additional axial misalignment was introduced. So one can say that the original residual stress state was maintained within the scope of accuracy. Nevertheless, due to the single-sided stiffener and the specimen shape, secondary bending effects cannot be avoided totally.

As already mentioned, a small deviation of the target and actual values of load amplitudes in fatigue tests generally occurs. The experimental data points given in the following diagrams of S-N curves and lifetime curves were determined by thorough analysis and filtering of the raw data. Reversal points that had a difference of less than 3 kN were not counted as turning points and were filtered out. With the assumption of a stress ratio of R=−1, an irregularity factor of I=0.99 and a symmetrically loading, the cycle number is calculated as the half of the number of reversal points of the filtered sequence. Possible deviations and effects of a different evaluation method, classification and counting algorithms and evaluation of cycles are necessary for a damage assessment, but are not part of this paper. The stress range values Δσ_n are given as the maximum values of the actual sequence. Therefore, the actual values of Δσ_n,max and N are shown in the diagrams according to the nominal stress concept.

The S-N curves in the following diagrams result from the evaluation of the data with the common used linear regression method with free slope. To specify the descriptive characteristic value of the S-N curve, the stress range Δσ_C corresponding to N_C=2E+6 cycles was calculated with the lower prediction bound for one single future test with 95% confidence [51, 53, 54]. The thus determined probability of survival P_S=95% is stated in the diagrams. In some figures, also the characteristic S-N curves of the FAT classes according to the IIW recommendations [14, 28] are given. One has to keep in mind that the values of the FAT classes assumed to represent a survival probability of at least 95%, even if they are calculated from the mean value on the basis of two-sided 75% tolerance limits of the mean. Despite the different methods of statistical evaluation and existing definitions, the characteristic values are practically equal for engineering applications [28].

The finite life region of low cycle fatigue (LCF), N_LCF<1E+4, and the infinite life region from high cycle fatigue (HCF) to ultra-high cycle fatigue (UHCF), N_HCF-UHCF>1E+7, were not topic of the project and are not considered. The following assessments are given only for the HCF region because there are data points available. But in respect to the recommended damage accumulation calculation, the second slope of the S-N curves is still shown in the diagrams, which changes under the knee-point of the constant amplitude fatigue limit (CAFL) at N_CAFL=1E+7 cycles and follows a value of m’=2m−1.

3.2.1 CAL fatigue test

To specify the characteristic stress range values Δσ_C,AW and Δσ_C,HFMI of the S-N curve, fatigue tests under CAL with a stress ratio of R=−1 were carried out. The fatigue results are shown in Fig. 9. To analyse the S-N curves of the AW and HFMI state, for each, a number of 5 specimens were tested. This is a very low number of tests, but due to the small scatter, these data could be evaluated. Specimens with N=5E+6 load cycles were defined as run outs and set to a higher level. Because in both states the S-N data point was within the scatter band, they were taken into account by the evolution of the S-N curve, which leads to a slightly greater scatter. The run outs were at values of Δσ_AW=84 MPa and Δσ_HFMI=294 MPa and set higher to a level of Δσ_AW=160 MPa and Δσ_HFMI=460 MPa of the respective series.

Fig. 9

CAL-AW and CAL-HFMI series

According to the real yield strength and the aim of this project, the fatigue tests of the HFMI series were performed outside the IIW restrictions, which have been described before. The specimen within the restrictions of the nominal yield strength led to a run out.

With respect to the small number of test specimen in both states, the AW series for CAL confirms with an experimental characteristic stress range value of Δσ_C,AW,CAL=100.3 MPa and a slope of m_AW,CAL=3.01 the detail category of FAT 80 quite good. The fracture pattern shows more or less the expected semi-elliptical surface crack at the weld toe (WT) (Fig. 10). On the other hand, in the HFMI series for CAL, a characteristic stress range value of Δσ_C,HFMI,CAL=304.3 MPa and a slope of m_HFMI,CAL=9.87 were determined, which is compared to the FAT 140 for transverse stiffeners (TS) and a recommended slope of m=5 a significant increase for the finite life region of HCF. The intersection point for the statistically evaluated S-N curves of the AW and HFMI series is at about N_i,AW,HFMI≈16,350 cycles which is associated to a stress range of Δσ_i,AW,HFMI≈495 MPa.

Fig. 10

Failure locations of the AW series (WT) and the HFMI series (BM) as well as typical fracture pattern of the one-sided T

However, it has to be considered that the failure location of the HFMI-treated specimen was exclusively in the base material (BM). Therefore in Fig. 9, the FAT class FAT 160 for base material is also given. At this point, it is important to emphasize that the fatigue strength of a steel structure is limited to the fatigue strength of the base material.

The result of this investigation shows that the efficiency of the HFMI treatment could be confirmed for the CAL study, but to indicate a final statement, further detailed analysis and evaluations concerning the local stress state and the surface layer state have to be conducted.

3.2.2 VAL fatigue test, random

As already mentioned, the fatigue tests under random VAL followed the approximated convex p value spectrum p (1/3) with a spectrum length of H₀=200,000 load cycles and an irregularity factor of I=0.99. The stress ratio associated to the maximum stress amplitude ${\overline{\upsigma}}_{\mathrm{a}}$ was given by $\overline{\mathrm{R}}$=-1. The fatigue results of the VAL series are shown in Fig. 11. For a better comparison, the results of the CAL series are also shown in this figure. Whereas the resultant slope of the AW series under VAL with a value of m_AW,VAL,R=2.63 is slightly steeper as under CAL, the slope of the HFMI series under VAL is with a value of m_HFMI,VAL,R=13.65 flatter than the slope of the HFMI series under CAL. For a rough assessment concerning the increase of the service fatigue strength under VAL, the estimation is given for the reference point of CAL, namely at N_C=2E+6 cycles. A service fatigue strength of Δσ_C,AW,VAL,R=180.2 MPa for the series VAL-random-AW and a value of Δσ_C,HFMI,VAL,R=481.0 MPa for the series VAL-random-HFMI are determined. The intersection point for the S-N curve with P_S=50% is at about N_i,AW,HFMI≈100,000 cycles which is associated to a stress range of Δσ_i,AW,HFMI≈675 MPa.

Fig. 11

VAL-random-AW and VAL-random-HFMI series

According to the CAL series, the failure location of the AW specimen was at the expected weld toe (WT) and in the base material (BM) for the HFMI-treated specimen (Fig. 12). In the AW series, the typical failure location WT and a typical fracture pattern with a semi-elliptical crack surface that resulted from multiple crack initiation locations which are growing into one single crack can be recognized. In the HFMI series, the failure location is in the BM, 2–4 mm before the HFMI-treated welds. The crack started differently from the BM surface or edges (Fig. 12); one can also see one specimen of the HFMI series for which the failure location is clearly in the BM, but additionally one can see a crack contour in the HFMI-treated zone. But the problem is that it is questionable at which time the crack occurred during the fatigue test. Further it cannot be stated whether it is (i) an initial crack due to the HFMI-treatment, (ii) a small crack with crack arrest or (iii) a small crack which occurred at the end of fatigue test due to the reduction in cross section of the specimen while the BM fails.VAL fatigue test, high-low

Fig. 12

Top left: VAL-random-HFMI, failure location BM. Top right: VAL-random-HFMI, failure location WT. Bottom: VAL-random-HFMI, failure location BM and crack contour in the HFMI-treated zone

To determine a load sequence effect, fatigue tests with a high-low ordered VAL of the p (1/3) spectrum were carried out (Fig. 13). The failure locations and the fracture pattern of the high-low series are similar to the CAL and random series (Fig. 14). In comparison to the CAL series of the AW and HFMI-treated state, one can see the change of slopes and the benefit of the HFMI treatment in the high-low series, as already seen in the random series (Fig. 13). But a closer look to the data points and the evaluated S-N curves of the series with VAL is worthwhile.

Fig. 13

VAL-high-low-AW and VAL-high-low-HFMI series

Fig. 14

Top: VAL-high-low-AW, failure location WT. Middle and bottom: VAL-high-low-HFMI, failure location BM, with some beach marks

At first glance, one can see the greater scatter of the high-low series in the AW state and the steeper slopes of the high-low series in the HFMI and AW states. But in detail, at the reference cycle number of N_C=2E+6 cycles, the mean value of the high-low series in the AW state with a value of Δσ_{50%,AW,VAL,HL}=197.4 MPa is a little bit lower than in the random series with a value of Δσ_50%,AW,VAL,R=211.5 MPa. The mean value of the high-low series in the HFMI state is with a value of Δσ_{50%,HFMI,VAL,HL}=554.0 MPa greater than in the random series with a value of Δσ_{50%,HFMI,VAL,R}=532.3 MPa. Due to the greater scatter in the AW state, the characteristic values of the high-low series with values of Δσ_C,AW,VAL,HL=140.5 MPa are lower than in the random series, while the characteristic values of the high-low series in the HFMI state are with a value of Δσ_{C,HFMI,VAL,HL}=492.3MPa a little bit higher than in the random series.

The resultant slope of the high-low series m_AW,VAL,HL=2.39 and the random series m_AW,VAL,R=2.63 in the AW state is practically equal. In the HFMI state, the slope of the high-low series is with a value of m_HFMI,VAL,HL=10.72 steeper as the evaluation and discussion of the sequence effect

3.2.3 Comparison of experimental and calculated fatigue lifetime curves

To be able to give a first statement for the application of a damage accumulation hypothesis, the experimental data points with the evaluated characteristic S-N curve and the calculated fatigue lifetime curves are shown in Figs. 15 and 16. To compare the experimental data and make an assessment to recommendations, the S-N curves and the calculated fatigue lifetime curves of the FAT classes are also shown.

Fig. 15

Calculated lifetime curves (modified Palmgren-Miner rule) of FAT classes and CAL-AW series vs. VAL-random-AW series

Fig. 16

Calculated lifetime curves (modified Palmgren-Miner rule) of FAT classes and CAL-HFMI series vs. VAL-random-HFMI series

As already mentioned, in the AW state (see Fig. 15), the slopes of VAL series are slightly steeper than in the CAL series. Because of the linear approach of the damage accumulation, the calculated fatigue lifetime curves are parallel to the reference S-N curve, which means that they have the same slope in the finite life region of HCF. In both cases, the FAT 80 curve and the experimental S-N curve, all experimental data points of the VAL-random-AW series lie above the calculated fatigue lifetime curves (Fig. 15). The experimental fatigue lifetime curve with a steeper slope of m_AW,VAL,R=2.63 intersects the calculated lifetime curve of the CAL-AW series with a slope of m_AW,CAL=3.01 in the region between 6E+5<N<1E+6. However, this could not be seriously assessed because in the region from N>1.5E+6, there are no experimental data points. Therefore, the fatigue lifetime curve in the region from N>1.5E+6 is just extrapolated from the assumption of the recommendations. With some more data points in this region, the actual S-N curve could maybe flatter than the experimental estimated one. To give a statement about this region, further fatigue tests under VAL have to be performed.

Figure 16 shows the results for the HFMI state. Similar to the AW state, the experimental data points of the HFMI state lie above the expected values using given FAT classes. The calculated fatigue lifetime curves for VAL based on the FAT classes for the HFMI state, FAT 160 for the base material (BM) and FAT 140 for the transverse stiffeners (TS), are underneath the experimental evaluated lifetime curves for the VAL-HFMI series, even if the curves would intersect in the region between 1E+4<N<6E+4 (Fig. 16). The calculated fatigue lifetime curve for VAL based on the experimental evaluated S-N curve lies clearly above the experimental fatigue lifetime curve. Because of the two different slopes of the curves under CAL and VAL, the distance of the calculated lifetime curve and the experimental lifetime curve is larger than in the range between 1E+6<N<2E+7. The evaluated scatter of the experimental S-N curve of CAL-HFMI series is quite small. The estimated standard deviation in terms of logarithmic cycle numbers amounts to a value of s_N,log,HFMI=0.101. A common value of standard deviation of welded joints is given with a value of about s_N,log=0.206, at a slope of m=3 [55]. For flatter slopes, the standard deviation commonly takes higher values up to approximately s_N,log=0.3, e.g. [43]. As already mentioned, only a small number of experiments have been carried out to estimate the S-N curves in both cases, the AW state and the HFMI state. This is taken into account in the statistical method, but the data points are unusually close to the regression line, which gives this uncommonly small scatter.

It should be mentioned again that a differentiated view is necessary with regard to the statements made about the fatigue lifetime curves in the HFMI state based on the FAT classes transverse stiffeners (TS) and base material (BM) and the experimental S-N curve for VAL-random-HFMI. The need of a differentiated approach results from the different failure locations. The failure location of the FAT classes will be assumed in the impact region of the weld toe (WT), while the experimental data under VAL are exclusively in the base material (BM).

3.2.4 Experimental scatter bands in comparison of two statistical evaluation methods

The low scatter of the experimentally determined and statistically evaluated S-N curve under CAL has already been pointed out. Standardized or normalized scatter bands are usually descripted with the value T_S, which is the stress range ratio between the lower and the upper bound of the logarithmic standard normal distribution for specific values of probability of survivals, typically P_S=90% and P_S=10%.

In order to quantitatively evaluate the small experimental scatter band compared to a standardized or normalized scatter bands as well as for a better classification of the experimental data and the subsequently calculated damage sums D, a conversion of the lower bound of the one-sided prediction interval to a two-sided scatter band of a logarithmic standard normal distribution is performed, as presented below.

Since the statistical evaluation was done with the lower prediction bound for a single future test with 95% confidence, and T_S is usually given for the logarithmic standard normal distribution, a conversion into equivalent values of probability of survivals for the equal stress range ratio T_S was made (Eqs. (9), (10), (11), and (12)). The statistically evaluated S-N curve shows a one-sided lower bound, but for scatter bands, the specification of two-sided intervals is common. The conversion achieves that the lower limit of the two-sided interval of the log-normal distribution, which also indicates an upper limit, is identical with the one-sided lower bound of the experimental evaluated S-N curve.

To distinguish the equal stress range ratio T_S of the different statistical assessment, an additional index for survival probabilities for the logarithmic standard normal distribution is given to the value of the stress range ratio.

The general representation of Eqs. (9)–(12) can be found analogously, e.g. in [43]. The designations of the equations contained there have been partially adapted for the conversion presented here.

The stress range ratio T_S can be calculated by the experimentally evaluated stress range values Δσ_50% for P_S=50% and Δσ_C for P_S=95% at the reference cycle number of N_C=2E+6 (Eq. (9)). To indicate the equal values of the stress range ratio T_S and the resulting probability of survival values P_S with the corresponding statistical method, additional index for T_S and P_S will be given. The value T_{S, (95% Prediction)} is determined from the experimentally evaluated lower prediction bound for P_{S, (95% Prediction)}=95%. This value T_{S, (95% Prediction)} is now used to determine the probability of survival values from the log-normal distribution P_{S, (log-normal)}. To have an assignment, the stress range ratio is marked in the index with the resulting survival probability values of the lower and upper bound, ${\mathrm{T}}_{\mathrm{S},\left({\mathrm{P}}_{\mathrm{S},\mathrm{lower}\ \mathrm{bound}}\%/{\mathrm{P}}_{\mathrm{S},\mathrm{upper}\ \mathrm{bound}}\%\right)}$.

$$ {\mathrm{T}}_{\mathrm{S},\left(95\%\mathrm{Prediction}\right)}=1:{\left(\raisebox{1ex}{$\Delta \upsigma 50\%,\mathrm{CAL}$}\!\left/ \!\raisebox{-1ex}{$\Delta \upsigma \mathrm{C},\mathrm{CAL},\left(95\%\mathrm{Prediction}\right)$}\right.\right)}^2 $$

(9)

While T_S indicates the stress range ratio, T_N indicates the ratio between the values of cycle numbers. The relationship between the stress range ratio and the cycle number ratio depends on the slope m of the given S-N curve (Eq. (10)).

$$ {\mathrm{T}}_{\mathrm{N},\left(95\%\mathrm{Prediction}\right)}={\mathrm{T}}_{\mathrm{S},\left(95\%\mathrm{Prediction}\right)}^{\mathrm{m}} $$

(10)

With the calculated cycle number ratio T_N and the estimated standard deviation s_N,log, the normal score u of the standard normal distribution could be calculated (Eq. (11)).

$$ \mathrm{u}=\frac{\log \left(1/{\mathrm{T}}_{\mathrm{N},\left(95\%\mathrm{Prediction}\right)}\right)}{2\cdotp {\mathrm{s}}_{\mathrm{N},\log }} $$

(11)

The probability of survival values of the log-normal distribution with the equal stress range ratio of the statistical evaluated lower prediction bound with 95% of confidence T_{S, (95% Prediction)} can be determined with Eq. (12).

$$ {\mathrm{P}}_{\mathrm{S},\left(\log -\mathrm{normal}\right)}=\Phi \left(\mathrm{u}\right)=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{2\uppi}$}\right.\underset{-\infty }{\overset{\mathrm{u}}{\int }}\exp \left(\raisebox{1ex}{$-{\mathrm{t}}^2$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)\mathrm{dt} $$

(12)

The calculated values of probability of survival P_{S,(log-normal)} of the descripted procedure can be found in the Figs. 17 and 18, which are discussed in the next chapter.

Fig. 17

Calculated lifetime curve (modified Palmgren-Miner rule) vs. VAL-random-AW series

Fig. 18

Calculated lifetime curve (modified Palmgren-Miner rule) vs. VAL-random-HFMI series

3.2.5 Evaluation of the damage accumulation

To give an assessment regarding the damage sums, one must have a look at Figs. 17 and 18. In the figures, the experimental data points of the CAL and random-VAL series, the statistically determined CAL S-N curve and the calculated fatigue lifetime curves in form of scatter bands are shown. The fatigue lifetime scatter band curves are calculated based on the experimental S-N curves of the AW, respectively, HFMI series and under the application of the modified Palmgren-Miner rule.

The illustrated S-N curves in Fig. 17 are given for the experimental evaluated scatter band with a value of T_{S, (95% Prediction)}=T_{S, (99.92%/0.08%)}=1:1.264. The stress range ratio T_{S, (99.92%/0.08%)}=1:1.264 is estimated from the statistically evaluated lower prediction bound with 95% of confidence. Therefore, in terms of the logarithmic standard normal distribution, the upper and the lower bounds give values of probability of survivals of P_{S, (log-normal)}=99.92% and P_{S, (log-normal)}=0.08%. These values of probability of survival again underline the unusually small scatter, as mentioned above. The estimated standard deviation in the AW state gives a value of s_N,log,AW=0.049 which is a quite smaller value as the common value of about s_N,log=0.206 [55]. The experimental evaluated value T_{S, (99.92%/0.08%)}=1:1.264 for P_{S, (log-normal)}=99.92% and P_{S, (log-normal)}=0.08% gives a smaller scatter than the normalized scatter bands based on the log-normal distribution with the common values for welded joints of T_S=1:1.45, respectively, T_N=1:3 according to [43], or T_S=1:1.5, respectively, T_N=1:3.375 according to [55], relating to a slope of m=3 for values of probability of survivals of P_S=90% and P_S=10%.

The experimental data points of the AW state are within the scatter band (Fig. 17). If, instead of the diagrams shown here, an evaluation according to the equivalent stress range method would be carried out, the modified experimental data points would lie within the scatter band of the S-N curve. This is due to the linear damage accumulation approach. This means that for the experimental reference S-N curve, a damage sum of D=1 can be assumed. As presented and discussed before, results prove a damage sum of D>1 based on a FAT 80 S-N curve.

Further, the HFMI data in Fig. 18 will be evaluated. The previously available data of S-N curves for HFMI-treated welded joints from the literature do not allow a uniform specification of the normalized scatter band for the HFMI state. The studies published so far by the experts with the wide range of test parameters such as weld details, dimensions, load condition, R ratio, etc. have so far provided different fatigue strengths and different slopes of the S-N curves even with similar weld details, so that the results are not yet uniform enough to indicate a standardized or normalized scatter band.

As mentioned above, the standard deviation of the CAL-HFMI series is given with a value of s_N,log,HFMI=0.101, which is a fairly small value compared to the usual values of standard deviations of welded joints and in conjunction with the very flat slope of m_HFMI,VAL,R=9.87.

Figure 18 shows that the experimental data points of the HFMI specimens lie on the left side of the calculated scatter band for the fatigue lifetime curves. This means that in case of a fatigue life assessment based on the experimental S-N curve (FAT 304), a damage sum of D<1 will be calculated. But, as the presented and discussed results above show, a damage sum of D≫1 would be calculated for the FAT 140 or the FAT 160 S-N curve.

In order to discuss the results of the calculated lifetime curves of the HFMI state, an alternative evaluation of the data points according to the recommendations [14, 43] has been performed and presented in Fig. 19. The evaluation of the data was done by use of the linear regression method with a fixed slope of m=5, which is recommended for HFMI-treated welded joints.

Fig. 19

Calculated lifetime curve (modified Palmgren-Miner rule) with fixed slope m=5 vs.VAL-random-HFMI series

The characteristic value of the S-N curve, the stress range Δσ_C corresponding to N_C=2E+6 cycles, was calculated with the lower prediction bound for one single future test with 95% confidence, with a small modification in the statistical evaluation compared to the previously evaluated results. The prediction limits are usually hyperbolae, but because of the fixed slope and the assumption that the characteristic value is not far removed from the statistical mean value of the regression analysis, the prediction limits were assumed to be parallel to the regression line [53, 54]. Without this assumption, the scatter band of the S-N curve would be even greater than it already is.

In Fig. 19 again, the estimated statistically evaluated lower prediction bound with 95% of confidence is shown, and the probability of survival values are given in terms of the upper and the lower bounds of the logarithmic standard normal distribution (Eqs. (9)–(12)). One can see that the experimental data points fill the whole region of the calculated lifetime scatter bands and that the scatter bands of the S-N curve and the lifetime curve overlap. From a purely mathematical point of view, such a consideration with a fixed slope could lead to an admissible damage sum of D=1 in the lifetime assessment in relation to the determined reference curve.

To give a final statement about the use of the linear damage accumulation, a differentiated consideration of the results with special attention to the different failure locations have to be performed.

Besides the discussion whether the modified linear damage accumulation is a suitable calculation method for the fatigue life assessment of the HFMI-treated welded joints or not, one has to discuss the slope and the fatigue strength of the recommended S-N curves for the different FAT classes. The evaluated S-N curves and the calculated lifetime curves in the HFMI state show the large deviations due to the different slopes and the resultant scatter bands. Therefore, a statement about the use of the linear damage accumulation is closely related to the specification of a standardized and normalized scatter band, valid for the respective notch detail.

Some other effects can influence the results, as already indicated by the unexpected location of the failure. However, these factors cannot be covered with the nominal stress concept at all. Nevertheless, it can be stated that the efficiency of the HFMI treatment under VAL can be confirmed, as the study has shown.

3.2.6 Results and discussion about the sequence effect

As the former discussed results of the high-low and the random series have shown, beside the slightly change of slopes in both states, the wider scatter band in the AW state is the most significant property between these series. In Fig. 20, the mean experimental fatigue lifetime curves of the high-low and the random series in the AW state and the mean experimental fatigue lifetime curves of the random curve are shown. Additionally, the characteristic curves for a probability of survival of P_S=95% of the series CAL-AW, CAL-HFMI, VAL-random-HFMI and VAL-high-low-AW are given. One can see that the experimental data points of the VAL-high-low-HFMI series lie above the characteristic curve of the VAL-random-HFMI series.

Fig. 20

Random series vs. high-low series

Even if the characteristic value of the VAL-high-low-AW series is clearly underneath the characteristic value of the VAL-random-AW series, the regression lines intersect at about a cycle number of N=3.5E+4. Both the experimental data points and the regression lines are superimposed in the region between 2E+5<N<7E+5. Only one experimental data point of the VAL-high-low-AW series lies underneath the experimental evaluated lifetime curve of the VAL-random-AW series. As already mentioned, the difference between the VAL-random-AW and the VAL-high-low-AW series is just due to the different scatter

According to the previous results based on the nominal stress concept, no sequence effect can be recognized. Therefore, an additional evaluation has been performed, in which the two series of the different VAL type were evaluated together for the AW and HFMI states, respectively (Fig. 21). This type of evaluation gives a better estimate for the scatter band of VAL fatigue tests without sequence effect, cause of the higher number of tests when evaluating the series together. Compared to the evaluation of the random series, there is just a tiny change in slopes of the together evaluated data with values of m_AW,VAL=2.50 and m_HFMI,VAL=13.8. The reference values of P_S=50% are Δσ_50%,AW,VAL=203.3 MPa for the AW state and Δσ_50%,HFMI,VAL=542.0 MPa for the HFMI state. The characteristic values of P_S=95% then result in Δσ_C,AW,VAL=163.0 MPa for the AW state and Δσ_C,HFMI,VAL=493.3 MPa for the HFMI state.

Fig. 21

Jointly evaluated VAL series

4 Conclusions

Fatigue tests under CAL, random VAL and high-low VAL on one-sided transverse stiffener specimen of mild steel (S355) in the AW and HFMI state were performed and evaluated. A p (1/3) spectrum with a sequence length of H₀=2E+5 and an irregularity factor of I=0.99 was applied with a stress ratio of R=−1 under axial force controlled loading.

The failure mechanisms of the performed fatigue tests of CAL, VAL random and VAL high-low series are similar within the respective AW or HFMI state. While for the AW state all specimens have shown a typical fracture pattern in the weld toe, all specimens of the HMFI series failed in the base material, which may indicate an influence of the chosen notch detail.

Compared to the AW series, the HFMI series shows a significant increase in fatigue strength as well as service fatigue strength and a change in slope in the finite life region of HCF, both in CAL and in VAL. In addition, the fatigue strength of the CAL HFMI series is significantly higher, and the slope is flatter than the recommended FAT classes, for both the FAT 140 for transverse stiffeners and FAT 160 for base material. The experimental data of VAL for the AW series lie within the scatter band of the calculated fatigue lifetime curves based on the reference S-N curve of the experimental evaluated fatigue tests under CAL considering the modified linear damage accumulation. In the HFMI state, the experimental data of VAL lie on the left side of the scatter band. A fatigue assessment for the HFMI-treated transverse stiffeners with the studied parameters based on the S-N curves of the recommended FAT classes instead would lead to a conservative result. Investigations show that the damage accumulation and the calculated damage sums have to be evaluated in relation to the notch effect of the details.

The experimental data of the fatigue tests under VAL with a random and high-low sequence lie more or less within the same scatter band, for both the AW and HFMI states. Evaluating the fatigue tests with the nominal stress concept, a sequence effect could not be identified. Even if an assessment based on the nominal stress concept is not accurate enough to generalize statements about the sequence effect, the trend that there is no sequence effect between random and high-low series in the finite life region of HCF is recognizable.

For a more precise statement about the sequence effect, further investigations and analyses are necessary. Future investigations within the project [21] with low-high series and further analyses will be able to specify the meaning of the statement made so far.