Mapping of scatter in fatigue life assessment of welded structures—a round-robin study

Abstract

A round-robin study has been carried out within a national project in Sweden with the addition of an international participant, where several industrial partners and universities are participating. The project aims to identify variation and sources of variation in welding production, map scatter in fatigue life estimation, and define and develop concepts to reduce these, in all steps of product development. The participating organisations were asked to carry out fatigue life assessment of welded box structures, which is a component in load-carrying structures. The estimations of fatigue life have also been compared with fatigue test results. Detailed drawings, loads and material data were also given to the participants. The participants were supposed to use assessment methods based on global and local stresses using the design codes or recommendations they currently use in-house. Differences were identified between both methods and participants using the same codes/recommendations. Applicability and conditions from the cases in the codes were also identified to be differently evaluated between the participants. It could be concluded that for the applied cases the nominal stress method often overestimated the fatigue life and had a high scatter in the estimations by different participants. The effective notch method is conservative in comparison to the life of tested components with little scatter between the results derived by the participants.

Introduction

The amount of variation introduced in the welding industry is significant. All process steps from customer requirements, design and analysis (assessment of fatigue properties), preparation, welding, all induce variation to some degree and are hence connected with a cost. In an ideal situation without variation, it is estimated that more than half of all welding could be removed, resulting in increased productivity, higher flexibility, and reduced cost [1]. Many structural machines and components are exposed to fatigue loads in their daily use, e.g. haulers, cranes and several other similar machines and structures. For this type of steel structures, it is of great importance to balance the fatigue strength and consequences of failure with a competitive cost for design and manufacturing. Increased knowledge about the sources of variation affecting fatigue properties opens the possibilities for weight reduction and hence an increased competitiveness of the product. The incorporation of variations and unknowns is usually done by conservative design of the structure; scatter of fatigue life and loading makes it difficult to obtain an optimal balance for fatigue design of such components [2, 3].

Pettersson and Barsoum [4] carried out fatigue life assessment of welded structure in an articulated hauler. Different fatigue life estimation concepts were used and compared work effort and accuracy of fatigue life assessments methods. They concluded that the nominal stress method overestimates the fatigue life of the component and that simplifications must be considered for each specific case. They also concluded that fracture mechanics and the effective notch stress method are the most accurate methods to assess the fatigue life of welded components. Öberg and Åstrand [5] described the consequences of variation in the welding industry and its effect on manufacturing productivity. They concluded that there is a hidden potential in unnecessary stringent requirements as well as over-processing. This is costly and may be targeted by reducing variation. Bennenbach et al. [6] summarised a collaborative effort, performed as a round-robin study, with the goal to challenge well documented and most promising weld idealisation models and converge towards the most capacitive ones. None of the methods employed in the study were able to estimate the fatigue life in the weld root side safely. In the round-robin study by Fricke [7], three different specimen geometries were studied regarding stress states by the effective notch stress approach. One outcome from the study was guidelines for element sizes for the finite element analysis and fatigue strength recommendations. Fricke et al. [8] performed a round-robin study where some unexpected scatter occurred and concluded that fatigue assessment with current approaches is not satisfactory. Fricke et al. [9] performed a round-robin study using hot spot and the effective notch stress concepts, where the objective was to quantify the uncertainties related to modelling and stress evaluation and identifying sources of scatter. The scatter in the study increased with the complexity of the assessed case. The main source of scatter was identified to be the different types and properties of the finite elements, the mesh density and type of stress extrapolation.

The current round-robin study has been carried out within a national project in Sweden with the addition of an international participant, where several industrial partners and universities have participated. The aim of the round-robin study has been to map scatter in fatigue life estimation. The participating organisations were asked to carry out fatigue life assessment of welded box structure, which is a component typically found in load carrying structures. Detailed drawings, loads and material data were given to the participants. The participants were supposed to use assessment methods based on global and local stresses using the design codes or recommendations they currently use in-house. The component had different sheet thicknesses of the circumferential sheet casing and different levels of weld penetration for the load carrying weld. The geometry was chosen to be similar to a geometry recognised from several codes. However, load insertion was chosen to be different, introducing bending stresses into the weld. Fatigue testing was then performed for one of the sheet thicknesses and the results from the assessments were compared accordingly.

Survey on challenges in fatigue design

Design engineers and analysts at the participating companies were asked to fill out a questioner survey regarding the challenges in fatigue strength assessment of welded structures. The survey was designed to be similar to a prior investigation carried out by the European Pressure Equipment Research Council in 2000 [10], presented in Fig. 1a. It was concluded that among the most troublesome tasks in the fatigue assessment were the estimation of loads acting on the structure, how to carry out the stress analysis and the lack of skilled personnel. Other difficulties encountered in the study with frequent reply were the complexity of the design rules and how to handle situations which fall outside the framework of the standards. The present study showed similar results, see Fig. 1b, where the majority stated that unclear load data is the biggest difficulty for fatigue assessment followed by limitations in the current standards when the load situation is not applicable.

Fig. 1

Survey on challenges in fatigue design from 2000 [10] to the left survey from the current study to the right. (a) European Pressure Equipment Research Council (2000). (b)Survey in current Study (2018).

Welded box structure

The evaluated structure is a box-shaped welded structure, as shown in Fig. 2a, that is designed to represent a non-trivial loading state that includes both normal and bending forces at the circumferential joints. The flanges are made out of 30 mm thick, S700QL sheets in which the loading pin is inserted to. Four different thicknesses are investigated for the web plates: 6 mm, 8 mm and 10 mm, where all are made from S600MC. The presented structure differentiates itself from the cases in current design codes [11,12,13], where the plate is assumed to be thick and/or the load is evenly distributed over the outer flange surface.

Fig. 2

The box-shaped structure used in the round-robin study as the investigated component. (a) Box specimen overview. (b) Box specimen geometry.

The structure is tack welded together at the corners prior to the manual welding procedure [14]. The web plates are then joined together using longitudinal welds (parallel to the loading direction) and the webs are joined to the flanges by circumferential single bevel tee joints made up of five manual weld passes, which are all presented in Table 1. No backing material was used when welding the circumferential joint, the geometry of which can be seen in Fig. 2b. The latter mentioned is the load-carrying weld that is crucial for the fatigue properties of the structural component. No information of which side of the weld that should be regarded as the critical (root/face) was given to the participants.

Table 1 Welding parameters for the circumferential joint

The participating companies were asked to evaluate eight different versions of the presented box specimen with varying web thickness and penetration depths. All individual configurations are presented in Table 2. The load is applied to the box specimen using two loading pins that are inserted into opposite sides of the specimen. The cyclic force applied is 305 kN.

Table 2 Specimen specific data

Nominal stress method

The participants of the study were asked to evaluate the fatigue strength of the box configurations based on the nominal stress method. They presented their calculations together with information regarding which design code and representative detail they implemented. Their results are discussed and compared in the following section. Six participants took part in the fatigue strength assessment using the nominal stress method.

Implemented design codes

The design codes implemented by the participants in the nominal stress method assessment are presented in Table 3 together with information on the applied geometrical detail, the FAT values used, and the failure probability implemented by the standards.

Table 3 Summary of the different approaches by the participants for the nominal stress method

Participant 1 and participant 2 have implemented the same detail from two different design codes: a single-sided V-butt weld with full penetration in the form of either a cruciform joint or a T-joint that is load carrying. It should however be noted that the structural details in the SSAB Design Handbook [13] are primarily based on the IIW recommendation [12], which is the case for the chosen detail. Both codes state that the FAT value of the chosen detail is 71 and potential failure from the weld toe might be expected provided that the full penetration is checked by inspection of the root. If no inspection is carried out, then root failure is expected, and the FAT value is representatively lowered to 36. Both participants have chosen to utilise FAT 71 for the box specimens with full penetration (A, D, F) and FAT 36 when the weld is partially penetrated.

The detail implemented by participant 3 represents a cylindrical hollow tube welded to a flange using a circumferential groove weld with a FAT-value of 63. The tube can be subjected to both axial and bending stresses, and the nominal stresses shall be calculated in the tube. The same detail has the option of utilizing the more representative case of square tube welded onto the flange which would decrease the FAT value to 45. The basic conditions specified for detail 3.33 states that it is governed by a fully penetrated grove weld and is therefore only applicable for box specimens A, D and F. In addition, it is stated that the flange thickness must be greater than two times the thickness of the tube which is true for all cases investigated [16].

Participant 4 and participant 5 have both chosen to implement details representing splices of rectangular hollow sections with an intermediate plate. One of the details, 424, is governed by a single-sided butt weld with potential failure from the weld toe, whereas detail 425 is governed by a single sided fillet weld where potential weld root failure would be expected. FAT values of both details are dependent on if the wall thickness of the hollow section is larger or smaller than 8 mm. If the thickness is above the threshold value, then the FAT values are 50/40 (detail 424/425) and if they are below the FAT values becomes 45/36 (detail 424/425). Participant 4 investigated and compared both details and concluded that weld root failure (detail 425) is to be regarded as the limiting failure mode in fatigue strength assessment for the presented box specimen. As this participant only presented calculations for box specimens A, B and C in the nominal stress method the FAT value of 40 was exclusively used as these cases all have web thicknesses of 10 mm. Participant 5 implemented detail 424 for the specimens with full penetration and detail 425 for the specimens with partial penetration considering the reduction of FAT based on the web thickness.

Participant 6 implemented detail 7.9 in the British Standard 7608:2014 [17] represented by a single-sided fillet weld as a corner or T-joint with either a full penetration or a partially penetrated weld that is subjected to both normal and bending stresses. The location of the potential crack initiation is prescribed to the weld root and the associated class for the nominal stress method is class G. A comparable FAT value for class G at 2·10⁶ cycles and a nominal probability of failure that is 2.3 % (two standard deviations from mean) is 50.

Four out of six participants have chosen to implement details with little to no bending stress over the throat section of the weld. This could potentially overestimate the fatigue life of the component as detrimental bending stresses can be expected over the throat section due to bending in the flange. Three of the four participants are in extension using details for the full penetration cases which either state that weld toe failure is the most plausible failure type or that root and toe failure can be regarded as equally plausible. Participant 3 and participant 6 are the only ones who implemented details where the bending contribution of the applied load over the throat of the weld is considered.

Nominal stress evaluation

Both analytical hand calculations as well as FE-based simulations were used to derive the nominal stress for each box configuration. The methods ranged from simple models considering only the membrane stresses as the ratio between the applied load and the nominal area to FEM simulations with stresses calculated over the weld throat. The approaches used by the participants are presented in Table 4. Participant 2 and participant 6 chose to include calculation results using both analytical models and numerical simulations.

Table 4 Model types used in the nominal stress method by the participants

Analytical methods

Two types of analytical methods were presented by the participants, those who only considered the membrane stresses and those who also accounted for bending stresses. The method for calculating the membrane stresses is similar for all participants, the applied force is equally distributed onto a reference area. The source of variation for the calculated membrane stresses is therefore given by the magnitude of the applied load and the size of the load carrying area, which in a simplified form can be expressed as

$$ {\sigma}_{\mathrm{m}}=\frac{F}{4{\mathrm{l}}_{weld}\alpha \left(\mathrm{a},\mathrm{p},{\mathrm{t}}_{\mathrm{web}}\right)}. $$

(1)

F is here the applied force, l_weld is the length of the weld along one of the web plates and α is a function describing the equivalent load carrying thickness. This latter parameter is by some used as either the total cross-sectional area of the web plates, or as a percentage of this area while other participants have used an effective throat thickness. The effective throat thickness is governed by the penetration depth and throat thickness (the definition of these two can be seen in Fig. 2b). The number of ways that this effective throat thickness was calculated equals the number participants who implemented this approach, all different versions are presented in Fig. 3. The parameters used by participants in the implementation of Eq. (1) are presented in Table 5.

Fig. 3

Different ways of calculating the effective throat thickness presented by the participants

Table 5 Effective cross-sectional properties used by the participants

Participant 4 and participant 6 have added analytical calculations of the bending stresses to capture a more complete stress state. Both have calculated these stresses by assuming that half of the box section resists half of the load applied at the load surfaces. The bending stresses were calculated using the area moment of inertia and the bending moment, both of which were calculated differently by the two participants. The estimation of the bending stresses thereby differs considerably between the two participants, with the method by participant 4 giving stresses around 37 MPa whereas the method by participant 6 gave stresses of 128 MPa. Both participants state that they are unsure on validity of the methods that they used. This shows the uncertainty in analytical models when the complexity of the problem studied exceeds that of typical textbook examples.

Simulation methods

Participants 1, 2 and 6 have all performed numerical simulations to derive the nominal stress. Both participants 1 and 2 investigated the far field stresses by looking at how the stresses in the web change along the load direction. They chose a stress path mid centre of the load surfaces to analyse, the same path on which the maximum principal surface stress was found. The far field stress was taken by both participants as the local minima along this line, as presented in Fig. 4.

Fig. 4

Nominal stress analyses by participant 1 and participant 2 on Box A. The stresses were extracted at the inner surface of the web

Participant 6 chose to implement the nominal stress method and fatigue class G found in the British Standard [17] with linearised stresses in the weld throat. The stress distribution over a path from the weld root to the weld toe on the web side was extracted from simulations with a refined mesh at the weld and around its close proximity. A linear fit was manually estimated to the stress distribution along the path from which the stresses at the weld root was extrapolated. This extrapolation of stresses at the weld toe shares resemblance to methods proposed by Søreensen et al.[18] and Fricke et al. [19], the FAT classes used by the participant are however not the same as in the mentioned methods.

Assessed fatigue strength

The critical stress levels determined by the participants for each box specimen are presented in Fig. 5. Almost no dependency of the penetration depth is seen for the participants, who only considered the nominal membrane stresses. The same is seen for the simulation results of participants 1 and 2 who also have a high level of agreement with each other. The analytical methods considering the bending stresses by participants 4 and 6 shows a clear dependency of the penetration depth; they do however not coheir well with each other as a factor of two separates them.

Fig. 5

Critical nominal stresses calculated by the participants for each box specimen configuration. (a) Web thickness – 10 mm. (b) Web thickness – 8mm. (c) Web thickness – 6 mm.

All participants were asked present the mean fatigue life for each box configuration using the nominal stress method. The recalculations of the results from the probability level given by the codes to the mean level prove to introduce some variations in the fatigue assessment. Participant 3 stood out the most with a scaling factor on the fatigue life that was approximately 10% lower than the rest of the group that lay within 2% of each other. The mean fatigue life for the specimens investigated by the nominal stress method is presented in Fig. 6. Large scatter is seen for all specimen configurations when comparing both the analytical results and the FEM results.

Fig. 6

Scatter in fatigue life estimations for the nominal stress approach

The numerical results of participant 6 estimate the lowest number of cycles, as can be expected with their approach of implementing local stress extrapolation over the throat. Little to no variation is seen between participant 1 and participant 2 who both used a numerical approach to derive the far field stress in contrast to the participants that utilised analytical approaches. This shows that numerical simulations are to recommend in situations where either a complex geometry or stress distribution gives rise to local bending effects that are hard to capture analytically.

Local stress-based fatigue assessment

The second task in the study was to use a local stress-based method for fatigue strength evaluation. Participant 1 to participant 5 took part in this task where both the structural hot spot stress method and the effective notch stress method were used. A detailed outline of the modelling approaches by the participants is presented in Table 6.

Table 6 Modelling approaches by different participants

Hot spot stress method

Participant 1 implemented the hot spot stress method with a FAT class for weld toe failure. The method includes the stress raising effects at the weld toe by linearising the stress in close proximity and then extrapolating the stress at the weld toe [12]. Niemi [22] states when using the nominal stress approach, that it is of importance that there is a well-defined nominal stress, not complicated by macro-geometric effects and that the structural discontinuity is comparable with the classified detail from the standard and that the detail is free from significant imperfections, such as lack of penetration.

Participant 1 chose to implement a shell model in their fatigue strength assessment, employing quadrilateral elements with a length of 2mm at the weld toe. The welds were modelled using elements with an axial length equal to

$$ {\mathrm{l}}_{\mathrm{weld}}=\frac{{\mathrm{t}}_{\mathrm{web}}}{2}+\sqrt{2\mathrm{a}}, $$

(2)

with an increased shell thickness equal to the plate thickness plus the throat thickness to account for the stiffness change at the weld. Participant 1 modelled one fourth of each specimen by applying symmetry conditions at the boundaries. The stress distribution in the web close to the flange for Box A can be seen in Fig. 7a. Axial constraints were added on the upper load area in the direction of the applied force. The force itself was applied onto the lower load area evenly and a uniform displacement that was prescribed by coupling the deflection of the nodes in the direction of the applied force. The hot spot stress was calculated along the circumferential weld to find its peak value, which showed to be located mid centre of the locking area; this can be seen in Fig. 7b.

Fig. 7

Hot spot stress evaluation by participant 1 for Box A. (a) Stress distribution in shell model. (b) Stress distribution along weld.

Effective notch stress method

The effective notch stress approach developed by Radaj [23] assumes a fictive notch radius of 1mm as the evaluation point for the stress extrema, used in fatigue life estimation. The assumptions are supported by the micro-structural effects proposed by Neuber. This approach has been included in the IIW Recommendations [12] and additional radii have been proposed [20, 21, 24, 25] with their corresponding FAT classes as extensions, when notch effects in thinner members are considered. Only participant 2 chose to use a fictive radius of 1 mm for all box specimens (even with web thicknesses below 10 mm). The other participants implemented the proposed extension of a 0.3 mm notch radius for thinner members with a thickness of at least 5 mm [20]. Participant 2 chose to simulate the complete box specimens and performed sub-modelling at the location of the highest notch stress in the root of the circumferential weld. Participants 3–5 on the other hand chose to simulate one quarter of the box specimens using symmetry conditions without any sub-modelling.

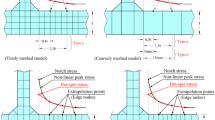
A U-notch geometry was implemented by participant 2, Fig. 8a, as this can lead to an underestimation of the potential failure in the weld throat using the effective notch method it is generally not recommended as stated in the IIW Guidelines for the Assessing root failure [26]. The participant did however not consider potential failure in the weld throat. Participant 4 and partly participant 3 modelled the root using the keyhole notch (also known as o-notch) as presented in standards and recommendations [12, 26,27,28], removing only a cylindrical volume and opening up a small path between the web and the flange without altering the length of the non-welded root face. Participant 3 did however alter this geometry slightly, as did participant 5, by removing more material so that the notch geometry, at the web side of the non-welded root face, shared resemblance with a U-notch. This altering can be seen in Fig. 8c, d for participant 3 and participant 5. Variation can also be seen on how the participants chose to discretise the root of the partially penetrated welds. Only participant 2 who employed a sub-modelling approach had a uniformed mesh in the periphery that gradually was refined in zones until it reached the U-notched area, where a uniform mesh edge size of 0.25 mm was prescribed (Fig. 8a), as recommended by the guidelines [26] and most similar to the mesh presented in Fig. 8e. The other participants chose either to refine the elements within a certain distance from the keyhole, as participant 3 in Fig. 8b, c, or to only prescribe the element length at the surface of the fictive notch, as participant 5 in Fig. 8d. These methods did not produce a gradual refinement of the mesh towards the notched region and high aspect elements where in some cases seen at the notch for those who only prescribed the element length at the surface. Participant 5 did not use the recommended element sizes around the complete notch, the reason for this is not clear.

Fig. 8

Examples of local mesh refinements and modelling methods for the fictitious notch. (a) Participant 2 (Box C). (b) Participant 3 (Box C). (c) Participant 3 (Box G). (d) Participant 5 (Box B). (e) IIW Recommendations.

There was less variation in the local modelling between participants for the specimen cases with full penetration. All except participant 3 implemented a fillet radius notch, type 1 in Fig. 9, at the root side of the weld for Box A, D and F whereas participant 3 implemented an undercut notch, type 2 in Fig. 9.

Fig. 9

Local modelling of the weld root for the case of full penetration

Assessed fatigue strength

The stresses computed by the participants are presented in Table 7 together with their corresponding location in the box structure. A graphical comparison of the stresses used in the effective notch stress approach by the participants is presented in Fig. 10. The smallest variation in the notch stress is seen for the box specimens with a 10 mm web thickness, Fig. 10a, where the only noteworthy difference is that participant 2, who implemented both a U-notch and a sub-modelling approach, consistently estimates a higher notch stress. Similar tendencies were seen in a study by Fricke [9] where the participants that implemented a U-notch geometry estimated higher root stresses than the participants who implemented a keyhole notch geometry, for the same element length at the root. The opposite trends are seen for the box specimens with thinner web thicknesses, where the variation between the estimated notch stress is more prominent. There is additionally a shift in order where participant 2, who previously estimated higher stresses, now lies below the results of the other participants, an effect of participant 2 being the only one who implemented a fictive notch radius of 1 mm. The undercut notch approach that participant 3 implemented for the fully penetrated box specimens produce lower notch stresses than the fillet radius approach implemented by the other participants, which is seen for Box D and Box F in Fig. 10b, c.

Table 7 Calculated stress values used in fatigue strength assessment using local approaches.

Fig. 10

Critical stresses used in effective notch stress method. (a) Web thickness – 10mm. (b) Web thickness – 8 mm. (c) Web thickness – 6 mm.

The mean fatigue life estimations using local stress methods are presented in Fig. 11. The scatter in the transformation to mean fatigue life from the probability levels utilised in the corresponding codes are the same as described in Sect. 4.3. Participant 1 who implemented the hot spot stress method did not consider root failure for the specimen so their presented results should only be regarded as valid if toe failure can be seen from the fatigue testing. A high conformity of the estimated fatigue life is seen for Box A–C between the participants that utilised the effective notch stress method. The only deviation is that participant 2 have estimated a slightly lower mean fatigue life than the remaining participants, which is expected due to the higher stresses that the same participant derived earlier (Fig. 10). The same conformity is not seen for the box specimens with thinner web sections. Scatter is seen both between the different radii used and within the group of participants who utilised a notch radius of 0.3 mm. The difference in notch radius seems to have a higher contribution to the mean fatigue life for the fully penetrated box specimens (Box F and Box D) than for the partially penetrated specimens where the results of the 1 mm notch radius lie within the scatter for the 0.3 mm notch.

Fig. 11

Scatter in fatigue life estimations for both the hot spot stress method and for the effective notch stress method

Fatigue testing

Fatigue testing was conducted on two specimen types to assess the fatigue strength evaluated by the participants, box specimen A and C. Several box specimens were serially tested using connection-beams to bridge together the specimens, this can be seen in Fig. 12. The chain of specimens was placed horizontally on a low-friction slider which minimise the heat build-up while not affecting the stress distribution in the specimens. A hydraulic load actuator was used to generate the loading at a testing frequency of 0.25 Hz. This ensured both that no dynamic effects were present as well as to avoid heat build-up between the jig and the specimens. Pulsating testing with a load ratio of 0.03 was used to keep tension in the setup and to prevent the connecting beams from falling out of position. The raw data of the testing conducted in this study, together with additional testing performed by Delkhosh et Al. [29], can be found in Table 9.

Fig. 12

Setup used for the fatigue testing. The specimens are connected in series using connection-beams and the force is generated using a servo hydraulic testing system

Strain gauge measurements

The accuracy of the modelling approaches presented by the participants is evaluated by comparing model strains with experimentally measured strains. Every box specimen is during the testing equipped with two linear strain gauges on opposites sides of the specimen that are measuring the strain parallel to the loading direction, one of which can be seen in Fig. 2. Each strain gauge is connected as individual channels using independent bridge completion modules. The strain results from the participants that shared this data are presented in Table 8. These results show a rather good agreement with the calculated values by the participants, with slightly higher average strains captured by the experimental measurements.

Table 8 Experimental strain data together with calculated strain results presented by the participants

Measured penetration depth

Macrographs of the weld geometry were produced from two specimens of different types (Box A and Box C) after fatigue testing. The penetration depth was measured at four positions along the un-cracked side of the specimen with the two outermost cuts located at the corners. The macrographs revealed that full penetration was not achieved along the complete circumferential weld for Box A. The desired full penetration was only seen at a few sites while the predominant lack of penetration depth for Box A was found to be 4 mm, Fig. 13a. The fatigue test results for Box A are therefore not a representative reference for the fatigue strength estimations proposed by the participants. What this however shows is the importance of knowing the limitation and variation in production. The fact that no backing was used [14] for the circumferential welds in combination with the general design of the specimen complicates root inspection. This implies that visual inspection of the root can only be carried out through the load pin insertion holes.

Fig. 13

Macrographs and fracture path investigation carried out on Box A by Delkhosh et al. [29]. (a) Sample of magrograps for Box A. Delkhosh et al. [29]. (b) Fracture path. Delkhosh et al. [29].

Four additional macrographs were produced where the fatigue crack initiated for one of the specimens. The path of root crack follows the leg plane for the majority of the distance with a slight deviation into the throat at the end.

Comparison of fatigue assessment methods

The assessed fatigue life of Box A and Box C are presented together with the fatigue test results in Fig. 14, which shows a large variation between the scatter of the different assessment methods. The nominal stress assessment presented by participant 6 clearly deviates from the general population with a fatigue assessment comparable to that of the effective notch stress method. The most prominent difference in the method by participant 6 is that the nominal stress method is used in conjunction with stresses calculated over the weld throat. This is done by extrapolating the linearised stress field through the weld throat to account for bending stresses. The effective notch stress method has a conservative mean fatigue life estimation for all participants and low scatter in comparison with the nominal stress method. The mean fatigue life estimated with hot spot stress method by participant 1 is included in the results; it is however not applicable for the tested structure as the predominant throat bending did not produce any weld toe failure. The analytical nominal stress method has the highest variation in the predicted mean fatigue life with result both on the conservative and the non-conservative side compared to the fatigue testing. This method is therefore not recommended in complex structures like the investigated specimen as it leaves a lot of interpretation to the user who implements it.

Fig. 14

Scatter of assessed fatigue life based on the method used together with the scatter of the fatigue testing

Influence of load application

The geometries of the presented box specimens share similarities with the standardised geometrical cases used in design codes for nominal stress assessment. One key difference however is the load application in the centre of the lifting plate by the connection beam which in combination with the deformable flange gives rise to bending stresses at the weld. As the stresses for the present case vary both through the plate thickness and around the circumferential weld, the position at which the stresses are evaluated will have a considerable effect in the fatigue strength assessment. For accurate results it is vital that that the ratio between the stresses at the crack initiation point and the location where the stresses are extracted is similar to the cases presented in the design codes.

To investigate the effect of bending deformation in the flange the present load application, Fig. 15a, is compared with that of a flange with no bending deformation, Fig. 15b. The stress distribution changes considerably between the two load cases, from being located only in the weld root as in the present study to being more equally distributed in the toe and root as in the case of a non-bending flange.

Fig. 15

Stress distribution around the critical weld joint, both for the present case with a flange that bends as well as for the fictive case of a flange not subjected to bending. The surface on which the stresses are plotted lies in the centre plane of the specimen. (a) With flange bending. (b) Without flange bending.

The IIW guideline for assessment of weld root fatigue by Fricke [26] contains recommendations and detail descriptions on how to include bending stresses in the fatigue assessment. One approach proposed by the same author, for fillet welds subjected predominantly by throat bending [19], is to linearise the normal stress in the leg plane (over A-A in Fig. 16c) which then serves as the basis for the fatigue strength assessment. The linearisation over this section is proposed based on previous research where it was seen that the root crack is frequently closer to the leg section than to the throat section, which adheres well to the crack path seen in Sect. 6.2. The proposed method is therefore used to compare the two load cases in Fig. 15. The stress distribution along section A-A is presented in Fig. 16a together with the linearised stress in Fig. 16b.

Fig. 16

Comparison of the stresses for the two loading applications. (a) True stress along A-A. (b) Linearized stress along A-A. (c) Linearisation over A-A Fricke et al. [19].

The structural stress for the two load cases becomes 240 MPa and 45 MPa, respectively, which is more than a fivefold increase of structural stress due to the deformable flange. The corresponding mean fatigue life using the proposed FAT value of 80 will therefore be given as 0.18 million cycles with the deformable flange and 29 million cycles for the rigid flange. The mean fatigue life of 0.18 million cycles for the analysed case coheres well with the average of the mean fatigue life calculated by the participants for Box A using the effective notch stress method. The larger mean fatigue life can be compared with the mean fatigue life for Box A calculated by participant 3 using the nominal stress method shown in Fig. 6.

Conclusions

Based on the analysis in this study the following can be concluded:

• The nominal stress method has limitations not known to all design engineers in the project.

• The application of the nominal stress method needs to be done with care since there is an obvious risk of misleading results when implementing the method for cases where the load application is in principle different compared to the cases in the codes.

• Analytical calculations for the nominal stress method cannot be recommended for structures where the far field stress state is nontrivial, such as for the investigated specimen. The fatigue life estimation by experienced users still shows a high level of scatter.

• The hot spot stress method with FAT classes for weld toe failure was implemented by one of the participants even though the structure is exposed to predominant throat bending and weld root failure. This indicates that that there is a lack of knowledge for when the method is valid.

• The effective notch stress method has a high conservatism in comparison to the fatigue test results which make the method safe to implement independent of the user experience in the present investigation.

Appendix. Raw data

Table 9 Fatigue test results