Abstract
Additive manufacturing enables the fabrication of lattice structures which are of particular interest to fabricate medical implants and lightweight aerospace parts. Product integrity is critical in these applications. This requests very challenging quality control for such complex geometries, particularly on detecting internal defects. It is important not only to detect whether there are missing struts for a product with a large size of lattices, but also to identify the number of missing struts for safety-critical applications. Resonant ultrasound spectroscopy is a promising method for fast and cost-effective non-destructive testing of complex geometries but data analytics methods are needed to systematically analyze resonant ultrasound signals for defect identification and classification. This study utilizes resonant acoustic method to obtain resonant frequency spectrum of test lattice structures. In addition, regularized linear discriminant analysis, combined with adaptive sampling and normalization, is developed to classify the number of missing struts. The result shows 80.95% testing accuracy on validation study, which suggests that the resonant acoustic method combined with machine learning is a powerful tool to inspect lattices.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Additive manufacturing (AM) enables production of parts with complex geometries such as lattice structures [1]. Comprising a network of nodes and beams, or struts, lattice structures can dramatically reduce weight and retain structural integrity. Interesting applications can be found in the medical sector for implantology [2, 3], where implants with lattices lead to better fixation due to cell growth inside lattices [4]. In aerospace industry, lattice structures contribute to the design of new lightweight components with better thermal performance to dissipate heat [5].
However, lattices fabricated by AM can contain several types of flaws, which include unconsolidated or trapped powder particles, voids and porosities inside the struts, or missing struts in the cells that potentially weaken the structures mechanically. Reliable and reproducible volumetric non-destructive testing (NDT) methods are essential to ensure the internal integrity of lattice structures, especially for safety-critical applications.
Volumetric non-destructive testing (NDT) of lattice quality faces a number of challenges [6, 7]. The golden standard nowadays is X-ray computed tomography (XCT) [8, 9]. However, XCT is time-consuming and expensive. Recently, resonant ultrasound spectroscopy (RUS) has emerged to be an efficient and cost-effective NDT method to check the internal flaws of complex AM parts [7, 10,11,12]. Yet applying RUS methods to lattice structures requires new research to evaluate its capability to distinguish different types of internal defects, as opposed to simple pass/fail decision. We propose to investigate and demonstrate the capability of RUS methods, named resonant acoustic method (RAM) [13], and combine it with machine learning for the detection of missing struts in metallic lattice structures produced by AM.
The paper is structured as follows. Following the “Introduction,” Section 2 describes the principle of RUS methods and more specifically the principle of the RAM implemented in this study. Section 3 is dedicated to the design and AM of the lattice structures dedicated to the RAM evaluation. Section 4 presents the visual and X-ray digital radiography (XDR) inspections of the manufactured lattice structures. Section 5 provides the RAM inspection of these lattices. Section 6 presents a machine learning method for defect classification of lattice structures based on RAM signals. Conclusion is given in Section 7.
2 Principle of the RAM
There are several variants of RUS methods, as described in ASTM E2001 [14], but their basic principles are similar. These whole-body inspection approaches compare the frequency spectrum of the mechanical resonances of a set of reference parts, supposedly flawless, to the frequency spectrum of the mechanical resonances of test parts. Two similar objects will have similar resonant frequency spectra. A shift of the frequency peaks of a part, compared to the statistical variation from the similar reference parts, will be the signature of a structural change of the part (e.g., changes in part geometry and/or material properties associated with the mass, stiffness, and damping). Consequently, the methods can be used to screen external and internal structural flaws or deviations in AM parts.
A typical characterization using RUS methods for pass/fail assessments includes several steps:
-
First step: to excite the natural resonant frequencies of a test part by mechanical impulse;
-
Second step: to monitor and collect the response of the test part by a sensor;
-
Third step: to process recorded data by performing a fast Fourier transform (FFT) to obtain the resonant frequency spectrum;
-
Fourth step: to compare the resonant spectrum of the test part to the spectra of the reference parts. The comparison, often requiring heavy human intervention, involves:
-
1.
Identification of well-defined resonant peaks based on testing all the reference parts and a few test parts with different structural properties than the reference parts;
-
2.
Selection of a subset of these well-defined resonant peaks that are consistent for all reference parts and have distinct separation with the peaks of the test parts for further consideration;
-
3.
Evaluation of the ranges in variations in each selected resonant peak frequency of the reference parts to define several “criteria.” Outliers of these variations are excluded from these ranges; and
-
4.
Sorting of the test parts with regard to the criteria to evaluate the quality of the test parts. All test parts with frequency peaks outside of the defined boundaries (criteria) are rejected as faulty parts.
-
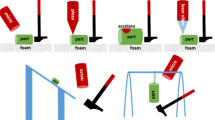
1.
The steps for a typical RAM test are also outlined in the graphic in Fig. 1.
The more reference parts available, the more clearly defined the criteria are and the more accurate the RUS methods are.
RAM [13] is an impulse excitation type of RUS method. In RAM, no preparation or fixturing of the test parts is required. The part is excited by dropping down a slide and onto an impact surface where it bounces off and drops a short distance (first step). The resulting acoustic frequency data are monitored by a microphone, while the part is falling and resonating in a free-free state (second step). The output of the microphone is converted into a frequency spectrum using a high-speed analog to digital converter (24 bits) performing a FFT to determine resonant peaks (third step). Finally, a statistical analysis conducted with software reveals if the test parts fall within the defined criteria or not (fourth step). If at least one of the measured resonant peak frequencies of a test part lies outside of the established frequency ranges of the reference parts, the test part is considered faulty. Clearly, this resonant acoustic method is easy to use and simple to implement.
3 Design and manufacturing of lattice structures for RAM evaluation
In order to evaluate the capability of the RAM method to detect missing struts in metallic lattice structures produced by AM, a large set of lattice structures, with different numbers of missing struts, was specifically designed and additively manufactured for this purpose at the National Institute of Standards and Technology (NIST). Since the more reference parts available, the more clearly defined the criteria are and the more accurate the RAM is, it was decided to build, on the same AM platform, one hundred reference parts.
Since a large number of parts needed to be manufactured on a single AM platform, small parts needed to be considered. However, we did not want to evaluate the RAM with a basic standard specimen, but with a specimen, as much as possible, representative of what is used in the industry. The lattices are very much used in the medical sector and the parts, in this sector, are generally smaller than those in the other industrial sectors. For example, spinal implants are small parts [15]. Thus, it was decided to design and manufacture lattice structures, which mimic in sizes a typical spinal implant regarding its global shape, the ratio dense lattice material, and the basic lattice cell. In addition, since cobalt-chromium (Co–Cr) is a commonly used material in implantology [3], it was decided to use Co–Cr among AM powders processed at NIST. With regard to the global shape of the specimen, it was chosen to be representative of the shape of a spinal implant, but also to facilitate the manufacturing and post-processing of as many of them as possible on a single AM platform. Therefore, the specimen global shape is in a door shape, the top is rounded to mimic spinal implant shape, and its base is flat to enable the part to be manufactured in a vertical position without support. Indeed, the vertical manufacturing enables optimizing the number of built parts on the AM platform, and the flat base to reduce the post-processing time needed for supports’ removal. Extra 1-mm height was added on the base of the specimens for their electrical discharge machining (EDM) removal from the AM platform. Since missing struts can be located inside or on the surface of the lattice, three layers of unit cells were considered (two surface layers and one internal layer). The missing struts were deleted directly from the CAD model on specific outer and inner positions. Finally, we ended with the design presented in Fig. 2 and the following number of parts:
-
100 reference parts without missing strut
-
10 parts with 1 visible missing strut on position 1
-
10 parts with 2 visible missing struts, 1 on each side of the part on position 1
-
10 parts with 4 visible missing struts, 2 on each side of the part on positions 1 and 2
-
10 parts with 6 visible missing struts, 3 on each side of the part on positions 1, 2, and 3
-
10 parts with 8 visible missing struts, 4 on each side of the part on positions 1 to 4
-
10 parts with 10 visible missing struts, 5 on each side of the part on positions 1 to 5
-
10 parts with 12 visible missing struts, 6 on each side of the part on positions 1 to 6
-
10 parts with 1 inner missing strut on inside position 1
-
10 parts with 2 inner missing struts on inside positions 1 and 2
-
10 parts with 4 inner missing struts on inside positions 1 to 4
-
10 parts with 6 inner missing struts on inside positions 1 to 6
The positions of the missing struts are specified on Fig. 2. A missing strut corresponds to the CAD removal of one of the six branches of the lattice unit cell. Visible strut means that the strut is located on one of the two surface layers of the lattice, whereas inner missing strut means that the strut is located on the intermediate layer of the lattice.
The lattice structures were manufactured at NIST with a cobalt-chrome-molybdenum-based superalloy powder (EOS MP1) using a laser power bed fusion (LPBF) machine EOS M290, and default built parameters for MP1. The distribution of the parts on the AM platform has been governed by the manufacture performance of the NIST EOS machine. Indeed, it had been noticed that, with this machine, the parts manufactured on the sides of the AM platform could show differences with the supposed similar parts manufactured on the center of the platform. Thus, it was decided that, to guarantee a better homogeneity of the one hundred reference parts, they would be manufactured at the center of the AM platform, and that the parts with missing struts would be manufactured around them as shown on Fig. 3. There can be several reasons explaining these inhomogeneities in the parts. They can be due to the laser focus in the corners of the platform. But it can also be due to the distribution of the shield gas used to dissipate vapor plume and spatters resulting from laser fusion of the powder.
The EOS machine encountered several unexpected stops during the AM process for unknown reasons. However, these stops happened systematically at the end of a complete layer process. So even if these stops had an influence of the part integrity, all the parts were impacted in the same way.
The fabrication in the laser PBF machine and the Co–Cr lattice structures on the AM platform at the end of the AM process are shown on Fig. 4.
4 Visual and XDR inspections of lattice structures with different numbers of missing struts
In order to check that the parts manufactured with missing struts complied with the specifications, visual inspections were performed for several parts with outer missing struts (Fig. 5).
With respect to lattices with inner missing struts, the inspection of three of them was performed with a two-dimensional (2D) XDR system from Safran (Fig. 6). The inspection was achieved on lattices with one, two, and six inner missing struts.
The Safran system included a Vario focus source from Comet with nominal voltage of 225 kV and focal spot size of 250 μm at P = 290 W, and a flat panel XRD0822 detector from Perkin Elmer with a pitch of 200 μm encoded in 16 bits. The chosen acquisition parameters are given in Table 1.
The inner missing struts are clearly visible on the XDR image (Fig. 7). From these visual and XRD inspections, we made the assumption that all the parts manufactured with missing struts complied with the specifications.
XDR image of the three inspected lattice structures with inner missing struts in Co–Cr lattice structures. On the left image, one missing strut is visible; on the center image, two missing struts are visible; and on the right image, six missing struts are visible (these missing struts are indicated by the red circles)
5 RAM tests of lattice structures with different numbers of missing struts
The RAM tests of the lattice structures were performed with the RAM-DROP system from The Modal Shop presented on Fig. 8. This system, dedicated to quick tests of small parts, provides automatic sorting of defective parts: simple pass/fail result is returned requiring no human interpretation.
The Drop System (RAM-DROP) is instrumented with a laboratory-grade force sensor, a prepolarized microphone (PCB 130 series) acting in the frequency range up to 50 kHz, and a 2-channel high-speed analog to digital converter (24 bits). The Drop system also includes an industrial PC mounted on a swivel arm to provide software interface control and a free-standing test cabinet. A light tower status indicator provides prominent visual display of passed or failed parts, indicating a system fault or providing warning that a preset number of parts have failed consecutively. In order to effectively capture the resonant frequency response of small parts, the part under test is fed onto a slide and then dropped onto an impact surface, thus creating the mechanical excitation required to excite the resonant frequencies of the part under test. The part then drops a short distance into the white drum in the center of the Drop System pictured in Fig. 8. Once the Drop System receives the Pass or Fail result from the NDT-RAM software, the drum will rotate clockwise for a good part, or counterclockwise for a defective part to automatically sort the parts that have been tested.
The tested lattices were dropped down the slide, rounded side first. All parts were impacted in the same location (rounded surface), with no twisting on the slide. The frequency window for analysis ranged from 500 Hz to 50 kHz (Fig. 9), and the resolution was 7.8 Hz. Four criteria were considered to sort the lattices with missing struts from the reference parts (Fig. 10). These criteria, defined from the ranges (boundaries) in variations in each resonant peak frequency of the reference parts, are shown by vertical green lines on Fig. 10.
The RAM software indicates as faulty parts (F) all tested parts with frequency peaks outside of the defined criteria, and as passed parts (P) all tested parts with frequency peaks inside of the defined criteria. All the lattices were tested using the four criteria (an excerpt of the RAM tests on the lattice structures is presented in Table 2). If a lattice is falling at least one of the criterion, it is considered as faulty part, i.e., part with at least one missing strut. The comparison between the reference lattices and the lattices with missing struts reveals that the RAM can detect all the lattice structures with missing struts. The parts were tested three times to confirm this result. The overall result was similar.
Then, one tried to compare the lattices structures with missing struts to each other and no longer in comparison with the reference parts. As displayed on Table 3, RAM is not differentiating:
-
The parts with 1/2 outer missing struts from the parts with 1/2/4/6 inner missing struts;
-
The parts with 1 outer missing strut from the parts with 2 outer missing struts;
-
The parts with 6 outer missing struts from the parts with 8/10/12 outer missing struts;
-
The parts with 8 outer missing struts from the parts with 6/10 outer missing struts;
-
The parts with 10 outer missing struts from the parts with 6/8/12 outer missing struts;
-
The parts with inner missing struts from the other parts with inner missing struts.
But RAM is differentiating:
-
Most of the parts with inner missing struts from the parts with 4/6/8/10/12 outer missing struts;
-
Most of the parts with 1/2 outer missing strut from the parts with 4/6/8/10/12 outer missing struts;
-
Most of the parts with 4 outer missing struts from the parts with outer missing struts;
-
Most of the parts with 6 outer missing strut from the parts with 1/2/4 outer missing struts;
-
Most of the parts with 8 outer missing struts from the parts with 1/2/4/12 outer missing struts;
-
Most of the parts with 10 outer missing strut from the parts with 1/2/4 outer missing struts;
-
Most of the parts with 12 outer missing struts from the parts with 1/2/4/8 outer missing struts.
To try to find an explanation why the parts with 6/10 outer missing struts could not be separated from other lattices with a different number of missing struts, we identified their location on the AM platform (Fig. 11). For the parts with 6 outer missing struts, one explanation could be the fact that these parts are right on the edge of the AM platform (red rectangles on Fig. 11). The manufacturing process of the used AM machine might not be optimum on the edges of the AM the platform of this machine. However, the part locations on the AM platform, for the 10 outer missing strut parts, cannot explain that these parts failed the test (green rectangles on Fig. 11). No other reasons could be found.
In a nutshell, the defined criteria of the RAM system were able to separate all the parts with missing struts from the reference parts. However, when the parts with inner missing struts are compared with parts with a different number of inner missing struts, RAM cannot effectively differentiate them from each other. In addition, RAM cannot distinguish parts with one outer missing strut from parts with two outer missing struts. It is only effective when the gap of missing struts in parts is more than two.
As mentioned previously, RUS is a whole-body test method which means that the entire structure is excited and evaluated during the RUS test. The primary factors that dictate the natural frequencies of any given part under test are the stiffness and the mass. The process of additively manufacturing a group of parts (or any other known manufacturing process for that matter) will inherently create minor variations in the stiffness and mass from part to part. The process variation from part to part is acceptable as long as the parts still meet the established specifications and are free from defects such as cracks, missing material, voids, and a number of other defects that would cause the part in question to fail to perform in its intended manner. The minor variations in stiffness and mass among the conforming parts are known as normal manufacturing process variation and result in variation in the natural frequency response of the parts during RUS testing. The same normal variation holds true for parts containing defects; however, the effect of a defect on the frequency response of a given part is generally much more pronounced than the normal process variation in the conforming parts. The normal manufacturing process variation from part to part can be defined as the noise in the RUS testing technique. As long as the change in stiffness and/or mass of the defective parts is greater than the effect of the noise from normal process variation, RUS testing is 100% successful in detecting defective parts and sorting them from conforming parts.
In the case of detecting size, location, or number of defects present in a part, RUS testing is generally not well suited. The noise from normal process variation, which is equally present in non-conforming parts as it is in conforming parts, plays a factor in creating variation in the response of the defective parts. A manufacturer of a given part will optimize their manufacturing process to minimize the normal variation in that part and meet or exceed the specification required of that part. The conforming parts that are manufactured have the same mechanical characteristics and resonant frequency response plus the added noise from normal process variation, meaning that the results of RUS testing will be predictable and repeatable. Defective parts, however, fall out of the predictable and repeatable range of frequency response. Defective parts represent a failure in the expected normal manufacturing process and therefore do not follow the same level of predictability and noise variation that is present in the conforming parts. In the case of the lattice structures used for this paper, the defects were intentional and printed. The RAM system was able to reliably differentiate all of the conforming parts from all of the defective parts, but not the different numbers of defects from each other or the variation in location of the defects.
While the change in stiffness and/or mass of the defective parts was significant enough to reliably separate them from the conforming parts, a small change in the number or location of defects was not significant enough to reliably sort the defective parts by number and location of defects. The same results generally hold true for all RUS testing regardless of part size, shape, and manufacturing processes.
In order to improve the reliability of separating defective parts by the number of defects present in the part, it was decided to analyze all the RAM data with machine learning.
6 Machine learning analysis of RAM data to sort lattice structures according to the number of missing struts
Physical modeling and simulation of RAM patterns in response to various defective prints can be impractical. Given RAM inspection signals and quality inspection, machine learning (ML) can be used to construct a model to make predictions and help in understanding the process [16]. For the RAM data, the classification methods in ML literature can be applied to predict the number of missing struts and their locations (in/out).
6.1 Regularized linear discriminant analysis to sort lattice structures
Linear discriminant analysis (LDA) is a commonly used supervised learning approach for classification and is applied in many areas, including signal processing, image recognition, economics, biomedical science, earth science, and so on [17,18,19,20,21,22,23]. By projecting the original data matrix into a lower dimensional space, the ratio of the between-class variance to the within-class variance is maximized to ensure the separability between different classes, while the redundant features could be eliminated to achieve dimensionality reduction [24]. LDA also provides insights into the importance of different frequencies collected from RAM.
A typical classification problem is that given N observations formulating the original data matrix X = {x1, …, xN}, where xi ∈ ℝp, and the corresponding labels y ∈ ℝN, where yi = 1, …, k for all i = 1, …, N, how to predict the class of a new sample x∗ ∈ ℝp. Essentially, k regions are defined to allocate each observation x. Assuming the data in each class follow the Gaussian distribution with mean μj and covariance matrix Σj for each class j, i.e.:
Then we know that:
By the Bayes’ rule, given the prior distribution of each class πj, we can maximize the posterior log probability to decide the label of the observation x:
which is known as quadratic discriminant analysis (QDA) since the right side is a quadratic function in x.
If we assume the homoscedasticity, i.e., Σj = Σ for all j = 1, …, k, Eq. (3) is changed to:
which is a linear function in x, and thus is called LDA. It requires must less data than QDA since there are fewer parameters to estimate. To avoid overfitting, we deploy the regularized LDA (or RLDA) by setting the covariance matrix as a function of the hyperparameter γ ∈ [0, 1], i.e.:
where I is the diagonal matrix.
Fisher [17] approaches the same formulation without any assumptions about data distribution by maximizing the ratio of the between-class variance to the within-class variance [19]. Given the transformation matrix W, the between-class variance is:
where μi is the mean of the ith class and μ is the total mean, and the within-class variance of the jth class is calculated as:
where xij is the ith sample in the jth class and nj is the number of samples in the jth class, which subjects to ∑jnj = N. Then, the best transformation matrix can be found by solving the following optimization problem:
where \( {S}_W={\sum}_j{S}_{W_j} \) is the total within-class variance.
All the lattice structures with missing struts are labeled by both their number of missing struts, and by their missing struts are either inside or outside the lattice, such as “1 out,” “2 out,” …, “6 in”; 80% of the data are used to train the RLDA model, and the rest (20%) form the testing set.
6.2 Adaptive sampling and normalization for RLDA
There exist two major issues for applying RLDA to RAM data: a large number of frequency features and robustness of RLDA classification. So we propose RLDA with adaptive sampling and normalization for the reference lattice structures.
Thousands of different frequencies are generated by FFT to form the resonant frequency spectrum. Considering all frequencies as features would cause unnecessary computational complexity and overload the MATLAB software. Therefore, the adaptive sampling strategy is proposed to reduce the inessential frequencies. Unlike random sampling, which selects each frequency with the same probability, the proposed adaptive sampling chooses the frequency according to the magnitude of its voltage. The larger the response is, the more likely the frequency is chosen. Also, the frequencies with the top 10 largest voltage would be kept with probability 1 to make sure no significant frequency is missed. Figure 12 shows the adaptive sampling result of a randomly selected lattice structure frequency spectrum. We can find that the patterns are similar to less than 10% of the original frequencies.
To achieve stable and faster computation, normalization is applied by computing the z-score [25] for each selected frequency. Also, the voltage collected could be affected by many non-defect-related causes, for example, the dropping position and recording distance. Then, normalization could help to improve the robustness of the proposed method.
After randomly selecting 80% of the 209 manufactured parts as the training set, we adaptively select 500 features from 6400 original frequencies and train the RLDA classifier with 5-fold cross validation. The training result is shown in Fig. 13. Note that even with the adaptive sampling strategy proposed in Section 6.2, the RAM data still have 500 different frequencies, so we have to project them onto a 2D plane to visualize the results. In Fig. 13, two random frequencies 125 Hz and 132.8 Hz are selected as the x- and y-axes, and different colors represent different numbers of missing struts and locations (in/out).
We achieved 100% training accuracy and 80.95% testing accuracy on the rest (20%) of the parts. Note that the train-test split is done within each type of the defect; for example, among ten lattice structures with 4 visible/outside missing struts, eight of them are in the training set and two of them are in the testing set. We also compared the proposed RLDA method with other machine learning methods after the same preprocessing procedures as shown in Table 4. As a popular classification method, linear support vector machine (SVM) finds the hyperplanes that separate data points of one class from those of other classes by maximizing the margins among classes, where the margin is decided by the closest data points called support vectors [26]. Since only the points close to the separating hyperplane are used, SVM is very flexible and robust at the cost of interpretability compared to LDA. In addition, random forest, as an ensemble learning method, consists of multiple decision trees, where each decision tree classifies the data following the decisions from the root node down to a leaf node. Each internal (non-leaf) node is labeled with an input feature, which is one specific frequency in our case, and leads to a subordinate decision node [27]. While the fine tree allows many leaves to be selected for a flexible distinction between classes, the coarse tree restricts the number of leaves for each node to be less than four.
7 Conclusions
This study presents a non-destructive testing (NDT) method to control the quality of lattice structures built by AM. Based on RAM to collect resonant frequency spectrums of test lattice structures, the RLDA with adaptive sampling and normalization could classify the defects with 100% training accuracy and 80.95% testing accuracy with a good reproducibility. The result shows that the RAM method combined with the machine learning method RLDA is an effective solution for detailed defect classification. Further study can be conducted to reduce the potential over-fitting problem in model training stage and improve the prediction accuracy for test data.
References
Nagesha BK, Dhinakaran V, Varsha Shree M, Manoj Kumar KP, Chalawadi D, Sathish T (2020) Review on characterization and impacts of the lattice structure in additive manufacturing. Mater Today Proc 21:916–919. https://doi.org/10.1016/j.matpr.2019.08.158
Culmone C, Smit G, Breedveld P (2019) Additive manufacturing of medical instruments: a state-of-the-art review. Addit Manuf 27:461–473. https://doi.org/10.1016/j.addma.2019.03.015
Lowther M, Louth S, Davey A, Hussain A, Ginestra P, Carter L, Eisenstein N, Grover L, Cox S (2019) Clinical, industrial, and research perspectives on powder bed fusion additively manufactured metal implants. Addit Manuf 28:565–584. https://doi.org/10.1016/j.addma.2019.05.033
Obaton A-F et al (2017) In vivo XCT bone characterization of lattice structured implants fabricated by additive manufacturing. Heliyon 3(8). https://doi.org/10.1016/j.heliyon.2017.e00374
Ngo TD, Kashani A, Imbalzano G, Nguyen KTQ, Hui D (2018) Additive manufacturing (3D printing): a review of materials, methods, applications and challenges. Compos Part B Eng 143:172–196. https://doi.org/10.1016/j.compositesb.2018.02.012
Todorov E, Spencer R, Gleeson SP, Jamshidinia M, Kelly SM (2014) America Makes: National Additive Manufacturing Innovation Institute (NAMII) Project 1: nondestructive evaluation (NDE) of complex metallic additive manufactured (AM) structures. https://doi.org/10.21236/ada612775
ISO TC261/ASTM F42, JG59, Additive manufacturing—general principles—non-destructive testing of additive manufactured products, International Organization for Standardization, On balloting 2020
Chiffre L, Carmignato S, Kruth J-P, Schmitt R, Weckenmann A (2014) Industrial applications of computed tomography. CIRP Ann - Manuf Technol 63. https://doi.org/10.1016/j.cirp.2014.05.011
du Plessis A, Yadroitsev I, Yadroitsava I, Le Roux SG (2018) X-Ray microcomputed tomography in additive manufacturing: a review of the current technology and applications, 3D Print. Addit Manuf 5(3):227–247. https://doi.org/10.1089/3dp.2018.0060
Obaton A-F, Lê MQ, Prezza V, Marlot D, Delvart P, Huskic A, Senck S, Mahé E, Cayron C (2018) Investigation of new volumetric non-destructive techniques to characterise additive manufacturing parts. Weld World 62(5):1049–1057. https://doi.org/10.1007/s40194-018-0593-7
Obaton A-F, Butsch B, Carcreff E, Laroche N, Tarr J, Donmez A (2020) Efficient volumetric non-destructive testing methods for additively manufactured parts. Weld World. https://doi.org/10.1007/s40194-020-00932-0
Obaton A-F et al (2020) Evaluation of nondestructive volumetric testing methods for additively manufactured parts. In: Shamsaei N, Daniewicz S, Hrabe N, Beretta S, Waller J, Seifi M (eds) Structural integrity of additive manufactured parts. ASTM International, West Conshohocken, pp 51–91
Bono R, Schiefer M Fundamentals of resonant acoustic method NDT. https://www.modalshop.com/filelibrary/White-Paper-Fundamentals-of-NDT-RAM-(MD-0269).pdf
ASTM E2001–18 (2018) Guide for resonant ultrasound spectroscopy for defect detection in both metallic and non-metallic parts. ASTM International. https://doi.org/10.1520/E2001-18
Paddock BW et al (2020) Partially resorbable implants and methods. US10537666B2
Alpaydin E (2020) Introduction to machine learning. MIT Press
Fisher RA (1936) The use of multiple measurements in taxonomic problems. Ann Eugenics 7(2):179–188
Frank CR, Cline WR (1971) Measurement of debt servicing capacity: an application of discriminant analysis. https://doi.org/10.1016/0022-1996(71)90004-3
Belhumeur PN, Hespanha JP, Kriegman DJ (1997) Eigenfaces vs. Fisherfaces: recognition using class specific linear projection. IEEE Trans Pattern Anal Mach Intell 19(7):711–720. https://doi.org/10.1109/34.598228
Chen C-Y, Wooster GA, Getchell RG, Bowser PR, Timmons MB (2003) Blood chemistry of healthy, nephrocalcinosis-affected and ozone-treated tilapia in a recirculation system, with application of discriminant analysis. https://doi.org/10.1016/S0044-8486(02)00499-4
David DE, Lynne AM, Han J, Foley SL (2010) Evaluation of virulence factor profiling in the characterization of veterinary Escherichia coli isolates. Appl Environ Microbiol 76(22):7509–7513
Tahmasebi P, Hezarkhani A, Mortazavi M (2010) Application of discriminant analysis for alteration separation. Sungun Copper Deposit, East Azerbaijan
Khalid MI, Alotaiby T, Aldosari SA, Alshebeili SA, al-Hameed MH, Almohammed FSY, Alotaibi TS (2016) Epileptic MEG spikes detection using common spatial patterns and linear discriminant analysis. IEEE Access 4:4629–4634. https://doi.org/10.1109/ACCESS.2016.2602354
Tharwat A, Gaber T, Ibrahim A, Hassanien AE (2017) Linear discriminant analysis: a detailed tutorial. AI Commun 30:169–190. https://doi.org/10.3233/AIC-170729
Triola MF, Goodman WM, Law R, Labute G (2006) Elementary statistics. Pearson/Addison-Wesley, Reading
Vapnik V (2013) The nature of statistical learning theory. Springer Science & Business Media.
Resende PAA, Drummond AC (2018) A survey of random forest based methods for intrusion detection systems. ACM Comput Surv 51(3):1–36
Acknowledgments
The authors would like to thank the National Institute of Standards and Technology (NIST), Gaithersburg, MD, USA, for the fabrication of the lattice structures.
Funding
This project has received funding from the EMPIR programme co-financed by the Participating States and from the European Union’s Horizon 2020 research and innovation programme.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Recommended for publication by Commission I - Additive Manufacturing, Surfacing, and Thermal Cutting
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Obaton, AF., Wang, Y., Butsch, B. et al. A non-destructive resonant acoustic testing and defect classification of additively manufactured lattice structures. Weld World 65, 361–371 (2021). https://doi.org/10.1007/s40194-020-01034-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40194-020-01034-7