1 Introduction

With modern automated welding processes, such as laser-hybrid welding, it is possible to produce high-quality welds with good resistance to fatigue. However, although the overall quality of the welds may be very good, the joints can still contain significant geometrical variation and geometrical imperfections at the weld notches. For instance, the previous research for laser-hybrid welded butt joints showed that small undercut-type imperfections exist both in toe and root side [1]. These imperfections are usually short along the weld length direction and may not be visible when the geometry of the weld is examined. However, such imperfections work as local stress risers and may influence the fatigue strength significantly based on the weakest link principle. Thus, the control and assessment of weld quality with respect to fatigue strength is of the greatest importance in fatigue critical structures.

Importance of weld quality is increased in small plate thicknesses, i.e. t < 5 mm, due to increased relative size of the weld geometry and notches. In thin plates, especially undercuts are observed to reduce the fatigue strength significantly [2]. Influence of geometrical imperfections on fatigue strength is also increased for high-strength steels and welds having high hardness, e.g. produced by laser-based welding processes. For welds in thin plates and high-strength steels, commonly used fatigue strength assessment approaches are observed to have high uncertainty and produce high scatter in stress-life (S-N) curve, lowering the design values for fatigue strength and limiting the structural optimization with respect to weight. To fully benefit from modern thin plate structures, fatigue strength assessment approaches and weld quality control methods need to be improved.

Link between local weld notch geometry and fatigue strength of the joint is still unclear. Several studies investigate the influence of actual weld notch geometry on the notch stresses and fatigue. Often, these investigations are conducted for 2D geometry cross-sections (see, e.g. [1, 3]). While the weld geometry in large scale is seemingly constant along the weld (and 2D simplification can be justified), in small scale, the varying geometry may cause stress redistribution in weld direction. This may cause 2D idealisation to result in notch stress overestimation in critical cross-sections due to assumption of continuous geometry. The load redistribution was already observed in [4], where in deep and narrow undercuts did not cause as high notch stresses as could be expected. In most of the studies conducted for measured 3D weld geometry, e.g. [5], investigation is focused on the maximum surface stress that is known to be incorrect reference stress for fatigue assessment, especially for sharp and small notches usually found in welded joints. In such cases, consideration of microstructural support should be included. In [6], thorough fatigue strength analysis was conducted for measured 3D weld geometry considering microstructural support. In the study, good correspondence between undercut defective and defect-free specimens was obtained by local stress approach.

Three-dimensional stress analysis requires measurement of full 3D geometry at the weld notch, which is difficult to acquire for larger weld samples with adequate accuracy, resolution and speed. In addition, the efficiency of 3D finite-element analysis (FEA) regarding model construction and computation is low compared to two-dimensional approach. Thus, 2D geometry measurement and FEA is highly preferred for analysis of large full-scale joints. However, the validity of 2D stress analysis for small-scale weld notch geometry is still unclear in the case of local geometrical imperfections.

This study investigates the accuracy of 2D analysis for effective notch stress assessment. The aim of the study is to reveal the amount of difference introduced by 2D idealisation in comparison to 3D analysis. The study is conducted for parametric weld geometries and undercuts having semi-elliptic depth in weld direction. In the study, focus is to examine the fatigue-effective stress at the notch instead of maximum surface stress.

2 Assessment of fatigue-effective stress

Currently, the most common method to assess the fatigue strength of welded joint, considering also the influence of weld geometry, is effective notch stress approach [7]. This utilises enlarged fictitious notch rounding rF at the weld notch to take into account the microsupport effects of the material. The theory of microsupport assumes that load on critical particles, such as grains in steel, is redistributed to surrounding material, increasing the fatigue strength from estimation based on linear-elastic notch factors [8]. The effective notch approach, or fictitious rounding approach, is based on the Neuber’s line method, where average stress is assessed along line, perpendicular to maximum principal stress direction, below notch by equation

$$ {\sigma}_{\mathrm{eff}}=\frac{1}{\rho^{\ast }}{\int}_0^{\rho^{\ast }}\sigma (y) dy $$
(1)

Here, σ(y) is the linear-elastic maximum principal stress as a function of depth y and ρ∗ is a material-dependent parameter; stress averaging length. According to Neuber, equivalent effective stress σeff can be derived by calculating surface stress in a notch with enlarged fictitious radius

$$ {r}_F=r+s{\rho}^{\ast } $$
(2)

where r is the actual radius of the notch and s is the support factor due to loading condition. Commonly used fictitious notch rounding rF = 1 mm for welds in steel, as proposed by Radaj [7], is derived from here using assumption of sharp notch (r = 0), flat plate (s = 2.5), and cast steel properties for weld (ρ∗ = 0.4 mm [8]). The effective notch stress method with rF = 1 mm has proven to be good fatigue assessment tool for arc welded thick plates (t > 5 mm) (see, e.g. [9]). However, as the method has observed to have some uncertainty regarding the assessment of thin plates (t < 5 mm) and mild notches, e.g. butt joints, several modifications has been proposed to the method in these cases. These modifications include use of smaller fictitious radius, i.e. rF = 0.05 mm [10], or use of stress averaging approach [1, 11]. Currently rF = 1 mm is not anymore considered to be based on the material properties but is just a one value for deriving reference stress for a sharp notch. Other radii can also be used, and corresponding S-N curve should be chosen based on the radius [12].

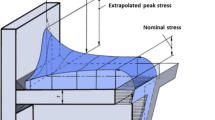
The fictitious notch rounding approach is effective fatigue assessment tool for design and structural analyses when the exact shape or quality of the weld is not known. However, for more detailed fatigue strength assessment of welds, taking into account also the actual notch shape and material properties, original theory of stress averaging (Eq. 1) could be used [1] (see Fig. 1 for an example on application). The original stress averaging approach is beneficial on analysing the influence of local notch geometry, as the notch shape does not need to be modified for the stress analysis.

Fig. 1
figure 1

Stress averaging approach applied in analysis of measured weld notch [1]

Full size image

With stress averaging approach, challenge lies in defining proper stress averaging length ρ∗, which defines how sensitive the material is to notches with respect to fatigue. Based on the original research by Neuber [7], the stress averaging length is ρ∗ < 0.15 mm for structural steel depending on the yield strength, while for cast steel it is around previously discussed ρ∗ = 0.4 mm. Welded steel has complex and inhomogeneous microstructure, and thus the proper values for ρ∗ are still open question. However, in [1], the smallest scatters for laser-hybrid welded butt joints in thin plates were derived with ρ∗ = 0.05…0.1 mm, which suggests that Neuber’s values for structural steel could be good approximation also for welded joints when actual weld geometry is considered.

Stress averaging approach and its simplification fictitious notch rounding approach are originally 2D approaches. For large-scale weld geometry, fictitious notch rounding approach is nowadays also commonly utilised in 3D analysis of complex joints by FEA. This application is acceptable considering the relatively constant geometry of the weld in large scale. However, the small-scale geometry has larger variation along the weld length and contains short notches, which cannot be considered continuous. When stress-averaging approach is applied on this small-scale geometry, understanding of the 3D effect of the stress distribution should be acquired. Influence of 3D effect and neglecting small-scale geometry can also be one reason why regression studies for stress averaging length had led to quite large averaging length, i.e. ρ∗ = 0.4 mm [12], compared to Neuber’s curves. With smaller stress averaging length, the influence of 3D notch geometry can be expected to increase due to closing scale between ρ∗ and local geometry variation. When 3D effect is studied, consideration of stress averaging length should thus be included.

3 Notch stress analysis of parametric models

3.1 Notch shape and parameters for notch in flat plate

To investigate the influence of geometry 2D simplification on the notch stress results, simplified case of a semi-elliptical notch in flat plate was examined. Examination was made by numerical analysis of parametric notch model. The geometry of the models was formed in Matlab software [13] based on commonly assumed blunt V-shape notch geometry in loading direction, i.e. normal to notch length.

Input parameters for the notch were the notch length l, notch depth d, notch opening angle β and notch root radius r (see Fig. 2). The shape of notch in weld direction was formed using notch depth as a driving parameter. The depth of the notch was determined to have semi-elliptic distribution in the weld direction. Radius and opening angle was defined to remain same for whole length of the notch.

Fig. 2
figure 2

Shape and parameters for flat plate notch and weld undercut models: notch depth d, notch length l, notch opening angle β, notch radius r, weld flank angle θ, weld bead width W and weld bead height H

Full size image

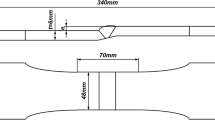
Parametric study was conducted as dimensionless. However, as stress averaging length ρ∗ introduces scaling parameter to the analysis, it is necessary to define realistic range for dimensionless parameters based on the actual welds. As discussed in Section 2, proper stress averaging length for analysis of welded joints is an open question. The traditional effective notch stress method is based on ρ* = 0.4 mm, while the research in [1] proposes smaller stress averaging lengths, i.e. 0.05 mm. Thus, the range of ρ* = 0.05 … 0.4 mm is covered in this study. For notch depth, reference was chosen to be d = 200 μm, based on observations in [14, 15]. Scaling of the geometry with respect to stress averaging length ρ∗ can be done based on the depth, resulting in the d/ρ∗ ratio range 0.5 … 4. Notch radius is hard to define accurately due to non-well-defined geometry of the weld [16, 17] and thus good reference value is hard to define. However, sensitivity of the stress difference between 2D and 3D analysis to notch radius can be conducted. In this study, ratio r/d in range 0.25 … 1 was studied. For the influence of notch opening angle, range β = 30 … 90° was studied. The shape of elliptic notch in weld direction is described by aspect ratio d/l. Depending on the welding process, d/l ratio of undercut may vary significantly. In this study, aspect ratio d/l range from 0.05 to 0.4 is studied as this is considered to fully cover normal aspect ratios in modern high quality welding. For example, based on the measurements of thin laser-hybrid welded joints, the typical ratio was around 0.1 (see Fig. 3). This is similar to the given example in [6] with the ratio around 1:20, while in [4], deepest studied undercut had a ratio of 1:8. Summary of the all studied parameter ranges are given in Table 1.

Fig. 3
figure 3

Example of measured undercut on root side of laser-hybrid weld

Full size image
Table 1 Range for geometric parameters studied for notch in a flat plate
Full size table

3.2 Notch shape and parameters for notch at weld toe

To extend the examination to a weld undercut, parametric model including weld bead was formed. Input parameters for geometry creation were plate thickness t, weld bead width W, weld bead height H, weld flank angle θ, notch length l, notch radius r, notch depth d, notch flank angle γ and notch opening angle β (see Fig. 2). To reduce the number of parameters, two weld bead geometries are chosen for examination; Geometry 1 represents typical root side and Geometry 2 typical top side of laser-hybrid butt weld in thin plates based on values in [15]. For the undercut, opening angle β = 60° in the middle of range in the flat plate notch analysis was chosen. Also, the same undercut depth d = 0.2 mm was chosen as in the flat plate analysis. For dimensionless parameter d/l range from 0.05 to 0.4 is analysed, and r/d range is from 0.25 to 1. All studied geometrical parameters for weld bead and undercut are given in Table 2.

Table 2 Values for geometric parameters studied for weld undercut
Full size table

3.3 Effective stress analysis by FEA

FE models were constructed and solved in Abaqus software version 6.14 [18]. The 3D models were 1/8 models assuming symmetry in three directions (see Fig. 4). With uniform tension loading applied to the free end of the model, this modelling results in pure tension case for the notch without secondary bending occurring from the eccentricity. For efficient calculation, sub-modelling technique was used for notch to allow refined meshing in critical area. The thickness of the model was set large enough for excluding the thickness effect (reduced cross-sectional area) from the results, while width of the model was set to be three times wider than the notch. The outer face of the model was restricted to move in transversal direction to loading, meaning that boundary conditions are similar to plane strain in 2D FEA. Poisson ratio was set to ν = 0.3 assuming steel properties.

Fig. 4
figure 4

FE model for notch in flat plate

Full size image

Global model was constructed from 8-noded brick elements with mesh refinement around the sub-model and notch (see Figs. 4 and 5). The loading was applied on the free end of the model as a negative unit pressure. From the global model solution, displacements were transferred to sub-model as boundary conditions. Sub-model had refined mesh with quadratic elements, mainly 20-noded bricks. Mesh size in critical location was set to be r/5, but with ρ∗/5 as maximum size limit. Thus, the element size varied depending of the notch shape, being 0.01 mm for the smallest notch radius.

Fig. 5
figure 5

3D global model and sub-model, and 2D model, for parametric undercut model. Global coordinate system is shown

Full size image

Effective notch stress in critical cross-sections, at the mid plane, was also analysed using 2D FE model. Due to the less degrees of freedom, 2D FEA did not require sub-modelling and fine mesh could be used directly. At the notch, mesh size was overly small (see Fig. 5). Elements were mainly 4-noded plane strain elements. Similar boundary conditions were applied on the 2D model excluding the weld direction, which was constrained by plane strain assumption to correspond with the restricted displacement of outer edge in 3D model.

For both 2D and 3D models, stress averaging approach by line method is used to assess effective notch stress. Assessment is made along lines perpendicular to the maximum principal stress direction starting from the notch root in centre cross-section, see the coordination axis x* in Fig. 6. For simplicity, the direction of principal stress is assessed at the depth half of the stress averaging length since this gave equal results to that of evaluation based on full averaging length. Due to symmetry, the stress assessment line is vertical for flat plate notch model. In the case of weld undercut, the line is slightly tilted due to curved stress field (see Fig. 6 for example). The effective stress is calculated using Eq. 1 by numerical integration of derived maximum principal stress distribution.

Fig. 6
figure 6

Definition of effective notch stress σρ∗ from 3D model

Full size image

4 Results

In order to simplify the results’ presentation, the 3D correction factor k3D is introduced. This factor describes the ratio between 2D and 3D effective stress results, and it is calculated by

$$ {k}_{3\mathrm{D}}=\frac{\sigma_{\rho \ast, 3\mathrm{D}}}{\sigma_{\rho \ast, 2\mathrm{D}}} $$
(3)

where σρ ∗ , 2D and σρ ∗ , 3D are effective notch stresses by 2D and 3D analyses, respectively. No examination of the absolute values of notch stresses, or notch factors, are conducted in this study. All results, including notch factors, are however given in number format in Appendix Table 3 for flat plate and Appendix Table 4 for weld undercut models.

4.1 Notch in flat plate with semi-elliptical undercut

As expected, notch stress results by 2D and 3D analysis for flat plate diverge when the shape of the notch is deep compared to the length, or other words “less continuous”. The main influencing geometric parameter for the 3D correction factor was observed to be depth to length ratio d/l. In Fig. 7, correction factor k3D is given as a function of d/l for different d/ρ∗ scaling parameters. As a reference for lower boundary, results are given also for surface stress without stress averaging.

Fig. 7
figure 7

3D correction factor of flat plate notch as a function of d/l for different d/ρ* ratios

Full size image

Correction factor decreases nearly linearly with the increasing d/l for selected parameter ranges. Lower boundary of correction factor is given by surface stress without averaging, and results for the smallest stress averaging length are close to this. For example, minimum correction factor for d/l = 0.1 is k3D = 0.951 for surface stress and k3D = 0.964 for d/ρ∗ = 4. For d/l = 0.4, minimum correction factors for corresponding sets are k3D = 0.677 (surface stress) and k3D = 0.696 (d/ρ∗ = 4). Difference between 2D and 3D solutions for the smallest scaling parameter d/ρ∗ = 0.5 are approximately half of the d/ρ∗ = 4 values, correction factors being approximately k3D = 0.82 and 0.92 for d/l = 0.1 and 0.4, respectively.

Scaling parameter d/ρ∗ is observed to define the slope in curves presented in Fig. 7. For smaller d/ρ∗ values, correction factor is larger as the highly stressed material layer becomes smaller compared to the stress averaging length. In Fig. 8, the same results shown in Fig. 7, are given as a function of d/ρ∗ for different d/l ratios. From this figure, it can be seen that when stress averaging length becomes smaller compared to the notch depth, the more the correction factor is defined by d/l ratio only. With smaller d/ρ∗, or larger ρ∗, the correction factor approaches 1 as the effective stress start to approach nominal stress of the cross-section.

Fig. 8
figure 8

3D correction factor of flat plate notch as a function of d/ρ* for different d/l ratios

Full size image

Both Figs. 7 and 8 includes the full notch opening angle αn range from 30 to 90°, and notch radius ratio r/d range from 0.25 to 1. It can be observed, that these parameters have minor influence on the 3D correction factor, but introduce some scatter on the results. The scatter is especially significant on the results with large d/ρ∗ ratios (small stress averaging length). However, with d/ρ∗ = 4 and d/l = 0.4, values with the largest scatter, correction factor varies only from k3D = 0.696 to 0.711 due to varying r/d and β.

4.2 Weld undercut with semi-elliptical depth

When weld bead is added to the model, the notch becomes approximation of weld undercut. The results for the parametric weld undercut model were similar to notch in a flat plate, although some difference exists. In Fig. 9, the 3D correction factors are presented as a function of d/l for different stress averaging lengths. Trendlines for the notch in a flat plate are plotted for the reference. It can be seen that the correction factor is larger with neighbouring weld bead, and the flat plate results describes the lower limit of factor. For the weld undercut, the scatter due to notch radius is a bit higher, although it is small compared to the influence of d/l and d/ρ∗.

Fig. 9
figure 9

3D correction factor of weld undercut as a function of d/l for ρ* = 0.05 mm and 0.4 mm (d = 0.2 mm)

Full size image

In Fig. 10, the results for undercut are translated to be a function of d/ρ∗ for different d/l. It is observed that for undercut, the correction factor behaves similarly to notch in flat plate, but is larger. For large d/ρ∗ values, the factor saturates to a constant value. When d/l is small, this saturation happens already with smaller d/ρ∗ ratios.

Fig. 10
figure 10

3D correction factor of weld undercut as a function of d/ρ* for different d/l ratios

Full size image

Comparison of results between two weld bead geometries shows that factor is higher for smaller weld, Geometry 1. For larger weld bead, Geometry 2, the difference is higher and closer to flat plate results. Although it would be expected that the correction factor with smaller weld bead would be closer to that of flat plate notch, it is not the case here.

4.3 Three-dimensional stress state under notch

Difference in effective notch stress between 2D and 3D notch geometries was observed to be consequence of geometrical support effect, i.e. reduction of notch opening deformation for short notch, and difference in three-dimensional stress state under notch, i.e. divergence from plane strain condition in 3D. This behaviour is illustrated in Fig. 11.

Fig. 11
figure 11

Stress components with respect to nominal stress (above) and maximum principal stress with respect to von Mises stress (below) under notch in flat plate (β = 30°, r/d = 0.5) for different notch aspect ratios (3D) in comparison to plane strain solution (2D). Enlarged notch opening displacements illustrated for comparison to principal stress

Full size image

In upper row of Fig. 11, stress components under notches (β = 30°, r/d = 0.5) with different aspect ratios in flat plate are presented as a function of depth (scaled with notch depth). Stress components are given as a factor with respect to nominal stress. Stress components of 2D plane strain solution are given for comparison, as well as illustrations of difference in notch opening under loading between 3D and plane strain solutions. It can be seen that for very short notch (d/l = 0.4) both the level and ratio of stress components differ from plane strain solution significantly. While the largest difference in stress is in longitudinal direction (σyy), relatively the largest difference is in transverse stress components, σxx and σzz. When notch is longer, the difference between 3D and plane strain solutions decreases, and 3D solution approaches to plane strain condition for very shallow notch (d/l = 0.05). It can also be observed that the difference in notch opening displacement between 3D and plane strain solution is almost equal to the difference in maximum principal stress at the notch surface. This behaviour is caused by geometrical support of the material surrounding the notch, decreasing the notch opening displacements and reducing the stresses at weld root.

In lower row of Fig. 11, stress three-dimensionality is presented as a ratio between maximum principal stress and von Mises stress. It is observed that near the surface of the notch, stress three-dimensionality is equal for plane strain and 3D notch. When going deeper, the stress states start to differ significantly for short notch, i.e. larger d/l ratio. The difference between plane strain and 3D solution exists for the whole examined stress averaging length range X∗/d = 0.25…2 (d/ρ∗ = 0.5…4), and it is the largest at depth X∗/d = 0.5…1 . The reduction of stress three-dimensionality below the finite length notch is caused by reduction of material deformation restrictions in transverse direction, resulting in divergence from plane strain condition.

5 Discussion

The results show that the effective notch stress, calculated by stress averaging approach, is overestimated in 2D (plane strain) analysis for finite length notch due to supporting factor of the surrounding material and difference in local boundary conditions at the notch. The 3D correction factor depends mainly on the notch shape and size in transversal direction (cross-section perpendicular to loading). For notch with finite length, the shape is defined by depth-to-length ratio d/l. The size of the notch is defined relative to used stress averaging length; here scaling parameter d/ρ∗ is used.

The correction factor behaved almost linearly with the d/l ratio for both flat plate notch and weld undercut (see Figs. 7 and 9). Figure 12 represents the comparison of the current results for the smallest average length and the results obtained by fracture mechanical calculations using the stress intensity factor (SIF) of semi-elliptical surface crack in uniform tension loading [19, 20]. The SIF corresponds the sharp undercut, in where the notch radius approaches zero. The SIF-based solution is in line with the current results and it provides good approximation of minimum k3D factor especially for smaller d/l (< 0.2) values. With more common d/l ratios for modern welding, from 1:20 to 1:10 (e.g. in Fig. 3 and [6]), k3D factor is above 0.92. In such cases, 2D stress analyses are easily justified.

Fig. 12
figure 12

Influence of d/l on SIF of semi-elliptical crack in tension and on effective stress for semi-elliptical notch with smallest analysed ρ*

Full size image

When the correction factor is plotted as a function of d/ρ∗ (see Figs. 8 and 10), the influence of used stress averaging on the analysis can be observed. With higher d/ρ∗ ratio, meaning smaller stress averaging length, the correction factor decreases until it starts to reach the surface stress solution. With larger stress-averaging length, the effective stress includes larger area of low stress region, which approaches to nominal stress far from the notch for both 2D and 3D analysis. This increases the factor. Resulting from this, larger stress averaging length, i.e. ρ∗ = 0.4 mm, can provide better reference stress for fatigue analysis in the case of joint with large geometrical variation and traditional 2D analysis as unrealistic high peak stresses are neglected.

Traditionally, fictitious notch rounding approach with rf = 1 mm has been used for welded joints with both von Mises and maximum principal stress using FAT classes 200 and 225 MPa, respectively, latter being recommended for most loading cases. Due to the observed differences in three-dimensional stress state of the material at different depths (see Fig. 11), use of von Mises stress instead of maximum principal stress would lead to very different results in fatigue strength assessment when stress-averaging approach is used. This is also the case for 2D analysis, as observed in convergence study for ρ∗ in [21].

The flat plate notch results provided the lower limit for the factor, with the studied parameter range (see Fig. 9). Weld undercut seems to have slightly smaller difference between 2D and 3D notch stress solutions than the flat plate notch throughout the tested parameter regions. However, the difference between the flat plate and undercut results is quite small, undercut models having approximately 20 to 30% smaller difference between 2D and 3D (see Fig. 12). Also, the two different shape and size weld beads resulted in different correction factors, which means that k3D factor is dependent also on the weld bead. These results suggest that flat plate results can be used to estimate maximum error caused by 2D simplification, but do not provide conservative approximation for k3D factor.

From the two analysed weld geometries, larger weld bead (Geometry #2) resulted in smaller correction factor and was surprisingly closer to the flat plate results than the smaller bead (see Fig. 9). However, Geometry #2 had also shallower weld flank angle than Geometry #1. Steeper flank angle can result in steeper stress gradient at the weld notch. Full understanding how the weld bead geometry affects on the results shown in this paper is hard to gain due to large number of affecting geometrical parameters.

Geometric parameters for notch shape in loading direction, e.g. notch opening angle and radius, seem to have minor influence on the correction factor with the studied parameter ranges. In weld undercut, the scatter of results due to notch radius is larger than for flat plate, but variation in k3D remains within 6% while radius of notch varies in factor of four. This behaviour simplifies the assessment of severity of short notch undercut in quality control as approximation of 3D correction factor can be based only on the depth and length of the notch in weld direction.

In previous research [1], use of mean value of analysed notch stress results for measured weld geometry resulted in smaller S-N scatter than use of 95% probability value for one specimen set, while for other set, this was other way around. Ninety-five percent probability stress value represents the worse end of the notch geometries found at the weld, or even defects. The observed behaviour might be a result of the notch stress overestimation of the local and short undercuts. For example, overestimation of stress by 20%, which would be approximately the case for ρ∗ = 0.05 mm and typical 200 μm deep undercut having 1:5 depth-to-length ratio, results in 45% shorter fatigue life according to [20]. As mean value of notch stress is more stable and weakly influenced by the local imperfections, it might provide better results in 2D space in some cases compared to the use of most critical sections. This filtering of overestimated notch factors is similar to the filtering effect of using larger stress averaging length. Deeper research in the statistics of notch stresses at the weld is required to study this issue.

The 3D correction factor studied here does not necessarily directly transfer to fatigue strength due to size effects. For long notch, a larger material volume is under high stress, resulting usually in lower fatigue strength than for short notch with the same effective notch stress. This is discussed for example in [22]. This means that there should be also statistical size effect to even further decrease the influence of short notches. Thus, the influence of notch 3D geometry on fatigue strength could be even larger in practice.

6 Summary and conclusions

The study examined the 3D correction factor, meaning the ratio of between effective notch stress in 2D and 3D stress analysis, for short notch in a flat plate and weld undercut. Effective notch stress was assessed by stress averaging approach and line method. Conducted numerical analyses for parametric models show that effective notch stress is overestimated in 2D analysis when notch is short and deep. For semi-elliptic notch shape, the main influencing parameter on the 3D correction factor was observed to be notch depth-to-length ratio, describing the shape of the notch in transversal direction to loading, and the scale of the notch compared to used stress averaging length. The overestimation of effective stress by 2D analysis is higher, when depth-to-length ratio becomes larger (deeper notch), or when stress averaging length is smaller compared to the notch depth. The shape parameters of the notch in direction longitudinal to loading, such as weld opening angle and notch radius, had minor influence on the correction factor with studied parameter range.

Maximum overestimation of effective stress by 2D analysis occurred with the smallest stress averaging length, and with typical 1:10 and 1:20 depth-to-length ratios, the stress overestimation by 2D analysis was below 5 and 10%, respectively. With such dimensions, 2D geometry simplification seem acceptable for notch stress analysis. Maximum error of 2D simplification can be estimated based on simple flat plate notch analysis, which provided lowest values for 3D correction factors in this study. For weld undercut, the overestimation is slightly smaller and is also affected by the shape of the weld bead.

Based on the study, consideration of notch length should be accounted in the fatigue strength analysis when the undercuts are short, i.e. depth-to-length ratio is larger than 1:10. The influence of undercut length is even further increased for smaller stress averaging lengths, meaning material with higher notch sensitivity (high-strength steels or welds with high hardness). Current weld quality rules for undercuts are based only on the depth of undercut. However, also the length matters. If weld quality control is based on dense measurement of weld geometry, individual exceeding of the depth limits might not be critical for fatigue strength of the joint. Assumption of continuous undercut (2D solution) is however conservative, while the consideration of undercut length in quality control requires further study and definitions.

It must be noted that analysis made in this study were focused on the typical weld and undercut shapes for thin, laser-hybrid welded butt joint. Also, the semi-elliptic shape of the notch is only rough approximation of the real undercut, which might be very irregular by its shape. However, the results can be used as a reference to estimate the error made in 2D geometry simplification and to assess the severity of finite-length undercut. To further study this topic, thickness effect should be examined as in thin plate thickness might increase the stress gradient at the notch. Also, being very relevant for butt joints in thin plates, sensitive to misalignments, bending loading should be examined. It is also clear that the line method used in this study to assess effective stress does not take into account the highly stressed volume (or area) which might have large influence on the fatigue strength of welded joint in real case. In any case, this size-effect should further decrease the influence of short undercuts on fatigue strength.