1 Introduction

As a result to increased demands in rail transport, producers around the world have developed modern high-performance rail steel grades with improved mechanical properties, especially at the head of the rail [1,2,3,4,5]. Moreover, for several reasons, it has become common today that rail tracks are continuously welded lines. Thus, the weld joints’ properties contribute an essential part to the overall performance of the railways for what concerns durability properties. In turn, this means that weldability of rails is a very crucial aspect in the track.

One important aspect with regard to the quality of a rail weld joint is the drop of hardness at the so called soft zones, which are located on both sides of the weld at the transition from HAZ to base metal (BM). These dips in hardness can appear differently pronounced for different steel grades and welding processes [6,7,8]. The reason for decreased hardness in this area are changes in the microstructure due to welding. A simple and also effective approach to cope with this challenge in rail welding is to keep the size of the HAZ as small as possible by reducing the heat input, compare [7, 9]. However, reduced heat input welding has a negative connotation, as it may cause flaws in the joint due to lack of sidewise fusion, which in turn can act as crack initiation points under cyclic loading and thus maybe represent an even more crucial aspect for rails. Furthermore, cooling rates are increased and lead to the formation of undesirable phases, such as Bainite and Martensite, which are also prohibited according to rail welding standards [10, 11]. There is demand for welding procedures for joining rails in the track welding which can be for these purpose optimized accurately enough at sufficient reliability and reasonable investment costs.

In our research project, the potential of a high performance automated gas metal arc welding process to replace the aluminothermic process is investigated. One very important task to overcome the above described challenges was to optimize the heat input for each layer such, sufficient fusion is constantly guaranteed on the one hand side and that the mechanical properties in the HAZ in comparison to the as produced material are least possible decreased on the other side. Numerical simulation was chosen to support the process development as the efforts for welding experiments for these heavy parts with large cross sections are very high.

Numerical simulation is used in many different fields in industry and research to support welding process-related tasks. Different phenomena can be studied, such as the evolution of the temperature field, weld pool behavior, distortions, and residual stresses as well as phase transformations and related changes of the microstructure and properties of the joint. Various commercially available software packages, e.g., SYSWELD, SimWeld, DynaWeld, and SimuFact as well as numerous generalized welding simulation textbooks, such as [12,13,14] proof that numerical simulation in welding can be considered as a state-of-the-art tool for many applications nowadays. The Johnson-Mehl-Avrami-Kolmorgorov (JMAK) equation can be used for calculating diffusive phase transformations phenomena in materials [15]. However, the JMAK-equations describe transformations under isothermal conditions. In order to predict phase changes during continuous temperature changes, like in welding, derivations of the equations are necessary [16,17,18,19].

With SYSWELD’s thermo-metallurgical calculation option, changes in phase fractions during heating and continuous cooling from welding can—among others—be studied. Two different models are available in the software, which’s derivation and generalization to include the JMAK-type transformation kinetics are described in the software’s manual [20] from page 7 on. Regardless of the chosen model, for each specific material and set of thermal cycles, a dedicated optimization of the comprised parameters is necessary. We have explained our model and the method for obtaining the necessary parameters for a simulation of GMAW of the investigated pearlitic rail steel in SYSWELD in our previous publication, s. in detail [21].

Only a limited number of publications on numerical simulation of rail welding are available. They deal with the calculation of the temperature field and residual stresses from aluminothermic [22,23,24] or flash butt-welded rails [25,26,27] and their influence on the strength of the weld joints. Research results of numerical simulation of GMAW of pearlitic rails cannot be found.

In rail welding, the microstructure of HAZ may only consist of Pearlite. Therefore, the hardness inside the HAZ can be attributed to Pearlite alone, namely its morphology, such as the interlamellar spacing or the width of the carbide lamellae [28,29,30,31,32]. One possible approach for calculating the hardness in pearlitic steel is via a calculation of the interlamellar spacing. Good results could be obtained by various researchers, [31, 33,34,35]. However, the investigated materials were not rail steels, and interest was either on fundamentals or on the production process and not the welding.

The purpose of the here presented work was the implementation and validation of a 3D-FE-simulation of multilayer GMAW of pearlitic rails as a tool for process optimization. More specifically, the hardness. It represents a use-case and proof the functionality of a previously presented model [21] for calculating phase transformation and hardness in the HAZ of pearlitic rail welds. Thus, it aims to depict metallurgical transformations inside the HAZ as a function of the transient temperature field in the weld zone during multilayer arc weld of pearlitic rails, and its effects on the mechanical properties inside the HAZ. The main advantage of this model is its novelty to enable more efficient process development for GMAW of pearlitic rails.

2 Experimental procedures

2.1 Used material

The used material was a R350HT rail steel according to European standard [36]. Rails of this grade are fully pearlitic. The hardness at the rail head is increased by faster cooling after the rolling process [37] and accounts in this way for better resistance to wear and rolling contact fatigue [38, 39]. The chemical composition and hardness at the running surface of the steel is given in Table 1.

Table 1 Chemical composition limitations and hardness requirements of R350HT rail steel according to European standard [36]
Full size table

2.2 Welding experiments

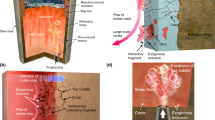
The used experimental setup is depicted in Fig. 1a. Experiments were carried under laboratory condition. A specifically designed narrow gap welding torch, which was mounted to an automated rack and a TPS 500 GMAW power source from Fronius were used. The movement of the welding torch as well as the power source settings was programmed via a separate programmable logic controller (PLC) unit. Welding parameters of each layer had been optimized beforehand for a stable process and sound welds. A 1.2-mm diameter G3Si1 filler wire was used for all layers. For the root layer (1st layer) the welding current was 150 A in pulsed mode and the traveling speed was 14 cm/min. For the subsequent layers, the welding current was increased to 180 A, still in pulsed mode, and the speed to 18 cm/min.

Fig. 1
figure 1

a Experimental setup for instrumented rail welds in the laboratory. (1) Welding torch (stand-by position). (2) Rail samples. (3) Thermocouples wiring. (4) Weld pool backing. (5) Glue aluminum foils (shielding gas traps). b Temperature measurement positions, Dimensions are in mm

Full size image

Seven hundred-millimeter-long samples of rails of 60E1 profile were accurately positioned and clamped to form a 15-mm weld gap. Additionally, the rail samples were preheated to 300 °C before welding, which is in accordance with the standard WPS used for manual arc welding of R350HT rails steel grade. Run-on and run-off plates were used sidewise. Copper shoes and ceramic inlays were used for weld metal backing. Glued aluminum foils were used as shielding gas traps. The weld sequence consisted of in total ten layers from the bottom of the rails foot up to the transition from rails foot to rail web. These layers were welded in continuous “to and fro” movements according the width of rail’s cross section.

2.3 Temperature measurements

One-millimeter-diameter type K thermocouples were point-welded at two positions on the surface of the top of the rail foot to capture the temperature evolution inside the HAZ during welding, s. Fig. 1b. At each of the two positions, three different distances from the weld flanks were defined as measurement point based on the size of the HAZ in macrographs of cross sections of preliminary welded samples. Additionally, two more thermocouples were placed on the lower side of the rail at both sides of the weld gap to monitor the preheating temperature.

2.4 Metallography

After welding, samples for metallography investigation were prepared. Therefore, the outer parts of the rail samples, as well as the web and head of the rail were cut-off. Then, three cross section samples were cut out at reference locations I, II, and III perpendicular to the weld path, whereof two at 10 mm from the side edges of the foot on both sides and one in the middle, s. Fig. 2. The width of the HAZ zone was measured by taking macrographs from the so obtained entire cross sections.

Fig. 2
figure 2

Top view of welded rail sample (outer parts, web, and head of rail cut off). Locations of sample extraction for macrographs of HAZ, LiMi, and SEM metallography as well as hardness investigations.

Full size image

Subsequently, these same macro samples were cut again at the center of the weld path. The so obtained samples were first off all for hardness measurements in the HAZ and base material. Therefore, 3 HV10 lines were done on each location from the weld center line until the base material. For better comparability, average hardness as a function of the distance from the line of fusion inside the HAZ was calculated out of the so gathered data.

Second, the samples were used for light microscopy of the microstructure in the HAZ. Furthermore, SEM investigations were done for measuring the interlamellar spacing of the Pearlite in dedicated locations.

3 Numerical procedures

3.1 Thermo-metallurgical simulation in SYSWELD

First, a 3D multilayer thermo-metallurgical coupled FE simulation was implemented in SYSWELD® in order to depict the temperature field evolution and calculate the phase transformations in the HAZ. The main dimensions of the implemented model, as well as all the implemented weld layers can be derived from Fig. 5a. The geometry of the rails as well as the weld layers corresponded to the carried out experiments described in the section above.

In order to reduce the actual process’s complexity and attain reasonable calculation times, some simplifications were done in the simulation. First of all, a symmetry condition was modeled at the y-z-plane along the center line of the weld path to reduce the number of elements, s. Fig. 5a. This symmetry condition was found in beforehand carried out experiments to be valid.

A second simplification is in regard to the weld path. Some smaller details in the travel of the welding torch, which were found to be necessary in the experiments for a stable process and sound welds, were neglected in the simulation. However, the overall welding sequence in terms of total time per layer and heat input per unit of length was defined such, that exact correspondence to the experiments was given. Still prevailing differences in the T (t) curves were fitted by multiple optimizations, using the welding velocity and efficiency coefficient of the heat input (s. Table 2) for each layer as variables.

Table 2 Welding parameters for each layer in the SYSWELD® simulation
Full size table

The geometry of the single layers in weld metal was implemented based on the macro images and cross section taken after welding. Still, some details of the weld had to be simplified. The reason was the in other ways excessive number of elements and partially bad element quality, due to pointy geometries at the intersection of the rail’s cross section and the weld metal. The weld path and the mesh of the weld metal of each layer are depicted in Fig. 6.

Furthermore, the used Goldak heat source was simplified in comparison to the arc of the actual process. Pulsed mode welding as well as the rotation of the arc of the therefore specifically designed narrow gap weld torch was neglected. However, its shape has been adapted to an almost spherical shape. This is accordance to the weld pool’s shape of the actual process. It was realized in the simulation by setting the fitting parameters of the Goldak [40] heat source to 16 mm for width and length, and power ratio to 1.0 and the length ratio to 0.9.

Heat transfer to the outside was defined by thermal boundary conditions on an enveloping layer of shell elements with temperature dependent radiative term, according to the Stefan-Boltzmann law (ε = 0.8), and a constant convective term of 25 W/m2 K. The ambient temperature was defined to constant 20 °C. This heat transfer surface is individually defined for each weld layer according the shape of the newly deposited weld metal.

Furthermore, element activation in the weld metal was implemented in two levels. The simulation is run layer after layer. At the start of each layer, only the elements of already welded and currently welded layers are defined in the simulation. Furthermore, all elements of the currently welded layer are initially deactivated by setting them to the so called “fictive phase.” The elements are then activated by a phase transformation into Austenite upon passage of the heat source at a temperature of 1000 °C.

The phase transformation model’s parameters PEQ, Tau, F, and N for the simulation in SYSWELD had been setup for the used R350HT rails based on dilatometry results as described in our previous publication [21]. Their derivation and also generalization to the JMAK-equation is described in the SYSWELD-Reference Manuals [20]. The parameters used for Austenite to Pearlite transformation can be seen in Fig. 3 those for the transformation from Austenite to Bainite in Fig. 4.

Fig. 3
figure 3

SYSWELD parameters for the calculation of Austenite to Pearlite transformation

Full size image
Fig. 4
figure 4

SYSWELD parameters for the calculation of Austenite to Bainite transformation

Full size image

The total number of 3D-hexagon-elements of SYSWELD’s type 3008, [20] for details, for the rail and the weld metal for all ten simulated layers was roughly 150,000. Furthermore, the number of enveloping 2d-shell elements to model the heat transfer via convection and radiation to the outside was roughly 65,000. There is also some 1d elements, which however only serve as a reference for the path of the heat source. The simulation was run on an Intel i7–2600 3,4Ghz 64Bit Win7 desktop computer with 16GB Ram memory. The calculation time for all ten layers was roughly 12 h.

Furthermore, thermo-physical properties (density, heat capacity, and thermal conductivity) were simulated in JMatPro® and introduced in the material database format of SYSWELD®. These properties are depicted as function of the temperature in Fig. 5b. Throughout beforehand carried out optimization work in the simulation, it was found that the temperature dependence has caused divergence problems in the transient calculation. Therefore, density was instead modeled as constant 7.815 kg/m3. Furthermore, the two significant peaks in the specific heat, which indicate latent heat of the phase changes from Ferrite to Austenite (720 °C) and solid to liquid state (1380–1480 °C), were smoothened and therefore lowered by 50% (compare Fig. 5b).

Fig. 5
figure 5

a Simulation model: main dimensions in mm and weld layers. b Thermo-physical properties of R350HT rail steel from JMatPro® simulation. Red lines show simplified properties used in SYSWELD®

Full size image

For what concerns the metallurgy part of the simulation, transformation properties of R350HT rail steel were defined for all elements of the model. This is another simplifying assumption in the simulation when compared to the actual process, where a filler wire with different chemical composition than the one of the rail steel was used. However, the weld metal was not inside the scope of investigation in this work. The transformation parameters were optimized according to [21].

3.2 Hardness simulation in the HAZ

Results from the above SYSWELD® simulation were used to extract T (t) curves and corresponding data of phase transformations at three dedicated points (1st:1 mm from the fusion boundary, 2nd: middle of HAZ at 9 mm from fusion boundary, and 3rd: at the minimum hardness inside soft zone at 15 mm from fusion boundary) for the corresponding three reference locations of the metallography samples. The data was then used in separate MatLab® routines to calculate the interlamellar spacing and the corresponding hardness in these points. There is no back-coupling of the hardness results into SYSWELD®. We have presented the principles of this calculation approach in a previous publication, s. [21].

In this work, in a first step, a calibration of the previously presented calculation routine for both the interlamellar spacing S and the hardness was done based on the measurement results from reference location I at the distance 1 mm from the fusion boundary line. After that, the calibrated calculation was run for all other presented points (Fig. 6).

Fig. 6
figure 6

Meshing details in the weld zone and schematic depiction of weld path in simulation

Full size image

4 Results and discussion

4.1 Thermal history

In Fig. 7, simulation results are compared to the corresponding T (t) curves in measurement position 1 and position 2. It can be derived that very good agreement in both positions could be attained in the welding phase of the simulation. For what regards the cooling, the simulation results show good agreement in the high temperature ranges. However, in the last cool down cycle from about 680 to 350 °C, a significant discontinuity in the measured T (t) curves can be observed. This aspect is less perceivable in the simulated T (t) curves. As a result, the t8/5-times in the simulation are shorter (Δt8/5 of P11-SIM vs. P11 is − 48 s, Δt8/5 of P21-SIM vs P21 is 41 s). The difference is believed to be a result of a combination of the implemented simplifications and the underestimated latent heat of the Pearlite transformation in the simulation.

Fig. 7
figure 7

Comparison of T (t) curves in measurements and in simulation. a Position 1. b Position 2

Full size image

Furthermore, it can be derived from the measurement results, that t8/5 times increase with increasing distance from the weld center line. This is the case for both measurement positions. However, there is a significantly faster cooling rates at measurement position 2. The cooling rates can be derived from Table 3.

Table 3 Cooling rates from thermocouples at measurement positions 1 and 2
Full size table

4.2 Size of HAZ

In Fig. 8, the simulated size of the HAZ (minimum and maximum width) in the three reference locations I, II, and III is shown. It is compared to the experimentally measured size of HAZ in the corresponding locations. It can be seen that for all three locations, very good agreement for what concerns the size as well as the shape of the HAZ was attained. Furthermore, it can be seen that the size of the HAZ is enlarged in the center of the rail and that it not symmetrical with regard to the rails longitudinal center plane.

Fig. 8
figure 8

Comparison of the size of the HAZ simulation and macrograph cross sections. Left-side images show the maximum austenitized area in the simulation. In the right side images, the size of the HAZ can be derived from the etched micro-structure

Full size image

4.3 Thermo-metallurgical simulation

The simulated temperature field is depicted at three different time steps in Fig. 9. It can be derived that the size of the HAZ continuously increases throughout the welding. The effect is more pronounced for the first three layers, compare Fig. 9a, b. For the remaining layers 3 to 10, the change is still present but much smaller. Overheating at the sides of the rails was found in the simulation due to the narrow geometry of the rail foot in comparison to the middle of the rail. Due to this fact, also the cooling rates are significantly influenced as a result of a non-homogenous temperature field evolution.

Fig. 9
figure 9

Simulated temperature fields at a start of first layer (root), b start of third layer, and c start of tenth layer

Full size image

Still, the simulation results show a fully pearlitic microstructure in all regions of the HAZ after cool down, s. Fig. 11a. This corresponds well to the microstructure found in light-microscopy samples.

The simulation was run a second time with the same parameters but without preheating in order to see whether preheating is necessary to avoid formation of Bainite and Martensite in the HAZ. The results are compared with the help of T (t) curves, peak temperatures TP, and t8/5 times, respectively cooling rates in Fig. 10 in P11 and P21. It can be derived that there is a significant difference in the cooling rates as well as the peak temperatures, and hence the influence from preheating is clearly given. This influence is also reflected in the results of the metallurgy simulation depicted in Fig. 11b. With preheating the entire HAZ, including the weld metal, fully retransforms into Pearlite. However, without preheating in the weld metal at the later layers, 15% transform into Bainite and also 1% into Martensite, and in HAZ of the root layer, close to the fusion boundary, 9% transform into Bainite.

Fig. 10
figure 10

Simulated thermal cycles at points P11 and P21 with and without preheating (noPH)

Full size image
Fig. 11
figure 11

Cross section view of simulated phase fraction of Pearlite after cool down for welding with a and without b preheating

Full size image

4.4 Hardness in the HAZ

In Table 5, results from the simulation (with preheating) of the hardness are presented together with additional relevant data at dedicated points and compared to measured hardness values at the corresponding locations.

From the measurement results, it can be derived that the hardness inside the HAZ for corresponding points at the same distance from the fusion boundary is varying at different the reference locations. However, for all three locations, the maximum hardness is reached closest to the fusion boundary and continuously decreases towards the absolute minimum inside the soft zone. Additionally, it can be derived that this relative decrease in hardness as well as the distance of the minimum hardness from the fusion boundary is for all locations practically the same (ΔH, 63–65 HV10; distance, 15–16 mm). Furthermore, it can be derived that the hardness of the base material is the same and higher in the sidewise reference locations I and III, but significantly lower in the middle location II.

From the results in Table 5, it can be derived that the interlamellar spacing increases and that the hardness decreases with increasing distance from the fusion line. Combining this fact with the peak temperatures and the t8/5-times from Table 3, it can be derived that the interlamellar spacing increases with decreasing peak temperature and decreasing cooling rates.

As a result, for what concerns the models capability, it can be stated that it can predict the hardness and its variation due to varying thermal cycles in the HAZ. However, the results are of variably good accuracy. It is very good for the sidewise reference locations I and III at the 9-mm distance (center of HAZ), where ΔΗminHAZ is equally as low as 1 HV10. However, average ΔHHAZ (excluding soft zone) is still 14.8 HV10, and the ΔHmaxHAZ is as high as 39 HV10. Comparing different parts of the HAZ, it can be derived that the inaccuracy of the simulation is significantly higher inside the soft zone, where average ΔHSZ is 17.7 HV10. Comparing the accuracy in the different reference location, it turns out that it is better in sidewise locations I and III, where ΔHI and III is only 11 HV10, whereas in the middle of the rail ΔHII is 24 HV10. The trend of relatively decreasing hardness from the fusion boundary towards the soft zone was depicted in all locations correctly (Table 4).

Table 4 Comparison of simulated results of t8/5-times, average cooling rates, and peak temperature TP of the last cooling cycles
Full size table
Table 5 Results of simulated and measured hardness
Full size table

5 Conclusions

With the help of the presented simulation, it was possible to show, that the size of the temperature field is inhomogeneous throughout the welding layers and although continuously welded pre heating is still necessary in order to have a fully pearlitic microstructure in all regions of the HAZ after welding.

However, given the fact that the amount of non-Pearlite phase is small, and moreover the simulation results showed faster cooling than the actual process and that the last layer lacks a “tempering layer” to slow down cooling even more, it is believed that for the used welding parameters, a fully pearlitic microstructure can be achieved even without preheating, especially if the entire cross sections is welded and a tempering layer is still applied at the last pass.

Furthermore, a non-symmetrical width and shape of the HAZ was derived with regard to the rail center plane. It is believed to be a result of the “to and fro” welding sequence in combination with the rail’s specific geometry. As a result, also a non-symmetrical hardness distribution inside the HAZ was found from the measurements as well as the simulation results.

The results of the proposed calculation approach for the hardness inside the HAZ showed partially very good results. The models applicability is therefore basically believed to be given. However, accuracy at the current state of the model was not sufficient.

The remaining differences in the hardness calculation are drawn back to the following aspects:

  • The initial microstructures vary in the rail cross section. This fact was also pointed out by the found variances of the measured hardness in the base metal, where in the middle of the rail the measured hardness was 20 HV10 less. The aspect is basically known to be a result from the rail production process.

  • The parameters for the model to calculate phase transformation in SYSWELD® was optimized with regard to the final phase fractions for a given thermal cycle. We could show in our previous work that compared to our dilatometry results, the final phase fractions can be estimated at an accuracy of maximum deviation of about 3% [21]. However, for a given cooling cycle, there are possibly many parameter sets which could lead to the same good result for final phase fractions. The course of the transformation as a function of temperature had not been validated proportionally in our previous work. The course of transformation can significantly influence the results for the calculation of interlamellar spacing, which is separately calculated for each temperature step of a given cooling cycle as a function of undercooling below the eutectoid temperature. It is then quantitatively weighted in the averaged final interlamellar spacing of given cooling cycle according to the formed phase proportion at the given temperature step. This influence was not checked in the present work.

  • The austenitization conditions in the HAZ vary with regard to their locations throughout the weld path. This is a result of the described non-homogeneous evolution of the temperature field. This fact in turn influences the hardness in the HAZ and specifically soft zone by influencing the Pearlite’s morphology.

    • Varying increase of austenite grains size and resolution and change of segregations from rail production influence the reformation of Pearlite for fully and partially austenitized regions of the HAZ.

    • In non or partially austenitized regions of the HAZ tempering and coagulation effects of the Pearlite appear differently pronounced as a function of the thermal cycle(s) from welding. This varyingly lowers the hardness of the Pearlite.

  • Another important influencing aspect on the Pearlite formation, which however has not been studied in this work, is the initial deformation state and residual stresses in the rail.

6 Outlook

Based on the findings from this work, we have identified the following future steps required to improve the results of our simulation:

  • Identify and quantify the influence of the variable initial microstructure and implement this aspect to the metallurgical model for the hardness calculation.

  • Identify and implement the hardness influencing factor in order to reduce found inaccuracies of the currently used model for the hardness calculation.

  • Implement a metallurgical model for the WM and study its phase transformation behavior and hardness with special regards to the transition zone. As a prerequisite, a suitable filler wire would need to be identified and characterized first. As a result, the behavior of the entire joint can be studied.

  • Run the simulation for all the necessary layer to weld the entire cross section.