Quantifying Dynamic Signal Spread in Real-Time High-Energy X-ray Diffraction

Abstract

Measured intensity in high-energy monochromatic X-ray diffraction (HEXD) experiments provides information regarding the microstructure of the crystalline material under study. The location of intensity on an areal detector is determined by the lattice spacing and orientation of crystals so that changes in the heterogeneity of these quantities are reflected in the spreading of diffraction peaks over time. High temporal resolution of such dynamics can now be experimentally observed using technologies such as the mixed-mode pixel array detector (MM-PAD) which facilitates in situ dynamic HEXD experiments to study plasticity and its underlying mechanisms. In this paper, we define and demonstrate a feature computed directly from such diffraction time series data quantifying signal spread in a manner that is correlated with plastic deformation of the sample. A distinguishing characteristic of the analysis is the capability to describe the evolution from the distinct diffraction peaks of an undeformed alloy sample through to the non-uniform Debye–Scherrer rings developed upon significant plastic deformation. We build on our previous work modeling data using an overcomplete dictionary by treating temporal measurements jointly to improve signal spread recovery. We demonstrate our approach in simulations and on experimental HEXD measurements captured using the MM-PAD. Our method for characterizing the temporal evolution of signal spread is shown to provide an informative means of data analysis that adds to the capabilities of existing methods. Our work draws on ideas from convolutional sparse coding and requires solving a coupled convex optimization problem based on the alternating direction method of multipliers.

Introduction

High-Energy X-ray Diffraction

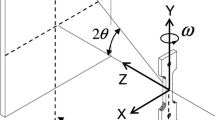
High-energy X-ray diffraction (HEXD) is an invaluable tool for studying the phenomena that underpin the macroscopic behaviors and properties of structural materials. Diffraction peaks produced by individual grains of a polycrystal can provide valuable information about the intermittent motion of dislocations that occurs when a metal plastically deforms [6, 14, 16, 17]. In the HEXD setting, a beam incident on a crystalline solid diffracts at an angle $2\theta$ determined by the lattice spacing and at an orientation $\eta$ determined by the crystal orientation as shown in Fig. 1. Rotation in $\omega$ can be used to change the set of crystals satisfying the diffraction condition in order to sample more of orientation space. Therefore changes in the heterogeneity of lattice spacing and misorientation can be captured by tracking the width of diffraction peaks in the Bragg angle coordinate $(2\theta$ or r) and orientation coordinates ($\eta$ and $\omega$), respectively [16].

Fig. 1

HEXD setup to capture entire Debye–Scherrer rings. The diffraction angle $2\theta$ is determined by the lattice spacing $d_{hkl}$ according to Bragg’s law $n\lambda = 2d_{hkl}\sin \theta$. The azimuthal diffraction angle $\eta$ is determined by the azimuthal orientation of underlying crystals. The sample can be rotated in $\omega$ to change which crystals satisfy the diffraction condition. Adapted from [6]

Fig. 2

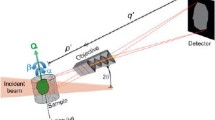
a MM-PAD experimental setup postioned to only capture partial Debye–Scherrer rings diffracting from the titanium sample. Adapted from [6] b Examples of partial Debye–Scherrer ring measurements captured by MM-PAD at $t = 0\text {s}, 25\text {s}$. c $\eta$ profile of {004} Debye–Scherrer ring obtained by summing in $2\theta$ (four pixel gap in the data is due to a four pixel gap in the detector). d First 25 s of the same {004} $\eta$ profile highlighting the evolution of peaks from a collection of discrete grains to a near-powder material. Red dotted line denotes 25s mark in both plots

Significance of Signal Spread

In a polycrystalline sample with relatively few lattice defects, an experiment may be designed to follow separable intensity peaks, resolving grain-averaged lattice orientation and strain [22]. As a material plastically deforms and its crystals become misoriented, the morphology of a diffracted intensity signal transitions from individual diffraction peaks to something resembling a uniform powder (as in the data of Fig. 2b). Under these conditions a peak center-of-mass becomes increasingly difficult to even define and thus decreasingly relevant. Nonetheless, the spreading of the signal in $\eta$ and $\omega$ still remains linked to the evolution of lattice defects in the material, regardless of whether the diffraction signal has distinct (but evolving) peaks associated with individual grains or represents the overlap of many grains having significant gradients in orientation. The goal of this paper is to define and demonstrate the utility of a meaningful feature capturing spread in a consistent manner across any morphological structure exhibited by the diffracted intensity of a deforming polycrystalline sample.

A complete picture of crystal reorientation would ideally be obtained by analyzing spread in two dimensions ($\eta$ and $\omega$), as shown in "Real-Time HEXD" section. Such analysis would build upon an experimental plan that provided $360^\circ$ coverage of $\omega$ with temporal resolution sufficient to resolve transients developed in the course of in situ loading. The challenges of such an experiment are significant, but realization of such studies is on course with present advances in detector technology and mechanical load frame design [24]. In this work, temporal resolution necessary to characterize the onset of plasticity during continuous loading is achieved by sampling a limited range of $\omega$, obtained by oscillating the sample about $\omega$. X-ray diffraction measurements are then integrated in both $2\theta$ and $\omega$ to produce a one-dimensional signal in $\eta$ over which to characterize the development of spread in time. Integrating in $2\theta$ additionally nullifies any effect potentially arising due to the finite bandwidth of the nominally monochromatic X-rays. We demonstrate—using experimental data—that the one-dimensional spread signal can be relativity insensitive to the details of $\omega$ integration providing useful insight into misorientation dynamics across time and between different modes of crystallographic slip. The present effort provides a foundation for (the more substantial effort) of integration in both $\eta$ and $\omega$, here envisioned as a prospective analysis technique to accompany developing experimental capability.

Motivation

Our work is motivated by the increasing availability of HEXD data sampled at rates on the order of 1kHz [11, 12, 21] which provide unprecedented opportunities for in situ experiments capable of resolving the detailed dynamics of plastic deformation. As a concrete example, we consider in "Real-Time HEXD" section data from an in situ experiment at the advanced photon source (APS) where a commercially pure Ti sample was deformed under tensile loading, followed by stress relaxation. The experiment was designed to observe the transients that occur during plastic deformation by taking HEXD data with the mixed-mode pixel array detector (MM-PAD) which allows for rapid, high dynamic range imaging of high-energy X-rays [21, 26]. The experimental setup of Fig. 2a [6] shows the arrangement of X-ray beam, sample, and MM-PAD placed to capture partial Bragg diffraction patterns. An initial pre-load was applied to the sample, and crystallographic orientations of grains within the diffraction volume were determined using the technique of high-energy diffraction microscopy [25], as detailed in [6]. Under displacement control, the sample is first deformed in tension with a nominal strain rate of $10^{-3}\;\mathrm{s}^{-1}$ and then held with fixed cross-head displacement. During the loading and subsequent stress relaxation, the sample was oscillated at 2 Hz about a rotation axis aligned with the loading direction. This rotation aids in maintaining the diffraction condition for distinct spots throughout the course of loading as images are collected with the MM-PAD. As plastic flow develops during tensile loading, the diffraction spots of discrete grains evolve into one another as shown in the raw data of Fig. 2b and one-dimensional $\eta$ profiles of Fig. 2c and d. Note that the partial Debye–Scherrer rings shown in Fig. 2b are developed by summing images collected over the sample rotation, to be detailed below. Further condensing the images into one-dimensional $\eta$ profiles of Fig. 2c and d, we track a data-derived indicator that serves to characterize the evolution of plasticity.

Previous Work

To address the challenges of this type of data, we build on our previous work [2] where ideas from compressed sensing [5, 9] were used to characterize the distribution of $\eta$ and $2\theta$ spread in samples under static loading. Of particular interest were materials that possessed mixed micro-structure characteristics at different locations in space. Previously, measurements were taken with minutes passing between each time step. The problem of interest in this work is to take advantage of the fast in situ measurements taken at a single location on the sample. The approach in [2] models each diffraction measurement as an independent sparse superposition of two-dimensional Gaussian peak functions in order to compute a signal spread feature. In practice, the spread feature is prone to “noise” as we do not account for the fact that the material state is, in a sense, correlated from one time point to the next (see Fig. 6a to see the “noisy” feature computed for real data).

Contributions

In this paper, diffraction images are modeled jointly in time to leverage temporal correlations and reduce variability in spread estimation. By treating the entire time series of diffraction images simultaneously, we find a cohesive global representation instead of many independent ones. Furthermore, we introduce a feature of peak spread that is computed over a region by averaging the widths of constituent peaks weighted by their amplitudes. In simulations with measurements taking the form of Gaussian peaks, we demonstrate that our recovered feature faithfully reproduces true peak width for simulated data with Poisson statistics.

Temporally coupling reconstructions using the MM-PAD measurements taken during the HEXD experiment described above improved the recovery of spreading dynamics and produced smooth distributions of peak function variances across time in which spurious variations due to detector noise and signal variation are effectively removed. As a result, we are able to show that the extent of the plasticity displayed in the azimuthal spreading of signal is consistent with the deformation modes of the titanium sample.

Despite our own experimental focus on HEXD, the method is general: it can be applied to any imaging technique involving intensity peak measurements and has the potential to be extended to two spatial dimensions at a computational cost. In reality any one-dimensional data could be processed using our temporal dictionary method in this manner to extract spread information or other features depending on the dictionary used. Furthermore, as the quantity of data captured in modern HEXD experiments exceeds researchers’ ability to analyze it, automated methods such as ours that can extract information from even the most unclean or challenging data are valuable in enabling next-generation analyses.

Paper Outline

As a preliminary, we will review the overcomplete dictionary model of [2] before presenting the proposed model that imposes smoothness on the dictionary representation as well as a one-dimensional spread feature. Simulated examples of measurements with Poisson statistics will then be used to demonstrate the behavior of the spread feature. Finally, our focus will shift to the dynamic MM-PAD experiment; the spread estimates extracted from the HEXD data let us relate the development of orientation heterogeneity in each lattice plane to the deformation modes of titanium. Detailed descriptions of algorithmic implementations will be included in Appendix A, and MATLAB code with data is available at https://github.com/dbanco/DynamicSignalSpread

Method

In the following section we will review the X-ray diffraction data model proposed in our previous work [2], describe a new model for temporal measurements, and introduce a feature for characterizing signal spread. The general approach is to model the X-ray diffraction data as a superposition of Gaussian peak functions drawn from a dictionary. The recovery algorithm selects a minimal number of entries from the dictionary to represent the signal where the elements of the dictionary as well as associated amplitudes are taken to evolve smoothly in time. Finally, the variances of the selected Gaussian peak functions are used to evaluate the degree of spread in the diffraction signal.

Problem Setup

We employ a model in which the X-ray detector signal is represented as a superposition of a small number of shifted Gaussians of varying widths. As we demonstrate in "Real-Time HEXD" section, the temporal evolution of the width parameters for the selected Gaussians provides insight into the evolution of lattice defects in the material sample itself. While the implemented model is discrete in time and space, we begin with a continuous formulation in an attempt to clearly connect the discrete model to the underlying sensor data. To that end, with $b(\eta ,t)$ being the diffraction signal from a given Debye–Scherrer ring (assuming we have integrated in $2\theta$ and $\omega$) at azimuth angle $\eta$ and time t, our model takes the form

$$\begin{aligned} b(\eta ,t)&= \int _{\underline{\sigma }}^{\overline{\sigma }} \int _{-\infty }^{\infty } \frac{1}{\sqrt{2\pi \sigma ^2}} \exp \left\{ -\frac{1}{2\sigma ^2}(\eta - \mu )^2 \right\} x(\eta ,\sigma ,t)d\mu d\sigma \\&= \int _{\underline{\sigma }}^{\overline{\sigma }} a_\sigma (\eta ) * x_{\sigma }(\eta ,t) d\sigma \end{aligned}$$

where $*$ denotes convolution in the $\eta$ variable, $a_\sigma (\eta ) = \frac{1}{\sqrt{2\pi \sigma ^2}}e^{-\frac{1}{2\sigma ^2}(\eta - \mu )^2}$ and $x_{\sigma }(\eta ,t)$ encodes “how much” of a Gaussian with parameters $\mu$ and $\sigma$ is contained in the diffraction signal at time t. The function $x_{\sigma }(\eta ,t)$ is constrained to be non-negative, $x_{\sigma }(\eta ,t) \ge 0$, as measured intensity signals are non-negative.

To obtain a discrete form of the model, we start by taking K equally spaced values for the Gaussian scale parameters: $\sigma _k = \underline{\sigma } + \frac{k-1}{K-1}(\overline{\sigma }-\underline{\sigma })$ for $k = 1, 2, \dots , K$. Using a Riemann approximation to the integral and absorbing the differential in $\sigma$ into $a_{\sigma _k}$ gives

$$\begin{aligned} b(\eta ,t) = \sum _{k=1}^K a_{\sigma _k}(\eta ) * x_{\sigma _k}(\eta ,t). \end{aligned}$$

(1)

To discretize in angle, we assume that the HEXD data are sampled N times between some minimum angle, $\underline{\eta }$, and maximum angle, $\overline{\eta }$. We define $\eta _n = \underline{\eta } + \frac{n-1}{N-1}(\overline{\eta }-\underline{\eta })$ for $n=1,2 \dots , N$ as the set of sampling points. Discretizing the convolution integral in (1) and collecting the samples in $\eta$ into column vectors, (1) becomes

$$\begin{aligned} \mathbf {b}(t) = \sum _{k=1}^K \mathbf {a}_{k} * \mathbf {x}_k(t) = \sum _{k=1}^K \mathbf {A}_k \mathbf {x}_k(t) = \mathbf {A}\mathbf {x}(t) \end{aligned}$$

(2)

where $\mathbf {a}_k$ and $\mathbf {x}_k(t)$ are column vectors holding discrete versions of their continuous counterparts, $a_{\sigma _k}(\eta )$ and $x_{\sigma _k}(\eta ,t)$, respectively. With some abuse of notation, $*$ denotes discrete circular convolution; $\mathbf {A}_k$ is the $N \times NK$ matrix implementing the operation “convolve with $\mathbf {a}_k$” and $\mathbf {A}= \left[ \mathbf {A}_1 \,|\, \mathbf {A}_2 \,|\, \cdots \,|\, \mathbf {A}_K \right]$. The matrix $\mathbf {A}$ can be viewed as an overcomplete dictionary containing K different entries located at every point in discrete $\eta$ space. In this case, each of the entries of the dictionary is a discrete Gaussian function with variance $\sigma ^2_k$ and corresponding dictionary block $\mathbf {A}_k$. Within each block, $\mathbf {A}_{n,m,k}$ denotes the entry on row n and column m of matrix $\mathbf {A}_k$ and is defined according to

$$\begin{aligned} \mathbf {A}_{n,m,k} = \frac{ \exp \left\{ -\frac{(\eta _n-\mu _m)^2}{2\sigma _k^2}\right\} }{\sqrt{\sum _{n=1}^N \exp \left\{ -\frac{(\eta _n-\mu _m)^2}{\sigma _k^2}\right\} }} \end{aligned}$$

(3)

where the normalization in the denominator assures that all columns of $\mathbf {A}$ have unit $l_2$-norm. Similarly $\mathbf {x}(t)$ is comprised of K blocks of N components a piece;

$$\begin{aligned} \mathbf {x}(t) = \begin{bmatrix} \mathbf {x}_1(t)&\mathbf {x}_2(t)&\hdots&\mathbf {x}_K(t) \end{bmatrix}^\top \end{aligned}$$

and we let $\mathbf {x}_{m,k}(t)$ denote the entry on row m of the column vector $\mathbf {x}_k(t)$. Thus, $\mathbf {x}_{m,k}(t)$ indicates the “amount” of the Gaussian centered at $\mu _m$ and of width $\sigma _k$ contributes to the HEXD data at time t. Figure 3 shows an example signal represented using a Gaussian peak dictionary, breaks down the representation according to peak width, and highlights $\mathbf {x}_{2}(t)$ values with delta functions. Assuming that data are acquired at times $t_1, t_2, \dots , t_T$, gathering all representations in time gives

$$\begin{aligned} \mathbf {X}= \begin{bmatrix} \mathbf {x}(t_1)&\mathbf {x}(t_2)&\hdots&\mathbf {x}(t_T) \end{bmatrix}^\top . \end{aligned}$$

Our goal is to recover the coefficients $\mathbf {X}$ and in turn a sparse superposition of Gaussian functions that represent a time series of diffraction signal measurements.

Boundary Handling

In the event that the data do not span a complete ring, discontinuities will be present at the boundaries as wrapping occurs between $\underline{\eta }$ and $\overline{\eta }$ during circular convolution. Extending the data at $\underline{\eta }$ and $\overline{\eta }$ assuming that the data are mirrored at the boundaries prevents discontinuities and any resulting artifacts. This symmetric extension approach for dealing with boundary artifacts is also used in [29]. To make this concrete, if

$$\begin{aligned} \mathbf {b}(t) = \begin{bmatrix} b_1(t)&b_2(t)&\hdots&b_N(t) \end{bmatrix}^\top , \end{aligned}$$

then the symmetric extension of $\mathbf {b}(t)$, $\hat{\mathbf {b}}(t)$, has elements

$$\begin{aligned} \hat{\mathbf {b}}(t) = \begin{bmatrix} b_\frac{N}{2}&\hdots&b_2(t)&b_1(t)&b_2(t)&\hdots&b_N(t)&b_{N-1}&\hdots&b_{\frac{N}{2}+1} \end{bmatrix}^\top , \end{aligned}$$

for even valued N. The boundaries are handled in this manner in "Real-Time HEXD" section where the measurements taken by the MM-PAD detector capture at most about a $4^\circ$ arc in $\eta$.

Fig. 3

Data $\mathbf {b}(t)$ are represented by a dictionary of peak functions $\mathbf {a}_1,\mathbf {a}_2,...,\mathbf {a}_{K}$. Representing $\mathbf {b}(t)$ as $\sum ^K_i \mathbf {a}_i * \mathbf {x}_i(t)$, the signal is decomposed into the components $\mathbf {a}_i * \mathbf {x}_i(t)$ to capture the contributions of Gaussian peak function of varying widths. Coefficient values $\mathbf {x}_2(t)$ are overlaid on the corresponding representation component; the weighted delta functions show each position where $\mathbf {a}_2$ contributes signal. The un-normalized variance distribution function (UVDF), defined as $\mathbf {q}(t)$ in (3), shows the sum of coefficient values for each dictionary entry $\mathbf {a}_i$ with variance $\sigma _i^2$ in this case highlighting the preponderance of structures with widths of $\sigma _1$, $\sigma _2$, and $\sigma _M$ in this particular signal

Variance Distribution Function

In preparation for defining our approach for recovering $\mathbf {X}$ and using this result to characterize the degree of diffraction signal spread, we define the following two quantities derived from $\mathbf {X}$:

$$\begin{aligned} \mathbf {q}(t) = \begin{bmatrix} \varvec{1}^T\mathbf {x}_1(t) \\ \varvec{1}^T\mathbf {x}_2(t) \\ \vdots \\ \varvec{1}^T\mathbf {x}_K(t) \end{bmatrix} = \mathbf {S}\mathbf {x}(t) \quad \text {and} \quad \mathbf {p}(t) = \frac{\mathbf {q}(t)}{\varvec{1}^T \mathbf {q}(t)} \end{aligned}$$

(4)

where $\varvec{1}$ is the vector of all ones and $\mathbf {S}$ is the matrix that implements this summing operation. The first vector $\mathbf {q}(t)$ can be interpreted as an un-normalized amplitude-weighted probability distribution function over the K different Gaussian functions in the representation $\mathbf {x}(t)$. Each entry in $\mathbf {q}(t)$ is obtained by summing spatially over the coefficients $\mathbf {x}_i(t)$ associated with dictionary entry $\mathbf {a}_i$. The second vector $\mathbf {p}(t)$ is then obtained by normalizing $\mathbf {q}(t)$ to sum to 1. The quantities $\mathbf {q}(t)$ and $\mathbf {p}(t)$ will be referred to as the un-normalized variance distribution function (UVDF) and variance distribution function (VDF). An example UVDF in Fig. 3 summarizes the scale components used to represent the data $\mathbf {b}(t)$. The UVDF is a reduced form of the original representation that solely tells how much of each scale component has been chosen. The degree of spread present in the diffraction signal should evolve smoothly; therefore, we would like to to enforce smoothness in the distribution of scale components (UVDF) in time. Intuitively, variations in peak width caused by noise will not persist in time, while the effects of real signal changes will be present across time steps. Ultimately, we will compute a scalar that measures the degree of signal spread (described in Sect. Signal Spread Feature). Smoothing the UVDF in time will reduce the variation we observe when modeling diffraction signals independently in time (as we will see in Fig. 6a).

Optimization Problem

The signal recovery problem is formulated as the constrained optimization

$$\begin{aligned} \hat{\mathbf {X}} = \mathop {\hbox {arg min}}\limits _{\mathbf {X}\ge 0} \sum _{i=1}^T \left[ \frac{\Vert \mathbf {b}(t_i) - \mathbf {A}\mathbf {x}(t_i)\Vert _2^2}{\Vert \mathbf {b}(t_i) \Vert _2^2} + \lambda (t_i)\Vert \mathbf {x}(t_i)\Vert _1 \right] + \gamma \varOmega (\mathbf {X}) \end{aligned}$$

(5)

where $\mathbf {X}\ge 0$ means each element of the matrix $\mathbf {X}$ should be non-negative. The objective function contains three terms: the first is a data fidelity term, the second is a sparsity term, and the third is a temporal coupling term designated by $\varOmega (\mathbf {X})$ and with parameter $\gamma$ that specifies the magnitude of the regularization. The first two terms form the approach originally proposed in [2]. Combining a squared error term with a $\lambda$-weighted $l_1$-norm penalty encourages the use of a minimal number of peak functions. The expression $\Vert \mathbf {v}\Vert _1$ is the $l_1$-norm of the vector $\mathbf {v}$, that is, the sum of the absolute values of the elements of the vector. Given our choice of peak function dictionary, parsimonious representations resulting from sparsity are those utilizing the broadest possible peaks from the dictionary. Ultimately, decomposing diffraction intensity into a sparse superposition of dictionary entries encodes information about signal spread. The time-dependent $\lambda (t_k)$ parameter manages the trade-off between data fidelity and sparsity. As the data evolve, so too does the signal-to-noise ratio, thus $\lambda (t_i)$ must be chosen at each time step $t_i$. Similarly, the data fidelity term is normalized to account for signal magnitude variations that could lead to biased solutions once temporal coupling is introduced. Recalling (3), one choice for temporal coupling term $\varOmega$ is

$$\begin{aligned} \varOmega (\mathbf {X}) = \sum _{i=1}^{T-1} \Vert \mathbf {p}(t_{i+1}) - \mathbf {p}(t_i) \Vert _1. \end{aligned}$$

(6)

The expression is desirable because it is a meaningful metric between probability mass functions: the total variation distance [19]. By penalizing VDF differences in time, we seek to mitigate the sporadic change in representations caused by signal noise while capturing signal changes that persist in time. To avoid complications of non-convexity in the optimization function introduced by the presence of $\mathbf {x}(t)$ in the denominator of $\mathbf {p}(t)$, we replace $\mathbf {p}(t)$ in (5) with its un-normalized counterpart to arrive at

$$\begin{aligned} \varOmega (\mathbf {X}) = \sum _{i=1}^{T-1} \Vert \mathbf {q}(t_{i+1}) - \mathbf {q}(t_i) \Vert _1 \end{aligned}$$

(7)

where we emphasize that (3) indicates that $\mathbf {q}(t)$ is a linear function of the components of $\mathbf {X}$.

The parameters $\lambda (t)$ and $\gamma$ are selected by constructing L-curves [27] and finding values that balance the sparsity or UVDF total variation with reconstruction fidelity. More details are provided in Appendix B. The data fidelity term is normalized by $||\mathbf{b}_t||_2$ and a separate sparsity parameter $\lambda (t_i)$ is used at each time step to address imbalance in the error and sparsity terms that can occur due to changes in the magnitude of the overall signal in time. An alternating direction method of multipliers (ADMM) algorithm is used to solve the optimization problem with the details provided in Appendix A. Once a Gaussian peak representation has been computed, the coefficients $\mathbf {X}$ are used to compute a scalar feature that quantifies the spreading of signal.

Signal Spread Feature

Upon recovering a sparse representation, we can take advantage of the known variances of the constituent Gaussian peaks to compute a spread feature. Each dictionary entry contributes a value proportional to its standard deviation $\sigma _k$ and weighted by corresponding coefficients $\mathbf {x}_k$. Hence, we refer to this spread feature as the amplitude-weighted mean variance (AWMV) and compute it as

$$\begin{aligned} \text {AWMV}(t)= \sum ^K_{k=1}\frac{\mathbf{1}^\top \mathbf {x}_k(t) \sigma _k}{\mathbf{1}^\top \mathbf {x}(t)} = \sum ^K_{k=1} \mathbf {p}_k(t) \sigma _k. \end{aligned}$$

(8)

Most of the summands in the above expression are zero because of the sparsity enforced on each $\mathbf {x}(t)$. Additionally, the AWMV can be viewed as the expectation of the VDF $\mathbf {p}(t)$ as in (7). As a result, smoothing the UVDF in time has the effect of indirectly smoothing the AWMV in time. The degree of signal spread as indicated by the AWMV has some dependence on experimental design choices, such as the extent to which we integrate in $\omega$, and thus does not provide a quantitative estimate of a physical, material property of the sample. Rather, the AWMV provides a feature that is easily computable directly from the data and, in the case of HEXD, is reflective of meaningful processes within a material sample. In the present setting, the process of interest is the onset and evolution of plasticity and association with particular crystallographic slip modes. However, as we demonstrate in "Robustness to $\omega$ Sweep Length" section, the AWMV exhibits some robustness to sweep length in this experimental data. Regardless of the structure of signal in a Debye–Scherrer ring, the one-dimensional intensity signal will be represented parsimoniously by Gaussian peak functions. Even if the detector pixels themselves do not appear to be sparse, a sparse representation can be ascertained regardless. More specifically, even in the case of a more full Debye–Scherrer, $\mathbf {x}(t)$ will still remain sparse as the dictionary is highly over-complete. Moreover, the degree of sparsity will be accommodated by our algorithm through the selection of the $\lambda (t_i)$ and $\gamma$ parameters. In the case when peaks are truly Gaussian and non-overlapping, we will show that this model recovers the true AWMV in Sect. Simulations. Section Simulations. In order to recover an accurate AWMV, the dictionary needs to be defined following a few guidelines that will be laid out in the following section. Afterward, we will demonstrate the advantage of modeling measurements jointly in time in Sects. Simulations and Real-Time HEXD. It is noteworthy that these considerations imply the capability of the AWMV to span the distinct peaks associated with a “rotating crystal” experiment to the (non-uniform) rings found in a polycrystalline powder-like diffraction—a capability that will be leveraged in the present work.

Dictionary Construction

The dictionary of Gaussian peak functions needs to be appropriately constructed in order for the AWMV to capture meaningful signal spread information. Given that each dictionary entry is defined according to (3), there are three parameters to be chosen: a minimum standard deviation $\underline{\sigma }$, maximum standard deviation $\overline{\sigma }$, and number of different variances K. To ensure that the smallest entry is just larger than a single point, we choose the minimum standard deviation for the dictionary to be half the distance between detector pixels

$$\begin{aligned} \underline{\sigma } \ge \eta _i-\eta _{i-1}. \end{aligned}$$

The maximum standard deviation is chosen so that the higher intensity values of the peak remain within the domain of the data

$$\begin{aligned} \overline{\sigma } \le \frac{1}{6} \overline{\eta }. \end{aligned}$$

In our HEXD measurements, the detector only captures a small arc of the diffraction data and the signal spreads out significantly almost becoming a powder. Therefore, choosing $\overline{\sigma } = \frac{1}{6} \overline{\eta }$ is appropriate, but when the signal is not expected to broaden significantly, a smaller $\overline{\sigma }$ can be chosen to gain resolution in the dictionary entries. Finally, the number of dictionary entries should be chosen to be the largest number that keeps the problem computationally practical. For the data presented in Sect. Real-Time HEXD, sufficient peak width resolution is achieved with $K = 20$.

Simulations

To develop an understanding of the performance of our approach, in this section we consider the recovery of the AWMV for a pair of model problems for which ground truth is known. We demonstrate success in tracking smoothly broadening peak functions and in detecting anomalous broadening events. In HEXD, it is important that the algorithm is able to detect anomalies so as to be able to identify events taking place during the deforming of a sample such as during the elasto-plastic transition. Both simulations employ a signal in the form of a single, temporally evolving one-dimensional Gaussian peak which is used to generate Poisson distributed data. We emphasize that the model is not aware the data contain only a single Gaussian and a Gaussian of the same variance is not present in the dictionary. As the AWMV is computed as a convex combination of dictionary entry standard deviations, the AWMV is expected to recover the standard deviation of these Gaussian peaks. Therefore, the true AWMV is the standard deviation of the Gaussian peak, $\text {AWMV}(t) = \sigma (t)$. In the following section, we show that leveraging temporal information improves recovery, specifically for Poisson distributed data.

Generating Simulated Data

The simulated data are modeled as time-varying Gaussian functions with Poisson statistics defined by

$$\begin{aligned} \mathbf {b}(t_i) = \text {Poisson}(\alpha \mathbf {g}(t_i)),\quad i=1,2,...,T \end{aligned}$$

(9)

where $\text {Poisson}({\varvec{\lambda }})$ generates a vector of N independent Poisson random variables, $\alpha$ is a scaling factor, and $\mathbf {g}(t_i) \in \mathbb {R}^N$ is a Gaussian function at time $t_i$. Examples of the Gaussian peak simulations can be seen in Fig. 4a and 5a. The Gaussian functions are defined by

$$\begin{aligned} \mathbf {g}(t_i) = \begin{bmatrix} g(\eta _1,t_i) \\ \vdots \\ g(\eta _N,t_i) \end{bmatrix} \end{aligned}$$

(10)

where

$$\begin{aligned} g(\eta _j,t_i) = \exp {\left\{ -\eta _j^2/2\sigma ^2(t_i)\right\} } \end{aligned}$$

for $N=101$ equally spaced samples $\eta _j$ between $\pm 50^\circ$. The scaling factor $\alpha$ serves to vary the average and thus determine the signal-to-noise ratio (SNR) of the simulations such that SNR increases with $\alpha$. We define the SNR for the simulated measurement $\mathbf {b}(t_i)$ to be

$$\begin{aligned} \text {SNR} = \frac{||\mathbf {g}(t_i)||_2}{||A(t_i)\mathbf {b}(t_i) - \mathbf {g}(t_i)||_2} \end{aligned}$$

(11)

With this scheme, we produce two time series described in Table 1: the first with a linearly increasing AWMV and the second with a step function AWMV.

Table 1 Parameters defining each simulated dataset

Fig. 4

Linearly broadening peak under Poisson statistics. a Generated data are shown alongside the recovered signal identified using the VDF smoothed model. b The relative mean squared error between the AWMV and standard deviation of the Gaussian peak is plotted as a function of the SNR. c The standard deviation of the Gaussian peak (black), AWMV computed with $\gamma =0$ (blue), and AWMV computed with $\gamma =\gamma ^*$ (red) are all plotted as a function of time for each SNR

Fig. 5

Step broadening peak under Poisson statistics. a Generated data are shown alongside the recovered signal identified using the VDF smoothed model. b The relative mean squared error between the AWMV and standard deviation of the Gaussian peak is plotted as a function of the SNR. c The standard deviation of the Gaussian peak (black), AWMV computed with $\gamma =0$ (blue), and AWMV computed with $\gamma =\gamma ^*$ (red) are all plotted as a function of time for each SNR

The first data sequence contains a Gaussian peak with standard deviation that increases linearly in time. This example was chosen to explore the utility of the temporal regularization term in (2) when the AWMV of the signal in question evolves smoothly. The second data sequence contains a Gaussian peak with standard deviation that follows a step function in time. That is, the width of the Gaussian peak is piece-wise constant with a single jump. At lower SNRs, the sudden broadening is not evident from looking at the data. We demonstrate that the AWMV step is more identifiable and does not become smoothed out in time with the addition of temporal regularization.

Recovery experiments were conducted with the following SNRs

$$\begin{aligned} \text {SNR} = [10, 5, 2.5, 2, 1.75, 1.5, 1.25, 1.1] \end{aligned}$$

(12)

obtained by choosing the scaling factors

$$\begin{aligned} {\varvec{\alpha }} = [136.55, 33.35, 8.34, 5.44, 4.07, 3.08, 2.08, 1.63]. \end{aligned}$$

(13)

Furthermore, we report the average results for 100 different random instances of the noisy data. In all cases, the dictionary $\mathbf {A}$ was constructed according to (3) with K = 20 different entries with parameters

$$\begin{aligned} \sigma _i = \frac{49}{38}(i-1) + \frac{1}{2} \text { for } i=1,2,...K. \end{aligned}$$

(14)

With a dictionary defined we can apply the approach described in Sect. 2. Initially, the optimization problem (4) is solved for a single instance, and then those same selected parameters are used across 100 random instances.

Results and Discussion

The resulting reconstructions of the data are displayed for three SNRs on the right of Figs. 4a, 5a. We evaluate recovery by computing the relative squared error (RSE),

$$\begin{aligned} \text {RSE} = \frac{||\mathbf{\sigma }(t)-\text {AWMV}(t)||_2}{||\mathbf{\sigma }(t)||_2}, \end{aligned}$$

(15)

of AWMV estimates; the average RSE for 100 trials is plotted in Figs. 4b, 5b. For a single instance, the AWMV is computed from each of the representations according to (7) to arrive at the AWMV curves shown in Figs. 4c, 5. Regardless of temporal regularization, the true AWMV can be recovered with RSE of 0.05 or less beyond an SNR of 10. Naturally, as the count values are scaled down, the AWMV is recovered with increased RSE on average. However, enforcing temporal smoothness reduces the RSE, especially in lower SNR cases. Recovery improvements are present in both simulations with the step function simulation of Fig. 5 seeing a reduced RSE by as much as half with temporal regularization. From the simulation with linearly increasing AWMV, we demonstrate the ability of our algorithm to identify a smoothly broadening signal in noise. From the simulation with step function AWMV, we show that by globally modeling in time our model can more readily detect sudden anomalous broadening.

Real-Time HEXD

Experiment

The goal of the experiment is to study the behavior of a commercially pure titanium sample deformed in uniaxial tension through the elasto-plastic transition and subsequent stress relaxation (under fixed cross-head displacement). From the in situ HEXD measurements, we apply our algorithm to extract signal spread information in order to study the plasticity behavior of the sample. In the titanium sample, prism slip and tensile twinning are expected to be the dominant deformation modes.

A total of 146 frames are captured per cycle over a sample rotation of $\pm 2.5^\circ$. For each half cycle, we sum over 73 frames (covering the full $5^\circ$ arc) giving a sampling rate of 4Hz. Additionally, the measurements are summed radially in the $2\theta$ coordinate to produce a diffraction signal profile that varies only in the azimuthal $\eta$ coordinate. The experimental setup and summed measurements are previously shown in Fig. 2. In Fig. 2a, the detector centered at $14.6^\circ$ is visible.

The Debye–Scherrer rings corresponding to four distinct lattice planes are present in the MM-PAD measurements; {004},{021},{112},{020}. We apply our algorithm to each one. The resolved shear stress experienced in each of the lattice planes due to prism slip and tensile twinning is expected to be distinct. That is, the stress undergone by the sample can be expected to manifest differently in each of the Debye–Scherrer rings of the sample’s lattice planes. The azimuthal domain slightly differs for each of the four Debye–Scherrer rings and is shown in Table 2.

Table 2 Domain parameters of each Debye–Scherrer ring captured by the MM-PAD during experiments

Processing

In order to avoid boundary effects, the intensity profiles are symmetrically extended by mirroring at the boundaries as described in Sect. 2.2. This way we can guarantee the signal to be continuous across the edges of the domain. As a result, the domain is doubled from about $4^\circ$ to $8^\circ$. The Gaussian peak dictionary $\mathbf {A}$ was constructed according to (3) with $K = 20$ different entries with parameters given by

$$\begin{aligned} \sigma _i = \frac{100\varDelta \eta - \frac{\varDelta \eta }{2}}{K-1}(i-1) + \frac{\varDelta \eta }{2} \text { for } i=1,2,...K \end{aligned}$$

(16)

so that the widths increase linearly from $\sigma _1 = \frac{\varDelta \eta }{2}$ to $\sigma _K = 100\varDelta \eta$. Solving the optimization problem of (4) renders an AWMV in the azimuthal $\eta$ coordinate for each time step (Fig. 6b).

In addition to spread, we extract the strain by tracking the radial shift in each of the Debye–Scherrer rings. The radial position of the signal in $2\theta$ is computed by locating the center of mass of the measured intensity signal. The radial shift is the change in this angle $\varDelta \theta$ and, given an initial diffraction angle $\theta _0$, then

$$\begin{aligned} \varDelta \text {Strain} = -\cot {(\theta _0)}\varDelta \theta . \end{aligned}$$

From the plot of strain in Fig. 6c, we can observe the direct dependence of strain on the stress curve associated with loading.

Fig. 6

Results computed from MMPAD measurements of commercially pure titanium under uniaxial tension. a $\varDelta$AWMV plotted for $\gamma = 0$ (independent in time) and $\gamma = \gamma ^*$ (coupling reconstructions in time) for each of the four Debye–Scherrer rings to make evident the benefit of temporal modeling. Variations in the independent solutions are reduced. b $\varDelta$AWMV plotted for $\gamma = \gamma ^*$ for each of the four Debye–Scherrer rings alongside the stress curve associated with the loading of the sample. Different events can be observed in each of the four rings as well as co-occurrence between the stress curve reaching the plastic regime and the development of AWMV. c The average lattice strain computed based on the radial shift of the portion of the individual Debye–Scherrer rings visible to the MMPAD. The strain matches the behavior of the stress curve as one would expect. d $\varDelta$AWMV plotted against the average lattice strain for each of the four Debye–Scherrer rings

Results and Discussion

As crystal orientation determines the azimuthal position of intensity signal, changes in the AWMV are indicative of changes in orientation heterogeneity. Figure 6a shows the change in AWMV, $\varDelta \text {AWMV}(t) = \text {AWMV}(t)-\text {AWMV}(t=0)$, for each Debye–Scherrer ring with/without temporal smoothing $(\gamma = \gamma * /\gamma = 0)$. The reduced variation in the AWMV signal is evident. The solutions resulting from the full temporal model $(\gamma = \gamma *)$ of Fig. 6b are more amenable to analysis.

In Fig. 6b, the stress signal provides indication of yield at $\sim \! 8$ s, followed by work hardening during continued cross-head displacement to $\sim \! 42$ s, then stress relaxation under fixed cross-head displacement. For all reflections, there are numerous transients in the measured $\varDelta \text {AWMV}$ over the course of yield and work hardening. Recent work by [28] draws an association between azimuthal spread of diffraction spots and (Taylor) work hardening in a commercial purity Ti (similar to that used in the present work). $\varDelta \text {AWMV}$ provides a similar, but more global, measure. Clearly, there is a trend of increasing $\varDelta \text {AWMV}$ developed during the work hardening prior to stress relaxation. These authors also noted the presence of (lattice) strain softening in some grains. The negative transients in $\varDelta \text {AWMV}$ for the $\{021\}$ and $\{112\}$ reflections support the notion of work softening through decrease of lattice misorientation—assuming the connection between azimuthal spread of peaks and work hardening taken in [28].

An average lattice strain associated with each reflection was computed based on radial displacement of the associated Debye–Scherrer ring (Fig. 6c). It should be noted that the diffraction vector is tilted from the loading direction by $\sim 15^\circ$. Also, this lattice strain is taken relative to that developed during the initial preloading of the sample. Still, this lattice strain computed on the basis of radial shift provides indication of the degree of tensile loading. Turning to the plot of $\varDelta \text {AWMV}$ vs. lattice strain, Fig. 6d, the strain initially increases with little development of $\varDelta \text {AWMV}$; the deformation is dominantly elastic. This is followed by a rapid evolution of $\varDelta \text {AWMV}$ during tensile deformation. Stress relaxation is associated with the decrease in lattice strain during relatively quiescent $\varDelta \text {AWMV}$ as relaxation proceeds.

Table 3 Resolved shear stress from finite element simulation

To draw a connection between the evolution of $\varDelta \text {AWMV}$ and slip modes in Ti, a finite element simulation was carried out to predict resolved shear stress as described in Appendix C. This resolved shear stress was computed for grains that would satisfy the diffraction condition for measurement with the MMPAD and is given in Table 3. Several observations can be made on the basis of the predicted resolved shear stress.

• The elasto-plastic transition is sharpest and occurs at the smallest lattice strain for the {020} reflection (Fig. 6d). Grains associated with this {020} reflection are well oriented for prism slip—the favored slip mode in this alloy.

• As stress relaxation develops, the magnitude of $\varDelta \text {AWMV}$ follows the ordering of predicted resolved shear stress for basal slip, as given in Table 3.

• Results for the {112} reflection show the greatest $\varDelta \text {AWMV}$ and lattice strain. This is consistent with increased evolution of geometric dislocation density with basal slip relative to prism slip [10]. Grains associated with this Debye–Scherrer ring are well oriented for basal slip, as compared to slip associated with other reflections.

As shown in Fig. 6d, upon yield and early in the rapid evolution of $\varDelta \text {AWMV}$, there are decreases in lattice strain for the {004} and {021} reflections. These decreases are accompanied by an inflection in the stress curve after yield. For all reflections, $\varDelta \text {AWMV}$ is increasing rapidly through the duration of this initial ‘flattening’ of the stress curve. This suggests that softening indicated by lattice strain decrease is associated with something other than the development of lattice misorientation. A similar initial softening transient was observed by Pagan et al. [18] in Ti-7Al.

Robustness to $\omega$ Sweep Length

Our discussion of the results relies on the assumption that the measurements observed at this angular interval will be representative of measurements taken at the other angular intervals as well. In order to demonstrate that the same analysis could be done even with smaller intervals than $\varDelta \omega = 5^\circ$, identical processing is done with MMPAD measurements over rotations of $4^\circ$, $3^\circ$, and $2^\circ$. Each of these windows in $\omega$ is centered in $\eta$ (at $14.6^\circ$) on the detector. Figure 7 shows the $\varDelta$AWMV curves obtained can be used to draw the same conclusions as the original results of Fig. 6b. It remains true in all cases that the elasto-plastic transition is sharpest and occurs at the smallest lattice strain for the {020} reflection. The negative transients that can be observed in the AWMV curves of the {021} and {112} at $\varDelta \omega = 5^\circ$ can also be seen at each other $\varDelta \omega$. The observation that there is a trend of increasing $\varDelta \text {AWMV}$ developed during the work hardening prior to stress relaxation also still holds for all cases. As our observations hold across these different $\omega$ sweep sizes and the AWMV curves maintain a strong resemblance across $\omega$ sweep lengths, we can conclude that the AWMV exhibits a fair degree of insensitivity to $\omega$ sweep length. The similarity of the $\varDelta$AWMV curves across $\omega$ sweep sizes can be seen in Fig. 8. While the curves do bear resemblance, once cause for the discrepancies present is the greater amount of signal observed as the $\omega$ sweep is increased. A smaller $\omega$ sweep means that more signal is likely to enter and exit the diffraction condition as the sample experiences bulk reorientation during loading.

Fig. 7

$\varDelta$AWMV computed from data integrated over $5^\circ$, $4^\circ$, $3^\circ$, and $2^\circ$ for each of the four Debye–Scherrer rings. Comparing to the $5^\circ$ case, reducing the $\omega$ sweep maintains similar AWMV curves

Fig. 8

$\varDelta$AWMV computed from data integrated over $5^\circ$, $4^\circ$, $3^\circ$, and $2^\circ$ for each of the four Debye–Scherrer rings. A high degree of similarity can be observed for all four rings as the $\omega$ sweep is reduced

Conclusion

Our approach for evaluating signal spread provides a highly general analysis tool that provides a meaningful feature regardless of the signal structure. Our global modeling succeeds in filtering out temporal variations while still picking up on local effects. In the context of HEXD, in situ experimentation offers the ability to capture events occurring at small timescales and modeling full time series enables the detection of transients in the signal spread caused by heterogeneous crystal misorientation.

Simulations verified that treating temporal data globally improves spread recovery increasingly at lower SNRs. In particular, we demonstrated improved AWMV estimation for a linearly broadening signal and a signal experiencing an anomalous broadening event. More importantly, we made use of our model to study signal spread in real data.

From experimental HEXD data, we extracted signal spread to study the development of orientation heterogeneity and subsequently draw connections to the slip modes of our Ti sample. The behavior of the $\Delta {\text{AWMV}}$ showed alignment with the resolved shear stress predicted in a finite element simulation. Our findings corroborate the possibility of observing work softening in some grains as observed in [28]. By applying our method directly to these data without any kind of supervision, we were immediately able to draw meaningful insights that complement existing HEXD analysis methods. As our algorithm is completely agnostic to the nature of the data itself, it could easily be used to the same effect in other domains.

There are two general directions for future work. The first avenue pertains to the adaptability of the algorithm itself. Currently, our dictionary model is limited in that it may only contain Gaussian peak functions and those entries are fixed. A Gaussian peak is not the optimal choice in every circumstance. It is typical in the literature for a convolutional dictionary to be learned from example data. In this problem, our fixed multi-width Gaussian dictionary could be replaced by a more general learned multi-scale dictionary. Doing so would remove the need to define a dictionary. The learned entries of the dictionary themselves also have the potential to provide additional insights. Dictionary entries could be allowed to take on asymmetric peak functions with more than one parameter. A parameterization representative of underlying physics could even be incorporated into entries. Beyond the dictionary itself, the regularization parameters $\lambda (t)$ and $\gamma$ can also be learned. Many simulated examples could be generated to train a model that would learn to choose the optimal parameters given an input signal. This would remove the need to estimate the SNR, conduct a grid search, and choose a parameter from the L-curve.

The second avenue for future work is to further explore applications and different experimental setups that can take advantage of this temporal modeling. Augmenting procedures for evaluation of lattice strain at the scale of individual grains [25] with the characterization advanced in the present work might reveal interesting spatio-temporal correlations. A comparison of the temporal plasticity behavior observed as in this paper for multiple identical samples under identical loading might provide insight about the dynamics of the material undergoing plasticity. Such experiments will also benefit from the latest version of the MM-PAD with 10 KhZ frame rate described in a recent submission [8]. A higher frame rate will offer greater opportunity to observe quick sporadic events during plastic deformation using our approach and/or provide for more complete coverage of $\omega$ and extension of the present analysis to the 2-D setting of $(\eta ,\omega )$ space over time.. Fast detection in combination with our general processing technique gives the ability to find correlations in high-dimensional data. In the context of HEXD, it would be fruitful to verify the connection between the spreading of particular diffraction spots in particular Debye–Scherrer rings to the activation of underlying slip systems as is done in [15]. A finite element and virtual diffractometer modeling simulation should be able to replicate the spreading of diffraction spots as captured by the AWMV; model validation would be facilitated through direct comparison of simulated and measured AWMV.

Appendices

Appendix A: ADMM Algorithm

The optimization problem resulting from the sparse dictionary model with total variation regularization on the UVDFs in time is

$$\begin{aligned} \hat{\mathbf {X}} = \mathop {\hbox {arg min}}\limits _{\mathbf {X}\ge 0} \sum _{i=1}^T \left[ \frac{\Vert \mathbf {b}(t_i) - \mathbf {A}\mathbf {x}(t_i)\Vert _2^2}{\Vert \mathbf {b}(t_i) \Vert _2^2} + \lambda (t_i)\Vert \mathbf {x}(t_i)\Vert _1 \right] + \gamma \sum _{i=1}^{T-1} \Vert \mathbf{q}(t_{i+1}) - \mathbf{q}(t_i) \Vert _1 \end{aligned}$$

(17)

Following the ADMM formulation allows us to optimize the two non-differentiable $l_1$-norm terms. The first step in reformulating (16) is to introduce $\mathbf {y}_1(t_i),\mathbf {y}_2(t_i)$ to split up objective terms and yield the following constrained optimization problem

$$\begin{aligned}&\mathop {\hbox {arg min}}\limits _{\mathbf {X},\mathbf {Y}_1 \ge 0,\mathbf {Y}_2} \sum _{i=1}^T \left[ \frac{\Vert \mathbf {b}(t_i) - \mathbf {A}\mathbf {x}(t_i)\Vert _2^2}{\Vert \mathbf {b}(t_i) \Vert _2^2} + \lambda (t_i)\left| \left| \mathbf {y}_1(t_i) \right| \right| _1 \right] + \gamma \sum _{i=1}^{T-1} \left| \left| \mathbf {y}_2(t_i) \right| \right| _1\\&\quad \text {subject to } \begin{array}{l} \mathbf {y}_1(t_i) = \mathbf {x}(t_i) \\ \mathbf {y}_2(t_i) = \mathbf {q}(t_{i+1}) - \mathbf {q}(t_i) \end{array} \end{aligned}$$

where

$$\begin{aligned} \mathbf {Y}_1= & {} \begin{bmatrix} \mathbf {y}_1(t_1)&\mathbf {y}_1(t_2)&\hdots&\mathbf {y}_1(t_T) \end{bmatrix}^\top \\ \mathbf {Y}_2= & {} \begin{bmatrix} \mathbf {y}_2(t_1)&\mathbf {y}_2(t_2)&\hdots&\mathbf {y}_2(t_T) \end{bmatrix}^\top . \end{aligned}$$

The job of finding solutions that acknowledge the sparsity and temporal smoothness constraints is relegated to $\mathbf {Y}_1$ and $\mathbf {Y}_2$, respectively. These constraints are then passed on to $\mathbf {X}$ by forcing $\mathbf {X}$ to match $\mathbf {Y}_1$ and $\mathbf {Y}_2$—something easier to accomplish than optimize the original problem. The new constraints are incorporated into the objective via the method of Lagrange multipliers. Additionally augmented Lagrangian terms are added to the objective to increase robustness without altering the solution. These two changes lead to the following unconstrained optimization problem

$$\begin{aligned} \mathcal {L}(\mathbf {X},\mathbf {Y}_1,\mathbf {Y}_2,\mathbf {U}_1,\mathbf {U}_2) =&\sum _{i=1}^T \left[ \frac{\Vert \mathbf {b}(t_i) - \mathbf {A}\mathbf {x}(t_i)\Vert _2^2}{\Vert \mathbf {b}(t_i) \Vert _2^2} + \lambda (t_i)\left| \left| { \mathbf{y}}_1(t_i) \right| \right| _1 \right] + \\&\gamma \sum _{i=1}^{T-1} \left| \left| { \mathbf{y}}_2(t_i) \right| \right| _1 + \\&\sum _{i=1}^T \mathbf {v}_1(t_i)^\top \left[ \mathbf {x}(t_i) - \mathbf {y}_1(t_i) \right] + \\&\sum _{i=1}^T \frac{\rho _1}{2} \left| \left| \mathbf {x}(t_i) - \mathbf {y}_1(t_i) \right| \right| _2^2 \\&+ \sum _{i=1}^{T-1} \mathbf {v}_2(t_i)^\top \left[ \mathbf {q}(t_{i+1}) - \mathbf {q}(t_i) - \mathbf {y}_2(t_i) \right] \\&+ \sum _{i=1}^{T-1} \frac{\rho _2}{2} \left| \left| \mathbf {q}(t_{i+1}) - \mathbf {q}(t_i) - \mathbf {y}_2(t_i) \right| \right| _2^2. \end{aligned}$$

The two new pairs of terms can be consolidated by scaling the dual variables $\mathbf {u}_1(t_i) = (1/\rho _1)\mathbf {v}_1(t_i)$ and $\mathbf {u}_2(t_i) = (1/\rho _2)\mathbf {v}_2(t_i)$ (as in Chapter 3.4 of [4]) to render a more convenient form. If we let $\mathbf {r}_1(t_i) = \left[ \mathbf {x}(t_i) - \mathbf {y}_1(t_i)\right]$ and $\mathbf {r}_2(t_i) = \left[ \mathbf {q}(t_{i+1}) - \mathbf {q}(t_i) - \mathbf {y}_2(t_i) \right]$, then we can rewrite

$$\begin{aligned} \sum _{i=1}^T \mathbf {v}_1(t_i)^\top \mathbf {r}_1 + \frac{\rho _1}{2} \left| \left| \mathbf {r}_1(t_i) \right| \right| _2^2&= \sum _{i=1}^T \rho _1 \mathbf {u}_1(t_i)^\top \mathbf {r}_1(t_i) + \frac{\rho _1}{2} \left| \left| \mathbf {r}_1(t_i) \right| \right| _2^2 \\&= \sum _{i=1}^T \frac{\rho _1}{2} \left| \left| \mathbf {r}_1(t_i) + \mathbf {u}_1(t_i) \right| \right| _2^2 - \frac{\rho _1}{2}\left| \left| \mathbf {u}_1(t_i)\right| \right| _2^2 \end{aligned}$$

and

$$\begin{aligned} \sum _{i=1}^{T-1} \mathbf {v}_2(t_i)^\top \mathbf {r}_2(t_i) + \frac{\rho _2}{2} \left| \left| \mathbf {r}_2(t_i) \right| \right| _2^2&= \sum _{i=1}^{T-1} \rho _2 \mathbf {u}_2(t_i)^\top \mathbf {r}_2(t_i) + \frac{\rho _1}{2} \left| \left| \mathbf {r}_2(t_i) \right| \right| _2^2 \\&= \sum _{i=1}^{T-1} \frac{\rho _2}{2} \left| \left| \mathbf {r}_2(t_i) + \mathbf {u}_2(t_i) \right| \right| _2^2 - \frac{\rho _2}{2}\left| \left| \mathbf {u}_2(t_i)\right| \right| _2^2 \end{aligned}$$

and we are left with shorter expressions as the $\frac{\rho _1}{2}\left| \left| \mathbf {u}_1(t_i)\right| \right| _2^2$ and $\frac{\rho _2}{2}\left| \left| \mathbf {u}_2(t_i)\right| \right| _2^2$ terms do not depend on $\mathbf {X},\mathbf {Y}_1,\mathbf {Y}_2$. The scaled form of the objective function is

$$\begin{aligned} \mathcal {L}(\mathbf {X},\mathbf {Y}_1,\mathbf {Y}_2,\mathbf {U}_1,\mathbf {U}_2) =&\sum _{i=1}^T \left[ \frac{\Vert \mathbf {b}(t_i) - \mathbf {A}\mathbf {x}(t_i)\Vert _2^2}{\Vert \mathbf {b}(t_i) \Vert _2^2} + \lambda (t_i)\left| \left| { \mathbf{y}}_1(t_i) \right| \right| _1 \right] + \\&\gamma \sum _{i=1}^{T-1} \left| \left| { \mathbf{y}}_2(t_i) \right| \right| _1 + \\& \sum _{i=1}^T \frac{\rho _1}{2} \left| \left| \mathbf {x}(t_i) - \mathbf {y}_1(t_i)+ \mathbf {u}_1(t_i) \right| \right| _2^2 + \\& \sum _{i=1}^{T-1} \frac{\rho _2}{2} \left| \left| \mathbf {q}(t_{i+1}) - \mathbf {q}(t_i) - \mathbf {y}_2(t_i) + \mathbf {u}_2(t_k) \right| \right| _2^2 . \end{aligned}$$

The ADMM updates are then

$$\begin{aligned} \mathbf {X}^{k+1}&= \mathop {\hbox {arg min}}\limits _{\mathbf {X}} \mathcal {L}(\mathbf {X},\mathbf {Y}_1^k,\mathbf {Y}_2^k,\mathbf {U}_1^k,\mathbf {U}_2^k) \end{aligned}$$

(18)

$$\begin{aligned} \mathbf {Y}_1^{k+1}, \mathbf {Y}_2^{k+1}&= \mathop {\hbox {arg min}}\limits _{\mathbf {Y}_1 \ge 0,\mathbf {Y}_2} \mathcal {L}(\mathbf {X}^{k+1},\mathbf {Y}_1,\mathbf {Y}_2,\mathbf {U}_1^k,\mathbf {U}_2^k) \end{aligned}$$

(19)

$$\begin{aligned} \mathbf {U}_1^{k+1}&= \mathbf {U}_1^{k} + \left( \mathbf {X}^{k+1} - \mathbf {Y}_1^{k+1} \right) \end{aligned}$$

(20)

$$\begin{aligned} \mathbf {U}_2^{k+1}&= \mathbf {U}_2^{k} + \left( \mathbf{\Phi } \mathbf {X}^{k+1} - \mathbf {Y}_2^{k+1} \right) \end{aligned}$$

(21)

where the value of $\mathbf {X}$ at iteration k is given by $\mathbf {X}^k$. The matrix $\mathbf{\Phi }$ computes the difference between each subsequent UVDF to produce a vector with the ith element defined as $[\mathbf{\Phi }\mathbf {X}]_i = \mathbf {q}(t_{i+1}) - \mathbf {q}(t_i)$ The algorithm alternates between updating $\mathbf {X}$, updating $\mathbf {Y}_1,\mathbf {Y}_2$, and updating $\mathbf {U}_1,\mathbf {U}_2$. The scaled dual variables $\mathbf {U}_1,\mathbf {U}_2$ keep a running sum of the residuals. The scaled dual-variable updates are gradient steps (weighted by $\rho _1,\rho _2$ in the unscaled form) where the gradients follow from the dual form of the optimization.

The $\mathbf {X}$ update of (17) is a large least squares problem

$$\begin{aligned} \mathbf {X}^{k+1}&= \mathop {\hbox {arg min}}\limits _{\mathbf {X}} \sum _{i=1}^T \frac{\Vert \mathbf {b}(t_i) - \mathbf {A}\mathbf {x}(t_i)\Vert _2^2}{\Vert \mathbf {b}(t_i) \Vert _2^2} + \\&\sum _{i=1}^T \frac{\rho _1}{2} \left| \left| \mathbf {x}(t_i) - \mathbf {y}_1(t_i)+ \mathbf {u}_1(t_i) \right| \right| _2^2 + \\&\sum _{i=1}^{T-1} \frac{\rho _2}{2} \left| \left| \mathbf {q}(t_{i+1}) - \mathbf {q}(t_i) - \mathbf {y}_2(t_i) + \mathbf {u}_2(t_k) \right| \right| _2^2 \end{aligned}$$

that we solve via the conjugate gradient method of Algorithm 1.

The updates for $\mathbf {Y}_1,\mathbf {Y}_2$ are both optimizations containing an $l_1$-norm term and $l_2$-norm term that are simpler compared to the original optimization. Here we have terms of the form $||\mathbf {x}-\mathbf {b}|^2_2$ instead of $||\mathbf {A}\mathbf {x}-\mathbf {b}||^2_2$. These follow the form for the definition of a proximal operator [20] and happen to have a known closed-form solution. Both updates

$$\begin{aligned} \mathbf {Y}_1^{k+1}&= \mathop {\hbox {arg min}}\limits _{\mathbf {Y}_1 \ge 0} \sum _{i=1}^T \lambda (t_i)\left| \left| { \mathbf{y}}_1(t_i) \right| \right| _1 + \frac{\rho _1}{2} \left| \left| \mathbf {x}(t_i) - \mathbf {y}_1(t_i)+ \mathbf {u}_1(t_i) \right| \right| _2^2\\ \mathbf {Y}_2^{k+1}&= \mathop {\hbox {arg min}}\limits _{\mathbf {Y}_2} \lambda _2\left| \left| \mathbf {Y}_2 \right| \right| _1 + \frac{\rho _2}{2} \left| \left| \mathbf{\Phi } \mathbf {X}^{k+1} - \mathbf {Y}_2 + \mathbf {V}_2^k \right| \right| _2^2. \end{aligned}$$

are the proximal operator for the $l_1$-norm which has a closed-form solution given by soft-thresholding. The update for $\mathbf {Y}_1$ additionally contains a non-negativity constraint; the resulting proximal operator in this case involves first soft thresholding followed by setting any negative values to zero [4]. The soft-thresholding operator is defined as

$$\begin{aligned} S_{\rho }(x) = \left\{ \begin{array}{l l l } x-\rho &{} &{} x > \rho \\ 0 &{} &{}|x| \le \rho \\ x+\rho &{} &{} x < -\rho \end{array} \right. \end{aligned}$$

and we define soft-thresholding with non-negativity as

$$\begin{aligned} S_{\rho }^+(x) = \left\{ \begin{array}{l l l } x-\rho &{} &{} x > \rho \\ 0 &{} &{} x \le \rho \end{array} \right. . \end{aligned}$$

The resulting updates are

$$\begin{aligned} \mathbf {Y}_1^{k+1}&= S^+_{\lambda _1/\rho _1} \left( \mathbf {X}^{k+1} + \mathbf {U}_1^k \right) \\ \mathbf {Y}_2^{k+1}&= S_{\lambda _2/\rho _2} \left( \mathbf{\Phi } \mathbf {X}^{k+1} + \mathbf {U}_2^k \right) . \end{aligned}$$

and when applied to a vector or matrix the operation is applied to each of its elements. These updates constitute the essential pieces of the ADMM algorithm. Additionally, there are two modifications that are made to this kind of ADMM algorithm. Firstly, $\rho _1,\rho _2$ need to be selected. They are initialized to $\rho _1,\rho _2 = 1$ and then adaptively updated to ensure that the magnitude of the primal and dual objectives is relatively close. Secondly, relaxation over-relaxation to improve convergence. These additions were found to be beneficial and further discussion can be found in Chapter 3.4 of [4]. The final ADMM algorithm is shown below.

Appendix B: Parameter Selection

The goal of the parameter selection process is to choose a value that balances objective terms. In our formulation, a signal could be recovered well using exclusively the narrowest basis function, but that would be entirely uninformative. The sparsity term enforces a cost on each basis function so that the narrowest are the most costly. As such, the sparsity parameter $\lambda$ must be large enough to ensure that the largest basis functions possible are used, but not too large so as to sacrifice reconstruction fidelity in order to use larger basis functions. The optimal value for the sparsity parameter is determined by the noise level present in the data. An L-curve is constructed by grid search—solving the optimization problem over a number of parameters and plotting the objective terms against one another to produce a curve such as the one in Fig. 9. The plot will reveal a point at a kink in the curve that balances the objective terms. If a clear kink is not present, a point closest to the origin with lower error is selected.

In order to choose the $\lambda (t_i)$ parameters, a grid search is completed with $\gamma = 0$ and an L-curve is obtained by plotting the reconstruction error term against the sparsity term. These T parameters are selected individually and then fixed to perform a grid search over the parameter $\gamma$. Again, an L-curve is constructed by plotting the UVDF total variation against the sum of the other two terms and selecting a balanced point.

Fig. 9

Example L-curve plot used to select a regularization parameter that balances the trade-off between objective terms

Appendix C: Estimation of Resolved Shear Stress

Estimates of the resolved shear stress for basal and prismatic slip modes based upon the crystallographic texture of the sample. The lattice orientation of grains in the unloaded sample was characterized using the technique of high-energy diffraction microscopy [22, 25]. This measurement was conducted with the sample under a tensile pre-load, prior to carrying out the in situ characterization using the MMPAD detector.

Rotating the sample about the tensile axis, diffraction images of complete Debye–Scherrer rings were collected at $0.25^\circ$ increments using a single GE amorphous silicon detector at APS 1-ID. The beam height was 0.4 mm, identical to that used in the in situ measurement. The HEXRD code [3] was used to identify (index) the crystallographic orientations of 876 distinct grains.

The FEniCS computing platform [1, 13] was used to carry out the simulation of linear elastic response. A mesh was generated using the Neper program [23] and the orientations developed through indexing of diffraction data were assigned to individual grains. Single-crystal elastic constants were taken from [7]. The average stress tensor, $\varvec{\sigma }_g$, was computed for each grain as part of post-processing.

For each grain, $\varvec{\sigma }_g$ was transformed to the local crystal frame and resolved shear stress computed for each of the basal and prismatic slip systems. The maximum values for basal and prismatic slip were identified and normalized by the stress magnitude, $\left| \varvec{\sigma }_g \right|$, to indicate driving force(s) for slip for a grain. A subset of grains were singled out which would have diffraction spots at positions measurable by the MMPAD detector. This selection was not restricted to the limited range of $\pm 2.5^\circ$ sample rotation taken in the in situ measurement; taking advantage of the uniaxial character of the test, grains with similar (mis-)orientation between the diffraction vector and the applied stress were grouped for the four Debye–Scherrer rings present on the MMPAD. A similar procedure was followed for tensile twinning (TTW), considering the directional nature of this deformation model. Average values for the normalized resolved shear stresses are given in Table 3.