Abstract
Local features of the internal structure or the microstructure dominate the overall performance of materials. An open problem in materials design with enhanced properties is to accurately identify and quantify salient features of the microstructure and understand its correlation with the material’s performance. This task is exacerbated when dealing with failure related properties that show strong correlations to higher-order details of the material microstructure. This paper presents a novel data-driven framework for quantitatively determining the highly complex correlations that exist between the higher-order details of the material microstructure and its failure-related properties, specifically its damage initiation properties. The enclosed work will address this challenge by significantly extending the Materials Knowledge Systems (MKS) framework and by leveraging concepts in extreme value distributions and machine learning. The developed framework was capable of successfully sorting nine different classes of synthetically generated two-phase microstructures for their sensitivity to damage initiation. The framework and approaches presented here open new research avenues for studying the microstructure-sensitive damage initiation properties associated with heterogeneous materials, and pave the way forward for practical multiscale materials design.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The precise connections between the material’s internal structure, generally referred to as the microstructure, and its effective performance characteristics are often very difficult to establish with sufficient accuracy and reliability [1,2,3,4,5,6,7]. This is mainly because the material microstructure spans a multitude of length/structure scales and exhibits a very large number of salient features that may or may not contribute significantly to a specific macroscale (effective) property or performance characteristic of interest. Because of this difficulty, one generally resorts to numerical approaches where the material microstructure is captured in a representative volume element (RVE) with sufficient accuracy, and simulates the effective response of the material to imposed loading conditions by invoking suitable descriptions of the material constitutive laws for all constituent phases. Although such numerical approaches provide new insights into the underlying physics of the materials phenomena, they are extremely time consuming and their computational cost is extremely high; factors that without doubt contribute to the slow pace of deployment and development of novel materials in advanced technology applications [8,9,10]. Therefore, a better strategy to account for the effects that material heterogeneities present at different length scales have on the performance characteristic of interest is required [2, 9]. A systematic and robust way to account for these effects is to develop/establish scale-bridging tools [9]. These tools effectively and efficiently communicate salient information among the different scales involved in the form of reduced-order models [11]. However, the fidelity, robustness, and ultimately the validity of the scale-bridging tools depend on the accuracy with which they communicate information among the different length scales [11]. This means that the reduced-order models need to accurately capture the highly complex effects that different microstructural features, at different length scales, have on its failure-related properties. As a result, the development of such reduced-order models requires a suitable framework capable of capturing the high-value quantitative connections between the complex material microstructure and its associated properties. This task represents a nontrivial challenge for most practically relevant material systems, and is exacerbated when dealing with failure-related properties that show strong correlations to higher-order details of the material microstructure. A clear example is damage initiation, where besides great effort, a robust framework that yields reliable reduced-order models has not been able to be developed. The main reason stems from the fact that current frameworks for establishing reduced-order models for damage initiation in heterogeneous microstructures employ highly simplified descriptors of the material microstructure, which typically include phase volume fractions, average particle size, etc. For example, several models in current literature aim to predict damage probability due to second-phase particle cracking in metal matrix composites [12,13,14,15,16,17,18]. In the work by Brechet et al. [13], a model was developed that calculates the probability of particle cracking depending on particle diameter. Subsequently, the model was extended to include particles’ size and aspect ratio as well as clustering effects [12]. Following the same ideas, an expanded model was developed to correlate ductility with a combined parameter accounting for particle aspect ratio and the particle equivalent circle diameter [14]. In another effort, an analytical model was developed for the prediction of the stress-strain response while accounting for particle size distribution and volume fraction [19]. As it can be clearly observed, the reduced-order models obtained with traditional approaches rely on simplified/idealized measures of microstructural features and do not take a systematic and a comprehensive approach to include all of the attributes of material’s structure that might control its damage-related properties. Consequently, the existing reduced-order models cannot be integrated into the aforementioned multi-scale efforts. Therefore, there is a clear need for a framework that enables one to capture and employ a more rigorous description of the microstructure when establishing reduced-order models for damage initiation-related properties or performance characteristics. The present study will address this challenge by defining a robust framework capable of generating reduced-order models that quantitatively account for the hierarchically complex aspects of the microstructure in damage initiation properties. As a result, this work lays the foundations for practical multiscale materials design for damage imitation properties.
The framework developed in this paper will extend significantly the work performed by Kalidindi and co-workers in order to address the incumbent challenges related to the establishment of accurate reduced-order, microstructure-sensitive, and damage initiation models. The work pioneered by Kalidindi and co-workers will be leveraged due to its success for establishing robust, accurate and computationally efficient reduced-order models [11, 20, 21]. The success of this work, called Materials Knowledge Systems (MKS) framework, stems from the rigorous statistical description (based on n-point spatial correlations) used for quantifying the material’s hierarchical structure employed by the framework. In addition, by employing low-dimensional representations (obtained using Principal Component Analysis) of the material microstructure, this framework is able to build accurate and computationally inexpensive Process-Structure and Structure-Property (PSP) linkages (also known as high-value linkages). Although the framework is cast in the form of n-point spatial correlations for generality, it has typically only used 2-point spatial correlations (often referred as 2-point statistics) to establish high-value linkages for different materials phenomena [20,21,22]. In addition, most of the prior implementations of the MKS framework have focused on properties that represent a bulk-averaged response over the entire RVE (often referred to as defect-insensitive properties) such as the effective elastic and yield properties of composite systems [20, 22]. However, in its current formulation the MKS framework is not capable of obtaining accurate reduced-order models for damage initiation properties, as its implementation is challenged by several factors. First, it is not at all clear that 2-point statistics carry the important microstructure information influencing the damage initiation properties of a microstructure because these properties might depend on even higher-order microstructure information (i.e., 3-point and higher-order spatial correlations). Second, while Principal Component Analysis (PCA) maximizes the capture of the variance in the given microstructure ensemble in the least number of terms possible, it is not expected to capture the exact microstructure information needed to correlate to the damage initiation properties of the microstructure. Third, one should anticipate the need to use a much larger number of PC scores (i.e., terms in the PCA representation). Consequently, the model building effort is likely to need significant enhancements (e.g., pruning the list of features to retain only the most important ones). Fourth, it is not at all clear how one would define an effective (global) damage initiation property given the field of damage parameters in the entire RVE predicted by a numerical approach (e.g., finite element method).
In order to address the challenges outlined above we have devised specific enhancements to the MKS framework. In addition, we have demonstrated the viability and utility of the extended MKS framework for producing reliable microstructure-sensitive reduced-order models for the sensitivity to damage initiation with a case study that employs an idealized damage initiation model. Finally, we have also shared the datasets and reduced-order models generated in this work through an open repository [23] to facilitate further curation by the broader community.
Materials Knowledge System (MKS) Framework for Damage Initiation Properties
The MKS framework is an extremely modular and generic framework that can be customized to develop scale-bridging tools for a vast variety of phenomena [20, 22, 24, 25]. The MKS framework digitally quantifies the internal structure of the material by discretizing both the spatial domain and the local state space. The local state space defines the complete set of all local states one might expect to encounter in a given material system and is typically defined as a combination of multiple attributes [11]. In the case of multiphase materials, the local state can be conveniently defined by each one of the different thermodynamic phases. The spatial domain is discretized by tessellating the microstructure into voxels (spatial cells) of uniform volume enumerated by s ∈ S [1, 11]; this index can be treated as a vector index for multidimensional domains and for the case of this work (where 3D microstructures are of interest), it is convenient to employ a three-index vector as s = (s1, s2, s3). Additionally, binning the local state space by considering each thermodynamic phase as a binned local state enables the MKS to digitize the microstructure with the array\( {m}_{\boldsymbol{s}}^h \). This array reflects the volume fraction of spatial bin s occupied by local state h. As a specific example, for a two-phase composite (H = 2), the digital representation of the microstructure exhibits the following properties [1, 11]:
Notice that all the definitions and relationships defined for \( {m}_{\boldsymbol{s}}^h \) are valid for any s ∈ S and h ∈ H. Building on this digital representation, the MKS employs n-point spatial correlations to quantify the hierarchically complex internal structure of the material. Prior work has identified the n-point spatial correlations as a valid measure of the statistics pertaining to the various neighborhoods encountered in the material microstructure [1, 11, 26, 27]. As a specific example, 2-point spatial correlations describe the probability of finding two local states (indexed by h and h′, respectively) in two different spatial locations separated by a vector indexed by r. The digital representation of the microstructure introduced above allows one to express the 2-point statistics of a periodic microstructure as [1, 11]:
where |S| denotes the total number of voxels (spatial bins) present in the spatial domain.
One of the main impediments for using n-point spatial correlations directly as measures of the microstructure comes from the fact that they constitute a very large set (note that the complete set covers a fairly large space of vectors). For that reason, the MKS leverages Principal Component Analysis (PCA) to obtain an objective (data-driven) low-dimensional representation of the defined statistical description of the material microstructure [28, 29].
PCA is an extremely powerful dimensionality reduction method that rotationally transforms the data into a new set of orthonormal axes that capture variance in a dataset with the fewest number of dimensions [30]. PCA starts by packing all spatial statistics deemed important for quantifying the microstructure into fq. Let Q denote the dimensionality of fq (i.e.,q = 1, 2, …, Q) and l enumerate the elements of the ensemble of microstructures on which the PSP linkages are to be established (e.g., l = 1, 2, …, L). In other words, \( {f}_q^{(l)} \)denotes the statistical measures that quantify the internal structure of one of the microstructures of the ensemble of interest. PCA produces an orthonormal representation of \( {f}_q^{(l)} \) in a new basis aligned with the natural directions of high orthogonal variance among the data of interest [31]. The basis vectors of this new frame are called principal components and the weights are called PC scores [11]. The fact that PCA transforms the data into a new frame organized by the variance causes for the data to cluster in the first few dimensions, and as a result, the representation of \( {f}_q^{(l)} \) in this new frame can be truncated to encompass only a small number of dimensions. The truncated representation is expressed as [11]:
where φjq denotes the new basis vectors (i.e., the principal components), \( {\overset{\sim }{f}}_q \) is the ensemble average for all microstructures in the ensemble, \( {\alpha}_j^{(l)} \) denotes the low-dimensional representation for the lth microstructure (i.e., the PC scores), and R∗ denotes the truncation level in this new orthogonal basis. The value of R∗ is usually selected based on the variance captured by the principal components and is typically very small compared to the size of the initial data matrix resulting in a highly effective dimensionality reduction [20, 32]. The succinct, objective, and low-dimensional representation of the microstructure captures the most salient distinguishing features of the hierarchical structure of the material with the fewest number of dimensions. As a result, it is now possible to establish a linkage between the low-dimensional representation of the microstructure and an effective property of interest, which in the case of this work is the initiation of damage. The established linkage is typically referred as a high-value linkage. Let P∗ denote an effective property which we desire to link to the low-dimensional representation of the microstructure (i.e., the PC scores). A multivariate polynomial expression in which the PC scores are considered as the independent variables has been found to be quite effective in prior work [11, 22]. This multivariate polynomial is expressed as follows:
where it can be seen that the \( {\overset{\sim }{\alpha}}_m \) are monomials of the PC scores and the Am denotes the coefficient associated with each monomial. Each monomial term (indexed by m = 0, 1, 2, …, M) is defined by power products of the different PC scores (identified by\( {\alpha}_1,\dots, {\alpha}_j,\dots {\alpha}_{R^{\ast }} \)), where each PC score (αj) is raised to a non-negative integer power nj. The MKS framework then calibrates the values of the Am coefficients to available data (typically generated using established numerical toolsets such as finite element models) for a chosen physical phenomenon using different regression techniques. For a more comprehensive treatment of the mathematical formulation of the general MKS and the theoretical background behind Eq. (4), please confer Refs. [11, 20].
A significant challenge in the development of microstructure-sensitive damage models comes from the lack of established measures for the effective damage initiation property of a given microstructure. Consequently, in order to proceed, we must first define a global measure capable of capturing the effective damage initiation of a microstructure. The initiation of damage in a microstructure is expected to be heavily influenced by spatial locations experiencing high values of damage drivers (colloquially referred as “hotspots”) and their frequency. Therefore, in order for the effective damage initiation property to be realistic, it needs to account in some measure for these hotspots. A recent MKS application established a clever approach for defining an effective property capable of capturing the effect of spatial locations exhibiting high values of a property of interest [33]. The approach first defines a threshold value of the property of interest. Then, an extreme value distribution that best fits the distribution of the spatial locations with values greater than defined threshold value is identified. Finally, the parameters that define the identified extreme value distribution are defined as the effective property. This clever approach is appealing for damage initiation properties because the defined global/effective property parametrically captures the frequency and distribution of these hotspots. As a result, we will incorporate this novel approach with the hopes it can lead us to develop accurate reduced-order models for damage initiation. At this point, it is important to highlight the generality of the extended MKS framework because no assumptions were made regarding the quantification of damage initiation to define the effective property. As a result, the extended MKS framework can be used to establish reduced-order models regardless of the damage model used to quantify the initiation of damage in the microstructure.
Following the direction defined by prior MKS implementations [20, 22], the reduced-order models described in Eq. (4) will be established using ordinary least squares regression and Leave-One-Out-Cross-Validation (LOOCV) will be performed during the model development to avoid overfitting. LOOCV removes one data point from the calibration dataset and uses it for validation of the model that is built with the remainder of the data. This process is repeated for all the data points in the calibration set. Error measures play an important role in the model selection process. This work will employ a normalized mean of absolute error (NMAE) and its standard deviation (SDE) defined as follows:
where P∗l denotes the actual value of the effective property, \( {\widehat{P^{\ast}}}_l \) is the corresponding predicted value from the reduced-order model, \( \overline{P^{\ast }} \) denotes the average value of the property over the ensemble being studied, and L is the total number of microstructures included in the ensemble. Normalization by the average value (\( \overline{P^{\ast }} \)) allows an easier interpretation of the mean of absolute error in terms of a percentage. During the process of model selection, the best model is chosen based on the minimum value of NMAE both for the developed model and its LOOCV. If there are models that have similar error magnitudes, then the model with the least number of terms will be selected as the best model [22].
A final factor that must be considered for developing accurate reduced-order models for damage initiation is that the expected number of microstructure features to influence damage initiation properties is quite large. This factor causes a significant increase in the number of PC scores that need to be probed in order to establish a robust high-value linkage. Under these circumstances, a brute-force application of the original MKS framework is not likely to produce any useful surrogate models [33]. The Pearson Correlation coefficient [34, 35] provides quantitative information about the linear dependency of each individual input to the desired output of the model. The value of this coefficient varies between − 1 and 1 (the closer the value is to 1 or − 1, the better the correlation). The Pearson correlation coefficient has been used successfully as a feature pruning technique in a few recent MKS case studies [22, 33]. As a result, we will incorporate the Pearson Correlation coefficient into the model building effort in order to identify the microstructure features that contribute the most to the initiation of damage.
In this paper, we extended the MKS framework to address the incumbent challenges related to the establishment of accurate reduced-order, microstructure-sensitive damage models. In order to demonstrate the viability of the extended framework, it is needed to critically evaluate it on a scenario where existing reduced-order models are not successful. A scenario where existing reduced-order models are not capable to provide accurate results is when the volume fractions of the composite are exactly the same since their results depend heavily on highly simplified descriptions of the material microstructure (like volume fraction). Therefore, as a critical validation of this work, a reduced-order model will be established to rank-order nine different classes of synthetically generated two-phase microstructures (whose phases have the same volume fraction) for their sensitivity to damage initiation.
Case Study
The extended MKS framework will be employed to establish a microstructure-sensitive reduced-order model to rank-order different two-phase composites according to their sensitivity to damage initiation. Figure 1 schematically depicts the workflow to be followed to establish the microstructure-sensitive damage initiation model for the defined case study.
Generation of the Dataset
The main strategy is to generate a substantial dataset using micromechanical finite element (FE) simulations, and to use the dataset to train the desired microstructure-sensitive models. Subsequently, the developed models will be critically evaluated using new microstructures that were not included in the training of the model. The generation of the dataset for this case study consisted of two main steps:
-
(i)
Generation of a large ensemble of microstructures exhibiting a rich diversity of microstructural features (our focus is on the morphological aspects of the individual phases present in the microstructure [36, 37]).
-
(ii)
Simulation of the local damage drivers using FE software for each of the microstructures in the ensemble.
A total of nine different classes of two-phase microstructures were generated for this case study. The volume fraction of each phase was ~ 50% in all of the microstructures. Table 1 schematically shows the different microstructure classes used in this case study. The generated dataset includes 20 different instantiations for each of the classes listed in Table 1 yielding a total of 180 different microstructures. Therefore, the ensemble of microstructures employed in this work was designed to include both intra-class and inter-class differences.
The volume size of 100 × 100 × 100 voxels was employed as a compromise between making sure that the volumes are large enough to represent the microstructure and keeping the computational costs reasonable (note that a large number of these volumes need to be analyzed for this study). One of the checks to ensure the adequacy of the volume size comes from comparing the 2-point spatial correlations of the instantiations contained in each class, which were found to be quite similar to each other. The similarity of the spatial correlations means that the selected size characterizes all the features of the microstructure adequately. The fact that the volume fraction of each phase is the same (~ 50%) for all the microstructures causes for any observed differences in the responses of the different microstructures to be attributed to the effect of the higher-order microstructure statistics. In addition, notice that defining an average feature size (i.e., average particle size, average diameter, etc.) is quite difficult for the selected microstructure classes. As a result, reduced-order models obtained with traditional approaches are not able to produce accurate results since their simplistic microstructure descriptors are ill-defined (difficult to obtain and not meaningful at all) for the classes employed in this case study. On the other hand, the reduced-order models developed with the extended MKS framework are capable to account for these effects.
We obtained the damage response for each one of the generated microstructures using a finite element software and a damage model. Each one of the generated microstructures was discretized with a 100 × 100 × 100 hexahedral mesh because it significantly simplifies the application of the MKS framework (which employs discrete Fourier transforms in computing the 2-point statistics) [1, 11]. We recognize that the selected mesh is not designed to accurately estimate the stress and strain fields at the interfaces. Damage parameters computed based on such highly local values of stress and strain fields at interfaces will be very sensitive to the details of the numerical implementation (such as mesh design, mesh size, magnitude of time steps). Therefore, it is more appropriate to compute these values on locally volume-averaged quantities. Using the simple hexahedral mesh employed in this work conveniently addresses this requirement. A common approach for simulating damage evolution in materials is to employ a void growth and coalescence model [38,39,40], which typically defines damage drivers using different combinations of equivalent plastic strain, stress triaxiality [41,42,43,44,45,46,47], maximum principal tensile stress [48], hydrostatic stress [49], and equivalent stress [50]. Taking these factors into account, it was decided to use an integral of the stress triaxiality with respect to equivalent plastic strain as a metric for damage initiation. The selected parameter captures the main underlying physics associated with damage initiation in ductile materials, and is calculated as follows [42, 43]:
where TF is the stress triaxiality, σH is the hydrostatic stress, σeq is the von-Mises equivalent stress, and εeq is the equivalent plastic strain. It should be noted that only positive values of triaxiality are included in the evaluation of Eq. (7) [42, 43]. In addition, since the focus of this case study is damage initiation (i.e., in the early stages of the imposed plastic deformations), it was decided to compute damage in a post-FE analysis step. We align damage nucleation with the propensity to grow a potential flaw population. In this vein, the post-processed, uncoupled metric is helpful for ranking the sensitivity of microstructures and is not intended to be employed for capturing the failure process. This means that the damage drivers computed in this work do not aim to capture the complete damage evolution, but only the damage initiation. It is recognized that the treatment of damage is simplified in this work. However, it is important to recall that the goal of this case study is to rank different microstructures by their sensitivity to damage initiation (which microstructure is most likely to nucleate damage), and as such, a simplified treatment of damage should suffice. Moreover, recall that the framework followed to establish the reduced-order model for this case study is quite general, and can be subsequently extended to account for broader, more complex and more rigorous definitions of damage initiation [51,52,53] in future studies.
FEM simulations of uniaxial tension along the Y-axis (cf. Table 1) up to 1% overall (average) strain were performed for each microstructure using Sandia’s solid mechanics code JAS3D [54]. Displacement-controlled boundary conditions were applied to nodes in +Y planes at a nominal strain rate of 10−4 s−1 while −X, −Y, and −Z planes were constrained along X, Y, and Z directions, respectively. Such boundary conditions inevitably produce spurious hotspots at or close to the boundary. To avoid their effects in our analyses, data from the five outer layers of elements from each side of the cube were removed. The simulations employed an elastic-perfectly plastic (no hardening) material model for each constituent phase in the microstructure. It was desired for the damage fields to be as heterogeneous as possible and the fact that we are employing synthetically generated data allows us to carefully tailor the properties of the phases to achieve this. Based on Eq. (7), we see that equivalent plastic strain plays a significant role in this definition. Therefore, in order to generate a heterogeneous field of damage parameters, the plastic properties of the phases need to be varied suitably to generate a highly heterogeneous state of strain. Taking these factors into consideration, each phase was assigned a Young’s modulus of 1000 GPA, a Poisson’s ratio of 0.3, and yield strengths of 100 MPa (softer phase) and 500 MPa (harder phase), respectively. As a result of these assignments, the contrast in the plastic properties produce heterogeneous stress and strain fields in the microstructure and the high value of Young’s modulus mitigates any effects from elasticity. Finally, it is pointed out that the employed FEM code has a single integration point per mesh element, and it is assumed that the obtained result is the average value over the voxel. As a result, the average value of damage driver per voxel is obtained by evaluating Eq. (7) for the FEM result obtained for each element in each microstructure generated. Finally, by deforming the different microstructures to the same amount of strain, it provides different levels of local damage in each microstructure. In the instantiations of the classes depicted in Table 1, the softer phase is colored in red and the harder phase is shown in blue.
As the reader can see, the employed material properties, the method for quantifying damage initiation, and the finite element mesh result in a highly idealized scenario. However, notice that the sensitivity to damage initiation of each of the microstructures varies significantly from class to class (see Figs. 2 and 3) and recall that reduced-order models obtained with traditional approaches are not capable of obtaining a robust prediction of their ranking. Therefore, in spite of all the simplifying assumptions, this problem is still a scenario for which traditional approaches fail to provide accurate responses, and thus constitutes an effective validation for the framework developed in the last section.
Figure 2(a1, a2) shows Y–Z cross-sections of a 3-D microstructure from class 6 and another microstructure from class 8, respectively. In these images, black domains correspond to the harder phase, while white domains correspond to the softer phase. Note also that the microstructures of class 8 correspond to the microstructures from class 6 rotated 90° about X-axis. The (b1, b2), (c1, c2), and (d1, d2) subplots in Fig. 2 depict its corresponding fields of stress triaxiality, equivalent plastic strain, and the damage parameter at 1% overall deformation. It can also be observed that the stress triaxialities computed at material interfaces in the soft phase are substantial. Further analysis of the figure shows that load redistribution perpendicular to the fibers (see Fig. 2(a2)) tends to produce higher local values of stress triaxiality, plastic strain, and damage in contrast to load redistribution along the fibers (see Fig. 2(a1)). We remark that while some effects of the microstructure, such as loading along fibers and perpendicular to fibers shown in Fig. 2, can be discerned very easily, many other aspects of the complex structure-property linkages in heterogeneous materials are very difficult to extract. The framework employed in this case study extracts these linkages with the objective, and largely automated, workflow proposed in the last section.
For this case study, it has been decided to employ two different measures to determine the effective initiation of damage in a microstructure according to which the generated microstructures will be ranked. The first one consists of a simple volume average of the local damage drivers as the effective damage initiation property that we will denote with\( \overline{\ D} \). This results in 180 different values, 1 for each microstructure. However, it is important to notice that this choice of effective property does not pay any attention to details of the frequency of “hotspots” (i.e., spatial locations experiencing high values of the damage drivers), which could be an important consideration in rank-ordering microstructures for their effective damage initiation properties. Therefore, taking advantage of the extension to the MKS framework defined in the previous section, we will employ parametric descriptions of the extremal distribution of the local damage parameters in the microstructure as surrogate measures of the damage initiation response, and define their associated parameters as the effective damage initiation property.
Extreme value distributions [55, 56] are very useful in quantifying the frequency of the occurrence of these hotspots in the material microstructure since they characterize the distribution of events that occur with very small probability. Extreme value theory states that the highest (or lowest) values of a large number of observations (when normalized appropriately) can only converge to three types of extreme value distributions: Gumbel, Frechet, and Weibull [55, 56]. The generalized extreme value distribution (GEVD) is a flexible three-parameter distribution that encompasses these three standard extreme value distributions [57, 58]. The cumulative distribution function (CDF) represents the probability that a random variable X will have a value equal or less than x, i.e., FX(x) = P(X ≤ x). The cumulative distribution function (CDF) associated with the GEVD is expressed as follows [57, 58]:
In Eq. (8), k, σ, and μ denote the shape, scaling, and location parameters of the GEVD function, respectively. The shape parameter (k) in Eq. (8) determines which extreme value distribution is represented [57,58,59,60]. The three parameters of GEVD are obtained with maximum likelihood estimation (MLE) [61, 62] as the best fit of Eq. (8) to extremal portions of the CDF curve for any given dataset. GEVD will be employed in this study to characterize the details of the frequency of the “hotspots” of interest due to its generality and flexibility. As a result, the effective damage initiation property defined with the help of the GEVD is likely to provide a more realistic microstructure ranking.
The extremal portion analyzed in this case study is delimited by the top 2% values of the damage parameter. In order to obtain the GEVD parameters that describe parametrically the distribution of these extreme values, we first obtain the CDF of the local damage parameter values and identify the top 2% portion for each simulation result.
Figure 3 displays the extremal portion of the CDFs analyzed in this study for all the microstructures in classes 6–9 (center of the figure). The contour plots depict the spatial distribution of the damage parameter values at the defined threshold (top 2%) for some microstructure instantiations of the classes 6–9. The contour plots show that the highest values of local damage parameter are clustered along the interfaces on the side of the softer phase (classes 6 and 8) or inside the softer phase when the average spacing between the hard phase is small (e.g., the microstructures of class 9). Figure 3 also shows that the microstructures loaded along the direction of the elongated phase, such as aligned cylinders (classes 6) and microstructures with elongated grains (class 7), have less sensitivity to damage initiation than those loaded perpendicular to the interfaces (i.e., class 8). Therefore, in Fig. 3, the microstructures corresponding to class 7 perform the best in terms of sensitivity to damage initiation while the microstructures of class 8 perform the worst. From Fig. 3, it can also be seen that CDFs of different microstructures close to each other have similar spatial distributions of damage parameter values. This analysis gave us confidence that the top 2% portion of the CDF adequately characterizes the extreme value response of the local damage values and that their distribution is a meaningful effective (global) damage initiation property. In addition to this fact, the top 2% portion was selected because it was the smallest CDF portion that yielded stable GEVD parameters. Obtaining a GEVD for smaller portions of the CDF (for example the top 1.5, 1, .99%, etc.) fitted the distribution to a reduced number of data points and introduced non-physical factors (such as mesh size) into the data on which the reduced-order model will be calibrated.
For each simulation result, maximum likelihood estimation (MLE) [62] was used to determine the k, σ, and μ that provided the closest agreement between Eq. (8) and the extremal portion (top 2%) of the CDF identified to be analyzed in this work. The MLE obtained values for k were in a narrow range and no clear distinction among the classes could be detected. The narrow range in the shape parameter (k) indicates that the top 2% values of the local damage parameter for all the microstructures analyzed converge to the same shape of extremal distribution. Under these circumstances, a GEVD having a constant k (shape parameter) value within the range of the previously obtained k’s will provide an accurate fit to the distribution of the top 2% damage values for all the microstructures in the ensemble. Therefore, it was decided to fix the value of k in Eq. (8) to the mean value of all the previously obtained k’s (this value is 0.48) and use MLE to obtain the σ and μ that maximized the agreement between the fixed shape parameter GEVD and the top 2% portion of the CDF of local damage values.
Figure 4 shows the extremal portion of the CDF curves of local damage parameter values analyzed in this work and their corresponding fixed shape parameter GEVD fits for one microstructure from each class. It can be clearly seen that the GEVD obtained with the fixed shape (k) parameter provides a good quality fit that adequately describes the distribution of the extremal values of the damage parameter and demonstrates that there is no need to establish a reduced-order model for the shape parameter.
A closer inspection of some of the FE results (cf. Figs. 2 and 3) revealed that the main microstructural features influencing damage initiation are the soft-hard interfaces perpendicular to the loading direction. This, of course, makes sense as one would expect these locations to exhibit high values of triaxiality and plastic strains. However, we note that this is a highly qualitative statement. We seek to establish a reduced-order model that will provide quantitative predictions by accounting for all features in the microstructures (e.g., the interfaces that are not precisely perpendicular to the loading direction). The insights gathered above provide us valuable guidance into what specific sets of spatial correlations should be considered in the model building effort. We have considered to incorporate the autocorrelations of the soft phase (i.e., soft-soft 2-point statistics) because they capture the information on shape and size distributions of the soft regions in the microstructure. Only one subset of the 2-point spatial correlations is incorporated into the model building effort because for a composite with two local states all other 2-point correlations (soft-hard, hard-soft, and hard-hard correlations) are completely determined once we specify the soft-soft correlations [63]. Therefore, including any other subset of 2-point statistics will not add any new features in the representation of the microstructure. Given the role the interfaces and their spatial distributions are likely to play (cf. Figs. 2 and 3), it was found necessary to add some more microstructure features capturing some of the higher-order microstructure statistics (beyond those captured in the 2-point statistics). In other words, our attempts at building a reduced-order model using only the 2-point statistics of the microstructures did not produce acceptable models. As a result, for this case study, higher-order statistics were added in the form of 2-point statistics on the interface voxels. In other words, all of the interface voxels were identified as a new local state (these were identified as voxels in the soft phase that had at least one of the six first neighboring voxels occupied by a hard phase), and then autocorrelations were computed for this local state. Since the identification of the interface voxels itself amounts to a first neighbor 2-point statistics, computing 2-point statistics on them is equivalent to computing a subset of higher-order statistics (in fact, this is a subset of 4-point statistics). The selection of this specific subset was guided by intuition and a qualitative assessment of the finite element results shown in Fig. 3. In the model-building process (discussed in later sections), it was observed that these higher-order statistics played an important role in obtaining a reliable model.
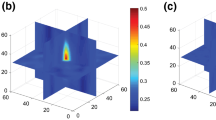
Figure 5a shows a microstructure from one of the different instantiations of class 9 (i.e., random spheres). Figure 5b shows three orthogonal slices of the 3D autocorrelations of the soft phase in this microstructure. The value of the 2-point statistics at r = 0 corresponds to the volume fraction of the soft phase. The sliced contours in Fig. 5b present a probability map of finding both the tail and the head of a randomly placed vector r in the soft phase. It is clear from these contours that this probability decreases with the length of the vector, and asymptotes to a value corresponding to the square of the volume fraction of the soft phase. Typically, the first minimum in the 2-point statistics corresponds to an average feature size [11, 26], which in this case corresponds to an effective sphere size. Figure 5c displays the soft phase voxels that are located at the interface of the two phases, and Fig. 5d shows three orthogonal slices of the autocorrelation of the interfaces. As before, the peak at the center of this plot provides the volume fraction of interface voxels and the next local peak corresponds to the effective radius of the spheres (lighter colored contours).
Combining the two autocorrelations into a single array yields a representation for each microstructure of a size of roughly 2 × 106 values. It is needless to say that this is a very large and unwieldy feature list for establishing surrogate models. Therefore, we will employ PCA analysis to drastically reduce the dimensionality of the data being analyzed. Before performing PCA, the dataset is split into a training set and test set: Class 4 is used as a test set and the other eight classes are used as the training set. PCA was performed using only the microstructures in the training set and as a consequence is completely uninformed of class 4. Recall that PCA represents the data on which it was performed (i.e., the calibration set) in a new orthonormal frame aligned with the natural directions of high variance among the data of interest. The orthogonality of the new frame enables for one to procure the PCA representation of the test set by performing a dot product between the statistics of the microstructures contained in the test set and the basis vectors obtained with the PCA (which was performed on the calibration set only). In other words, the microstructures in the test set are projected into the PCA space using the principal components (φjq) of the training set. It is also important to mention that the autocorrelation values for the interfaces are significantly smaller in values compared to the autocorrelation values for the soft phase (compare the numbers in Fig. 5b, d). Therefore, to give equal importance to both correlations in the PCA, it becomes necessary to scale the autocorrelations of the interfaces. This scaling factor was treated as a hyper-parameter in the model selection process (i.e., it was adjusted to obtain the best model).
Figure 6a shows the low-dimensional representation of the training set and the projected representation of the test set in this new reduced-order frame. It can be seen that the microstructures of the test set fall within the range of the microstructures in the training set. This bodes well for the application of the reduced-order models established in this work on the test set [1, 11]. Figure 6b shows the variance explained by each principal component along with accumulated variance. From Fig. 6b, we can observe that the first two principal components capture about 95% of variance in dataset while subsequent principal components capture significantly less variance of the data.
As stated in the previous section, the PC scores serve as the low-dimensional representations of the microstructure in establishing robust, high-value, and structure-property linkages. The microstructures in the test set are not used at all during the development of these models. The features that represent the microstructures in building these models are typically selected as monomials of the PC scores (see Eq. (4)) [11, 20, 22]. In this work, monomial combinations comprised in a 4th order polynomial generated using the first ten PC scores were considered in building the model. The list of features obtained with such a high value of the exponent is excessively large since it encompasses all the monomials that comprise a polynomial of degree 4 with ten independent variables. Clearly, not all of these features contribute significantly to the initiation of damage. Therefore, it is necessary to prune the list of potential features to identify those that have the biggest potential influence on damage initiation in order to effectively build a reliable model.
Following the extended MKS framework outlined in the previous section, the features that have the greatest influence on the damage initiation properties were identified using Pearson correlation coefficients, which were computed individually for each potential feature variable considered. The Pearson correlation coefficients were obtained for all the monomials comprised in a polynomial of degree 4 with ten independent variables, and only the top values (both positive and negative correlations) are selected for model building. The model building protocol employed in this work treated the cutoff value of the Pearson correlation coefficient used to prune the feature list as a hyper-parameter. As mentioned earlier, another hyper-parameter in the model building process was the scaling factor applied between the two autocorrelations before performing the PCA. Once a value for each of the hyper-parameters was defined, a reduced-order model is obtained using an ordinary least squares regression technique. As a result, different models corresponding to different values for the two hyper-parameters were built. The best model is selected based on the smallest magnitude of the error measurement (i.e., NMAE; see Eq. (5)) both for the model and the cross validation (LOOCV). It is also important to mention that the best model will have similar error for the model and for cross validation.
Microstructure-Sensitive Reduced-Order Damage Initiation Models
The model for the volume-averaged damage parameter that fulfilled the aforementioned error requirements (and therefore identified as the best model) has the following polynomial expression:
where \( \overline{D} \) denotes the average value of damage in the whole microstructure. The normalized error measures (Eq. (5)) for the identified model are 0.0825 (corresponds to average error of 8.25%) for the training set and 0.0871 for LOOCV on the training set. The corresponding standard deviations of the normalized errors are 0.0610 and 0.0646 (for LOOCV).
Finally, employing the same criteria, the best models for μ and σ were identified and have the following expressions:
The corresponding normalized error measures for the developed models are presented in Table 2, where NMAE and standard deviation of normalized error (SDE) are given for the developed models and their cross validation.
The identified reduced-order models (defined by Eqs. (9), (10), and (11)) need to be critically validated using new microstructures that were not used in the calibration process. Precisely for this reason, we set aside microstructures of class 4 as the test set.
Figure 7 shows the goodness of fit for the volume-averaged damage parameter predicted by Eq. (9) as a parity plot for all microstructures included in this study. The diagonal black line in this plot represents a perfect fit. The predictions for class 4 microstructures (the test set) exhibited a mean normalized error of 0.0936 and a standard deviation in the normalized error of 0.0623; these are similar to the values obtained in the training sets. The reduced-order model for the volume-averaged damage parameter ranks the microstructures of class 3 and class 8 to be the worst and the microstructures of class 6 and class 7 to be the best in terms of their sensitivity to initiate damage.
Figure 8 presents the goodness of fit for the values of μ and σ predicted using Eqs. (10) and (11) as a parity plot for all the microstructures analyzed in this work. The errors associated with the predictions of the test set (class 4) are summarized in Table 3.
Before we define a protocol for ranking the microstructures based on the model-predicted values of μ and σ, it is essential to demonstrate that the GEVD fits obtained with the model predicted values in conjunction with the previously fixed value of k (recall that the shape parameter value was fixed to the mean value of the shape parameters for all the microstructures analyzed in this study) characterize the extremal response of the damage parameters for all the microstructures analyzed in this study to adequate accuracy. Therefore, the CDFs were reconstructed using Eq. (8) with the previously set fixed value for k and the model predicted μ and σ values for all the microstructures (both in the test set and the training set). Figure 9 shows the reconstructed CDF for all the microstructures considered in this work using the MLE-obtained GEVD parameters and the model-predicted GEVD parameters. For convenience of viewing, the plots are presented as four groups in Fig. 9. The shaded area in each plot represents the range of the MLE-obtained GEVD fits for each microstructure class and the dashed lines depict the GEVDs fits obtained with the model-predicted values. The model-predicted GEVD parameters reconstructed the CDFs of most classes within the range of the MLE-obtained GEVD fits. Notice also that the reduced-order models predicted with great accuracy the GEVD fit for the test set (class 4). It can be clearly seen that the GEVD parameters predicted with the reduced-order models accurately describe the extremal distribution of damage parameter values for the different microstructure classes. Therefore, we can confidently proceed to establish a ranking protocol based on the values for μ and σ predicted with the reduced-order models, because it is now clear that they will provide a reliable and valid ranking.
Ranking the sensitivity for damage initiation of a microstructure based on its location parameter (μ) value for the extremal portion identified in this case study is logical because this parameter defines the value at which the reconstructed CDF extremal portion starts. Therefore, the microstructures with the lowest μ value will have the lowest sensitivity towards damage initiation. The behavior of the μ parameter observed in Fig. 8a validates the suggested ranking protocol since we can clearly observe that the μ parameter is distinctly different for each microstructure class and effectively ranks the damage initiation response of the different microstructure. The value of the shape parameter (σ) can be used as a second discriminatory value in the case where the location parameter of two microstructures is the same. Following the protocol proposed above, microstructures belonging to class 3 and class 8 were identified to have the highest sensitivity to damage initiation, since they have the highest value of the μ parameter. On the other hand, the microstructures that exhibit the lowest sensitivity to damage initiation are those that belong to class 6 and class 7, since they have the lowest value of the μ parameter and possess the least amount soft-hard interfaces in the direction perpendicular to the loading direction. Finally, it can be seen that the microstructure ranking based on the reduced-order models for μ and σ is consistent with the ranking defined by the volume-averaged damage parameter reduced-order model. In the subsequent subsection, an analysis of the results produced by the best identified reduced-order models is going to be performed.
Discussion of the Results
The reduced-order models for both different effective damage measurements identified that microstructures belonging to class 3 and class 8 exhibit the highest values of the effective damage initiation property. The microstructures of both these classes are characterized by the elongated phases offering several soft-hard interfaces in the direction perpendicular to the loading direction. In addition, both models also identified that the microstructures that belong to classes 6 and 7 have the best damage resistant properties. Recall that class 6 and class 7 are essentially rotated versions of microstructures from classes 8 and 3, respectively. As such, the microstructures in classes 6 and 7 offer the least amount of soft-hard interface in the direction perpendicular to the loading direction. As a result, the established reduced-order models effectively reflect our qualitative expectations in terms of ranking of the microstructures studied, but accomplish this in a highly quantitative manner.
Another insight obtained from the results presented above is that the effect of the low-dimensional representation of the microstructure (based on PCA) on the resulting effective properties is palpable. For example, the microstructures of class 9 exhibited the smallest intra-class variance in the PC representations of their 2-point statistics and as a result, they exhibit a very small intra-class variance in their damage sensitivity. Another example is obtained by analyzing the responses of classes 1, 2, 4, and 5, which are the classes that are comprised of randomly placed equiaxed hard phases in their microstructures. Notice that the values of the averaged damage parameter for microstructures in class 4 seem to overlap with those from classes 1, 2, and 5. This is also the case for their GEVD parameters since these four classes show similar values of the μ parameter and consequently exhibit similar sensitivity towards damage initiation. The fact that the models generated in this case study can identify this similarity in the microstructures on its own (note that none of the microstructures are in any way tagged by how they are generated or what features they contain) is indeed remarkable, and attests to the power of the techniques presented in this work. Most importantly, it is seen that the developed models provided overall good predictions and provided a valid rank-ordering of the sensitivity of the different classes of microstructures.
We also notice that α4 and α5 consistently play dominant roles in all the established reduced-order linkages (see Eqs. (9), (10), and (11)). These dominant PC scores were identified because they exhibited the highest Pearson coefficients among the different damage parameters studied here. PCA is unsupervised and completely uninformed of the damage sensitivity of the microstructures studied. Therefore, even though α1 is the best parameter for the discrimination of the microstructures based on their topological features, it is clearly not the best indicator of the damage sensitivity of the microstructure. The ability to identify the important microstructure features for any selected property in automated workflows is indeed one of the distinctive features of the extended MKS framework developed in this work and validated with this case study. The main advantage of the PCA is that it provides a consistent and unbiased set of objective low-dimensional representations of the microstructure on which the high-value linkages can be explored and established. Therefore, one should expect that different properties associated with a given class of microstructures are likely dominated by a different set of PC scores. In the present study, it is reassuring that the same set of PC scores (α4 and α5) play a strong role in the two substantially different effective damage initiation properties defined. In order to obtain further insights on the microstructure features that are captured by any specific PC score, one needs to examine the corresponding eigenvector. As an example, to understand the features captured by α4, one needs to examine its associated basis vector φ4q (see Eq. (3)). Recall that φ4q contains two autocorrelations because the size of the eigenvector is the same as the original dataset on which PCA was performed.
Figure 10a, b presents the components of φ4q as autocorrelation maps. For convenience, the loading direction (LD) is indicated in the axes within Fig. 10. Figure 10 shows that higher α4 scores lead to an alignment of both the soft phase and the interfaces in directions that are perpendicular to the loading direction. Further analysis showed that microstructures in PC space with higher α4 scores are more sensitive to damage initiation than those with lower values of α4 score. The microstructures of class 3 and class 8, which were consistently ranked as having the highest sensitivity to damage initiation, have the highest α4 scores in the entire ensemble studied. The insights obtained by analyzing the eigenvector of α4 are consistent with our expectations for the problem studied. However, it is really important to reiterate that the developed models capture highly quantitative linkages that cover a very large set of microstructure configurations (beyond the simple notion of hard-soft interfaces being perpendicular to the loading direction). Unfortunately, as is the case with almost all dimensionality reduction techniques, the complete interpretation of the reduced-order models is currently not possible. That is an ongoing field of study, not just in materials science, but also in other disciplines.
The microstructure-sensitive damage initiation models developed in this paper take into account a fairly large set of microstructures. In fact, we are confident that the diversity of microstructures selected for our work is significantly larger than any that has been explored in any previous study on damage initiation models in published literature. However, the set of all theoretically possible microstructures is infinite, and as such, we recognize that the developed model can be further improved by encompassing a bigger set of microstructures. All the tools employed to establish the reduced-order model developed in this work are available through www.pymks.org and the dataset employed in this work is being hosted in the MATIN repository [23]. It is hoped that the broader research community will be able to further curate these models.
Conclusion
The present study establishes a new foundational framework for pursuing the formulation and curation of microstructure-sensitive, reduced-order models that capture a more rigorous description of the microstructure for failure-related properties. This new framework, based on the previously established MKS framework, leverages the formalism of microstructure quantification using the concept of n-point spatial correlations together with emerging toolsets in data science and informatics. The performed case study shows that this new approach holds tremendous promise for a systematic study of microstructure-sensitive damage models. In particular, it was demonstrated that the emerging toolsets in materials data sciences and informatics can offer new opportunities for an unbiased automated exploration of a very large model space, and help identify reliable and robust models that not only are consistent with the qualitative trends expected by the domain experts but also are highly quantitative in their predictive capabilities for a diverse set of microstructures.
The generalized and modular nature of the framework developed in this work enable it to be extended as deemed necessary. For example, the local state can be extended to include more complex local states (e.g., crystal lattice orientation for polycrystalline materials). Similarly, the damage criterion can be customized as needed to the selected material system. All of these extensions, and many more not mentioned, can be pursued by the broader research community using the tools are available through the open-source code repository PyMKS (www.pymks.org).
References
Adams BL, Kalidindi S, Fullwood DT (2013) Microstructure-sensitive design for performance optimization. Butterworth-Heinemann, Waltham
McDowell DL, Panchal J, Choi H-J, Seepersad C, Allen J, Mistree F (2009) Integrated design of multiscale, multifunctional materials and products. Butterworth-Heinemann, Waltham
Song K, Zhang Y, Meng J, Green EC, Tajaddod N, Li H, Minus ML (2013) Structural polymer-based carbon nanotube composite fibers: understanding the processing–structure–performance relationship. Materials 6(6):2543–2577
McDowell DL, Ghosh S, Kalidindi SR (2011) Representation and computational structure-property relations of random media. JOM 63(3):45–51
McDowell DL, Olson GB (2008) Concurrent design of hierarchical materials and structures. Sci Model Simul 15(1–3):207–240
Olson GB (1997) Computational design of hierarchically structured materials. Science 277(5330):1237–1242
Adams BL, Olson T (1998) The mesostructure—properties linkage in polycrystals. Prog Mater Sci 43(1):1–87
N.R. Council (2008) Integrated computational materials engineering: a transformational discipline for improved competitiveness and national security. National Academies Press, Washington DC
J Oden, T Belytschko, J Fish, T Hughes, C Johnson, D Keyes, A Laub, L Petzold, D Srolovitz, S Yip (2006) Simulation-based engineering science: revolutionizing engineering science through simulation. Report of NSF Blue Ribbon Panel on Simulation-Based Engineering Science
N. Science, T. Council (2011) Materials genome initiative for global competitiveness, Executive Office of the President. National Science and Technology Council, Washington D.C.
Kalidindi SR (2015) Hierarchical materials informatics. Butterworth Heinemann, Waltham
Brechet Y, Embury J, Tao S, Luo L (1991) Damage initiation in metal matrix composites. Acta Metall Mater 39(8):1781–1786
Brechet Y, Newell J, Tao S, Embury JD (1993) A note on particle comminution at large plastic strains in Al-SiC composites. Scr Metall Mater 28(1):47–51
Caceres CH, Griffiths JR (1996) Damage by the cracking of silicon particles in an Al-7Si-0.4Mg casting alloy. Acta Mater 44(1):25–33
Caceres CH, Griffiths JR, Reiner P (1996) The influence of microstructure on the Bauschinger effect in an Al-Si-Mg casting alloy. Acta Mater 44(1):15–23
Wilkinson DS, Maire E, Fougeres R (1999) A model for damage is a clustered particulate composite. Mater Sci Eng A-Struct 262(1–2):264–270
Wilkinson DS, Maire E, Embury JD (1997) The role of heterogeneity on the flow and fracture of two-phase materials. Mat Sci Eng A-Struct 233(1–2):145–154
Segurado J, Gonzalez C, Llorca J (2003) A numerical investigation of the effect of particle clustering on the mechanical properties of composites. Acta Mater 51(8):2355–2369
Nan CW, Clarke DR (1996) The influence of particle size and particle fracture on the elastic/plastic deformation of metal matrix composites. Acta Mater 44(9):3801–3811
Gupta A, Cecen A, Goyal S, Singh AK, Kalidindi SR (2015) Structure–property linkages using a data science approach: application to a non-metallic inclusion/steel composite system. Acta Mater 91:239–254
Paulson NH, Priddy MW, McDowell DL, Kalidindi SR (2017) Reduced-order structure-property linkages for polycrystalline microstructures based on 2-point statistics. Acta Mater 129:428–438
Latypov MI, Kalidindi SR (2017) Data-driven reduced order models for effective yield strength and partitioning of strain in multiphase materials. J Comput Phys 346:242–261
D Montes de Oca Zapiain, A Fadi, L Hojun, E Popova, SR Kalidindi (2017) 2-Phase composite damage initiation sensitivity dataset, https://matin.gatech.edu/resources/296
Brough DB, Kannan A, Haaland B, Bucknall DG, Kalidindi SR (2017) Extraction of process-structure evolution linkages from X-ray scattering measurements using dimensionality reduction and time series analysis. Integr Mater Manuf Innov 6(2):147–159
CeCen A, Fast T, Kumbur E, Kalidindi S (2014) A data-driven approach to establishing microstructure–property relationships in porous transport layers of polymer electrolyte fuel cells. J Power Sources 245:144–153
S Torquato (2013) Random heterogeneous materials: microstructure and macroscopic properties. Springer Science & Business Media
Kroner E (1986) Statistical modelling. In: Gittus J, Zarka J (eds) Modelling small deformations of polycrystals. Elsevier Science Publishers, London, pp 229–291
Kalidindi SR, Niezgoda SR, Salem AA (2011) Microstructure informatics using higher-order statistics and efficient data-mining protocols. JOM 63(4):34–41
Niezgoda SR, Kanjarla AK, Kalidindi SR (2013) Novel microstructure quantification framework for databasing, visualization, and analysis of microstructure data. Integr Mater Manuf Innov 2(1):3
Jolliffe I (2005) Principal component analysis, encyclopedia of statistics in behavioral science. Wiley, Hoboken
Suh C, Rajagopalan A, Li X, Rajan K (2002) The application of principal component analysis to materials science data. Data Sci J 1:19–26
Niezgoda SR, Yabansu YC, Kalidindi SR (2011) Understanding and visualizing microstructure and microstructure variance as a stochastic process. Acta Mater 59(16):6387–6400
NH Paulson, MW Priddy, DL McDowell, SR Kalidindi (2017) Data-driven reduced-order models for rank-ordering the high cycle fatigue performance of polycrystalline microstructures, Submitted for review
Benesty J, Chen J, Huang Y, Cohen I (2009) Pearson correlation coefficient, noise reduction in speech processing. Springer, Berlin, pp 1–4
P. Sedgwick (2012) Pearson’s correlation coefficient. BMJ 345(7)
Bienias J, Debski H, Surowska B, Sadowski T (2012) Analysis of microstructure damage in carbon/epoxy composites using FEM. Comput Mater Sci 64:168–172
Ghosh S, Moorthy S (1998) Particle fracture simulation in non-uniform microstructures of metal-matrix composites. Acta Mater 46(3):965–982
Needleman A, Tvergaard V (1984) An analysis of ductile rupture in notched bars. J Mech Phys Solids 32(6):461–490
Tvergaard V, Needleman A (1984) Analysis of the cup-cone fracture in a round tensile bar. Acta Metall Mater 32(1):157–169
Gurson AL (1977) Continuum theory of ductile rupture by void nucleation and growth. 1. Yield criteria and flow rules for porous ductile media. J Eng Mater Trans ASME 99(1):2–15
Rice JR, Tracey DM (1969) On ductile enlargement of voids in Triaxial stress fields. J Mech Phys Solids 17(3):201–217
Bao Y, Wierzbicki T (2004) On fracture locus in the equivalent strain and stress triaxiality space. Int J Mech Sci 46(1):81–98
Mirone G (2008) Elastoplastic characterization and damage predictions under evolving local triaxiality: axysimmetric and thick plate specimens. Mech Mater 40(9):685–694
Mirone G (2007) Role of stress triaxiality in elastoplastic characterization and ductile failure prediction. Eng Fract Mech 74(8):1203–1221
Mcclintock FA (1968) A criterion for ductile fracture by growth of holes. J Appl Mech 35(2):363–371
Mcclintock FA (1968) Local criteria for ductile fracture. Int J Fract Mech 4(2):101–130
Mackenzie AC, Hancock JW, Brown DK (1977) On the influence of state of stress on ductile failure initiation in high strength steels. Eng Fract Mech 9(1):167–188
Cockcroft M, Latham D (1968) Ductility and the workability of metals. J Inst Met 96(1):33–39
P Brozzo, B Deluca, R Rendina (1972) A new method for the prediction of formability limits in metal sheets, Proc. 7th biennal Conf. IDDR
Clift SE, Hartley P, Sturgess C, Rowe G (1990) Fracture prediction in plastic deformation processes. Int J Mech Sci 32(1):1–17
Zhang KS, Bai JB, François D (2001) Numerical analysis of the influence of the lode parameter on void growth. Int J Solids Struct 38(32):5847–5856
Xue L (2007) Damage accumulation and fracture initiation in uncracked ductile solids subject to triaxial loading. Int J Solids Struct 44(16):5163–5181
Xue L, Wierzbicki T (2008) Ductile fracture initiation and propagation modeling using damage plasticity theory. Eng Fract Mech 75(11):3276–3293
Biffle JH (1993) JAC3D—a three-dimensional finite element computer program for the nonlinear quasi-static response of solids with the conjugate gradient method. Yucca Mountain Site Characterization Project, Sandia National Labs, Albuquerque
Ahsanullah M (2016) Extreme value distributions. Atlantis Press, Paris
IF Alves, C Neves (2011) Extreme value distributions. 493–496
Jenkinson AF (1955) The frequency distribution of the annual maximum (or minimum) values of meteorological elements. Q J R Meteorol Soc 81(348):158–171
Bali TG (2003) The generalized extreme value distribution. Econ Lett 79(3):423–427
Singh VP (1998) Generalized extreme value distribution, entropy-based parameter estimation in hydrology. Springer, Berlin, pp 169–183
Coles S, Bawa J, Trenner L, Dorazio P (2001) An introduction to statistical modeling of extreme values. Springer, Berlin
Martins ES, Stedinger JR (2000) Generalized maximum-likelihood generalized extreme-value quantile estimators for hydrologic data. Water Resour Res 36(3):737–744
Hosking J (1985) Algorithm as 215: maximum-likelihood estimation of the parameters of the generalized extreme-value distribution. J R Stat Soc: Ser C: Appl Stat 34(3):301–310
Niezgoda SR, Fullwood DT, Kalidindi SR (2008) Delineation of the space of 2-point correlations in a composite material system. Acta Mater 56(18):5285–5292
Acknowledgments
Sandia National Laboratories is a multi-mission laboratory managed and operated by the National Technology and Engineering Solutions of Sandia, LLC., a wholly owned subsidiary of Honeywell International, Inc., for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-NA0003525.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Montes de Oca Zapiain, D., Popova, E., Abdeljawad, F. et al. Reduced-Order Microstructure-Sensitive Models for Damage Initiation in Two-Phase Composites. Integr Mater Manuf Innov 7, 97–115 (2018). https://doi.org/10.1007/s40192-018-0112-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40192-018-0112-0