Abstract
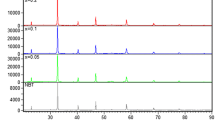
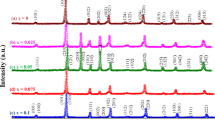
Polycrystalline powders of (1–x)Na0.5Bi0.5TiO3–xCaTiO3 ((1–x)NBT–xCT, 0 ≤ x ≤ 0.55) have been synthesized by solid state route. The effects of simultaneous substitution of Na+/Bi3+ at A-site in NBT on structural and dielectric properties were investigated. X-ray diffraction analysis revealed the phase transition from rhombohedral structure (x = 0) to orthorhombic structure (x ≥ 0.15). A distinct behaviour in dielectric properties was obtained, where for x = 0, a normal ferroelectric behaviour was observed, whereas for x ≥ 0.15, a broad dielectric anomaly was revealed such that the maximum temperature (Tm) strongly depended on the frequency and shifted towards low temperature with CT. The dielectric dispersion indicated a relaxor behaviour revealed by the degree of diffuseness and modelled via Vogel–Fulcher relation. The study highlighted the relaxor behaviour as a function of frequency and proved the transformation from a relaxor high-frequency dependence to a paraelectric phase at temperature Ts. The distinct variation of the Raman spectra at room temperature was correlated with X-ray diffraction results and proved the already mentioned transition. On heating (-193–500 °C), the Raman spectra confirmed the structural stability (Pnma) of the materials. The phonon behaviour for x = 0.15 was discussed in terms of the appearance of polar nanoregions (PNRs) into a non-polar orthorhombic matrix responsible of the relaxor behaviour. For x = 0.20, unchanged phonon behaviour confirmed the variation in dielectric behaviour where the solids transformed from a relaxor to a paraelectric state without structural phase transition.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Ravez J, Simon A. Some solid state chemistry aspects of lead-free relaxor ferroelectrics. J Solid State Chem 2001, 162: 260–265.
Ye Z-G. Relaxor ferroelectric complex perovskites: Structure, properties and phase transitions. Key Eng Mat 1998, 155–156: 81–122.
Ge W, Yao J, DeVreugd C, et al. Electric field dependent phase stability and structurally bridging orthorhombic phase in Na0.5Bi0.5TiO3–x%BaTiO3 crystals near the MPB. Solid State Commun 2011, 151: 71–74.
Chen M, Xu Q, Kim BH, et al. Structure and electrical properties of (Na0.5Bi0.5)1-xBa x TiO3 piezoelectric ceramics. J Eur Ceram Soc 2008, 28: 843–849.
Suchanicz J, Jankowska-Sumara I, Kruzina TV. Raman and infrared spectroscopy of Na0.5Bi0.5TiO3–BaTiO3 ceramics. J Electroceram 2011, 27: 45–50.
Chu B-J, Chen D-R, Li G-R, et al. Electrical properties of Na1/2Bi1/2TiO3–BaTiO3 ceramics. J Eur Ceram Soc 2002, 22: 2115–2121.
Jo W, Daniels JE, Jones JL, et al. Evolving morphotropic phase boundary in lead-free (Bi1/2Na1/2)TiO3–BaTiO3 piezoceramics. J Appl Phys 2011, 109: 014110.
Ma C, Guo H, Beckman SP, et al. Creation and destruction of morphotropic phase boundaries through electrical poling: A case study of lead-free (Bi1/2Na1/2TiO3)–BaTiO3 piezoelectrics. Phys Rev Lett 2012, 109: 107602.
Gomah-Pettry JR, Marchet P, Salak A, et al. Electrical properties of Na0.5Bi0.5TiO3–SrTiO3 ceramics. Integrated Ferroelectrics 2004, 61: 159–162.
Hiruma Y, Imai Y, Watanabe Y, et al. Large electrostrain near the phase transition temperature of (Bi0.5Na0.5)TiO3–SrTiO3 ferroelectric ceramics. Appl Phys Lett 2008, 92: 262904.
Rout D, Moon K-S, Kang S-JL, et al. Dielectric and Raman scattering studies of phase transitions in the (100–x)-Na0.5Bi0.5TiO3–xSrTiO3 system. J Appl Phys 2010, 108: 084102.
Krauss W, Schütz D, Mautner FA, et al. Piezoelectric properties and phase transition temperatures of the solid solution of (1–x)(Bi0.5Na0.5)TiO3–xSrTiO3. J Eur Ceram Soc 2010, 30: 1827–1832.
Wang T, Du H, Shi X. Dielectric and ferroelectric properties of (1–x)Na0.5Bi0.5TiO3–xSrTiO3 lead-free piezoceramics system. J Phys: Conf Ser 2009, 152: 012065.
Praharaj S, Rout D, Kar BB, et al. Study of glassy behavior in 60(Na0.5Bi0.5)TiO3–40SrTiO3 lead-free relaxor. AIP Conference Proceedings 2016, 1731: 140017.
Jin L, Huo R, Guo R, et al. Diffuse phase transitions and giant electrostrictive coefficients in lead-free Fe3+-doped 0.5Ba(Zr0.2Ti0.8)O3–0.5(Ba0.7Ca0.3)TiO3 ferroelectric ceramics. ACS Appl Mater Interfaces 2016, 8: 31109–31119.
Zhang L, Xu Z, Li Z, et al. Preparation and characterization of high Tc (1–x)BiScO3-xPbTiO3 ceramics from high energy ball milling process. J Electroceram 2008, 21: 605–608.
Khansur NH, Glaum J, Clemens O, et al. Uniaxial compressive stress and temperature dependent mechanical behavior of (1–x)BiFeO3–xBaTiO3 lead-free piezoelectric ceramics. Ceram Int 2017, 43: 9092–9098.
Cheng R, Xu Z, Chu R, et al. Large piezoelectric effect in Bi1/2Na1/2TiO3-based lead-free piezoceramics. Ceram Int 2015, 41: 8119–8127.
Jo W, Daniels J, Damjanovic D, et al. Two-stage processes of electrically induced-ferroelectric to relaxor transition in 0.94(Bi1/2Na1/2)TiO3–0.06BaTiO3. Appl Phys Lett 2013, 102: 192903.
Bokov AA, Ye Z-G. Recent progress in relaxor ferroelectrics with perovskite structure. J Mater Sci 2006, 41: 31–52.
Sciau Ph, Calvarin G, Ravez J. X-ray diffraction study of BaTi0.65Zr0.35O3 and Ba0.92Ca0.08Ti0.75Zr0.25O3 compositions: Influence of electric field. Solid State Commun 1999, 113: 77–82.
Simon A, Ravez J, Maglione M. The crossover from a ferroelectric to a relaxor state in lead-free solid solutions. J Phys: Condens Matter 2004, 16: 963.
Yasuda N, Ohwa H, Arai K, et al. Effect of hydrostatic pressure in barium titanate stannate solid solution Ba(Ti1–xSn x )O3. J Mater Sci Lett 1997, 16: 1315–1318.
Chu F, Setter N, Tagantsev AK. The spontaneous relaxor-ferroelectric transition of Pb(Sc0.5Ta0.5)O3. J Appl Phys 1993, 74: 5129–5134.
Dai X, Xu Z, Viehland D. The spontaneous relaxor to normal ferroelectric transformation in La-modified lead zirconate titanate. Philos Mag B 1994, 70: 33–48.
Bobnar V, Kutnjak Z, Pirc R, et al. Electric-field-temperature phase diagram of the relaxor ferroelectric lanthanum-modified lead zirconate titanate. Phys Rev B 1999, 60: 6420–6427.
Setter N, Cross LE. The role of B-site cation disorder in diffuse phase transition behavior of perovskite ferroelectrics. J Appl Phys 1980, 51: 4356–4360.
Burns G, Dacol FH. Glassy polarization behavior in ferroelectric compounds Pb(Mg1/3Nb2/3)O3 and Pb(Zn1/3Nb2/3)O3. Solid State Commun 1983, 48: 853–856.
Bonneau P, Garnier P, Calvarin G, et al. X-ray and neutron diffraction studies of the diffuse phase transition in PbMg1/3Nb2/3O3 ceramics. J Solid State Chem 1991, 91: 350–361.
Bonneau P, Garnier P, Husson E, et al. Structural study of PMN ceramics by X-ray diffraction between 297 and 1023 K. Mater Res Bull 1989, 24: 201–206.
Uesu Y, Tazawa H, Fujishiro K, et al. Neutron scattering and nonlinear-optical studies on the phase transition of ferroelectric relaxor Pb(Mg1/3Nb2/3)O3. Journal of the Korean Physical Society 1996, 29: S703–S705.
Vakhrushev S, Nabereznov A, Sinha SK, et al. Synchrotron X-ray scattering study of lead magnoniobate relaxor ferroelectric crystals. J Phys Chem Solids 1996, 57: 1517–1523.
Moriya Y, Kawaji H, Tojo T, et al. Specific-heat anomaly caused by ferroelectric nanoregions in Pb(Mg1/3Nb2/3)O3 and Pb(Mg1/3Ta2/3)O3 relaxors. Phys Rev Lett 2003, 90: 205901.
De Mathan N, Husson E, Calvarn G, et al. A structural model for the relaxor PbMg1/3Nb2/3O3 at 5 K. J Phys: Condens Matter 1991, 3: 8159.
Jeong I-K, Darling TW, Lee JK, et al. Direct observation of the formation of polar nanoregions in Pb(Mg1/3Nb2/3)O3 using neutron pair distribution function analysis. Phys Rev Lett 2005, 94: 147602.
Xu G, Shirane G, Copley JRD, et al. Neutron elastic diffuse scattering study of Pb(Mg1/3Nb2/3)O3. Phys Rev B 2004, 69: 064112.
Shvartsman VV, Kholkin AL, Orlova A, et al. Polar nanodomains and local ferroelectric phenomena in relaxor lead lanthanum zirconate titanate ceramics. Appl Phys Lett 2005, 86: 202907.
You H, Zhang QM. Diffuse X-ray scattering study of lead magnesium niobate single crystals. Phys Rev Lett 1997, 79: 3950.
La-Orauttapong D, Toulouse J, Robertson JL, et al. Diffuse neutron scattering study of a disordered complex perovskite Pb(Zn1/3Nb2/3)O3 crystal. Phys Rev B 2001, 64: 212101.
Dkhil B, Kiat JM, Calvarin G, et al. Local and long range polar order in the relaxor-ferroelectric compounds PbMg1/3Nb2/3O3 and PbMg0.3Nb0.6Ti0.1O3. Phys Rev B 2001, 65: 024104.
Hirota K, Ye Z-G, Wakimoto S, et al. Neutron diffuse scattering from polar nanoregions in the relaxor Pb(Mg1/3Nb2/3)O3. Phys Rev B 2002, 65: 104105.
Dorcet V, Trolliard G, Boullay P. The structural origin of the antiferroelectric properties and relaxor behavior of Na0.5Bi0.5TiO3. J Magn Magn Mater 2009, 321: 1758–1761.
Lee J-K, Hong KS, Kim CK, et al. Phase transitions and dielectric properties in A-site ion substituted (Na1/2Bi1/2)TiO3 ceramics (A = Pb and Sr). J Appl Phys 2002, 91: 4538.
Otonicar M, Škapin SD, Spreitzer M, et al. Compositional range and electrical properties of the morphotropic phase boundary in the Na0.5Bi0.5TiO3–K0.5Bi0.5TiO3 system. J Eur Ceram Soc 2010, 30: 971–979.
Hiruma Y, Nagata H, Takenaka T. Detection of morphotropic phase boundary of (Bi1/2Na1/2)TiO3–Ba(Al1/2Sb1/2)O3 solid-solution ceramics. Appl Phys Lett 2009, 95: 052903.
Watanabe Y, Hiruma Y, Nagata H, et al. Phase transition temperatures and electrical properties of divalent ions (Ca2+, Sr2+ and Ba2+) substituted (Bi1/2Na1/2)TiO3 ceramics. Ceram Int 2008, 34: 761–764.
Yuan Y, Li EZ, Li B, et al. Effects of Ca and Mn additions on the microstructure and dielectric properties of (Bi0.5Na0.5)TiO3 ceramics. J Electron Mater 2011, 40: 2234–2239.
Ranjan R, Garg R, Kothai V, et al. Phases in the (1-x)Na0.5Bi0.5TiO3–(x)CaTiO3 system. J Phys: Condens Matter 2010, 22: 075901.
Du HL, Du X, Li HL. Phase structure and electrical properties of lead free Na0.5Bi0.5TiO3–CaTiO3 ceramics. Adv Appl Ceram 2013, 112: 277–281.
Birks E, Dunce M, Ignatans R, et al. Structure and dielectric properties of Na0.5Bi0.5TiO3–CaTiO3 solid solutions. J Appl Phys 2016, 119: 074102.
Aksel E, Forrester JS, Jones JL, et al. Monoclinic crystal structure of polycrystalline Na0.5Bi0.5TiO3. Appl Phys Lett 2011, 98: 152901.
Roukos R. Transitions de phases dans des oxydes complexes de structure pérovskite: cas du système (1–x)Na0.5Bi0.5TiO3–xCaTiO3. Université de Bourgogne, 2015.
Roukos R, Geoffroy N, Chaumont D. Electric field induced monoclinic phase stability in Ca doped Na0.5Bi0.5TiO3: Case of 0.93Na0.5Bi0.5TiO3–0.07CaTiO3 ferroelectric ceramics. AIP Advances 2017, 7: 015030.
Craciun F, Galassi C, Birjega R. Electric-field-induced and spontaneous relaxor-ferroelectric phase transitions in (Na1/2Bi1/2)1-xBaxTiO3. J Appl Phys 2012, 112: 124106.
Parija B, Badapanda T, Rout SK, et al. Morphotropic phase boundary and electrical properties of 1-x[Bi0.5Na0.5]TiO3–xBa[Zr0.25Ti0.75]O3 lead-free piezoelectric ceramics. Ceram Int 2013, 39: 4877–4886.
Zheng H, Csete de Györgyfalva GDC, Quimby R, et al. Raman spectroscopy of B-site order–disorder in CaTiO3-based microwave ceramics. J Eur Ceram Soc 2003, 23: 2653–2659.
Selvamani R, Singh G, Sathe V, et al. Dielectric, structural and Raman studies on (Na0.5Bi0.5TiO3)(1-x)(BiCrO3) x ceramic. J Phys: Condens Matter 2011, 23: 055901.
Xu C, Lin D, Kwok KW. Structure, electrical properties and depolarization temperature of (Bi0.5Na0.5)TiO3–BaTiO3 lead-free piezoelectric ceramics. Solid State Sci 2008, 10: 934–940.
Sapper E, Schaab S, Jo W, et al. Influence of electric fields on the depolarization temperature of Mn-doped (1–x)-Bi1/2Na1/2TiO3–xBaTiO3. J Appl Phys 2012, 111: 014105.
Jo W, Schaab S, Sapper E, et al. On the phase identity and its thermal evolution of lead free (Bi1/2Na1/2)TiO3–6 mol% BaTiO3. J Appl Phys 2011, 110: 074106.
Barick BK, Mishra KK, Arora AK, et al. Impedance and Raman spectroscopic studies of (Na0.5Bi0.5)TiO3. J Phys D: Appl Phys 2011, 44: 355402.
Bai W, Chen D, Zheng P, et al. Composition- and temperature-driven phase transition characteristics and associated electromechanical properties in Bi0.5Na0.5TiO3-based lead-free ceramics. Dalton Trans 2016, 45: 8573–8586.
Bai W, Chen D, Zheng P, et al. NaNbO3 templates-induced phase evolution and enhancement of electromechanical properties in <00l> grain oriented lead-free BNT-based piezoelectric materials. J Eur Ceram Soc 2017, 37: 2591–2604.
Wang K, Hussain A, Jo W, et al. Temperature-dependent properties of (Bi1/2Na1/2)TiO3–(Bi1/2K1/2)TiO3–SrTiO3 lead-free piezoceramics. J Am Ceram Soc 2012, 95: 2241–2247.
Chu B-J, Chen D-R, Li G-R, et al. Electrical properties of Na1/2Bi1/2TiO3–BaTiO3 ceramics. J Eur Ceram Soc 2002, 22: 2115–2121.
Oh T. Dielectric relaxor properties in the system of (Na1–xK x )1/2Bi1/2TiO3 ceramics. Jpn J Appl Phys 2006, 45: 5138.
Jarupoom P, Pengpat K, Pisitpipathsin N, et al. Development of electrical properties in lead-free bismuth sodium lanthanum titanate–barium titanate ceramic near the morphotropic phase boundary. Curr Appl Phys 2008, 8: 253–257.
Singh AK, Pandey D. Evidence for MB and MC phases in the morphotropic phase boundary region of (1–x)-[Pb(Mg1/3Nb2/3)O3]– x PbTiO3: A Rietveld study. Phys Rev B 2003, 67: 064102.
Ma HY, Chen XM, Wang J, et al. Structure, dielectric and ferroelectric properties of 0.92Na0.5Bi0.5TiO3–0.06BaTiO3–0.02K0.5Na0.5NbO3 lead-free ceramics: Effect of Co2O3 additive. Ceram Int 2013, 39: 3721–3729.
Li Y, Chen W, Zhou J, et al. Dielectric and ferroelectric properties of lead-free Na0.5Bi0.5TiO3–K0.5Bi0.5TiO3 ferroelectric ceramics. Ceram Int 2005, 31: 139–142.
Talik B. Ferroelectric relaxor behavior and spectroscopic properties of Ba2+ and Zr4+ modified sodium bismuth titanate. Am J Mater Sci 2012, 2: 110–118.
Tagantsev AK. Vogel–Fulcher relationship for the dielectric permittivity of relaxor ferroelectrics. Phys Rev Lett 1994, 72: 1100.
Grigalaitis R, Ivanov M, Macutkevic J, et al. Size effects in a relaxor: Further insights into PMN. J Phys: Condens Matter 2014, 26: 272201.
Liu J, Duan C-G, Yin W-G, et al. Dielectric permittivity and electric modulus in Bi2Ti4O11. J Chem Phys 2003, 119: 2812–2819.
Grigalaitis R, Banys J, Kania A, et al. Distribution of relaxation times in PMN single crystal. J Phys IV France 2005, 128: 127–131.
Kreisel J, Glazer AM, Bouvier P, et al. High-pressure Raman study of a relaxor ferroelectric: The Na0.5Bi0.5TiO3 perovskite. Phys Rev B 2001, 63: 174106.
Luo L, Ge W, Li J, et al. Raman spectroscopic study of Na1/2Bi1/2TiO3–x%BaTiO3 single crystals as a function of temperature and composition. J Appl Phys 2011, 109: 113507.
Aksel E, Forrester JS, Kowalski B, et al. Structure and properties of Fe-modified Na0.5Bi0.5TiO3 at ambient and elevated temperature. Phys Rev B 2012, 85: 024121.
Bai W, Li P, Li L, et al. Structure evolution and large strain response in BNT–BT lead-free piezoceramics modified with Bi(Ni0.5Ti0.5)O3. J Alloys Compd 2015, 649: 772–781.
Wakimoto S, Stock C, Birgeneau RJ, et al. Ferroelectric ordering in the relaxor Pb(Mg1/3Nb2/3)O3 as evidenced by low-temperature phonon anomalies. Phys Rev B 2002, 65: 172105.
Li F, Zuo R, Zheng D, et al. Phase-composition-dependent piezoelectric and electromechanical strain properties in (Bi1/2Na1/2)TiO3–Ba(Ni1/2Nb1/2)O3 lead-free ceramics. J Am Ceram Soc 2015, 98: 811–818.
Schütz D, Deluca M, Krauss W, et al. Lone-pair-induced covalency as the cause of temperature- and field-induced instabilities in bismuth sodium titanate. Adv Funct Mater 2012, 22: 2285–2294.
Sasaki A, Chiba T, Mamiya Y, et al. Dielectric and piezoelectric properties of (Bi0.5Na0.5)TiO3–(Bi0.5K0.5)TiO3 systems. Jpn J Appl Phys 1999, 38: 5564.
Ragini, Ranjan R, Mishra SK, et al. Room temperature structure of Pb(Zr x Ti1-xO3) around the morphotropic phase boundary region: A Rietveld study. J Appl Phys 2002, 92: 3266–3274.
Daniels JE, Jo W, Rödel J, et al. Electric-field-induced phase transformation at a lead-free morphotropic phase boundary: Case study in a 93%(Bi0.5Na0.5)TiO3–7%BaTiO3 piezoelectric ceramic. Appl Phys Lett 2009, 95: 032904.
Viehland D, Wuttig M, Cross LE. The glassy behavior of relaxor ferroelectrics. Ferroelectrics 1991, 120: 71–77.
Hiruma Y, Nagata H, Takenaka T. Thermal depoling process and piezoelectric properties of bismuth sodium titanate ceramics. J Appl Phys 2009, 105: 084112.
Acknowledgements
R. Roukos and the other authors wish to acknowledge the French Ministry of Higher Education and Research and give special thanks to Dr. Fatima Barakat and Nathalie Azar for supporting this work. This work was supported by the Nanosciences Department of Université de Bourgogne.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is published with open access at Springerlink.com
Rights and permissions
Open Access The articles published in this journal are distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Roukos, R., Zaiter, N. & Chaumont, D. Relaxor behaviour and phase transition of perovskite ferroelectrics-type complex oxides (1–x)Na0.5Bi0.5TiO3–xCaTiO3 system. J Adv Ceram 7, 124–142 (2018). https://doi.org/10.1007/s40145-018-0264-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40145-018-0264-6