Abstract
Purpose
The proper choice of an intraocular lens (IOL) power calculation formula is an important aspect of phacoemulsification. In this study, the formulas most commonly used today are described and their accuracy is evaluated.
Methods
This review includes papers evaluating the accuracy of IOL power calculation formulas published during the period from January 2015 to December 2022. The articles were identified by a literature search of medical and other databases (PubMed/MEDLINE, Crossref, Web of Science, SciELO, Google Scholar, and Cochrane Library) using the terms “IOL formulas,” “Barrett Universal II,” “Kane,” “Hill-RBF,” “Olsen,” “PEARL-DGS,” “EVO,” “Haigis,” “SRK/T,” and “Hoffer Q.” Twenty-nine of the most recent peer-reviewed papers in English with the largest samples and largest number of formulas compared were considered.
Results
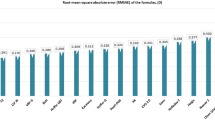
Outcomes of mean absolute error and percentage of predictions within ±0.5 D and ±1.0 D were used to evaluate the accuracy of the formulas. In most studies, Barrett achieved the smallest mean absolute error and PEARL-DGS the highest percentage of patients with ±0.5 D in short eyes, while Kane obtained the highest percentage of patients with ±0.5 D in long eyes.
Conclusions
The third- and fourth-generation formulas are gradually being replaced by more accurate ones. The Barrett Universal II among vergence formulas and Kane and PEARL-DGS among artificial intelligence-based formulas are currently most often reported as the most precise.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
The accuracy of the refractive power of the intraocular lens (IOL) implant depends on the exactness of the IOL power calculation formula. |
There is no consensus in the literature regarding the choice of formula. |
A review of the current literature will help cataract surgeons to choose the appropriate IOL power calculation formula before phacoemulsification. |
The Barrett Universal II among vergence formulas and the Kane and PEARL-DGS among artificial intelligence-based formulas are currently most often reported as the most precise. |
The accuracy of IOL formulas depends on the axial length and corneal curvature. |
Introduction
Refractive accuracy is one of the basic goals of successful cataract surgery [1]. However, according to the European Registry of Quality Outcomes for Cataract and Refractive Surgery, the percentage of prediction error within ±0.5 D after cataract surgery is 73.7% [2]. The accuracy of the refractive power of the intraocular lens (IOL) implant depends not only on the accuracy of the preoperative biometric data such as axial length (AL), keratometry (K), and anterior chamber depth (ACD), where inaccuracy in measurement can contribute to 36%, 22%, and 42% of error, respectively, but most of all on effective lens position (ELP) estimation resulting from the selection of the appropriate formula [3, 4].
Over the years, many IOL power calculation formulas have been introduced in efforts to obtain the most precise postoperative refractive results. Traditionally they were classified by generations, as shown in Table 1 [5]. However, categorizing formulas based on a logical approach is much more useful (Table 2).
In addition, there are formulas that are used in special cases, such as the phakic lens formulas (Linz–Homburg–Castrop, Holladay, and Olsen–Feingold) [6] or post-refractive formulas listed in Table 3 [7,8,9].
Most IOL power calculation formulas have satisfactory refractive outcomes for eyes with AL ranging between 22.0 and 25.0 mm [10]. The accuracy of IOL power calculation formulas for eyes shorter than 22.0 mm and longer than 25.0 mm is less precise [11,12,13,14]. So far, the Barrett Universal 2 formula has appeared to be the most accurate in calculating IOL power for myopic eyes [5, 14,15,16,17], and Kane for hyperopic eyes [18,19,20,21]. But the newly developed methods have very promising results as well [22,23,24]. However, there is no consensus in the literature regarding the choice of the formula.
To the best of the authors’ knowledge, there are no peer-reviewed review articles considering 18 newer IOL power calculation formulas. This is probably because new formulas have just been introduced. The aim of this paper is to describe and to compare the exactness of most of the formulas on the market.
Methods
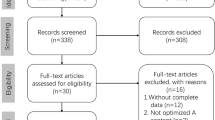
The methodology follows the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) guidelines. This review includes papers concerning the accuracy of IOL power calculation formulas published during the period 2015–2022. The papers were identified by a literature search of medical and other databases (PubMed/MEDLINE, Web of Science, SciELO, Crossref, Google Scholar, Cochrane Library) using the terms “IOL formulas,” “Barrett Universal II,” “Kane,” “Hill-RBF,” “Olsen,” “PEARL-DGS,” “EVO,” “Haigis,” “SRK/T,” and “Hoffer Q.” Duplicates were removed at the screening. The preliminary search was based on abstracts. Only peer-reviewed articles in English were considered. Studies presented as editorials were excluded. After the preliminary manual search, only 26 papers were selected for further analysis. The articles with data obtained with ultrasound biometry using the contact technique were excluded, but no distinction was made between optical biometers. Studies with the largest samples (> 170 eyes for entire AL or > 40 short eyes or > 65 long eyes), with the largest number of IOL power calculation formulas (> 8) compared, and which were published most recently (from the last 5 years) were used. Papers with risk of bias were excluded. Articles in which the author’s formula achieved the best outcomes were excluded. Additionally, papers with bilateral eyes were excluded according to Hoffer’s protocol [25]. However, preliminary sample size calculation was not considered.
This article is based on previously conducted studies and does not contain any new studies with human participants or animals performed by any of the authors.
Results
The removal of duplicates resulted in 192 articles being retrieved and analyzed. After the preliminary search, 26 papers were selected for further analysis. A detailed PRISMA flow chart (Fig. 1) shows the identification, screening, and selection of papers for this review. It was found that different formulas could have advantages and disadvantages for individual patients in terms of eyeball AL: the longer or shorter the eye, the less accurate some formulas become.
Many different tools could be employed to assess the accuracy of the chosen formula. Most research in this area is based on observation of mean absolute error (MAE) and percentage of eyes within ±0.5 D, less often of median absolute error (MedAE). Hoffer et al. recommended the use of MedAE as a primary outcome in this type of study due to the non-normal distribution of absolute refractive prediction error [25]. In turn, Cooke et al. proposed a mean rank score for subgroup analysis (e.g., in terms of AL) [26], and Haigis developed his own rank [25]. Detailed outcomes of recent studies (MAE, percentage of eyes within ±0.5 D and ±1.0 D) are summarized in Table 4.
The Third- and Fourth-Generation Formulas
At the turn of the twenty-first century, several third- and fourth-generation formulas had dominated IOL power calculations for over 30 years [27]. The Holladay 1 formula was launched in 1988 by Jack T. Holladay and was based on variables AL, K, and specific surgeon factor (SF). This produced accurate outcomes in short eyes [28]. The SRK/T (for Sanders, Retzlaff, Kraff; T for theoretical) formula was developed by Donald R. Sanders, John A. Retzlaff, and Manus C. Kraff in 1990. This is a combination of a linear regression method with a theoretical eye model [29]. In 1993, Kenneth J. Hoffer published the Hoffer Q formula based on AL, K, and personalized ACD (pACD) [30]. This formula was recommended for short eyes [18, 31]. The Holladay 2 formula launched in 1996 determines ELP using seven parameters (in order of importance): AL, average K, horizontal white-to-white (WTW), preoperative refraction, ACD, lens thickness (LT), and age [32]. Wolfgang Haigis published the Haigis formula in 2000. This empirical formula uses the variables AL, K, and ACD, and three constants a0, a1 (associated with measured ACD), and a2 (associated with measured AL) [27].
The Newer Formulas
The FullMonte Method
In 1997, Gerald Clarke and Jeanne Burmeister proposed the first neural network for biometric computations specifically to predict IOL power using a personalized Holladay program and clinical data from 200 subsequent cases of one surgeon's outcomes with one IOL. Input data included preoperative AL, K, ACD, and LT. The neural network was trained to obtain the actual postoperative refractive error, and the Holladay surgeon factor was continuously refined using the same results. Then, after the network was successfully trained against the clinical data, it was used to compute IOL power in a double-masked study. FullMonte is a hybrid formula. Clarke and Kalpener launched a combined method based on the SRK/T formula and an artificial intelligence (AI) algorithm called Bayesian additive regression trees (BART), optimized with a Markov chain Monte Carlo simulator to create its refractive predictions [33].
The Olsen Formula
The Olsen formula was developed by Thomas Olsen in 2006. It is based on ray-tracing tools to account for the true physical dimensions of an eye’s optical system. The Olsen formula precisely estimates the physical position of the IOL using a newly developed concept, the C-constant (a ratio by which the empty capsular bag will encapsulate and fixate an IOL following in-the-bag implantation). This unique approach considers the IOL position as a function of preoperative ACD and LT; therefore, traditional factors such as AL, K, WTW, IOL power, age, and gender are unnecessary. The great advantage is the ability for exact calculation of the implant power in any type of eye, including eyes after refractive surgery, because its only requirements are accurate measurements of ACD and LT [34].
The T2 Formula
In 2010, Richard M. Sheard, Guy T. Smith, and David L. Cooke introduced the T2 formula. It is a modification of SRK/T to improve the original formula, especially in cases of extreme K. The T2 formula was developed to correct a non-physiological behavior of the corneal height prediction (so-called cusp phenomenon). It uses the same optical A-constant of the SRK/T and intensified regression algorithm for postoperative prognosis of the anterior segment of the eye. It was programmed into Excel according to the original data [35].
The Barrett Universal II Formula
The Barrett Universal II formula launched in 2010 by Graham Barrett was based on Gaussian simplification of the Snellen refraction law in the paraxial space. It investigates the change from principal planes that occurs with different IOL power. It also considers the shift of the optic configuration from biconvex to meniscus lens. And finally, it views the modification in vergence that occurs when the lens changes from a plus to a minus, and as such it does not require additional correction elements or constants customized for patients with high myopia and very long AL. The Barrett Universal II formula has a unique theoretical model to predict the ELP which differs quite significantly from the other ones. As a theoretical formula, it uses traditional mathematics for IOL power calculation based on obligatory data (lens factor or A-constant, AL, K, ACD, target refraction) and optional data such LT and WTW; however, it was demonstrated that Barrett could be calculated even without ACD [2, 5, 36] The formula is available online, https://calc.apacrs.org/barrett_universal2105/.
The Ladas Super Formula
In 2015, John G. Ladas, Albert Jun, Aazim Siddiqui, and Uday Devgan proposed the concept of an IOL “super formula” which combined the advantages of previous models. They considered the Hoffer Q, Holladay 1, Holladay 1 with Koch adjustment, SRK/T, and Haigis formulas. All these formulas were thought of as two-dimensional algebraic equations. Ladas et al. found a novel methodology of describing these formulas as mathematical equations with the potential to be graphically plotted on the x, y, and z axes and represented in three dimensions (AL [mm], corneal power [D], IOL power [D]). In this way they provided a framework for analyzing these formulas in terms of their accuracy. Using this concept, from the peer-reviewed literature, the best sections identified for each of the abovementioned IOL formulas were chosen, and an IOL super surface was developed [37]. Retrospective analyses showed that SRK/T tends to be better for longer eyes [5], while the Hoffer Q is more accurate for very short eyes [38]. In addition, due to AL or corneal power, some eyes require further optimization; for example, hyperopic eyes are difficult to calculate, as the smallest of changes in ELP can alter the lens power calculations significantly. From this super surface, the Ladas formula was derived. The last step was the adjustment of existing formulas using deep learning. This was introduced by Ladas and colleagues and is called the Ladas PLUS method [39]. A formula calculator is accessible online, https://iolcalc.com.
The Hill Radial Basis Function (RBF) Formula
The Hill-RBF, as the first purely AI formula, was launched in 2016 by Warren E. Hill, MD, and was based on radial basis functions. The Hill-RBF formula is a purely data-driven IOL calculation approach. It employs pattern recognition developed in MATLAB and a sophisticated form of data interpolation. It uses a large dataset (more than 12,000 eyes in version 2.0 and over 30,000 eyes in version 3.0, which has been available since September 2020). Initially, Hill-RBF would not provide a refractive prediction if it was likely to be inaccurate, and early versions were restricted to plano target refraction. Currently, it always provides the prediction, just appending a warning sign next to it when the outcome is doubtful. Data inputs for the Hill-RBF 3.0 formula include AL, K, ACD, LT, WTW, central corneal thickness (CCT), and gender [28]. The formula is available online, https://rbfcalculator.com.
The PEARL-DGS Formula
In 2017, Debellemanière, Gatinel, and Saad launched a new formula based on optical and machine learning modeling called PEARL-DGS (PEARL: Prediction Enhanced by ARtificial Intelligence and output Linearization; DGS named after the formula developers). As a thick lens formula it uses the prediction of the theoretical distance between the posterior corneal surface and the anterior IOL surface called the theoretical internal lens position (TILP). At the same time, as an AI-based formula, it uses postoperative data to back-calculate TILP, which is independent of both the lens principal plane positions and the corneal thickness. The PEARL-DGS formula employs various machine learning algorithms (e.g., gradient boosted trees, regular multiple regression, and support vector regression) to predict TILP. Data inputs of the PEARL-DGS formula include AL, K, ACD, LT, WTW, and CCT. Adjustable IOL constants are the same as for the third-generation formulas. The corneal index was determined empirically during the formula development process, while other refractive index values are typical as in the Atchison model eye. Output linearization and no re-training for new IOL models are characteristic for the PEARL-DGS formula [40, 41]. Online access is available, https://iolsolver.com.
The Kane Formula
Jack X. Kane, MD, from Australia developed a new IOL power calculation formula in September 2017 using about 30,000 highly accurate cases from selected surgeons. The Kane formula uses a combination of theoretical optics, thin lens formulas, and “big data” techniques to make its predictions. As a hybrid formula, it is based on optics and includes both regression and AI elements to further improve its outcomes [42]. The formula was developed using high-performance cloud-based computing, which is a way to leverage the power of the cloud to create a virtual supercomputer capable of accelerated computing. A focus of the formula was to reduce the errors seen at the extreme eyeball AL. A-constant (very similar to the SRK/T A-constant, although surgeon’s optimized A-constant is recommended), AL, K, ACD, and patient biological sex are compulsory variables used in the Kane formula. In turn, LT and CCT as optional input data improve the prediction. This approach allows those with older biometers to use the formula. The formula is accessible online, https://iolformula.com.
The Panacea Formula
Panacea was developed by David Flikier in 2017. This is a thin-lens vergence formula using four types of variables: biometric (AL, ACD, LT), keratometric, and topometric data. Keratometric data include mean K of the anterior face and IOL and A-constant (ideally should be readjusted by each surgeon according to the type of IOL, but the values reported by ULIB [User Group for Laser Interference Biometry] for SRK/T can be used as well). Panacea is the only formula enabling surgeons to enter topometric data—the corneal asphericity (Q-value) of the anterior surface and the ratio between the anterior and posterior corneal curvature—which should improve the refractive accuracy [27]. Online access is available, https://panaceaiolandtoriccalculator.com.
The K6 Formula
David L. Cooke and Timothy L. Cooke proposed K6 in 2018. This vergence formula was developed in three stages. First, it was considered with SN60WF IOL using a thick-lens formula for the IOL and back-calculation for the ideal corneal power. Then the prediction formula for the ideal corneal power (the reason for the name “K formula”) was developed. The prediction formula for ideal corneal power with sum-of-segment AL (a form of Cooke-modified AL called CMAL) was used to determine a thin-lens ELP prediction. Finally, an A-constant was added to work with other IOLs. K6 requires six variables: AL, K, CCT, LT, WTW, and aqueous depth (AQD) calculated by subtracting the CCT from the ACD [21]. The formula is available online, https://cookeformula.com.
The Voytsekhivskyy Regression Function (VRF) Formula
VRF was developed and published by Oleksiy V. Voytsekhivskyy, MD, from Ukraine in 2018. This is a vergence-based thin-lens formula using ACD constant for optical biometry (CACD optical) and four variables for estimation of postoperative lens position, including AL, K, preoperative ACD (epithelium to lens), and the horizontal CD. It was programmed into Excel by the author. The VRF algorithm is empirical [43].
The Næser 2 Formula
In 2019, Kristian Næser published the Næser 2 formula. This is a thick-lens vergence formula. Instead of ELP, it calculates the anatomical postoperative ACD. The IOL thickness and anterior/posterior curvatures are calculated for each IOL power. Postoperative optimization on a separate dataset of 300 eyes with AL ranging from 21.46 to 27.96 mm was used to obtain regression for different types of IOLs; therefore, refractive outcomes are equally good in hyperopic, emmetropic, and myopic eyes. This formula is available in Excel (Microsoft Corporation, Redmond, WA, USA) from its author via personal communication [44].
The Emmetropia Verifying Optical (EVO) Formula
EVO was developed by Tun Kuan Yeo from Singapore in 2019. This is a thick-lens formula based on the theory of emmetropization that generates an “emmetropia factor” for each eye and can manage different IOL geometry and power. It is unknown whether any AI element is included. EVO version 2.0 is available online at www.evoiolcalculator.com (accessed on November 30, 2022) and uses AL, K, and ACD as the predictors (LT and CCT are optional). It was recently demonstrated that EVO could calculate even without ACD [36]. Version 2.0 has improved prediction for long and short eyes, and toric IOLs [27]. The formula calculator is accessible online, https://evoiolcalculator.com.
The Voytsekhivskyy Regression Function-Gender (VRF-G) Formula
In 2020, Oleksiy V. Voytsekhivskyy published the VRF-G formula as a modification and improvement of the VRF. The VRF-G formula is based on theoretical optics with regression and ray-tracing components. This very sophisticated formula uses the optical A-constant for SRK/T and operates eight variables including four mandatory, i.e., AL, K, ACD, and gender, and four optional, i.e., LT, horizontal CD, CCT and preoperative refraction [45].
The Karmona Formula
The Karmona formula was designed and programmed in Shiny-RStudio version 1.1.423 (R Foundation, Boston, USA) by David Carmona González (Madrid, Spain, 2018–2021). It is a result of pure AI without optics (either linear Gaussian optics or ray tracing). It is based on two combined machine learning models, which were selected from 11 nonlinear regression strategies that showed the best performance. They were then hyperparametrized and tuned to improve their metrics. Finally, an ensemble model was generated that combined prediction from separate strategies (regularized Bayesian neural network and cubist decision tree) [22]. Karmona requires the AL, ACD, K, WTW, and corneal anterior surface central radius, and optionally LT and corneal posterior surface central radius, anterior segment depth as the sum of ACD and LT, ratio of the back to front corneal surface central radius, and gender.
As a new method, Karmona was developed with a database of only 386 eyes, with AL ranging mainly between 22.0 and 25.0 mm, but as with any other AI-based formula, it is constantly learning, so its predictive capacity is continuously improving. Using unique data input such as anterior segment depth and ratio of the back to front corneal surface central radius as a separate parameter, Karmona is designed to increase the accuracy in extreme and atypical eyes. The formula can be obtained online, https://karmona-iol.com.
The Hoffer QST Formula
In 2021, Kenneth Hoffer (USA), Giacomo Savini (Italy), and Leonardo Taroni (Italy) proposed the Hoffer QST (Hoffer Q/Savini/Taroni) formula as an improvement of the third-generation vergence-based Hoffer Q by using AI [24]. In particular, they aimed to increase accuracy in long eyes. For this purpose, a customized AL adjustment was developed from a sample with more than 300 eyes longer than 25.0 mm. Additionally, the ACD prediction of the Hoffer Q was replaced with the pACD and the T-factor. This was created by entering the parameters K, AL, ACD measured from corneal epithelium to lens, and gender into a linear machine learning model. It was developed on an independent sample of 537 eyes. The formula is available online, https://hofferqst.com.
The Castrop Formula
The Castrop formula was published in 2021 by Achim Langenbucher (Germany) and Peter Hoffmann (Germany). This is a paraxial vergence formula based on a pseudophakic model eye with the following refractive surfaces: spectacle plane, cornea described with corneal front and back surface curvature and central thickness, and an IOL implant. Castrop uses three constants—C, H, and R. The C-constant is in accordance with the Olsen formula, H is for a systematic shift of the IOL plane (characterized by the optics and haptics design), and R is for an offset in predicted refraction.
It requires the variables AL, CCT, ACD, LT, mean corneal radius of curvature (Rmean), and the corneal back surface radius [46]. The formula is accessible online, https://iolcon.org.
The Okulix Formula
Okulix is a numerical ray-tracing software which was developed in Mainz (Germany) by Preussner et al. It calculates the path and the focal point of the entire beams passing through the pupils at each optical level (intravitreal, lens, aqueous humor, and cornea) in terms of Snell's law. AL, IOL central thickness, IOL curvature radii, asphericity, and refractive index, as well as corneal topography measurements (anterior/posterior corneal keratometric values and CCT) are used in Okulix software for more precise IOL power calculation. The software demonstrated acceptable performance in eyes with long AL [47].
Subgroup Analysis
The detailed results of several published studies on the application of IOL power calculation formulas in short eyes (AL < 22.0 mm) and long eyes (AL > 26.0 mm) are summarized in Tables 5 and 6, respectively.
Discussion
Short Eyes
Accurate IOL power calculation is a very important aspect of phacoemulsification because patients’ expectations for perfect vision after cataract surgery continue to increase [48]. In short eyes, small AL combined with high-power IOL can cause a large refractive surprise with a minimal shift in ELP. Additionally, the tolerance for IOLs with a power higher than 30 D is ±1.00 D, and therefore such IOLs could have different standards to tag the optical power by their producers [21].
In 2018, Wang et al. published a meta-analysis based on ten observational studies involving 1161 eyes (218 with Holladay 2, 512 with Haigis, 1161 with Hoffer Q, 986 with Holladay 1, 1071 with SRK/T, and 84 with SRK II). They found that Haigis was significantly superior to Hoffer Q, SRK/T, and SRK II, although they did not identify any statistical difference between Haigis and Holladay 1 and Holladay 2. The Holladay 2 formula obtained the smallest MAE, and the largest MAE difference was observed between Holladay 2 and SRK II. However, the meta-analysis did not consider the latest IOL power calculation formulas such as Hill-RBF, Kane, EVO, Ladas, or K6 [13]. On the other hand, Kane et al. in their 2017 study concluded that new IOL power calculation formulas such Ladas, Hill-RBF, and FullMonte had failed to yield more accurate results than the current Barrett Universal II and Holladay 1 methods. However, they did not include either the Kane formula or the EVO formula [28].
A meta-analysis by Shrivastava et al. in 2022 including 15 studies, 2395 eyes, and 11 formulas (Barrett Universal II, FullMonte, Haigis, Hill-RBF, Hoffer Q, Holladay 1, Holladay 2, Olsen, Ladas super formula, SRK/T, and T2) found no statistically significant difference in any of the comparisons in terms of MAE, ±0.5 D, or ±1.0 D, although the Barrett Universal II formula achieved the lowest MAE and the Holladay 1 and Hill-RBF had the highest percentage of eyes within ±0.50 D and ±1.0 D of target refraction, respectively. Thus, in their meta-analysis, none of the 11 formulas was found to be significantly superior to others in hyperopic eyes [49].
The most recent meta-analysis published by Luo et al. in June 2022 included 1476 eyes from 14 studies comparing 13 formulas (Barrett Universal II, Castrop, Haigis, Hoffer Q, Holladay 1, Holladay 2, Kane, Ladas super formula, Okulix, Olsen, PEARL-DGS, SRK/T, and T2). PEARL-DGS obtained the highest percentage of eyes within ±0.5 D, which was significantly higher than Hoffer Q (P = 0.0003), Barrett Universal II (P = 0.001), Holladay 2 (P = 0.007), Holladay 1 (P = 0.01), Haigis (P = 0.02), and Olsen (P = 0.05). In turn, in the ±1.0 D range, Okulix received the highest percentage, and it was significantly higher than Barrett Universal II, Castrop, Hoffer Q, and Holladay 2 (P = 0.0005, P = 0.03, P = 0.003, P = 0.02, respectively). Therefore, they showed that new-generation formulas, based on AI or the ray-tracing principle, were more accurate than the vergence formulas in short eyes [11].
Long Eyes
Inaccuracy in the calculation of the implant power in long eyes is often due to incorrect AL measurement caused by poor eye fixation and the existence of posterior staphyloma. Additionally, the wide range of myopic eyeball length increases the risk of prediction errors. Chen et al. showed that for the SRK/T and Hoffer Q formulas, a 1-mm increase in AL led to an increase in absolute error (AE) by about 0.1 D when AL > 26 mm, while in the case of AL > 33 mm, a 1-mm increase in AL increased the AE by as much as about 1.1 D [10].
Eleven observational studies involving 4047 eyes (2529 calculated with Barrett Universal II, 2318 with Haigis, 2210 with Holladay 2, 4050 with SRK/T, 3687 with Hoffer Q, and 3916 with Holladay 1) were investigated in a meta-analysis by Wang et al. in 2018. The heterogeneity was minimized by dividing eyes into two groups—the first with AL < 26.0 mm and the second with AL ≥ 26.0 mm. The MAE of Barrett Universal II was statistically lower than that of Holladay 2 (P = 0.0002), SRK/T (P < 0.00001), Hoffer Q (P < 0.00001), and Holladay 1 (P < 0.00001). There was no significant difference in MAE for the comparison between Barrett Universal II and Haigis, although the subgroup analysis showed that Barrett Universal II performed better than Haigis when the AL was < 26.0 mm. Barrett Universal II obtained a significantly higher percentage of eyes within ±0.50 D than the other formulas. The authors also compared the Olsen formula with Barrett Universal II and Haigis in a meta-analysis. They observed no statistical difference in the comparison between Olsen and Barrett Universal II (P = 0.86), or between Olsen and Haigis (P = 0.14) [14].
The most recent meta-analysis published by Li et al. in September 2022 compared 13 formulas (SRK/T, Hoffer Q, Holladay 1, Holladay 2, and Haigis as traditional, and Barrett Universal II, Olsen, T2, VRF, EVO, Kane, Hill-RBF, and Ladas as the new-generation formulas). A total of 2273 eyes in 15 studies were included. Overall, the new-generation formulas showed more accurate results than the traditional formulas. The percentage of eyes with a predictive refraction error within ±0.5 D of Kane, EVO, and Ladas was higher than 80%, and those within ±1.0 D exceeded 95%, which was only significantly different from Hoffer Q (all P < 0.05). Moreover, another two new-generation formulas, Barrett Universal II and Olsen, had higher percentages than SRK/T, Hoffer Q, Holladay 1, and Haigis for eyes with predictive refraction error within ±0.5 D and ±1.0 D (all P < 0.05). In the ±0.5 D group, Hill-RBF was better than SRK/T (P = 0.02), Holladay 1 was better than EVO (P = 0.03) and Ladas (P = 0.009), and Hoffer Q had a lower percentage than EVO, Kane, Hill-RBF, and Ladas (P = 0.007, 0.004, 0.002, 0.03, respectively). Barrett Universal II was better than T2 (P = 0.02), and Hill-RBF was better than SRK/T (P = 0.009). No significant difference was found in other pairwise comparisons [12].
This study has noteworthy limitations. First, constant optimization by zeroing out the mean error in studied articles was not considered. According to most updated protocols in IOL power calculation studies, constant optimization is essential to make all formulas comparable, and without it, important biases could affect the reliability of data [26]. However, the authors recognized that constant optimization is a standard in peer-reviewed articles. Second, accuracy of only nine formulas was considered (Barrett Universal II, Kane, Hill-RBF, Olsen, PEARL-DGS, EVO, Haigis, SRK/T, Hoffer Q). However, the authors selected the most popular among those currently used. Third, the authors did not consider how the biometric data were obtained. Although data obtained with ultrasound biometry using the contact technique were excluded, no distinction was made between optical biometers using group refractive index (GRI) and those using sum-of-segments technology. GRI-based biometers could be affected by lens opacity, and they generally overestimate AL in long eyes and underestimate AL in short eyes [50]. In addition, preliminary sample size calculation was not considered. Finally, MedAE was not considered, which was not consistent with Hoffer’s recommendation [25].
Conclusions
With the continuous improvement of phacoemulsification, an increasing number of IOL power calculation formulas have appeared. They are based on a growing number of parameters, from the initial AL and K, through ACD, to the current ones, i.e., LT, WTW, CCT, age, gender, and others. However, there is no consensus in the literature regarding the choice of IOL power calculation formula. The third- and fourth-generation formulas are being replaced by more accurate ones. The Barrett Universal II [5, 14, 16, 17, 28, 31, 48, 51,52,53,54,55] among vergence formulas and Kane [1, 15, 20, 34, 36, 42, 45, 56, 57] and PEARL-DGS [18, 24, 40, 58] among AI-based formulas are currently most often reported as the most precise. Overall, IOL power calculation formulas based on machine learning are very promising and can have a positive effect on the outcomes of postoperative refraction; additionally, machine learning methods can also be incorporated into a variety of existing IOL power formulas to refine their accuracy [59]. However, based on the available literature, there is no gold standard as yet that can be applied to all patients. Moreover, each patient should be managed individually considering their unique eye features.
Data Availability
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
References
Kane JX, Melles RB. Intraocular lens formula comparison in axial hyperopia with a high-power intraocular lens of 30 or more diopters. J Cataract Refract Surg. 2020;46(9):1236–9. https://doi.org/10.1097/j.jcrs.0000000000000235.
Nemeth G, Modis L Jr. Accuracy of the Hill-radial basis function method and the Barrett Universal II formula. Eur J Ophthalmol. 2021;31(2):566–71. https://doi.org/10.1177/1120672120902952.
Stopyra W. The exactness of intraocular lens power calculation formulas for short eyes and correlation between method accuracy and eyeball axial length. Cesk Slov Oftal. 2022;78(5):236–40. https://doi.org/10.31348/2022/24.
Lee AC, Quazi MA, Pepose JS. Biometry and intraocular lens power calculation. Curr Opin Ophthalmol. 2008;19(1):13–7. https://doi.org/10.1097/ICU.0b013e3282f1c5ad.
Stopyra W. Comparison of the accuracy of six intraocular lens power calculation formulas for eyes of axial length exceeding 25.0 mm. J Fr Ophthalmol. 2021;44(9):1332–9. https://doi.org/10.1016/j.jfo.2021.04.009.
Wendelstein JA, Hinterberger S, Hoffmann PC, Hirnschnall N, Koss MJ, Langenbucher A, Jirak P, Bolz M. Evaluation of phakic IOL power calculation using the new LHC formula and comparison with four conventional methods. J Cataract Refract Surg. 2022. https://doi.org/10.1097/j.jcrs.0000000000001055.
Li H, Nan L, Li J, Song H. Accuracy of intraocular lens power calculation formulae after laser refractive surgery in myopic eyes: a meta-analysis. Eye Vis (Lond). 2020;1(7):37. https://doi.org/10.1186/s40662-020-00188-1.
Wang L, Koch DD. Intraocular lens power calculations in eyes with previous corneal refractive surgery: review and expert opinion. Ophthalmology. 2021;128(11):e121–31. https://doi.org/10.1016/j.ophtha.2020.06.054.
Rosa N, Cione F, Pepe A, Musto S, De Bernardo M. An advanced lens measurement approach (ALMA) in post refractive surgery IOL power calculation with unknown preoperative parameters. PLoS One. 2020;15(8): e0237990. https://doi.org/10.1371/journal.pone.0237990.
Chen C, Xu X, Miao Y, Zheng G, Sun Y, Xu X. Accuracy of intraocular lens power formulas involving 148 eyes with long axial lengths: a retrospective chart-review study. J Ophthalmol. 2015;2015: 976847. https://doi.org/10.1155/2015/976847.
Luo Y, Li H, Gao L, Du J, Chen W, Gao Y, Ye Z, Li Z. Comparing the accuracy of new intraocular lens power calculation formulae in short eyes after cataract surgery: a systemic review and meta-analysis. Int Ophthalmol. 2022;42(6):1939–56. https://doi.org/10.1007/s10792-021-02191-4.
Li H, Ye Z, Luo Y, Li Z. Comparing the accuracy of new-generation intraocular lens power calculation formulae in axial myopic eyes: a meta-analysis. Int Ophthalmol. 2022. https://doi.org/10.1007/s10792-022-02466-4.
Wang Q, Jiang W, Lin T, Wu X, Lin H, Chen W. Meta-analysis of Accuracy of intraocular lens power calculation formulas in short eyes. Clin Exp Ophthalmol. 2018;46(4):356–63. https://doi.org/10.1111/ceo.13058.
Wang Q, Jiang W, Lin T, Zhu Y, Chen C, Lin H. Accuracy of intraocular lens power calculation formulas in long eyes: a systemic review and meta-analysis. Clin Exp Ophthalmol. 2018;46(7):738–49. https://doi.org/10.1111/ceo.13184.
Pereira A, Popovic MM, Ahmed Y, Lloyd JC, El-Defrawy S, Gorfinkel J, Schlenker MB. A comparative analysis of 12 intraocular lens power formulas. Int Ophthalmol. 2021;4(12):4137–50. https://doi.org/10.1007/s10792-021-01966-z.
Rong X, He W, Zhu Q, Qian D, Lu Y, Zhu X. Intraocular lens power calculation fin eyes with extreme myopia: comparison of Barrett Universal II, Haigis and Olsen formulas. J Cataract Refract Surg. 2019;45(6):732–7. https://doi.org/10.1016/j.jcrs.2018.12.025.
Liu J, Wang L, Chai F, Han Y, Qian S, Koch DD, Weikert MP. Comparison of intraocular lens power calculation formulas in Chinese eyes with axial myopia. J Cataract Refract Surg. 2019;45(6):725–31. https://doi.org/10.1016/j.jcrs.2019.01.018.
Rocha-de-Lossada C, Colmenero-Reina E, Flikier D, Castro-Alonso FJ, Rodriguez-Raton A, García-Madrona JL, Peraza-Nieves J, Sánchez-González JM. Intraocular lens power calculation formula accuracy: Comparison of 12 formulas for trifocal hydrophilic intraocular lens. Eur J Ophthalmol. 2021;31(6):2981–8. https://doi.org/10.1177/1120672120980690.
Carmona-González D, Castillo-Gómez A, Palomino-Bautista C, Romero-Domínguez M, Gutiérrez-Moreno MÁ. Comparison of the accuracy of 11 intraocular lens power calculation formulas. Eur J Ophthalmol. 2021;31(5):2370–6. https://doi.org/10.1177/1120672120962030.
Darcy K, Gunn D, Tavassoli S, Sparrow J, Kane JX. Assessment of the accuracy of new and updated intraocular lens power calculation formulas in 10930 eyes from the UK National Health Service. J Cataract Refract Surg. 2020;46(1):2–7. https://doi.org/10.1016/j.jcrs.2019.08.014.
Voytsekhivskyy OV, Hoffer KJ, Savini G, Tutchenko LP, Hipólito-Fernandes D. Clinical accuracy of 18 IOL power formulas in 241 short eyes. Curr Eye Res. 2021;46(12):1832–43. https://doi.org/10.1080/02713683.2021.1933056.
Carmona-González D, Palomino-Bautista C. Accuracy of a new intraocular lens power calculation method based on artificial intelligence. Eye (Lond). 2021;35(2):517–22. https://doi.org/10.1038/s41433-020-0883-3.
Lin L, Xu M, Huang S, Qi X, Gu S, Sun W, Su Q, Li J, Zhao Y. Accuracy of never generation IOL power calculation formulas in eyes with high axial myopia. J Refract Surg. 2021;37(11):754–8. https://doi.org/10.3928/1081597X-20210712-08.
Shammas HJ, Taroni L, Pellegrini M, Shammas MC, Jivrajka RV. Accuracy of never IOL power formulas in short and long eyes using sum-of-segment biometry. J Cataract Refract Surg. 2022. https://doi.org/10.1097/j.jcrs.0000000000000958.
Hoffer KJ, Savini G. Update on intraocular lens power calculation study protocols: the better way to design and report clinical trials. Ophthalmology. 2021;128(11):e115–20. https://doi.org/10.1016/j.ophtha.2020.07.05.
Cooke DL, Cooke TL. Comparison of 9 intraocular lens power calculation formulas. J Cataract Refract Surg. 2016;42(8):1157–64. https://doi.org/10.1016/j.jcrs.2016.06.029.
Savini G, Taroni L, Hoffer KJ. Recent developments in intraocular lens power calculation methods-update 2020. Ann Transl Med. 2020;8(22):1553. https://doi.org/10.21037/atm-20-2290.
Kane JX, Van Heerden A, Atik A, Petsoglou C. Accuracy of 3 new method for intraocular lens power selection. J Cataract Refract Surg. 2017;43(3):333–9. https://doi.org/10.1016/j.jcrs.2016.12.021.
Retzlaff JA, Sanders DR, Kraff MC. Development of the SRK/T intraocular lens implant power calculation formula. J Refract Surg. 1990;16(3):333–40. https://doi.org/10.1016/s0886-3350(13)80705-5.
Hoffer KJ. The Hoffer Q formula: a comparison of theoretic and regression formulas. J Refract Surg. 1993;19(6):700–12. https://doi.org/10.1016/s0886-3350(13)80338-5.
Melles RB, Holladay JT, Chang WJ. Accuracy of intraocular lens calculation formulas. Ophthalmology. 2018;125(2):169–78. https://doi.org/10.1016/j.ophtha.2017.08.027.
Hoffer KJ. Clinical results using the Holladay 2 intraocular lens power formula. J Refract Surg. 2000;26(8):1233–7. https://doi.org/10.1016/s0886-3350(00)00376-x.
Clarke GP, Burmeister J. Comparison of intraocular lens computations using a neural network versus the Holladay formula. J Cataract Refract Surg. 1997;23(10):1585–9. https://doi.org/10.1016/s0886-3350(97)80034-x.
Olsen T, Hoffmann P. C constant: new concept for raytracing-assisted intraocular lens power calculation. J Cataract Refract Surg. 2014;40:764–73. https://doi.org/10.1016/j.jcrs.2013.10.037.
Sheard RM, Smith GT, Cooke DL. Improving the prediction accuracy of the SRK/T formula: the T2 formula. J Cataract Refract Surg. 2010;36(11):1829–34. https://doi.org/10.1016/j.jcrs.2010.05.031.
Savini G, Di Maita M, Hoffer KJ, Næser K, Schiano-Lomoriello D, Vagge A, Di Ciello L, Traverso CE. Comparison of 13 formulas for IOL power calculation with measurements from partial coherence interferometry. Br J Ophthalmol. 2021;105(4):484–9. https://doi.org/10.1136/bjophthalmol-2020-316193.
Ladas JG, Siddiqui AA, Devgan U, Jun A. A 3-D “super surface” combining intraocular lens formulas to generate a “super formula” and maximize accuracy. JAMA Ophthalmol. 2015;133(12):1431–6. https://doi.org/10.1001/jamaophthalmol.2015.3832.
Stopyra W. Effectiveness, sensitivity and specificity of intraocular lens power calculation formulas for short eyes. Turk J Ophthalmol. 2022;52(3):201–7. https://doi.org/10.4274/tjo.galenos.2021.83704.
Grzybowski A. et al. Artificial intelligence in ophthalmology. Switzerland: Springer Nature; 2021. p. 1–286. ISBN 978-3-030-78601-4 (eBook). https://doi.org/10.1007/978-3-030-78601-4.
Debellemanière G, Dubois M, Gauvin M, Wallerstein A, Brenner L, Rampat R, Saad A, Gatinel D. The PEARL-DGS formula: the development of an open-source machine learning-based thick IOL calculation formula. Am J Ophthalmol. 2021;232:58–69. https://doi.org/10.1016/j.ajo.2021.05.004.
Gatinel D, Debellemanière G, Saad A, Dubois M, Rampat R. Determining the theoretical effective lens position of thick intraocular lenses for machine learning-based IOL power calculation and simulation. Transl Vis Sci Technol. 2021;10(4):27. https://doi.org/10.1167/tvst.10.4.27.
Connell BJ, Kane JX. Comparison of the Kane formula with existing formulas for intraocular lens power selection. BMJ Open Ophthalmol. 2019;4(1): e000251. https://doi.org/10.1136/bmjophth-2018-000251.
Voytsekhivskyy OV. Development and clinical accuracy of a new intraocular lens power formula (VRF) compared to other formulas. Am J Ophthalmol. 2018;185:56–67. https://doi.org/10.1016/j.ajo.2017.10.020.
Næser K, Savini G. Accuracy of thick-lens intraocular lens power calculation based on cutting-card or calculated data for lens architecture. J Cataract Refract Surg. 2019;45(10):1422–9. https://doi.org/10.1016/j.jcrs.2019.05.021.
Hipólito-Fernandes D, Luís ME, Gil P, Maduro V, Feijão J, Yeo TK, Voytsekhivskyy O, Alves N. VRF-G, a new intraocular lens power calculation formula: a 13-formulas comparison study. Clin Ophthalmol. 2020;16(14):4395–402. https://doi.org/10.2147/OPTH.S290125.
Langenbucher A, Szentmáry N, Cayless A, Weisensee J, Fabian E, Wendelstein J, Hoffmann P. Considerations on the Castrop formula for calculation of intraocular lens power. PLoS One. 2021;16(6): e0252102. https://doi.org/10.1371/journal.pone.0252102.
Jamali A, Jabbarvand M, Asharlous A, Doostdar A, Bordbar S, Khabazkhoob M. Assessing accuracy of Okulix ray-tracing software in calculating intraocular lens power in long cataractous eyes. J Curr Ophthalmol. 2022;34(1):67–73. https://doi.org/10.4103/joco.joco_136_20.
Gökce SE, Zeiter JH, Weikert MP, Koch DD, Hill W, Wang L. Intraocular lens power calculations in short eyes using 7 formulas. J Cataract Refract Surg. 2017;43(7):892–7. https://doi.org/10.1016/j.jcrs.2017.07.004.
Shrivastava AK, Nayak S, Mahobia A, Anto M, Pandey P. Accuracy of intraocular lens power calculation formulae in short eyes: a systemic review and meta-analysis. Indian J Ophthalmol. 2022;70(3):740–8. https://doi.org/10.4103/ijo.IJO_934_21.
De Bernardo M, Cione F, Capasso L, Coppola A, Rosa N. A formula to improve the reliability of optical axial length measurement in IOL power calculation. Sci Rep. 2022;12(1):18845. https://doi.org/10.1038/s41598-022-23665-0.
Cooke DL, Cooke TL. A comparison of two methods to calculate axial length. J Cataract Refract Surg. 2019;45(3):284–92. https://doi.org/10.1016/j.jcrs.2018.10.039.
Abulafia A, Barrett GD, Rotenberg M, Kleinmann G, Levy A, Reitblat O, Koch DD, Wang L, Assia EI. Intraocular lens power calculation for eyes with an axial length greater than 26.0 mm: comparison of formulas and methods. J Cataract Refract Surg. 2015;41(3):548–56. https://doi.org/10.1016/j.jcrs.2014.06.033.
Rong X, He W, Zhu Q, Qian D, Lu Y, Zhu X. Intraocular lens power calculation in eyes with extreme myopia: comparison of Barrett Universal II, Haigis and Olsen formulas. J Cataract Refract Surg. 2019;45(6):732–7. https://doi.org/10.1016/j.jcrs.2018.12.025.
Zhou D, Sun Z, Deng G. Accuracy of the refractive prediction determined by intraocular lens power calculation formulas in high myopia. Indian J Ophthalmol. 2019;67(4):484–9. https://doi.org/10.4103/ijo.IJO_937_18.
Zhang JQ, Zou XY, Zheng DY, Chen WR, Sun A, Luo LX. Effect of lens constant optimization on the accuracy of intraocular lens power calculation formulas for highly myopic eyes. Int J Ophthalmol. 2019;12(6):943–8. https://doi.org/10.18240/ijo.2019.06.10.
Cheng H, Kane JX, Liu L, Li J, Cheng B, Wu M. Refractive predictability using the IOLMaster 700 and artificial intelligence-based IOL power formulas compared to standard formulas. J Refract Surg. 2020;36(7):466–72. https://doi.org/10.3928/1081597X-20200514-02.
Cheng H, Wang L, Kane JX, Li J, Liu L, Wu M. Accuracy of artificial intelligence formulas and axial length adjustments for highly myopic eyes. Am J Ophthalmol. 2021;223:100–7. https://doi.org/10.1016/j.ajo.2020.09.019.
Hipólito-Fernandes D, Luís ME, Serras-Pereira R, Gil P, Maduro V, Feijão J, Alves N. Anterior chamber depth, lens thickness and intraocular lens calculation formula accuracy: nine formulas comparison. Br J Ophthalmol. 2022;106(3):349–55. https://doi.org/10.1136/bjophthalmol-2020-317822.
Chang P, Qian S, Wang Y, Li S, Yang F, Hu Y, Liu Z, Zhao Y. Accuracy of new-generation intraocular lens calculation formulas in eyes with variations in predicted refraction. Graefes Arch Clin Exp Ophthalmol. 2022. https://doi.org/10.1007/s00417-022-05748-w.
Doshi D, Limdi P, Parekh N, Gohil N. A comparative study to assess the predictability of different IOL power calculation formulas in eyes of short and long axial length. J Clin Diagn Res. 2017;11(1):NC01–4. https://doi.org/10.7860/JCDR/2017/22095.9136.
Moschos MM, Chatziralli IP, Koutsandrea C. Intraocular lens power calculation in eyes with short axial length. Indian J Ophthalmol. 2014;62(6):692–4. https://doi.org/10.4103/0301-4738.129791.
Ang RE, Rapista AJ, Remo JT, Tan-Daclan MA, Cruz EM. Clinical outcomes and comparison of intraocular lens calculation formulas in eyes with long axial myopia. Taiwan J Ophthalmol. 2021;12(3):305–11. https://doi.org/10.4103/tjo.tjo_7_21.
Funding
No funding or sponsorship was received for this study or publication of this article.
Author information
Authors and Affiliations
Contributions
Wiktor Stopyra: study design; acquisition, analysis and data interpretation; writing and drafting; revision; verification; Achim Langenbucher: support; reviewing; Andrzej Grzybowski: planning; data acquisition; supervision. All authors participated in final approval of the article and agreed to be accountable for all aspects of the work.
Corresponding authors
Ethics declarations
Conflict of Interest
Wiktor Stopyra and Achim Langenbucher have nothing to disclose. Andrzej Grzybowski has Grants/Contracts from Alcon, Bausch & Lomb, Zeiss, Hoya, Thea, Viatris, Teleon, J&J, Cooper Vision, Essilor and Polpharma; consulting fees/honoraria from Thea, Polpharma, Viatris and stock with GoCheckKids.
Ethical Approval
This article is based on previously conducted studies and does not contain any new studies with human participants or animals performed by any of the authors.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, which permits any non-commercial use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc/4.0/.
About this article
Cite this article
Stopyra, W., Langenbucher, A. & Grzybowski, A. Intraocular Lens Power Calculation Formulas—A Systematic Review. Ophthalmol Ther 12, 2881–2902 (2023). https://doi.org/10.1007/s40123-023-00799-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40123-023-00799-6