Abstract
Introduction
Combination antiretroviral therapy has become the standard care of human immunodeficiency virus (HIV)-infected patients and has further led to a dramatically decreased progression probability to acquired immune deficiency syndrome (AIDS) for patients under such a therapy. However, responses of the patients to this therapy have recorded heterogeneous complexity and high dynamism. In this paper, we simultaneously model long-term viral suppression, viral rebound, and state-specific duration of HIV-infected patients.
Methods
Full-parametric and semi-parametric Markov multistate models were applied to assess the effects of covariates namely TB co-infection, educational status, marital status, age, quality of life (QoL) scores, white and red blood cell parameters, and liver enzyme abnormality on long-term viral suppression, viral rebound and state-specific duration for HIV-infected individuals before and after treatment. Furthermore, two models, one including and another excluding the effect of the frailty, were presented and compared in this study.
Results
Results from the diagnostic plots, Akaike information criterion (AIC) and likelihood ratio test showed that the Weibull multistate frailty model fitted significantly better than the exponential and semi-parametric multistate models. Viral rebound was found to be significantly associated with many sex partners, higher eosinophils count, younger age, lower educational level, higher monocyte counts, having abnormal neutrophils count, and higher liver enzyme abnormality. Furthermore, viral suppression was also found to be significantly associated with higher QoL scores, and having a stable sex partner. The analysis result also showed that patients with a stable sex partner, higher educational levels, higher QoL scores, lower eosinophils count, lower monocyte counts, and higher RBC indices were more likely to spend more time in undetectable viral load state.
Conclusions
To achieve and maintain the UNAIDS 90% suppression targets, additional interventions are required to optimize antiretroviral therapy outcomes, specifically targeting those with poor clinical characteristics, lower education, younger age, and those with many sex partners. From a methodological perspective, the parametric multistate approach with frailty is a flexible approach for modeling time-varying variables, allowing for dealing with heterogeneity between the sequence of transitions, as well as allowing for a reasonable degree of flexibility with a few additional parameters, which then aids in gaining a better insight into how factors change over time.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Why carry out this study? |
Highly active antiretroviral therapy (ART) has allowed for improvements in CD4 cell counts, suppression of human immunodeficiency virus (HIV) RNA and increased life expectancy of HIV-infected patients. |
However, in some patients, suppression of HIV-RNA has been shown not to fall to undetectable levels, while, for other patients, viral rebound occurred after initially becoming undetectable. |
In this paper, we simultaneously model long-term viral suppression, viral rebound and length of stay in better clinical stages. |
What was learned from the study? |
Viral rebound was found to be significantly associated with many sexual partners, higher eosinophils count, younger age, lower educational level, higher monocytes counts, having abnormal neutrophils count, and higher liver enzyme abnormality. |
To achieve and maintain the UNAIDS 90% suppression targets, additional interventions are required to optimize ART outcomes, specifically targeting those with poor clinical characteristics, lower education, younger age, and those with many sex partners. |
Parametric multistate with frailty approach is a flexible approach for modeling time-varying variables factors, allowing for dealing with heterogeneity between the sequence of transitions, as well as allowing for a reasonable degree of flexibility with a few additional parameters, which then aids in gaining a better insight in how factors change over time. |
Introduction
Care for HIV-infected patients has changed dramatically over the last two decades, [1] largely due to advances in antiretroviral therapy (ART), which has, in turn, allowed for improvements in CD4 cell counts, suppression of HIV RNA and increased life expectancy of human immunodeficiency virus (HIV)-infected patients [2, 3]. However, in some patients, suppression of HIV-RNA concentration has been shown not to fall to undetectable levels, while, for other patients, viral rebound occurred after initially becoming undetectable [4]. Such cases are termed virologic failure and have been conjectured to possibly be associated with poor adherence [5], drug–drug interactions, treatment failure, drug-resistance, or unobserved factors [6, 7]. To allow timely detection of virologic failure, the World Health Organization (WHO) recommended the use of HIV-RNA testing as the gold standard for monitoring of HIV-infected patients’ response to therapy [8]. Assessment of the factors that affect viral load dynamics (i.e., viral suppression and rebound) is important in order to identify whether a patient is in need of more intensive adherence counseling and the timely detection of treatment failure in order to minimize the chances of development of drug resistance and unnecessary switching to an expensive regimen [9].
In 2015, the UNAIDS set the 90-90-90 global targets in order to end the AIDS epidemic, whereby the third 90 represents the target to achieve a viral load suppression in at least 90% of HIV-infected patients under ART [10]. Identifying the possible factors that may affect virologic failure is key to achieving these targets. Findings from previous studies highlight a number of factors that may affect the viral suppression status among HIV-infected patients initiating ART, including gender, clinician skill level, suboptimal adherence, age, treatment history, WHO stage, and baseline CD4 cell count [5, 11,12,13,14]. Although clinical covariates are more capable of explaining and capturing realistic behavioral patterns of the VL responses, and are more sensitive to the source of variations in the viral load (VL), no previous study has directly examined the effects of several clinical attributes [i.e., white blood cell (WBC) parameters, red blood cell (RBC) parameters, blood chemistry parameters, and quality of life (QoL) domain scores] on VL dynamics. In addition, the relative role of various factors related to HIV VL responses may also further be dependent on the local context and the ART program setting. This study thus gives an insight into assessing the effect of several clinical, risk, and socio-demographic factors on long-term HIV VL dynamics. Therefore, we emphasize a comparison of viral rebound and viral suppression across different clinical attributes, and identify factors contributing to virologic failure which are key to informing adjustments in the program-level strategies most amenable to intervention in this context and key to achieving UNAIDS global target goals.
Mathematical models have been used extensively in research into HIV VL dynamics because they play an important role in improving our understanding of major factors contributing to the VL dynamics of the disease. These models range from logistic regression [5, 15,16,17], Cox regression analysis [18,19,20], accelerated failure time models [21], generalized estimating equations [22,23,24], to generalized linear mixed-effects models [25]. It has also been argued that multistate Markov models are useful tools for studying the complex dynamics of chronic diseases such as HIV VL progression, and are further valuable for identifying factors associated with disease progression of HIV/AIDS [26,27,28]. However, several multi-state Markov models assume that the intensities are homogeneous, conditional on the observed covariates. Unfortunately, it is hardly ever possible to include all the relevant factors, either due to it not being possible to measure all the relevant factors or because the researchers do not know all the relevant factors. Ignoring such frailty or unobserved heterogeneity may have a huge impact on the estimation of the parameters in multistate Markov models.
In this study, full-parametric and semi-parametric multistate Markov frailty models were used to model viral rebound, viral suppression, and state-specific duration in HIV-infected patients under treatment. Multistate frailty models are a powerful tool for modeling complex cycles of chronic diseases, encompassing the life history of a cohort [29], considering all possible pathways [30], and further allowing for dealing with heterogeneity between the sequence of transitions [31, 32]. These models can also accommodate competing risks, censored data, recurrent outcomes ,and multiple outcomes [33]. In this study, we classified the sequential adverse events by the degree of chronicity based on VL, with classifications defined by patients going through undetectable, low, moderate, and high VL. Most importantly, we have presented full and semi-parametric multistate Markov models, with patient-level frailties on all VL rebound, VL suppression and state-specific duration in HIV-infected patients, thus making the current study different from previous studies. Additionally, among the surrogate markers of HIV progression and ART responses, both the CD4 cell and VL counts are included in the same model. As discussed by Chikobvu and Shoko [34], the effects of multi-collinearity on the VL count transitions can be corrected using the principal component approach. Therefore, in this study, we have presented a parametric multistate frailty model for predicting transition intensities between sequential events of HIV infection, which takes into account the CD4 cell count, in order to study several factors that may affect viral suppression, viral rebound and state-specific duration of HIV-infected patients.
Methods
Data Description
The data are from an ongoing prospective cohort study conducted among HIV-infected women from the Centre for the AIDS Programme of Research in South Africa (CAPRISA). The original study, which started in 2004, enrolled a cohort of HIV-uninfected women whose age was greater than 18 years with the aim of describing immunologic, clinical, and virologic characteristics of HIV-1 disease [35]. In this study, the participants’s enrollment was conducted from August 2004 to December 2017. The participant who seroconverted during the HIV-uninfected stage of CAPRISA_002 and other CAPRISA prevention and seroincidences trials (including the CAPRISA_004 trials), were enrolled into the Acute HIV Infection phase, and then followed-up during chronic infection, ART initiation, and for up to 6 years on ART. Participants were recruited at two sites in KwaZulu-Natal-South Africa, a rural site in Vulindlela and an urban site in the city of Durban. Women without well-documented estimated date of HIV infection, and those who did not have at least two follow-up clinical attribute measurements, were excluded from the analysis. Finally, 219 participants were included in the study. Further information about the above-mentioned ongoing prospective HIV cohort study (CAPRISA_002), including women’s eligibility criteria and the enrollment procedure, were reported in [35,36,37]. All procedures performed in this study were approved by the Research Ethics Committee of the University of KwaZulu-Natal and CAPRISA. Written informed consent was obtained from all participants, and ethical approval for the original study was granted by the University of KwaZulu-Natal (E013/04), the University of Cape Town (025/2004), and the University of the Witwatersrand (M040202).
Variables and Measurements
CAPRISA initially enrolled HIV-negative (phase I) women into different study cohorts. The women who seroconverted were enrolled again into acute infection (i.e., phase II: weekly visits up to 3 months post-infection), early infection (i.e., phase III: monthly visits from 3 to 12 months), established infection (i.e., phase IV: quarterly visits for more than 12 months), and on ART (phase V). Samples for immunological, virological, and clinical attributes (such as VL, WBC parameters, RBC parameters, blood chemistry parameters, CD4 cell count, etc.) were measured at each visit [38]. These longitudinal immunologic, virologic, and clinical measurements were recorded for several follow-up visits. A total of 8760 follow-up visits were recorded for 219 HIV-infected women.
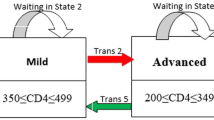
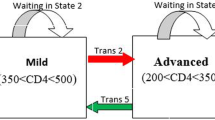
The primary outcomes in this current paper were viral rebound, viral suppression and state-specific duration of stay of AIDS patients. We defined disease progression of HIV/AIDS into four disease states: high VL (state 1), moderate VL (state 2), low VL (state 3), and undetectable VL (state 4) (Fig. 1). It is assumed that patients can have transitions from undetectable to detectable states and vice versa. Viral suppression transitions correspond to being from high VL to moderate VL (trans 1), or from moderate VL to low VL (trans 2), or from low VL to undetectable VL (trans 3). Likewise, viral rebound transition corresponds to a transition from undetectable VL to low VL (trans 4), or from low VL to moderate VL (trans 5), or from moderate VL to high VL (trans 6). Furthermore, state-specific duration corresponds to time spent in the high VL state, moderate VL state, low VL state, and undetectable VL state.
The effect of numerous possible factors on viral suppression, viral rebound, and state-specific duration of stay of HIV patients was evaluated, including (1) demographics: date of the clinical visit, age, gender, marital status, and educational status; (2) risk variables: sex under the influence of alcohol, contraceptive use and substance use; (3) past opportunistic illness: tuberculosis and hypertension; (4) clinical attributes: blood chemistry [chloride, sodium, calcium, aspartate aminotransferase (AST), alanine aminotransferase (ALT), total protein and lactate dehydrogenase (LDH)], WBC parameters (lymphocyte count, neutrophils, leucocyte count, monocytes and eosinophils), RBC parameters [hemoglobin (Hb), red cell distribution width (RDW), mean corpuscular hemoglobin (MCH), mean corpuscular volume (MCV), mean corpuscular hemoglobin concentration (MCHC), and hematocrit], lipid parameters [cholesterol, triglycerides and low-density lipoproteins (LDL)] and physical examination parameters [blood pressure (BP), pulse rate (PR), weight and height]; and (5) QoL domain scores. The WHO QoL questionnaire [39] was used to measure the QoL of the participants. Therefore, the QoL scales contain the following domain scores. The first is physical health scores, which measure the impact of the disease on the activities of daily living, dependence on therapeutic substances, fatigue, lack of energy, presence of pain, and initiative and perceived working capacity. The second is the psychological wellbeing score domain, which assesses the patient’s thoughts about body appearance, positive and negative feelings, personal beliefs and self-esteem, suicide, higher cognitive functions, anxiety, spirituality, and depression. The third domain is social relationships, which assesses personal relationships, social contacts, social support, and sexual activity. The fourth domain is devoted to the level of independence and assesses areas such as mobility, activities of daily living, dependence on treatments and work capacity. Further information about the above-mentioned factors has been reported in [40, 41] (Fig. 2).
Statistical Method
Since our data have a large number of clinical variables, we used exploratory factor analysis to group and minimize the number of variables. Factor analysis was carried out by creating the principal components of the original variables and then creating the eigenvectors. By using the Kaiser criterion, eigenvectors with eigenvalues greater than 1 were kept [42]. A maximum likelihood extraction method with varimax rotation was used. Factor loadings describe the relationship of each clinical variable with each factor. The factor loading is considered strong if greater than 0.6, moderate if 0.4–0.6, and weak if less than 0.4 [43]. Each observation was assigned a score for each rotated factor based on the loading of the subject’s original variable levels. Accordingly, we managed to group the 20 clinical variables in the study, to create 6 latent variables, defined as RBC component, red blood cell indices, liver abnormality component, electrolyte component, lipid component, and protein component (Table 1).
Multistate Markov Frailty Modeling
To assess the effect of possible factors on the viral rebound, viral suppression and length of stay in each VL category of HIV/AIDS patients, we adopted a multistate frailty model to describe how patients move between a series of four VL count categories, from high VL to undetectable VL, in continuous time (Fig. 1).
Let S(t) represent the state occupied by a randomly chosen patient at time t. The transition probability of the patient being in state j at time t, given that the individual was in state m at time z, is defined by \(P_{mj} \left( {z,t} \right) = P\left( {S\left( t \right) = j |S\left( z \right) = m} \right);\) where \(\mathop \sum \nolimits_{j \in S} P_{mj} = 1\). The corresponding transition intensity is defined as
Consequently, the 4×4 transition intensity matrix Q(t) is defined as
Note that the rows sum to zero since \(\sum\nolimits_{j \in S} {P_{mj} = 1}\). The off-diagonal entries are the viral suppression and the viral rebound transition intensities, respectively). The diagonal entries are defined by \(q_{mm} \left( t \right) = - \sum\nolimits_{m \ne j} {q_{mj} \left( t \right)} .\) The average length of stay in a single state before making any transitions to either higher or lower VL states is estimated by a negative inverse of the mth diagonal entry of Q(t), that is \(\frac{ - 1}{{q_{mm} }}\).
To examine the effect of covariates namely the educational status, age, marital status, QoL [physical health (PH) score, psychological wellbeing (PW) score, level of independence (LI) score, social relationship (SR) score], TB co-infection, RBC indices, hemoglobin and hematocrits (HH), eosinophils, neutrophils, monocytes, electrolyte components and liver enzyme abnormality on such transitions, we employ both fully-parametric and semi-parametric multistate frailty models. In all models,
where \(q_{mj} \left( {t;{\mathbf{x}},\varvec{v}} \right)\) represent the transition intensity from state m to state j, after adjusting a set of covariates \({\mathbf{x}}_{mj} .\) The random effect or frailty of a patient is \({\text{v}}_{mj}^{i} ,\) \(\varvec{\alpha}_{mj}\) is the effect of the covariates on the transitions hazard (\(q_{mj} )\), \({\text{where }}q_{mj}^{0} \left( t \right)\) represents the baseline intensity from state m to state j. We assumed \(v_{mj}^{i}\) to be independent and identically distributed with a Gamma probability distribution \(v_{mj}^{i} \sim \varGamma \left( {\frac{1}{{\gamma_{mj} }},\frac{1}{{\gamma_{mj} }}} \right), {\text{mean}}\left( {v_{mj}^{i} } \right) = 1 \;{\text{and var}} \left( {v_{mj}^{i} } \right) = \gamma_{mj}\). The variance \(\gamma_{mj}\) represents the heterogeneity of the overall underlying baseline risk for the transition m → j. For this model, if m < j, it is termed as the viral suppression transitions, while a transition where m > j is termed as viral rebound and for m = j, it is termed as the probability of staying in the same diseasing state. Thus the labeling is 1 for high VL, 2 for moderate VL, 3 for low VL, and 4 for undetectable VL states (See Fig. 1). Thus, viral suppression transition, viral rebound transition, and the state-specific duration of stay for a patient I in the current study are defined as:
In the fully parametric cases, the baseline intensity is given by a full parametric function of time \(q_{mj}^{0} \left( t \right) = {\mathfrak{g}}\left( {t,\theta } \right)\), so that the intensity model is a standard parametric distribution. In the current study, we used the Weibull distribution with parameters (\(\theta ,\varvec{\alpha})\varvec{ }\) and transition intensity, \(q_{mj} \left( {t;{\mathbf{x}},\varvec{u}} \right) = \theta_{mj} t^{{\varvec{\theta}_{mj} - 1}} {\text{v}}_{mj}^{i} \exp \left( {\varvec{\alpha}_{mj}^{'} {\mathbf{x}}_{mj} } \right)\). An important special case, which we also considered, was \(\theta_{mj} = 1\), for all m and j, where the transition rate is constant, conditional on the value of any time-dependent variables. Since these variables are assumed to be constant between event times, the transition rate is a step function of time, and the waiting time in each state has an exponential model. Thus, the full likelihood function for all observed multistate data is given by
where h is the transition for patient i, \(\delta_{hi}\) is the event indicator, \(\theta\) is a vector of parameters relating to the cumulative baseline intensity \({\text{Q}}_{\text{h}}^{0} \left( {{\text{t }}_{\text{i}} } \right)\) and \(L_{\text{M}} \left( {\varvec{\alpha},\theta } \right) {\text{is}}\) the marginal likelihood for the multistate frailty model. For the computations of the above likelihood function, a maximum penalized likelihood estimation with gamma frailty (as discussed by Rondeau and Gonzalez [44]), can be applied to estimate the integrals and thereby avoids the need for intensive computations.
In the semi-parametric case, the baseline intensity, \(q_{mj}^{0} \left( t \right),\) is left completely unspecified and estimated non-parametrically. The log-linear effect of the covariates \(\varvec{\alpha}_{mj}\), are estimated by maximizing the partial loglikelihood function. Thus, the partial loglikelihood for all the observed multistate data is given by
where h is the transition for patient I, \(d_{h} = \sum \delta_{hi}\) is the number of events, and R(t) is the risk set at time t for making a transition h. In this study, we used a more efficient Quasi–Newton iterative approach proposed by Kalbfleisch and Lawless [45] , for the computations of the above partial loglikelihood function.
In addition to adding the frailty term, a principal component variable is created to improve the efficiency of the above models. In order to create a principal component variable, as explained by Chikobvu and Shoko [34], we carried out the following regression analysis to estimate β0 and β1 in the model: \(y_{\varvec{i}}^{{{\text{CD}}4}} = \beta_{0} + \beta_{1} x_{\varvec{i}}^{\text{VL}} + \varepsilon_{i} .\) We then defined an orthogonal CD4 cell count variable = \(\varepsilon_{i}\) = \(\varvec{ }y_{i}^{{{\text{CD}}4}} \varvec{ }{-} \left( {\beta_{0} + \beta_{1} x_{i}^{\text{VL}} } \right)\). The orthogonal CD4 cell count in the model explains the component of disease progression of HIV that cannot be explained by the VL alone. In order to deal with multicollinearity of the CD4 cell count and VL count, the orthogonal CD4 cell count component was used. The residual from the fitted principal component model was included with the original HIV/AIDS data model to form the new CD4 cell count component.
Prediction from Multistate Model
To predict the probability of occupying a particular state at a given time, we calculated, pmj(z, t), the probability of being in state j at a time t, given being in state m at time z. Under all models, we used a simulation approach, which can be considered to be a more efficient and general approach (proposed by Crowther and Lambert [46]). This can be achieved by simulating a large number of patient states history from multistate frailty models, given the cumulative hazard for each transition, or covariate-specific hazard. The flexsurv and mstate commands have utilities to do this for the parametric and semiparametric multistate Markov model, respectively. All the analyses were carried out using statistical packages R-3.6 (mstate and felxsurv) and SAS 9.4.
Results
Characteristics of the ART Cohort at Enrolment
All participants were black women (n = 219), with a mean age of 26.67 years (standard deviation of 6.9 years). The majority of participants were married or with a stable partner 174 (79.5%), not co-infected with TB 201 (91.8%), not with anemia 208 (95.0%) and overweight 137 (62.8%), based on their body mass index (BMI) measurements. Over two-thirds, 153 (69.9%), reported having completed grades 11/12 of schooling. Considering the baseline virologic state, 40.2% and 32.4% of patients had an initial VL of 10,000 < VL < 1000,000 copies/ml and 50 < VL < 10,000 copies/ml, respectively. The median baseline CD4 count of the participants included in the analysis was 519.0 cells/mm3 (IQR 419–655.5 cells/mm3) (Table 2).
Estimated Transition Probability and Length of Stay
The plot in Fig. 3 displays the non-parametric estimated probability of transitions of viral suppression, viral rebound, and the state-specific length of stay of AIDS patients. From Fig. 3a, b, it is interesting to observe that, when a patient’s VL is above 10,000, rates of change of viral rebound (transitions 5 and 6), are smaller than the rates of change of viral suppression (transitions 1 and 2). However, the probability of achieving an undetectable VL for patients (transition 3) is smaller than the probability of a viral rebound from the undetectable VL (transition 4) (Fig. 3c). Furthermore, patients with lower VL (particularly those in the undetectable VL state) had a higher probability of staying in the same state throughout the duration of follow-up periods, compared to those with a higher VL (Fig. 3d).
Assessment of the Fitted Models
We applied three Markov multistate models, the Exponential, Weibull, and the Semi-Parametric Multistate models. The estimates of these full and semi-parametric multistate models were compared with non-parametric estimates to assess the goodness of fit of the model (as discussed by Ieva et al. [47] and Titman and Sharples [48]) (Fig. 4). From this plot, we noted that the Weibull model accounted better for the decrease in the survival function of the length of stay and transitions since the time of the last visit. The model selection criteria in Table 3 further confirm this finding.
Besides selecting the best fit model for our data, the effect of patient-level frailties and orthogonal CD4 cell count components on VL dynamics were also analyzed. This was achieved by fitting a Weibull multistate model without patient-level frailties and orthogonal CD4 cell count components on VL dynamics. Secondly, we fitted a Weibull model for the effects of the factors, where only a frailty term was included in the model. Finally, we fitted a Weibull multistate model with patient-level frailties and orthogonal CD4 cell counts. A comparison of these three models was based on the AIC and likelihood ratio tests (LRT). The AIC and LRT from Table 4 showed that the Weibull multistate model with patient-level frailties and with CD4 cell count orthogonal adjustment gives the best fit to the data (i.e., gives improvements in estimation) (Table 4).
Predictors of Viral Suppression
Analysis results for modeling viral suppression, viral rebound, and length of stay using Weibull multistate frailty are presented in Figs. 5, 6 and 7, respectively. Focusing on the effect of predictors on viral suppression, an increase in eosinophils count decreases the probability of experiencing viral suppression from high to moderate VL (aHR = 0.33, 95% CI 0.14–0.78). Compared to patients without TB co-infection, we note that patients with TB co-infection were associated with a decreased probability of achieving viral suppression to undetectable VL (aHR = 0.44, 95% CI 0.23–0.83) and to low VL (aHR = 0.60, 95% CI 0.38–0.95). Considering QoL domain scores of the patients, as the score of psychological wellbeing (aHR = 1.02, 95% CI 1.01–1.15) increases, the transitions to viral suppression (particularly from high VL to moderate VL) increase. Similarly, having a high level of independence score was associated with a higher probability of achieving viral suppression.
Age was shown to have a strong association with suppression of VL (particularly from high VL → moderate VL). These results suggest that the likelihood of achieving viral suppression to moderate VL is lower for patients in the younger age group (age < 20 years) (aHR = 0.19, 95% CI 0.08–0.46) and middle age group (21–39 years), evidenced by (aHR = 0.41, 95% CI 0.26–0.66), compared to those in an older age group (age > 40 years). In addition, the time for transition from high VL to moderate VL (aHR = 1.65, 95% CI 1.03–2.64) and from moderate VL to low VL (aHR = 1.67, 95% CI 1.22–2.29), s accelerated for patients with stable sex partners (married), compared to those with no sex partner. Moreover, the result further showed that patients with many sex partners (aHR = 0.24, 95% CI 0.08–0.70), ad significantly decreased viral suppression to undetectable levels, as compared to those with no sex partner (Fig. 5).
Predictors of Viral Rebound
The effect of several predictors on viral rebound of HIV/AIDS is given in Fig. 6. Based on the parameter estimates, we noted that the neutrophils had significantly decreased transition intensity to viral rebound. As the score of this covariate increases, the probability of experiencing viral rebound from low VL to moderate VL (aHR = 0.88, 95% CI 0.80–0.97), and from moderate VL to high VL (aHR = 0.70, 95% CI 0.59–0.84) decreases. In addition, having high monocyte counts accelerates viral rebound from low to moderate VL (aHR = 2.20, 95% CI 1.90–3.31) and from moderate to high VL (aHR = 1.25, 95% CI 1.01–1.67). Similarly, having a higher eosinophil score was associated with an increased probability of experiencing viral rebound, from low to moderate VL (aHR = 1.83, 95% CI 1.41–2.38) and from moderate to high VL (aHR = 2.36, 95% CI 1.64–3.88). Furthermore, having high liver abnormality scores accelerates viral rebound from moderate to high VL (aHR = 1.23, 95% CI 1.01–1.67).
Considering QoL domain scores of the patients, we note that, as the score of physical health increases, the transitions to viral rebound from low to moderate VL (aHR = 0.91, 95% CI 0.83–0.99) and from moderate to high VL (aHR = 0.85, 95% CI 0.75–0.97), decreases Patients in the younger age group (age < 20 years) were more likely to experience viral rebound (aHR = 1.26, 95% CI 1.09–2.25), compared to those in older age groups (age > 40 years). In addition, patients with higher educational levels were less likely to experience viral rebound from moderate to high VL. Furthermore, having many sex partners accelerates viral rebound from moderate to high VL (aHR = 1.32, 95% CI 1.02–3.36) see Fig. 6.
Predictors of Length of Stay
As seen from Fig. 7, monocytes and eosinophils were shown to have a strong association with time spent in this moderate VL state. These results suggest that patients with high monocytes (aHR = 1.78, 95% CI 1.29–2.46) and high eosinophils (aHR = 1.54, 95% CI 1.12–2.12) are more likely to stay longer in a moderate VL state (between 10,000 and 100,000). In addition, patients with high neutrophils were less likely to stay longer in a high VL state (aHR = 0.76, 95% CI 0.63–0.92) and moderate VL (aHR = 0.90, 95% CI 0.84–0.96). High RBC indices scores (aHR = 0.75, 95% CI 0.62–0.92) and high electrolyte component scores (HR = 0.78, 95% CI 0.63–0.97) were significantly associated with a decreased probability of staying in a higher VL state. Furthermore, having high liver abnormality scores were associated with an increased probability of staying in a higher VL state (aHR = 1.35, 95% CI 1.16–1.57).
Patients with higher educational levels were found to be associated with an increased probability of staying in a lower VL state. Considering QoL domain scores of the patients, high physical health scores were significantly associated with an increased probability of staying at an undetectable level (aHR = 1.09, 95% CI 1.01–1.26). Patients in the younger age group (age < 20 years) were also associated with an increased probability of staying in a higher VL state (aHR = 1.81, 95% CI 1.23–3.39), compared to those in the older age group. Furthermore, an increased probability of staying in moderate VL states (between 10,000 and 100,000) was associated with having many sex partners (aHR = 2.36, 95% CI 1.63–3.42), as compared to those with no sex partner (Fig. 7).
Discussion
The current study was aimed to simultaneously model viral rebound, viral suppression, and state-specific duration of stay of AIDS patients, and to determine how these depend on level of educational status, age, marital status, quality of life scores, TB co-infection, RBC indices, hemoglobin and hematocrits, eosinophils, neutrophils, monocytes, electrolyte components, and liver enzyme abnormality. These factors may not adequately be modeled using constant hazards, although the bias in estimates of the hazard ratios was not large in this population. Thus, we have presented and compared full-parametric and semi-parametric multistate models. Results from the diagnostic plots, AIC and LRT, showed that the Weibull multistate model, fitted significantly better than the exponential and semi-parametric multistate models. We also improved the selected model, the Weibull multistate model, by including patient-level frailties and an orthogonal CD4 cell count component. This further improved the efficiency and predictive accuracy of the model.
Some of the results of this study supported the previous literature findings, while some results of this study provided new insights. The results of this study showed that young adolescents were significantly associated with decreased viral suppression and were associated with an increased probability of experiencing viral rebound, compared to those patients in older age groups (age > 40 years). This was supported by previous studies ([5, 49, 50]), in which older age groups were more likely to achieve viral suppression compared to those in younger age groups. A plausible reason for this is that the treatment for adolescents may be affected by alcohol and recreational drug use [51], lack of disclosure, stress, HIV-associated discrimination and stigma [5, 52], and feelings of invulnerability to the consequences of HIV disease [53]. These factors may mediate the observed association among younger aged individuals and viral rebound. We also found that patients with lower educational levels were associated with an increased probability of experiencing viral rebound, a finding that is in accordance with the literature [54,55,56], where patients who have lower educational attainment were associated with viral rebound. It may reflect lower levels of health literacy or indicate a marker of overall poverty. Lower health literacy and greater poverty-related stress have been linked to medication non-adherence and poor virologic outcomes [57, 58].
Having a high QoL domain score in our study was associated with increased suppression and reduced likelihood of viral rebound. As has been previously shown [59, 60], patients with anxiety, depression, and low QoL are less likely to exhibit adherence to ART. Poor adherence may be associated with increased probability of experiencing viral rebound [61,62,63], showing that at least part of the effect of low QoL scores on incomplete viral suppression is mediated through combination ART adherence. Patients diagnosed with TB after ART initiation are associated with increases in plasma HIV viremia [64,65,66]. The risk of viral suppression may also be decreased by patients with TB co-infection, due to an increased risk of drug toxicity, drug–drug interactions, and the potential for lower adherence due to the high pill burden [67]. Our data add to this literature by showing that patients with TB co-infection were associated with a decreased probability of experiencing viral suppression. Therefore, patients on ART with active TB should thus be prioritized for VL monitoring and adherence support. Furthermore, having many sex partners exposes them to an accelerated risk of viral rebound, from moderate to high VL.
Among the different hematological parameters for HIV-infected patients, as expected, an abnormally high number of eosinophils in the blood significantly decreased viral suppression and increased the probability of experiencing viral rebound, a finding that is in accordance with the literature [68], where it has been found that patients with a higher eosinophils counts were more likely to have higher long-term viral rebound. We also found that patients having higher neutrophil counts were significantly associated with a decreased probability of experiencing viral rebound. This finding agrees with studies that have shown that worsening HIV disease, demonstrated by increasing VL rebound, has been associated with abnormality of neutrophils (neutropenia: absolute neutrophil counts < 500) [69, 70]. We further observed that patients with high monocyte count were associated with a higher probability of experiencing viral rebound. Our finding is concurrent with those from prior reports, which noted that the monocyte CD69 expression rate was significantly positively correlated with the HIV-1 RNA [71]. Consequently, caution is needed for risk assessment measures to monitor and screen patients’ pre- and post-ART initiation in African clinical settings to curtail potential risks associated with an increased probability of experiencing viral rebound. Moreover, liver enzyme abnormalities were significantly associated with a higher probability of experiencing viral rebound. Our findings are concurrent with those from prior reports [72, 73], which noted that a positive correlation exists between VL and aminotransferase (ALT and AST). Thus, there is a need to monitor ALT and AST levels after initiation of ART, mainly in high-risk patients, to reduce side effect concerns.
We further found that patients having higher educational levels were more likely to spend a longer time in good states (particularly lower VL state), as compared to those with lower educational levels. This could be due to better knowledge about their treatment and disease, access to health services, or functional status. Similarly, higher QoL scores (particularly physical health scores) were significantly associated with longer time spent in lower VL states. Furthermore, those of younger age (< 20 years) with high liver abnormality scores and high social relationship scores were associated with an increased probability of staying in a higher VL state.
Readers should be cautious when interpreting the findings of this study since the study findings were limited to adult females, and hence the findings may not be generalized to all HIV-infected patients. In addition, this study has also some limitations, including missing data, which are expected for a study conducted on data collected from patients’ files and when dealing with a long-term follow-up period. Moreover, we did not assess some other clinical and risk factors, such as adherence level, hepatitis status, treatment change, drug–drug interactions, and drug abuse, that may affect VL dynamics. Despite these limitations, important information regarding clinical factors associated with viral rebound and viral suppression for women were identified. This information is of value in identifying women at risk for suboptimal therapeutic outcomes. Additionally, it will help to inform cART retention strategies for HIV-infected patients.
Conclusions
We have simultaneously modeled long-term viral suppression, viral rebound, and state-specific duration of stay of AIDS patients in seroconversion among South African women, using the Weibull multistate frailty model. This has resulted in precise estimates of covariate effects, time spent in each state, and expected survival times. Additionally, we have examined important information regarding factors that affect long-term viral dynamics. This information is of value in identifying women at risk for suboptimal therapeutic outcomes. Moreover, to achieve and maintain the UNAIDS 90% suppression targets, additional interventions are required to optimize ART outcomes, specifically targeting poor clinical characteristics, lower education, younger age individuals, and those with many sex partners.
From a methodological perspective, the parametric multistate with frailty approach is a flexible approach for modeling time-varying variable factors, allowing for dealing with heterogeneity between the sequence of transitions, allowing for a reasonable degree of flexibility with few additional parameters, and gaining a better insight into how the factors change over time. Furthermore, the parametric multistate frailty model further extends the knowledge as to the HIV disease burden transitions and can be used to learn more about the disease progression of other chronic diseases.
REFERENCES
Trickey A, May MT, Vehreschild J-J, Obel N, Gill MJ, Crane HM, Boesecke C, Patterson S, Grabar S, Cazanave C. Survival of HIV-positive patients starting antiretroviral therapy between 1996 and 2013: a collaborative analysis of cohort studies. Lancet HIV. 2017;4(8):e349–56.
Slim J, Saling CF. A review of management of inflammation in the hiv population. Biomed Res Int. 2016;2016:3420638.
Cohen MS, Chen YQ, McCauley M, Gamble T, Hosseinipour MC, Kumarasamy N, Hakim JG, Kumwenda J, Grinsztejn B, Pilotto JH. Prevention of HIV-1 infection with early antiretroviral therapy. N Engl J Med. 2011;365(6):493–505.
Conway JM, Perelson AS, Li JZ. Predictions of time to HIV viral rebound following ART suspension that incorporate personal biomarkers. PLoS Comput Biol. 2019;15(7):e1007229.
Bulage L, Ssewanyana I, Nankabirwa V, Nsubuga F, Kihembo C, Pande G, Ario AR, Matovu JK, Wanyenze RK, Kiyaga C. Factors associated with Virological non-suppression among HIV-positive patients on antiretroviral therapy in Uganda, August 2014–July 2015. BMC Infect Dis. 2017;17(1):326.
Wainberg MA, Zaharatos GJ, Brenner BG. Development of antiretroviral drug resistance. N Engl J Med. 2011;365(7):637–46.
Bvochora T, Satyanarayana S, Takarinda KC, Bara H, Chonzi P, Komtenza B, Duri C, Apollo T. Enhanced adherence counselling and viral load suppression in HIV seropositive patients with an initial high viral load in Harare, Zimbabwe: operational issues. PLoS ONE. 2019;14(2):e0211326.
World Health Organization. Consolidated guidelines on the use of antiretroviral drugs for treating and preventing HIV infection: recommendations for a public health approach. 2nd ed. Geneva, Switzerland: WHO; 2016.
World Health Organization. Technical brief on HIV viral load technologies. Geneva, Switzerland: WHO; 2010.
UNAIDS. 90-90-90: the ambitious target to help end the AIDS epidemic. Geneva, Switzerland: UNAIDS; 2014. http://www.unaids.org/sites/default/files/media_asset/90-90-90_en_0.pdf.
Aghokeng AF, Monleau M, Eymard-Duvernay S, Dagnra A, Kania D, Ngo-Giang-Huong N, Toni TD, Touré-Kane C, Truong LX, Delaporte E. Extraordinary heterogeneity of virological outcomes in patients receiving highly antiretroviral therapy and monitored with the World Health Organization public health approach in sub-saharan Africa and southeast Asia. Clin Infect Dis. 2013;58(1):99–109.
Gupta RK, Jordan MR, Sultan BJ, Hill A, Davis DH, Gregson J, Sawyer AW, Hamers RL, Ndembi N, Pillay D. Global trends in antiretroviral resistance in treatment-naive individuals with HIV after rollout of antiretroviral treatment in resource-limited settings: a global collaborative study and meta-regression analysis. Lancet. 2012;380(9849):1250–8.
Hamers RL, Sigaloff KC, Wensing AM, Wallis CL, Kityo C, Siwale M, Mandaliya K, Ive P, Botes ME, Wellington M. Patterns of HIV-1 drug resistance after first-line antiretroviral therapy (ART) failure in 6 sub-Saharan African countries: implications for second-line ART strategies. Clin Infect Dis. 2012;54(11):1660–9.
Kiweewa F, Esber A, Musingye E, Reed D, Crowell TA, Cham F, Semwogerere M, Namagembe R, Nambuya A, Kafeero C. HIV virologic failure and its predictors among HIV-infected adults on antiretroviral therapy in the African Cohort Study. PLoS ONE. 2019;14(2):e0211344.
Chhim K, Mburu G, Tuot S, Sopha R, Khol V, Chhoun P, Yi S. Factors associated with viral non-suppression among adolescents living with HIV in Cambodia: a cross-sectional study. AIDS Res Ther. 2018;15(1):20.
Crawford KW, Wakabi S, Magala F, Kibuuka H, Liu M, Hamm T. Evaluation of treatment outcomes for patients on first-line regimens in US President’s Emergency Plan for AIDS Relief (PEPFAR) clinics in U ganda: predictors of virological and immunological response from RV 288 analyses. HIV Med. 2015;16(2):95–104.
Nsubuga-Nyombi T, Sensalire S, Karamagi E, Aloyo J, Byabagambi J, Rahimzai M, Nabitaka LK, Calnan J. Multivariate analysis of covariates of adherence among HIV-positive mothers with low viral suppression. AIDS Res Ther. 2018;15(1):9.
Kazooba P, Mayanja BN, Levin J, Masiira B, Kaleebu P. Virological failure on first-line antiretroviral therapy; associated factors and a pragmatic approach for switching to second line therapy–evidence from a prospective cohort study in rural South-Western Uganda, 2004-2011. Pan Afr Med J. 2018;29(1):1–16.
Ocampo JMF, Plankey M, Zou K, Collmann J, Wang C, Young MA, Liu C, Ripple JA, Kassaye S. Trajectory analyses of virologic outcomes reflecting community-based HIV treatment in Washington DC 1994–2012. BMC Public Health. 2015;15(1):1277.
Tsondai PR, Wilkinson LS, Grimsrud A, Mdlalo PT, Ullauri A, Boulle A. High rates of retention and viral suppression in the scale-up of antiretroviral therapy adherence clubs in Cape Town, South Africa. J Int AIDS Soc. 2017;20:21649.
Palmer A, Gabler K, Rachlis B, Ding E, Chia J, Bacani N, et al. Viral suppression and viral rebound among young adults living with HIV in Canada. Medicine. 2018;97:e10562.
Duarte HA, Harris DR, Tassiopoulos K, Leister E, Negrini SFBDM, Ferreira FF, Cruz MLS, Pinto J, Allison S, Hazra R. Relationship between viral load and behavioral measures of adherence to antiretroviral therapy in children living with human immunodeficiency virus in Latin America. Brazil J Infect Dis. 2015;19(3):263–71.
Kunzweiler CP, Bailey RC, Mehta SD, Okall DO, Obondi E, Djomand G, Nyunya BO, Otieno FO, Graham SM. Factors associated with viral suppression among HIV-positive Kenyan gay and bisexual men who have sex with men. AIDS Care. 2018;30(sup5):S76–88.
Loeliger KB, Altice FL, Desai MM, Ciarleglio MM, Gallagher C, Meyer JP. Predictors of linkage to HIV care and viral suppression after release from jails and prisons: a retrospective cohort study. The Lancet HIV. 2018;5(2):e96–106.
Kemp CG, Lipira LL, Huh D, Nevin PE, Turan J, Simoni JM, Cohn SE, Bahk M, Berzins B, Andrasik M. HIV stigma and viral load among African-American women receiving treatment for HIV. AIDS. 2019;33(9):1511–9.
Dessie ZG. Modeling of HIV/AIDS dynamic evolution using non-homogeneous semi-markov process. SpringerPlus. 2014;3(1):537.
Naresh R, Tripathi A, Omar S. Modelling the spread of AIDS epidemic with vertical transmission. Appl Math Comput. 2006;178(2):262–72.
Shoko C, Chikobvu D. Determinants of viral load rebound on HIV/AIDS patients receiving antiretroviral therapy: results from South Africa. Theoret Biol Medi Model. 2018;15(1):10.
Schoen R, Kim YJ. A dynamic multistate model of robustness and frailty. Math Popul Stud. 2000;8(4):293–304.
Postmus D, van Veldhuisen DJ, Jaarsma T, Luttik ML, Lassus J, Mebazaa A, Nieminen MS, Harjola VP, Lewsey J, Buskens E. The COACH risk engine: a multistate model for predicting survival and hospitalization in patients with heart failure. Eur J Heart Fail. 2012;14(2):168–75.
Oliveira RDVCD, Shimakura SE, Campos DP, Victoriano FP, Ribeiro SR, Veloso VG, Grinsztejn B, Carvalho MS. Multi-state models for defining degrees of chronicity related to HIV-infected patient therapy adherence. Cad Saude Publica. 2013;29:801–11.
Putter H, van Houwelingen HC. Frailties in multi-state models: are they identifiable? Do we need them? Stat Methods Med Res. 2015;24(6):675–92.
Abner EL, Nelson PT, Schmitt FA, Browning SR, Fardo DW, Wan L, Jicha GA, Cooper GE, Smith CD, Caban-Holt AM. Self-reported head injury and risk of late-life impairment and AD pathology in an AD center cohort. Dement Geriatr Cogn Disord. 2014;37(5–6):294–306.
Chikobvu D, Shoko C. A Markov model to estimate mortality due to HIV/AIDS using CD4 cell counts based states and viral load: a principal component analysis approach. Biomed Res. 2018;29(15):3090–8.
van Loggerenberg F, Mlisana K, Williamson C, Auld SC, Morris L, Gray CM, Karim QA, Grobler A, Barnabas N, Iriogbe I. Establishing a cohort at high risk of HIV infection in South Africa: challenges and experiences of the CAPRISA 002 acute infection study. PLoS ONE. 2008;3(4):e1954.
Garrett N, Norman E, Leask K, Naicker N, Asari V, Majola N, Karim QA, Karim SSA. Acceptability of early antiretroviral therapy among South African women. AIDS Behav. 2018;22(3):1018–24.
Karim QA, Karim SSA, Frohlich JA, Grobler AC, Baxter C, Mansoor LE, Kharsany AB, Sibeko S, Mlisana KP, Omar Z. Effectiveness and safety of tenofovir gel, an antiretroviral microbicide, for the prevention of HIV infection in women. Science. 2010;329(5996):1168–74.
Mlisana K, Werner L, Garrett NJ, McKinnon LR, van Loggerenberg F, Passmore J-AS, Gray CM, Morris L, Williamson C, Abdool Karim SS. Rapid disease progression in HIV-1 subtype C–infected South African Women. Clin Infect Dis. 2014;59(9):1322–31.
WHOQoL Group. Development of the World Health Organization WHOQOL-BREF quality of life assessment. Psychol Med. 1998;28(3):551–8.
Dessie ZG, Zewotir T, Mwambi H, North D. Modelling of viral load dynamics and CD4 cell count progression in an antiretroviral naive cohort: using a joint linear mixed and multistate Markov model. BMC Infect Dis. 2020;20(1):1–14.
Dessie ZG, Zewotir T, Mwambi H, North D. Multivariate multilevel modeling of quality of life dynamics of HIV-infected patients. Health Qual Life Outcomes. 2020;18(1):1–14.
Byrne BM. Factor analytic models: viewing the structure of an assessment instrument from three perspectives. J Pers Assess. 2005;85(1):17–32.
Kaiser HF. The varimax criterion for analytic rotation in factor analysis. Psychometrika. 1958;23(3):187–200.
Rondeau V, Gonzalez JR. Frailtypack: a computer program for the analysis of correlated failure time data using penalized likelihood estimation. Comput Methods Programs Biomed. 2005;80(2):154–64.
Kalbfleisch J, Lawless JF. The analysis of panel data under a Markov assumption. J Am Stat Assoc. 1985;80(392):863–71.
Crowther MJ, Lambert PC. Parametric multistate survival models: flexible modelling allowing transition-specific distributions with application to estimating clinically useful measures of effect differences. Stat Med. 2017;36(29):4719–42.
Ieva F, Jackson CH, Sharples LD. Multi-State modelling of repeated hospitalisation and death in patients with Heart Failure: the use of large administrative databases in clinical epidemiology. Stat Methods Med Res. 2017;26(3):1350–72.
Titman AC, Sharples LD. Model diagnostics for multi-state models. Stat Methods Med Res. 2010;19(6):621–51.
Shoko C, Chikobvu D. A superiority of viral load over CD4 cell count when predicting mortality in HIV patients on therapy. BMC Infect Dis. 2019;19(1):169.
Nasuuna E, Kigozi J, Babirye L, Muganzi A, Sewankambo NK, Nakanjako D. Low HIV viral suppression rates following the intensive adherence counseling (IAC) program for children and adolescents with viral failure in public health facilities in Uganda. BMC Public Health. 2018;18(1):1048.
Reisner MSL, Mimiaga MJ, Skeer MM, Perkovich MB, Johnson MCV, Safren SA. A review of HIV antiretroviral adherence and intervention studies among HIV–infected youth. Topics HIV Med. 2009;17(1):14.
Katz IT, Ryu AE, Onuegbu AG, Psaros C, Weiser SD, Bangsberg DR, Tsai AC. Impact of HIV-related stigma on treatment adherence: systematic review and meta-synthesis. J Int AIDS Soc. 2013;16:18640.
Hadland SE, Milloy M-J, Kerr T, Zhang R, Guillemi S, Hogg RS, Montaner JS, Wood E. Young age predicts poor antiretroviral adherence and viral load suppression among injection drug users. AIDS Patient Care STDs. 2012;26(5):274–80.
Burch LS, Smith CJ, Anderson J, Sherr L, Rodger AJ, O’Connell R, Geretti A-M, Gilson R, Fisher M, Elford J. Socioeconomic status and treatment outcomes for individuals with HIV on antiretroviral treatment in the UK: cross-sectional and longitudinal analyses. Lancet Public Health. 2016;1(1):e26–36.
Burch LS, Smith CJ, Phillips AN, Johnson MA, Lampe FC. Socioeconomic status and response to antiretroviral therapy in high-income countries: a literature review. AIDS. 2016;30(8):1147–62.
Sobrino-Vegas P, Rodríguez-Urrego J, Berenguer J, Caro-Murillo AM, Blanco JR, Viciana P. Educational gradient in HIV diagnosis delay, mortality, antiretroviral treatment initiation and response in a country with universal health care. Antivir Ther. 2012;17(1):1.
Kalichman SC, Grebler T. Stress and poverty predictors of treatment adherence among people with low-literacy living with HIV/AIDS. Psychosom Med. 2010;72(8):810.
Katz IT, Leister E, Kacanek D, Hughes MD, Bardeguez A, Livingston E, Stek A, Shapiro DE, Tuomala R. Factors associated with lack of viral suppression at delivery among highly active antiretroviral therapy–naive women with HIV: a cohort study. Ann Intern Med. 2015;162(2):90–9.
Gonzalez JS, Batchelder AW, Psaros C, Safren SA. Depression and HIV/AIDS treatment nonadherence: a review and meta-analysis. J Acquir Immune Defic Syndr. 2011;58(2):181–7.
Mannheimer SB, Matts J, Telzak E, Chesney M, Child C, Wu AW, Friedland G, AIDS TBCPfCRo. Quality of life in HIV-infected individuals receiving antiretroviral therapy is related to adherence. AIDS Care. 2005;17(1):10–22.
Glass TR, Sterne JA, Schneider M-P, De Geest S, Nicca D, Furrer H, Günthard HF, Bernasconi E, Calmy A, Rickenbach M. Self-reported nonadherence to antiretroviral therapy as a predictor of viral failure and mortality. AIDS. 2015;29(16):2195–200.
Musinguzi N, Mocello RA, Boum Y, Hunt PW, Martin JN, Haberer JE, Bangsberg DR, Siedner MJ. Duration of viral suppression and risk of rebound viremia with first-line antiretroviral therapy in rural Uganda. AIDS Behav. 2017;21(6):1735–40.
Shah B, Walshe L, Saple DG, Mehta SH, Ramnani JP, Kharkar R, Bollinger RC, Gupta A. Adherence to antiretroviral therapy and virologic suppression among HIV-infected persons receiving care in private clinics in Mumbai, India. Clin Infect Dis. 2007;44(9):1235–44.
El-Khatib Z, Ekström AM, Ledwaba J, Mohapi L, Laher F, Karstaedt A, Charalambous S, Petzold M, Katzenstein D, Morris L. nViremia and drug resistance among HIV-1 patients on antiretroviral treatment–a cross-sectional study in Soweto, South Africa. AIDS (London, England). 2010;24(11):1679.
Gupta A, Wood R, Kaplan R, Bekker L-G, Lawn SD. Prevalent and incident tuberculosis are independent risk factors for mortality among patients accessing antiretroviral therapy in South Africa. PLoS ONE. 2013;8(2):e55824.
Komati S, Shaw PA, Stubbs N, Mathibedi MJ, Malan L, Sangweni P, Metcalf JA, Masur H, Hassim S. Tuberculosis risk factors and mortality for HIV-infected persons receiving antiretroviral therapy in South Africa. AIDS (London, England). 2010;24(12):1849.
Curran A, Falco V, Pahissa A, Ribera E. Management of tuberculosis in HIV-infected patients. AIDS Rev. 2012;14(4):231–46.
Al MM, Villarreal-Williams E, Andrade RA, Giordano TP, Serpa JA. Eosinophilia and associated factors in a large cohort of patients infected with human immunodeficiency virus. South Med J. 2014;107(9):554–8.
Levine AM, Karim R, Mack W, Gravink DJ, Anastos K, Young M, Cohen M, Newman M, Augenbraun M, Gange S. Neutropenia in human immunodeficiency virus infection: data from the women’s interagency HIV study. Arch Intern Med. 2006;166(4):405–10.
Shi X, Sims MD, Hanna MM, Xie M, Gulick PG, Zheng Y-H, Basson MD, Zhang P. Neutropenia during HIV infection: adverse consequences and remedies. Int Rev Immunol. 2014;33(6):511–36.
Zhou L, Shang H, Zhang Z, Wang Y, Li G, Shi W, Ding H. Correlation between the function of monocytes/macrophages and disease progression in people living with HIV/AIDS in several provinces in China. Zhonghua yi xue za zhi. 2007;87(34):2394–7.
Mata-Marín JA, Gaytán-Martínez J, Grados-Chavarría BH, Fuentes-Allen JL, Arroyo-Anduiza CI, Alfaro-Mejía A. Correlation between HIV viral load and aminotransferases as liver damage markers in HIV-infected naive patients: a concordance cross-sectional study. Virol J. 2009;6(1):181.
Zechini B, Pasquazzi C, Aceti A. Correlation of serum aminotransferases with HCV RNA levels and histological findings in patients with chronic hepatitis C: the role of serum aspartate transaminase in the evaluation of disease progression. Eur J Gastroenterol Hepatol. 2004;16(9):891–6.
Acknowledgements
We would like to acknowledge Dr Nonhlanhla Yende-Zuma, Dr Nigel Garrett and the entire CAPRISA Acute Infection team including research leaders who formulated the research ideas that generated such rich data, thank you very much for allowing us to use this dataset. We also thank the participants for their involvement in this study. We would also like to thank the School of Mathematics, Statistics and Computer Science, University of KwaZulu-Natal, South Africa for providing their guidance and support.
Funding
This study was supported through the DELTAS Africa Initiative SSACAB (Grant No. 107754/Z/15/Z). The DELTAS Africa Initiative is an independent funding scheme of the African Academy of Sciences (AAS) Alliance for Accelerating Excellence in Science in Africa (AESA) and is supported by the New Partnership for Africa’s Development Planning and Coordinating Agency (NEPAD Agency) and the UK Government. No funding or sponsorship was received for the publication of this article.
Authorship
All named authors meet the International Committee of Medical Journal Editors (ICMJE) criteria for authorship of this article, take responsibility for the integrity of the work as a whole, and have given their approval for this version to be published.
Authorship Contributions
Zelalem G. Dessie designed the study, collected the data, analysed the data and wrote the article. Temesgen Zewotir designed the study, advised on analysis and edited the manuscript. Henry Mwambi and Delia North reviewed the study designed and critically edited the manuscript. All authors read and approved the final manuscript.
Disclosures
Zelalem G. Dessie, Temesgen Zewotir, Henry Mwambi and Delia North declare that they have no conflict of interest.
Compliance with Ethics Guidelines
All procedures performed in this study were approved by the Research Ethics Committee of the University of KwaZulu-Natal and Centre for the AIDS Programme of Research in South Africa (CAPRISA). Written informed consent was obtained from all participants, and ethical approval for the original study was granted by the University of KwaZulu-Natal (E013/04), the University of Cape Town (025/2004), and the University of the Witwatersrand (M040202).
Data Availability
The datasets during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Author information
Authors and Affiliations
Corresponding author
Additional information
Digital Features
To view digital features for this article go to https://doi.org/10.6084/m9.figshare.12058938.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, which permits any non-commercial use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc/4.0/.
About this article
Cite this article
Dessie, Z.G., Zewotir, T., Mwambi, H. et al. Modeling Viral Suppression, Viral Rebound and State-Specific Duration of HIV Patients with CD4 Count Adjustment: Parametric Multistate Frailty Model Approach. Infect Dis Ther 9, 367–388 (2020). https://doi.org/10.1007/s40121-020-00296-4
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40121-020-00296-4