Introduction

The class of partial integro-differential equations (PIDEs) is the one that combines the unknown function’s partial differentiation and integration. It is used in many cases where the memory effect should be considered. PIDEs appear in different fields of engineering and physics such as heat conduction [1], compression of poro-viscoelastic media [2], reaction diffusion problems [3], and nuclear reactor dynamics [4].

Many techniques are used to solve PIDEs. These include for example semianalytic techniques such as in [1] where He’s variational iteration technique is employed. Some numerical methods have been proposed like the finite difference method (FDM) [2]. Also, the collocation method is used to solve PIDE as in [3]. A Fixed-Point Theorem of type Monch–Krasnosel’skii is introduced in [5]. The authors of [6] considered a nonlinear form of PIDE that arises in viscoelasticity applications and solved it numerically using graded meshes. In [7], an approach that depends on unsupervised deep learning is also used to solve PIDEs. Time fractional PIDEs are solved with different methods as in [8], where a compact FDM is utilized. Also, we see in [9] that a new FDM is proposed to approximate time fractional PIDE and the stability and convergence of the mentioned numerical scheme areas proved. PIDEs have been generalized to fractional order modeling and are referred to as fractional partial integro-differential equations (FPIDEs) as in [10].

During the past decades, great attention has been paid to the so-called fractional calculus, with which we can consider integration and differentiation not only of integer order but also of fractional ones. It is applied to generalize different types of differential equations. This produces fractional differential equations, which are distinguished from integer ones as being able to describe the memory effect, which increases its modeling ability. Publications [11,12,13,14] have included a summary of fractional differential equations. Fractional derivatives are defined using many definitions, such as Caputo, Riemann–Liouville, Riesz fractional derivatives, and many others.

The Riesz fractional derivative is usually used with space fractional derivatives. It was defined on finite and infinite domains as well. Riesz definition on infinite domains was considered in [15,16,17,18,19,20], where semianalytic techniques were used, and in [21] where similarity solution was used. While Riesz definition on finite domains was considered in [22], where the McCormack numerical method was utilized. One of the numerical methods used to solve Riesz fractional partial differential equations is the finite element method (FEM), as in [23, 24].

The FEM is a powerful method that is useful and effective in solving different types of differential equations. Recently, some appraised papers have been concerned with the FEM solution for fractional differential equations. Adolfsson [25] and [26] proposed a numerical method based on the FEM for integrating the constitutive response of fractional order viscoelasticity. Roop and Ervin [27,28,29,30] analyzed theoretically the approximation of the Galerkin finite element method to some kinds of fractional partial differential equations (FPDEs). Li [31] approximated numerically the fractional differential equations with subdiffusion and superdiffusion by using the difference method and the finite element method.

For the FEM to be more reliable, adaptive techniques can be used to control the error under some predefined tolerance. Adaptive techniques are procedures that iterate until the error reaches a predefined tolerance. A significant improvement is achieved by a posteriori treatment of the finite element data. This is a post-process called recovery, which is utilized in the implementation of the recovery-based error estimator. Then, the mesh is adaptively refined so that the accuracy satisfies the requirements of the user. Adaptive FEMs for different types of equations have been considered by many authors; see, [32,33,34]. Adaptive techniques sometimes depend on recovery techniques as in [35] where solution recovery is considered, and in [36,37,38,39,40] where gradient recovery is considered.

In [23], an algorithm was proposed to solve FPIDEs using FEM on a uniform mesh. In this work, we apply an adaptive FEM which is a recovery-based technique, and this causes the mesh to be nonuniform. We modified the algorithm in [23] so that it is applicable in the case of nonuniform mesh. This is illustrated by applying the gradient recovery technique known as the polynomial preserving recovery (PPR) technique to Riesz FPIDEs of the form

$$\begin{aligned} \frac{\partial u}{\partial t}=c\frac{\partial ^{1+\alpha }u(x,t)}{\partial \left| x\right| ^{1+\alpha }}+\int \limits _{0}^{t}K(t,s)u(x,s)ds+f(x,t),\qquad x\in (a,b),\;t\in (0,T), \end{aligned}$$
(1)

with an initial condition

$$\begin{aligned} u(x,0)=\psi (x),\qquad a\le x\le b, \end{aligned}$$
(2)

and boundary conditions

$$\begin{aligned} u(a,t)=0,\qquad u(b,t)=0,\qquad 0\le t\le T, \end{aligned}$$
(3)

where \(0<\alpha <1,\) and u(x, t), f(x, t) are continuous functions.

Here, the space fractional derivative \(\frac{\partial ^{1+\alpha }u(x,t)}{ \partial \left| x\right| ^{1+\alpha }}\) is the Riesz fractional derivative of order \((1+\alpha )\), defined by [41]

$$\begin{aligned} \frac{\partial ^{1+\alpha }u(x,t)}{\partial \left| x\right| ^{1+\alpha }}=-\frac{1}{2cos\frac{\pi (1+\alpha )}{2}}\left[ \frac{\partial ^{1+\alpha }u(x,t)}{\partial x^{1+\alpha }}+\frac{\partial ^{1+\alpha }u(x,t) }{\partial \left( -x\right) ^{1+\alpha }}\right] , \end{aligned}$$
(4)

and

$$\begin{aligned} \frac{\partial ^{1+\alpha }u(x,t)}{\partial x^{1+\alpha }}&= \frac{1}{ \Gamma (1-\alpha )}\int \limits _{a}^{x}(x-\zeta )^{-\alpha }\frac{\partial ^{2}}{\partial x^{2}}u(\zeta ,t)d\zeta , \nonumber \\ \frac{\partial ^{1+\alpha }u(x,t)}{\partial (-x)^{1+\alpha }}&= \frac{1}{ \Gamma (1-\alpha )}\int \limits _{x}^{b}(\zeta -x)^{-\alpha }\frac{\partial ^{2}}{\partial x^{2}}u(\zeta ,t)d\zeta . \end{aligned}$$
(5)

The outline of the paper is as follows: the fundamental relations of the Riesz approximation on nonuniform mesh are introduced in “Section Riesz approximation on nonuniform mesh”. The method of solution to the FPIDE is introduced in “Section Description of method”. “Section Gradient recovery and adaptive refinement” is about the gradient recovery using the PPR technique and the proposed adaptive refinement algorithm. “Section Error analysis and stability condition” contains the error analysis and the stability for the proposed scheme. “Section 6” contains the numerical examples section where the results are presented and compared with the exact solution. The last section offers some conclusions regarding the work presented in this article.

Riesz approximation on nonuniform mesh

Here, the basic relations and lemmas that are utilized in the next sections are stated.

First, we refer to the finite domain by \(\Omega =[a,b]\) and (, ) to be the inner product on the \(L_{2}(\Omega )\) space. Then, for some integer m,  the nodes \(x_{0},x_{1},\ldots ,x_{m-1},x_{m}\) partition the domain \(\Omega\) into m nonuniform subintervals. The set of all nodes in the partition forms the mesh \(M_{h}.\)

We denote the set of polynomials that are piecewise linear over the mesh nodes to be the space \(V_{h},\) which is defined as follows:

$$\begin{aligned} V_{h}=\left\{ v:v|_{\Omega _{i}}\in P_{1}(\Omega _{i}),\quad v\in C(\Omega )\right\} \end{aligned}$$
(6)

where \(P_{1}(\Omega _{i})\) denotes the space of linear polynomials defined on \(\Omega _{i}\). Then, the following is the representation of any \(v\in V_{h}\)

$$\begin{aligned} v=\sum \limits _{j=0}^{m}v(x_{j})\phi _{j}, \end{aligned}$$

where the nodal-based functions \(\phi _{0}\), \(\phi _{1}\),..., \(\phi _{m}\) of \(V_{h}\) are defined as follows:

$$\begin{aligned} \phi _{i}(x)=\left\{ \begin{array}{c} \frac{x-x_{i-1}}{x_{i}-x_{i-1}},\qquad x\in \left[ x_{i-1},x_{i}\right] \\ \frac{x_{i+1}-x}{x_{i+1}-x_{i}},\qquad x\in \left[ x_{i},x_{i+1}\right] \\ 0,\qquad \ \ otherwise. \end{array} \right. \end{aligned}$$
(7)

where i is an integer that takes values from 1 to \(m-1\), and

$$\begin{aligned} \phi _{0}(x)&= \left\{ \begin{array}{c} \frac{x_{1}-x}{x_{1}-x_{0}},\qquad x\in \left[ x_{0},x_{1}\right] \\ 0,\qquad \ \ otherwise \end{array} \right. , \nonumber \\ \phi _{m}(x)&= \left\{ \begin{array}{c} \frac{x-x_{m-1}}{x_{m}-x_{m-1}},\qquad x\in \left[ x_{m-1},x_{m}\right] \\ 0,\qquad \ \ \ \ \ otherwise. \end{array} \right. \end{aligned}$$
(8)

Lemma 1

If i takes the values of \(1,2,\ldots ,m-1,\) the inner product between the basic functions is given by

$$\begin{aligned} (\phi _{i}(x),\phi _{j}(x))=\frac{1}{6}\left\{ \begin{array}{l} (x_{i}-x_{i-1}),\quad \ \ \ \ j=i-1, \\ (x_{i+1}-x_{i}),\quad \ \ \ \ j=i+1, \\ 2(x_{i+1}-x_{i-1}),\qquad j=i,\quad \\ 0,\qquad otherwise. \end{array} \right. \end{aligned}$$
(9)

Proof

Let \(i=j\), from definition of inner product and the definition of \(\phi _{i}(x)\), we have:

$$\begin{aligned} (\phi _{i}(x),\phi _{i}(x))&= \int \limits _{x_{i-1}}^{x_{i}}\frac{ (x-x_{i-1})^{2}}{(x_{i}-x_{i-1})^{2}}dx+\int \limits _{x_{i}}^{x_{i+1}}\frac{ (x_{i+1}-x)^{2}}{(x_{i+1}-x_{i})^{2}}dx \\&= \frac{(x_{i}-x_{i-1})}{3}+\frac{(x_{i+1}-x_{i})}{3}=\frac{ (x_{i+1}-x_{i-1})}{3}. \end{aligned}$$

For \(j=i-1\), it follows that

$$\begin{aligned} (\phi _{i}(x),\phi _{i-1}(x))=\int \limits _{x_{i-1}}^{x_{i}}\frac{(x-x_{i-1}) }{(x_{i}-x_{i-1})}\frac{(x_{i}-x)}{(x_{i}-x_{i-1})}dx=\frac{(x_{i}-x_{i-1})}{ 6}. \end{aligned}$$

For \(j=i+1,\) we have

$$\begin{aligned} (\phi _{i}(x),\phi _{i+1}(x))=\int \limits _{x_{i}}^{x_{i+1}}\frac{(x_{i+1}-x) }{(x_{i+1}-x_{i})}\frac{(x-x_{i})}{(x_{i+1}-x_{i})}dx=\frac{(x_{i+1}-x_{i})}{ 6}. \end{aligned}$$

Otherwise, from the definition of \(\phi _{i}(x)\), the inner product will always equal zero. \(\square\)

Lemma 2

If i takes the values of \(1,2,\ldots ,m-1,\) the fractional derivative of order \(\alpha\) for the basic functions will be given by

$$\begin{aligned} \frac{\partial ^{\alpha }\phi _{i}(x)}{\partial x^{\alpha }}=\frac{1}{\Gamma (2-\alpha )}\left\{ \begin{array}{c} 0,\qquad \qquad \qquad \qquad \qquad \qquad \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ a\le x\le x_{i-1} \\ \frac{(x-x_{i-1})^{1-\alpha }}{(x_{i}-x_{i-1})},\qquad \ \ \ \ \ \ \ \ \ \qquad \qquad \qquad \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x_{i-1}\le x\le x_{i} \\ \frac{(x-x_{i-1})^{1-\alpha }}{(x_{i}-x_{i-1})}-\frac{(x-x_{i})^{1-\alpha }}{ (x_{i}-x_{i-1})}-\frac{(x-x_{i})^{1-\alpha }}{(x_{i+1}-x_{i})},\qquad \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x_{i}\le x\le x_{i+1} \\ \frac{(x-x_{i-1})^{1-\alpha }}{(x_{i}-x_{i-1})}-\frac{(x-x_{i})^{1-\alpha }}{ (x_{i}-x_{i-1})}-\frac{(x-x_{i})^{1-\alpha }}{(x_{i+1}-x_{i})}+\frac{ (x-x_{i-1})^{1-\alpha }}{(x_{i+1}-x_{i})},\quad \ \ \ \ \ x_{i+1}\le x\le b \end{array} \right. \end{aligned}$$
(10)
$$\begin{aligned} \frac{\partial ^{\alpha }\phi _{i}(x)}{\partial (-x)^{\alpha }}=\frac{1}{ \Gamma (2-\alpha )}\left\{ \begin{array}{c} \frac{(x_{i+1}-x)^{1-\alpha }}{(x_{i+1}-x_{i})}-\frac{(x_{i}-x)^{1-\alpha }}{ (x_{i}-x_{i-1})}-\frac{(x_{i}-x)^{1-\alpha }}{(x_{i+1}-x_{i})}+\frac{ (x_{i-1}-x)^{1-\alpha }}{(x_{i}-x_{i-1})},\qquad a\le x\le x_{i-1} \\ \frac{(x_{i+1}-x)^{1-\alpha }}{(x_{i+1}-x_{i})}-\frac{(x_{i}-x)^{1-\alpha }}{ (x_{i}-x_{i-1})}-\frac{(x_{i}-x)^{1-\alpha }}{(x_{i+1}-x_{i})},\qquad \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x_{i-1}\le x\le x_{i} \\ \frac{(x_{i+1}-x)^{1-\alpha }}{(x_{i+1}-x_{i})},\qquad \qquad \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \hspace{0.14in} x_{i}\le x\le x_{i+1} \\ 0,\qquad \qquad \qquad \qquad \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x_{i+1}\le x\le b \end{array} \right. \end{aligned}$$
(11)

Proof

From the definition of the first order left Caputo derivative,

$$\begin{aligned} \frac{\partial ^{\alpha }\phi _{i}(x)}{\partial x^{\alpha }}=\frac{1}{\Gamma (1-\alpha )}\int \limits _{a}^{x}\frac{\partial \phi _{i}(\zeta )}{\partial \zeta }\frac{d\zeta }{(x-\zeta )^{\alpha }}. \end{aligned}$$

If \(x_{i-1}\le x\le x_{i}\), and from definition of \(\phi _{i}(x)\), we have

$$\begin{aligned} \frac{\partial ^{\alpha }\phi _{i}(x)}{\partial x^{\alpha }}&= \frac{1}{ \Gamma (1-\alpha )}\int \limits _{x_{i-1}}^{x}\frac{1}{(x_{i}-x_{i-1})}\frac{ d\zeta }{(x-\zeta )^{\alpha }} \nonumber \\&= \frac{1}{\Gamma (2-\alpha )}\frac{(x-x_{i-1})^{1-\alpha }}{(x_{i}-x_{i-1}) }. \end{aligned}$$
(12)

If \(x_{i}\le x\le x_{i+1}\), it follows that

$$\begin{aligned} \frac{\partial ^{\alpha }\phi _{i}(x)}{\partial x^{\alpha }}&= \frac{1}{ \Gamma (1-\alpha )}\left[ \int \limits _{x_{i-1}}^{x_{i}}\frac{1}{ (x_{i}-x_{i-1})}\frac{d\zeta }{(x-\zeta )^{\alpha }}\right. \nonumber \\{} & \quad \left. +\int \limits _{x_{i}}^{x} \frac{-1}{(x_{i+1}-x_{i})}\frac{d\zeta }{(x-\zeta )^{\alpha }}\right] \nonumber \\&= \frac{1}{\Gamma (2-\alpha )}\left[ \frac{(x-x_{i-1})^{1-\alpha }}{ (x_{i}-x_{i-1})}-\frac{(x-x_{i})^{1-\alpha }}{(x_{i}-x_{i-1})}\right. \nonumber \\{} & \quad \left. -\frac{ (x-x_{i})^{1-\alpha }}{(x_{i+1}-x_{i})}\right] . \end{aligned}$$
(13)

If \(\ x\ge x_{i+1},\) we have

$$\begin{aligned} \frac{\partial ^{\alpha }\phi _{i}(x)}{\partial x^{\alpha }}= & {} \frac{1}{ \Gamma (1-\alpha )}\left[ \int \limits _{x_{i-1}}^{x_{i}}\frac{1}{ (x_{i}-x_{i-1})}\frac{d\zeta }{(x-\zeta )^{\alpha }}\right. \nonumber \\{} & {} \left. +\int \limits _{x_{i}}^{x_{i+1}}\frac{-1}{(x_{i+1}-x_{i})}\frac{d\zeta }{(x-\zeta )^{\alpha }}\right] \nonumber \\= & {} \frac{1}{\Gamma (2-\alpha )}\left[ \frac{(x-x_{i-1})^{1-\alpha }}{ (x_{i}-x_{i-1})}-\frac{(x-x_{i})^{1-\alpha }}{(x_{i}-x_{i-1})}-\frac{ (x-x_{i})^{1-\alpha }}{(x_{i+1}-x_{i})}\right. \nonumber \\{} & {} \left. +\frac{(x-x_{i-1})^{1-\alpha }}{ (x_{i+1}-x_{i})}\right] . \end{aligned}$$
(14)

If \(x\le x_{i-1},\) \(\phi _{i}(x)\) equal zero and \(\frac{\partial ^{\alpha }\phi _{i}(x)}{\partial x^{\alpha }}=0.\)

Also, from the definition of the first order right Caputo derivative

$$\begin{aligned} \frac{\partial ^{\alpha }\phi _{i}(x)}{\partial (-x)^{\alpha }}=\frac{-1}{ \Gamma (1-\alpha )}\int \limits _{x}^{b}\frac{\partial \phi _{i}(\zeta )}{ \partial \zeta }\frac{d\zeta }{(\zeta -x)^{\alpha }}. \end{aligned}$$
(15)

If \(x\le x_{i-1},\) and from definition of \(\phi _{i}(x),\), we have

$$\begin{aligned} \frac{\partial ^{\alpha }\phi _{i}(x)}{\partial (-x)^{\alpha }}= & {} \frac{-1}{ \Gamma (1-\alpha )}\left[ \int \limits _{x_{i-1}}^{x_{i}}\frac{1}{ (x_{i}-x_{i-1})}\frac{d\zeta }{(\zeta -x)^{\alpha }}\right. \nonumber \\{} & {} \left. +\int \limits _{x_{i}}^{x_{i+1}}\frac{-1}{(x_{i+1}-x_{i})}\frac{d\zeta }{(\zeta -x)^{\alpha }}\right] \nonumber \\= & {} \frac{1}{\Gamma (2-\alpha )}\left[ \frac{(x_{i+1}-x)^{1-\alpha }}{ (x_{i+1}-x_{i})}-\frac{(x_{i}-x)^{1-\alpha }}{(x_{i}-x_{i-1})}\right. \nonumber \\{} & {} \left. -\frac{ (x_{i}-x)^{1-\alpha }}{(x_{i+1}-x_{i})}+\frac{(x_{i-1}-x)^{1-\alpha }}{ (x_{i}-x_{i-1})}\right] . \end{aligned}$$
(16)

If \(x_{i-1}\le x\le x_{i},\) it follows that

$$\begin{aligned} \frac{\partial ^{\alpha }\phi _{i}(x)}{\partial (-x)^{\alpha }}= & {} \frac{-1}{ \Gamma (1-\alpha )}\left[ \int \limits _{x}^{x_{i}}\frac{1}{(x_{i}-x_{i-1})} \frac{d\zeta }{(\zeta -x)^{\alpha }}\right. \nonumber \\{} & {} \left. +\int \limits _{x_{i}}^{x_{i+1}}\frac{-1}{ (x_{i+1}-x_{i})}\frac{d\zeta }{(\zeta -x)^{\alpha }}\right] \nonumber \\= & {} \frac{1}{\Gamma (2-\alpha )}\left[ \frac{(x_{i+1}-x)^{1-\alpha }}{ (x_{i+1}-x_{i})}\right. \nonumber \\{} & {} \left. -\frac{(x_{i}-x)^{1-\alpha }}{(x_{i}-x_{i-1})}-\frac{ (x_{i}-x)^{1-\alpha }}{(x_{i+1}-x_{i})}\right] . \end{aligned}$$
(17)

If \(x_{i}\le x\le x_{i+1}\), we have

$$\begin{aligned} \frac{\partial ^{\alpha }\phi _{i}(x)}{\partial (-x)^{\alpha }}&= \frac{-1}{ \Gamma (1-\alpha )}\left[ \int \limits _{x}^{x_{i+1}}\frac{-1}{(x_{i+1}-x_{i}) }\frac{d\zeta }{(\zeta -x)^{\alpha }}\right] \nonumber \\&= \frac{1}{\Gamma (2-\alpha )}\left[ \frac{(x_{i+1}-x)^{1-\alpha }}{ (x_{i+1}-x_{i})}\right] . \end{aligned}$$
(18)

If \(x\ge x_{i+1},\) \(\phi _{i}(x)\) equal zero and \(\frac{\partial ^{\alpha }\phi _{i}(x)}{\partial (-x)^{\alpha }}=0.\)

From (12)–(18), Lemma 2 is proved. \(\square\)

Lemma 3

Let \(B=(x_{j}-x_{j-1})\) and \(M=(x_{j+1}-x_{j}),\), then, for \(i=1,2,\ldots ,m-1,\) we have

$$\begin{aligned} \int \limits _{x_{i-1}}^{x_{i}}(\frac{\partial ^{\alpha }\phi _{j}(x)}{ \partial x^{\alpha }}-\frac{\partial ^{\alpha }\phi _{j}(x)}{\partial (-x)^{\alpha }})dx=\frac{1}{\Gamma (3-\alpha )}g_{i,j}^{(3)}, \end{aligned}$$
(19)
$$\begin{aligned} \int \limits _{x_{i}}^{x_{i+1}}(\frac{\partial ^{\alpha }\phi _{j}(x)}{ \partial x^{\alpha }}-\frac{\partial ^{\alpha }\phi _{j}(x)}{\partial (-x)^{\alpha }})dx=\frac{1}{\Gamma (3-\alpha )}g_{i,j}^{(4)}, \end{aligned}$$
(20)

where

$$\begin{aligned} g_{i,j}^{(3)}= & {} \left\{ \begin{array}{c} \begin{array}{c} (\frac{(x_{i}-x_{j-1})^{2-\alpha }}{B}-\frac{(x_{i}-x_{j})^{2-\alpha }}{B}- \frac{(x_{i}-x_{j})^{2-\alpha }}{M}+\frac{(x_{i}-x_{j+1})^{2-\alpha }}{M}) \\ -(\frac{(x_{i-1}-x_{j-1})^{2-\alpha }}{B}-\frac{(x_{i-1}-x_{j})^{2-\alpha }}{ B}-\frac{(x_{i-1}-x_{j})^{2-\alpha }}{M}+\frac{(x_{i-1}-x_{j+1})^{2-\alpha } }{M}) \end{array},\ \ \ \ \ \ j\le i-2 \\ \\ \frac{(x_{i}-x_{i-2})^{2-\alpha }}{B}-\frac{(x_{i}-x_{i-1})^{2-\alpha }}{B} -2M^{1-\alpha }-B^{1-\alpha },\qquad \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ j=i-1 \\ \\ 2B^{1-\alpha }+M^{1-\alpha }-\frac{(x_{i+1}-x_{i-1})^{2-\alpha }}{M}+\frac{ (x_{i}-x_{i-1})^{2-\alpha }}{M},\qquad \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ j=i \\ \\ \begin{array}{c} -(\frac{(x_{j}-x_{i})^{2-\alpha }}{B}-\frac{(x_{j-1}-x_{i})^{2-\alpha }}{B}- \frac{(x_{j+1}-x_{i})^{2-\alpha }}{M}+\frac{(x_{j}-x_{i})^{2-\alpha }}{M}) \\ +(\frac{(x_{j}-x_{i-1})^{2-\alpha }}{B}-\frac{(x_{j-1}-x_{i-1})^{2-\alpha }}{ B}-\frac{(x_{j+1}-x_{i-1})^{2-\alpha }}{M}+\frac{(x_{j}-x_{i-1})^{2-\alpha } }{M}) \end{array},\ \ \ \ \ \ j\ge i+1 \end{array} \right. , \end{aligned}$$
(21)
$$\begin{aligned} g_{i,j}^{(4)}= & {} \left\{ \begin{array}{c} \begin{array}{c} (\frac{(x_{i+1}-x_{j-1})^{2-\alpha }}{B}-\frac{(x_{i+1}-x_{j})^{2-\alpha }}{B }-\frac{(x_{i+1}-x_{j})^{2-\alpha }}{M}+\frac{(x_{i+1}-x_{j+1})^{2-\alpha }}{ M}) \\ -(\frac{(x_{i}-x_{j-1})^{2-\alpha }}{B}-\frac{(x_{i}-x_{j})^{2-\alpha }}{B}- \frac{(x_{i}-x_{j})^{2-\alpha }}{M}+\frac{(x_{i}-x_{j+1})^{2-\alpha }}{M}) \end{array},\ \ \ \ j\le i-1 \\ \\ \frac{(x_{i+1}-x_{i-1})^{2-\alpha }}{B}-\frac{(x_{i+1}-x_{i})^{2-\alpha }}{B} -2M^{1-\alpha }-B^{1-\alpha },\qquad \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ j=i \\ \\ 2B^{1-\alpha }+M^{1-\alpha }-\frac{(x_{j+1}-x_{i})^{2-\alpha }}{M}+\frac{ (x_{j}-x_{i})^{2-\alpha }}{M},\qquad \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ j=i+1 \\ \begin{array}{c} -(\frac{(x_{j}-x_{i+1})^{2-\alpha }}{B}-\frac{(x_{j-1}-x_{i+1})^{2-\alpha }}{ B}-\frac{(x_{j+1}-x_{i+1})^{2-\alpha }}{M}+\frac{(x_{j}-x_{i+1})^{2-\alpha } }{M}) \\ +(\frac{(x_{j}-x_{i})^{2-\alpha }}{B}-\frac{(x_{j-1}-x_{i})^{2-\alpha }}{B}- \frac{(x_{j+1}-x_{i})^{2-\alpha }}{M}+\frac{(x_{j}-x_{i})^{2-\alpha }}{M}) \end{array},\ \ \ \ j\ge i+2 \end{array} \right. . \end{aligned}$$
(22)

Proof

From Eq. (19) along with Lemma 2, we get for \(j=i\)

$$\begin{aligned}{} & {} \int \limits _{x_{i-1}}^{x_{i}}(\frac{\partial ^{\alpha }\phi _{j}(x)}{ \partial x^{\alpha }}\nonumber \\{} & {} -\frac{\partial ^{\alpha }\phi _{j}(x)}{\partial (-x)^{\alpha }})dx \nonumber \\= & {} \frac{1}{\Gamma (2-\alpha )}\int \limits _{x_{i-1}}^{x_{i}}\frac{ (x-x_{i-1})^{1-\alpha }}{(x_{i}-x_{i-1})}\nonumber \\{} & {} -\frac{(x_{i+1}-x)^{1-\alpha }}{ (x_{i+1}-x_{i})}+\frac{(x_{i}-x)^{1-\alpha }}{(x_{i}-x_{i-1})}+\frac{ (x_{i}-x)^{1-\alpha }}{(x_{i+1}-x_{i})}dx \nonumber \\= & {} \frac{1}{\Gamma (3-\alpha )}\left[ 2B^{1-\alpha }+M^{1-\alpha }\right. \nonumber \\{} & {} \left. -\frac{ (x_{i+1}-x_{i-1})^{2-\alpha }}{M}+\frac{(x_{i}-x_{i-1})^{2-\alpha }}{M} \right] , \end{aligned}$$
(23)

where \(B=(x_{j}-x_{j-1})\) and \(M=(x_{j+1}-x_{j}).\)

For \(j=i-1,\) we have

$$\begin{aligned}{} & {} \int \limits _{x_{i-1}}^{x_{i}}(\frac{\partial ^{\alpha }\phi _{j}(x)}{ \partial x^{\alpha }}-\frac{\partial ^{\alpha }\phi _{j}(x)}{\partial (-x)^{\alpha }})dx \nonumber \\{} & {} \quad =\frac{1}{\Gamma (2-\alpha )}\int \limits _{x_{i-1}}^{x_{i}}\frac{ (x-x_{i-2})^{1-\alpha }}{(x_{i-1}-x_{i-2})}\nonumber \\{} & {} \qquad -\frac{(x-x_{i-1})^{1-\alpha }}{ (x_{i-1}-x_{i-2})}-\frac{(x-x_{i-1})^{1-\alpha }}{(x_{i}-x_{i-1})}-\frac{ (x_{i}-x)^{1-\alpha }}{(x_{i}-x_{i-1})}dx \nonumber \\{} & {} \quad =\frac{1}{\Gamma (3-\alpha )}\left[ \frac{(x_{i}-x_{i-2})^{2-\alpha }}{B}\right. \nonumber \\{} & {} \qquad \left. -\frac{(x_{i}-x_{i-1})^{2-\alpha }}{B}-2M^{1-\alpha }-B^{1-\alpha }\right] . \end{aligned}$$
(24)

If \(\ j\le i-2,\) it follows that

$$\begin{aligned}{} & {} \int \limits _{x_{i-1}}^{x_{i}}(\frac{\partial ^{\alpha }\phi _{j}(x)}{ \partial x^{\alpha }}-\frac{\partial ^{\alpha }\phi _{j}(x)}{\partial (-x)^{\alpha }})dx \nonumber \\{} & {} \quad =\frac{1}{\Gamma (2-\alpha )}\int \limits _{x_{i-1}}^{x_{i}}\frac{ (x-x_{j-1})^{2-\alpha }}{(x_{j}-x_{j-1})}\nonumber \\{} & {} \qquad -\frac{(x-x_{j})^{2-\alpha }}{ (x_{j}-x_{j-1})}-\frac{(x-x_{j})^{2-\alpha }}{(x_{j+1}-x_{j})}+\frac{ (x-x_{j+1})^{2-\alpha }}{(x_{j+1}-x_{j})}-0\text { }dx \nonumber \\{} & {} \quad =\frac{1}{\Gamma (3-\alpha )}\left[ \begin{array}{c} (\frac{(x_{i}-x_{j-1})^{2-\alpha }}{B}-\frac{(x_{i}-x_{j})^{2-\alpha }}{B}- \frac{(x_{i}-x_{j})^{2-\alpha }}{M}+\frac{(x_{i}-x_{j+1})^{2-\alpha }}{M}) \\ -(\frac{(x_{i-1}-x_{j-1})^{2-\alpha }}{B}-\frac{(x_{i-1}-x_{j})^{2-\alpha }}{ B}-\frac{(x_{i-1}-x_{j})^{2-\alpha }}{M}+\frac{(x_{i-1}-x_{j+1})^{2-\alpha } }{M}) \end{array} \right] . \end{aligned}$$
(25)

If \(\ j\ge i+1\), we have

$$\begin{aligned}{} & {} \int \limits _{x_{i-1}}^{x_{i}}(\frac{\partial ^{\alpha }\phi _{j}(x)}{ \partial x^{\alpha }}-\frac{\partial ^{\alpha }\phi _{j}(x)}{\partial (-x)^{\alpha }})dx \nonumber \\{} & {} \quad =\frac{1}{\Gamma (2-\alpha )}\int \limits _{x_{i-1}}^{x_{i}}0-\frac{ (x_{j+1}-x)^{1-\alpha }}{(x_{j+1}-x_{j})}+\frac{(x_{j}-x)^{1-\alpha }}{ (x_{j}-x_{j-1})}\nonumber \\{} & {} \qquad +\frac{(x_{j}-x)^{1-\alpha }}{(x_{j+1}-x_{j})}-\frac{ (x_{j-1}-x)^{1-\alpha }}{(x_{j}-x_{j-1})}dx \nonumber \\{} & {} \quad =\frac{1}{\Gamma (3-\alpha )}\left[ \begin{array}{c} -(\frac{(x_{j}-x_{i})^{2-\alpha }}{B}-\frac{(x_{j-1}-x_{i})^{2-\alpha }}{B}- \frac{(x_{j+1}-x_{i})^{2-\alpha }}{M}+\frac{(x_{j}-x_{i})^{2-\alpha }}{M}) \\ +(\frac{(x_{j}-x_{i-1})^{2-\alpha }}{B}-\frac{(x_{j-1}-x_{i-1})^{2-\alpha }}{ B}-\frac{(x_{j+1}-x_{i-1})^{2-\alpha }}{M}+\frac{(x_{j}-x_{i-1})^{2-\alpha } }{M}) \end{array} \right] . \end{aligned}$$
(26)

From (23)–(26), it is proved that

$$\begin{aligned} \int \limits _{x_{i-1}}^{x_{i}}(\frac{\partial ^{\alpha }\phi _{j}(x)}{ \partial x^{\alpha }}-\frac{\partial ^{\alpha }\phi _{j}(x)}{\partial (-x)^{\alpha }})dx=\frac{1}{\Gamma (3-\alpha )}g_{i,j}^{(3)}, \end{aligned}$$

where \(g_{i,j}^{(3)}\) is defined as in (21).

In the same way, Eq. (20) is proved where \(g_{i,j}^{(4)}\) is defined as in (22). \(\square\)

Description of method

Consider the FPIDE with the Riesz space fractional derivative of the form (1)–(3). The equations can be written as follows:

$$\begin{aligned}{} & {} \frac{\partial u}{\partial t}=-\frac{c}{2\cos \frac{\pi (1+\alpha )}{2}}( \frac{\partial ^{1+\alpha }u(x,t)}{\partial x^{1+\alpha }}+\frac{\partial ^{1+\alpha }u(x,t)}{\partial \left( -x\right) ^{1+\alpha }} )\nonumber \\{} & {} \quad +\int \limits _{0}^{t}K(t,s)u(x,s)ds+f(x,t) \nonumber \\{} & {} \quad =-\rho \frac{\partial }{\partial x}H(x,t)+\int \limits _{0}^{t}K(t,s)u(x,s)ds+f(x,t), \end{aligned}$$
(27)

where

$$\begin{aligned} \rho =\frac{c}{2\cos \frac{\pi (1+\alpha )}{2}},\qquad H(x,t)=\frac{\partial ^{\alpha }u(x,t)}{\partial x^{\alpha }}-\frac{\partial ^{\alpha }u(x,t)}{ \partial \left( -x\right) ^{\alpha }}. \end{aligned}$$
(28)

The weak form of this problem is given by

$$\begin{aligned}{} & {} (\frac{\partial u}{\partial t},v)=\rho (H,\frac{\partial v}{\partial x} )\nonumber \\{} & {} \quad +(\int \limits _{0}^{t}K(t,s)u(x,s)ds,v)+(f,v),\quad \forall \text { }v\in V_{h} \end{aligned}$$
(29)

Discretizing the first order time derivative by the finite difference method (FDM) with a time step \(\Delta t\) as follows:

$$\begin{aligned} \frac{\partial u}{\partial t}=\frac{u^{n}-u^{n-1}}{\Delta t}, \end{aligned}$$
(30)

also, using the trapezoidal rule to approximate the integral term as follows

$$\begin{aligned}{} & {} \int \limits _{0}^{t}K(t,s)u(x,s)ds=\frac{\Delta t}{2} K(t_{n},t_{0})u(x,t_{0})\nonumber \\{} & {} \quad +\Delta t\sum \limits _{j=1}^{n-1}K(t_{n},t_{j})u(x,t_{j})+\frac{\Delta t}{2} K(t_{n},t_{n})u(x,t_{n}), \end{aligned}$$
(31)

we get

$$\begin{aligned} (u^{n},v)-(u^{n-1},v)= & {} \rho \Delta t(H^{n},\frac{\partial v}{\partial x})+ \frac{(\Delta t)^{2}}{2}(K(t_{n},t_{0})u(x,t_{0}),v) \nonumber \\{} & {} +(\Delta t)^{2}(\sum \limits _{j=1}^{n-1}K(t_{n},t_{j})u(x,t_{j}),v) \nonumber \\{} & {} +\frac{(\Delta t)^{2}}{2}(K(t_{n},t_{n})u(x,t_{n}),v)+\Delta t(f,v). \end{aligned}$$
(32)

Let\(\ u_{h}^{n}=\sum \limits _{j=0}^{m}u_{j}^{n}\phi _{j}(x)\in V_{h}(a,b),\) while \(V_{h}(a,b)\) represents the space of functions that are continuous and piecewise linear regarding the partition of the space, and they take the value of zero at the boundaries, and \(u_{j}^{n}=u_{h}(x_{j},t_{n}).\) Also choosing every function v to be \(\phi _{i}(x),i=1,2,\ldots ,m\), it follows that

$$\begin{aligned}{} & {} (\sum \limits _{j=0}^{m}u_{j}^{n}\phi _{j}(x),\phi _{i}(x))-\frac{(\Delta t)^{2}}{2}(K(t_{n},t_{n})u(x,t_{n}),\phi _{i}(x)) \nonumber \\{} & {} \quad -\rho \Delta t(\sum \limits _{j=1}^{m+1}u_{j}^{n}\int \limits _{a}^{b}(\frac{ \partial ^{\alpha }\phi _{j}(x)}{\partial x^{\alpha }}-\frac{\partial ^{\alpha }\phi _{j}(x,t)}{\partial \left( -x\right) ^{\alpha }}).\frac{ \partial \phi _{i}(x)}{\partial x}dx) \nonumber \\{} & {} \quad =(\sum \limits _{j=0}^{m}u_{j}^{n-1}\phi _{j}(x),\phi _{i}(x))+\frac{ (\Delta t)^{2}}{2}(K(t_{n},t_{0})u(x,t_{0}),\phi _{i}(x)) \nonumber \\{} & {} \qquad +(\Delta t)^{2}(\sum \limits _{j=1}^{n-1}K(t_{n},t_{j})u(x,t_{j}),\phi _{i}(x))+\Delta t(f(x,t_{n}),\phi _{i}(x)). \end{aligned}$$
(33)

From definition (7), it follows that

$$\begin{aligned}{} & {} (\sum \limits _{j=0}^{m}u_{j}^{n}\phi _{j}(x),\phi _{i}(x))-\frac{(\Delta t)^{2}}{2}(K(t_{n},t_{n})u(x,t_{n}),\phi _{i}(x)) \nonumber \\{} & {} \quad -\rho \Delta t(\sum \limits _{j=1}^{m+1}\frac{u_{j}^{n}}{(x_{i}-x_{i-1})} \int \limits _{x_{i-1}}^{x_{i}}(\frac{\partial ^{\alpha }\phi _{j}(x)}{ \partial x^{\alpha }}-\frac{\partial ^{\alpha }\phi _{j}(x,t)}{\partial \left( -x\right) ^{\alpha }})dx \nonumber \\{} & {} \quad -\sum \limits _{j=1}^{m+1}\frac{u_{j}^{n}}{(x_{i+1}-x_{i})} \int \limits _{x_{i}}^{x_{i+1}}(\frac{\partial ^{\alpha }\phi _{j}(x)}{ \partial x^{\alpha }}-\frac{\partial ^{\alpha }\phi _{j}(x,t)}{\partial \left( -x\right) ^{\alpha }})dx) \nonumber \\{} & {} =(\sum \limits _{j=0}^{m}u_{j}^{n-1}\phi _{j}(x),\phi _{i}(x))+\quad \frac{ (\Delta t)^{2}}{2}(K(t_{n},t_{0})u(x,t_{0}),\phi _{i}(x)) \nonumber \\{} & {} \quad +(\Delta t)^{2}(\sum \limits _{j=1}^{n-1}K(t_{n},t_{j})u(x,t_{j}),\phi _{i}(x))+\Delta t(f(x,t_{n}),\phi _{i}(x)). \end{aligned}$$
(34)

From Lemma 1 and Lemma 3, it follows that

$$\begin{aligned}{} & {} \frac{1}{6} ((x_{i}-x_{i-1})u_{i-1}^{n}+2(x_{i+1}-x_{i-1})u_{i}^{n}\nonumber \\{} & {} \quad +(x_{i+1}-x_{i})u_{i+1}^{n}) \nonumber \\{} & {} \quad -\frac{(\Delta t)^{2}}{2}(K(t_{n},t_{n})u(x,t_{n}),\phi _{i}(x))\nonumber \\{} & {} \quad -\rho \Delta t(\sum \limits _{j=1}^{m+1}u_{j}^{n}(\frac{g_{i,j}^{(3)}}{(x_{i}-x_{i-1})}- \frac{g_{i,j}^{(4)}}{(x_{i+1}-x_{i})})) \nonumber \\{} & {} =\frac{1}{6} ((x_{i}-x_{i-1})u_{i-1}^{n-1}+2(x_{i+1}\nonumber \\{} & {} \quad -x_{i-1})u_{i}^{n-1}+(x_{i+1}-x_{i})u_{i+1}^{n-1}) \nonumber \\{} & {} \quad +\frac{(\Delta t)^{2}}{2}(K(t_{n},t_{0})u(x,t_{0}),\phi _{i}(x)) \nonumber \\{} & {} \quad +(\Delta t)^{2}(\sum \limits _{j=1}^{n-1}K(t_{n},t_{j})u(x,t_{j}),\nonumber \\{} & {} \quad \phi _{i}(x))+\quad \Delta t(f(x,t_{n}),\phi _{i}(x)). \end{aligned}$$
(35)

Now, we have a system of linear equations that can be solved for \(u_{i}^{n}.\)

Gradient recovery and adaptive refinement

There are many techniques that were developed for the recovery of the gradient, and these techniques have been used in practice due to their efficiency as a posteriori error estimators, ease of implementation, and superconvergence (see [42,43,44,45,46,47,48] and references therein).

In [43, 49], the PPR technique was introduced for the recovery of the gradient, which works methodically in FEMs of different orders. It possesses a superconvergence property, which means that the a posteriori error estimator based on recovery is asymptotically precise.

The way the PPR technique works to recover the gradient at a mesh node d can be illustrated as follows:

Let \(M_{h}\) denotes the set of mesh nodes. For any node \(d\in M_{h},\) we first construct a patch of elements which is denoted by \(\chi _{d},\) which contains the union of elements in the first n layers around d,  i.e.,

$$\begin{aligned} \chi _{d}(d,n)=\cup \{E:E\in \textbf{E}_{h},\text { }E\cap \chi _{d}(d,n-1)\ne \phi \}, \end{aligned}$$
(36)

where \(\textbf{E}_{h}\) is the set of mesh elements and \(\chi _{d}(d,0)=\{d\}.\)

Then, we define a polynomial \(P_{d}\) that best fits the FEM solution \((u_{h})\) at the mesh nodes in \(\chi _{d}\) in the least squares sense. This polynomial is the least squares approximation of \(u_{h}\) at d. Then, the recovered gradient \(R_{h}\) is defined as follows:

$$\begin{aligned} R_{h}= & {} \sum _{d\in M_{h}}R_{h}(d)\phi _{d}, \nonumber \\ R_{h}(d)= & {} \nabla P_{d}(d). \end{aligned}$$
(37)

Depending on the recovered gradient, an adaptive procedure is applied, and it can be illustrated as follows: The procedure starts with an initial mesh and the system is solved for the FEM solution. Then, using the PPR technique, the recovered gradient \(R_{h}\) is calculated. After that, the error (\(e_{k}\) ) in the finite element gradient on every element is calculated using the recovered gradient instead of the exact one. When compared to some predefined tolerance \(\tau\), the maximum error is checked so that the algorithm ends if the tolerance is reached. Otherwise, we use a marking strategy to mark certain elements that meet the criteria \(e_{k}>\eta *\tau\) for a positive parameter \(\eta <1\). The marked elements are refined; then, the mesh is adapted. Here, the system is solved using our formulation for Riesz FPIDE with nonuniform mesh. Again, the PPR technique is applied; then, the error is checked, and the procedure continues until the tolerance is reached.

Error analysis and stability condition

In this section, we present the error analysis and stability condition of the proposed scheme. We begin by listing some of the definitions and symbols that are used in this section.

The inner product and norm of the space \(L_{2(\Omega )}\) are defined by

$$\begin{aligned} (u,v)_{L_{2}(\Omega )}= & {} \int \limits _{\Omega }uv\text { \ }dx, \end{aligned}$$
(38)
$$\begin{aligned} \text {and}{} & {} \nonumber \\ \text { \ }\left\| u\right\| _{L_{2}}= & {} (u,u)_{L_{2(\Omega )}}^{1/2} \text {, \ \ }\forall u,v\in L_{2(\Omega )}, \end{aligned}$$
(39)

respectively.

For any \(\sigma >0,\) we define \(^{l}H_{0}^{\sigma }(\Omega )\) and \(^{r}H_{0}^{\sigma }(\Omega )\) to be the closure of \(C_{0}^{\infty }(\Omega )\) with respect to the norms \(\left\| v\right\| _{^{l}H_{0}^{\sigma }(\Omega )}\) and \(\left\| v\right\| _{^{r}H_{0}^{\sigma }(\Omega )},\) respectively, where

$$\begin{aligned} \left\| v\right\| _{^{l}H_{0}^{\sigma }(\Omega )}= & {} (\left\| v\right\| _{L_{2}}^{2}+\left| v\right| _{^{l}H_{0}^{\sigma }(\Omega )}^{2})^{1/2}, \end{aligned}$$
(40)
$$\begin{aligned} \left\| v\right\| _{^{r}H_{0}^{\sigma }(\Omega )}= & {} (\left\| v\right\| _{L_{2}}^{2}+\left| v\right| _{^{r}H_{0}^{\sigma }(\Omega )}^{2})^{1/2}, \end{aligned}$$
(41)

where

$$\begin{aligned} \left| v\right| _{^{l}H_{0}^{\sigma }(\Omega )}^{2}= & {} \left\| _{a}^{c}D_{x}^{\sigma }v\right\| _{L_{2}(\Omega )}^{2}, \end{aligned}$$
(42)
$$\begin{aligned} \left| v\right| _{^{r}H_{0}^{\sigma }(\Omega )}^{2}= & {} \left\| _{x}^{c}D_{b}^{\sigma }v\right\| _{L_{2}(\Omega )}^{2}. \end{aligned}$$
(43)

In the usual Sobolev space \(H_{0}^{\sigma }(\Omega ),\) we also have the definition

$$\begin{aligned} \left\| v\right\| _{H_{0}^{\sigma }(\Omega )}=(\left\| v\right\| _{L_{2}(\Omega )}^{2}+\left| v\right| _{H_{0}^{\sigma }(\Omega )}^{2})^{1/2}, \end{aligned}$$
(44)

where

$$\begin{aligned} \left| v\right| _{H_{0}^{\sigma }(\Omega )}^{2}=(\frac{ (_{a}^{c}D_{x}^{\sigma }v,_{x}^{c}D_{b}^{\sigma }v)_{L_{2}(\Omega )}}{\cos (\pi \sigma )}). \end{aligned}$$
(45)

Error analysis

Lemma 4

(see [41, 50]) For real \(0<\gamma <1,\) \(0<\delta <1\) if \(v(0)=0,\) \(x\in (a,b)\) then

$$\begin{aligned} (1)\text { \ \ }_{a}^{c}D_{x}^{\gamma +\delta }v(x)= & {} (_{a}^{c}D_{x}^{\gamma })(_{a}^{c}D_{x}^{\delta })v(x)\text { \ }\forall v\in H^{\gamma +\delta }(a,b), \\ (2)\text { }(_{a}^{c}D_{x}^{\gamma }w,v)_{L_{2}}= & {} (w,_{x}^{c}D_{b}^{\gamma }v)_{L_{2}}\text { \ }\forall w\in H^{\gamma }(a,b),\text { }v\in C_{0}^{\infty }(a,b). \end{aligned}$$

Lemma 5

(see [50]) Let \(0<\gamma <1,\) then for any \(w,v\in H_{0}^{\gamma /2}(\Omega )\)

$$\begin{aligned} (_{a}^{c}D_{x}^{\gamma }w,v)_{L_{2}}=(_{a}^{c}D_{x}^{\gamma /2}w,_{x}^{c}D_{b}^{\gamma /2}v)_{L_{2}}. \end{aligned}$$

Lemma 6

(see [51]) For \(\gamma >0,v\in C_{0}^{\infty }(R),\) then

$$\begin{aligned} (_{a}^{c}D_{x}^{\gamma }v,_{x}^{c}D_{b}^{\gamma }v)= & {} \cos (\pi \gamma )\left\| _{a}^{c}D_{x}^{\gamma }v\right\| _{L_{2(\Omega )}}^{2}, \\ (_{a}^{c}D_{x}^{\gamma }v,_{x}^{c}D_{b}^{\gamma }v)= & {} \cos (\pi \gamma )\left\| _{x}^{c}D_{b}^{\gamma }v\right\| _{L_{2(\Omega )}}^{2}. \end{aligned}$$

Lemma 7

(see [52]) Let \(u\in H^{r}(\Omega ),\) \(0<r\le m,\) and \(0\le s\le r\), then, there exists a constant \(C_{A}\) depending only on \(\Omega\) such that

$$\begin{aligned} \left\| u-I_{h}u\right\| _{H^{s}(\Omega )}\le C_{A}h^{r-s}\left\| u\right\| _{H^{r}(\Omega )}, \end{aligned}$$

where \(I_{h}\) is a projection operator from \(H^{r}(\Omega )\cap H^{s}(\Omega )\) to \(V_{h}.\)

Based on lemma 4, the variational form of Eq. (32) can be written in the following form

$$\begin{aligned}{} & {} (1-0.5(\Delta t)^{2}K(t_{n},t_{n}))(u^{n},v)+\rho \Delta t(_{a}^{c}D_{x}^{\gamma /2}u^{n},_{x}^{c}D_{b}^{\gamma /2}v)\nonumber \\{} & {} \quad +\rho \Delta t(_{x}^{c}D_{b}^{\gamma /2}u^{n},_{a}^{c}D_{x}^{\gamma /2}v) \nonumber \\{} & {} \quad =(G(x,t),v)\text { \ \, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }v\in H_{b}^{\gamma /2}, \end{aligned}$$
(46)

where

$$\begin{aligned}{} & {} G(x,t)=u^{n-1}+\frac{(\Delta t)^{2}}{2}K(t_{n},t_{0})u(x,t_{0})\nonumber \\{} & {} \quad +(\Delta t)^{2}\sum _{j=1}^{n-1}K(t_{n},t_{j})u(x,t_{j})+\Delta tf(x,t). \end{aligned}$$
(47)

The semidiscrete problem of (27) is to find the approximate solution \(u_{h}(x,t)\in V_{h}\) such that

$$\begin{aligned}{} & {} (1-0.5(\Delta t)^{2}K(t_{n},t_{n}))(u_{h}^{n},v)+\rho \Delta t(_{a}^{c}D_{x}^{\gamma /2}u_{h}^{n},_{x}^{c}D_{b}^{\gamma /2}v)\nonumber \\{} & {} \quad +\rho \Delta t(_{x}^{c}D_{b}^{\gamma /2}u_{h}^{n},_{a}^{c}D_{x}^{\gamma /2}v) \nonumber \\{} & {} \quad =(G(x,t),v),\text { \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }v\in V_{h}. \end{aligned}$$
(48)

Let \(J_{h}:H^{\gamma /2}(\Omega )\longrightarrow V_{h}\) be the elliptic projection defined by

$$\begin{aligned}{} & {} \rho (_{a}^{c}D_{x}^{\gamma /2}J_{h}u,_{x}^{c}D_{b}^{\gamma /2}v)_{L_{2}}+\rho (_{x}^{c}D_{b}^{\gamma /2}J_{h}u,_{a}^{c}D_{x}^{\gamma /2}v)_{L_{2}} \nonumber \\{} & {} \quad =\rho (_{a}^{c}D_{x}^{\gamma /2}u,_{x}^{c}D_{b}^{\gamma /2}v)_{L_{2}}+\rho (_{x}^{c}D_{b}^{\gamma /2}u,_{a}^{c}D_{x}^{\gamma /2}v)_{L_{2}},\text { \ \ } v\in V_{h}. \end{aligned}$$
(49)

Lemma 8

For \(J_{h}\) defined by (49) and any \(v\in H^{r}(\Omega )\cap H_{0}^{\gamma /2},\) the following inequality holds

$$\begin{aligned} \left\| _{a}^{c}D_{x}^{\gamma /2}(J_{h}u-u)\right\| _{L_{2}}\le h^{r-\gamma /2}\left\| v\right\| _{H^{r}(\Omega )}. \end{aligned}$$

Proof

Let \(I_{h}\) be a projection operator from \(H^{r}(\Omega )\cap H^{\gamma /2}(\Omega )\) to \(V_{h},\) and from definition of \(L_{2(\Omega )}\), we obtain

$$\begin{aligned}{} & {} (_{a}^{c}D_{x}^{\gamma /2}(J_{h}u-u),_{x}^{c}D_{b}^{\gamma /2}(J_{h}u-u))_{L_{2}}\nonumber \\{} & {} \quad +(_{x}^{c}D_{b}^{\gamma /2}(J_{h}u-u),_{a}^{c}D_{x}^{\gamma /2}(J_{h}u-u))_{L_{2}} \nonumber \\{} & {} \quad =(_{a}^{c}D_{x}^{\gamma /2}(J_{h}u-u),_{x}^{c}D_{b}^{\gamma /2}(J_{h}u-I_{h}u))_{L_{2}}\nonumber \\{} & {} \quad +(_{x}^{c}D_{b}^{\gamma /2}(J_{h}u-u),_{a}^{c}D_{x}^{\gamma /2}(J_{h}u-I_{h}u))_{L_{2}} \nonumber \\{} & {} \quad +(_{a}^{c}D_{x}^{\gamma /2}(J_{h}u-u),_{x}^{c}D_{b}^{\gamma /2}(I_{h}u-u))_{L_{2}}\nonumber \\{} & {} \quad +(_{x}^{c}D_{b}^{\gamma /2}(J_{h}u-u),_{a}^{c}D_{x}^{\gamma /2}(I_{h}u-u))_{L_{2}}. \end{aligned}$$
(50)

Let \(v=J_{h}u-I_{h}u\) in (49), we obtain

$$\begin{aligned}{} & {} (_{a}^{c}D_{x}^{\gamma /2}(J_{h}u-u),_{x}^{c}D_{b}^{\gamma /2}(J_{h}u-u))_{L_{2}}\nonumber \\{} & {} \quad +(_{x}^{c}D_{b}^{\gamma /2}(J_{h}u-u),_{a}^{c}D_{x}^{\gamma /2}(J_{h}u-u))_{L_{2}} \nonumber \\{} & {} \quad \le \left\| _{a}^{c}D_{x}^{\gamma /2}(J_{h}u-u)\right\| _{L_{2}}\left\| _{x}^{c}D_{b}^{\gamma /2}(I_{h}u-u)\right\| _{L_{2}}\nonumber \\{} & {} \quad +\left\| _{x}^{c}D_{b}^{\gamma /2}(J_{h}u-u)\right\| _{L_{2}}\left\| _{a}^{c}D_{x}^{\gamma /2}(I_{h}u-u)\right\| _{L_{2}} \nonumber \\{} & {} \quad \le (\left\| _{a}^{c}D_{x}^{\gamma /2}(J_{h}u-u)\right\| _{L_{2}}\nonumber \\{} & {} \quad +\left\| _{x}^{c}D_{b}^{\gamma /2}(J_{h}u-u)\right\| _{L_{2}})*(\left\| _{a}^{c}D_{x}^{\gamma /2}(I_{h}u-u)\right\| _{L_{2}}\nonumber \\{} & {} \quad +\left\| _{x}^{c}D_{b}^{\gamma /2}(I_{h}u-u)\right\| _{L_{2}}). \end{aligned}$$
(51)

Note that

$$\begin{aligned}{} & {} (_{a}^{c}D_{x}^{\gamma /2}(J_{h}u-u),_{x}^{c}D_{b}^{\gamma /2}(J_{h}u-u))_{L_{2}}\nonumber \\{} & {} \quad +(_{x}^{c}D_{b}^{\gamma /2}(J_{h}u-u),_{a}^{c}D_{x}^{\gamma /2}(J_{h}u-u))_{L_{2}} \nonumber \\{} & {} \quad \gtrsim (\left\| _{a}^{c}D_{x}^{\gamma /2}(J_{h}u-u)\right\| _{L_{2}}+\left\| _{x}^{c}D_{b}^{\gamma /2}(J_{h}u-u)\right\| _{L_{2}})^{2}, \end{aligned}$$
(52)

where the expression \(A\lesssim B\) \((A\gtrsim B)\) means that there exists a positive real number c such that \(A\le cB\) \((A\ge cB)\).

Combining Eqs. (51) and (52), we obtain

$$\begin{aligned}{} & {} \left\| _{a}^{c}D_{x}^{\gamma /2}(J_{h}u-u)\right\| _{L_{2}}+\left\| _{x}^{c}D_{b}^{\gamma /2}(J_{h}u-u)\right\| _{L_{2}} \nonumber \\{} & {} \quad \lesssim \left\| _{a}^{c}D_{x}^{\gamma /2}(I_{h}u-u)\right\| _{L_{2}}+\left\| _{x}^{c}D_{b}^{\gamma /2}(I_{h}u-u)\right\| _{L_{2}}. \end{aligned}$$
(53)

From lemma 7,

$$\begin{aligned} \left\| _{a}^{c}D_{x}^{\gamma /2}(I_{h}u-u)\right\| _{L_{2}}\lesssim \left\| I_{h}u-u\right\| _{H^{\gamma /2}(\Omega )}\lesssim h^{r-\gamma /2}\left\| u\right\| _{H^{r}(\Omega ).} \end{aligned}$$
(54)

Similarly,

$$\begin{aligned} \left\| _{x}^{c}D_{b}^{\gamma /2}(I_{h}u-u)\right\| _{L_{2}}\lesssim \left\| I_{h}u-u\right\| _{H^{\gamma /2}(\Omega )}\lesssim h^{r-\gamma /2}\left\| u\right\| _{H^{r}(\Omega ).} \end{aligned}$$
(55)

Combining Eqs. (53), (54) and (55), we obtain

$$\begin{aligned} \left\| _{a}^{c}D_{x}^{\gamma /2}(J_{h}u-u)\right\| _{L_{2}}\lesssim h^{r-\gamma /2}\left\| u\right\| _{H^{r}(\Omega ).} \end{aligned}$$
(56)

\(\square\)

Theorem 1

Let \(u^{n}\) and \(u_{h}^{n}\) be the solution of (46) and (48 ), respectively, the following estimate holds

$$\begin{aligned} \left\| u^{n}-u_{h}^{n}\right\| =O((\Delta t)^{2})+O(h^{r-\gamma /2}). \end{aligned}$$

Proof

$$\begin{aligned} u_{h}^{n}-u^{n}=\psi +\phi , \end{aligned}$$
(57)
$$\begin{aligned} \psi =u_{h}^{n}-J_{h}u^{n}\text {,\ \ \ \ \ }\phi =J_{h}u^{n}-u^{n}. \end{aligned}$$

From lemma 8,

$$\begin{aligned} \left\| \phi \right\| ^{2}\lesssim h^{2r-\gamma }\left\| u^{n}\right\| _{H^{r}(\Omega ).}^{2} \end{aligned}$$
(58)

Subtracting (48)–(46) and taking \(v=\psi =u_{h}^{n}-J_{h}u^{n},\) we get

$$\begin{aligned}{} & {} C_{B}(u_{h}^{n}-u^{n},u_{h}^{n}-J_{h}u^{n})\nonumber \\{} & {} \quad +\rho \Delta t(_{a}^{c}D_{x}^{\gamma /2}(u_{h}^{n}-J_{h}u^{n}),_{x}^{c}D_{b}^{\gamma /2}(u_{h}^{n}-J_{h}u^{n})) \nonumber \\{} & {} \quad +\rho \Delta t(_{x}^{c}D_{b}^{\gamma /2}(u_{h}^{n}-J_{h}u^{n}\text { } ),_{a}^{c}D_{x}^{\gamma /2}(u_{h}^{n}-J_{h}u^{n})) \nonumber \\{} & {} \quad =zero+O((\Delta t)^{2}), \end{aligned}$$
(59)

where \(C_{B}=(1-0.5(\Delta t)^{2}K(t_{n},t_{n})).\) By lemma 6, we get

$$\begin{aligned}{} & {} \quad C_{B}(u_{h}^{n}-J_{h}u^{n},u_{h}^{n}-J_{h}u^{n})\nonumber \\{} & {} \quad +C_{B}(J_{h}u^{n}-u^{n},u_{h}^{n}-J_{h}u^{n})+C_{D}\left| u_{h}^{n}-J_{h}u^{n}\right| _{H^{\gamma /2}}^{2} \nonumber \\{} & {} \quad =zero+O((\Delta t)^{2}), \end{aligned}$$
(60)

where \(C_{D}=2\cos (\frac{\pi \gamma }{2})\rho \Delta t.\) Arranging the terms of Eq. (60), we get

$$\begin{aligned}{} & {} C_{B}(u_{h}^{n}-J_{h}u^{n},u_{h}^{n}-J_{h}u^{n})+C_{D}\left| u_{h}^{n}-J_{h}u^{n}\right| _{H^{\gamma /2}}^{2}\nonumber \\{} & {} \quad =C_{B}(u^{n}-J_{h}u^{n},u_{h}^{n}-J_{h}u^{n})+O((\Delta t)^{2}). \end{aligned}$$
(61)

For any small \(\varepsilon >0,\) we have

$$\begin{aligned}{} & {} \left\| u_{h}^{n}-J_{h}u^{n}\right\| _{H^{\gamma /2}}^{2}\lesssim C_{\varepsilon }\left\| u^{n}-J_{h}u^{n}\right\| ^{2}\nonumber \\{} & {} \quad +\varepsilon \left\| u_{h}^{n}-J_{h}u^{n}\right\| ^{2}+O((\Delta t)^{2}), \end{aligned}$$
(62)

where \(C_{\varepsilon }\) is a constant with respect to \(\varepsilon .\)

$$\begin{aligned}{} & {} \left\| u_{h}^{n}-J_{h}u^{n}\right\| _{H^{\gamma /2}}\lesssim C_{\varepsilon }\left\| \phi \right\| _{H^{\gamma /2}}+\nonumber \\{} & {} \quad O((\Delta t)^{2})\lesssim h^{r-\gamma /2}\left\| u^{n}\right\| _{H^{r}}+O((\Delta t)^{2}). \end{aligned}$$
(63)

Combining Eqs. (58) and (62), we get

$$\begin{aligned} \left\| u^{n}-u_{h}^{n}\right\| _{H^{\gamma /2}}=\left\| \psi +\phi \right\| _{H^{\gamma /2}}=O(h^{r-\gamma /2})+O((\Delta t)^{2}). \end{aligned}$$
(64)

\(\square\)

Stability

Theorem 2

The FEM defined in (46) is unconditionally stable.

Proof

Let \(v=u^{n}\), \(f(x,t)=0,\) from Eq. (46), we have

$$\begin{aligned}{} & {} (1-0.5(\Delta t)^{2}K(t_{n},t_{n}))(u^{n},u^{n})\nonumber \\{} & {} \quad +\rho \Delta t(_{a}^{c}D_{x}^{\gamma /2}u^{n},_{x}^{c}D_{b}^{\gamma /2}u^{n})+\rho \Delta t(_{x}^{c}D_{b}^{\gamma /2}u^{n},_{a}^{c}D_{x}^{\gamma /2}u^{n}) \nonumber \\{} & {} \quad =(u^{n-1},u^{n})+\frac{(\Delta t)^{2}}{2}K(t_{n},t_{0})(u^{0},u^{n})\nonumber \\{} & {} \quad +( \Delta t)^{2}\sum _{j=1}^{n-1}K(t_{n},t_{j})(u^{j},u^{n}). \end{aligned}$$
(65)

Using Cauchy–Schwarz inequality, we obtain

$$\begin{aligned} (u^{n-k},u^{n})\le \frac{1}{2}[\left\| u^{n-k}\right\| ^{2}+\left\| u^{n}\right\| ^{2}]. \end{aligned}$$

From Eq. (65) and Cauchy–Schwarz inequality, we obtain

$$\begin{aligned}{} & {} (1-0.5(\Delta t)^{2}K(t_{n},t_{n}))\left\| u^{n}\right\| _{L_{2}}^{2}\nonumber \\{} & {} \quad +2\rho (\Delta t)(\cos \pi \gamma )\left\| _{a}^{c}D_{x}^{\gamma }u^{n}\right\| _{L_{2}}^{2} \nonumber \\{} & {} \quad \le \frac{1}{2}[\left\| u^{n-1}\right\| ^{2}+\left\| u^{n}\right\| ^{2}]+\frac{(\Delta t)^{2}}{4}K(t_{n},t_{0})[\left\| u^{0}\right\| ^{2}\nonumber \\{} & {} \quad +\left\| u^{n}\right\| ^{2}]+\frac{(\Delta t)^{2} }{2}\sum _{j=1}^{n-1}K(t_{n},t_{j})[\left\| u^{j}\right\| ^{2}+\left\| u^{n}\right\| ^{2}]. \end{aligned}$$
(66)

Equation (66) can be simplified to

$$\begin{aligned}{} & {} [\frac{1}{2}-\frac{1}{2}(\Delta t)^{2}K(t_{n},t_{n})-\frac{(\Delta t)^{2}}{ 4}K(t_{n},t_{0})\nonumber \\{} & {} \quad -\frac{(\Delta t)^{2}}{2}\sum _{j=1}^{n-1}K(t_{n},t_{j})] \left\| u^{n}\right\| ^{2} \nonumber \\{} & {} \quad \le \frac{1}{2}\left\| u^{n-1}\right\| ^{2}+\frac{(\Delta t)^{2}}{4} K(t_{n},t_{0})\left\| u^{0}\right\| ^{2}\nonumber \\{} & {} \quad +\frac{(\Delta t)^{2}}{2} \sum _{j=1}^{n-1}K(t_{n},t_{j})\left\| u^{j}\right\| ^{2}. \end{aligned}$$
(67)

We prove the stability of Eq. (48) by induction, at \(n=1\), we have

$$\begin{aligned}{} & {} [\frac{1}{2}-\frac{1}{2}(\Delta t)^{2}K(t_{1},t_{1})-\frac{(\Delta t)^{2}}{4}K(t_{1},t_{0})]\left\| u^{1}\right\| _{L_{2}}^{2}\le [\frac{1}{2}+\nonumber \\{} & {} \quad \frac{(\Delta t)^{2}}{4}K(t_{1},t_{0})]\left\| u^{0}\right\| ^{2}, \end{aligned}$$
(68)

which leads to

$$\begin{aligned} \left\| u^{1}\right\| \lesssim \left\| u^{0}\right\| . \end{aligned}$$

For the induction step, we have

$$\begin{aligned} \left\| u^{n-1}\right\| \lesssim \left\| u^{n-2}\right\| \lesssim \cdots \lesssim \left\| u^{0}\right\| . \end{aligned}$$

Using this result, we obtain

$$\begin{aligned}{} & {} [\frac{1}{2}-\frac{1}{2}(\Delta t)^{2}K(t_{n},t_{n})-\frac{(\Delta t)^{2}}{ 4}K(t_{n},t_{0})\nonumber \\{} & {} \quad -\frac{(\Delta t)^{2}}{2}\sum _{j=1}^{n-1}K(t_{n},t_{j})] \left\| u^{n}\right\| ^{2} \nonumber \\{} & {} \quad \le [\frac{1}{2}+\frac{(\Delta t)^{2}}{4}K(t_{n},t_{0})+\frac{(\Delta t)^{2}}{2}\sum _{j=1}^{n-1}K(t_{n},t_{j})]\left\| u^{0}\right\| ^{2}, \end{aligned}$$
(69)

which leads to

$$\begin{aligned} \left\| u^{n}\right\| \lesssim \left\| u^{0}\right\| . \end{aligned}$$

\(\square\)

Numerical examples

The following examples are introduced to illustrate the accuracy of the procedure proposed. For this purpose, two figures are shown for each example. The first figure shows the \(L_{2}\)norm of error with respect to the number of degrees of freedom (DOFs), and the second figure shows the \(L_{\infty }\)norm of error. In the following examples, \(\alpha\) will denotes the fractional order of Riesz, T denotes the final time, \(\tau\) denotes the tolerance, and \(\Delta t\) denotes the time step. The three examples are presented at different values for \(\alpha ,\) \(\Delta t\) and T to present different cases for the problems.

Example 1

Consider the following problem

$$\begin{aligned}{} & {} \frac{\partial u}{\partial t}=\frac{\partial ^{1+\alpha }u(x,t)}{\partial \left| x\right| ^{1+\alpha }}+\int \limits _{0}^{t}(t^{2}+s^{2})u(x,s)ds+f(x,t),\nonumber \\{} & {} \qquad x\in (0,1),\;t\in (0,T), \end{aligned}$$
(70)

with the boundary and initial conditions given as follows

$$\begin{aligned} u(x,0)= & {} 0,\qquad \qquad \qquad \qquad \quad 0<x<1, \nonumber \\ u(0,t)= & {} 0,\qquad u(1,t)=0,\qquad 0<t<T, \end{aligned}$$
(71)

while the exact solution is provided by

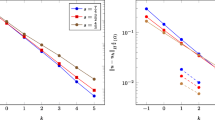
$$\begin{aligned} u(x,t)=2^{5}*e^{-t}x^{6}(1-x)^{6}. \end{aligned}$$
(72)

In this example, we take \(\alpha =0.9,T=1,\tau =10^{-4},\Delta t=0.01.\) Fig. 1 shows the \(L_{2}\)norm of error calculated for the gradient in two cases, the adaptive case and the uniform refinement case, whereas Fig. 2 shows the \(L_{\infty }\)norm of the error over all the elements in the whole domain, which is also calculated for the two cases.

Fig. 1
figure 1

\(L_{2}\)norm of error over the domain of example (1)

Full size image
Fig. 2
figure 2

\(L_{\infty }\)norm of error over the domain of example (1)

Full size image

Example 2

Consider Eq. (70) with boundary and initial conditions as in (71), while the exact solution is provided by

$$\begin{aligned} u(x,t)=x^{(2a)}(1-x^{(2a)})\frac{1}{1+t}. \end{aligned}$$

Here, we take \(\alpha =0.9,T=0.5,\tau =10^{-3},\Delta t=0.01.\)The \(L_{2}\) norm of error and the \(L_{\infty }\)norm of the error are calculated for the gradient and shown in Figs. 3 and 4, respectively.

Fig. 3
figure 3

\(L_{2}\)norm of error over the domain of example (2)

Full size image
Fig. 4
figure 4

\(L_{\infty }\)norm of error over the domain of example (2)

Full size image

Example 3

Consider Eq. (70), while the exact solution is provided by

$$\begin{aligned} u(x,t)=(1-x^{2})\sin ^{-1}(x)e^{-t}, \end{aligned}$$

with boundary and initial conditions as in (71). In this example, we take \(\alpha =0.5,T=1,\tau =10^{-2},\Delta t=0.001.\)The proposed procedure is applied and the \(L_{2}\)norm and the \(L_{\infty }\)norm of the error of the gradient and shown in Figs. 5 and 6, respectively.

Fig. 5
figure 5

\(L_{2}\)norm of error over the domain of example (3)

Full size image
Fig. 6
figure 6

\(L_{\infty }\)norm of error over the domain of example (3)

Full size image

Figs. 1, 2, 3, 4, 5 and 6 in the three examples show that the error of the adaptive refinement is better than that of the uniform refinement at the same number of nodes. This reflects the strength of the proposed procedure as it indicates that the adaptive scheme was successful in refining the mesh at the elements which have the higher error.

Conclusion

The aim of this work is to increase the accuracy of FEM approximations to space fractional partial integro-differential equation defined in Riesz sense via using an adaptive refinement scheme. Thus, we deduced the fractional derivatives of FEM bases at nonuniform mesh. These derivatives were successfully employed to recover the gradient of the considered problem and use this recovered gradient as an a posteriori error estimator that controls the adaptive refinement process. Some numerical simulations were performed, and the results clearly show that the proposed adaptive scheme yields better accuracy than the uniform refinement at the same number of nodes. Also, the theoretical analysis for the error estimate and the stability of the scheme was presented. These findings can help researchers to obtain high-accuracy results for problems that involve Riesz fractional order derivative where the solution exhibits fast changes while maintaining low computational cost. The non-classical differentiation of the basic functions for FEM solutions to problems should be designed to suit nonuniform meshes to allow for adaptive refinement techniques.