Introduction

Delay differential equations in neutral type and integro-differential equations are of an attractive interest in many applications in science and engineering. In applied mathematics, they have an increasing enthusiasm by their implementation in dynamical systems, electrodynamics and mechanics as well. In recent years, numerical treatment of the neutral type integro-differential equations has been arised [1]. These type of equations occur in mechanics, physics, technical problems such as progress for showing cutting and infeed grinding. Besides, they describe some procedures in chemistry and physics for reactors. Moreover, some well-known biological processes growth, death and birth are determined by neutral type equations. In ecological phenomena, some models with respect to the neutral type integro-differential equations are used for evolution equations of single species [2]. Furthermore, many applications of these types of equations exist in medicine. For instance, sugar quantity in blood is modeled by using them; immunology, epidemiology, cancer chemotherapy may explain different aspects of human body interaction with diseases. As another example, in Fig. 1 model of pressure regulation of model of arterial blood is represented by the formulation of functional differential equations. In this figure, arterial vessels are shown by A and B. These arterial vessels have connections to each other, blood flow from A to B has a rate which is shown by Q, R represents peripheral resistance, and the heart productivity is denoted by \({Q}_{\mathrm{h}}\). The incoming liquid rate is \({Q}_{\mathrm{in}}\) while the outcoming rate is \({Q}_{\mathrm{out}}\) [3]. Furthermore, epidemic of the human immunodeficiency virus (HIV) is modeled by the system of functional integro-differential equations. Besides, fishing process, river pollution control can be described and these examples are ecological applications in the ecology field.

Fig. 1
figure 1

A diagram to describe the cardiovascular system

Full size image

Neutral type delay integro-differential equations under the initial condition are of numerical solutions which have been reached by many authors. Such problems have difficulties in motivation but also often appear at numerical investigations. Functional integro-differential equations including Volterra type integrals have been searched with regard to numerical analysis aspect by Brunner [4]. Collocation methods have been applied for solving Volterra functional integral equations including non-vanishing delays [5]. Besides, in the literature, continuous spline collocation methods [6], Lagrange interpolation and Chebyshev interpolation [7], Adams–Moulton method [8], backward substitution method [9], continuous Runge–Kutta method [10,11,12], Spectral method [13] have been implemented in order to find the solutions of neutral type integro-differential equations including variable delays.

In this work, the following first-order integro-differential equation including neutral terms and variable delays is considered as

$$ y^{\prime}(t) + P_{1} (t)y^{\prime}(t - \tau (t)) = P_{0} (t)y(t) + \int\limits_{t - u(t)}^{t - v(t)} {K(t,s)y(s){\text{d}}s} + g(t),\quad 0 \le t,s \le b, $$
(1)

under the initial condition

$$ y^{\prime}(0) = \lambda_{0} , $$
(2)

where \({P}_{0}\left(t\right), {P}_{1}\left(t\right), u\left(t\right), v\left(t\right), g(t)\) and the delay term \(\tau (t)\) are defined as continuous functions for \(\infty > b > t \ge 0\). Here the aim is about finding a numerical solution \(y_{N} (t)\) by using the truncated Laguerre series of given problem (1)–(2):

$$ y_{N} (t) = \sum\limits_{n = 0}^{N} {a_{n} } L_{n} (t), $$
(3)

where \(a_{n} ,\,n = 0,1,...,N\) are unknown coefficients; \(L_{n} (t)\) are the Laguerre polynomials for \(n = 0,1,...,N\) and defined as

$$ L_{n} (t) = \sum\limits_{r = 0}^{n} {\frac{{( - 1)^{r} }}{r!}\left( {\begin{array}{*{20}c} n \\ r \\ \end{array} } \right)t^{r} } . $$
(4)

Numerical method

In this section, the numerical method based on Laguerre polynomials is introduced. The main advantage of the method lies in its straightforwardness since it has no aim for discretization as a reliable tool. On the other hand, Laguerre polynomials give powerful solutions, especially on the positive interval since its applications in several fields with these types of properties.

Fundamental relations

In here, the matrix forms of Eq. (1) are composed. First of all, it is organized as

$$ D_{3} + D_{2} = D_{1} + I + G, $$
(5)

where

$$ D_{1} = P_{0} (t)y(t);\,\,\,\,D_{2} = P_{1} (t)y^{\prime}(t - \tau (t));\,\,\,D_{3} = y^{\prime}(t)\,;\,\,\,\,I = \int\limits_{t - u(t)}^{t - v(t)} {K(t,s)y(s){\text{d}}s} ;\quad G = g(t). $$

Then, the matrix form of the numerical solution (3) is considered as

$$ \left[ {y(t)} \right] = {\mathbf{L}}(t){\mathbf{A}}, $$
(6)

where

$$ \;{\mathbf{L}}(t) = \left[ {\begin{array}{*{20}c} {L_{0} (t)} & {L_{1} (t)} & {L_{2} (t)} & \ldots & {L_{N} (t)} \\ \end{array} } \right]\;{\text{and}}\;{\mathbf{A}} = [a_{0} \;a_{1} \;...\;a_{N} ]^{T} . $$

here \({\mathbf{L}}(t)\) is defined as in the matrix form:

$$ {\mathbf{L}}(t) = {\mathbf{X}}(t){\mathbf{H}} $$
(7)

where

$$ {\mathbf{X}}(t) = \left[ {\begin{array}{*{20}c} 1 & t & {t^{2} } & \ldots & {t^{N} } \\ \end{array} } \right], $$
$$ {\mathbf{H}} = \left[ {\begin{array}{*{20}c} {\frac{{( - 1)^{0} }}{0!}\left( {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right)} & {\frac{{( - 1)^{0} }}{0!}\left( {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right)} & {\frac{{( - 1)^{0} }}{0!}\left( {\begin{array}{*{20}c} 2 \\ 0 \\ \end{array} } \right)} & \cdots & {\frac{{( - 1)^{0} }}{0!}\left( {\begin{array}{*{20}c} N \\ 0 \\ \end{array} } \right)} \\ 0 & {\frac{{( - 1)^{1} }}{1!}\left( {\begin{array}{*{20}c} 1 \\ 1 \\ \end{array} } \right)} & {\frac{{( - 1)^{1} }}{1!}\left( {\begin{array}{*{20}c} 2 \\ 1 \\ \end{array} } \right)} & \cdots & {\frac{{( - 1)^{1} }}{1!}\left( {\begin{array}{*{20}c} N \\ 1 \\ \end{array} } \right)} \\ 0 & 0 & {\frac{{( - 1)^{2} }}{2!}\left( {\begin{array}{*{20}c} 2 \\ 2 \\ \end{array} } \right)} & \cdots & {\frac{{( - 1)^{2} }}{2!}\left( {\begin{array}{*{20}c} N \\ 2 \\ \end{array} } \right)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & {\frac{{( - 1)^{N} }}{N!}\left( {\begin{array}{*{20}c} N \\ N \\ \end{array} } \right)} \\ \end{array} } \right]. $$

Thus, the connection between \({\mathbf{X}}(t)\) and \({\mathbf{X^{\prime}}}(t)\) is defined as

$$ {\mathbf{X^{\prime}}}(t) = {\mathbf{X}}(t){\mathbf{B}} $$
(8)

in which

$$ {\mathbf{B}} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & \ldots & 0 \\ 0 & 0 & 2 & \ldots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & N & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]. $$

Therefore, the matrix relations (7) and (8) are used and \({\mathbf{L^{\prime}}}(t)\) is defined as follows

$$ {\mathbf{L^{\prime}}}(t) = {\mathbf{X}}(t){\mathbf{BH}} $$
(9)

So that, from (7) and (9)

$$ {\mathbf{X}}(t) = {\mathbf{L}}(t){\mathbf{H}}^{ - 1} ;\,\,\,{\mathbf{L^{\prime}}}(t) = {\mathbf{L}}(t){\mathbf{C}}, $$
(10)

is obtained in which \({\mathbf{C}}\) is described as

$$ {\mathbf{C}} = \left[ {c_{pq} } \right],\,\,\,\,\,\,c_{pq} = \left\{ {\begin{array}{*{20}c} { - 1,\,\,p < q} \\ {0,\,\,\,p \ge q} \\ \end{array} } \right.. $$

Thus, from (6), (7), and (10) [14]:

$$ \left[ {y^{\prime}(t)} \right] = {\mathbf{L}}(t){\mathbf{CA}} $$
(11)

By replacing \(t \to t - \tau (t)\) into (11) and by using (9), we obtain

$$ \left[ {y^{\prime}(t - \tau (t))} \right] = {\mathbf{L}}(t - \tau (t)){\mathbf{CA}} = {\mathbf{X}}(t - \tau (t)){\mathbf{BHA}} = {\mathbf{X}}(t){\mathbf{T}}(t - \tau (t)){\mathbf{BHA}} $$
(12)

where

$$ {\mathbf{T}}\left( { - \tau (t)} \right) = \left[ {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right)\left( { - \tau (t)} \right)^{0} } & {\left( {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right)\left( { - \tau (t)} \right)^{1} } & \ldots & {\left( {\begin{array}{*{20}c} N \\ 0 \\ \end{array} } \right)\left( { - \tau (t)} \right)^{N} } \\ 0 & {\left( {\begin{array}{*{20}c} 1 \\ 1 \\ \end{array} } \right)\left( { - \tau (t)} \right)^{0} } & \ldots & {\left( {\begin{array}{*{20}c} N \\ 1 \\ \end{array} } \right)\left( { - \tau (t)} \right)^{N - 1} } \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & {\left( {\begin{array}{*{20}c} N \\ N \\ \end{array} } \right)\left( { - \tau (t)} \right)^{0} } \\ \end{array} } \right]. $$

Diversely, the kernel function \(K(t,s)\) is obtained by using the Taylor series as

$$ K(t,s) = \sum\limits_{i,j = 0}^{N} {k_{ij} t^{i} s^{j} \,} \,,\,\,\,k_{ij} = \frac{1}{i!j!}\frac{{\partial^{i + j} K(0,0)}}{{\partial t^{i} \partial s^{j} }},\,\,K = \left[ {k_{ij} } \right],\,\,i,j = 0,1,...,N. $$

Then, its matrix form is written as

$$ {\mathbf{K}}(t,s) = {\mathbf{X}}(t){\mathbf{KX}}^{T} (s). $$
(13)

By means of the relations (9) and (13), the integral part of Eq. (1) has a matrix form as

$$ \int\limits_{t - u(t)}^{t - v(t)} {{\mathbf{X}}(t){\mathbf{KX}}^{T} (s){\mathbf{L}}(s){\mathbf{A}}ds} = {\mathbf{X}}(t){\mathbf{K}}\int\limits_{t - u(t)}^{t - v(t)} {{\mathbf{X}}^{T} (s){\mathbf{X}}(s)ds} {\mathbf{HA}} = {\mathbf{X}}(t){\mathbf{KQ}}(t){\mathbf{HA}}, $$
(14)

where

$$ {\mathbf{Q}}(t) = \int\limits_{t - u(t)}^{t - v(t)} {{\mathbf{X}}^{T} (s){\mathbf{X}}(s)ds} = \int\limits_{t - u(t)}^{t - v(t)} {[s^{i + j} ]ds} = [q_{ij} (t)], $$

and

$$ q_{ij} (t) = \frac{{(t - v(t))^{i + j + 1} - (t - u(t))^{i + j + 1} }}{i + j + 1},\quad i,j = 0,1, \ldots ,N. $$

Similarly, from (11), the initial condition in Eq. (2) has the matrix form as

$$ \left[ {y^{\prime}(0)} \right] = {\mathbf{L}}(0){\mathbf{CA}} = \left[ {\lambda_{0} } \right]. $$
(15)

Therefore, we obtain the matrix forms of \(D_{1} ,\,D_{2} ,\,D_{3}\) and \(I\) in Eq. (5), from (6), (12), (11), and (14), respectively, as

$$ \begin{aligned} D_{1} & = {\mathbf{P}}_{0} (t){\mathbf{L}}(t){\mathbf{A}} \\ D_{2} & = {\mathbf{P}}_{1} (t){\mathbf{X}}(t){\mathbf{T}}(t - \tau (t)){\mathbf{BHA}} \\ D_{3} & = {\mathbf{L}}(t){\mathbf{CA}} \\ I & = {\mathbf{X}}(t){\mathbf{KQ}}(t){\mathbf{HA}}. \\ \end{aligned} $$

So that, Eq. (1) can be represented by the following matrix equation as

$$ {\mathbf{L}}(t){\mathbf{CA}} + {\mathbf{P}}_{1} (t){\mathbf{X}}(t){\mathbf{T}}(t - \tau (t)){\mathbf{BHA}} = {\mathbf{P}}_{0} (t){\mathbf{L}}(t){\mathbf{A}} + {\mathbf{X}}(t){\mathbf{KQ}}(t){\mathbf{HA}} + {\mathbf{G}}(t). $$
(16)

Method of solution

In this section, the collocation points are defined by

$$ t_{i} = \frac{b}{N}i,\quad i = 0,1, \ldots ,N $$
(17)

Thus, the collocation points (17) are substituted into Eq. (16) and the fundamental matrix is obtained asor

$$ {\mathbf{L}}(t_{i} ){\mathbf{CA}} + {\mathbf{P}}_{1} (t_{i} ){\mathbf{X}}(t_{i} ){\mathbf{T}}(t_{i} - \tau (t_{i} )){\mathbf{BHA}} = {\mathbf{P}}_{0} (t_{i} ){\mathbf{L}}(t_{i} ){\mathbf{A}} + {\mathbf{X}}(t_{i} ){\mathbf{KQ}}(t_{i} ){\mathbf{HA}} + {\mathbf{G}}(t_{i} ) $$
$$ \left\{ {{\mathbf{LC}} + {\mathbf{P}}_{1} {\mathbf{XT}}_{\tau } {\mathbf{BH}} - {\mathbf{P}}_{0} {\mathbf{L}} - {\mathbf{XKQH}}} \right\}{\mathbf{A}} = {\mathbf{G}} $$
(18)

where

$$ \begin{aligned} {\mathbf{L}} & = \left[ {\begin{array}{*{20}c} {L_{0} (t_{0} )} & {L_{1} (t_{0} )} & \ldots & {L_{N} (t_{0} )} \\ {L_{0} (t_{1} )} & {L_{1} (t_{1} )} & \ldots & {L_{N} (t_{1} )} \\ \vdots & \vdots & \ddots & \vdots \\ {L_{0} (t_{N} )} & {L_{1} (t_{N} )} & \ldots & {L_{N} (t_{N} )} \\ \end{array} } \right],\,\,{\mathbf{A}} = \left[ {\begin{array}{*{20}c} {a_{0} } \\ {a_{1} } \\ \vdots \\ {a_{N} } \\ \end{array} } \right],\,{\mathbf{G}} = \left[ {\begin{array}{*{20}c} {g(t_{0} )} \\ {g(t_{1} )} \\ \vdots \\ {g(t_{N} )} \\ \end{array} } \right], \hfill \\ \hfill \\ {\mathbf{P}}_{0} &= diag\left[ {\begin{array}{*{20}c} {P_{0} (t_{0} )} & {P_{0} (t_{1} )} & \ldots & {P_{0} (t_{N} )} \\ \end{array} } \right], \hfill \\ {\mathbf{P}}_{1} &= diag\left[ {\begin{array}{*{20}c} {P_{1} (t_{0} )} & {P_{1} (t_{1} )} & \ldots & {P_{1} (t_{N} )} \\ \end{array} } \right], \hfill \\ {\mathbf{X}} &= diag\left[ {\begin{array}{*{20}c} {X(t_{0} )} & {X(t_{1} )} & \ldots & {X(t_{N} )} \\ \end{array} } \right], \hfill \\ {\mathbf{T}}_{\tau } &= diag\left[ {\begin{array}{*{20}c} {X(t - \tau (t_{0} ))} & {X(t - \tau (t_{1} ))} & \ldots & {X(t - \tau (t_{N} ))} \\ \end{array} } \right]. \hfill \\ \end{aligned} $$

Briefly,

$$ {\mathbf{WA}} = {\mathbf{G}}\;{\text{or}}\;\left[ {{\mathbf{W}};\,{\mathbf{G}}} \right] $$
(19)

Here we have the augmented matrix form of Eq. (18). Besides, we consider the initial condition which is given in Eq. (2). Its matrix form is defined in Eq. (15). By putting the row from (15) in place of the last row of (19),

$$ {\tilde{\mathbf{W}}} = \left[ {\begin{array}{*{20}c} {\omega_{00} } & {\omega_{01} } & {\omega_{02} } & \ldots & {\omega_{0N} } \\ {\omega_{10} } & {\omega_{11} } & {\omega_{12} } & \ldots & {\omega_{1N} } \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {\omega_{(N - 1)0} } & {\omega_{(N - 1)1} } & {\omega_{(N - 1)2} } & \ldots & {\omega_{(N - 1)N} } \\ {u_{00} } & {u_{01} } & {u_{02} } & \ldots & {u_{0N} } \\ \end{array} } \right],\,\,\,{\tilde{\mathbf{G}}} = \left[ {\begin{array}{*{20}c} {g(t_{0} )} \\ {g(t_{1} )} \\ \vdots \\ {g(t_{N - 1} )} \\ {\lambda_{0} } \\ \end{array} } \right]. $$

Then, we construct the new augmented matrix as

$$ {\tilde{\mathbf{W}}\mathbf{A}} = {\tilde{\mathbf{G}}}\;{\text{or}}\;\left[ {{\tilde{\mathbf{W}}};{\tilde{\mathbf{G}}}} \right]. $$
(20)

In Eq. (20), if \({\text{rank}}\left[ {{\tilde{\mathbf{W}}}} \right] = {\text{rank}}\left[ {{\tilde{\mathbf{W}}};{\tilde{\mathbf{G}}}} \right] = N + 1\), then the coefficients matrix \({\mathbf{A}}\) is uniquely determined with the help of Gauss Elimination procedure [15,16,17,18,19,20,21,22]. Then, by using Eq. (3), the problem (1)–(2) is solved numerically and its numerical solution is obtained as in the form

$$ y(t) \cong y_{N} (t) = \sum\limits_{n = 0}^{N} {a_{n} } L_{n} (t). $$

Analysis of the method

In this section, some properties of the method are introduced. The stability of the collocation methods has been investigated previously by Brunner et al. [23, 24]. Besides, the stability of the related problem has been also considered by some authors [25, 26]. However, existence and uniqueness theorems and convergence of the method are given as follows.

Convergence of the method

Definition 1

Let \(y_{N} (t)\) be the approximate solution of the problem (1)–(2) which has an exact solution as \(y(t)\). Then, the collocation method is said to be convergent if an only if

$$ \mathop {\lim }\limits_{h \to 0} \left| {y_{N} (t_{i} ) - y(t_{i} )} \right| \to 0,\,\,\,\,i = 0,1, \ldots ,N, $$
(21)

where \(h\) is the step size and \(h \to 0,\,\,N \to \infty\) [27,28,29,30,31].

Definition 2

If the largest number is p for the finite constant C, then the method is of order p such that [27,28,29,30,31]

$$ \left| {y_{N} (t_{i} ) - y(t_{i} )} \right| \le Ch^{p} ,\,\,\,\,i = 0,1, \ldots ,N. $$
(22)

where \(h\) is the step size and \(h \to 0,\,\,N \to \infty\) [27,28,29].

Theorem 1

Consider the first-order integro-differential equation including neutral terms and variable delays in Eq. (1) under the initial condition (2). Then,

  1. i.

    \(g(t)\) is continuous in \(0 \le t \le b\),

  2. ii.

    \(K(t,s)\) is a continuous function for \(0 \le t \le b\) and \(\left\| y \right\| < \infty\),

  3. iii.

    \(K(t,s)\) satisfies a Lipschitz condition as follows

    $$ \left\| {K(t,s)y_{1} - K(t,s)y_{2} } \right\| \le L\left\| {y_{1} - y_{2} } \right\| $$
    (23)

for all \(0 \le t,s \le b\). Then, the problem (1)–(2) has a unique solution [27,28,29,30,31].

Theorem 2

Consider that \(g(t) \in C[I \times {\mathbb{R}}^{N} ,{\mathbb{R}}^{N} ]\), \(K(t,s) \in C[I \times I \times {\mathbb{R}}^{N} ,{\mathbb{R}}^{N} ]\) and \(K(t,s) \in C[I \times I \times {\mathbb{R}}^{N} ,{\mathbb{R}}^{N} ]\) for \(\int\limits_{t - u(t)}^{t - v(t)} {\left| {K(t,s)y(s)} \right|ds} \le N\) for \(0 \le t,s \le b\), \(y \in \Omega = \left\{ {\phi \in C[I,{\mathbb{R}}^{N} ]:\phi_{0} (0) = t_{0} \,{\text{and}}\,\left| {\phi (x) - \lambda_{0} \,} \right| \le b} \right\}\). Then, our initial value problem (IVP) (1)-(2) has at least one solution [27,28,29,30].

Existence and uniqueness

Theorem 3

Consider the first-order integro-differential equation including neutral terms and variable delays in Eq. (1) under the initial condition (2). Assume that \(g(t)\) and \(K(t,s)\) are continuous functions which satisfy the Lipschitz conditions. Then,

$$ \begin{gathered} \left\| {g(t)y_{1} - g(t)y_{2} } \right\| \le L\left\| {y_{1} - y_{2} } \right\|, \hfill \\ \left\| {K(t,s)y_{1} - K(t,s)y_{2} } \right\| \le L\left\| {y_{1} - y_{2} } \right\|, \hfill \\ \end{gathered} $$
(24)

for every \(\left| {t - t_{0} } \right| \le a\) and \(\left| {s - t_{0} } \right| \le a\) for any initial value \(t_{0}\) and the positive constant \(a > 0\), \(\left\| {y_{1} } \right\| < \infty\) and \(\left\| {y_{2} } \right\| < \infty\). Then, the IVP has a unique solution.

Proof

[28,29,30].

Accuracy

In this section, the accuracy of the approximate solution is investigated. As an important factor for the numerical methods in the literature, the approximate solutions are corrected with regard to the residual error correction procedure. On the other hand, a brief error analysis is given in order to reach the approximation for the problem (1)–(2).

Residual correction

In here, the residual correction is given in order to improve the solutions and for the comprehensive error analysis for the approximate solution of the problem (1)–(2) [17, 18, 32,33,34,35,36,37].

$$ R_{N} (t) = \left| {y^{\prime}_{N} (t) + P_{1} (t)y^{\prime}_{N} (t - \tau (t)) - P_{0} (t)y_{N} (t) - \int\limits_{t - u(t)}^{t - v(t)} {K(t,s)y_{N} (s){\text{d}}s} } \right|,\quad y^{\prime}(0) = \lambda_{0} . $$
(25)

Now, let us consider the error function as \(e_{N} (t) = y(t) - y_{N} (t)\). Then, we construct an error problem in the form

$$ e^{\prime}_{N} (t) + P_{1} (t)e^{\prime}_{N} (t - \tau (t)) = P_{0} (t)e_{N} (t) + \int\limits_{t - u(t)}^{t - v(t)} {K(t,s)e_{N} (s){\text{d}}s} ,\quad e^{\prime}_{N} (0) = 0. $$
(26)

Subsequently, the numerical method is applied on the error problem in Eq. (26) and we have the approximate solution for the error function in the form as follows

$$ e_{N,M} (t) = \sum\limits_{n = 0}^{M} {a_{n}^{*} } L_{n} (t). $$
(27)

Thus, the corrected approximate solution is obtained as

$$ y_{N,M} (t) = y_{N} (t) + e_{N,M} (t). $$
(28)

Error analysis

In this section, we investigate the absolute error function \(E_{N} (t)\) for \(t = t_{p} \in \left[ {a,b} \right],\,\,\,p = 0,1,2,...\).

$$ E_{N} (t_{p} ) = \left| {y_{N} (t_{p} ) - y^{\prime}(t_{p} ) - P_{1} (t_{p} )y^{\prime}(t_{p} - \tau (t_{p} )) + P_{0} (t_{p} )y(t_{p} ) + \int\limits_{t - u(t)}^{t - v(t)} {K(t_{p} ,s)y(s){\text{d}}s} } \right| \cong 0 $$
(29)

and the accuracy of the numerical solutions is checked. Specifically, if \(E_{N} (t_{q} ) \le 10^{{ - k_{q} }}\) (\(k_{q}\) any positive integer) is small enough, then the approximation has its reliability.

Algorithm

In here, the present method is shown by its algorithm. The steps are explained clearly in order to see the implementation of the computer programming part of the work.

Step 0

Input initial data: \(P_{0} (t)\), \(P_{1} (t)\), \(u(t)\), \(v(t)\) and \(\tau (t)\)

Step 1

Set \(m \le N\) for \(m \in {\mathbb{N}}\)

Step 2

Construct the matrices such as \({\mathbf{L}}(t),\,\,{\mathbf{B}},\,{\mathbf{H}}\)

Step 3

Replace in the fundamental equation

Step 4

Put the collocation points, \(t_{i} = \frac{b}{N}i,\quad i = 0,1, \ldots ,N\) into the fundamental equation in S3

Step 5

Calculate \(\left[ {{\mathbf{W}};{\mathbf{G}}} \right]\)

Step 6

Compute the matrix for the initial condition

Step 7

Substitute the outcome from S6 into the matrix in S5 and get \(\left[ {{\tilde{\mathbf{W}}};{\tilde{\mathbf{G}}}} \right]\)

Step 8

Determine the system in S7. Output: \(y_{N} (t)\)

Step 9

Accuracy check:\(E_{N} (t)\)

Step 10

If \(E_{N} (t_{q} ) \cong 0\). Stop

Step 11

Else back S1

Numerical experiments

Numerical experiments section gives us an idea about the method and its applicability, validity and reliability. The applications of this method have been implemented by using some numerical illustrations. Here Maple and MATLAB computer programs are used for the calculation algorithm and plotting.

Example 1

Firstly, the first-order Volterra integro-differential equation including neutral term and variable delay.

$$ y^{\prime}(t) + \left( {\frac{{15t^{2} }}{2} + t + 1} \right)y^{\prime}(t - y(t)) = y(t) + \int\limits_{t - 1}^{t - (1 - 3t)} {y(s){\text{d}}s} ,\quad 0 \le t \le 1 $$
(30)

under the initial condition

$$ y^{\prime}(0) = 1 $$
(31)

Hereby approximate solution of (30)–(31) is found by using the algorithm of the present method for N = 4.

$$ y(t) \cong y_{4} (t) = \sum\limits_{n = 0}^{4} {a_{n} } L_{n} (t) $$
(32)

The collocation points (17) are set for N = 4 on the interval [0,1] which are as follows.

$$ t_{0} = 0,\,\,t_{1} = \frac{1}{4},\,\,t_{2} = \frac{1}{2}\,,\,\,t_{3} = \frac{3}{4}\,,\,\,t_{4} = 1. $$

Then, Eq. (1) has its fundamental matrix equation as

\(\left\{ {{\mathbf{LC}} + {\mathbf{P}}_{1} {\mathbf{XT}}_{\tau } {\mathbf{BH}} - {\mathbf{P}}_{0} {\mathbf{L}} - {\mathbf{XKQH}}} \right\}{\mathbf{A}} = {\mathbf{G}}\)

where

$$ \begin{aligned} {\mathbf{P}}_{1} & = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 \\ 0 & {55/32} & 0 & 0 & 0 \\ 0 & 0 & {27/8} & 0 & 0 \\ 0 & 0 & 0 & {191/32} & 0 \\ 0 & 0 & 0 & 0 & {19/2} \\ \end{array} } \right],\quad {\mathbf{P}}_{0} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right],\quad {\mathbf{G}} = \left[ {\begin{array}{*{20}c} 1 \\ {5/4} \\ {3/2} \\ {7/4} \\ 2 \\ \end{array} } \right], \\ {\mathbf{L}} & = \left[ {\begin{array}{*{20}c} {L_{0} (0)} & {L_{1} (0)} & {L_{2} (0)} & {L_{3} (0)} & {L_{4} (0)} \\ {L_{0} (1/4)} & {L_{1} (1/4)} & {L_{2} (1/4)} & {L_{3} (1/4)} & {L_{4} (1/4)} \\ {L_{0} (1/2)} & {L_{1} (1/2)} & {L_{2} (1/2)} & {L_{3} (1/2)} & {L_{4} (1/2)} \\ {L_{0} (3/4)} & {L_{1} (3/4)} & {L_{2} (3/4)} & {L_{3} (3/4)} & {L_{4} (3/4)} \\ {L_{0} (1)} & {L_{1} (1)} & {L_{2} (1)} & {L_{3} (1)} & {L_{4} (1)} \\ \end{array} } \right],\quad {\mathbf{C}} = \left[ {\begin{array}{*{20}c} 0 & { - 1} & { - 1} & { - 1} & { - 1} \\ 0 & 0 & { - 1} & { - 1} & { - 1} \\ 0 & 0 & 0 & { - 1} & { - 1} \\ 0 & 0 & 0 & 0 & { - 1} \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right], \\ {\mathbf{X}} & = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 \\ 1 & {1/4} & {1/16} & {1/64} & {1/256} \\ 1 & {1/2} & {1/4} & {1/8} & {1/16} \\ 1 & {3/4} & {9/16} & {27/64} & {81/256} \\ 1 & 1 & 1 & 1 & 1 \\ \end{array} } \right],\quad {\mathbf{B}} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 \\ 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right],\quad {\mathbf{H}} = \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 1 & 1 \\ 0 & { - 1} & { - 2} & { - 3} & { - 4} \\ 0 & 0 & {1/2} & {3/2} & 3 \\ 0 & 0 & 0 & { - 1/6} & { - 2/3} \\ 0 & 0 & 0 & 0 & {1/24} \\ \end{array} } \right]. \\ \end{aligned} $$

So, the augumented matrix is found as

$$ \left[ {{\text{W}};\,{\text{G}}} \right] = \left[ {\begin{array}{*{20}c} {2/5} & { - 1/5} & 0 & 0 & 0 & ; & 1 \\ {1/2} & { - 1/4} & 0 & 0 & 0 & ; & {5/4} \\ {3/5} & { - 3/10} & 0 & 0 & 0 & ; & {3/2} \\ {7/10} & { - 7/20} & 0 & 0 & 0 & ; & {7/4} \\ {4/5} & { - 2/5} & 0 & 0 & 0 & ; & 2 \\ \end{array} } \right]. $$

Now, the initial condition is defined in (31) has the matrix form as

$$ \left[ {y^{\prime}(0)} \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 \\ \end{array} } \right]. $$

So that the new augmented matrix is constructed as

$$ \left[ {{\tilde{\text{W}}};\,{\tilde{\text{G}}}} \right] = \left[ {\begin{array}{*{20}c} {2/5} & { - 1/5} & 0 & 0 & 0 & ; & 1 \\ {1/2} & { - 1/4} & 0 & 0 & 0 & ; & {5/4} \\ {3/5} & { - 3/10} & 0 & 0 & 0 & ; & {3/2} \\ {7/10} & { - 7/20} & 0 & 0 & 0 & ; & {7/4} \\ 1 & 0 & 0 & 0 & 0 & ; & 0 \\ \end{array} } \right]. $$

By following the procedure, the system is solved, and then, \(a_{n}\) Laguerre coefficients are found as follows

$$ a_{0} = 2,\,\,\,\,\,\,a_{1} = - 1,\,\,\,\,\,\,a_{2} = 0,\,\,\,\,\,a_{3} = 0,\,\,\,\,\,a_{4} = 0. $$

Consequently, these calculated coefficients are established and they are replaced in Eq. (32). Then, the exact solution of (30)–(31) is acquired as

$$ y(t) = t + 1. $$
(33)

Example 2

As a second example, the first-order Volterra integro-differential equation including neutral term and delay is considered [37]

$$ y^{\prime}(t) = (\lambda - 1){\text{e}}^{(1 - t)} - (\lambda + 1)y(t) + y(t - 1) - \lambda \int\limits_{t - 1}^{t} {y(s){\text{d}}s} ,\quad t \ge 0, $$
(34)

and the initial condition

$$ y(0) = 1, $$
(35)

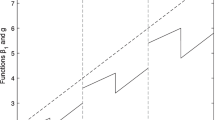
corresponding to the exact solution \(y_{{{\text{exact}}}} (t) = e^{t}\). Correspondingly, the problem (34)-(35) is solved by the similar approach which is followed in Example 1. In Table 1, absolute errors for different N truncation values are demonstrated for their comparison. Herein this error comparison with different numerical methods: Laguerre collocation method (LCM) for \(M=10\) and \(N=9\) and mixed spline/spectral method (MSSM) with \(h=0.2\) in Table 2 and in Fig. 1. From these comparisons, we can see apparently that more suitable and efficient results are obtained for the smaller when we have increasing N value.

Table 1 Error comparison for different truncation values: \(N\)=6, 8 and 10 for \(0\le t\le 1\) of Example 2 with \(\lambda =2\)
Full size table
Table 2 Errors comparison for \(\lambda =3\) and different numerical methods for \(2\le t\le 10\) of Example 2
Full size table

Example 3

Consider the first-order Volterra integro-differential equation including neutral term and delay from Eq. (1) with \(P_{1} (t) = v(t) = g(t) = 0\), \(K(t,s) = u(t) = 1\) and including a delay term \(y(t - 1)\) together with \(P_{0} (t) = 1\). Moreover, the initial condition is given as \(y(0) = 1\) and the exact solution is \(y_{exact} (t) = e^{t}\). Then, the absolute errors for different N truncation values are demonstrated for their comparison in Table 3 and Fig. 2. Besides, we can see the numerical solutions with regard to Laguerre approach and exact solution of the problem in Fig. 3. From these comparisons, we can see apparently that more suitable and efficient results are obtained for the smaller when we have increasing N value. Subsequently, there are improved results with related to the Sect. 4.1. Residual correction helps for a better approximation and give smaller values for the error function which is shown in Table 4.

Table 3 Error comparison for different truncation values: \(N\)=5, 6, 8 and 10 for \(0\le t\le 1\) of Example 3
Full size table
Fig. 2
figure 2

\({E}_{N}(t)\) error comparison for Example 2

Full size image
Fig. 3
figure 3

Comparison between exact solution with the numerical solutions with regard to Laguerre approach for \(N=4, 5, 6, 8\) and \(10\) in Example 3

Full size image
Table 4 Error functions for different iterations with improved results of Example 3
Full size table

Conclusion

In this study, a powerful numerical technique to determine the numerical solutions of first-order integro-differential equations including neutral terms and variable delays is proposed. The technique affords approximate solutions of the problem which are mainly close enough to the exact solutions with respect to \(N\). Accuracy and applicability of the method have been proved by the visible results at the tables and the figures. The main advantages of this technique are including but not limited to straightforward coding, its apparent algorithm and accessible matrix calculations. Moreover, the error analysis including the residual correction supports the results with the additional error problem solution which is explained and applied in an example.

As a future outlook, this numerical study and the technique can be extended to other models with related to Volterra integro-differential equations including retarded term. However, some modifications are required [38].