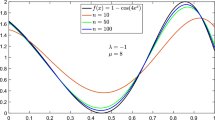
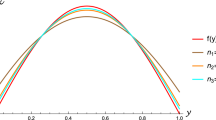
Abstract
In the present paper, we consider the complete asymptotic expansion of certain exponential-type operators connected with \(2x^{3/2}\). Also, a modification of such exponential-type operators is provided, which preserve the function \(\mathrm{e}^{Ax}\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Ismail and May [5, (3.16)] defined the operators
where \(x\in (0,\infty )\). The kernel is given by
where \(\delta (t)\) is the Dirac delta function and \(I_1\) denotes the modified Bessel function of first kind defined by
The operators (1) are exponential-type operators as the kernels \(k_n(x,t)\) of the operators \(T_n\) satisfy the partial differential equation
with \(p(x)=2x^{3/2}.\) The operators (1) reproduce constant and linear functions.
Note that the operators (1) can alternatively be written in the form
where \(x\in \left( 0,\infty \right)\) and
We observe that the operators \(T_{n}\) are closely related to the well-known Phillips operators given by
Obviously, we have \(\left( P_{n/\sqrt{x}}f\right) \left( x\right) =\left( T_{n}f\right) \left( x\right)\), but unlike the operators \(T_n\), Phillips operators are not exponential type operators.
The operators \(T_n\) individually have not been studied by researchers much, due to its complicated behaviour. Very recently, Abel and Gupta [1] studied the rate of convergence of these operators on functions of bounded variation. Also, Gupta [2] and Gupta et al. [3] resp. gave some direct results in ordinary and simultaneous approximation. In the present article, we establish the complete asymptotic expansion of the operators \(T_n\) as n tends to infinity.
Asymptotic expansion
In the following, we use the falling factorial given by \(z^{\underline{0}}=1\) , and \(z^{\underline{m}}=z\left( z-1\right) \left( z-2\right) \cdots \left( z-m+1\right)\), for \(m\in \mathbb {N}\).
Firstly, we derive a concise representation of the r-th order moment \(\left( T_{n} e_{r}\right) (x)\) where \(e_{r}\left( t\right) =t^{r},\) \(r\in \mathbb {N}_{0}\), denote the monomials. Obviously, we have \(\left( T_{n} e_{0}\right) (x) =1\).
Lemma 1
For \(r\in \mathbb {N}\), the r-th order moment of the Ismail–May operators \(T_{n}\) has the representation
Proof
For \(r\in \mathbb {N}\), we have
Application of the Leibniz rule for differentiation yields
which is the desired formula. \(\square\)
Now we turn to the central moments \(\left( T_{n} \psi _{x}^{s}\right) (x)\). For real x, we define \(\psi _{x}\left( t\right) =t-x\).
Lemma 2
For \(s=1,2,\ldots\), the central moment of the Ismail-May operator \(T_{n}\) possesses the representation
Proof
For \(s\in \mathbb {N}\), we have
Using the binomial identity \({\left( {\begin{array}{c}{s}\\ {r}\end{array}}\right) }{\left( {\begin{array}{c}{r}\\ {k}\end{array}}\right) }={\left( {\begin{array}{c}{s} \\ {k}\end{array}}\right) }{\left( {\begin{array}{c}{s-k}\\ {r-k}\end{array}}\right) }\) we obtain
and the desired formula follows by an application of the Leibniz rule for differentiation. \(\square\)
Lemma 3
The central moments of the operators \(T_n\) satisfy
Let \(C_{\gamma }\left[ 0,\infty \right)\) be the class of continuous functions f on \(\left[ 0,\infty \right)\) satisfying the exponential growth condition \({f}\left( t\right) =O\left( \mathrm{e}^{\gamma t}\right)\) as \(t\rightarrow \infty\), for some \(\gamma >0\).
The next theorem is the main result of this section.
Theorem 1
Let \(q\in \mathbb {N}\) and \(x\in (0,\infty )\). For each function \(f\in C_{\gamma }\left[ 0,\infty \right)\), which has a derivative of order 2q at the point x, the operators \(T_{n}\) possess the asymptotic expansion
as \(n\rightarrow \infty\).
Proof
We apply a general result by Sikkema [7]. In view of the localization result (Proposition 1), we can assume that the function f has (at most) polynomial growth as the variable tends to infinity. Using Lemma 2, we obtain
as \(n\rightarrow \infty\). \(\square\)
More explicitly, we have
as \(n\rightarrow \infty\).
A direct corollary is the following Voronovskaja-type formula.
Corollary 1
Let \(x\in \mathbb {R}\). For each function \(f\in C_{\gamma }\left[ 0,\infty \right)\), which has a second derivative at the point x, we have the asymptotic relation
Now we prove a localization result which is of use in the proof of Theorem 1. It is of interest in its own. In what follows let \(\exp\) denote the exponential function. For real \(\gamma\), we write \(\exp _{\gamma }\left( t\right) :=\mathrm{e}^{\gamma t}\).
Proposition 1
(Localisation theorem) Let \(\gamma ,\delta >0\) and fix \(x>0\). If \(f\in C_{\gamma }\left[ 0,\infty \right)\) vanishes on the interval \(\left( x-\delta ,x+\delta \right) \cap \left( 0,\infty \right)\) then
for arbitrary large \(m>0\).
Proof
Let \(m\in {N}\). For a certain positive constant C, we have
Application of the Schwarz inequality yields
The first root is finite, by [5, Prop. 2.5], if n is sufficiently large. The second root satisfies
by Lemma 3. This completes the proof. \(\square\)
Preservation of the exponential function \(\mathrm{e}^{Ax}\)
King [6] considered a modification of the Bernstein polynomials so as to preserve the function \(e_{2}\). Also the moments of several operators have been discussed in [4]. We start with the following modified form of operators (1) with \(\left( \widetilde{T} _{n}f\right) (x)=\left( T_{n}f\right) (a_{n}(x))\), i.e.,
such that
which is the case if
This modified form of operators preserves constants as well as the exponential function \(\exp _{A}\), but loose to preserve the linear functions. We have the following limits:
Also, we have
After simple computations, we derive the following representation.
Lemma 4
For real numbers C, it holds
We may observe here that the r-th order moment \(\widetilde{T}_{n}e_{r}\) is given by
In particular, we have
Remark 1
The central moments of the operators \(\widetilde{T}_{n}\) have the representation
Direct computation yields
Hence, for \(s=0,1,2,3,4\), the central moments satisfy
The proof of the next lemma uses standard techniques.
Corollary 2
Let \(\gamma\) and \(\delta\) be any two positive real numbers and \([a,b]\subset (0,\infty )\) be any bounded interval. Then, for any \(m>0\) there exists a constant M depending on m only such that
where \(\Vert .\Vert\) is the sup-norm over [a, b].
By Remark 1 and Corollary 2, we have the following asymptotic formula for the modified operators \(\widetilde{T}_{n}\).
Theorem 2
Let \(f\in C_{\gamma }(0,\infty )\) for some \(\gamma >0.\) If \(f^{\prime \prime }\) exists at a point \(x\in (0,\infty )\), then we have
Without a proof, we state the following formula for the first derivative.
Theorem 3
Let \(f\in C_{\gamma }(0,\infty )\) admitting the derivative of 3 -rd order at a fixed point \(x\in (0,\infty )\), then we have
The above result can be derived by using the fact that the kernel of the operator \(\left( \widetilde{T}_nf\right) (x)\) satisfies the partial differential equation
Change history
08 April 2021
Added Funding note.
References
Abel, U., Gupta, V.: Rate of convergence of exponential type operators related to \(p\left( x\right) =2x^{3/2}\) for functions of bounded variation. RACSAM 114,188 (2020). https://doi.org/10.1007/s13398-020-00919-y
Gupta, V.: Convergence estimates of certain exponential type operators. In: Deo et al. (eds.) Mathematical Analysis: Approximation Theory, vol. 306, pp. 47–55. Springer Proceedings in Mathematics and Statistics (2020)
Gupta, V., López-Pellicer, M., Srivastava, H. M.: Convergence estimates of a family of approximation operators of exponential type. Filomat (to appear)
Gupta, V., Rassias, M.T.: Moments of Linear Positive Operators and Approximation, Series: Springer Briefs in Mathematics. Springer, Switzerland (2019)
Ismail, M., May, C.P.: On a family of approximation operators. J. Math. Anal. Appl. 63, 446–462 (1978)
King, J.P.: Positive linear operators which preserve \(x^{2}\). Acta Math. Hungar. 99(3), 203–208 (2003)
Sikkema, P.C.: On some linear positive operators. Indag. Math. 32, 327–337 (1970)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Abel, U., Gupta, V. & Kushnirevych, V. Asymptotic expansions for certain exponential-type operators connected with \(2x^{3/2}\). Math Sci 15, 311–315 (2021). https://doi.org/10.1007/s40096-021-00382-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40096-021-00382-9