Introduction

Throughout this paper, all graphs are finite, simple, undirected and connected. Let G be a graph with vertex set V(G) and edge set E(G). We will use \(P_n\) to denote the path of order n.

The inverse degree and first Zagreb index of a graph G are defined as \(r(G)= \sum _{u\in V(G)} \frac{1}{\deg _G(u)}\) and \(M_1(G)= \sum _{u\in V(G)} \deg _G^2(u)=\sum _{uv\in E(G)} \big (\deg _G(u) +\deg _G(v) \big )\), respectively [1, 7].

The lexicographic product \(G_1 [G_2]\) of two graphs \(G_1\) and \(G_2\) is a graph with vertex set \(V(G_1)\times V(G_2)\) in which two vertices \((u_1,v_1)\) and \((u_2,v_2)\) of \(G_1 [G_2]\) are adjacent if and only if \(\left[ u_1=u_2 ~{\text {and}} ~ v_1 v_2 \in E(G_2)\right]\) or \(\left[ u_1u_2\in E(G_1) ~{\text {and}}~ v_1,v_2 \in V(G_2)\right]\).

For a graph G, there are several related graphs such as line graph L(G), subdivision graph S(G), t-subdivision graph \(S_t(G)\), vertex-semitotal graph R(G), edge-semitotal graph Q(G) and total graph T(G), defined as follows [2, 6, 15]:

L(G) has as its vertices the edges of G; adjacency in L(G) is defined as adjacency for the corresponding edges of G.

S(G) is obtained from G by replacing each edge of G by a path of length 2.

\(S_t(G)\) is obtained from G by replacing each edge of G by a path of length \(t+1\). Obviously, \(S_1(G) = S(G)\).

R(G) is obtained from G by adding a new vertex corresponding to each edge of G and then joining each new vertex to the end vertices of the corresponding edge.

Q(G) is obtained from G by inserting a new vertex into each edge of G and then joining with edges those pairs of new vertices on adjacent edges of G.

T(G) has as its vertices, the edges and vertices of G; adjacency in T(G) is defined as adjacency or incidence for the corresponding elements of G.

Let \(F\in \{S,R,Q,T\}\). The F-product \(G_1[G_2]_F\) of two graphs \(G_1\) and \(G_2\) is a graph with vertex set \(\left( V(G_1)\cup E(G_1) \right) \times V(G_2)\) in which two vertices \((u_1,v_1)\) and \((u_2,v_2)\) of \(G_1[G_2]_F\) are adjacent if and only if \(\left[ u_1=u_2 \in V(G_1) ~{\text {and}} ~ v_1 v_2 \in E(G_2)\right]\) or \(\left[ u_1u_2\in E(F(G_1)) ~{\text {and}} ~\right.\) \(\left. v_1, v_2 \in V(G_2) \right]\) [12].

We refer to the vertices in \(V(G_1)\) and \(V(F(G_1)) -V(G_1)\) as black vertices and white vertices, respectively, where \(F\in \{S,R,Q,T\}\).

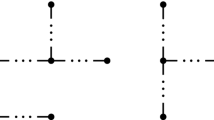
\(P_4 [P_2]_S\), \(P_4 [P_2]_R\), \(P_4 [P_2]_Q\) and \(P_4 [P_2]_T\) are shown in Fig. 1.

Fig. 1
figure 1

\(P_4[P_2]_F\), where \(F\in \{S,R,Q,T\}\)

Full size image

For a graph G, the Randić index R(G) is defined as \(R(G)=\sum _{uv\in E(G)} \left( \deg _G(u) \deg _G(v) \right) ^{-\frac{1}{2}}\) [11]. The sum-connectivity index \(\chi (G)\) and general sum-connectivity index \(\chi _{\alpha } (G)\) are closely related variants of Randić index, defined as \(\chi (G)=\sum _{uv\in E(G)} \left( \deg _G(u) + \deg _G(v) \right) ^{-\frac{1}{2}}\) and \(\chi _{\alpha }(G)=\sum _{uv\in E(G)} \left( \deg _G(u) + \deg _G(v) \right) ^\alpha\), where \(\alpha\) is a real number [19, 20]. It has been found that the (general) sum-connectivity index and Randić index correlate well among themselves and with the \(\pi\)-electronic energies of benzenoid hydrocarbons [4, 5].

In this paper, we consider the harmonic index, which is another variant of Randić index. For a graph G, the harmonic index H(G) is defined as \(H(G)=\sum _{uv\in E(G)} \frac{2}{\deg _G(u) +\deg _G(v)}\) [1]. In recent years, this vertex-degree-based topological index has been extensively studied. For example, Zhong [16] gave the minimum and maximum values of the harmonic index for simple connected graphs and trees and characterized the corresponding extremal graphs. Recently, Onagh investigated the harmonic index of product graphs, subdivision graphs, t-subdivision graphs, vertex-semitotal graphs, edge-semitotal graphs, total graphs and F-sum of graphs, where \(F\in \{S,S_t,R,Q,T\}\) [8,9,10]. More results on the harmonic index can be found in [3, 13, 14, 17, 18].

In this paper, we extend the definition of F-product to \(S_t\)-product of graphs and give an upper bound for the harmonic index of F-product of graphs, where \(F\in \{S,S_t,R,Q,T\}\).

The harmonic index for F-products of graphs

First, we give an upper bound for the harmonic index of \(G_1[G_2]_F\) in terms of \(H(S(G_1))\), \(H(G_2)\), \(r(G_1)\) and \(r(G_2)\), where \(F\in \{S,S_t\}\).

Theorem 2.1

Let \(G_1\) and \(G_2\) be two graphs. Then

$$\begin{aligned}&H(G_1[G_2]_S) < \frac{1}{4} n_2 H(S(G_1)) + \frac{1}{4} n_1 H(G_2)\\&\qquad \qquad \qquad+ \frac{1}{4} \frac{m_2}{n_2} r(G_1) + n_2 m_1 r(G_2), \end{aligned}$$

where \(n_i=|V(G_i)|\) and \(m_i=|E(G_i)|\), \(i=1,2\).

Proof

Let \(\deg (u,v)=\deg _{G_1 [G_2]_S } (u,v)\) be the degree of a vertex (u, v) in \(G_1[G_2]_S\). By the definition of the harmonic index, we have

$$\begin{aligned} H(G_1 [G_2]_S)&\displaystyle = \sum _{u\in V(G_1)} \sum _{v_1v_2\in E(G_2)} \frac{2}{\deg (u,v_1)+\deg (u,v_2)}\\&\quad \displaystyle + \sum _{v_1\in V(G_2)}\sum _{v_2\in V(G_2)} \sum _{u_1u_2\in E(S(G_1))}\\&\quad \frac{2}{\deg (u_1,v_1)+\deg (u_2,v_2)}\\&\displaystyle =: \sum 1 +\sum 2. \end{aligned}$$

Then,

$$\begin{aligned} \displaystyle \sum 1&\displaystyle = \sum _{u\in V(G_1)} \sum _{v_1v_2\in E(G_2)}\\&\quad \frac{2}{ \left( n_2\deg _{G_1}(u) + \deg _{G_2}(v_1) \right) + \left( n_2\deg _{G_1}(u) + \deg _{G_2}(v_2) \right) }\\&\displaystyle = \sum _{u\in V(G_1)} \sum _{v_1v_2\in E(G_2)}\\&\quad \frac{2}{ 2 n_2 \deg _{G_1}(u) + \left( \deg _{G_2}(v_1) + \deg _{G_2}(v_2) \right) }. \end{aligned}$$

By Jensen’s inequality, for every \(u\in V(G_1)\) and \(v_1v_2 \in E(G_2)\), we have

$$\begin{aligned}&\frac{2}{2 n_2 \deg _{G_1}(u) + \left( \deg _{G_2}(v_1) + \deg _{G_2}(v_2) \right) } \nonumber \\& \le \frac{1}{4n_2} \frac{1}{\deg _{G_1}(u)} + \frac{1}{4} \frac{2}{\deg _{G_2}(v_1) + \deg _{G_2}(v_2) } , \end{aligned}$$
(2.1)

with equality if and only if \(2n_2 \deg _{G_1}(u) = \deg _{G_2}(v_1) + \deg _{G_2}(v_2)\).

So,

$$\begin{aligned} \displaystyle \sum 1&\displaystyle \le \frac{1}{4n_2} \sum _{u\in V(G_1)} \sum _{v_1v_2\in E(G_2)} \frac{1}{\deg _{G_1}(u)} \\&\quad + \frac{1}{4} \sum _{u\in V(G_1)} \sum _{v_1v_2\in E(G_2)} \frac{2}{\deg _{G_2}(v_1) + \deg _{G_2}(v_2) }\\&\displaystyle = \frac{1}{4n_2} \sum _{u\in V(G_1)} \left( m_2 \times \frac{1}{\deg _{G_1}(u)} \right) + \frac{1}{4} \sum _{u\in V(G_1)} H(G_2) \\&\displaystyle =\frac{1}{4} \frac{m_2}{n_2} r(G_1) + \frac{1}{4} n_1 H(G_2). \end{aligned}$$

Also,

$$\begin{aligned} \displaystyle \sum 2&=\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _{u_1u_2\in E(S(G_1))} \frac{2}{\deg (u_1,v_1)+\deg (u_2,v_2)}\\&= \displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(S(G_1)) \\ u_1 \in V(G_1),~ u_2 \in V(S(G_1))-V(G_1) \end{subarray}} \\&\quad \frac{2}{\deg (u_1,v_1)+\deg (u_2,v_2)}\\&= \displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(S(G_1)) \\ u_1 \in V(G_1),~ u_2 \in V(S(G_1))-V(G_1) \end{subarray}} \\&\quad \frac{2}{ \left( n_2 \deg _{G_1}(u_1) + \deg _{G_2}(v_1) \right) + 2n_2}\\&= \displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _{u_1\in V(G_1)} \\&\quad\frac{2\deg _{G_1}(u_1)}{ \left( n_2 \deg _{G_1}(u_1) + \deg _{G_2}(v_1) \right) + 2n_2}\\&= \displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _{u_1\in V(G_1)}\\&\quad \frac{2\deg _{G_1}(u_1)}{ n_2 \left( \deg _{G_1}(u_1) + 2 \right) + \deg _{G_2}(v_1)} . \end{aligned}$$

Similarly, for every \(u_1\in V(G_1)\) and every \(v_1 \in V(G_2)\), we have

$$\begin{aligned}&\frac{2}{ n_2 \left( \deg _{G_1}(u_1) + 2 \right) + \deg _{G_2}(v_1) }\nonumber \\ & \le \frac{1}{4n_2} \frac{2}{\deg _{G_1}(u_1) + 2}+ \frac{1}{2} \frac{1}{\deg _{G_2}(v_1)}, \end{aligned}$$
(2.2)

with equality if and only if \(n_2 \left( \deg _{G_1}(u_1) + 2 \right) = \deg _{G_2}(v_1)\).

Thus,

$$\begin{aligned} \displaystyle \sum 2&\displaystyle \le \frac{1}{4n_2} \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _{u_1\in V(G_1)} \frac{2\deg _{G_1}(u_1)}{\deg _{G_1}(u_1) + 2 } \\&\quad + \frac{1}{2} \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _{u_1\in V(G_1)} \frac{\deg _{G_1}(u_1)}{\deg _{G_2}(v_1) }\\&\displaystyle = \frac{1}{4n_2} \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} H(S(G_1)) \\&\quad + \frac{1}{2} \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \left( 2m_1 \times \frac{1}{\deg _{G_2}(v_1) } \right) \\&\displaystyle = \frac{1}{4} n_2 H(S(G_1)) + n_2 m_1 r(G_2). \end{aligned}$$

Therefore,

$$\begin{aligned}&\displaystyle H(G_1[G_2]_S) \le \frac{1}{4} n_2 H(S(G_1))+ \frac{1}{4} n_1 H(G_2) \\ &\qquad \qquad\qquad + \frac{1}{4} \frac{m_2}{n_2} r(G_1) + n_2 m_1 r(G_2). \end{aligned}$$

Moreover, equality holds in above inequality if and only if the inequalities (2.1) and (2.2) be equalities, i.e., \(G_1\) and \(G_2\) are \(k_1\)-regular and \(k_2\)-regular graphs, respectively, such that \(2 n_2 k_1=k_2+k_2\) and \(n_2(k_1+2)=k_2\), a contradiction. This completes the proof. \(\square\)

Example 2.2

For any \(n\ge 2\),

$$\begin{aligned} H(P_n [P_2]_S )&= \left( \frac{2}{3} +\frac{1}{5}(n-2) \right) + \left( \frac{16}{7}+ \frac{16}{9} (n-2) \right) \\ & = \frac{62}{21} + \frac{89}{45}(n-2). \end{aligned}$$

In the following, we extend the definition of F-product to \(S_t\)-product of graphs.

Definition 2.3

Let \(G_1\) and \(G_2\) be two graphs. The \(S_t\)-product \(G_1 [G_2]_{S_t}\) is a graph with vertex set \(V(S_t(G_1))\times V(G_2)\) in which two vertices \((u_1,v_1)\) and \((u_2,v_2)\) of \(G_1 [G_2] _{S_t}\) are adjacent if and only if \(\left[ u_1=u_2 \in V(G_1) ~{\text {and}} ~ v_1 v_2 \in E(G_2)\right]\) or \(\left[ u_1u_2\in E(S_t(G_1)) ~{\text {and}}~ v_1,v_2\right.\) \(\left. \in V(G_2)\right]\).

Similarly, we refer to the vertices in \(V(G_1)\) and \(V(S_t(G_1)) -V(G_1)\) as black vertices and white vertices, respectively.

\(P_4 [P_2]_{S_3}\) is shown in Fig. 2.

Fig. 2
figure 2

\(P_4 [P_2]_{S_3}\)

Full size image

Theorem 2.4

Let \(G_1\) and \(G_2\) be two graphs. Then

$$\begin{aligned}&H(G_1[G_2]_{S_t}) < \frac{1}{4} n_2 H(S(G_1)) + \frac{1}{4} n_1 H(G_2)+ \frac{1}{4} \frac{m_2}{n_2} r(G_1) \\ &\qquad\qquad \qquad + n_2 m_1 r(G_2) + \frac{1}{ 2} (t-1) n_2 m_1, \end{aligned}$$

where \(n_i=|V(G_i)|\) and \(m_i=|E(G_i)|\), \(i=1,2\).

Proof

Let \(\deg (u,v)=\deg _{G_1 [G_2]_{S_t}} (u,v)\) be the degree of a vertex (u, v) in \(G_1 [G_2]_{S_t}\). Then,

$$\begin{aligned} H(G_1 [ G_2]_{S_t} )&\displaystyle = \sum _{u\in V(G_1)} \sum _{v_1v_2\in E(G_2)}\\&\quad \frac{2}{\deg (u,v_1)+\deg (u,v_2)} \\&\quad \displaystyle + \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _{u_1u_2\in E(S_t(G_1))} \\&\quad\frac{2}{\deg (u_1,v_1)+\deg (u_2,v_2)} \\ &\displaystyle =: \sum 1 +\sum 2. \end{aligned}$$

By the proof of Theorem 2.1, one can get

$$\begin{aligned} \displaystyle \sum 1 \le \frac{1}{4} \frac{m_2}{n_2} r(G_1) + \frac{1}{4} n_1 H(G_2), \end{aligned}$$

with equality \(2n_2 \deg _{G_1}(u)= \deg _{G_2}(v_1) + \deg _{G_2}(v_2)\) for all \(u\in V(G_1)\) and \(v_1 v_2 \in E(G_2)\).

Note that

$$\begin{aligned} \displaystyle \sum 2 &=\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(S_t(G_1))\\ u_1 \in V(G_1),~ u_2 \in V(S_t(G_1))-V(G_1) \end{subarray}}\\&\quad \frac{2}{\deg (u_1,v_1)+\deg (u_2,v_2)}\\&\quad +\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(S_t(G_1))\\ u_1 , u_2 \in V(S_t(G_1))-V(G_1) \end{subarray}} \\&\quad \frac{2}{\deg (u_1,v_1)+\deg (u_2,v_2)}\\&=\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(S_t(G_1))\\ u_1 \in V(G_1),~ u_2 \in V(S_t(G_1))-V(G_1) \end{subarray}}\\&\quad\frac{2}{ \left( n_2 \deg _{G_1}(u_1) + \deg _{G_2}(v_1) \right) + 2n_2 }\\&\quad +\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)}\sum _ {\begin{subarray}{c} u_1u_2\in E(S_t(G_1)) \\ u_1 , u_2 \in V(S_t(G_1))-V(G_1)\end{subarray}} \\&\quad\frac{2}{ 2n_2 + 2n_2}\\&=\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(S(G_1)) \\ u_1 \in V(G_1),~ u_2 \in V(S(G_1))-V(G_1) \end{subarray}}\\&\quad \frac{2}{ \left( n_2 \deg _{G_1}(u_1) + \deg _{G_2}(v_1) \right) + 2n_2 }\\&\quad +\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \frac{1}{ 2n_2} m_1 (t-1)\\&=\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(S(G_1))\\ u_1 \in V(G_1),~ u_2 \in V(S(G_1))-V(G_1) \end{subarray}} \\&\quad\frac{2}{ \left( n_2 \deg _{G_1}(u_1) + \deg _{G_2}(v_1) \right) + 2n_2 } \\& \quad+\displaystyle \frac{1}{ 2} (t-1) n_2 m_1.\end{aligned}$$

According to the proof of Theorem 2.1, we have

$$\begin{aligned} \sum 2 \le \frac{1}{4} n_2 H(S(G_1)) + n_2 m_1 r(G_2) + \frac{1}{ 2} (t-1) n_2 m_1, \end{aligned}$$

with equality if and only if \(n_2 \left( \deg _{G_1}(u_1) +2 \right) =\deg _{G_2}(v_1)\) for all \(u_1\in V(G_1)\) and \(v_1 \in V(G_2)\).

Therefore,

$$\begin{aligned}&H(G_1 [G_2]_{S_t}) \le \frac{1}{4} n_2 H(S(G_1)) + \frac{1}{4} n_1 H(G_2)+ \frac{1}{4} \frac{m_2}{n_2} r(G_1) \\&\qquad \qquad\qquad+ n_2 m_1 r(G_2) + \frac{1}{ 2} (t-1) n_2 m_1 . \end{aligned}$$

One can see that equality in above inequality cannot occur. This completes the proof. \(\square\)

Example 2.5

For any \(n\ge 2\),

$$\begin{aligned} H(P_n [P_2]_{S_t} )&= \left( \frac{2}{3} +\frac{1}{5}(n-2) \right) \\&\quad + \left( \frac{16}{7}+ \frac{16}{9} (n-2) + (t-1)(n-1) \right) \\&= \frac{62}{21} + \frac{89}{45}(n-2) + (t-1)(n-1). \end{aligned}$$

In the following, we give an upper bound for the harmonic index of \(G_1[G_2]_R\) in terms of \(H(R(G_1))\), \(H(G_1)\), \(H(G_2)\), \(r(G_1)\) and \(r(G_2)\).

Theorem 2.6

Let \(G_1\) and \(G_2\) be two graphs. Then

$$\begin{aligned}&H(G_1 [G_2]_R ) < \frac{1}{4} n_2 H(R(G_1)) + \frac{1}{4} n_1 H(G_2)-\frac{5}{72} n_2 H(G_1) \\&\qquad \qquad \qquad + \frac{1}{8} \frac{m_2}{n_2} r(G_1) +\frac{13}{9} n_2 m_1 r(G_2) , \end{aligned}$$

where \(n_i=|V(G_i)|\) and \(m_i=|E(G_i)|\), \(i=1,2\).

Proof

Let \(\deg (u,v)=\deg _{G_1[G_2]_R } (u,v)\) be the degree of a vertex (u, v) in \(G_1[G_2]_R\). Then,

$$\begin{aligned} H(G_1 [G_2]_R)&\displaystyle = \sum _{u\in V(G_1)} \sum _{v_1v_2\in E(G_2)} \\&\quad\frac{2}{\deg (u,v_1)+\deg (u,v_2)} \\&\quad \displaystyle + \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _{u_1u_2\in E(R(G_1))} \\&\quad\frac{2}{\deg (u_1,v_1)+\deg (u_2,v_2)}\\&\displaystyle =: \sum 1 +\sum 2. \end{aligned}$$

Note that

$$\begin{aligned} \displaystyle \sum 1&\displaystyle = \sum _{u\in V(G_1)} \sum _{v_1v_2\in E(G_2)} \frac{2}{ \left( 2 n_2\deg _{G_1}(u) + \deg _{G_2}(v_1) \right) + \left( 2n_2\deg _{G_1}(u) + \deg _{G_2}(v_2) \right) }\\&\displaystyle = \sum _{u\in V(G_1)} \sum _{v_1v_2\in E(G_2)} \\&\quad\frac{2}{ 4n_2\deg _{G_1}(u) + \left( \deg _{G_2}(v_1) + \deg _{G_2}(v_2) \right) }. \end{aligned}$$

Similar to the proof of Theorem 2.1, one can get

$$\begin{aligned} \displaystyle \sum 1 \le \frac{1}{8} \frac{m_2}{n_2} r(G_1) + \frac{1}{4} n_1 H(G_2), \end{aligned}$$
(2.3)

with equality \(4n_2 \deg _{G_1}(u)= \deg _{G_2}(v_1) + \deg _{G_2}(v_2)\) for all \(u\in V(G_1)\) and \(v_1 v_2 \in E(G_2)\).

Also,

$$\begin{aligned} \displaystyle \sum 2&=\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ { u_1u_2\in E(G_1)} \\&\quad \frac{2}{\deg (u_1,v_1)+\deg (u_2,v_2)}\\&\quad +\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(R(G_1)) \\ u_1\in V(G_1) ,~ u_2 \in V(R(G_1))-V(G_1) \end{subarray}}\\&\quad \frac{2}{\deg (u_1,v_1)+\deg (u_2,v_2)}\\&\displaystyle =: \sum 2^{'} +\sum 2^{''}. \end{aligned}$$

Note that

$$\begin{aligned} \displaystyle \sum 2^{'}&\displaystyle = \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _{u_1u_2\in E(G_1)} \\&\quad \frac{2}{\deg (u_1,v_1)+\deg (u_2,v_2)} \\&\displaystyle = \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _{u_1u_2\in E(G_1)} \\&\quad \frac{2}{\left( 2n_2 \deg _{G_1}(u_1) + \deg _{G_2}(v_1) \right) + \left( 2n_2\deg _{G_1}(u_2) + \deg _{G_2}(v_2) \right) } \\&\displaystyle = \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _{u_1u_2\in E(G_1)} \\&\quad\frac{2}{ 2n_2\left( \deg _{G_1}(u_1) + \deg _{G_1}(u_2) \right) + \deg _{G_2}(v_1) + \deg _{G_2}(v_2) } . \end{aligned}$$

By Jensen’s inequality, for every \(u_1u_2\in E(G_1)\) and \(v_1,v_2 \in V(G_2)\), we have

$$\begin{aligned}&\frac{2}{ 2 n_2\left( \deg _{G_1}(u_1) + \deg _{G_1}(u_2) \right) + \deg _{G_2}(v_1) + \deg _{G_2}(v_2) } \nonumber \\& \le \frac{1}{18n_2} \frac{2}{\deg _{G_1}(u_1) + \deg _{G_1}(u_2) } +\frac{2}{9} \frac{1}{\deg _{G_2}(v_1) } + \frac{2}{9} \frac{1}{\deg _{G_2}(v_2)} , \end{aligned}$$
(2.4)

with equality if and only if \(2n_2 \left( \deg _{G_1 }(u_1 )+\deg _{G_1 }(u_2 ) \right) =\deg _{G_2} (v_1)=\deg _{G_2} (v_2)\).

So, \(\displaystyle \sum 2^{'} \le \frac{1}{18}n_2 H(G_1) +\frac{4}{9} m_1 n_2 r(G_2)\).

Finally,

$$\begin{aligned} \displaystyle \sum 2^{''}&\displaystyle = \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(R(G_1)) \\ u_1 \in V(G_1),~ u_2 \in V(R(G_1))-V(G_1) \end{subarray}}\\&\quad \frac{2}{\left( 2 n_2 \deg _{G_1}(u_1) + \deg _{G_2}(v_1) \right) + 2n_2 } \\&\displaystyle = \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(R(G_1)) \\ u_1 \in V(G_1),~ u_2 \in V(R(G_1))-V(G_1) \end{subarray}} \\&\quad\frac{2}{ 2 n_2 \left( \deg _{G_1}(u_1) + 1 \right) + \deg _{G_2}(v_1) } . \end{aligned}$$

By the similar argument as above, for every \(u_1 \in V(G_1 )\) and \(v_1 \in V(G_2 )\), we have

$$\begin{aligned}&\frac{2}{ 2 n_2 \left( \deg _{G_1}(u_1) + 1 \right) + \deg _{G_2}(v_1) } \nonumber \\& \le \frac{1}{4n_2} \frac{1}{ \deg _{G_1}(u_1) + 1 } + \frac{1}{2} \frac{1}{\deg _{G_2}(v_1)} , \end{aligned}$$
(2.5)

with equality if and only if \(2 n_2 \left( \deg _{G_1}(u_1) + 1 \right) = \deg _{G_2}(v_1)\).

Hence,

$$\begin{aligned} \displaystyle \sum 2^{''}&\displaystyle \le \frac{1}{4n_2}\sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {u_1\in V(G_1) } \frac{\deg _G(u_1)}{ \deg _{G_1}(u_1) + 1} \\&\quad + \frac{1}{2}\sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \left( 2m_1\times \frac{1}{\deg _{G_2}(v_1)} \right) \\&\displaystyle = \frac{1}{4} n_2 \left( H(R(G_1)) -\frac{1}{2} H(G_1) \right) + n_2 m_1 r(G_2). \end{aligned}$$

Therefore,

$$\begin{aligned}&H(G_1 [ G_2]_R) \le \frac{1}{4} n_2 H(R(G_1)) + \frac{1}{4} n_1 H(G_2)-\frac{5}{72} n_2 H(G_1) \\&\qquad \qquad\qquad + \frac{1}{8} \frac{m_2}{n_2} r(G_1) +\frac{13}{9} n_2 m_1 r(G_2) . \end{aligned}$$

Furthermore, equality holds in above inequality if and only if the inequalities (2.3), (2.4) and (2.5) be equalities, i.e., \(G_1\) and \(G_2\) are \(k_1\)-regular and \(k_2\)-regular graphs, respectively, such that \(4n_2 k_1=k_2+k_2\), \(2n_2(k_1+k_1)=k_2\) and \(2n_2(k_1+1)=k_2\), a contradiction. This completes the proof. \(\square\)

Example 2.7

For any \(n\ge 3\),

$$\begin{aligned} \displaystyle H(P_n [P_2]_R )&\displaystyle = \left( \frac{2}{5}+\frac{1}{9}(n-2) \right) + \left( \frac{8}{7}+ \frac{4}{9} (n-3) \right) \\&\quad +\left( \frac{16}{9}+ \frac{16}{13}(n-2) \right) \\&\displaystyle = \frac{1046}{315} +\frac{157}{117}(n-2) + \frac{4}{9} (n-3) . \end{aligned}$$

Now, we give an upper bound for the harmonic index of \(G_1[G_2]_Q\) in terms of \(H(Q(G_1))\), \(H(L(G_1))\), \(H(G_2)\), \(M_1(G_1)\), \(r(G_1)\) and \(r(G_2)\).

Theorem 2.8

Let \(G_1\) and \(G_2\) be two graphs. Then

$$\begin{aligned} H(G_1[ G_2]_Q)&\displaystyle < \frac{1}{4}n_2 H(Q(G_1)) +\frac{3}{16}n_2 H(L(G_1)) \\&\quad +\frac{1}{4} n_1 H(G_2) + \frac{3}{64}n_2 M_1(G_1)\\&\quad +\frac{1}{4} \frac{m_2}{n_2} r(G_1) + n_2 m_1 r(G_2) - \frac{3}{32}n_2 m_1, \end{aligned}$$

where \(n_i=|V(G_i)|\) and \(m_i=|E(G_i)|\), \(i=1,2\).

Proof

Let \(\deg (u,v)=\deg _{G_1[ G_2]_Q } (u,v)\) be the degree of a vertex (u, v) in \(G_1[G_2]_Q\). Then,

$$\begin{aligned} H(G_1 [G_2]_Q)&\displaystyle = \sum _{u\in V(G_1)} \sum _{v_1v_2\in E(G_2)} \\&\quad\frac{2}{\deg (u,v_1)+\deg (u,v_2)}\\&\quad \displaystyle + \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} ~\sum _{u_1u_2\in E(Q(G_1))} \\&\quad\frac{2}{\deg (u_1,v_1)+\deg (u_2,v_2)} \\&\displaystyle =: \sum 1 +\sum 2. \end{aligned}$$

Note that

$$\begin{aligned} \displaystyle \sum 1&\displaystyle = \sum _{u\in V(G_1)} \sum _{v_1v_2\in E(G_2)} \\&\quad\frac{2}{ \left( n_2\deg _{G_1}(u) + \deg _{G_2}(v_1) \right) + \left( n_2\deg _{G_1}(u) + \deg _{G_2}(v_2) \right) }\\&\displaystyle = \sum _{u\in V(G_1)} \sum _{v_1v_2\in E(G_2)} \\&\quad\frac{2}{ 2n_2 \deg _{G_1}(u) + \left( \deg _{G_2}(v_1) + \deg _{G_2}(v_2) \right) }. \end{aligned}$$

By the proof of Theorem 2.1, we have

$$\begin{aligned} \displaystyle \sum 1 \le \frac{1}{4} \frac{m_2}{n_2} r(G_1) + \frac{1}{4} n_1 H(G_2), \end{aligned}$$
(2.6)

with equality \(2n_2 \deg _{G_1}(u)= \deg _{G_2}(v_1) + \deg _{G_2}(v_2)\) for all \(u\in V(G_1)\) and \(v_1 v_2 \in E(G_2)\).

Also,

$$\begin{aligned} \displaystyle \sum 2&=\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(Q(G_1)) \\ u_1 \in V(G_1),~u_2 \in V(Q(G_1))-V(G_1) \end{subarray}}\\&\quad \frac{2}{\deg (u_1,v_1)+\deg (u_2,v_2)}\\&\quad +\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(Q(G_1)) \\ u_1 , u_2 \in V(Q(G_1))-V(G_1) \end{subarray}} \\&\quad\frac{2}{\deg (u_1,v_1)+\deg (u_2,v_2)}\\&=\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(Q(G_1))\\ u_1 \in V(G_1),~ u_2 \in V(Q(G_1))-V(G_1) \end{subarray}}\\&\quad \frac{2}{\left( n_2 \deg _{Q(G_1)}(u_1)+ \deg _{G_2} (v_1) \right) +n_2\deg _{Q(G_1)}(u_2)}\\&\quad +\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(Q(G_1)) \\ u_1 , u_2 \in V(Q(G_1))-V(G_1) \end{subarray}} \\&\quad\frac{2}{ n_2\deg _{Q(G_1)}(u_1) + n_2 \deg _{Q(G_1)}(u_2)}\\&=\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(Q(G_1)) \\ u_1 \in V(G_1),~ u_2 \in V(Q(G_1))-V(G_1) \end{subarray}} \\&\quad\frac{2}{ n_2 \left( \deg _{Q(G_1)}(u_1) + \deg _{Q(G_1)}(u_2) \right) +\deg _{G_2}(v_1) }\\&\quad +\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(Q(G_1)) \\ u_1 , u_2 \in V(Q(G_1))-V(G_1) \end{subarray}}\\&\quad \frac{2}{ n_2 \left( \deg _{Q(G_1)}(u_1) + \deg _{Q(G_1)}(u_2) \right) } . \end{aligned}$$

For every \(v\in V(G_2)\) and \(u_1u_2 \in E(Q(G_1))\) with \(u_1 \in V(G_1)\) and \(u_2 \in V(Q(G_1))-V(G_1)\), we have

$$\begin{aligned}&\frac{2}{ n_2 \left( \deg _{Q(G_1)}(u_1) + \deg _{Q(G_1)}(u_2) \right) +\deg _{G_2}(v_1)} \nonumber \\& \le \frac{1}{4 n_2} \frac{2}{\deg _{Q(G_1)}(u_1) + \deg _{Q(G_1)}(u_2)}+ \frac{1}{2}\frac{1}{\deg _{G_2}(v)} , \end{aligned}$$
(2.7)

with equality if and only if \(n_2 \left( \deg _{Q(G_1)}(u_1) + \deg _{Q(G_1)}(u_2) \right) = \deg _{G_2}(v_1)\).

Thus,

$$\begin{aligned}&\displaystyle \sum _ {\begin{subarray}{c} u_1u_2\in E(Q(G_1)) \\ u_1 \in V(G_1),~ u_2 \in V(Q(G_1))-V(G_1) \end{subarray}}\\&\quad \frac{2}{ n_2 \left( \deg _{Q(G_1)}(u_1) + \deg _{Q(G_1)}(u_2) \right) + \deg _{G_2}(v_1) }\\&\displaystyle \le \frac{1}{4n_2} \sum _ {\begin{subarray}{c} u_1u_2\in E(Q(G_1)) \\ u_1 \in V(G_1),~ u_2 \in V(Q(G_1))-V(G_1) \end{subarray}} \\&\quad\frac{2}{\deg _{Q(G_1)}(u_1) + \deg _{Q(G_1)}(u_2)}\\&\quad + \displaystyle \frac{1}{2} \sum _ {\begin{subarray}{c} u_1u_2\in E(Q(G_1)) \\ u_1 \in V(G_1),~ u_2 \in V(Q(G_1))-V(G_1) \end{subarray}} \frac{1}{\deg _{G_2}(v_1)}\\&\displaystyle = \frac{1}{4n_2} \sum _{u_1u_1'\in E(G_1)} \left( \frac{2}{\deg _{Q(G_1)}(u_1) + \deg _{Q(G_1)}(u_2)} + \frac{2}{\deg _{Q(G_1)}(u_2) + \deg _{Q(G_1)}(u_1')} \right) \\&\qquad {\text {(where }} u_2 {\text { is the vertex inserted into the edge }} u_1u_1' {\text { of }} G_1)\\&\quad +\displaystyle \frac{m_1}{\deg _{G_2}(v_1)} \\&\displaystyle = \frac{1}{4n_2} \left( H(Q(G_1)) - \sum _{ww'\in E(L(G_1))} \frac{2}{\deg _{Q(G_1)}(w) +\deg _{Q(G_1)}(w') } \right) + \frac{m_1}{\deg _{G_2}(v_1)}. \end{aligned}$$

So,

$$\begin{aligned} \displaystyle \sum 2&\le \displaystyle \frac{1}{4n_2} \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \left( H(Q(G_1)) - \sum _{ww'\in E(L(G_1))} \frac{2}{\deg _{Q(G_1)}(w) +\deg _{Q(G_1)}(w') } \right) \\&\quad + \displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \frac{m_1}{\deg _{G_2}(v_1)}\\&\quad + \displaystyle \frac{1}{n_2} \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(Q(G_1)) \\ u_1 , u_2 \in V(Q(G_1))-V(G_1) \end{subarray}} \frac{2}{\deg _{Q(G_1)}(u_1) + \deg _{Q(G_1)}(u_2)}\\&\displaystyle =\frac{1}{4}n_2 H(Q(G_1)) + n_2 m_1 r(G_2)\\&\quad \displaystyle -\frac{1}{4}n_2\sum _{ww'\in E(L(G_1))} \frac{2}{\deg _{Q(G_1)}(w) +\deg _{Q(G_1)}(w') }\\&\quad \displaystyle + n_2 \sum _ {u_1u_2 \in E(L(G_1)) } \frac{2}{\deg _{Q(G_1)}(u_1) + \deg _{Q(G_1)}(u_2)}\\&\displaystyle =\frac{1}{4}n_2 H(Q(G_1)) + n_2 m_1 r(G_2)\\&\quad+\frac{3}{4}n_2 \sum _{ww'\in E(L(G_1))} \frac{2}{\deg _{Q(G_1)}(w) +\deg _{Q(G_1)}(w') }\\&\displaystyle =\frac{1}{4}n_2 H(Q(G_1)) + n_2 m_1 r(G_2) \\&\quad +\frac{3}{4}n_2\sum _{ww'\in E(L(G_1))} \frac{2}{4+ \left( \deg _{L(G_1)}(w) +\deg _{L(G_1)}(w') \right) } . \end{aligned}$$

Similarly, one can verify that

$$\begin{aligned}&\sum _{ww'\in E(L(G_1))} \frac{2}{4+ \left( \deg _{L(G_1)}(w) +\deg _{L(G_1)}(w') \right) } \nonumber \\&\le \frac{1}{4} H(L(G_1)) +\frac{1}{16} M_1(G_1) -\frac{1}{8}m_1, \end{aligned}$$
(2.8)

with equality if and only if \(\deg _{L(G_1)}(w) +\deg _{L(G_1)} (w') =4\) for all \(ww'\in E(L(G_1))\).

Therefore,

$$\begin{aligned} H(G_1[ G_2]_Q)&\displaystyle \le \frac{1}{4}n_2 H(Q(G_1)) +\frac{3}{16}n_2 H(L(G_1)) \\&\quad +\frac{1}{4} n_1 H(G_2) + \frac{3}{64}n_2 M_1(G_1) \\&\quad \displaystyle +\frac{1}{4} \frac{m_2}{n_2} r(G_1) + n_2 m_1 r(G_2) - \frac{3}{32}n_2 m_1. \end{aligned}$$

Moreover, equality holds in above inequality if and only if the inequalities (2.6), (2.7) and (2.8) be equalities, i.e., \(G_1\) and \(G_2\) are \(k_1\)-regular and \(k_2\)-regular graphs, respectively, such that \(2n_2k_1=k_2+k_2\), \(n_2\left( k_1 +2k_1 \right) =k_2\) and \((2k_1-2)+(2k_1-2)=4\), a contradiction. This completes the proof. \(\square\)

Example 2.9

For any \(n\ge 4\),

$$\begin{aligned} H(P_n[ P_2]_Q)&\displaystyle = \left( \frac{2}{3}+\frac{1}{5}(n-2) \right) + \left( \frac{320}{99}+\frac{16}{13} (n-3) \right) \\&\quad + \left( \frac{8}{7} +\frac{1}{2}(n-4) \right) \\&\displaystyle = \frac{3494}{693}+\frac{1}{5}(n-2) +\frac{16}{13}(n-3)+ \frac{1}{2}(n-4). \end{aligned}$$

Finally, we give an upper bound for the harmonic index of \(G_1[G_2]_T\) in terms of \(H(T(G_1))\), \(H(L(G_1))\), \(H(G_1)\), \(H(G_2)\), \(M_1(G_1)\), \(r(G_1)\) and \(r(G_2)\).

Theorem 2.10

Let \(G_1\) and \(G_2\) be two graphs. Then

$$\begin{aligned} H(G_1 [G_2]_T)&< \frac{1}{4} n_2 H(T(G_1)) + \frac{3}{16} n_2 H(L(G_1)) \\&\quad + \frac{1}{4} n_1 H(G_2) -\frac{5}{72}n_2 H(G_1) \\&\quad + \frac{3}{64} n_2 M_1(G_1) + \frac{1}{8} \frac{m_2}{n_2} r(G_1)\\&\quad + \frac{13}{9}n_2 m_1 r(G_2) - \frac{3}{32}n_2 m_1, \end{aligned}$$

where \(n_i=|V(G_i)|\) and \(m_i=|E(G_i)|\), \(i=1,2\).

Proof

Let \(\deg (u,v)=\deg _{G_1 [G_2]_T} (u,v)\) be the degree of a vertex (u, v) in \(G_1 [ G_2]_T\). Then,

$$\begin{aligned} H(G_1 [ G_2]_T) &\displaystyle= \sum _{u\in V(G_1)} \sum _{v_1v_2\in E(G_2)} \frac{2}{\deg (u,v_1)+\deg (u,v_2)}\\& \displaystyle \quad+ \sum _{v_1\in V(G_2)}\sum _{v_2\in V(G_2)} \sum _{u_1u_2\in E(T(G_1))} \frac{2}{\deg (u_1,v_1)+\deg (u_2,v_2)}\\&\displaystyle = \sum _{u\in V(G_1)} \sum _{v_1v_2\in E(G_2)} \frac{2}{\deg (u,v_1)+\deg (u,v_2)}\\& \quad+\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ { u_1u_2\in E(G_1) } \frac{2}{\deg (u_1,v_1)+\deg (u_2,v_2)}\\& \quad+\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(T(G_1)) \\ u_1 \in V(G_1),u_2 \in V(T(G_1))-V(G_1) \end{subarray}} \frac{2}{\deg (u_1,v_1)+\deg (u_2,v_2)}\\& \quad+\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(T(G_1)) \\ u_1 , u_2 \in V(T(G_1))-V(G_1) \end{subarray}} \frac{2}{\deg (u_1,v_1)+\deg (u_2,v_2)}\\&\displaystyle = \sum _{u\in V(G_1)} \sum _{v_1v_2\in E(G_2)} \frac{2}{ 4n_2\deg _{G_1}(u) + \left( \deg _{G_2}(v_1) + \deg _{G_2}(v_2) \right) }\\& \quad+\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {u_1u_2\in E(G_1) } \frac{2}{ 2n_2\left( \deg _{G_1}(u_1)+ \deg _{G_1}(u_2)\right)+ \left( \deg _{G_2} (v_1) +\deg _{G_2} (v_2)\right) }\\& \quad +\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(T(G_1)) \\ u_1 \in V(G_1), u_2 \in V(T(G_1))-V(G_1) \end{subarray}}\frac{2}{ n_2 \left( \deg _{T(G_1)}(u_1) + \deg _{T(G_1)}(u_2) \right) + \deg _{G_2}(v_1) }\\& \quad+\displaystyle \sum _{v_1\in V(G_2)} \sum _{v_2\in V(G_2)} \sum _ {\begin{subarray}{c} u_1u_2\in E(T(G_1)) \\ u_1 , u_2 \in V(T(G_1))-V(G_1) \end{subarray}} \frac{2}{\deg _{T(G_1)}(u_1) + \deg _{T(G_1)}(u_2)} . \end{aligned}$$

By the similar argument as proof of Theorems 2.6 and 2.8, we have

$$\begin{aligned} H(G_1 [ G_2]_T)&\le \frac{1}{8} \frac{m_2}{n_2} r(G_1) + \frac{1}{4} n_1 H(G_2) \\&\quad +\frac{1}{18}n_2 H(G_1) +\frac{4}{9} n_2 m_1 r(G_2)\\&\quad + \frac{1}{4} n_2 H(T(G_1)) - \frac{1}{8} n_2H(G_1) + n_2 m_1 r(G_2)\\&\quad +\displaystyle \frac{3}{4} n_2 \left( \frac{1}{4} H(L(G_1)) + \frac{1}{16} M_1(G_1) -\frac{1}{8}m_1 \right) . \end{aligned}$$

So,

$$\begin{aligned} H(G_1 [G_2]_T)&\le \frac{1}{4} n_2 H(T(G_1)) + \frac{3}{16} n_2 H(L(G_1)) \\&\quad + \frac{1}{4} n_1 H(G_2) -\frac{5}{72}n_2 H(G_1)\\&\quad + \frac{3}{64} n_2 M_1(G_1) + \frac{1}{8} \frac{m_2}{n_2} r(G_1)\\&\quad + \frac{13}{9}n_2 m_1 r(G_2) - \frac{3}{32}n_2 m_1 . \end{aligned}$$

Moreover, equality holds in above inequality if and only if \(G_1\) and \(G_2\) be \(k_1\)-regular and \(k_2\)-regular graphs, respectively, such that \(4n_2k_1=k_2+k_2\), \(2n_2\left( k_1+k_1\right) =k_2\), \(n_2\left( 2k_1 +2k_1 \right) =k_2\) and \((2k_1-2)+(2k_1-2)=4\), a contradiction. This completes the proof. \(\square\)

Example 2.11

For any \(n\ge 4\),

$$\begin{aligned} H(P_n [P_2]_T)&= \left( \frac{2}{5}+\frac{1}{9}(n-2) \right) + \left( \frac{8}{7}+ \frac{4}{9} (n-3) \right)\\&\quad + \left( \frac{416}{165}+ \frac{16}{17}(n-3) \right) + \left( \frac{8}{7} +\frac{1}{2}(n-4) \right)\\&= \frac{6014}{1155}+ \frac{1}{9}(n-2)+\frac{212}{153}(n-3)+ \frac{1}{2}(n-4). \end{aligned}$$