Introduction

Weibull (W) distribution is one of the most important and well-recognized continuous probability models in research and also in teaching. It has become important because if you have right-skewed, left-skewed or symmetric data, you can use this distribution to model it. Moreover, the hazard rate of its can be constant, increasing or decreasing. That flexibility of W distribution and its generalizations has made many researchers using it into their data analysis in different fields such as medicine, pharmacy, engineering, reliability, industry, social sciences, economics and environmental. See for example, Mudholkar and Srivastara [41], Bebbington et al. [4], Sarhan and Apaloo [49], El-Gohary et al. [12, 13], El-Bassiouny et al. [9,10,11], El-Morshedy et al. [23, 30], Eliwa et al. [19, 21, 2], El-Morshedy and Eliwa [22], among others.

Sometimes, it is very difficult to measure the life length of a machine on a continuous scale, for example, on-off switching machines, bulb of photocopier device, etc. Thus, several discrete distributions have been derived by discretizing a known continuous distribution. See for example, Nakagawa and Osaki [42], Stein and Dattero [51], Roy [47, 48], Johnson et al. [31], Krishna and Pundir [35], Gomez-Deniz and Calderin-Ojeda [27], Farbod and Gasparian [26], Nekoukhou et al. [43], EL-Bassiouny and El-Morshedy [8, 1], El-Morshedy et al. [24], Eliwa and El-Morshedy [16], Emrah [25], among others.

Unfortunately, we cannot use the previous univariate models for modeling the bivariate data, and therefore, several authors aimed to propose bivariate models to discuss various phenomena in many fields. For bivariate continuous model, see Jose et al. [32], Kundu and Gupta [37], Sarhan et al. [50], Wagner and Artur [52], El- Bassiouny et al. [6], Rasool and Akbar [46], El-Gohary et al. [14], Mohamed et al. [40], Eliwa and El-Morshedy [17, 18], Eliwa et al. [20], among others. Whereas for bivariate discrete models, see Kocherlakota and Kocherlakota [34], Basu and Dhar [3], Kumar [36], Kemp [33], Lee and Cha [39], Nekoukhou and Kundu [44], Kundu and Nekoukhou [38], Eliwa and El-Morshedy [15], El-Bassiouny, et al. [7] among others. Although there are a large number of bivariate discrete models in studies, there still a needing to propose flexible models to analyze different types of data. In this paper, we propose a flexible model, in the so-called the bivariate exponentiated discrete Weibull (BEDsW) distribution. The proposed discrete model can be obtained from three independent exponentiated discrete Weibull (EDsW) distributions by using the maximization method as suggested by Lee and Cha [39].

The BEDsW distribution

Recently, Nekoukhou and Bidram [45] proposed a new three parameters distribution called the exponentiated discrete Weibull (EDsW) distribution. The CDF of the EDsW distribution is given by

$$\begin{aligned} F_{EDsW}(x;\alpha ,p,\beta )=[1-p^{(x+1)^{\alpha }}]^{\beta };\quad x\in {\mathbb {N}} _{\circ }, \end{aligned}$$
(1)

where \(\alpha ,\beta >0\), \(0<p<1\) and \( {\mathbb {N}} _{\circ }=\{0,1,2,\ldots \}\). The corresponding PMF of Equation (1) can be written as

$$\begin{aligned} f_{EDsW}\left( x;\alpha ,p,\beta \right) =[1-p^{(x+1)^{\alpha }}]^{\beta }-[1-p^{x^{\alpha }}]^{\beta };\quad x\in {\mathbb {N}} _{\circ }. \end{aligned}$$
(2)

For integer values of \(\beta \), Eq. (2) can be represented as

$$\begin{aligned} f_{EDsW}\left( x;\alpha ,p,\beta \right) =\overset{\infty }{\underset{k=1}{\sum }}(-1)^{k+1}\left( \begin{array}{c}{\beta }\\ {k}\end{array}\right) [p^{kx^{\alpha }}-p^{k(x+1)^{\alpha }}];\quad x\in {\mathbb {N}} _{\circ }. \end{aligned}$$
(3)

Table 1 presents some discrete distributions which can be obtained as special cases from the EDsW distribution.

Table 1 Special univariate models
Full size table

Suppose that \(V_{i};\)\(i=1,2,3\) are three independently distributed random variables which \(V_{i}\sim EDsW(\alpha ,p,\beta _{i})\). If \(X_{1}=\max \{V_{1},V_{3}\}\) and \(X_{2}=\max \{V_{2},V_{3}\}\), then the bivariate vector \({\mathbf {X}}=(X_{1},X_{2})\) has the BEDsW distribution with parameter vector \({\boldsymbol{\Omega }}=(\alpha ,p,\beta _{1},\beta _{2},\beta _{3})\). The joint CDF of \({\mathbf {X}}\) is given by

$$\begin{aligned} F_{X_{1},X_{2}}(x_{1},x_{2})&=P(V_{1}\le x_{1},V_{2}\le x_{2},V_{3} \le \min \{x_{1},x_{2}\}) \\&=F_{EDsW}(x_{1};\alpha ,p,\beta _{1}) \\&\quad F_{EDsW}(x_{2};\alpha ,p,\beta _{2})F_{EDsW}(z;\alpha ,p,\beta _{3}) \\&=\left\{ \begin{array}{ll} F_{1}(x_{1},x_{2})&\quad {\text {if}}\; x_{1}<x_{2}\\ F_{2}(x_{1},x_{2})&\quad {\text {if}}\; x_{2}<x_{1}\\ F_{3}(x)&\quad {\text {if}}\; x_{1}=x_{2}=x, \end{array} \right. \end{aligned}$$
(4)

where

$$\begin{aligned} F_{1}(x_{1},x_{2})&= F_{EDsW}(x_{1};\alpha ,p,\beta _{1}+\beta _{3})F_{EDsW} (x_{2};\alpha ,p,\beta _{2}), \\ F_{2}(x_{1},x_{2})&= F_{EDsW}(x_{1};\alpha ,p,\beta _{1})F_{EDsW}(x_{2} ;\alpha ,p,\beta _{2}+\beta _{3}) \end{aligned}$$

and

$$\begin{aligned} F_{3}(x)=F_{EDsW}(x;\alpha ,p,\beta _{1}+\beta _{2}+\beta _{3}) \end{aligned}$$

and \(z=\min \{x_{1},x_{2}\}.\) The marginal CDF of \(X_{i}\), \((i=1,2)\) can be written as

$$\begin{aligned} F_{X_{i}}(x_{i})=P(\max \{V_{i},V_{3}\}\le x_{i})=F_{EDsW}(x_{i} ;\alpha ,p,\beta _{i}+\beta _{3});\quad x_{i}\in {\mathbb {N}} _{\circ }. \end{aligned}$$
(5)

The corresponding marginal probability mass function (PMF) to Equation (5) can be proposed as

$$\begin{aligned} f_{X_{i}}(x_{i})=f_{EDsW}(x_{i};\alpha ,p,\beta _{i}+\beta _{3});\quad x_{i}\in {\mathbb {N}} _{\circ }. \end{aligned}$$
(6)

The joint PMF of the bivariate vector \({\mathbf {X}}\) can be easily obtained by using the following relation

$$\begin{aligned}&f_{X_{1},X_{2}}(x_{1},x_{2})=F_{X_{1},X_{2}}(x_{1},x_{2})-F_{X_{1},X_{2} }(x_{1}-1,x_{2}) \\&-F_{X_{1},X_{2}}(x_{1},x_{2}-1)+F_{X_{1},X_{2}}(x_{1} -1,x_{2}-1). \end{aligned}$$
(7)

Thus, the corresponding joint PMF to Eq. (4) can be written as

$$\begin{aligned} f_{X_{1},X_{2}}(x_{1},x_{2})=\left\{ \begin{array}{ll} f_{1}(x_{1},x_{2})&\quad {\text {if}}\; x_{1}<x_{2}\\ f_{2}(x_{1},x_{2})&\quad {\text {if}}\; x_{2}<x_{1}\\ f_{3}(x) &\quad {\text {if}}\;x_{1}=x_{2}=x, \end{array} \right. \end{aligned}$$
(8)

where

$$\begin{aligned} f_{1}(x_{1},x_{2})&= f_{EDsW}(x_{1};\alpha ,p,\beta _{1}+\beta _{3})f_{EDsW} (x_{2};\alpha ,p,\beta _{2}), \\ f_{2}(x_{1},x_{2})&= f_{EDsW}(x_{1};\alpha ,p,\beta _{1})f_{EDsW} (x_{2};\alpha ,p,\beta _{2}+\beta _{3}) \end{aligned}$$

and

$$\begin{aligned} f_{3}(x)\text { }=p_{1}f_{EDsW}(x;\alpha ,p,\beta _{2}+\beta _{3})-p_{2} f_{EDsW}(x;\alpha ,p,\beta _{2}), \end{aligned}$$

with \(p_{1}=[1-p^{(x+1)^{\alpha }}]^{\beta _{1}}\) and \(p_{2}=[1-p^{x^{\alpha } }]^{\beta _{1}+\beta _{3}}\). Figure 1 shows the scatter plot of the joint PMF of the BEDsW distribution for various values of the parameters.

Fig. 1
figure 1

The joint PMF of the BEDsW distribution for different values of \({\boldsymbol{\Omega }}\): a\({\boldsymbol{\Omega }}=(0.9,0.9,0.3,3.3,2)\), b \({\boldsymbol{\Omega }}=(0.5,0.9,0.3,3.3,2)\) and c\({\boldsymbol{\Omega }}=(0.5,0.6,0.3,3.3,2)\)

Full size image

As expected, the joint PMF of the BEDsW distribution can take various shapes depending on the values of its parameter vector \({\boldsymbol{\Omega }}.\) Suppose \((X_{j1},X_{j2})\)\(\sim \ \)BEDsW\((\alpha ,p,\beta _{j1},\beta _{j2} ,\beta _{j3})\) for \(j=1,\ldots ,n\), and they are independently distributed. If \(Z_{1}=\max \{x_{11},\ldots ,x_{n1}\}\) and \(Z_{2}=\max \{x_{12},\ldots ,x_{n2}\}\), then

$$\begin{aligned} (Z_{1},Z_{2})\sim \text {BEDsW}\left( \alpha ,p,\overset{n}{\underset{j=1}{\sum }}\beta _{j1},\overset{n}{\underset{j=1}{\sum }}\beta _{j2},\overset{n}{\underset{j=1}{\sum }}\beta _{j3}\right) . \end{aligned}$$
(9)

The joint survival function (SF) of the random vector \({\mathbf {X}}\) can be defined as

$$\begin{aligned} S_{X_{1},X_{2}}(x_{1},x_{2})=1-F_{X_{1}}(x_{1})-F_{X_{2}}(x_{2})+F_{X_{1} ,X_{2}}(x_{1},x_{2}). \end{aligned}$$
(10)

Thus, the joint SF of the BEDsW distribution is given by

$$\begin{aligned} S_{X_{1},X_{2}}(x_{1},x_{2})=\left\{ \begin{array}{ll} S_{1}(x_{1},x_{2})&\quad {\text {if}}\,x_{1}<x_{2}\\ S_{2}(x_{1},x_{2})&\quad {\text {if}}\,x_{2}<x_{1}\\ S_{3}(x)&\quad {\text {if}}\,x_{1}=x_{2}=x, \end{array} \right. \end{aligned}$$
(11)

where

$$\begin{aligned} S_{1}(x_{1},x_{2})&= 1-\text { }\left[ 1-p^{(x_{2}+1)^{\alpha }}\right] ^{\beta _{2}+\beta _{3}}\\&-\left[ 1-p^{(x_{1}+1)^{\alpha }}\right] ^{\beta _{1}+\beta _{3}}\left( 1-\left[ 1-p^{(x_{2}+1)^{\alpha }}\right] ^{\beta _{2} }\right) , \\ S_{2}(x_{1},x_{2})&= 1-\left[ 1-p^{(x_{1}+1)^{\alpha }}\right] ^{\beta _{1}+\beta _{3}}\\&-\left[ 1-p^{(x_{2}+1)^{\alpha }}\right] ^{\beta _{2}+\beta _{3}}\left( 1-\left[ 1-p^{(x_{1}+1)^{\alpha }}\right] ^{\beta _{1}}\right) \end{aligned}$$

and

$$\begin{aligned} S_{3}(x)=1-\left[ 1-p^{(x+1)^{\alpha }}\right] ^{\beta _{3}}\left( \left[ 1-p^{(x+1)^{\alpha }}\right] ^{\beta _{1}}+\left[ 1-p^{(x+1)^{\alpha }}\right] ^{\beta _{2}}-\left[ 1-p^{(x+1)^{\alpha }}\right] ^{\beta _{1}+\beta _{2} }\right) . \end{aligned}$$

If \({\mathbf {X}}\)\(\sim \) BEDsW\(\left( {\boldsymbol{\Omega }}\right) \), then the stress–strength reliability can be expressed as

$$\begin{aligned}&P(X_{1}<X_{2})=\overset{\infty }{\underset{i=0}{\sum }}\{[1-p^{(i+2)^{\alpha } }]^{\beta _{2}} \\&\quad -[1-p^{(i+1)^{\alpha }}]^{\beta _{2}}\}[1-p^{(i+1)^{\alpha } }]^{\beta _{1}+\beta _{3}}. \end{aligned}$$
(12)

The joint hazard rate function (HRF) can be written as

$$\begin{aligned} h_{X_{1},X_{2}}(x_{1},x_{2})=\left\{ \begin{array}{ll} h_{1}(x_{1},x_{2})&\quad {\text {if}}\,x_{1}<x_{2}\\ h_{2}(x_{1},x_{2})&\quad {\text {if}}\,x_{2}<x_{1}\\ h_{3}(x)&\quad {\text {if}}\,x_{1}=x_{2}=x, \end{array} \right. \end{aligned}$$
(13)

where \(h_{i}(x_{1},x_{2})=\frac{f_{i}(x_{1},x_{2})}{S_{i}(x_{1-1},x_{2} -1)};i=1,2\ \) and \(h_{3}(x)=\frac{f_{3}(x)}{S_{3}(x-1)}\). The scatter plot of the joint HRF of the BEDsW distribution is shown in Fig. 2.

Fig. 2
figure 2

The joint HRF of the BEDsW distribution for different values of \({\boldsymbol{\Omega }}\): a\({\boldsymbol{\Omega }}=(1.5,0.9,0.3,0.3,0.3)\), b\({\boldsymbol{\Omega }}=(1.5,0.5,0.3,0.3,0.3)\) and c\({\boldsymbol{\Omega }}=(1.3,0.5,0.7,0.7,0.7)\)

Full size image

It is observed that the joint HRF of the proposed model can take various shapes depending on the model parameters which makes this model more flexible to fit different data sets.

Statistical properties

The positive quadrant dependent (PQD) and total positivity of order two (TP2) properties

Assume \({\mathbf {X}}\)\(\sim \) BEDsW\(\left( {\boldsymbol{\Omega }}\right) \), then \(X_{1}\) and \(\ X_{2}\) are PQD for some values of \(x_{1}\) and \(x_{2}\) where

$$\begin{aligned} F_{X_{1},X_{2}}(x_{1},x_{2};{\boldsymbol{\Omega }})\ge F_{EDsW}(x_{1};\alpha ,p,\beta _{1}+\beta _{3})F_{EDsW}(x_{2};\alpha ,p,\beta _{2}+\beta _{3}). \end{aligned}$$
(14)

Further, for every pair of increasing functions \(f_{X_{1}}(.)\) and \(f_{X_{2} }(.)\), we get \(Cov\left\{ f_{X_{1}}(X_{1}),f_{X_{2}}(X_{2})\right\} \ge 0\). Let us recall that the function \(\varUpsilon (p,q):R\times R\rightarrow R\) is said to have TP2 property if \(\varUpsilon (p,q)\) satisfies

$$\begin{aligned} \varUpsilon (p_{1},q_{1})\times \varUpsilon (p_{2},q_{2)}\ge \varUpsilon (p_{2} ,q_{1})\times \varUpsilon (p_{1},q_{2}), \end{aligned}$$
(15)

for all \(p_{1},q_{1},p_{2},q_{2}\in R\). Assume \(x_{11},x_{21},x_{12},x_{22} \in \mathbf { {\mathbb {N}} }_{0}\) and \(x_{11}<x_{21}<x_{12}<x_{22}\) from \({\mathbf {X}}\)\(\sim \) BEDsW\(\left( {\boldsymbol{\Omega }}\right) \), then the joint SF of \({\mathbf {X}}\) satisfies the TP2 property for some values of \(x_{1}\) and \(x_{2}\) where

$$\begin{aligned} \frac{S_{X_{1},X_{2}}(x_{11},x_{21})\times S_{X_{1},X_{2}}(x_{12},x_{22} )}{S_{X_{1},X_{2}}(x_{12},x_{21})\times S_{X_{1},X_{2}}(x_{11},x_{22})}\ge 1. \end{aligned}$$
(16)

Similarly, when \(x_{11}=x_{21}<x_{12}<x_{22},\)\(x_{21}<x_{11}<x_{12}<x_{22}\), etc.

The joint probability generating function (PGF)

If \(\ {\mathbf {X}}\thicksim \ \)BEDsW(\({\boldsymbol{\Omega }}\)), then the joint PGF can be expressed as

$$\begin{aligned}&G(u,v) =E(u^{X_{1}}v^{X_{2}})=\overset{\infty }{\underset{i=0}{\sum } }\underset{j=0}{\overset{\infty }{\sum }}P(X_{1}=i,X_{2}=j)u^{i}v^{j} \\&\quad \underset{i=0}{=\ \overset{\infty }{\sum }}\overset{\infty }{\underset{j=i+1}{\sum }}\underset{k=1}{\overset{\infty }{\sum }}\overset{\infty }{\underset{l=1}{\sum }}(-1)^{k+l}\left( {\begin{array}{c}\beta _{1}+\beta _{3}\\ k\end{array}}\right) \left( {\begin{array}{c}\beta _{2}\\ l\end{array}}\right) \left[ p^{ki^{\alpha }}-p^{k(i+1)^{\alpha }}\right] \left[ p^{kj^{\alpha }} -p^{k(j+1)^{\alpha }}\right] u^{i}v^{j} \\&\qquad + \underset{j=0}{\overset{\infty }{\sum }}\overset{\infty }{\underset{i=j+1}{\sum }}\underset{k=1}{\overset{\infty }{\sum }}\overset{\infty }{\underset{l=1}{\sum }}(-1)^{k+l}\left( {\begin{array}{c}\beta _{1}\\ k\end{array}}\right) \left( {\begin{array}{c}\beta _{2}+\beta _{3}\\ l\end{array}}\right) \left[ p^{ki^{\alpha }}-p^{k(i+1)^{\alpha }}\right] \left[ p^{lj^{\alpha }} -p^{l(j+1)^{\alpha }}\right] u^{i}v^{j} \\&\qquad +\underset{j=0}{\overset{\infty }{\ \sum }}\underset{i=0}{\overset{\infty }{\sum }}\underset{k=1}{\overset{\infty }{\sum }}(-1)^{j+k+l}\left( {\begin{array}{c}\beta _{1}\\ k\end{array}}\right) \left( {\begin{array}{c}\beta _{2}+\beta _{3}\\ j\end{array}}\right) p^{j(i+1)^{\alpha }} \left[ p^{ki^{\alpha } }-p^{k(i+1)^{\alpha }}\right] u^{i}v^{i} \\&\qquad - \underset{j=0}{\overset{\infty }{\sum }}\underset{i=0}{\overset{\infty }{\sum }}\underset{k=1}{\overset{\infty }{\sum }}(-1)^{j+k+l}\left( {\begin{array}{c}\beta _{1}+\beta _{3}\\ k\end{array}}\right) \left( {\begin{array}{c}\beta _{2}\\ j\end{array}}\right) p^{ji^{\alpha }} \left[ p^{ki^{\alpha } }-p^{k(i+1)^{\alpha }}\right] u^{i}v^{i}, \end{aligned}$$
(17)

where \(\left| v\right| <1.\) Hence, different moments and product moments of the BEDsW distribution can be obtained, as infinite series, using the joint PGF.

The conditional expectation (COEX) of \(X_{1}\ \)given \(X_{2}=x_{2}\)

If \(\ {\mathbf {X}}\thicksim \ \hbox {BEDsW}({\boldsymbol{\Omega }}\)), then the conditional PMF of \(\ X_{1}\mid X_{2}=x_{2},\) say \(f_{X_{1}\mid X_{2}=x_{2} }(x_{1}\mid x_{2}),\) is given by

$$\begin{aligned} f_{X_{1}\mid X_{2}=x_{2}}(x_{1}\mid x_{2})=\left\{ \begin{array}{ll} f_{1}(x_{1}\mid x_{2})&\quad {\text {if}}\;0\le x_{1}<x_{2}\\ f_{2}(x_{1}\mid x_{2})&\quad {\text {if}}\;0\le x_{2}<x_{1}\\ f_{3}(x_{1}\mid x_{2})&\quad {\text {if}}\;0\le x_{1} =x_{2}=x, \end{array} \right. \end{aligned}$$
(18)

where

$$\begin{aligned} f_{1}(x_{1} \mid x_{2})&=\frac{\left( [1-p^{(x_{1}+1)^{\alpha }}]^{\beta _{1}+\beta _{3}}-[1-p^{x_{1}^{\alpha }}]^{\beta _{1}+\beta _{3}}\right) \left( [1-p^{(x_{2}+1)^{\alpha }}]^{\beta _{2}}-[1-p^{x_{2}^{\alpha }}]^{\beta _{2} }\right) }{[1-p^{(x_{2}+1)^{\alpha }}]^{\beta _{2}+\beta _{3}}-[1-p^{x_{2} ^{\alpha }}]^{\beta _{2}+\beta _{3}}},\\ f_{2}(x_{1} \mid x_{2})&=[1-p^{(x_{1}+1)^{\alpha }}]^{\beta _{1}} -[1-p^{x_{1}^{\alpha }}]^{\beta _{1}} \end{aligned}$$

and

$$\begin{aligned} f_{3}(x_{1}\mid x_{2})=[1-p^{(x+1)^{\alpha }}]^{\beta _{1}}-\frac{[1-p^{x^{\alpha }}]^{\beta _{1}+\beta _{3}}\left( [1-p^{(x+1)^{\alpha }} ]^{\beta _{2}}-[1-p^{x^{\alpha }}]^{\beta _{2}}\right) }{[1-p^{(x+1)^{\alpha } }]^{\beta _{2}+\beta _{3}}-[1-p^{x^{\alpha }}]^{\beta _{2}+\beta _{3}}}. \end{aligned}$$

Therefore, the COEX of \(X_{1}\mid X_{2}=x_{2},\) say \({\mathbf {E}}(X_{1}\mid X_{2}=x_{2}),\) can be expressed as

$$\begin{aligned}&{\mathbf {E}}(X_{1} \mid X_{2}=x_{2})=\overset{\infty }{\underset{x_{1}=0}{\sum }}x_{1}f_{X_{1}\mid X_{2}=x_{2}}(x_{1}\mid x_{2}) \\&\quad =\overset{\infty }{\underset{x_{1}=x_{2}+1}{\sum }}x_{1}f_{1}(x_{1}\mid x_{2})+\overset{x_{2}-1}{\underset{x_{1}=0}{\sum }}x_{1}f_{2}(x_{1}\mid x_{2})+x_{2}f_{3}(x_{1}\mid x_{2}) \\&\quad =\frac{[1-p^{(x_{2}+1)^{\alpha }}]^{\beta _{2}}-[1-p^{x_{2}^{\alpha }} ]^{\beta _{2}}}{[1-p^{(x_{2}+1)^{\alpha }}]^{\beta _{2}+\beta _{3}}-[1-p^{x_{2} ^{\alpha }}]^{\beta _{2}+\beta _{3}}}\overset{\infty }{\underset{x_{1}=x_{2} +1}{\sum }}x_{1}\left( [1-p^{(x_{1}+1)^{\alpha }}]^{\beta _{1}+\beta _{3} }\right. \\&\qquad \left. -[1-p^{x_{1}^{\alpha }}]^{\beta _{1}+\beta _{3}}\right) \\&\qquad +\overset{x_{2}-1}{\underset{x_{1}=0}{\ \sum }}x_{1}\left( [1-p^{(x_{1} +1)^{\alpha }}]^{\beta _{1}}-[1-p^{x_{1}^{\alpha }}]^{\beta _{1}}\right) +x_{2}[1-p^{(x_{2}+1)^{\alpha }}]^{\beta _{1}} \\&\qquad -\frac{x_{2}[1-p^{x_{2}^{\alpha }}]^{\beta _{1}+\beta _{3}}\left( [1-p^{(x_{2}+1)^{\alpha }}]^{\beta _{2}}-[1-p^{x_{2}^{\alpha }}]^{\beta _{2} }\right) }{[1-p^{(x_{2}+1)^{\alpha }}]^{\beta _{2}+\beta _{3}}-[1-p^{x_{2} ^{\alpha }}]^{\beta _{2}+\beta _{3}}}. \end{aligned}$$
(19)

The conditional probability can be used in various areas, especially, in diagnostic reasoning and decision making. Table 2 lists the COEX for some specific parameter selections.

Table 2 The COEX for some specific parameter selections
Full size table

Maximum likelihood (ML) estimation

In this section, we use the method of the ML to estimate the unknown parameters \(\alpha ,p,\beta _{1},\beta _{2}\) and \(\beta _{3}\) of the BEDsW distribution. Suppose that, we have a sample of size n, of the form \(\left\{ (x_{11},x_{21}),(x_{12},x_{22}),\ldots ,(x_{1n},x_{2n})\right\} \) from the BEDsW distribution. We use the following notations: \(I_{1}=\{x_{1j} <x_{2j}\},\)\(I_{2}=\{x_{2j}<x_{1j}\},\)\(I_{3}=\{x_{1j}=x_{2j}=x_{j}\},\)\(I=I_{1}\cup I_{2}\cup I_{3},\)\(\left| I_{1}\right| =n_{1},\)\(\left| I_{2}\right| =n_{2},\)\(\left| I_{3}\right| =n_{3}\) and \(n=n_{1}+n_{2}+n_{3}.\) Based on the observations, the likelihood function is given by

$$\begin{aligned} l({\boldsymbol{\Omega }})=\underset{j=1}{\overset{n_{1}}{\prod }}f_{1}(x_{1j} ,x_{2j})\underset{j=1}{\overset{n_{2}}{\prod }}f_{2}(x_{1j},x_{2j} )\underset{j=1}{\overset{n_{3}}{\prod }}f_{3}(x_{j}). \end{aligned}$$

The log-likelihood function becomes

$$\begin{aligned} L({\boldsymbol{\Omega }})&=\overset{n_{1}}{\underset{j=1}{\sum }}\ln \left( g_{1}(x_{1j};\beta _{1}+\beta _{3})\right) +\overset{n_{1}}{\underset{j=1}{\sum }}\ln \left( g_{1}(x_{2j};\beta _{2})\right) \\&\quad +\overset{n_{2}}{\underset{j=1}{\sum }}\ln \left( g_{1}(x_{1j};\beta _{1})\right) +\overset{n_{2}}{\underset{j=1}{\sum }}\ln \left( g_{1}(x_{2j};\beta _{2} +\beta _{3})\right) \\&\quad +\overset{n_{3}}{\underset{j=1}{\sum }}\ln \left( [1-p^{(x_{j}+1)^{\alpha } }]^{\beta _{1}}g_{1}(x_{j};\beta _{2}+\beta _{3})\right. \\&\left. \quad -\,[1-p^{x_{j}^{\alpha }} ]^{\beta _{1}+\beta _{3}}g_{1}(x_{j}+1;\beta _{2})\right) , \end{aligned}$$
(20)

where \(g_{1}(x;\beta )=[1-p^{(x+1)^{\alpha }}]^{\beta }-[1-p^{x^{\alpha } }]^{\beta }.\) The ML estimation of the parameters \(\alpha ,p,\beta _{1},\beta _{2}\) and \(\beta _{3}\) can be obtained by computing the first partial derivatives of (20) with respect to \(\alpha ,p,\beta _{1},\beta _{2}\) and \(\beta _{3}\), and then putting the results equal zeros. We get the likelihood equations as in the following form

$$\begin{aligned} \frac{\partial L}{\partial \alpha }&=\overset{n_{1}}{\underset{j=1}{\sum } }\frac{g_{4}(x_{1j}+1;\beta _{1}+\beta _{3})-g_{4}(x_{1j};\beta _{1}+\beta _{3} )}{g_{1}(x_{1j};\beta _{1}+\beta _{3})} \\&\quad +\overset{n_{1}}{\underset{j=1}{\sum } }\frac{g_{4}(x_{2j}+1;\beta _{2})-g_{4}(x_{2j};\beta _{2})}{g_{1}(x_{2j} ;\beta _{2})} \\&\quad +\overset{n_{2}}{\underset{j=1}{\sum }}\frac{g_{4}(x_{1j}+1;\beta _{1} )-g_{4}(x_{1j};\beta _{1})}{g_{1}(x_{1j};\beta _{1})} \\&\quad +\overset{n_{2}}{\underset{j=1}{\sum }}\frac{g_{4}(x_{2j}+1;\beta _{2}+\beta _{3})-g_{4} (x_{2j};\beta _{2}+\beta _{3})}{g_{1}(x_{2j};\beta _{2}+\beta _{3})} \\&\quad +\overset{n_{3}}{\underset{j=1}{\sum }}\frac{[1-p^{(x_{j}+1)^{\alpha } }]^{\beta _{1}}\left( g_{4}(x_{j}+1;\beta _{2}+\beta _{3})-g_{4}(x_{j};\beta _{2}+\beta _{3})\right) +g_{4}(x_{j}+1;\beta _{1})g_{1}(x_{j};\beta _{2} +\beta _{3})}{[1-p^{(x_{j}+1)^{\alpha }}]^{\beta _{1}}g_{1}(x_{j};\beta _{2} +\beta _{3})-[1-p^{x_{j}^{\alpha }}]^{\beta _{1}+\beta _{3}}g_{1}(x_{j} +1;\beta _{2})} \\&\quad -\overset{n_{3}}{\underset{j=1}{\sum }}\frac{[1-p^{x_{j}^{\alpha }} ]^{\beta _{1}+\beta _{3}}\left( g_{4}(x_{j}+1;\beta _{2})-g_{4}(x_{j};\beta _{2})\right) +g_{4}(x_{j};\beta _{1}+\beta _{3})g_{1}(x_{j};\beta _{2} )}{[1-p^{(x_{j}+1)^{\alpha }}]^{\beta _{1}}g_{1}(x_{j};\beta _{2}+\beta _{3})-[1-p^{x_{j}^{\alpha }}]^{\beta _{1}+\beta _{3}}g_{1}(x_{j}+1;\beta _{2} )}, \end{aligned}$$
(21)
$$\begin{aligned} \frac{\partial L}{\partial p}&=\overset{n_{1}}{\underset{j=1}{\sum }} \frac{g_{3}(x_{1j}+1;\beta _{1}+\beta _{3})-g_{3}(x_{1j};\beta _{1}+\beta _{3} )}{g_{1}(x_{1j};\beta _{1}+\beta _{3})} \\&\quad +\overset{n_{1}}{\underset{j=1}{\sum } }\frac{g_{3}(x_{2j}+1;\beta _{2})-g_{3}(x_{2j};\beta _{2})}{g_{1}(x_{2j} ;\beta _{2})} \\&\quad +\overset{n_{2}}{\underset{j=1}{\sum }}\frac{g_{3}(x_{1j}+1;\beta _{1} )-g_{3}(x_{1j};\beta _{1})}{g_{1}(x_{1j};\beta _{1})} \\&\quad +\overset{n_{2}}{\underset{j=1}{\sum }}\frac{g_{3}(x_{2j}+1;\beta _{2}+\beta _{3})-g_{3} (x_{2j};\beta _{2}+\beta _{3})}{g_{1}(x_{2j};\beta _{2}+\beta _{3})} \\&\quad +\overset{n_{3}}{\underset{j=1}{\sum }}\frac{[1-p^{(x_{j}+1)^{\alpha } }]^{\beta _{1}}\left( g_{3}(x_{j}+1;\beta _{2}+\beta _{3})-g_{3}(x_{j};\beta _{2}+\beta _{3})\right) +g_{3}(x_{j}+1;\beta _{1})g_{1}(x_{j};\beta _{2} +\beta _{3})}{[1-p^{(x_{j}+1)^{\alpha }}]^{\beta _{1}}g_{1}(x_{j},;\beta _{2}+\beta _{3})-[1-p^{x_{j}^{\alpha }}]^{\beta _{1}+\beta _{3}}g_{1} (x_{j}+1;\beta _{2})} \\&\quad -\overset{n_{3}}{\underset{j=1}{\sum }}\frac{[1-p^{x_{j}^{\alpha }} ]^{\beta _{1}+\beta _{3}}\left( g_{3}(x_{j}+1;\beta _{2})-g_{3}(x_{j};\beta _{2})\right) +g_{3}(x_{j};\beta _{1}+\beta _{3})g_{1}(x_{j};\beta _{2} )}{[1-p^{(x_{j}+1)^{\alpha }}]^{\beta _{1}}g_{1}(x_{j};\beta _{2}+\beta _{3})-[1-p^{x_{j}^{\alpha }}]^{\beta _{1}+\beta _{3}}g_{1}(x_{j}+1;\beta _{2} )}, \end{aligned}$$
(22)
$$\begin{aligned} \frac{\partial L}{\partial \beta _{1}}&=\overset{n_{1}}{\underset{j=1}{\sum } }\frac{g_{2}(x_{1j}+1;\beta _{1}+\beta _{3})-g_{2}(x_{1j};\beta _{1}+\beta _{3} )}{g_{1}(x_{1j};\beta _{1}+\beta _{3})} \\&\quad +\overset{n_{2}}{\underset{j=1}{\sum } }\frac{g_{2}(x_{1j}+1;\beta _{1})-g_{2}(x_{1j},\beta _{1})}{g_{1}(x_{1j} ;\beta _{1})} \\&\quad +\overset{n_{3}}{\underset{j=1}{\sum }}\frac{g_{2}(x_{j}+1;\beta _{1} )g_{1}(x_{j};\beta _{2}+\beta _{3})-g_{2}(x_{j};\beta _{1}+\beta _{3})g_{1} (x_{j};\beta _{2})}{[1-p^{(x_{j}+1)^{\alpha }}]^{\beta _{1}}g_{1}(x_{j};\beta _{2}+\beta _{3})-[1-p^{x_{j}^{\alpha }}]^{\beta _{1}+\beta _{3}}g_{1} (x_{j}+1;\beta _{2})}, \end{aligned}$$
(23)
$$\begin{aligned} \frac{\partial L}{\partial \beta _{2}}&=\overset{n_{1}}{\underset{j=1}{\sum } }\frac{g_{2}(x_{2j}+1;\beta _{2})-g_{2}(x_{2j};\beta _{1})}{g_{1}(x_{2j} ;\beta _{2})} \\&\quad +\overset{n_{2}}{\underset{j=1}{\sum }}\frac{g_{2}(x_{2j} +1;\beta _{2}+\beta _{3})-g_{2}(x_{2j};\beta _{2}+\beta _{3})}{g_{1}(x_{2j} ;\beta _{2}+\beta _{3})} \\&\quad +\overset{n_{3}}{\underset{j=1}{\sum }}\frac{[1-p^{(x_{j}+1)^{\alpha } }]^{\beta _{1}}\left( g_{2}(x_{j}+1;\beta _{2}+\beta _{3})-g_{2}(x_{j};\beta _{2}+\beta _{3})\right) }{[1-p^{(x_{j}+1)^{\alpha }}]^{\beta _{1}}g_{1} (x_{j};\beta _{2}+\beta _{3})-[1-p^{x_{j}^{\alpha }}]^{\beta _{1}+\beta _{3} }g_{1}(x_{j}+1;\beta _{2})} \\&\quad -\overset{n_{3}}{\underset{j=1}{\sum }}\frac{[1-p^{x_{j}^{\alpha }} ]^{\beta _{1}+\beta _{3}}\left( g_{2}(x_{j}+1;\beta _{2})-g_{2}(x_{j};\beta _{2})\right) }{[1-p^{(x_{j}+1)^{\alpha }}]^{\beta _{1}}g_{1}(x_{j};\beta _{2}+\beta _{3})-[1-p^{x_{j}^{\alpha }}]^{\beta _{1}+\beta _{3}}g_{1} (x_{j}+1;\beta _{2})} \end{aligned}$$
(24)

and

$$\begin{aligned} \frac{\partial L}{\partial \beta _{3}}&=\overset{n_{1}}{\underset{j=1}{\sum } }\frac{g_{2}(x_{1j}+1;\beta _{1}+\beta _{3})-g_{2}(x_{1j};\beta _{1}+\beta _{3} )}{g_{1}(x_{1j};\beta _{1}+\beta _{3})} \\&\quad +\overset{n_{2}}{\underset{j=1}{\sum } }\frac{g_{2}(x_{2j}+1;\beta _{2}+\beta _{3})-g_{2}(x_{2j};\beta _{2}+\beta _{3} )}{g_{1}(x_{2j};\beta _{2}+\beta _{3})} \\&\quad +\overset{n_{3}}{\underset{j=1}{\sum }}\frac{[1-p^{(x_{j}+1)^{\alpha } }]^{\beta _{1}}\left( g_{2}(x_{j}+1;\beta _{2}+\beta _{3})-g_{2}(x_{j};\beta _{2}+\beta _{3})\right) -g_{2}(x_{j};\beta _{1}+\beta _{3})g_{1}(x_{j};\beta _{2})}{[1-p^{(x_{j}+1)^{\alpha }}]^{\beta _{1}}g_{1}(x_{j};\beta _{2}+\beta _{3})-[1-p^{x_{j}^{\alpha }}]^{\beta _{1}+\beta _{3}}g_{1}(x_{j}+1;\beta _{2} )}, \end{aligned}$$
(25)

where

$$\begin{aligned} g_{2}(x;\beta )&=[1-p^{x^{\alpha }}]^{\beta }\ln (1-p^{x^{\alpha }}),\\ g_{3}(x;\beta )&=-\beta x^{\alpha }p^{x^{\alpha }-1}[1-p^{x^{\alpha } }]^{\beta -1},\\ g_{4}(x;\beta )&=-\beta \ln (x)x^{\alpha }p^{x^{\alpha }}\ln (p)[1-p^{x ^{\alpha }}]^{\beta -1}. \end{aligned}$$

The ML estimation of the parameters \(\alpha ,\)p,  \(\beta _{1},\)\(\beta _{2} \) and \(\beta _{3}\) can be obtained by solving the above system of five nonlinear equations from (21) to (25). The solution of these equations is not easy to solve, so we need a numerical technique to get the ML estimators like the Newton–Raphson method.

Simulation

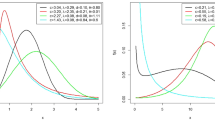
In this section, we estimate the bias and mean square error (MSE) for the proposed model parameters using simulations under complete sample. The population parameter is generated using software “R” package program. The sampling distributions are obtained for different sample sizes \(n=20,22,24,\ldots ,200\) from \(N=1000\) replications for different values of the model parameters. It is very useful in simulation study for EDsW distribution to know the following relation: If the continuous random variable Y has exponentiated Weibull (EW) distribution, say Y\(\sim EW(\alpha ,\lambda ,\beta ),\)\(\lambda =-\ln (p),\) then \(X=[Y]\sim EDsW(\alpha ,p,\beta ).\) So, to generate a random sample from the EDsW distribution, we first generate a random sample from a continuous EW distribution by using the inverse CDF method, and then by considering \(X=[Y], \) we find the desired random sample. The empirical results are shown in Figures 3 and 4 for BEDsW(0.4, 0.5, 0.8, 0.9, 1.3) and BEDsW(1.1, 0.2, 1.5, 1.5, 0.6), respectively.

Fig. 3
figure 3

The biases and MSEs when \({\boldsymbol{\Omega }}=(0.4,0.5,0.8,0.9,1.3)\)

Full size image
Fig. 4
figure 4

The biases and MSEs when \({\boldsymbol {\Omega}} =(1.1,0.2,1.5,1.5,0.6)\)

Full size image

It is clear that the bias and MSE are reduced as the sample size is increased. This shows the consistency of the estimators, and therefore, the ML method is a proper for estimating the model parameters.

Data analysis

In this section, we explain the experimental importance of the BEDsW distribution using two applications to real data sets. The tested distributions are compared using some criteria, namely, the maximized log-likelihood (\(-L\)), Akaike information criterion (AIC) (see [29]), and Hannan–Quinn information criterion (HQIC) (see [28]).

Data set I: football data

These data are reported in Lee and Cha [39], and it represents a football match score in Italian football match (Serie A) during 1996 to 2011, between ACF Fiorentina(\(X_{1}\)) and Juventus(\(X_{2}\)). We shall compare the fits of BEDsW distribution with some competitive models like BDsE, BDsR, BDsW, bivariate Poisson with minimum operator (BPo\(_{\min }\)), bivariate Poisson with three parameters (BPo-3P), independent bivariate Poisson (IBPo), bivariate discrete inverse exponential (BDsIE) and bivariate discrete inverse Rayleigh (BDsIR) distributions. Before trying to analyze the data by using the BEDsW distribution, we fit at first the marginals \(X_{1}\) and \(X_{2}\) separately and the \(\min (X_{1},X_{2})\) on these data. The ML estimation of the parameters \(\alpha ,p\) and \(\beta \) of the corresponding EDsW distribution for \(X_{1}\), \(X_{2}\) and \(\min (X_{1},X_{2})\) are (0.665, 0.059, 22.543), (1.974, 0.716, 1.673) and (0.722, 0.054, 20.223), respectively. Moreover, the \(-L\) values are 31.224, 31.735 and 28.265, respectively. Figure 5 shows the estimated PMF plots for the marginals \(X_{1} \), \(X_{2}\) and \(\min (X_{1},X_{2})\) by using data set I.

Fig. 5
figure 5

The estimated PMF for the marginals \(X_{1}\), \(X_{2}\) and \(\min (X_{1},X_{2})\) by using football data set

Full size image

From Figure 5, it is clear that EDsW distribution fits the data for the marginals. Now, we fit BEDsW distribution on these data. The ML estimators (MLEs), \(-L\), AIC and HQIC values for the tested bivariate models are reported in Table 3.

Table 3 The MLEs, \(-L\) , AIC and HQIC values
Full size table

From Table 3, it is clear that BEDsW distribution provides a better fit than the other tested distributions, because it has the smallest values among \(-L\), AIC and HQIC. Figure 6 shows the profiles of the L function, which indicate that the estimators are unique.

Fig. 6
figure 6

The profiles of the L function using football data set

Full size image

Figure 7 shows the estimated joint PMF for BEDsW, BDsW, BDsR and BDsE distributions by using data set I.

Fig. 7
figure 7

The estimated joint PMFs using football data set

Full size image

From Fig. 7, it is clear that the BEDsW model is the best among all tested models, which support the results of Table 3.

Data set II: nasal drainage severity score

These data are reported in Davis [5], and it represents the efficacy of steam inhalation in the treatment of common cold symptoms. We shall compare the fits of the BEDsW distribution with some competitive models like bivariate Poisson with four parameters (BPo-4P), IBPo, BDsE, BDsIE and BDsIR distributions. We fit at first the marginals \(X_{1}\) and \(X_{2}\) separately and the \(\min (X_{1},X_{2})\) on these data. The MLEs of the parameters \(\alpha ,p\) and \(\beta \) of the corresponding DsEW distribution for \(X_{1}\), \(X_{2}\) and \(\min (X_{1},X_{2})\) are (4.171, 0.981, 0.570), (1.857, 0.692, 1.658) and (2.906, 0.877, 0.766), respectively. Moreover, the \(-L\) values are 35.868, 37.804 and 34.047, respectively. Figure 8 shows the estimated PMF plots for the marginals \(X_{1}\), \(X_{2}\) and \(\min (X_{1},X_{2})\) by using data set II.

Fig. 8
figure 8

The estimated PMF for the marginals \(X_{1}\), \(X_{2}\) and \(\min (X_{1},X_{2})\) by using nasal drainage severity score

Full size image

It is clear that the EDsW distribution fits the data for the marginals. Now, we fit BEDsW distribution on these data. The MLEs, \(-L\), AIC and HQIC values for the tested bivariate models are reported in Table 4.

Table 4 The MLEs, \(-L\) , AIC and HQIC values
Full size table

From Table 4, it is clear that BEDsW distribution provides a better fit than the other tested distributions. Figure 9 shows the profiles of the L function.

Fig. 9
figure 9

The profiles of the L function using nasal drainage severity score

Full size image

Figure 10 shows the estimated joint PMF for BEDsW and BDsE distributions by using these data, which support the results of Table 4.

Fig. 10
figure 10

The estimated joint PMFs using nasal drainage severity score

Full size image

Conclusions

In this paper, we have introduced a new five parameters bivariate discrete distribution, in the so-called the bivariate exponentiated discrete Weibull distribution. Several of its statistical properties have been studied, and it is found that the marginals are positive quadrant dependent. Moreover, the joint reliability function satisfies the total positivity of order two for some values of \(x_{1}\) and \(x_{2}\). The maximum likelihood method has been used to estimate the model parameters. Simulation has been performed, and it is found that the maximum likelihood method works quite well in estimating the model parameters. Finally, two real data sets have been analyzed, and it is found that the proposed model provides better fit than other well-known discrete distributions like bivariate discrete Weibull, bivariate discrete Rayleigh, bivariate discrete exponential, bivariate Poisson with minimum operator, bivariate Poisson with three parameters, independent bivariate Poisson, bivariate discrete inverse exponential and bivariate discrete inverse Rayleigh distributions.