Introduction

Hyperbolic partial differential equations (HPDEs) constitute an important subclass of partial differential equations. The HPDEs are used in many disciplines of science and engineering, such as studying the transmission and propagation of electrical signals [1], wave propagation [2], hypoelastic solids [3], astrophysics [4], process engineering [5], acoustic transmission [6] and random walk theory [7]. The HPDEs are used in shaping the vibrational motion of structures (e.g., beams, machines and buildings) and represent basis for fundamental equations of atomic physics [8, 9]. Recently, the study of exact and numerical solutions of either hyperbolic or parabolic PDEs has received increasing attention [10,11,12,13,14,15].

Spectral techniques have been successfully applied for approximating the solution of differential problems defined in unbounded domains. For problems with sufficient smooth analytic solutions, they exhibit exponential rates of convergence, high accuracy and low computational cost. Doha et al. [16] used a Jacobi rational spectral technique for solving Lane–Emden initial value problems, in astrophysics, on a semi-infinite interval. Hafez et al. [17] applied a new collocation scheme for solving hyperbolic equations of second order in a semi-infinite domain. Doha et al. [18] proposed a new spectral Jacobi rational-Gauss collocation method for solving the multi-pantograph delay differential equations on the half line. Bhrawy et al. [19] solved some higher order ordinary differential equations using a new exponential Jacobi pseudospectral method.

In this study, we used exponential Jacobi functions for numerically solving the HPDEs. The operational matrices of derivatives and products of exponential Jacobi functions were derived. These matrices were jointly implemented with the collocation approach to evaluate the solutions of the HPDEs. Collocation method [20,21,22,23,24] is an effective technique for numerically approximating different kinds of equations.

The workflow of this paper encompass: In the next section, we present some notations and other mathematical facts. “Operational matrix of differentiation for exponential Jacobi” section is devoted to the operational matrix of differentiation for exponential Jacobi functions. In “Implementation of the method” section, the operational matrix of differentiation for exponential Jacobi was used in a combination with the exponential Jacobi collocation method to solve the HPDEs. The error analysis was executed in “Error analysis” section. Two numerical examples are given in “Numerical results” section. Finally, some concluding remarks are mentioned in “Conclusion” section.

Mathematical preliminaries

Here, we list some useful mathematical relations and identities needed in the construction of the exponential Jacobi operational matrix.

Exponential Jacobi functions

Consider the standard classical Jacobi polynomials \(J^{(\rho ,\sigma )}_k(z)\) on the interval \([-1,1]\) with the weight function \(\omega ^{(\rho ,\sigma )}(z)=(1-z)^{\rho }(1+z)^{\sigma }, \rho ,\sigma >-1\),

$$\begin{aligned} J^{(\rho ,\sigma )}_0(z)=1,\quad J^{(\rho ,\sigma )}_1(z)= \frac{1}{2} (\rho -\sigma +z (\rho +\sigma +2)), \end{aligned}$$

the set \(\{J^{(\rho ,\sigma )}_k(z):k=0,1,\ldots \}\) forms a complete orthogonal system in the weighted Hilbert space \(L_{\omega ^{\rho ,\sigma }(x)}^2[-1,1]\) equipped with the inner product

$$\begin{aligned} (f,g)_{\omega ^{(\rho ,\sigma )}(x)}:=\int _{-1}^{1}f(x)g(x)\omega ^{(\rho ,\sigma )}(x)dx, \end{aligned}$$

and the norm

$$\begin{aligned} \Vert f\Vert _{\omega ^{(\rho ,\sigma )}(x)}=(f,f)_{\omega ^{(\rho ,\sigma )}(x)}^{\frac{1}{2}}. \end{aligned}$$

Let us define the exponential Jacobi functions by replacing z by \(1-2 e^{-\frac{x}{L}}\). Denoting the exponential Jacobi functions \(J^{(\rho ,\sigma )}_i (1-2 e^{-\frac{x}{L}})\) by \(\Upsilon ^{(\rho ,\sigma )}_i(x)\), \(x\in [0,\infty )\). Therefore, \(\Upsilon ^{(\rho ,\sigma )}_i(x)\) may be generated by the following recurrence relation:

$$\begin{aligned}&\Upsilon ^{(\rho ,\sigma )}_{k+1}(x)=\frac{(2 k+\rho +\sigma +1) (2 k+\rho +\sigma +2)}{(k+1) (k+\rho +\sigma +1)} \\&\quad \left[ \left( \frac{((\rho +1) (\rho +\sigma )+2 k^2+2 k (\rho +\sigma +1))}{(2 k+\rho +\sigma )(2 k+\rho +\sigma +2)}-e^{-\frac{x}{L}}\right) \Upsilon ^{(\rho ,\sigma )}_{k}(x)\right. \\&\left. \quad -\frac{(k+\rho )( k+\sigma )}{(2 k+\rho +\sigma ) (2 k+\rho +\sigma +1)}\Upsilon ^{(\rho ,\sigma )}_{k-1}(x)\right] ,\quad k\ge 1, \end{aligned}$$
(1)

where

$$\begin{aligned} \Upsilon ^{(\rho ,\sigma )}_0(x)= 1,\quad \Upsilon ^{(\rho ,\sigma )}_1(x) = (\rho +1)-(\rho +\sigma +2) e^{-\frac{x}{L}}, \end{aligned}$$

and

$$\begin{aligned} (k+\rho +\sigma )\Upsilon _{i}^{(\rho ,\sigma )}(x)=(k+\sigma ) \Upsilon _{i}^{(\rho ,\sigma -1)}(x)+(k+\rho )\Upsilon _{i}^{(\rho -1,\sigma )}(x). \end{aligned}$$

The exponential Jacobi functions \(\Upsilon ^{(\rho ,\sigma )}_i(x)\) of degree i can be written as

$$\begin{aligned} \Upsilon ^{(\rho ,\sigma )}_i(x)=\sum \limits _{k=0}^{i}(-1)^k\frac{\Gamma (i+\rho +1)\Gamma (i+k+\rho +\sigma +1)}{\Gamma (\rho +k+1)\Gamma (i+\rho +\sigma +1)(i-k)!k!}exp(-k x/L), \end{aligned}$$

where

$$\begin{aligned} \Upsilon _{i}^{(\rho ,\sigma )}(0)=\frac{(-1)^{i}\ \Gamma (\sigma +i+1)}{i!\ \Gamma (\sigma +1)}. \end{aligned}$$
(2)

The set \(\{\Upsilon _{i}^{(\rho ,\sigma )}(x): i=0,1,\ldots \}\), satisfy the following orthogonality relation:

$$\begin{aligned} \displaystyle \int _0^{\infty }\Upsilon _{i}^{(\rho ,\sigma )}(x)\,\Upsilon _{j}^{(\rho ,\sigma )}(x)\,w^{(\rho ,\sigma )}\,dx=h^{(\rho ,\sigma )}_{i}\,\delta _{ij}, \end{aligned}$$
(3)

where

$$\begin{aligned} w^{(\rho ,\sigma )}&= e^{-\frac{\rho +1}{L}x}(1-e^{-\frac{x}{L}})^{\sigma },\\ h^{(\rho ,\sigma )}_{i}&= \displaystyle \frac{L\,\Gamma (i+\rho +1)\, \Gamma (i+\sigma +1)}{i!\,(2i+\rho +\sigma +1)\,\Gamma (i+\rho +\sigma +1)}, \end{aligned}$$

and \(\delta _{ij}\) is the well-known kronecker delta.

Function approximation

Now, approximation of u(x) by \(N+1\) terms of exponential Jacobi functions yields

$$\begin{aligned} u(x)\simeq \sum \limits _{j=0}^{N} c_j \Upsilon ^{(\rho ,\sigma )}_j(x)=\textbf{C}^{T}\phi (x), \end{aligned}$$
(4)

where C and \(\phi (x)\) are the unknown coefficients vector and the exponential Jacobi function vector, respectively, and are given by:

$$\begin{aligned}\textbf{ C}= [c_0,c_1,\ldots ,c_N]^{T},\end{aligned}$$
(5)
$$\begin{aligned} c_i= \frac{1}{h^{(\rho ,\sigma )}_{i}}\displaystyle \int _0^{\infty }u(x)\, \Upsilon _{i}^{(\rho ,\sigma )}(x)\,w^{(\rho ,\sigma )}\,dx, \end{aligned}$$
(6)

and

$$\begin{aligned} \phi (x)=[\Upsilon _{0}^{(\rho ,\sigma )}(x),\Upsilon _{1}^{(\rho ,\sigma )}(x), \ldots ,\Upsilon _{N}^{(\rho ,\sigma )}(x)]^{T}. \end{aligned}$$
(7)

Operational matrix of differentiation for exponential Jacobi

Here, we report the derivation of the operational matrix of derivatives of the exponential Jacobi functions, which is of important use to our numerical scheme.

Theorem 1

Let\(\phi (x)\)be the exponential Jacobi vector defined in (7). The derivative of the vector\(\phi (x)\)can be expressed by

$$\begin{aligned} \phi ^{\prime }(x)=\frac{d\phi (x)}{dx}\simeq \mathbf{D }\phi (x), \end{aligned}$$
(8)

where\(\mathbf{D }\)is \((N+1)\times (N+1)\)operational matrix of the derivative. Then, the nonzero elements\(d_{k\,\ell }\)for\(0\le k, \ell \le N\)are given as follows:

$$\begin{aligned} \begin{aligned} d_{k+1,k}&=\frac{(\rho +k+1)(\rho +\sigma +2k+1)}{L(\rho +\sigma +k+1)}, \quad d_{kk}=-\frac{k}{L},\\ d_{k\,\ell }&=\frac{(-1)^{k+\ell +1}(2\ell +\rho +\sigma +1)}{L} \prod \limits _{r=1}^{k-\ell } \frac{(\rho +k-r+1)}{(\rho +\sigma +k-r+1)},\quad \ell <k-1. \end{aligned} \end{aligned}$$

It easily noted that\(\mathbf{D }\)is a lower-Heisenberg matrix.

Proof

See, Bhrawy et al. [19].

Studying the class of exponential Jacobi functions yields many special orthogonal functions as a direct special cases, and these cases are reported in the following corollaries:

Corollary 1

(Legendre Case) If\(\rho = \sigma = 0\), then the nonzero elements, of the operational matrix of the exponential Legendre functions,\(d_{k\,\ell }\) for \(0\le k,\ell \le N\)are given as follows:

$$\begin{aligned} \begin{aligned} d_{k+1,k}&=\frac{2k+1}{L}, \quad d_{kk}=-\frac{k}{L},\\ d_{k\,\ell }&=(-1)^{k+\ell +1}\frac{(2 \ell +1)}{L},\quad \ell <k-1. \end{aligned} \end{aligned}$$

Corollary 2

(ChebyshevT Case) If\(\rho = \sigma =- \frac{1}{2}\), then the nonzero elements, of the operational matrix of the exponential Chebyshev functions of the first kind,\(d_{k\,\ell }\)for\(0\le k,\ell \le N\)are given as follows:

$$\begin{aligned} \begin{aligned} d_{k+1,k}&=\frac{2 k+1}{L}, \quad d_{kk}=-\frac{k}{L},\\ d_{k\,\ell }&=\frac{2(-1)^{k+\ell +1}\ell (k-\frac{1}{2})_{k-\ell }}{L(1-k)_{k-\ell }} ,\quad \ell <k-1. \end{aligned} \end{aligned}$$

Corollary 3

(ChebyshevU Case) If\(\rho = \sigma = \frac{1}{2}\), then the nonzero elements, of the operational matrix of the exponential Chebyshev functions of the second kind,\(d_{k\,\ell }\) for \(0\le k,\ell \le N\)are given as follows:

$$\begin{aligned} \begin{aligned} d_{k+1,k}&=\frac{(2k+3)(k+1)}{L(k+2)}, \quad d_{kk}=-\frac{k}{L},\\ d_{k\,\ell }&=\frac{2(-1)^{k+\ell +1}(\ell +1) \left( k-\frac{1}{2}\right) _{k-\ell }}{L(-k-1)_{k-\ell }},\quad \ell <k-1. \end{aligned} \end{aligned}$$

Corollary 4

(ChebyshevV Case) If\(\rho = -\frac{1}{2},\ \sigma = \frac{1}{2}\), then the nonzero elements\(d_{k\,\ell }\) for \(0\le k,\ell \le N\)are given as follows:

$$\begin{aligned} \begin{aligned} d_{k+1,k}&=\frac{(2 k+1)^{2} }{ 2L(k+1)}, \quad d_{kk}=-\frac{k}{L},\\ d_{k\,\ell }&=\frac{(2\ell +1) (-1)^{k+\ell +1} \Gamma (-k) \left( \frac{1}{2}-k\right) _{k-\ell }}{L\Gamma (-\ell )},\quad \ell <k-1. \end{aligned} \end{aligned}$$

Corollary 5

(ChebyshevW Case) If\(\rho = \frac{1}{2},\ \sigma =- \frac{1}{2}\), then the nonzero elements\(d_{k\,\ell }\)for\(0\le k,\ell \le N\)are given as follows:

$$\begin{aligned} \begin{aligned} d_{k+1,k}&=\frac{(2 k+3) (2 k+1)}{2L (k+1)}, \quad d_{kk}=-\frac{k}{L},\\ d_{k,\ell }&=\frac{2 (-1)^{k+\ell } \Gamma (-k) \Gamma \left( \frac{1}{2}-\ell \right) }{L\Gamma \left( -k-\frac{1}{2}\right) \Gamma (-\ell )},\quad \ell <k-1, \end{aligned} \end{aligned}$$

Remark 1

The operational matrix for r-th derivative can be derived as

$$\begin{aligned} \frac{d^r \phi (x)}{dx^r}=(\mathbf{D }^{(1)})^{r} \phi (x), \end{aligned}$$
(9)

where \(r \in N\) and the superscript in \({\mathbf{D }}^{(1)}\) denote matrix powers. Thus,

$$\begin{aligned} {\mathbf{D }}^{(r)}=({\mathbf{D }}^{(1)})^{r},\quad r=1,2,\ldots . \end{aligned}$$
(10)

Implementation of the method

The target of this part is to derive a scheme for the exponential Jacobi spectral collocation method based on the operational matrix of derivative of exponential Jacobi function to numerically solve the HPDEs on the half line. Let us consider the HPDEs of the form [25]

$$\begin{aligned} \frac{\partial v(x,t)}{\partial t}=\xi _1 \frac{\partial v(x,t)}{\partial x}+\xi _2 v(x,t) +\mathcal {S}(x,t),\ (x,t)\in [0,\infty )\times [0,\infty ), \end{aligned}$$
(11)

subject to the initial conditions

$$\begin{aligned} v(x,0)= k_0(x),\quad x\in [0,\infty ), \end{aligned}$$
(12)
$$\begin{aligned} v(0,t)= k_1(t),\quad t\in [0,\infty ). \end{aligned}$$
(13)

We approximate \(v(x,t),\ \frac{\partial v(x,t)}{\partial t}\) and \(\frac{\partial v(x,t)}{\partial x}\) by the double exponential Jacobi functions as

$$\begin{aligned} v(x,t)\approx v_{N,M}(x,t)&= \sum _{i=0}^{M}\sum _{j=0}^{N}c_{ij}\Upsilon _{i}^{(\rho _1,\sigma _1)}(x) \Upsilon _{j}^{(\rho _2,\sigma _2)}(t) \\&= \phi _{N}(t)\mathbf{C }^{T}\phi _{M}(x), \end{aligned}$$
(14)
$$\begin{aligned} \frac{\partial v_{N,M}(x,t)}{\partial t}&= \sum _{i=0}^{M}\sum _{j=0}^{N}c_{ij}\Upsilon _{i}^{(\rho _1,\sigma _1)}(x) \frac{\partial \Upsilon _{j}^{(\rho _2,\sigma _2)}(t)}{\partial t} \\ &= \phi _{N}^{'}(t)\mathbf{C }^{T}\phi _{M}(x), \end{aligned}$$
(15)
$$\begin{aligned} \frac{\partial v_{N,M}(x,t)}{\partial x}&= \sum _{i=0}^{M}\sum _{j=0}^{N}c_{ij}\frac{\partial \Upsilon _{i}^{(\rho _1,\sigma _1)}(x)}{\partial x} \Upsilon _{j}^{(\rho _2,\sigma _2)}(t) \\ &= \phi _{N}(t)\mathbf{C }^{T}\phi _{M}^{'}(x), \end{aligned}$$
(16)

where \(\mathbf{C }^{T}\) is \((N + 1)\times (M + 1)\) unknown matrix. Now, using Eqs. (14), (15) and (16), then it is easy to write

$$\begin{aligned} \phi _{N}^{'}(t)\mathbf{C }^{T}\phi _{M}(x)= \xi _1 \phi _{N}(t)\mathbf{C }^{T}\phi _{M}^{'}(x)+\xi _2 \phi _{N}(t)\mathbf{C }^{T}\phi _{M}(x) +\mathcal {S}(x,t), \end{aligned}$$
(17)
$$\begin{aligned} \phi _{N}(0)\mathbf{C }^{T}\phi _{M}(x)= k_0(x), \end{aligned}$$
(18)
$$\begin{aligned} \phi _{N}(t)\mathbf{C }^{T}\phi _{M}(0)= k_1(t), \end{aligned}$$
(19)

Now, we tame the collocation procedure for solving Eqs. (17)–(19). Suppose \(x^{(\rho _1,\sigma _1)}_{i}\ (\ 0\leqslant i\leqslant M)\) are the exponential Jacobi collocation points of \(\Upsilon _{i}^{(\rho _1,\sigma _1)}(x)\) and \(t^{(\rho _2,\sigma _2)}_{j}\ (0\leqslant j\leqslant N-1)\) are the exponential Jacobi collocation points of \(\Upsilon _{j}^{(\rho _2,\sigma _2)}(t)\). We substitute these collocation points in (17)–(19); therefore, the collocation scheme can be written as:

$$\begin{aligned}&\phi _{N}^{'}(t^{(\rho _2,\sigma _2)}_{j})\mathbf{C }^{T}\phi _{M} (x^{(\rho _1,\sigma _1)}_{i})=\xi _1 \phi _{N}(t^{(\rho _2,\sigma _2)}_{j})\mathbf{C }^{T}\phi _{M}^{'} (x^{(\rho _1,\sigma _1)}_{i}) \\ &\quad +\xi _2 \phi _{N}(t^{(\rho _2,\sigma _2)}_{j})\mathbf{C }^{T}\phi _{M} (x^{(\rho _1,\sigma _1)}_{i}) +\mathcal {S}(x^{(\rho _1,\sigma _1)}_{i},t^{(\rho _2,\sigma _2)}_{j}), \\ &\quad 1\le i\le M,\ 0\le j\le N-1. \end{aligned}$$
(20)
$$\begin{aligned}&\phi _{N}(0)\mathbf{C }^{T}\phi _{M}(x^{(\rho _1,\sigma _1)}_{i}) =k_0(x^{(\rho _1,\sigma _1)}_{i}) ,\ 0\le i\le M, \end{aligned}$$
(21)
$$\begin{aligned}&\phi _{N}(t^{(\rho _2,\sigma _2)}_{j})\mathbf{C }^{T}\phi _{M}(0) =k_1(t^{(\rho _2,\sigma _2)}_{j}),\quad 0\le j\le N-1. \end{aligned}$$
(22)

This yields a algebraic system of \((N + 1)\times (M + 1)\) equations in the required double exponential Jacobi coefficients \(c_{ij}, i=0,1,\ldots ,M;\,j=0,1,\ldots ,N,\) which can be solved by using any standard iteration technique, like Newton’s iteration solver. Consequently, the approximate solution \(v_{N,M}(x,t)\) can be evaluated.

Error analysis

Here, we discuss the convergence rate of the suggested double basis expansion, for this target, the following lemmas are needed:

Lemma 1

The following definite integral is valid:

$$\begin{aligned} \displaystyle \int _0^{\infty }\Upsilon _{i}^{(\rho ,\sigma )}(x)\,w^{(\rho +\mu +1,\sigma )} \,dx=\displaystyle \frac{L\,\Gamma (i+\sigma +1)\,\Gamma (\rho +\mu +1)\,(-\mu )_i}{i!\,\Gamma (i+\rho +\sigma +\mu +2)};\quad \rho +\mu>-1,\quad \sigma >-1, \end{aligned}$$

where \((a)_i\) denote the Pochhammer notation, i.e., \((a)_i=\Gamma (a+i)/\Gamma (a).\)

Lemma 2

For all\(\rho >-1\), there exist two generic constants\(0<\kappa _1<\kappa _2\)such that:

$$\begin{aligned} \kappa _1\,n^{\rho -1}\,n!\le \Gamma (n+\rho )\le \kappa _2\,n^{\rho -1}\,n!;\quad \forall n\in \mathbb {N}. \end{aligned}$$

Lemma 3

If\(\rho ,\sigma >-1\)then\(\mid \Upsilon _{i}^{(\rho ,\sigma )}(x)\mid \le J/i^q\)where\(q=\max (\rho ,\sigma ,-\frac{1}{2})\), whereJis a generic positive constant.

In this theorem, we ascertain the vanishing rate of the unknown expansion coefficients of the approximate solution, under certain constrains on the exact smooth solution of the solved problem.

Theorem 2

Ifv(x, t) is separable, i.e.,\(v(x,t)=v_1(x)\,v_2(t)\)and\(v_1, v_2\)are of exponential order, in the sense that, there exist\(A_1, A_2, \mu _1\)and\(\mu _2\)positive constants, such that\(|v_1(x)|\le A_1\,e^{-\mu _1\,x}\)and\(|v_2(t)|\le A_2\,e^{-\mu _2\,t}\), then the expansion coefficients in (14) satisfy the following estimate:

$$\begin{aligned} |c_{ij}|\le \displaystyle \frac{C}{i^{\rho _1+2\mu _1+1}\,j^{\rho _2+2\mu _2+1}}. \end{aligned}$$

Proof

By the hypothesis of theorem, we have,

$$\begin{aligned} v(x,t)=v_1(x)\,v_2(t)=\displaystyle \sum _{m=0}^{\infty }\displaystyle \sum _{k=0}^{\infty }c_{km}\,\Upsilon _{k}^{(\rho _1,\sigma _1)} (x)\,\Upsilon _{m}^{(\rho _2,\sigma _2)}(t), \end{aligned}$$

applying the inner product, and by the orthogonality relation (3), we get,

$$\begin{aligned} \left( v_1(x)\,v_2(t),\Upsilon _{i}^{(\rho _1,\sigma _1)}(x)\, \Upsilon _{j}^{(\rho _2,\sigma _2)}(t)\right) _{w^{(\rho _1,\sigma _1)} \,w^{(\rho _2,\sigma _2)}} =c_{ij}\,h^{(\rho _1,\sigma _1)}_{i}\,\,h^{(\rho _2,\sigma _2)}_{j}, \end{aligned}$$

i.e.,

$$\begin{aligned} c_{ij}&= \frac{1}{h_i^{(\rho _1,\sigma _1)}\,h_j^{(\rho _2,\sigma _2)}} \displaystyle \int _0^{\infty }\displaystyle \int _0^{\infty }v(x,t)\Upsilon _{i}^{(\rho _1,\sigma _1)}(x) \,\Upsilon _{j}^{(\rho _2,\sigma _2)}(t)\, w^{(\rho _1,\sigma _1)}\,w^{(\rho _2,\sigma _2)}\,dx\,dt \\ &= \frac{1}{h_i^{(\rho _1,\sigma _1)}\,h_j^{(\rho _2,\sigma _2)}} \left( \displaystyle \int _0^{\infty }v_1(x)\Upsilon _{i}^{(\rho _1,\sigma _1)}(x) \,w^{(\rho _1,\sigma _1)}\,dx\right) \left( \displaystyle \int _0^{\infty }v_2(t)\Upsilon _{j}^{(\rho _2,\sigma _2)}(t) \,w^{(\rho _2,\sigma _2)}\,dt\right) \\ &= I^{(\rho _1,\sigma _1)}_1(i)\,I^{(\rho _2,\sigma _2)}_2(j), \end{aligned}$$

where,

$$\begin{aligned} I^{(\rho _r,\sigma _r)}_r(k)=\frac{1}{h_k^{(\rho _r,\sigma _r)}} \displaystyle \int _0^{\infty }v_r(z)\Upsilon _{k}^{(\rho _r,\sigma _r)}(z)\,w^{(\rho _r,\sigma _r)} \,dz,\quad r=1,2. \end{aligned}$$

Now by application of integration by parts on \(I^{(\rho _1,\sigma _1)}_1(i)\) and \(I^{(\rho _2,\sigma _2)}_2(j)\), since \(v_1\) and \(v_2\) are of exponential order, by the integral formula in Lemma 1, repeated use of the estimate in Lemma 2 on \(I^{(\rho _1,\sigma _1)}_1(i)\) and \(I^{(\rho _2,\sigma _2)}_2(j)\), the theorem is proved. \(\square\)

In this theorem, based on the result of the previous theorem, we ascertain the convergence of the approximate solution as the number of retained modes increases.

Theorem 3

If\(\min (\rho _1+2\mu _1,\rho _2+2\mu _2)> \frac{1}{2}\)and\(-1<\max (\rho _1,\rho _2,\sigma _1,\sigma _2)<-\frac{1}{2}\), then series in (14) converges absolutely.

Proof

We show that the series \(|\displaystyle \sum _{0}^{\infty }\displaystyle \sum _{0}^{\infty }c_{ij}\,\Upsilon _{i}^{(\rho _1,\sigma _1)}(x) \,\Upsilon _{j}^{(\rho _2,\sigma _2)}(t)|\) converges absolutely.

By the estimate in Theorem 2, using Lemma 3, then

$$\begin{aligned} |c_{ij}\,\Upsilon _{i}^{(\rho _1,\sigma _1)}(x) \,\Upsilon _{j}^{(\rho _2,\sigma _2)}(t)|\le \frac{A}{i^{\rho _1+2\mu _1+\frac{1}{2}}\,j^{\rho _2+2\mu _2+\frac{1}{2}}}, \end{aligned}$$

which completes the proof of the theorem. \(\square\)

In this theorem, we control the estimate of two consecutive approximate solutions, to ascertain the stability when the number of retained modes increases.

Theorem 4

If\(\min (\rho _1+2\mu _1,\rho _2+2\mu _2)>\frac{1}{4}\)and\(-1<\max (\rho _1,\rho _2,\sigma _1,\sigma _2)<-\frac{1}{2}\), then

$$\begin{aligned} \displaystyle \lim _{N,M\rightarrow \infty }\Vert u_{N+1,M+1}-u_{N,M}\Vert _2=0. \end{aligned}$$

Proof

By the triangle inequality, we have,

$$\begin{aligned}&\Vert u_{N+1,M+1}-u_{N,M}\Vert _2=\Vert u_{N+1,M+1}-u_{N,M+1}+u_{N,M+1}-u_{N,M}\Vert _2\\&\quad \le \Vert u_{N+1,M+1}-u_{N,M+1}\Vert _2+\Vert u_{N,M+1}-u_{N,M}\Vert _2\\&\quad =\left\| \displaystyle \sum _{j=0}^{M+1}c_{N+1,j}\,\Upsilon _{N+1}^{(\rho _1,\sigma _1)}(x) \,\Upsilon _{j}^{(\rho _2,\sigma _2)}(t)\right\| _2\\&\qquad +\left\| \displaystyle \sum _{i=0}^{N} c_{i,M+1}\,\Upsilon _{i}^{(\rho _1,\sigma _1)}(x) \,\Upsilon _{M+1}^{(\rho _2,\sigma _2)}(t)\right\| _2. \end{aligned}$$

Now, application of Lemma 2, Lemma 3 to the two norms of the R.H.S of the later inequality, respectively, and by the result of Theorem 3, we get

$$\begin{aligned} \Vert u_{N+1,M+1}-u_{N,M}\Vert _2<\frac{B}{M^{2\rho _1+4\mu _1-\frac{1}{2}}\,\,N^{2\rho _2+4\mu _2-\frac{1}{2}}}, \end{aligned}$$

which completes the proof of the theorem. \(\square\)

Numerical results

In this section, we test our algorithm by exibiting two numerical experiments to check the applicability and accuracy of the proposed scheme. Comparison of the numerical results obtained by the suggested technique with those obtained by generalized Laguerre–Gauss–Radau collocation approach [25] confirms that the presented scheme is very effective and convenient. Thereby, we assert that the proposed scheme is more appropriate for solving these kinds of problems.

The absolute errors in the given tables are

$$\begin{aligned} E(x,t)=|v(x,t)-v_{N,M}(x,t)|, \end{aligned}$$
(23)

where v(x, t) and \(v_{N,M}(x,t)\) are the exact solution and the numerical solution, respectively, at the point (x, t), respectively. Moreover, the maximum absolute errors are given by

$$\begin{aligned} L^\infty =\text {Max}\{E(x,t):\forall (x,t)\in [0,\infty )\times [0,\infty )\}. \end{aligned}$$
(24)

Example 1

[25] Consider the hyperbolic equation of first-order of the form

$$\begin{aligned} \frac{\partial v(x,t)}{\partial t}= \frac{\partial v(x,t)}{\partial x}+v(x,t)+\mathcal {S}(x,t),\quad ,x\in [0,\infty ),\quad t\in [0,\infty ), \end{aligned}$$
(25)

subject to initial conditions,

$$\begin{aligned} v(x,0)=e^{-x},\quad x\in [0,\infty ),\quad v(0,t)=e^{-\sqrt{2}t},\quad t\in [0,\infty ), \end{aligned}$$

where

$$\begin{aligned} \mathcal {S}(x,t)=- \sqrt{2}e^{-\sqrt{2}t-x}. \end{aligned}$$

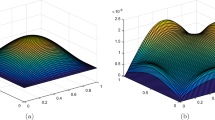
The exact solution is given by

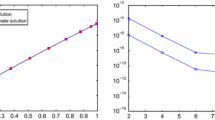
$$\begin{aligned} v(x,t)= e^{-(\sqrt{2}t+x)}. \end{aligned}$$

In Tables 1, 2 and 3, we give the absolute errors with \(\rho _1=\sigma _1=\rho _2= \sigma _2=-\frac{1}{2}\) (first kind exponential Chebyshev functions), \(\rho _1=\sigma _1=\rho _2= \sigma _2=0\) (exponential Legendre functions) and \(\rho _1=\sigma _1=\rho _2= \sigma _2=\frac{1}{2}\) (second kind exponential Chebyshev functions), respectively, at \(N=M=16\). Moreover, the results obtained by our method are compared with these obtained by generalized Laguerre–Gauss–Radau collocation method [25]. Figure 1 shows \(L^{\infty }\) error versus \(N = M\) and \(\rho _1=\sigma _1=\rho _2=\sigma _2\).

Table 1 Comparison of the absolute errors for Example 1 at \(t=0.1\) and \(N=M=16\)
Full size table
Table 2 Comparison of the absolute errors for Example 1 at \(t=0.5\) and \(N=M=16\)
Full size table
Table 3 Comparison of the absolute errors for Example 1 at \(t=1\) and \(N=M=16\)
Full size table
Fig. 1
figure 1

\(L^{\infty }\) error for Example 1 versus \(N = M\) and \(\rho _1=\sigma _1= \rho _2=\sigma _2\)

Full size image

Example 2

[25] Consider the following hyperbolic equation of first-order

$$\begin{aligned} \begin{aligned} \frac{\partial v(x,t)}{\partial t}&= \frac{\partial v(x,t)}{\partial x}+v(x,t)+e^{-t-x}(\cos (t)-\sin (t)),\,x\in [0,\infty ),\\&\quad t\in [0,\infty ), \end{aligned} \end{aligned}$$
(26)

subject to initial conditions,

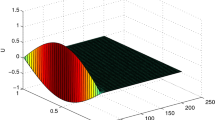
$$\begin{aligned} v(x,0)=0,\quad x\in [0,\infty ),\quad v(0,t)=e^{-t}\sin (t),\quad t\in [0,\infty ). \end{aligned}$$

The exact solution is given by

$$\begin{aligned} v(x,t)= e^{-(t+x)}\sin (t). \end{aligned}$$

Table 4 lists the results obtained by the our method in terms of absolute errors at \(N = M = 16\) for different values of \(\rho _1,\sigma _1,\rho _2,\sigma _2,x\) and t. Figure 2 shows the \(L^{\infty }\) error versus \(\rho _1=\sigma _1=\rho _2=\sigma _2\) and \(N=M\). Moreover, the results in Table 5 are more accurate if compared with these obtained by generalized Laguerre–Gauss–Radau collocation method [25].

Table 4 The absolute errors for Example 2 at \(N=M=16\)
Full size table
Table 5 Comparison of the maximum absolute errors for Example 2 versus \(\rho _1=\sigma _1,\ \rho _2=\sigma _2\) at \(N=M=16\)
Full size table
Fig. 2
figure 2

\(L^{\infty }\) error for Example 2 versus \(N = M\) and \(\rho _1=\sigma _1= \rho _2=\sigma _2\)

Full size image

Conclusion

We developed an accurate numerical technique and applied it to solve hyperbolic partial differential equations. The proposed operational matrix in combination with the exponential Jacobi spectral-collocation approach was elaborated for reducing the solution of hyperbolic first-order partial differential equations on the semi-infinite domain to an algebraic system of equations, which can be solved more easily. The operational matrices of derivatives of exponential Legendre, ChebyshevT, U, V, W functions can be obtained as direct special cases of the operational matrix of exponential Jacobi functions. The numerical results evince the high efficiency and accuracy of our approach.