Haar wavelet collocation method for solving singular and nonlinear fractional time-dependent Emden–Fowler equations with initial and boundary conditions

Abstract

In this paper, we have applied an iterative method to the singular and nonlinear fractional partial differential of Emden–Fowler equations types. Haar wavelets operational matrix of fractional integration will be used to solve the problem with the Picard technique. The singular equations turn to Sylvester equations that will be solved so that numerically solvable is very cost- effective. Moreover, the proposed technique is reliable enough to overcome the difficulty of the singular point at $x = 0$. Numerical examples are providing to illustrate the efficiency and accuracy of the technique.

Introduction

Most phenomena are modeled using differential equations in most fields of science such as chemistry, biology, and technology. Meantime, many real phenomena are modeled by nonlinear and singular differential equations. Recently, differential equations have attracted the attention of many researchers in science and engineering due to their vast applications in most branches of science (see for more details [4, 6, 10, 11, 16, 17]). The Emden–Fowler equation is a differential equation which arises in mathematical physics and astrophysics. Due to the singularity behavior at the point ($x=0$), it is numerically challenging to solve the Emden–Fowler problem, as well as other various linear and nonlinear singular initial value problems in quantum mechanics and astrophysics. This paper deals with the numerical solution for the singular and nonlinear fractional partial differential Emden–Fowler equation using the Haar wavelet collocation method. Various methods for solving these equations are cited in [1,2,3, 5, 7, 13, 18, 24]. Wavelets are widely used in approximation theory and have been used repeatedly for solving differential equations over recent years. Wavelet-based, numerical methods are used for solving the system of equations with faster convergence and low computational cost. In the last two decades, wavelets have been used for the solution of partial differential equations. The wavelet algorithms for solving PDE (partial differential equation) are based on the Galerkin technique or the collocation method. Among them, the Haar wavelets consist of piecewise constant functions, and therefore, they are the simplest orthonormal wavelets with compact support [17, 20].

In this work, we have proposed a collocation method by the Haar wavelet for solving nonlinear and singular fractional time-dependent Emden–Fowler equations [8, 19, 21]. The existence of a singularity at the point $x = 0$, as well as a nonlinear part, makes find the approximate solution of these categories of equations difficult.

The model is of the form:

$$\begin{aligned}&\frac{\partial ^{2} u}{\partial x^{2}}+\frac{\zeta }{x}\frac{\partial u}{\partial x} +a f(x,t)F(u)+h(x,t)\\&\quad =\frac{\partial ^{\alpha } u}{\partial t^{\alpha }},\qquad 0\le x,t\le 1,\qquad 0< \alpha \le 1, \end{aligned}$$

with initial and boundary conditions:

$$\begin{aligned} u(x,0)=g_{1} (x), u(0,t)=Y_{1} (t), u(1,t)=Y_{2}(t), \end{aligned}$$

where $g_{1}(x), Y_{1}(t)$ and $Y_{2}(t)$ are known functions. $\frac{\partial ^{\alpha } u}{\partial t^{\alpha }}$ donate the Caputo fractional derivative to time t. Here, u is the temperature, $f ( x , t ) F ( u ) + h ( x , t )$ is the nonlinear heat source, and t is the time variable. If $h ( x , t ) = 0$, this equation is the Emden–Fowler equation [8] which has been given by:

$$\begin{aligned} u_{xx}+\frac{\alpha }{x}u_{x} + af(x)F(u)=0, \end{aligned}$$

for $f ( x ) = 1$ and $F ( u ) = u^{n}$, this equation is known as the first kind, while the second kind is obtained when $F ( u ) = e^{u}$. These equations are solved by methods such as Adomian decomposition method (ADM) [15, 22, 23], modified homotopy perturbation method (MHPM) [12, 19], and homotopy perturbation method (HPM) [3]. See the details for more information about recent works on Lane–Emden equations [8, 9].

It is necessary to note that the Emden–Fowler singular partial fractional differential equation is the first one to be solved by the Haar wavelets collocation method and the Picard technique. There are no similar works with this method for these equations. The key idea in this paper is to convert the nonlinear equation using the Picard technique to a system of linear equations and then using the Haar wavelet collocation method for finding the approximate solutions of such equations.

Haar wavelet, fractional integral and derivative

Fractional integral and derivative

In this section, we first review some basic definitions of fractional calculus, which are required for establishing our results [14].

Definition 2.1

The Riemann–Liouville fractional integral operator of order $\alpha \ge 0$ of function u(t) is defined as:

$$\begin{aligned}&J^{\alpha } u(t)=\frac{1}{\Gamma (\alpha )} \int ^{t}_{0} (t-\tau )^{\alpha -1} u(\tau ) \hbox {d}\tau ,\nonumber \\&\quad \alpha , t>0,\qquad J^{0} u(t)=u(t). \end{aligned}$$

(1)

The properties of the operator $J^{\alpha }$ are given as follows:

$$\begin{aligned}&(i) J^{\alpha } J^{\beta } u(t)=J^{\alpha +\beta } u(t),\\&(ii) J^{\beta } J^{\alpha } u(t)=J^{\alpha } J^{\beta } u(t),\\&(iii) J^{\alpha } t^{\gamma }=\frac{\Gamma (\gamma +1)}{\Gamma (\alpha +\gamma +1)} t^{\alpha +\gamma }. \end{aligned}$$

Definition 2.2

The fractional derivative of u(t) in the Caputo sense is defined as:

$$\begin{aligned} D^{\alpha } u(t)=\left\{ \begin{array}{ll} \frac{\hbox {d}^{r} u(t)}{\hbox {d}t^{r}} &{} \quad \alpha =r\in N;\\ \frac{1}{\Gamma (r-\alpha )} \int ^{t}_{0} \frac{u^{(r)}}{(1-\tau )^{\alpha -r+1}}\hbox {d}\tau &{} \quad 0\le r-1<\alpha <r. \end{array} \right. \end{aligned}$$

(2)

Haar wavelets

The Haar functions contain just one wavelet during some subinterval of time and remain zero elsewhere and orthogonal. The $l\hbox {th}$ Haar wavelet $h_{l}(x),\quad x\in [0,1)$ is defined as:

$$\begin{aligned} h_{l} (x)=\left\{ \begin{array}{ll} 1\qquad &{} \quad a(l)\le t<b(l)\\ -1\qquad &{} \quad b(l)\le t <c(l)\\ 0\qquad &{} \quad \hbox {otherwise} \end{array}\right. \end{aligned}$$

(3)

where $a(l)=\frac{k}{m}, b(l)=\frac{k+0.5}{m}, c(l)=\frac{k+1}{m}, l=2^{j} +k+1, j=0,1,2,3,\ldots ,J$ are dilation parameters, $m=2^{j}$ and $k=0,1,2,\ldots 2^{j} -1$ are translation parameters. When $k=0$ , $j=0$, we have $l=2$ , which is the minimal value of l and the maximal value of l is 2M where $M=2^{j}$, J is maximal level of resolution. For the Haar wavelets, the wavelet collocation method is applied. The collocation points for the Haar wavelets are usually taken as $x_{j} =\frac{j-0.5}{2M}, j=1,2,3,\ldots , 2M.$ For convenience, 2M is equal to m. For instance $J=2$, then $m=8$.

Fractional integral of the Haar wavelets

The Riemann–Liouville fractional integral of the Haar scaling function and the Haar wavelets are given as:

$$\begin{aligned} p_{\alpha , 1} (x)= & {} I^{\alpha }_{a(1)} h_{1} (x)=\frac{1}{\Gamma (\alpha )} \int _{a(l)}^{x} (x-s)^{\alpha -1} \hbox {d}s, \qquad \alpha >0. \end{aligned}$$

(4)

$$\begin{aligned} p_{\alpha ,l} (x)= & {} ( I^{\alpha }_{a} h_{l}) (x)\nonumber \\= & {} \frac{1}{\Gamma (\alpha )} \left\{ \begin{array}{ll} \int _{a(l)}^{x} (x-s)^{\alpha -1} \hbox {d}s, &{} a(l)\le x< b(l);\\ \int _{a(l)}^{b(l)} (x-s)^{\alpha -1} \hbox {d}s - \int _{b(l)}^{x} (x-s)^{\alpha -1} \hbox {d}s, &{} b(l)\le x<c(l);\\ \int _{a(l)}^{b(l)} (x-s)^{\alpha -1} \hbox {d}s - \int _{b(l)}^{c(l)} (x-s)^{\alpha -1} \hbox {d}s, &{} x\ge c(l). \end{array}\right. \end{aligned}$$

(5)

Equations (4) and (5) imply that:

$$\begin{aligned} p_{\alpha ,1} (x)=\frac{(x-a(1))^{\alpha }}{\Gamma (\alpha +1)}, \end{aligned}$$

(6)

and

$$\begin{aligned}&p_{\alpha ,l} (x)\nonumber \\&\quad =\frac{1}{\Gamma (\alpha +1)} \left\{ \begin{array}{ll} (x-a(l))^{\alpha }, &{} a(l)\le x< b(l)\\ (x-a(l))^{\alpha }-2(x-b(l))^{\alpha }, &{} b(l)\le x< c(l)\\ (x-a(l))^{\alpha }-2(x-b(l))^{\alpha } +(x-c(l))^{\alpha }, &{} c(l)\le x. \end{array}\right. \end{aligned}$$

(7)

Any function $y\in L_{2} [0,1]$ can be represented in terms of the Haar series as:

$$\begin{aligned} y(x)=\sum \limits _{l=1}^{\infty } b_{l} h_{l} (x), \end{aligned}$$

(8)

where $b_{l}$ are the Haar wavelet coefficients given by $b_{l}= \int _{0}^{1} y(x) h_{l} (x) \hbox {d}x.$ The function y(x) can be approximated by the truncated Haar wavelets series as:

$$\begin{aligned}&y(x)\approx Y_{m} (x)= \sum \limits _{l=1}^{m} b_{l} h_{l}(x),\nonumber \\&\quad l=2^{j} +k+1,\quad j=0,1,\ldots , J\quad k=0,1,\ldots 2^{j}-1. \end{aligned}$$

(9)

In order to find the numerical approximation of a function, we put the Haar into a discrete form. So, we utilized the collocation method. The collocation points for the Haar wavelets are taken as $x_{c} (i) =\frac{i-0.5}{m}$, where $i=1,2,\ldots , m$.

Any function of two variables $u(x,t)\in L_{2}( [a,b]\times [a,b])$ can be approximated as:

$$\begin{aligned} u(x,t)\approx \sum \limits _{l=1}^{m} \sum \limits _{i=1}^{m} c_{l,i} h_{l} (x) h_{i} (t) =H^\mathrm{T} (x) C H(t), \end{aligned}$$

(10)

where C is $m\times m$ coefficient matrix which can be determined by the inner product $c_{l,i} =\langle h_{l} (x) ,\langle u(x,t), h_{i} (t) \rangle \rangle .$

Taking the collocation points as $x(i)=\frac{i-0.5}{m}$, where $i=1, 2, \ldots , m$, we define the Haar matrix as:

$$\begin{aligned} H_{m\times m}= \left[ \begin{array}{cccc} h_{1} (x_{c} (1)) &{} h_{1} (x_{c} (2)) &{} \ldots &{} h_{1} (x_{c} (m)) \\ h_{2} (x_{c} (1)) &{} h_{2} (x_{c} (2)) &{} \ldots &{} h_{2} (x_{c} (m)) \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ h_{m} (x_{c} (1)) &{} h_{m} (x_{c} (2)) &{} \ldots &{} h_{m} (x_{c} (m)) \end{array} \right] \end{aligned}$$

For instance, for $J=2$ , we get $m=8$ and the Haar matrix is given by:

$$\begin{aligned} H_{8\times 8}=\left[ \begin{array}{cccccccc} 1&{}1&{}1&{}1&{}1&{}1&{}1&{}1\\ 1&{}1&{}1&{}1&{}-1&{}-1&{}-1&{}-1\\ 1&{}1&{}-1&{}-1&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}1&{}1&{}-1&{}-1\\ 1&{}-1&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}1&{}-1&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}1&{}-1&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}1&{}-1 \end{array} \right] . \end{aligned}$$

The Haar coefficients $b_{l}$ can be determined by matrix inversion

$$\begin{aligned} b=yH^{-1}, \end{aligned}$$

(11)

where $H^{-1}$ is the inverse of H. Equation (11) gives the Haar coefficients $b_{l}$ which are used in (9) to get the solution y(x).

Similarly, we can obtain the fractional order integration matrix P of the Haar function by substituting the collocation points in Eqs. (6) and (7), $P(l,i)=p_{\alpha ,l} (x_{c} (i))),$ as:

$$\begin{aligned} P_{m\times m}= \left[ \begin{array}{cccc} p_{1} (x_{c} (1)) &{} p_{1} (x_{c} (2)) &{} \ldots &{} p_{1} (x_{c} (m)) \\ p_{2} (x_{c} (1)) &{} p_{2} (x_{c} (2)) &{} \ldots &{} p_{2} (x_{c} (m)) \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ p_{m} (x_{c} (1)) &{} p_{m} (x_{c} (2)) &{} \ldots &{} p_{m} (x_{c} (m)) \end{array} \right] . \end{aligned}$$

For instance, with $\alpha = 0.25, J=2 (m=8)$, we get the Haar wavelet operational matrix of fractional integration as:

$$\begin{aligned} P_{8 \times 8}=\left[ \begin{array}{cccccccc} 0.5516&{} 0.7259&{} 0.8248&{} 0.8972&{} 0.9554&{} 1.0046&{} 1.0474&{} 1.0856\\ 0.5516&{} 0.7259&{} 0.8248&{} 0.8972&{}- 0.1478&{}- 0.4473&{}- 0.60239&{}- 0.7089\\ 0.5516&{} 0.7259&{}- 0.2783&{}- 0.5547&{}- 0.14267&{}- 0.0639&{}- 0.0385&{}- 0.0263\\ 0&{} 0&{} 0&{} 0&{} 0.5516&{} 0.7259&{}- 0.2783&{}- 0.5547\\ 0.5516&{}- 0.3772&{}- 0.0754&{}- 0.0265&{}- 0.0142&{}- 0.0090&{}- 0.0063&{}- 0.0046\\ 0&{} 0&{} 0.5516&{}- 0.3772&{}- 0.0754&{}- 0.0265&{}- 0.01420&{}- 0.0090\\ 0&{} 0&{} 0&{} 0&{} 0.5516&{}- 0.3772&{}- 0.0754&{}- 0.0265\\ 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0.5516&{}- 0.3772 \end{array}\right] . \end{aligned}$$

We derive another operational matrix of fractional integration to solve the fractional boundary value problems. Let $\zeta >0$ and $z:[0,\zeta ]\rightarrow R$ be a continuous function and assume that the Haar function has $[0,\zeta ]$ as compact support, we have:

$$\begin{aligned} z(x) I_{0}^{\alpha } h_{1} (\zeta )= z(x) \int \limits _{0}^{\zeta } (\zeta -s)^{\alpha } \hbox {d}s,\quad v^{\alpha ,\zeta ,1}=z(x) C_{\alpha ,1}, \end{aligned}$$

(12)

and

$$\begin{aligned}&z(x)I^{\alpha }_{0} h_{l} (\zeta ) =z(x) \left[ \int \limits _{a(l)}^{b(l)} (\zeta -s)^{\alpha -1} \hbox {d}s - \int \limits _{b(l)}^{\zeta } (\zeta -s)^{\alpha -1} \hbox {d}s\right] ,\nonumber \\&v^{\alpha ,\zeta ,1} =z(x) C_{\alpha ,l}. \end{aligned}$$

(13)

For instance, $\zeta =1,z(x)= x, \alpha =1.25, m=8$, we have:

$$\begin{aligned} V_{8\times 8}^{1.25,1}= \left[ \begin{array}{cccccccc} 0.8826&{} 0.8826&{} 0.8826&{} 0.8826&{} 0.88261&{} 0.8826&{} 0.88261&{} 0.8826\\ 0.1404&{} 0.1404&{} 0.1404&{} 0.1404&{} 0.1404&{} 0.1404&{} 0.1404&{} 0.1404\\ 0.0216&{} 0.0216&{} 0.0216&{} 0.0216&{} 0.0216&{} 0.0216&{} 0.0216&{} 0.0216\\ 0.0590&{} 0.0590&{} 0.0590&{} 0.0590&{} 0.0590&{} 0.0590&{} 0.0590&{} 0.0590\\ 0.0047&{} 0.0047&{} 0.0047&{} 0.0047&{} 0.0047&{} 0.0047&{} 0.0047&{} 0.0047\\ 0.0061&{} 0.0061&{} 0.0061&{} 0.0061&{} 0.0061&{} 0.0061&{} 0.0061&{} 0.0061\\ 0.00910&{} 0.0091&{} 0.0091&{} 0.0091&{} 0.0091&{} 0.0091&{} 0.0091&{} 0.0091\\ 0.0248&{} 0.0248&{} 0.0248&{} 0.0248&{} 0.0248&{} 0.0248&{} 0.0248&{} 0.0248 \end{array}\right] . \end{aligned}$$

(14)

Method of solution

In this section, we describe the procedure of implementing the method for singular and nonlinear fractional Emden–Fowler equations. First, we convert the singular fractional partial differential equation into discrete fractional PDE (partial differential equations) by the Picard technique. Then, we solve it to obtain the approximate solution of the singular and nonlinear fractional partial differential equation by the Haar wavelet collocation method.

Consider the following singular and nonlinear fractional time-dependent Emden–Fowler partial differential equation:

$$\begin{aligned}&\frac{\partial ^{\alpha } u}{\partial t^{\alpha }} =\frac{\partial ^{2} u}{\partial x^{2}} +\frac{\zeta }{x} \frac{\partial u}{\partial x}+a f(x,t) F(u)+h(x,t), \nonumber \\&0<\alpha \le 1, \qquad 0\le x,t\le 1, \end{aligned}$$

(15)

with initial and boundary conditions:

$$\begin{aligned}&u(x,0)=g_{1} (x),\nonumber \\&u(0,t)=Y_{1} (t),\qquad u(1,t)=Y_{2}(t), \end{aligned}$$

(16)

and applying the Picard technique to Eq. (15), we get:

$$\begin{aligned}&\frac{\partial ^{\alpha } u_{r+1}}{\partial t^{\alpha }} =\frac{\partial ^{2} u_{r+1}}{\partial x^{2}} +\frac{\zeta }{x} \frac{\partial u_{r+1}}{\partial x}+m(x,t,u_{r}),\nonumber \\&0<\alpha \le 1,\quad \quad , r\ge 0 \end{aligned}$$

(17)

with the initial and boundary conditions:

$$\begin{aligned}&u_{r+1}(x,0)=g_{1} (x), \quad 0\le x <1.\nonumber \\&u_{r+1}(0,t)=Y_{1} (t),\qquad u_{r+1}(1,t)=Y_{2}(t), \qquad t\in [0,1] \end{aligned}$$

(18)

where $m(x,t,u_{r}):=af(x,t)F(u)+h(x,t)$. Applying the Haar wavelet method to Eq. (17), we approximate the higher order term by the Haar wavelet series as:

$$\begin{aligned} \frac{\partial ^{2} u_{r+1}}{\partial x^{2}}= \sum \limits _{l=1}^{m} \sum \limits _{p=1}^{m} c_{lp}^{r+1} h_{l} (x) h_{p} (t) = H^\mathrm{T} (x) C^{r+1} H(t). \end{aligned}$$

(19)

Applying the fractional integral operator $I^{2}_{x}$ on Eq. (19) gives:

$$\begin{aligned} u_{r+1} (x,t) =(P_{x}^{2})^\mathrm{T} C^{r+1} H(t) +p(t)x+q(t), \end{aligned}$$

(20)

where p(t) and q(t) are functions of t. Using the boundary conditions and Eqs. (5), (6), we get

$$\begin{aligned}&q(t)=Y_{1} (t) \nonumber \\&p(t)=-\sum \limits _{l=1}^{m} \sum \limits _{p=1}^{m} c_{lp}^{r+1}(I_{x}^{2} h_{l}(x))h_{p}(t)+Y_{2} (t) -Y_{1} (t). \end{aligned}$$

(21)

Equation (20) can be written as:

$$\begin{aligned} u_{r+1}(x,t)= & {} (P_{x}^{2})^\mathrm{T} C^{r+1} H(t) -x((P_{x}^{2}(1))^\mathrm{T} C^{r+1} H(t))\nonumber \\&-x(Y_{2}(t)-Y_{1}(t))+Y_{1}(t), \end{aligned}$$

(22)

take derivative with respect to x of order 1 to Eq. (22)

$$\begin{aligned} \frac{\partial u_{r+1}}{\partial x}=(P_{x}^{1})^\mathrm{T} C^{r+1} H(t)-(P_{x}^{2}(1))^\mathrm{T} C^{r+1} H(t) - Y_{2}(t)+Y_{1}(t). \end{aligned}$$

(23)

For simplicity, let

$$\begin{aligned} S(x,t)= & {} m(x,t,u_{r})\nonumber \\= & {} \sum \limits _{l=1}^{m} \sum \limits _{p=1}^{m} m_{lp} h_{l} (x) h_{p} (t)=H^\mathrm{T}(x) M H(t), \end{aligned}$$

(24)

where $m_{lp}=\langle h_{l} (x) ,\langle S(x,t), h_{p} (t) \rangle \rangle$. By substituting Eqs. (24), (19) and (23) in Eq. (15), we obtain:

$$\begin{aligned} \frac{\partial ^{\alpha } u_{r+1}}{\partial t^{\alpha }}= & {} H^\mathrm{T}(x) C^{r+1} H(t)\nonumber \\&+\frac{\zeta }{x} ((P_{x}^{1})^\mathrm{T} C^{r+1} H(t) -(P_{x}^{2}(1))^\mathrm{T} C^{r+1} H(t) \nonumber \\&+ Y_{2}(t)-Y_{1}(t)) + H^\mathrm{T}(x) M H(t). \end{aligned}$$

(25)

Apply fractional integral operator $I^{\alpha }_{t}$ to (25) and use the initial conditions to obtain:

$$\begin{aligned} u_{r+1} (x,t)= & {} H^\mathrm{T} C^{r+1} P_{t}^{\alpha } +\frac{\zeta }{x}((P_{x}^{1})^\mathrm{T} C^{r+1} P_{t}^{\alpha } +I_{t}^{\alpha }(Y_{2}(t)-Y_{1}(t))) \nonumber \\&+ H^\mathrm{T} M P_{t}^{\alpha } +g_{1}(x). \end{aligned}$$

(26)

Let $K(x,t)=-g_{1} (x) +x(Y_{2} (t)-Y_{1} (t))+\frac{\zeta }{x} I_{t}^{\alpha }(Y_{2} (t)-Y_{1}(t))$. From Eqs. (26), (22),

$$\begin{aligned}&(P_{x}^{2})^\mathrm{T} C^{r+1} H(t) -x ((P_{x}^{2}(1))^\mathrm{T} C^{r+1} H(t) )+K(x,t) \nonumber \\&\quad = H^\mathrm{T} C^{r+1} P_{t}^{\alpha }+\frac{\zeta }{x} ((P_{x}^{1})^\mathrm{T} C^{r+1} P_{t}^{\alpha }\nonumber \\&\quad \quad -(P_{x}^{2}(1))^\mathrm{T} C^{r+1} H(t))+ H^\mathrm{T} M P_{t}^{\alpha }. \end{aligned}$$

(27)

In discrete form, Eq. (27) and using the collocation points, we have matrix form:

$$\begin{aligned}&(P_{x}^{2})^\mathrm{T} C^{r+1} H-V^{2 ,1,f(x)} C^{r+1} H -H^\mathrm{T} C^{r+1} P_{t}^{\alpha } \nonumber \\&\quad +\frac{\zeta }{x}((P_{x}^{1})^\mathrm{T} C^{r+1})P_{t}^{\alpha } -V^{1,1,f(x)}C^{r+1}P_{t}^{\alpha })\nonumber \\&\quad \quad - H^\mathrm{T} M^{'} P^{\alpha }_{t} +K=0, \end{aligned}$$

(28)

where H is $m\times m$ the Haar matrix, $V^{2 ,1, f(x)} =f(x) I^{2}_{1} H^\mathrm{T}$ is $m\times m$ is the fractional integration matrix for boundary value problems, and $P^{2}_{x} = I^{2}_{x} H^\mathrm{T}, P^{\alpha }_{t} = I^{\alpha }_{t} H$ are $m\times m$ matrices of fractional integration of the Haar functions. $M'$ is $m\times m$ the coefficient matrix determined by inner products $m'_{lp}=\langle h_{l} (x) ,\langle S(x,t), h_{p} (t) \rangle \rangle$, and $f(x)=x$.

Let $L:=(H^\mathrm{T}+A((P^{1})^\mathrm{T}-(V^{1,1,f(x)})^\mathrm{T})^{-1}$ is $m\times m$ matrix, where A is a diagonal matrix and is given by:

$$\begin{aligned} A= \left[ \begin{array}{cccc} a (x (1)) &{} 0 &{} \ldots &{}0 \\ 0&{} a (x (2)) &{} \ldots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0&{} 0 &{} \ldots &{} a (x (m)) \end{array} \right] \hbox {with} \quad a(x(i))=\frac{\zeta }{x(i)}. \end{aligned}$$

So Eq. (28) can be written as:

$$\begin{aligned} L((P_{x}^{2})^\mathrm{T}-V^{2 ,1,f(x)}) C^{r+1} -C^{r+1} P_{t}^{\alpha }H^{-1} +L(K- H^\mathrm{T} M^{'} P^{\alpha }_{t}) =0, \end{aligned}$$

(29)

which is Sylvester equation $(AX+XB=C)$. Solving Eq. (29) for $C^{r+1}$ and substituting in Eq. (20) or Eq. (26), we get the solution $u_{r+1}$ at the collocation points. In particular, given an initial approximation $u_{0} (x,t)$, we get a linear fractional singular problem in $u_{1} (x,t)$ by substituting $r=0$ in Eq. (20), which is solved by mentioned procedure to get $u_{1} (x,t)$ at the collocation points.

Numerical results and examples

In this section, we have used the above technique for solving the singular and nonlinear fractional time-dependent Emden–Fowler equation. In these examples, exact solutions are being and comparison between Haar–Picard technique approximate solution and the exact solution do to show the efficiency of our method to solve such equations.

Example 4.1

We consider the singular and nonlinear fractional time-dependent Emden–Fowler heat-type equation [19, 22]:

$$\begin{aligned} \frac{\partial ^{2} u}{\partial x^{2}}+\frac{\zeta }{x} \frac{\partial u}{\partial x} -(24t+16t^{2}x^{2})e^{u} -2x^2e^{u/2}=\frac{\partial ^{\alpha } u}{\partial t^{\alpha }} \end{aligned}$$

(30)

where $\zeta =5$, with initial and boundary conditions:

$$\begin{aligned}&u(x,0)=0,\quad u(0,t)=0,\nonumber \\&u(1,t)=-2 \ln (1+t),\qquad 0\le x,t\le 1, \end{aligned}$$

(31)

Exact solution for $\alpha =1$ is $u(x,t)= -2 \ln (1+tx^{2})$.

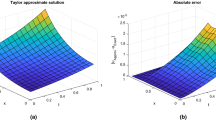
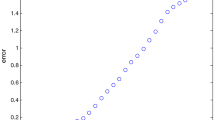
We use $u_{0}=0$ as an initial approximation and apply our method, we get the approximate solution of this singular equation. We see in Table 1 the different values of $\alpha$ when it goes to $\alpha =1$; the absolute errors show that the solution of method converges to exact solution. We also compare our results on the absolute error by the method introduced in [19, 22]. In Fig. 1, absolute errors show that increasing the number of iterations, approximate solutions to the present method approach the exact solution, and also we plotted absolute errors of approximate solutions in different values m for $\alpha =1$ in Fig. 2, as can be seen, by increasing the resolution m approximate solutions approach the exact solution.

Table 1 Absolute error $|u_{r+1}(x,t)- u(x,t)|_{t=0.5}$, for $m=64$, $\alpha$ when it goes to $\alpha =1$ at $6\hbox {th}$ iteration, and comparison of the absolute error with the methods MHMP [19], and ADM [22] in Example 4.1

Example 4.2

Consider the singular and nonlinear fractional time-dependent Emden–Fowler heat-type equation [19]:

$$\begin{aligned}&\frac{\partial ^{2} u}{\partial x^{2}}+\left( \frac{\zeta }{x}\right) \frac{\partial u}{\partial x} -\theta t ( t x)^{-2+\theta }\nonumber \\&\quad (x^{2}-t(-1+\zeta +\theta )e^{u} -t^{2} (tx))^{-2+2\theta } \theta ^{2} e^{2u}= \frac{\partial ^{\alpha } u}{\partial t^{\alpha }} \end{aligned}$$

(32)

with initial and boundary conditions

$$\begin{aligned}&u(x,0)=-\ln (3),\quad u(0,t)=-\ln (3),\nonumber \\&u(1,t) =-\ln (3+t^{\theta }),\quad 0\le x,t\le 1, \end{aligned}$$

(33)

where $\zeta$ and $\theta$ are constants and exact solution for $\alpha =1$ is $u(x,t)=-\ln (3+(tx)^{\theta })$.

We use $u_{0}(x,t)=-\ln (3)$ as an initial approximation and apply our technique, we get approximate solution of this singular problem. In Table 2, we set $\zeta =1, \theta =1$. In Table 2, we see the different values of $\alpha$ when it goes to $\alpha =1$; the absolute error shows the solution of method converges to the exact solution. We have got a comparison with the numerical results in [19], and our solution by present method is in Table 2. Another case of Example 4.2 is that $\zeta =2, \theta =2$. In Table 3, we see the different values of $\alpha$ when it goes to $\alpha =1$. Absolute error shows the solution of method converges to exact solution. We have got a comparison with numerical results in [19], and our solution by present method is in Table 3. We note that the methods in [19, 22] are modified homotopy perturbation method, and the Adomian decomposition method (ADM) that solve Examples 4.1 and 4.2 in integer derivative with respect to t that means $\alpha =1$. For two cases of values of $\zeta , \theta$, we plotted in Figs. 3, 4 absolute errors of different iterations for $m=64$, $\alpha =1$, as can be seen, increasing the iterations approximate solutions approach the exact solutions, also Figs. 5, 6 show that increasing the resolution m, absolute errors becomes less each time.

Table 2 Absolute error $|u_{r+1}(x,t)- u(x,t)|_{t=0.5}$, for $m=64$, $\alpha$ when it goes to $\alpha =1$ at $6\hbox {th}$ iteration, and comparison of the absolute error with MHPM [19], ADM [22] in Example 4.2

Table 3 Absolute error $|u_{r+1}(x,t)- u(x,t)|_{t=0.5}$, for $m=64$, $\alpha$ when it goes to $\alpha =1$ at $6\hbox {th}$ iteration, and comparison of the absolute error with the MHPM [19], ADM [22] in Example 4.2

Example 4.3

Consider the following singular and nonlinear fractional time-dependent in homogeneous Emden–Fowler equation:

$$\begin{aligned} \frac{\partial ^{2} u}{\partial x^{2}} + \frac{\zeta }{x} \frac{\partial u}{\partial x} + e^{u} - e^{\frac{u}{2}} +h(x,t)=\frac{\partial ^{\alpha } u}{\partial t^{\alpha }} \end{aligned}$$

(34)

where $h(x,t)=\frac{((-x^{4}-x^{2}+20)t-5x^{2}-5) \sqrt{tx^{2}+5}+(tx^{2}+5)^{2}}{(t x^{2}+5)^{\frac{5}{2}}}$, with initial and boundary condition:

$$\begin{aligned}&u(x,0)=-\ln (5),\quad u(0,t)=-\ln (5),\nonumber \\&u(1,t)=-\ln (5+t), \quad 0\le x,t\le 1, \end{aligned}$$

(35)

where $\zeta$ is constant and $\zeta =1$, and exact solution for $\alpha =1$ is $u(x,t)=-\ln (5+tx^{2}).$

We use $u_{0}=-\ln (5)$ as an initial approximation and apply our technique, we get the approximate solution of this singular problem. We see in Fig. 7 increasing the iterations at each stage, the absolute errors show that the solution of the method converges to the exact solution. In Table 4, we list the absolute errors for different values of $\alpha$, as can be seen, when $\alpha$ tends to 1, absolute errors also decrease and the approximate solution approaches the exact solution.

Table 4 Absolute error $|u_{r+1}(x,t)- u(x,t)|$, for $m=64$, when $\alpha$ goes to 1 at $4\hbox {th}$ iteration in Example 4.3

Fig. 1

Absolute errors for $\alpha =1, m=64$ of different iterations, Example 4.1

Fig. 2

Absolute errors for different values of m, $\alpha =1,$ in $6\hbox {th}$ iteration, Example 4.1

Fig. 3

Absolute errors for $\alpha =1, m=64$ of different iterations, Example 4.2$\zeta =1, \theta =1$

Fig. 4

Absolute errors for $\alpha =1, m=64, \theta =2,\zeta =2$ in $6\hbox {th}$ iteration, Example 4.2

Fig. 5

Absolute errors for different values of m, $\alpha =1, \theta =1,\zeta =1$ in $6\hbox {th}$ iteration, Example 4.2

Fig. 6

Absolute errors for different values of m, $\alpha =1, \theta =2,\zeta =2$ in $6\hbox {th}$ iteration, Example 4.2

Fig. 7

Absolute errors for $\alpha =1, m=64$ of different iterations, Example 4.3

Conclusion

We have proposed the Haar wavelet collocation–Picard method for solving the singular and nonlinear time-dependent Emden–Fowler-type equations with initial and boundary conditions of the fractional order. Indeed, we combined the Haar wavelet and the Picard technique to solve singular and nonlinear fractional partial differential equations such as Examples 4.1, 4.2, and 4.3. The main advantage of this method is that the singular and nonlinear fractional partial differential equation can be converted into an algebraic system of linear equations. We note that the use of the Haar wavelets and the Picard technique for solving these singular and nonlinear fractional equations is the first one to occur. We clearly realized that the method is more accurate on computing the approximate solutions and the results showed the efficiency of the method. Tables 1 and 3 show that our results are more accurate as compared to modified homotopy perturbation method introduced in [19] and Adomian decomposition method [22]. The method proposed in this paper is easy to implement for this type of singular and nonlinear fractional partial differential equations and does not require complex computations.