Abstract
In this study, a new algorithm that can be used for copyright protection is proposed for the embedding and detection of a watermark in the domain of discrete wavelet transform (DWT). The elements of the logo watermark are embedded directly to the three-level DWT decomposed subbands. In addition to that, the scheme is considered as a completely blind scheme for both host image and watermark. Two kinds of security attacks have also been considered which confirms the security of the scheme. The experimental results and computer simulation of the proposed scheme have shown that the proposed approach has the desired properties such as invisibility, blind detection, and robustness against various geometrical and non-geometrical attacks.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
With the fast growth of the Internet, people have paid more and more attention to the security of the network information. The protection of the digital data is an important topic to the owners of the multimedia products. Digital watermarking is embedding hidden data into the multimedia in such a manner that it cannot be removed and its detection to verify the ownership of digital products.
To be used as a means of copyright protection, the two main requirements of high robustness and capacity and high imperceptibility (low visibility) should be ensured for watermarking schemes. The peak signal-to-noise ratio (PSNR) is criteria that are used to evaluate imperceptibility. There exists a reverse relation between capacity, robustness, and imperceptibility and making a developed compromise between these conflict parameters is the core motivation of the most watermarking schemes.
The watermarking procedure in which the techniques first transform an image into a set of frequency-domain coefficients is frequency-domain techniques [1]. These techniques include discrete cosine transform (DCT) [2, 3], discrete Fourier transform (DFT) [4], radon transform [5], discrete wavelet transform (DWT) [6,7,8,9], etc. In these techniques, the watermark is embedded in the transform coefficients of the image. Then, the coefficients are inverse-transformed to form the watermarked image. In this way, the watermark is less visible and more robust to some image-processing operations and attacks. Extraction process of watermark may be dependent or independent of the original image or embedded watermark, which is based on level of required information that are classified into non-blind, semi-blind, or blind detection process. These classes are application-dependent and directly affect on the capacity of the watermarking scheme.
Most of the algorithms of watermarking schemes which are proposed have this common disadvantage that in the extracting process, they require a lot of information of host image and/or embedded watermark and this process is dependent on some information of host image or watermark. It is clear that in some situations and applications, it may be impossible to access to these information. On the other hand, each watermark has own data, and if too many watermarks are used, then too many available data are needed to be stored and utilized when they are required. Obviously, these drawbacks make serious restrictions for application of these methods.
In [8, 9], the authors use SVD (singular value decomposition) of subbands of one-level redundant wavelet and integer wavelet decomposition and add the singular values of the watermark to the singular values of the subbands. However, in the detection process, the presented methods require the orthogonal matrices of SVD of the watermark as well as the singular values of the subbands. In Lai et al. [6], the authors decomposed the host image into four subbands (LL, LH, HL, and HH) using DWT and then applied SVD to only the LH and HL subbands. Finally, the watermark image was divided into two halves and then embedded into the singular values of LH and HL, respectively. Again, there is necessity of the orthogonal matrices and singular values of the subbands in the extraction process. Other works such as [10,11,12,13] suffer from the same problem.
Although apparently, these algorithms declare high capacity and blind detection, but in fact, only the singular values of the watermark are embedded in the host image and a large percentage of the data of the watermark are stored in an available place apart from the host image. On the other hand, the detection process can not be blind because of dependency to a lot of data of the host image and watermark.
The work which is done in this study is to present an algorithm that does not have the above-mentioned difficulties and also preserves the desired properties of a watermarking procedure. The watermark, which is embedded, is a binary string derived from a logo watermark. The whole of the watermark is embedded in the host image and no additional data of watermark or host image are remained to be preserved beside the algorithm. Using discrete wavelet transform, the watermark is embedded in all detail subbands of three-level decomposition of the image. The extracting procedure is not dependent on any part of the host image or the watermark, and then, the process is fully blind. The algorithm showed good imperceptibility, capacity, and security, and with having high robustness, the proposed scheme is an ideal choice for copyright protection applications.
The remainder of this paper is organized as follows: “Discrete wavelet transformation of images” presents a brief overview regarding the transform applied in the proposed scheme. In the next section, the proposed scheme (i.e., the watermark embedding and extraction procedures) is stated. The experimental setup and results are presented in “Experimental results”. Finally, our conclusions are stated in the last section.
Discrete wavelet transformation of images
In this section, a brief overview of application of DWT for image decomposition is presented. A function (signal) f(x) using discrete wavelet transform can be decomposed into a weighted sum of basis functions \(\phi _{j_0,k}(x)\) and \(\psi _{j,k}(x)\) (scaling and wavelets functions):
where \(j_0\) is starting scale, M is the length of the signal, \(W_{\phi }(j_0,k)\), and \(W_{\psi }(j,k)\) are approximation and details coefficients, respectively.
In two-dimensional signals (like an image), wavelets and scaling functions are tensor products of the one dimension:
and the decomposition of signal f(x, y) of size \(M\times N\) will be as
for \(j,m,n\in \mathbb {Z}\). With this decomposition, the 2D signal is filtered by the filter coefficients \(h_{\phi }\) (low-pass filter) and \(h_{\psi }\) (high-pass filter) that have two directions X and Y along with a downsampling in each direction to produce the coefficients of the four subbands \(W_{\phi }(j,.,.)\), \(W_{\psi }^H(j,.,.)\), \(W_{\psi }^V(j,.,.)\), and \(W_{\psi }^D(j,.,.)\), where \(W_{\phi }(j+1,.,.)\) is the coefficients of the input image. This procedure is one-level analysis filter bank and an image is divided into four subbands LL, LH, HL, and HH. LH (low–high) is generated by the approximation coefficients (low-pass filter) in X direction and details coefficients (high-pass filter) in Y direction (see Fig. 1).
The inverse discrete wavelet transform is easy and can be accomplished by the upsampling and filtering by the inverse low-pass and high-pass filters and exchanging the split by merging. After decomposition of the image, the details and approximation coefficients are used by inverse DWT to recompose the original image. This process is synthesis filter bank and the filter coefficients (low-pass and high-pass filters) are chosen, such that the reconstruction is perfect [14,15,16]. Figure 2 illustrates the discrete wavelet and inverse discrete wavelet transforms steps. The basic approach of wavelets in many applications and their usefulness in image processing is demonstrated in three steps: computing a 2D DWT of an image, altering the coefficients of the transform, and finally computing the inverse transform to reconstruct the modified image. DWT properties can be utilized to enhance the robustness and preserve the imperceptibility in the watermarking. Accordingly, this technique is adopted by the scheme proposed in this paper.
The proposed scheme
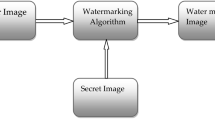
The proposed scheme is presented in this section. This scheme includes watermark embedding and extracting processes, as shown in Figs. 3 and 4. The embedding and detection procedures steps are listed in Algorithms 1 and 2, respectively. The watermark \(w = \{w_1,w_2,\ldots ,w_k\}\), which will be embedded, is a binary string with values \(w_j=0,1\) for \(j=1,\ldots ,k\) derived by listing the rows of a logo watermark. In addition, we name \(W_\psi ^i(j,m,n) = Y_i(m,n)\) the components of the subband \(i\in \{\mathrm{LH},\mathrm{HL},\mathrm{HH}\}\).
The watermark embedding procedure
The human eye is able to detect modifications to the lower frequencies. Therefore, it is better to embed a watermark into an image by modifying large detail coefficients of its multiresolution representation [19, 20]. Detail coefficients belong to the edges and borders of the images, where the frequency is high and embedding of the watermark in these locations is robust against human visual system.
The original image is decomposed into three levels. The subbands LH3, HL3, and HH3 in three levels are selected for the embedding of the watermark, since these subbands involve a wide range of the frequency spectrum of the image, and then, the robustness of the watermarking scheme will be increased. As mentioned before, all components of the watermark are embedded and no extra data of the watermark remain to be preserved out of the host image. The steps of the embedding process are as follows:

The watermark extraction procedure
For the detection of the watermark, the inverse of the embedding operations is implemented. Along with the detection procedure, no information of host image or embedded watermark is required, and then, the extraction procedure is completely blind. The watermarked image \( A^{*w} \) may be distorted by geometrical and non-geometrical attacks (image-processing attacks). After decomposition of the watermarked image \( A^{*w} \) in the same level as embedding, Algorithm 2 on the subbands LH3, HL3, and HH3 will be implemented.

Algorithm 2 of detection steps is independent of the original image and embedded watermark and this property makes the scheme more applicable in watermarking areas such as fingerprint and copy and copyright protections.
Experimental results
The proposed procedure simulation is implemented in MATLAB. Popular test images of size \(512\times 512\) have been used as host images and the Cameraman logo image is selected as a binary watermark. The examination of the efficiency of the proposed scheme under different conditions is considered in terms of imperceptibility and robustness under various attacks. To this end, we compute peak signal-to-noise ratio (PSNR) and normalized correlation coefficient (NCC) which are used repeatedly in the literature. The PSNR, which is used to estimate the imperceptibility, is criteria to evaluate the similarity between the host image x and the watermarked image y by the following relation:
where M, N are the size of the image and MSE is the mean square error between the two images. A high PSNR implies good imperceptibility of the watermarked image and its high similarity to the original image, and then, the host image is very slightly affected by the embedding process. The least acceptable value for PSNR is about 38 dB [17].
The similarity between the original watermark w and the extracted watermark \(\bar{w}\) is evaluated by the NCC which is criteria for the robustness of the scheme and is calculated as follows:
The NCC has a value between 0 and 1. If this value is closer to 1 under a special attack, then the process has higher robustness against the attack and vice versa. An acceptable value for the NCC is at least 0.75 [18].
The imperceptibility test of the proposed scheme
The imperceptibility of the test images with various sizes of the logo watermark is examined. Obviously, there is a reverse relation between the size of the watermark (the capacity of the watermarking scheme) and PSNR; hence, an optimal size of the watermark must be selected, such that an acceptable imperceptibility of the watermarked image to be obtained. These results are observed in Fig. 5.
According to these results and to the acceptable value of PSNR, \(64\times 64\) is selected as the size of the watermark. Table 1 displays some of the host and watermarked images in which the size of the embedded watermark is \(64\times 64\). The figure shows the efficiency of the proposed scheme in terms of the imperceptibility and invisibility of the embedded watermark.
The robustness test of the proposed scheme
Robustness is the resistance of the embedded watermark against distortions of the watermarked image. These criteria are an important necessity in developing the watermarking algorithms. The distortions may be geometrical or non-geometrical attacks. Tables 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 represent the NCC values of the detected watermark of the proposed scheme when it is impressed by the various attack types. Geometrical attacks such as scaling, rotation, cutting, shearing, and translation were applied. Noise addition (salt and pepper, Gaussian, and speckle noise), filtering, gamma correction, and jpeg compression attacks were selected as non-geometrical attacks (image-processing attacks). The proposed scheme showed good resistance under all attacks with high NCC values, which are shown in Table 2.
First considered that geometrical attack is scaling attack. The scaling is changing the image size and then resizing it to the original one. This attack is considered in Table 3 and the watermarked image is tested under various scaling attacks with different scaling parameters. The NCC values of the table show good resistance of the scheme against this attack. Rotation attack is rotating the watermarked image to a particular angle and then rotating back to the original angle. The watermarked image is considered under various rotation angles and the NCC values in Table 4 shows how the scheme is robust under this attack. Cutting attack also is applied to the watermarked image with different parameters to show the robustness of the procedure and the results of NCC values are presented in Table 5 verifying resistance of the scheme against this kind of attacks. Finally, shearing and translation attacks are used on the proposed scheme. Tables 6 and 7 show the NCC values of the attacks under different parameters, confirming the robustness of the scheme.
The second kind of attacks is non-geometrical attacks. Noise addition is considered as one of the image-processing attacks. Gaussian, salt and pepper, and speckle noises are considered as noise addition attacks and added to the watermarked image. The NCC values are reported for different selections of variances and densities of noises. These NCC results exhibit good resistance of the scheme against this kind of attack and are shown in Tables 8, 9, and 10. The second type of non-geometrical attacks which are examined are filtering or de-noising attacks. Two classes of these types of attacks are employed for our scheme. Wiener and median filters with different filter block sizes (e.g., \(3\times 3\), \(5\times 5\), \(7\times 7\), \(9\times 9\), and \(11\times 11\)) are employed and the related NCC values of the extracted watermarks are observed in Tables 11 and 12. These results show the high robustness of the procedure under filtering attacks. The compression of the images is a tool which is employed in many application areas of digital image processing. The watermarking technique must be able to detect the watermark after compression of the watermarked image with a high NCC value. The Jpeg compression is the most important of the compression procedures of the images. To test the resistance of the process, in our experiments, the different compression rates 90, 80, 70, 50, 30, and 10 were selected to compress the watermarked image. The NCC values of the detected watermark are presented in Table 13 which show good robustness of the scheme against the compression attack. Gamma correction of the images is usually applied in some image-processing applications. We altered the watermarked image by gamma correction with several gamma values varying from 0.1 to 0.9 and then evaluated the NCC of the extracted watermark. High resistance of the scheme is proved against the gamma correction attack. Table 14 shows these NCC values for different gamma values.
The security test of the proposed scheme
In this section, we consider two kinds of security attacks which are discussed in [21] to show the security of the proposed scheme. These attacks are copy attack and ambiguity attack with blind detection and we show that our scheme is resistant against these two attacks, and then, it is a secure scheme.
Copy attack
A copy attack occurs when an adversary copies a watermark from a watermarked image to an arbitrary target image \(A^t\) to include it as a watermarked image [22]. Given a legitimately watermarked image, \(A^w\), and an unwatermarked target image, \(A^t\), this method begins by applying a watermark removal attack to \(A^w\) to obtain an approximation of the original image, \(\tilde{A}\). For this step, the authors in [22] proposed using a noise-reduction filter. According to the weak robustness results, the median filtering is the best filter to eliminate the watermark and estimate the original image A. The next step is to estimate the added watermark pattern \(\tilde{w}\) by subtracting the estimated original from the watermarked work:
Finally, the estimated watermark pattern \(\tilde{w}\) is added to the unwatermarked image \(A^t\) to obtain a watermarked version and thus
This method has been implemented to the test images Peppers as a watermarked image \(A^w\) and Lena, Boat, and Cameraman as unwatermarked images \(A^t\). The obtained results for different block sizes m of median filtering are shown in Table 15. Due to weak NCC values we see that our scheme is resistant against this kind of attack.
Ambiguity attack with blind detection
An ambiguity attack against a scheme that uses blind detection is as follows: after watermarking of the original image A by the owner and creating \(A^w\), the adversary embed the fake watermark \(w^F\) on the watermarked image \(A^w\) and makes rewatermarked image \(A^{wF}\). Then, the detection process tries to extract the fake watermark \(w^F\).
In this case, first, we notice that our embedding scheme is invertible, and using the embedded watermark, we can derive the original image A. Now, if we invert the embedding process on the rewatermarked image \(A^{wF}\) using original watermark w, we derive the original image A, while applying this process with fake watermark \(w^F\), will give the watermarked image \(A^w\).
Comparative analysis of the proposed scheme
In this section, the comparison of the proposed scheme with the scheme in [23] is considered under approximately the same conditions. The scheme proposed in [23] represents a blind digital watermarking algorithm based on probabilistic neural network (PNN) in the wavelet domain. The watermarking procedure is performed by embedding a logo watermark of size \(64\times 64\) in the middle-frequency coefficient block of three DWT levels. The PNN is used during watermark extraction.
The robustness test of the scheme in [23] is done under few attacks (only JPEG compression, rotation, Gaussian noise, cropping, and median filter) and the other attacks examined in our discussion are not considered. On the other hand, the security requirement is not discussed. Then, our comparison is limited to the common considered attacks. The used watermarks in both schemes are the UM and Cameraman logos of size \(64\times 64\) (Fig. 6). This comparison is presented in Table 16 and the best NCC value is bolded in each attack. An overall comparison shows the priority of our scheme in the common considered attacks.
Conclusion
In this study, a new robust image watermarking based on discrete wavelet transform (DWT) is proposed. This scheme uses DWT properties to achieve the watermarking requirements. These properties are the edge detection and perfect reconstruction of the DWT. In the detection process of the proposed algorithm, there is no need to any data of watermark or host image and this procedure is completely blind. To the blind extraction and its security properties, the proposed scheme is more appropriate for watermarking applications such as fingerprint, copy, and copyright protections. The experimental results showed that the scheme is invisible with a high PSNR and resistant against many geometrical and non-geometrical attacks with a good NCC values. Two security attacks also are considered that confirms the security property of the scheme.
References
Shih, F.Y.: Image Processing and Patern Recognition. Wiley, Hoboken (2010)
Lin, S., Chen, C.F.: A robust DCT-based watermarking for copyright protection. IEEE Trans. Consum. Electron. 46(3), 415–421 (2000)
Patra, J.C., Phua, J.E., Bornand, C.: A novel DCT domain CRT-based watermark-ing scheme for image authentication surviving JPEG compression. Digit. Signal Process. 20(6), 1597–1611 (2010)
Premaratne, P., Ko, C.: A novel watermark embedding and detection scheme for images in DFT domain. In: 7th International Conference on Image Processing and Its Applications, pp. 780–783 (1999)
Rastegar, S., Namazi, F., Yaghmaie, K., Aliabadian, A.: Hybrid watermarking algorithm based on singular value decomposition and radon transform, AE. Int. J. Electron. Commun. 65(7), 658–663 (2011)
Lai, C.C., Tsai, C.C.: Digital image watermarking using discrete wavelet transform and singular value decomposition. IEEE Trans. Instrum. Meas. 59(11), 3060–3063 (2010)
Lagzian, S., Soryani, M., Fathy, M.: Anew robust watermarking scheme based on RDWT-SVD. Int. J. Intell. Inf. Process. 2(1), 22–29 (2011)
Makbol, N.M., Khoo, B.E.: Robust blind image watermarking scheme based on redundant discrete wavelet transform and singular value decomposition, AE. Int. J. Electron. Commun. 67(2), 102–112 (2013)
Makbol, N.M., Khoo, B.E.: A new robust and secure digital image watermarking scheme based on the integer wavelet transform and singular value decomposition. Digit. Signal Process. 33, 134–147 (2014)
Liu, R., Tan, T.: An SVD-based watermarking scheme for protecting rightful ownership. IEEE Trans. Multimed. 4(1), 121–128 (2002)
Ganic, E., Eskicioglu, A.M.: Robust embedding of visual watermarks using discrete wavelet transform and singular value decomposition. J. Electron. Imaging 14(4), 043004 (2005)
Loukhaoukha, K., Chouinard, J.Y., Haj Taieb, M.: Optimal image watermarking algorithm based on LWTSVD via multi-objective ant colony optimization. J. Inf. Hiding Multimed. Signal Process. 2, 303–319 (2011)
Gupta, A., Raval, M.: Arobust and secure watermarking scheme based on singular values replacement. Sadhana 37, 425–440 (2012)
Gonzalez, R.C., Woods, R.E.: Digital Image Processing, 3rd edn. Pearson International Edition, London (2008)
Daubechies, I.: Ten Lectures on Wavelets. Society for Industrial and Applied Mathematics, Pennsylvania (1992)
Goswami, J.C., Chan, A.K.: Fundamentals of Wavelets, Theory, Algorithms, and Applications. Wiley, New York (1999)
Lee, Y.P., Lee, J.C., Chen, W.K., Chang, K.C., Su, I.J., Chang, C.P.: High-payload image hiding with quality recovery using tri-way pixel-value differencing. Inf. Sci. 191, 214–225 (2012)
Al-Haj, A.: Combined DWT-DCT digital image watermarking. J. Comput. Sci. 3(11), 740–746 (2007)
Bounkong, S., Toch, B., Saad, D., Low, D.: ICA for watermarking digital images. J. Mach. Learn. Res. 4, 1471–1498 (2003)
Schyndel, R.G.V., Tirkel, A.Z., Osborne, C.F.: A digital watermark. IEEE Proc. Int. Conf. Image Process. 2, 86–90 (1994)
Cox, I., Miller, M., Bloom, J.: Digital Watermarking. The Morgan Kaufmann Publishers, San Francisco (2001)
Kutter, M., Voloshynovskiy, S., Herrigel, A.: The Watermark Copy Attack, in Security and Watermarking of Multimedia Contents II, SPIE-3971:371380 (2000)
Al-Nabhani, Y., et al.: Robust watermarking algorithm for digital images using discrete wavelet and probabilistic neural network. J. King Saud Univ. Comput. Inf. Sci. (2015) doi:10.1016/j.jksuci.2015.02.002
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Najafi, E. A robust embedding and blind extraction of image watermarking based on discrete wavelet transform. Math Sci 11, 307–318 (2017). https://doi.org/10.1007/s40096-017-0233-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40096-017-0233-1