Introduction

Proper design for engineering applications requires detailed information of the system-property distributions such as temperature, velocity, density, etc., in space and time domain. This information can be obtained by either experimental measurement or computational simulation. Although experimental measurement is reliable, it needs a lot of labor efforts and time. Therefore, the computational simulation has become a more and more popular method as a design tool, since it needs only a fast computer with a large memory [45].

The solutions of integral equations have a major role in the field of science and engineering. The theory and application of integral equation are an important subject within applied mathematics. Integral equations are used as mathematical models for many physical situations, and integral equations also occur as reformulations of other mathematical problems, such as partial differential equations and ordinary differential equations. A physical even can be modeled by the differential equation, an integral equation. Since few of these equations cannot be solved explicitly, it is often necessary to resort to numerical techniques which are appropriate combinations of numerical integration and interpolation [3, 4, 6, 7, 30]. There are several numerical methods for solving linear Volterra integral equation [16, 49] and system of nonlinear Volterra integral equations [9, 51]. Biazar [12] presented differential transform method for solving systems of integral equations. Kauthen in [25] used a collocation method to solve the Volterra–Fredholm integral equation numerically. Borzabadi and Fard in [14] obtained a numerical solution of nonlinear Fredholm integral equations of the second kind.

In recent years, meshless methods have been developed as alternative numerical approaches in effort to eliminate known shortcomings of the mesh-based methods [8]. The main advantage of these methods is to approximate the unknowns by a linear combination of shape functions. Shape functions are based on a set of nodes and a certain weight function with a local support associated with each of these nodes. Therefore, they can solve many engineering problems that are not suited to the conventional computational methods [17, 47, 53]. Bhrawy et al. [10] reported a new spectral collocation technique for solving second kind Fredholm integral equations (FIEs). They developed a collocation scheme to approximate FIEs by means of the shifted Legendre–Gauss–Lobatto collocation (SL–GL–C) method. Then, they developed an efficient direct solver for solving numerically the high-order linear Fredholm integro-differential equations (FIDEs) with piecewise intervals under the initial-boundary conditions [11]. Maleknejad et al. [33] introduced an approach for obtaining the numerical solution of the nonlinear Volterra–Fredholm integro-differential (NVFID) equations using hybrid Legendre polynomials and block-pulse functions. These hybrid functions and their operational matrices are used for representing matrix form of these equations. Hashemizadeh and Rostami [20] obtained numerical solution of Hammerstein integral equations of mixed type by means of Sinc collocation method is presented. This proposed approximation reduces these kinds of nonlinear Hammerstein integral equations of mixed type to a nonlinear system of algebraic equations.

FNN systems are hybrid systems that combine the theories of fuzzy logic and neural networks. Designing the FNN system based on the input–output data is a very important problem. Several authors investigated FNN, to compute crisp and even fuzzy information with neural network (NN). There existed only a few approaches to learning algorithms for FNN when Ishibuchi et al. presented two NNs which can be trained with interval vectors and with vectors of fuzzy numbers. In both networks, Ishibuchi et al. used crisp weights. For these networks, they presented a backpropagation based on learning algorithm. In a later paper [23], Ishibuchi et al. developed an FNN with symmetric triangular fuzzy numbers as weights. For this NN, they evolved a learning algorithm in which the backpropagation algorithm is used to compute the new lower and upper limits of the support of the weights. The modal value of the new fuzzy weight is calculated as an average of the newly computed limits. Recently, FNN successfully was used for solving fuzzy polynomial equation and systems of fuzzy polynomials [1, 2], approximate fuzzy coefficients of fuzzy regression models [37, 38, 40, 41], approximate solution of fuzzy linear systems and fully fuzzy linear systems [42, 43], and fuzzy differential equations [34,35,36, 44].

In this work, we propose a new solution method for the approximate solution of integral equations using innovative mathematical tools and neural-like systems of computation. This hybrid method can result in improved numerical methods for solving integral equations. In this proposed method, NNM is applied as universal approximator. Neural computation research, together with related areas in approximation theory, has developed powerful methods for approximating continuous and integrable functions on compact subsets. In such schemes, function approximation capabilities critically depend on the activation function nature of the hidden layer. Ito and Saito [24] proved that if the activation function is continuous and nondecreasing sigmoidal function, then the interpolation can be made with inner weights.

Neural network model

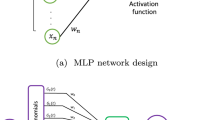
Artificial neural networks are an exciting form of artificial intelligence, which mimic the learning process of the human brain to extract patterns from historical data [2, 48]. For many years, this technology has been successfully applied to a wide variety of real-world applications [46]. Simple perceptrons need a teacher to tell the network what the desired output should be. These are supervised networks. In an unsupervised net, the network adapts purely in response to its inputs. Such networks can learn to pick out structure in their input. Figure 1 shows typical three-layered perceptron as a basic structural architecture with an input layer, a single hidden layer, and an output layer [19]. Here, the dimension of NNM is denoted by the number of neurons in each layer, that is N × M × S NNM, where N, M, and S are the number of neurons in the input layer, the hidden layer, and the output layer, respectively. The architecture of the model shows how NNM transforms the N inputs (t 1, …, t i , …, t N ) into the s outputs (x 1, …, x k , …, x S ) throughout the m hidden neurons (z 1, …, z j , …, z M ), where the cycles represent the neurons in each layer. Let b j be the bias for neuron z j , c k be the bias for neuron x k , w ji be the weight connecting neuron x i to neuron z j , and w kj be the weight connecting neuron z j to neuron x k . Then, the output of NNM \( f:{\text{R}}^{N} \to {\text{R}}^{S} \) can be determined as follows:

Fig. 1
figure 1

Multiple layer feed-forward NNM

Full size image
$$ x_{k} = f_{k} \left( {\sum\limits_{j = 1}^{M} w_{kj} z_{j} + c_{k} } \right), $$
(1)

with

$$ z_{j} = f_{j} \left( {\sum\limits_{i = 1}^{N} w_{ji} t_{i} + b_{j} } \right), $$
(2)

where f k and f j are the activation functions which are linear, piecewise linear, hard limiter, unipolar sigmoidal, and bipolar sigmoidal functions. The usual choices of the activation function [21, 28, 45] are the unipolar sigmoidal of the form:

$$ f(\theta ) = \frac{1}{1 + \exp ( - \theta )}. $$
(3)

Multi-layered perceptrons with more than three layers, which use more hidden layers [21, 26]. Multi-layered perceptrons correspond the input units to the output units by a specific nonlinear mapping [50]. The most important application of multi-layered perceptrons is their ability in function approximation [15]. From Kolmogorov existence theorem, we know that a three-layered perceptron with n(2n + 1) nodes can compute any continuous function of n variables [22, 31]. The accuracy of the approximation depends on the number of neurons in the hidden layer and does not depend on the number of the hidden layers [27].

Hammerstein–Volterra delay integral equations

The present paper deals with the investigation of the Volterra integral equation having a constant delay:

$$ x(t) = g(t) + \lambda \int_{t - \tau }^{t} H(t,s) \cdot x(s){\text{d}}s,\quad t \in [0,T], $$
(4)

with the initial condition

$$ x(t) = \psi (t),\quad t \in [ - \tau ,0], $$
(5)

where τ > 0 and T > 0 are such that T = p ∙ τ for given \( p \in {\text{N}} \), and g and ψ are known functions and \( H:[0,T] \times [ - \tau ,T] \to {\text{R}} \) is a weight function. This equation is a mathematical model for the spread of certain infectious diseases with a contact rate that varies seasonally. Here, x(t) is the proportion of infectives in the population at time t, τ > 0  is the length of time in which an individual remains infectious, and H(t, s).x(s) is the proportion of new infectives per unit time [39]. Throughout this paper, we always assume that the solution of (4) and (5) exists and is unique. Now, we study the NNM to approximate the solution of Eqs. (4) and (5).

The integral Eq. (4) contains a constant delay and its variant is the generalization of an epidemic model (see [18]), where H(t, s) = P(t − s). First, we define the operator:

$$ T_{1} (t,x(t)) = x(t) - g(t) - \lambda \int_{t - \tau }^{t} H(t,s) \cdot x(s){\text{d}}s, $$
(6)
$$ T_{2} (t,x(t)) = x(t) - \psi (t). $$
(7)

To obtain approximate solution x M (t, P), we solve unconstrained optimization problem that is simpler to deal with; we define the trial function to be in the following form:

$$ x_{M} (t,P) = N_{M} (t,P), $$
(8)

where the term in the right-hand side is a feed-forward neural network consisting of an input t and P is the vector containing all the adjustable parameters of NNM [32]. This NNM with some weights and biases is considered, and we train to compute the approximate solution of HVDIEs.

Substituting (8) into Eqs. (4) and (5), we can obtain the expression:

$$ T_{1} (t,x_{M} (t)) = x_{M} (t) - g(t) - \lambda \int_{t - \tau }^{t} H(t,s).x_{M} (s){\rm d}s,\quad t \in [0,T], $$
(9)
$$ T_{2} (t,x_{M} (t)) = x_{M} (t) - \varPhi (t),\quad t \in [ - \tau ,0]. $$
(10)

For any \( t \in [ - \tau ,0],R_{{M_{2} }} (t) = T_{2} (t,x_{M} (t)) - T_{2} (t,x(t)) \) and for any \( t \in [0,T],R_{{M_{1} }} (t) = T_{1} (t,x_{M} (t)) - T_{1} (t,x(t)) \) is called the remaining items of Eqs. (4) and (5), where M is the numbers of neurons or hidden layers for NNM; also in addition, we have:

$$ R_{{M_{1} }} (t) = (x_{M} (t) - x(t)) - \lambda \int_{t - \tau }^{t} H(t,s) \cdot (x_{M} (s) - x(s)){\text{d}}s, $$

and

$$ R_{{M_{2} }} (t) = x_{M} (t) - x(t). $$

Remark 1

For any t ∊ [ −τ, T],  if \( R_{{M_{1} }} (t) = 0 \) and \( R_{{M_{2} }} (t) = 0, \) then x(t) = x M (t);  if \( \lim_{M \to \infty } R_{{M_{1} }} (t) = 0 \) and \( \lim_{M \to \infty } R_{{M_{2} }} (t) = 0, \) then lim  M→∞ x M (t) = x(t).

Remark 2

For any t ∊ [ −τ, T],  if \( R_{{M_{1} }} (t) \equiv 0 \) and \( R_{{M_{2} }} (t) \equiv 0, \) then x M (t) is an exact solution of Eqs. (4) and (5); if \( \lim_{M \to \infty } R_{{M_{1} }} (t) = 0 \) and \( \lim_{M \to \infty } R_{{M_{2} }} (t) = 0, \) then x M (t) converges to the exact solution of Eqs. (4) and (5).

Remark 3

If \( \lim_{M \to \infty } \frac{1}{2}\int_{ - \tau }^{0} T_{2}^{2} (t,x_{M} (t)){\text{d}}t + \frac{1}{2}\int_{0}^{T} T_{1}^{2} (t,x_{M} (t)){\text{d}}t = 0, \), then the approximation solution x M (t) converges to the exact solution x(t) of Eqs. (4) and (5).

To compute the integrals from Eqs. (4) and (5), we consider the uniform partition of [ −τ, T]:

$$ \Delta : - \tau = t_{0} < t_{1} < \cdots < t_{n} = 0 < t_{n + 1} < \cdots < t_{q} = T $$

with \( q = (p + 1)n,t_{i} = t_{i - 1} + \frac{\tau }{n} = - \tau + \frac{i\tau }{n},i = \overline{1,q} . \) On these knots, the terms of the sequence of successive approximations are the following:

$$ x(t_{i} ) = \psi (t_{i} ),\quad i = \overline{0,n} , $$
$$ x(t_{i} ) = g(t_{i} ) + \lambda \int_{{t_{i} - \tau }}^{{t_{i} }} H(t_{i} ,s) \cdot x(s){\text{d}}s,\quad i = \overline{n + 1,q} . $$
(11)

The numerical calculation can be implemented to determine the integration of Eq. (11). Let us consider a three-layered NNM (see Fig. 2) with one unit entry t, one hidden layer consisting of M activation functions, and one unit output N M (t, P). In this paper, we use the unipolar sigmoidal activation function f(.). Here, the dimension of NNM is 1 × M × 1.

Fig. 2
figure 2

NNM with one input unit and one output unit

Full size image

Hence, in our proposed UAM, the solution of HVDIEs can be simply obtained with the algorithm of optimization; in addition, the adjustable parameters of NNM are systematically updated in such a way. Hence, the problem formulation can be expressed as the typical minimization problem:

$$ {\text{Minimize}}\quad J(P) $$
(12)

where P is the vector containing all the adjustable parameters. For instance, we can use the penalty method for the minimization problem. Therefore, for solving HVDIEs by Eq. (12), we have:

$$ {\text{Minimize}}\quad \sum\limits_{g = 1}^{G} \frac{1}{2}T_{2}^{2} (t_{g} ,x_{M} (t_{g} )) + \frac{1}{2}T_{1}^{2} (t_{g} ,x_{M} (t_{g} )), $$
(13)

where G is the total number of points chosen within the domain of [−τ, T] and g is the point index.

Below, we present the following algorithm that gives the approximate solution using NNM:

Step 1  Choose the numbers of neurons and hidden layers for NNM as small as possible at the beginning.

Step 2  Apply an optimization technique to determine the sub-optimal adjustable parameters of NNM in such a way that the residual errors are minimized.

Step 3  If the residual errors are less than tolerance then stop.

If not, then try to increase the various numbers in Step 1 and go to Step 2.

Figure 3 shows the overall diagram of the proposed UAM in determining the solution of HVDIEs.

Fig. 3
figure 3

Diagram of proposed NNM

Full size image

Numerical examples

In this section, two examples are given to illustrate the technique proposed in this paper.

Example 4.1

Consider the initial value problem:

$$ x(t) = \left\{ {\begin{array}{*{20}l} {{\text{e}}^{t - \tau } + \int_{t - \tau }^{t} x (s){\text{d}}s,} \hfill & {\quad t \in [0,0.5],} \hfill \\ {\psi (t),} \hfill & {\quad t \in [ - \tau ,0],} \hfill \\ \end{array} } \right. $$

with τ = 0.5, T = 0.5, and ψ:[ −0.5, 0] → R is defined by ψ(t) = e t, t ∊ [ −τ, 0]. The exact solution is x:[ −0.5, 0.5] → R given by x(t) = e t, t ∊ [ −0.5, 0.5]. Applying for M = 9, the above presented method, we obtain approximate solution with the error 3.21e−13. The exact and obtained solutions of Hammerstein–Volterra delay integral equation in this example are shown in Fig. 4. We see that the approximate solution obtained by the NNM has good accuracy on the whole interval. In Table 1, we compare the error of the present method (Method 1), method 2 in [13], method 3 in [5], method 4 in [52], and method 5 in [39].

Fig. 4
figure 4

Compares the exact solution and obtained solution

Full size image
Table 1 Comparison of the errors for Example 4.1
Full size table

Example 4.2

According to the epidemic model presented in [18], we consider that x(t) be the proportion of infectious individuals at the moment s, f(x(s)) be the proportion of new infected cases on unit time, and g(t) be the proportion of immigrants that still have the disease at the moment t. Considering P(s) as the probability of having the infection for a time at least s after infection, the spread of infection is governed by the integral equation:

$$ x(t) = \left\{ {\begin{array}{*{20}l} {g(t) + \int_{t - \tau }^{t} P (t - s) \cdot f(x(s)){\text{d}}s,} \hfill & {\quad t \in [0,T],} \hfill \\ {\psi (t),} \hfill & {\quad t \in [ - \tau ,0].} \hfill \\ \end{array} } \right. $$

Suppose that the proportion of new infected cases on unit time, f(x(s)) is proportional with x(s), and P is a positive decreasing function with P(0) = 1. Let τ = T = 0.5. Since it is natural to suppose that the proportion of immigrants that still have the disease is decreasing in time according to the decisions of the authorities, we were shown to the following model:

$$ x(t) = \left\{ {\begin{array}{*{20}l} {g(t) + \int_{t - \tau }^{t} {{\text{e}}^{ - (t - s)} } \,\cdot\,x(s){\text{d}}s,} \hfill & {\quad t \in [0,0.5],} \hfill \\ {\psi (t),} \hfill & {\quad t \in [ - 0.5,0],} \hfill \\ \end{array} } \right. $$

with g(t) = 0.5e−t and ψ(t) = e−t. The exact solution is x:[ −0.5, 0.5] → R given by x(t) = e−t, t ∊ [ −0.5, 0.5]. Applying, for M = 10, the above presented method, we obtain approximate solution with the error 4.23e−9. The exact and obtained solutions of Hammerstein–Volterra delay integral equation in this example are shown in Fig. 5.

Fig. 5
figure 5

Compares the exact solution and obtained solution

Full size image

Conclusions

Solving Hammerstein–Volterra delay integral equations using the universal approximators, that is, NNM was presented in this paper. We proposed NNM approximation method based on unipolar sigmoidal functions. The reliability and efficiency of the proposed method are demonstrated on the numerical experiments. In addition, we can execute this method in a computer simply.