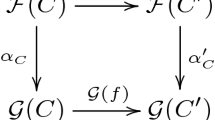Ideal extension of semigroups and their compactifications

Abstract

In this paper we consider compactification spaces of ideal extension for topological semigroups. As a consequence, we characterize compactification spaces for Brandt λ-extension of topological semigroups.

Introduction

Ideal extension for semigroups was studied by Clifford and Preston in [2]. Afterward, ideal extension for topological semigroup was considered by Chiristoph in [3]. He showed that if S and T are two disjoint topological semigroups such that T has a zero, then $H={\overline{T}}^{*}\cup (0\times S)$ is an ideal extension of S by T where $\overline{T^{*}}=\{(t,f(t)):t\in T\backslash \{0\}\}.$ Now, the natural question is: if H is an ideal extension of topological semigroup S by T and H′, S′ and T′ are compactifications of H, S and T respectively, can H′ be naturally characterized by S′ and T′? In this paper we investigate ideal extension for topological semigroups using congruences of semigroups, then we apply this method to characterize compactification spaces of this structure.

Preliminaries

Throughout, we use the notations introduced in [1]. For terms which are not introduced here, the reader may refer to [1, 2, 5, 6]. Let $\mathcal{B}(S)$ be the C^*-algebra of all bounded complex valued functions on S, $\mathfrak{F}$ be a unital C^*-subalgebra of $\mathcal{B}(S),$$S^{\mathcal{F}}$ be the set of all multiplicative means on $\mathcal{F}$ and $\mathit{\epsilon }:S\to S^{\mathcal{F}}$ be the evaluation mapping. $\mathcal{F}$ is called m-admissible if $T_{\mathit{\mu }}(\mathcal{F})\subseteq \mathcal{F}$ for all $\mathit{\mu }\in S^{\mathcal{F}},$ where T _μ (f)(s) = μ(L _s (f)), s ∈ S, $f\in \mathcal{F}.$ Now, $S^{\mathcal{F}}$ with the Gelfand topology and multiplication $\mathit{\mu }\mathit{\nu }(f)=\mathit{\mu }(T_{\mathit{\nu }}(f)),\mathit{\mu },\mathit{\nu }\in S^{\mathcal{F}}$ is a compact Hausdorff right topological semigroup. Also if (ψ, X) is a compactification of S, then ψ^*(C(X)) is an m-admissible subalgebra of C(S). Conversely, if $\mathcal{F}$ is an m-admissible subalgebra of C(S), then there exists a unique (up to isomorphism) compactification (ψ, X) of S such that ${\mathit{\psi }}^{\ast }(C(X))=\mathcal{F}.$ The compactification corresponding to the m-admissible subalgebra $\mathcal{F}$ is $(\mathit{\epsilon },S^{\mathcal{F}})$ and ${\mathit{\epsilon }}^{\ast }(C(S^{\mathcal{F}}))=\mathcal{F}.$ A compactification with a given property $\mathcal{P}$ is called a $\mathcal{P}$-compactification. A universal $\mathcal{P}$-compactification of S is a $\mathcal{P}$-compactification of which every $\mathcal{P}$-compactification of S is a factor. Universal $\mathcal{P}$-compactifications, if they exist, are unique (up to isomorphism). We denote the universal $\mathcal{P}$-compactification of S by $S^{\mathcal{P}}.$

Compactifications of ideal extensions of semigroup

In this paper S and T^* = T − {0} are semigroups with identities 1 _S ,1 _T respectively.

By a partial homomorphism we mean a mapping $A\mapsto \overline{A}$ of T^* = T − {0} into S such that $\overline{AB}=\overline{A}\overline{B},$ whenever AB ≠ 0 and $\overline{1_T}=1_S.$ It is known that a partial homomorphism $A\to \overline{A}$ of the semigroup T^* into S determines an extension $\mathrm{\Omega }$ of S by T as follows. For A, B ∈ T and s, t ∈ S, 

$$\begin{array}{cc}\hfill (P1)AoB& =\left\{\begin{array}{cc}AB\hfill & \mathrm{if}AB\ne 0\hfill \\ \overline{A}\overline{B}\hfill & \mathrm{if}AB=0\hfill \end{array}\right.\hfill \\ \hfill (P2)Aos& =\overline{A}s,(P3)soA=s\overline{A},(P4)sot=st.\hfill \end{array}$$

and every extension can be so constructed [2, 4.19].

Let S and T be disjoint topological semigroups, with T having a zero element 0. A topological semigroup $\mathrm{\Omega }$ is called an ideal extension of S by T if $\mathrm{\Omega }$ contains S as an ideal and the Rees factor semigroup $\frac{\mathrm{\Omega }}{S}$ is topologically isomorphic to T. The existence of ideal extension of topological semigroups was expressed in [3]. In the next Theorem we introduce the ideal extension of topological semigroups using congruences technique on semigroups which is our main tool in the following.

Theorem 1

LetSandTbe disjoint topological semigroups such thatThas a zero and$\mathrm{\Omega }$be ideal extension ofSbyT. Then there exists a congruence ρ on$\mathrm{\Omega }$such that$\frac{\mathrm{\Omega }}{\mathit{\rho }}\simeq \frac{\mathrm{\Omega }}{S}\simeq T.$

Proof

We regard $\mathrm{\Omega }\times \mathrm{\Omega }$ with the product topology. Let τ be the equivalence relation generated by $\{(u,s{u}^{\prime })\mid s\in S,u,u^{\prime }\in \mathrm{\Omega }\}$ and ${\mathit{\rho }}_{{}_{\mathrm{\Omega }}}=\{(x,y)\in \mathrm{\Omega }\times \mathrm{\Omega }\mid (uxv,uyv)\in \mathit{\tau },\mathrm{for}\mathrm{all}u,v\in \mathrm{\Omega }\}.$ By Proposition 1.5.10 [5], ${\mathit{\rho }}_{{}_{\mathrm{\Omega }}}$ is the largest congruence on $\mathrm{\Omega }\times \mathrm{\Omega }$ contained in τ. We use the techniques of Proposition 8.1.8 [5] to show that if $u_1{\mathit{\rho }}_{{}_{\mathrm{\Omega }}}{u}_2,$ then u₁ = u₂ or there exists $s\in S$ such that u₁ = su₂. Since $\mathrm{\Omega }$ is a topological semigroup, ${\mathit{\rho }}_{{}_{\mathrm{\Omega }}}$ is closed congruence on $\mathrm{\Omega }.$ Thus, $\frac{\mathrm{\Omega }}{{\mathit{\rho }}_{{}_{\mathrm{\Omega }}}}$ is a topological semigroup with quotient topology. Let $\mathit{\pi }:\mathrm{\Omega }\to \frac{\mathrm{\Omega }}{{\mathit{\rho }}_{{}_{\mathrm{\Omega }}}}$ be the natural quotient map. If $v\in ker(\mathit{\pi })={[1]}_{{\mathit{\rho }}_{{}_{\mathrm{\Omega }}}},$ then v = s.1 = s. Hence, $ker(\mathit{\pi })=\{u\in \mathrm{\Omega }\mid [u]=1\}=S.$ This implies that $\frac{\mathrm{\Omega }}{{\mathit{\rho }}_{{}_{\mathrm{\Omega }}}}\simeq \frac{\mathrm{\Omega }}{S}\simeq T.$

Let S and T be disjoint topological semigroups such that T has a zero and $\mathrm{\Omega }$ be an ideal extension of S by T. Let (ψ, X) be a topological semigroup compactification of $\mathrm{\Omega }$ and ${\mathit{\tau }}_{{}_X}$ be the equivalence relation generated by $\{(x,\mathit{\psi }(s)y)\mid x,y\in X,s\in S\}$ and ${\mathit{\rho }}_{{}_X}$ be the closure of the largest congruence on X × X contained in ${\mathit{\tau }}_{{}_X}.$ We fixed these notations for the rest of this paper. □

Theorem 2

LetS, Tbe disjoint topological semigroups such thatThas a zero and$\mathrm{\Omega }$be an ideal extension ofSbyT. Let (ψ, X) be a topological semigroup compactification of$\mathrm{\Omega }.$Then$\frac{X}{{\mathit{\rho }}_{{}_X}}$is a topological semigroup compactification of $\frac{\mathrm{\Omega }}{S}\simeq T.$

Proof

Let ${\mathit{\sigma }}_1{\mathit{\rho }}_{{}_{\mathrm{\Omega }}}{\mathit{\sigma }}_2,$ then $\mathit{\psi }({\mathit{\sigma }}_1){\mathit{\rho }}_{{}_X}\mathit{\psi }({\mathit{\sigma }}_2).$ Thus ψ preserves congruence. This implies that there exists a continuous homomorphism $\widehat{\mathit{\psi }}:\frac{\mathrm{\Omega }}{{\mathit{\rho }}_{{}_{\mathrm{\Omega }}}}\to \frac{X}{{\mathit{\rho }}_{{}_X}}$ such that $\widehat{\mathit{\pi }}\circ \mathit{\psi }=\widehat{\mathit{\psi }}\circ \mathit{\pi },$ where $\mathit{\pi }:\mathrm{\Omega }\to \frac{\mathrm{\Omega }}{{\mathit{\rho }}_{{}_{\mathrm{\Omega }}}},\widehat{\mathit{\pi }}:X\to \frac{X}{{\mathit{\rho }}_{{}_X}}.$ Since ρ _X is closed and X is a compact Hausdorff topological semigroup, $\frac{X}{{\mathit{\rho }}_{{}_X}}$ is a compact Hausdorff topological semigroup. We have $\overline{\widehat{\mathit{\psi }}\left(\frac{\mathrm{\Omega }}{{\mathit{\rho }}_{{}_{\mathrm{\Omega }}}}\right)}=\overline{\widehat{\mathit{\psi }}o\mathit{\pi }(\mathrm{\Omega })}=\overline{\widehat{\mathit{\pi }}o\mathit{\psi }(\mathrm{\Omega })}\supseteq \widehat{\mathit{\pi }}(\overline{\mathit{\psi }(\mathrm{\Omega })})=\widehat{\mathit{\pi }}(X)=\frac{X}{{\mathit{\rho }}_{{}_X}}.$ Also $\widehat{\mathit{\psi }}\left(\frac{\mathrm{\Omega }}{{\mathit{\rho }}_{{}_{\mathrm{\Omega }}}}\right)=\widehat{\mathit{\psi }}o\mathit{\pi }(\mathrm{\Omega })=\widehat{\mathit{\pi }}o\mathit{\psi }(\mathrm{\Omega })\subseteq \widehat{\mathit{\pi }}(\mathrm{\Lambda }(X))=\mathrm{\Lambda }(\widehat{\mathit{\pi }}(X))=\left(\frac{X}{{\mathit{\rho }}_{{}_X}}\right).$ Therefore, $\frac{X}{{\mathit{\rho }}_{{}_X}}$ is a topological semigroup compactification of $\frac{\mathrm{\Omega }}{{\mathit{\rho }}_{{}_{\mathrm{\Omega }}}}\simeq T.$ □

Theorem 3

LetSandTbe disjoint topological semigroups such thatThas a zero and$\mathrm{\Omega }$be an ideal extension ofSbyT. Let$({\mathit{\epsilon }}_T,T^{\mathcal{P}})$and$({\mathit{\epsilon }}_{\mathrm{\Omega }},{\mathrm{\Omega }}^{\mathcal{P}})$be the universal$\mathcal{P}$-compactifications ofTand$\mathrm{\Omega }$respectively. Then$T^{\mathcal{P}}\simeq \frac{{\mathrm{\Omega }}^{\mathcal{P}}}{{\mathit{\rho }}_{{}_{{\mathrm{\Omega }}^{\mathcal{P}}}}}$ if

• 1. $\mathcal{P}$ is invariant under homomorphism,

• 2. universal $\mathcal{P}$ -compactification is a topological semigroup.

Proof

By Theorem 2, $\left(\widehat{\mathit{\epsilon }}{}_{{}_{\mathrm{\Omega }}},\frac{{\mathrm{\Omega }}^{\mathcal{P}}}{{\mathit{\rho }}_{{}_{{\mathrm{\Omega }}^{\mathcal{P}}}}}\right)$ is a compactification of $\frac{\mathrm{\Omega }}{S}\simeq T.$ By universal property of $\mathcal{P}$-compactification $({\mathit{\epsilon }}_T,T^{\mathcal{P}})$ of T [1, 1.4.10], there exists a continuous homomorphism ${\mathit{\varphi }}_1:T^{\mathcal{P}}⟶\frac{{\mathrm{\Omega }}^{\mathcal{P}}}{{\mathit{\rho }}_{{}_{{\mathrm{\Omega }}^{\mathcal{P}}}}}$ such that ${\mathit{\phi }}_1\circ {\mathit{\epsilon }}_T=\widehat{{\mathit{\epsilon }}_{{}_{\mathrm{\Omega }}}}.$ Also homomorphism $\mathit{\eta }={\mathit{\epsilon }}_T\circ \mathit{\pi }:\mathrm{\Omega }\to \frac{\mathrm{\Omega }}{S}\simeq T\to T^{\mathcal{P}}$ provides a continuous homomorphism ${\mathit{\phi }}_2:{\mathrm{\Omega }}^{\mathcal{P}}⟶T^{\mathcal{P}}$ such that ${\mathit{\phi }}_2\circ {\mathit{\epsilon }}_{\mathrm{\Omega }}=\mathit{\eta }.$ Let ${\widehat{\mathit{\sigma }}}_1{\mathit{\rho }}_{{}_{{\mathrm{\Omega }}^{\mathcal{P}}}}{\widehat{\mathit{\sigma }}}_2$ (${\widehat{\mathit{\sigma }}}_1,{\widehat{\mathit{\sigma }}}_2\in {\mathrm{\Omega }}^{\mathcal{P}}$). Choose nets {u_α}, {v_α} in $\mathrm{\Omega }$ such that ${lim}_{\mathit{\alpha }}{\mathit{\epsilon }}_{{}_{\mathrm{\Omega }}}(u_{\mathit{\alpha }})={\widehat{\mathit{\sigma }}}_1,$${lim}_{\mathit{\alpha }}{\mathit{\epsilon }}_{{}_{\mathrm{\Omega }}}(v_{\mathit{\alpha }})={\widehat{\mathit{\sigma }}}_2$. We have ${\widehat{\mathit{\sigma }}}_1=\widehat{s}{\widehat{\mathit{\sigma }}}_2,$ where $\widehat{s}={\mathit{\epsilon }}_{{}_{\mathrm{\Omega }}}(s)$ for some s  ∈ S. Thus,

$$\begin{array}{cc}\hfill {\mathit{\phi }}_2({\widehat{\mathit{\sigma }}}_1)={\mathit{\phi }}_2(\widehat{s}{\widehat{\mathit{\sigma }}}_2)& ={\mathit{\phi }}_2({\mathit{\epsilon }}_{\mathrm{\Omega }}(s)\underset{\mathit{\alpha }}{lim}{\mathit{\epsilon }}_{\mathrm{\Omega }}(v_{\mathit{\alpha }}))\hfill \\ \hfill & =\underset{\mathit{\alpha }}{lim}{\mathit{\phi }}_{2}o{\mathit{\epsilon }}_{\mathrm{\Omega }}(s{v}_{\mathit{\alpha }})=\underset{\mathit{\alpha }}{lim}\mathit{\eta }(s{v}_{\mathit{\alpha }})\hfill \\ \hfill & =\underset{\mathit{\alpha }}{lim}\mathit{\eta }(s)\mathit{\eta }(v_{\mathit{\alpha }})=\underset{\mathit{\alpha }}{lim}{\mathit{\phi }}_{2}o{\mathit{\epsilon }}_{\mathrm{\Omega }}(v_{\mathit{\alpha }})\hfill \\ \hfill & ={\mathit{\phi }}_2({\widehat{\mathit{\sigma }}}_2)\hfill \end{array}$$

Then, ${\mathit{\phi }}_2$ preserves congruence. Thus there exists a continuous homomorphism ${\mathit{\phi }}_3:\frac{{\mathrm{\Omega }}^{\mathcal{P}}}{{\mathit{\rho }}_{{}_{{\mathrm{\Omega }}^{\mathcal{P}}}}}⟶T^{\mathcal{P}}$ such that ${\mathit{\phi }}_3\circ {\mathit{\pi }}_{{}_{{\mathrm{\Omega }}^{\mathcal{P}}}}={\mathit{\phi }}_2,$ where ${\mathit{\pi }}_{{}_{{\mathrm{\Omega }}^{\mathcal{P}}}}:{\mathrm{\Omega }}^{\mathcal{P}}\to \frac{{\mathrm{\Omega }}^{\mathcal{P}}}{{\mathit{\rho }}_{{}_{{\mathrm{\Omega }}^{\mathcal{P}}}}}.$We show that ${\mathit{\phi }}_{1}o{\mathit{\phi }}_3={\mathrm{id}}_{\frac{{\mathrm{\Omega }}^{\mathcal{P}}}{{\mathit{\rho }}_{{}_{{\mathrm{\Omega }}^{\mathcal{P}}}}}}.$ If ${\mathit{\pi }}_{{}_{{\mathrm{\Omega }}^{\mathcal{P}}}}(t)\in \frac{{\mathrm{\Omega }}^{\mathcal{P}}}{{\mathit{\rho }}_{{}_{{\mathrm{\Omega }}^{\mathcal{P}}}}},$ then we can find a net $\{{\mathit{\sigma }}_{\mathit{\alpha }}\}$ in $\mathrm{\Omega }$ such that ${lim}_{\mathit{\alpha }}{\mathit{\epsilon }}_{{}_{\mathrm{\Omega }}}({\mathit{\sigma }}_{\mathit{\alpha }})=t.$ we have

$$\begin{array}{cc}\hfill {\mathit{\phi }}_{1}o{\mathit{\phi }}_3({\mathit{\pi }}_{{}_{{\mathrm{\Omega }}^{\mathcal{P}}}}(t))& ={\mathit{\phi }}_{1}o{\mathit{\phi }}_2(t)=\underset{\mathit{\alpha }}{lim}{\mathit{\phi }}_{1}o{\mathit{\phi }}_2({\mathit{\epsilon }}_{{}_{\mathrm{\Omega }}}({\mathit{\sigma }}_{\mathit{\alpha }}))\hfill \\ \hfill & =\underset{\mathit{\alpha }}{lim}{\mathit{\phi }}_{1}o\mathit{\eta }({\mathit{\sigma }}_{\mathit{\alpha }})=\underset{\mathit{\alpha }}{lim}{\mathit{\phi }}_{1}o{\mathit{\epsilon }}_{T}o\mathit{\pi }({\mathit{\sigma }}_{\mathit{\alpha }})\hfill \\ \hfill & =\underset{\mathit{\alpha }}{lim}\widehat{{\mathit{\epsilon }}_{{}_{\mathrm{\Omega }}}}o\mathit{\pi }({\mathit{\sigma }}_{\mathit{\alpha }})=\underset{\mathit{\alpha }}{lim}{\mathit{\pi }}_{{}_{{\mathrm{\Omega }}^{\mathcal{P}}}}({\mathit{\epsilon }}_{{}_{\mathrm{\Omega }}}({\mathit{\sigma }}_{\mathit{\alpha }}))\hfill \\ \hfill & ={\mathit{\pi }}_{{}_{{\mathrm{\Omega }}^{\mathcal{P}}}}(\underset{\mathit{\alpha }}{lim}{\mathit{\epsilon }}_{{}_{\mathrm{\Omega }}}({\mathit{\sigma }}_{\mathit{\alpha }}))={\mathit{\pi }}_{{}_{{\mathrm{\Omega }}^{\mathcal{P}}}}(t).\hfill \end{array}$$

Similarly, ${\mathit{\phi }}_{3}o{\mathit{\phi }}_1=i{d}_{T^{\mathcal{P}}}.$ Therefore, $T^{\mathcal{P}}\simeq \frac{{\mathrm{\Omega }}^{\mathcal{P}}}{{\mathit{\rho }}_{{}_{{\mathrm{\Omega }}^{\mathcal{P}}}}}.$ □

Corollary 1

Let$\mathrm{\Omega }$be an ideal extension of topological semigroupSby topological semigroupT. Let$({\mathit{\epsilon }}_s,S^{\mathrm{sap}}),({\mathit{\epsilon }}_{\mathrm{\Omega }},{\mathrm{\Omega }}^{\mathrm{sap}})$[resp. $({\mathit{\epsilon }}_s,S^{\mathrm{ap}}),({\mathit{\epsilon }}_{\mathrm{\Omega }},{\mathrm{\Omega }}^{\mathrm{ap}})]$be the strongly almost periodic compactifications[resp. almost periodic compactifications ] ofSand$\mathrm{\Omega },$respectively. Then$T^{\mathrm{sap}}\simeq \frac{{\mathrm{\Omega }}^{\mathrm{sap}}}{{\mathit{\rho }}_{{}_{{\mathrm{\Omega }}^{\mathrm{sap}}}}}$[resp. $T^{\mathrm{ap}}\simeq \frac{{\mathrm{\Omega }}^{\mathrm{ap}}}{{\mathit{\rho }}_{{}_{{\mathrm{\Omega }}^{\mathrm{ap}}}}}],$where$\widehat{S}={\mathit{\rho }}_{{}_{{\mathrm{\Omega }}^{\mathrm{sap}}}}$[resp. where$\widehat{S}={\mathit{\rho }}_{{}_{{\mathrm{\Omega }}^{\mathrm{ap}}}}].$

Example 1

Let $S={\mathcal{M}}^0(G,P,I,J)$ be the Rees matrix semigroup where G is a topological group, I and J are arbitrary nonempty sets and P = (p _ji ) is a J × I matrix with entries in G⁰ = G∪{0}. In [7], it is shown that there is a continuous partial homomorphism $\mathit{\theta }:S\to G;$ then there exists an extension $\mathrm{\Omega }$ of G by S and $\frac{\mathrm{\Omega }}{G}\simeq \frac{\mathrm{\Omega }}{\mathit{\rho }}\simeq S$ where ${\mathit{\rho }}_{{}_{\mathrm{\Omega }}}=\{(u,v)\in \mathrm{\Omega }\times \mathrm{\Omega }\mid u=gv\mathrm{for}\mathrm{some}g\in G\}.$ Also, $S^{\mathrm{ap}}\simeq \frac{{\mathrm{\Omega }}^{\mathrm{ap}}}{{\mathit{\rho }}_{{}_{{\mathrm{\Omega }}^{\mathrm{ap}}}}}$ and $S^{\mathrm{sap}}\simeq \frac{{\mathrm{\Omega }}^{\mathrm{sap}}}{{\mathit{\rho }}_{{}_{{\mathrm{\Omega }}^{\mathrm{sap}}}}}$ □

Theorem 4

LetSandTbe disjoint topological semigroups such thatThas a zero and$\mathrm{\Omega }$be ideal extension ofSbyT. Let (ψ _S , X _S ) and (ψ _T , X _T ) be topological semigroup compactifications ofSandT, respectively, such thatX _S ∩ X _T  = $\mathrm{\varnothing }$. Then the following assertion holds.

• (a) Ideal extension$X_{\mathrm{\Omega }}$ of X _S by X _T exist.

• (b) Topological center $\mathrm{\Lambda }(\mathrm{\Omega })$ is an ideal extension of $\mathrm{\Lambda }(S)$ by $\mathrm{\Lambda }(T).$

• (c) $({\mathit{\psi }}_{\mathrm{\Omega }},X_{\mathrm{\Omega }})$ is a topological semigroup compactification of $\mathrm{\Omega }$ where ${\mathit{\psi }}_{{}_{\mathrm{\Omega }}}{{|}_T={\mathit{\psi }}_T,{\mathit{\psi }}_{{}_{\mathrm{\Omega }}}|}_S={\mathit{\psi }}_S.$

Proof

(a) First, we note that if 0 be zero element of T, then ψ _T (0) is zero element of X _T . It is enough to show that there is a continuous partial homomorphism $\widehat{\mathit{\theta }}:X_T^{\ast }=X_T-\{0\}\to X_S.$ Let $x_T\in X_T^{*}$ then there exists net {u_α } in T such that ${\mathit{\psi }}_T(u_{\mathit{\alpha }})\to x_T.$ Now $\{{\mathit{\psi }}_S\circ \mathit{\theta }(u_{\mathit{\alpha }})\}$ is a net in X _S and by compactness of X _S , there exists $x_s\in X_S$ such that ${\mathit{\psi }}_S\circ \mathit{\theta }(u_{\mathit{\alpha }})\to x_S.$ Let $\widehat{\mathit{\theta }}:X_T^{\ast }\to X_S$ by $\widehat{\mathit{\theta }}(x_T)=x_S.$ Obviously, $\widehat{\mathit{\theta }}$ is well defined. Suppose $x_T,y_T\in X_T$ and {u_α}, {v_α} are nets in T such that ${lim}_{\mathit{\alpha }}({\mathit{\psi }}_S\circ \mathit{\theta }(u_{\mathit{\alpha }}))=\widehat{\mathit{\theta }}(x_T)$ and ${lim}_{\mathit{\alpha }}({\mathit{\psi }}_S\circ \mathit{\theta }(v_{\mathit{\alpha }}))=\widehat{\mathit{\theta }}(y_T).$ We have

$$\begin{array}{cc}\hfill \widehat{\mathit{\theta }}(x_T)\widehat{\mathit{\theta }}(y_T)& =\underset{\mathit{\alpha }}{lim}({\mathit{\psi }}_S(\mathit{\theta }(u_{\mathit{\alpha }})){\mathit{\psi }}_S(\mathit{\theta }(v_{\mathit{\alpha }})))\hfill \\ \hfill & =\underset{\mathit{\alpha }}{lim}{\mathit{\psi }}_S(\mathit{\theta }(u_{\mathit{\alpha }}{v}_{\mathit{\alpha }}))\hfill \\ \hfill & =\widehat{\mathit{\theta }}(x_T{y}_T)\hfill \end{array}$$

Clearly, $\widehat{\mathit{\theta }}$ is continuous. Thus by Theorem 1, ideal extension $X_{\mathrm{\Omega }}$ of X _S by X _T exist.

(b) Obviously, $\mathrm{\Lambda }(T)\cap \mathrm{\Lambda }(S)=\mathrm{\varnothing }.$ Define ${\mathit{\theta }}^{\prime }:\mathrm{\Lambda }{(T)}^{*}=\mathrm{\Lambda }(T)-\{0\}\to \mathrm{\Lambda }(S)$ by ${\mathit{\theta }}^{\prime }({\mathit{\lambda }}_t)={\mathit{\lambda }}_{\mathit{\theta }(t)}(t\in T).$ Now θ′ is a continuous partial homomorphism then there exists an ideal extension ω of $\mathrm{\Lambda }(S)$ by $\mathrm{\Lambda }(T).$ Let ${\mathit{\lambda }}_{\mathit{\sigma }}\in \mathrm{\Lambda }(\mathrm{\Omega }).$ Then, if $\mathit{\sigma }\in S$ so ${\mathit{\lambda }}_{\mathit{\sigma }}\in \mathrm{\Lambda }(S)$ and if $\mathit{\sigma }\in T$ so ${\mathit{\lambda }}_{\mathit{\sigma }}\in \mathrm{\Lambda }(T).$ Thus $\mathrm{\Lambda }(\mathrm{\Omega })\subseteq \mathit{\omega }.$ Obviously, $\mathit{\omega }\subseteq \mathrm{\Lambda }(\mathrm{\Omega }).$ Then $\mathrm{\Lambda }(\mathrm{\Omega })=\mathit{\omega }.$

(c) By (a) ideal extension $X_{\mathrm{\Omega }}$ of X _S by X _T exist. Suppose $x\in X_{\mathrm{\Omega }}=X_S\cup X_T^{*},$ then there exists $\{u_{\mathit{\alpha }}\}\in \mathrm{\Omega }=S\cup T^{*}$ such that ${\mathit{\psi }}_{{}_{\mathrm{\Omega }}}(u_{\mathit{\alpha }})\to x.$ Thus $\overline{{\mathit{\psi }}_{{}_{\mathrm{\Omega }}}(\mathrm{\Omega })}=X_{\mathrm{\Omega }}.$ Also,

$$\begin{array}{c}\hfill {\mathit{\psi }}_{{}_{\mathrm{\Omega }}}(S)={\mathit{\psi }}_{{}_{\mathrm{\Omega }}}{|}_S(S)={\mathit{\psi }}_S(S)\subseteq \mathrm{\Lambda }(X_S)\\ \hfill {\mathit{\psi }}_{{}_{\mathrm{\Omega }}}(T)={\mathit{\psi }}_{{}_{\mathrm{\Omega }}}{|}_T(T)={\mathit{\psi }}_T(T)\subseteq \mathrm{\Lambda }(X_T)\end{array}$$

Now by (b), ${\mathit{\psi }}_{{}_{\mathrm{\Omega }}}(\mathrm{\Omega })\subseteq \mathrm{\Lambda }(X_{\mathrm{\Omega }}).$

The following theorem shows that topological semigroup compactifications of S and T can be constructed by topological semigroup compactification of their ideal extension. □

Theorem 5

LetSandTbe disjoint topological semigroups such thatThas a zero and$\mathrm{\Omega }$be an ideal extension ofSbyT. Suppose$({\mathit{\psi }}_{\mathrm{\Omega }},X_{\mathrm{\Omega }})$is a topological semigroup compactification of$\mathrm{\Omega }.$Then there are topological semigroups compactifications (ψ _S , X _S ), (ψ _T , X _T ) ofSandT, respectively, such that$X_{\mathrm{\Omega }}$is an ideal extension ofX _S byX _T .

Proof

Set ${\mathit{\psi }}_S={\mathit{\psi }}_{\mathrm{\Omega }}{\mid }_S:S\to X_{\mathrm{\Omega }}$ and $\overline{{\mathit{\psi }}_S(S)}=X_S.$ It is clear that $X_S\subseteq X_{\mathrm{\Omega }}$ is a compact topological subsemigroup of $X_{\mathrm{\Omega }}$ and $\mathit{\psi }(S)\subseteq \mathrm{\Lambda }(X_S).$ Thus (ψ _S , X _S ) is a topological semigroup compactification of S . Now we show that for every $x,x^{\prime }\in X_{\mathrm{\Omega }},$$(x{X}_S)(x^{\prime }{X}_S)\subseteq x^{\prime \prime }{X}_S$ for some $x^{\prime \prime }\in X_{\mathrm{\Omega }}.$ Let g  ∈ (xX _S )(x′X _S ) then there exist nets {u_α}, {v_α} in $\mathrm{\Omega }$ and u₁,v₁ in X _S such that $g={lim}_{\mathit{\alpha }}{\mathit{\psi }}_{\mathrm{\Omega }}(u_{\mathit{\alpha }})u_1{\mathit{\psi }}_{\mathrm{\Omega }}(v_{\mathit{\alpha }})v_1.$ Also there exist nets {s_α}, {t_α} in S such that ${lim}_{\mathit{\alpha }}{\mathit{\psi }}_S(s_{\mathit{\alpha }})\to u_1,{lim}_{\mathit{\alpha }}{\mathit{\psi }}_S(t_{\mathit{\alpha }})\to v_1.$ Then,

$$\begin{array}{cc}\hfill g& =\underset{\mathit{\alpha }}{lim}{\mathit{\psi }}_{\mathrm{\Omega }}(u_{\mathit{\alpha }}){\mathit{\psi }}_S(s_{\mathit{\alpha }}){\mathit{\psi }}_{\mathrm{\Omega }}(v_{\mathit{\alpha }}){\mathit{\psi }}_S(t_{\mathit{\alpha }})\hfill \\ \hfill & =\underset{\mathit{\alpha }}{lim}{\mathit{\psi }}_{\mathrm{\Omega }}(u_{\mathit{\alpha }}{s}_{\mathit{\alpha }}{v}_{\mathit{\alpha }}{t}_{\mathit{\alpha }})\hfill \end{array}$$

On the other hand, $\frac{\mathrm{\Omega }}{S}\simeq T$ so for every $a,b\in \mathrm{\Omega },$ there exists $c\in \mathrm{\Omega }$ such that aS.bS = cS. Thus for every α, there exists $\{w_{\mathit{\alpha }}\}\in \mathrm{\Omega }$ and $q_{\mathit{\alpha }}\in S$ such that u_αs_αv_αt_α = w_αq_α. The compactness of $X_{\mathrm{\Omega }}$ and X _S allows us to assume g = x′′ q′′ for some $x^{\prime \prime }\in X_{\mathrm{\Omega }},q^{\prime \prime }\in X_S.$ This implies that $\frac{X_{\mathrm{\Omega }}}{X_S}$ is semigroup. Also, $\frac{X_{\mathrm{\Omega }}}{X_S}$ is compact topological semigroup [1, 1.3.8]. Let $X_T=\frac{X_{\mathrm{\Omega }}}{X_S},$ then $X_{\mathrm{\Omega }}$ is a topological extension of X _S by X _T . Let $t\in T\simeq \frac{\mathrm{\Omega }}{S}$ then $t=\mathit{\pi }(\mathit{\sigma })$ for some $\mathit{\sigma }\in \mathrm{\Omega }.$ Define ${\mathit{\psi }}_T:T\to X_T$ by $\mathit{\psi }(t)={\mathit{\pi }}^{\prime }\circ {\mathit{\psi }}_{\mathrm{\Omega }}(\mathit{\sigma })$ where ${\mathit{\pi }}^{\prime }:X_{\mathrm{\Omega }}\to \frac{X_{\mathrm{\Omega }}}{X_S}=X_T.$ It remains to show that (ψ _T , X _T ) is a topological semigroup compactification of T . We have

$$\overline{{\mathit{\psi }}_T(T)}=\overline{{\mathit{\pi }}^{\prime }\circ {\mathit{\psi }}_{\mathrm{\Omega }}(\mathrm{\Omega })}\supseteq {\mathit{\pi }}^{\prime }\circ \overline{{\mathit{\psi }}_{\mathrm{\Omega }}(\mathrm{\Omega })}={\mathit{\pi }}^{\prime }(X_{\mathrm{\Omega }})=\frac{X_{\mathrm{\Omega }}}{X_S}=X_T$$

and

$${\mathit{\psi }}_T(T)={\mathit{\pi }}^{\prime }\circ {\mathit{\psi }}_{\mathrm{\Omega }}(\mathrm{\Omega })\subseteq {\mathit{\pi }}^{\prime }\circ \mathrm{\Lambda }(X_{\mathrm{\Omega }})=\mathrm{\Lambda }({\mathit{\pi }}^{\prime }(X_{\mathrm{\Omega }}))=\mathrm{\Lambda }\left(\frac{X_{\mathrm{\Omega }}}{X_S}\right)=\mathrm{\Lambda }(X_T).$$

□

Compactification of Brant λ-extensions

An important class of semigroups which has been considered from various points of view is completely 0-simple semigroup and Brandt λ-extension [see 2, 4, 5, 6, 7, for instance]. In this section we use topological extension technique to characterize compactification spaces of Brandt λ-extension.

Let G⁰ = G ∪ {0} [resp. G] be a group with zero [resp. group] and, E and F be arbitrary nonempty sets. Let P be a E × F matrix over G⁰ [resp. G]. The set S = G × E × F ∪ {0} [resp. S = G × E × F] is a semigroup under the composition

$$(i,a,j)\circ (l,b,k)=\left\{\begin{array}{cc}(i,a{p}_{jl}b,k)\hfill & \mathrm{if}{p}_{jl}\ne 0\hfill \\ o\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

This semigroup is denoted by S = M(G, P, E, F) and is called Rees E × F matrix semigroup over G⁰ [resp. G] with the sandwich matrix P.

In the special case, if P = I is an identity matrix, S = G⁰ is semigroup with zero, and E = F = I_λ is a set of cardinality λ ≥ 1. Define the semigroup operation on the set B_λ(S) = M(S, I, I_λ, I_λ) by

$$(i,a,j)\circ (l,b,k)=\left\{\begin{array}{cc}(i,ab,k)\hfill & \mathrm{if}j=l\hfill \\ 0,\hfill & \mathrm{if}j\ne l\hfill \end{array}\right.$$

and (i, a, j).0 = 0.(i, a, j) = 0.0 = 0 for all $a,b\in S,i,j,l,k\in I_{\mathit{\lambda }}.$ The semigroup B_λ(S) is called Brandt λ-extension of S [4]. Now let $i\to u_i$ and $j\to v_j$ be mappings of E and F to S such that $u_k.u_k=1_S,\forall k\in \mathit{\lambda }.$ Then mapping $\mathit{\theta }:B_{\mathit{\lambda }}{(S)}^{*}=B_{\mathit{\lambda }}(S)-\{0\}\to S$ by θ (i, s, j) = u _i su _j is a partial homomorphism.

Let S be a topological semigroup with zero and Brandt λ-extension of S , B_λ(S) be equipped with product topology then B_λ(S) is a topological semigroup. Now $\mathit{\theta }:B_{\mathit{\lambda }}{(S)}^{*}=B_{\mathit{\lambda }}(S)-\{0\}\to S^{*}=S-\{0\}$ by θ (i, s, j) = u _i su _j is a continuous partial homomorphism. Then there exists an ideal extension $\mathrm{\Omega }$ of $S^{*}$ by B_λ(S) and $\frac{\mathrm{\Omega }}{S^{*}}\simeq B_{\mathit{\lambda }}(S).$

The following Corollaries are immediately results of Theorems 3.4, 3.5, 3.6.

Corollary 2

LetSbe a topological semigroup with zero and$\mathrm{\Omega }$be an ideal extension of$S^{*}=S-\{0\}$byB_λ(S). Let (ψ , X) be a topological semigroup compactification of topological semigroup$\mathrm{\Omega }.$Then,$\frac{X}{{\mathit{\rho }}_{{}_X}}$is a topological semigroup compactification ofB_λ(S).

Corollary 3

LetSbe a topological semigroup with zero and$\mathrm{\Omega }$be an ideal extension of$S^{*}=S-\{0\}$byB_λ(S). Suppose$({\mathit{\epsilon }}_{B_{\mathit{\lambda }}(S)},B_{\mathit{\lambda }}{(S)}^{\mathcal{P}})$and$({\mathit{\epsilon }}_{\mathrm{\Omega }},{\mathrm{\Omega }}^{\mathcal{P}})$are the universal$\mathcal{P}$-compactifications ofB_λ(S) and$\mathrm{\Omega },$respectively. Then$B_{\mathit{\lambda }}{(S)}^{\mathcal{P}}\simeq \frac{{\mathrm{\Omega }}^{\mathcal{P}}}{{\mathit{\rho }}_{{}_{{\mathrm{\Omega }}^{\mathcal{P}}}}},$if

• 1. $\mathcal{P}$ is invariant under homomorphism,

• 2. universal $\mathcal{P}$ -compactification is a topological semigroup.

Corollary 4

LetSbe a topological semigroup with zero and$\mathrm{\Omega }$be an ideal extension of$S^{*}=S-\{0\}$byB_λ(S). Let$({\mathit{\epsilon }}_{B_{\mathit{\lambda }}(S)},B_{\mathit{\lambda }}{(S)}^{sap})$ [resp. $({\mathit{\epsilon }}_{B_{\mathit{\lambda }}(S)},B_{\mathit{\lambda }}{(S)}^{ap})]$and$({\mathit{\epsilon }}_{\mathrm{\Omega }},{\mathrm{\Omega }}^{sap})$ [resp. $({\mathit{\epsilon }}_{\mathrm{\Omega }},{\mathrm{\Omega }}^{ap})]$be the strongly almost periodic compactifications [resp. almost periodic compactifications] ofB_λ(S) and$\mathrm{\Omega },$respectively. Then$B_{\mathit{\lambda }}{(S)}^{sap}\simeq \frac{{\mathrm{\Omega }}^{sap}}{{\mathit{\rho }}_{{}_{{\mathrm{\Omega }}^{sap}}}}$ [resp. $B_{\mathit{\lambda }}{(S)}^{ap}\simeq \frac{{\mathrm{\Omega }}^{ap}}{{\mathit{\rho }}_{{}_{{\mathrm{\Omega }}^{ap}}}}].$