Introduction

Many studies in the past have been conducted to evaluate the feasibility of using reactors comprising ion transport membrane for the oxy-fuel combustion applications with gaseous fuels [1, 2]. However, to the author’s knowledge there are no studies on utilizing liquid fuels for the same application. CO2 emissions from combustion of fossil fuels in many industries pose a serious threat to the environment. Several CO2 capture technologies [3, 4] are now available, out of which membrane technology appears promising and has the potential to capture CO2 efficiently.

A considerable progress in the application of ion transport membrane technology in the area of gas separation in industry is achieved [5]. In the past, pressure swing adsorption and cryogenic distillation presented conventional ways for the separation of oxygen from air. During the past 20 years, oxygen separation from air utilizing ion transport membranes has shown a considerable progress. This technology offers significant advantages over conventional means through the reduction of energy requirements, operational, and capital costs. Accordingly, it leads to a better plant efficiency. The use of ceramic based membrane technology is expected to gain much commerciality in the near future due to its promising potential for a better and clean environment [6].

In recent decades, the ionic/electronic conducting membranes were used in the process of oxygen separation from atmospheric air in coal gasification plants and power generation cycles utilizing the oxy-fuel combustion technology. Integrating dense mixed-conducting membranes (MCMs) into power cycles with CO2 capture has been considered as the most advanced technology for high efficiency and clean power production. Membrane separation plays an important role in these technologies for CO2 reduction. Especially, the dense mixed-conducting membranes (MCMs) have shown some possibilities of implementation in power generation plants because of their better thermal and chemical stability, and typically higher selectivity [7].

Dense perovskite membranes demonstrate high oxygen ion permeability when subjected to an oxygen partial pressure gradient at high temperatures [8,9,10]. Moreover, the use of ITMs for oxygen separation comes with a penalty of relatively small pressure drop across the unit compared to the existing cryogenic process. It may be noted here that integrating ITMs with a power plant still faces many challenges and operational constraints that needs to be addressed.

ITM units operate at elevated temperatures [11], and are mostly depends on O2 partial pressure difference across the membrane for separation process [12]. In order for the cost of ITM to be reduced and their commercialization to be feasible, next generation ITMs should achieve high permeation fluxes while operating at low temperatures. The aforementioned approaches for ITMs, if developed successfully can commercialize ITM reactor systems [13]. However, important process parameters including ion exchange at the surface, diffusion in porous media and mass transfer either by convection or diffusion should not be neglected [14]. Other expressions such as mixed conducing membranes (MCM), and oxygen transport membranes (OTM) are also used for ion transport membranes [7].

Ion transport membranes (ITMs) are composed of different inorganic compounds combinations. These compounds have a perovskite or fluorite configured crystal lattice structure [15]. The utilization of membranes in gas or air separation processes is expected to increase to five times of its current value by 2020 [16]. Many studies are presently performed to enhance their chemical stability as well as gas separation performance at typical operational conditions [15]. Air Products Company has manufactured small-scale (O2 production of 500 kg every day) ITM units that require only 40% of energy per kg of O2 that are required by conventional large-scale cryogenic systems [16]. As well, the cost of oxygen separation is reduced by 35%. In large-scale power generation applications, in particular, ITM technology is conceded to be the most-promising substitute for cryogenic O2 production technology [7]. Many fundamental research works are to be performed before the integration of ITM technology in the power producing sector. Ceramic materials of the perovskite type are frequently used more than any other materials in ITM reactors. BSCF and LSCF perovskite materials have the potential for industrial applications and can provide oxygen fluxes up to ten times higher than non-perovskite material membranes. Currently, BSCF membranes can deliver oxygen fluxes of more than of 5 ml/(min cm2), [17]. In other cases of membrane materials such as LSCF, LNO or BSCF, the oxygen transport is mainly restricted by oxygen diffusion across the membrane [15].

The performance of oxy-fuel combustors was reviewed by Habib et al. [13]. They also reviewed the materials used in the ITMs and the implementation of these ITMs in reactors that can be integrated in power generation plants. An oxygen permeation investigation in a tubular BSCF oxygen permeable membrane was conducted by Wang et al. [18]. For the case of constant temperature, it was indicated that increase in feed side O2 partial pressure enhances O2 permeation flux. The stability of BSCF membranes with regard to CO2 was also discussed. It was also shown that BSCF membranes exhibit the highest permeability [19].

Several studies have been conducted on BSCF membranes for investigation of their oxygen permeation and other characteristics [20,21,22,23,24]. Many modeling efforts are also made to understand the underlying process of BSCF membranes but in non-reactive environments [25]. However, very few works have been carried out under reactive conditions [26]. Hunt et al. [27] investigated limitations of permeate surface exchange mechanism under non-reactive conditions and suggested that reactive (fuel) operation is essential to improve surface chemistry for future work.

BSCF membranes [28] produce the highest oxygen fluxes under given operating conditions. Recent research papers [29,30,31] indicate that there are substantial efforts to enhance the performance and the stability of BSCF based membranes, especially hollow fiber membranes [30, 31]. Though, there is little work conducted on ITMs performance under reactive conditions, there is absolutely no work carried out on ITMs utilizing liquid fuels as oxidizers. Therefore, the present article presents the investigation of characteristics of liquid fuels in a BSCF parallel tube ITM reactor. The advantages of using liquid fuels include high specific energy, storage safety and availability. Oxy-combustion of liquid fuels has been investigated recently as a solution for carbon capture and reduction of soot and NOx emissions [32]. The use of ITMs to produce oxygen for the conversion of liquid fuels into thermal energy in an oxygen transport reactor (OTR) while capturing CO2 is presented. In this case, the OTR will have two functions: O2 separation and reaction of evaporated liquid fuel with oxygen. A parametric study of the influence of parameters such as oxygen pressure in the feed and the permeate sides on the performance of the OTR is conducted.

Numerical modeling

To model the flow process, it is necessary that the mass, momentum, energy, and species conservation equations should be considered in the axi-symmetric domain. The physical processes in OTR include momentum and energy transport phenomena in addition to the species and their chemical reactions. For the present liquid fuel oxy-combustion case, we have modeled the breakup and/or atomization of liquid fuel, the heating and the evaporation of the fuel droplets and then the combustion of the fuel vapor close to the ITM. We have used a Lagrangian approach to track the fuel droplet through the evaporation process.

Mathematical model equations

The processes of flow, heat transfer and reaction in the ITM reactor are so complicated. The 2D conservation equations used in the present study can be expressed as:

$${\text{Continuity}}\;{\text{equation:}}\;\;\nabla .(\rho U) = S_{i} ,$$
(1)
$${\text{Momentum conservation:}}\;\;\nabla .(\rho UU) = - \nabla p + \mu \nabla^{2} U + \rho \vec{g},$$
(2)
$${\text{Energy}}\;{\text{conservation:}}\;\;(\rho C_{\text{p}} )_{\text{f}} U \cdot \nabla T = \nabla (k_{\text{eff}} \nabla T) + S_{\text{rad}} ,$$
(3)
$${\text{Species conservation:}}\;\;\nabla \cdot (\rho UY_{\text{i}} ) - \nabla \cdot (\rho D_{{i , {\text{m}}}} \nabla Y_{i} ) = S_{i} .$$
(4)

In the present study, the heat transfer by all modes including surface and gas radiation is considered in the energy equation. Initial studies were conducted to investigate the effect of radiation heat transfer. It was found that neglecting the radiation results in very high temperature levels. The inclusion of radiation resulted in lower temperatures by 300–400 K, depending on the concentration of the fuel in the mixture. Therefore, in the present study, the heat transfer through radiation is considered through the solution of complete radiative transfer equations including both gas and surface radiations. These equations can be expressed as

$$\nabla \cdot I(\vec{r},\vec{s}) = \kappa \left[ {\frac{{\sigma T^{4} }}{\pi } - I(\vec{r},\vec{s})} \right],$$
(5)

where I is the radiation intensity and \(\vec{r},\vec{s}\) are, respectively, the position vector and intensity resolved direction in a given coordinate system.

The Euler–Lagrange approach is used in the present study to solve the present multiphase problem. The main phase (gases) is treated as continuum via the Navier–Stokes equations presented above. The dispersed phase is solved by tracking the liquid fuel droplets through the flow field. Exchange of mass, momentum and energy can take place between the two phases. The trajectory of discrete particle is calculated through the integration of the force balance on the particle in the Lagrangian approach:

$$\frac{{{\text{d}}u_{\text{p}} }}{{{\text{d}}t}} = F_{\text{D}} (u - u_{\text{p}} ) + \frac{{g_{\text{x}} (\rho_{\text{p}} - \rho )}}{{\rho_{\text{p}} }} + F_{\text{x}} ,$$
(6)

where F D(u − u p) is the drag force. F x is the force created by the existing pressure gradient along the fluid.

Heat and mass transfer of the discrete phase are considered through the implementation of three different laws as explained in the following. The inert heating law is applied when the droplet temperature is less than the vaporization temperature as given by the following equation:

$$m_{\text{p}} c_{\text{p}} \frac{{{\text{d}}T_{\text{p}} }}{{{\text{d}}t}} = hA_{\text{p}} \left( {T_{\infty } - T_{p} } \right) + \varepsilon_{\text{p}} A_{\text{p}} \sigma \left( {\theta_{\text{R}}^{4} - T_{\text{p}}^{4} } \right).$$
(7)

The coefficient of heat transfer is calculated using the correlation of Ranz and Marshall [33],

$$h = \frac{{k_{\infty } }}{{d_{\text{D}} }}\left[ {2 + 0.6\text{Re}_{\text{d}}^{1/2} \Pr^{1/3} } \right].$$
(8)

When temperature of the droplet is above vaporization temperature and below the boiling point, the present calculation considers the Droplet Vaporization Law,

$$N_{\text{v}} = \kappa_{\text{c}} \left( {C_{\text{v,D}} - C_{{{\text{v}},\infty }} } \right).$$
(9)

When droplet temperature reaches the boiling point, the Droplet Boiling Law is applied for the calculations of the convective boiling of the droplet as follows,

$$- r\frac{{{\text{d}}m_{\text{D}} }}{{{\text{d}}t}} = hA_{\text{D}} \left( {T_{\infty } - T_{\text{D}} } \right) + \varepsilon_{\text{D}} A_{\text{D}} \sigma \left( {T_{\text{R}}^{4} - T_{\text{D}}^{4} } \right).$$
(10)

Two phenomena are considered for the calculation of the oxygen transport through the ITM and for the modeling of combustion of the liquid vapor fuel with O2 on the permeate side of the OTR. For O2 permeation across ITM, a zero order model is used for the calculation of complete permeation process. This process includes three steps; (i) the first is the adsorption and disassociation of O2 on feed side, (ii) the second is the diffusion of the ions as well as electrons of O2 through the membrane thickness, and (iii) the third step is the recombination of O2 ions on permeate side of membrane. The details of this model are initially reported by Xu and Thomson [14]. This zero order DKK (D v, K f and K r coefficients) model for O2 transport through the ion transport membrane can be written as:

$$J_{{O_{2} }} = \frac{{D_{v} k_{r} \left[ {(P_{1} )^{0.5} - (P_{2} )^{0.5} } \right]}}{{2Lk_{\text{f}} (P_{1} )^{0.5} (P_{2} )^{0.5} + ((P_{1} )^{0.5} + (P_{2} )^{0.5} )D_{\text{v}} }},$$
(11)

O2 permeation through the membrane is function of membrane temperature and partial pressure of O2 on two sides of the ITM.

In the above equation, P 1 is the partial pressure of O2 on the feed side (air-side) and P 2 is the partial pressure of O2 in the permeate side. D v is the diffusion coefficient of O2 ions across the ITM, k f is the forward surface exchange rate constant, k r is the reverse surface exchange rate constant and L is the ITM thickness.

Starting with the generalized DKK model with the pressure exponent n,

$$J_{{O_{2} }} = \frac{{D_{\text{v}} k_{\text{r}} \left[ {(P_{1} )^{n} - (P_{2} )^{n} } \right]}}{{2Lk_{\text{f}} (P_{1} )^{n} (P_{2} )^{n} + ((P_{1} )^{n} + (P_{2} )^{n} )D_{\text{v}} }}.$$
(12)

Behrouzifar et al. [29] suggested that if the surface reactions (13) and (14) are associated with the oxygen adsorption/dis-association on the feed side and then the oxygen recombination/desorption on the permeate side are elementary (single step) as assumed by Xu and Thomson (1999) [14] then n = 0.5. Behrouzifar et al. [29] have accounted for non-elementary (multi-step) surface reactions and the derived a new value for n = 0.25. This value will be used in validating our CFD model against their experimental data,

$$\frac{1}{2}{\text{O}}_{2} + V^{ \cdot \cdot } \overset {k_{\text{f}} /k_{\text{r}} } \longleftrightarrow O_{0}^{x} + 2h^{ \cdot } \quad ( {\text{feed}}\;{\text{air}}\;{\text{side),}}$$
(13)
$${\text{O}}_{0}^{x} + 2h^{ \cdot } \overset {k_{\text{r}} /k_{\text{f}} } \longleftrightarrow \frac{1}{2}O_{2} + V_{0}^{ \cdot \cdot } \quad ( {\text{sweep}}\;{\text{permeate}}\;{\text{side)}}.$$
(14)

Furthermore, Behrouzifar et al. [29] have introduced a correction on the feed and sweep oxygen partial pressure to take into account the effect of Reynolds number on both sides. In our CFD calculations, this effect should be automatically taken care of because we determine the oxygen flux based on the local pressure not on the bulk or global partial pressures measure at the inlet of the fee side and outlet of the permeate side. Hence, we will not put this correction in, otherwise our CFD computations becomes futile.

To implement the oxygen mass flux source terms in a computationally efficient way, we have reformulated Eq. (12) as follows:

$$J_{{O_{2} }} = \frac{{1 - (P_{2} /P_{1} )^{n} }}{{\left( {\frac{2L}{{D_{\text{v}} }}} \right)\left( {\frac{{k_{\text{f}} }}{{k_{\text{r}} }}} \right)(P_{2} )^{n} + \left( {\frac{{k_{\text{f}} }}{{k_{\text{r}} }}} \right)\left( {1 + (P_{2} /P_{1} )^{n} } \right)}}.$$
(15)

The new form has two major benefits; (1) it reduces the number of computer operation, and hence the time to obtain converged solution and (2) it gives more insight into the physics of the oxygen flux model summarized in the following observations: (a) the oxygen permeation faces two resistance R 1 = (2L/D v)(k f /k r)(P 2)n and R 2 = (1/k r)(1 + (P 2/P 1)n), (b) the first resistance R 1 is a function of the ratio of membrane thickness to diffusion coefficient, the ratio forward to reverse surface coefficient and the oxygen partial pressure on the permeate side, and (c) the second resistance is a function of the reverse surface coefficient and the ratio of oxygen permeate partial pressure to feed partial pressure.

The generalized finite-rate model [34] is used for the calculation of the combustion modeling. The reaction rates are calculated from the Arrhenius reaction rate expressions and are presented as source terms in the species transport equations. One step reaction mechanism was used in the present study. The laminar finite-rate model is used to solve the flow-combustion interaction. For the species transport, the mixture diffusion coefficient, \(D_{{i,{\text{m}}}}\), is calculated as [34]

$$D_{{i,{\text{m}}}} = \frac{{1 - X_{i} }}{{\sum\limits_{j,j \ne i}^{{}} {\left( {\frac{{X_{i} }}{{D_{i,j} }}} \right)} }}$$
(16)

The mathematical model comprising the above described equations including the boundary conditions designated in the following section is numerically integrated by the finite volume approach. The finite volume method guarantees conservation of mass, momentum and chemical species. The uncertainty in the calculated results can be calculated based on the uncertainty of the applied models. In the present numerical simulations, the most accurate models based on previous literature works are applied. To ensure higher accuracy, second order upwind discretization is utilized. The PRESTO scheme is used for pressure to avoid interpolation errors and pressure gradient assumption on boundaries, while the semi-implicit method for pressure-linked equations (SIMPLE) algorithm is used for the pressure–velocity coupling [35]. Under-relaxation of the scalars and variables was considered to avoid divergence. The problem utilizes a segregated algorithm by solving the individual governing equations sequentially [36].

The ITM membrane was implemented through the development of the required model code in a separately developed user-defined function (UDF). This UDF membrane model is joined with fluent as mass source/sink terms that consider the mass flow of species across the membrane as written below:

$$S_{\text{cell}} = \left\{ \begin{aligned} {ll}+ \frac{{M_{{{\text{O}}_{ 2} }} J_{{{\text{O}}_{ 2} }} A_{\text{cell}} }}{{V_{\text{cell}} }}&\quad {\text{at}}\;{\text{permeate}}\;{\text{side}} \hfill \\ - \frac{{M_{{{\text{O}}_{ 2} }} J_{{{\text{O}}_{ 2} }} A_{\text{cell}} }}{{V_{\text{cell}} }}&\quad {\text{at}}\;{\text{the}}\;{\text{feed}}\;{\text{side}}\; ( {\text{air}}\;{\text{side)}} \hfill \\ \end{aligned} \right..$$
(17)

In the above equation, we needed to multiply by the molar mass of oxygen \(M_{{{\text{O}}_{ 2} }}\) to convert the molar flux \(J_{{{\text{O}}_{ 2} }}\) into a mass flux. The subscript cell refers to the control local finite volume to which the mass sourced is applied.

To solve the problem progressively as indicated in the above strategy, we started our investigation with the modeling of the oxygen separation process along with liquid fuel atomization, heating, and evaporation. Then we look at the fuel–oxygen (and sweep gases, CO2) mixing to investigate the oxygen to fuel ratios across the system and judge the flammability limits across the computational domain. Once we decide the correct percentage that should be fed to have close-to-complete reaction then we model the oxy-combustion of the fuel vapor inside the OTR.

Geometric modeling

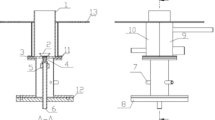
The geometry for the present investigations is shown in Fig. 1. It consists of two concentric parallel tubes. The inner tube is also called the feed zone where air is passed through it while the outer tube is called permeate zone or sweep zone where permeated oxygen reacts with fuel. The inner tube wall is the BSCF ion transport membrane (ITM) while the outer tube wall can be made of a proper material depending on the application. In this case, the outer tube wall is made out of steel. The diameter of the inner tube, i.e., BSCF membrane is 10 mm while the diameter of the outer steel tube is 20 mm. The length of both tubes is taken as 500 mm. As air (feed) flows through the feed zone, oxygen permeates through the BSCF ITM into the permeate zone where it reacts with vaporized liquid fuel and sweep for reactions to occur.

Fig. 1
figure 1

Schematic diagram of the present OTR model

Full size image

Boundary conditions

Given the small size of this model OTR and flow rates that we deal with, the flow is laminar in the system. Species transport and chemical reactions takes place due to liquid vapor fuel combustion. Moreover, there is transport of O2 through the ITM. Since the whole set up is axi-symmetric, a 2D axi-symmetric model is used to study the present investigations. The inner tube wall is the BSCF membrane and the outer tube is steel that surrounds the membrane. Air and sweep gases are introduced through the feed and permeate zones, respectively. The outer steel tube is given a boundary condition of zero heat flux. Pressure outlet boundary condition is used for both the feed and sweep zones flow exit. Air supply has to be sufficient enough for any reactor to efficiently utilize its capacity. Therefore, for the present model the mass flow rate of air/feed and sweep gas are varied in the range of 8e−4 to 6e−3 kg/s and 8e−6 to 5e−4 kg/s, respectively. Air is assumed to contain O2 and N2 only. With these very small mass flow rates used, the flow is laminar. Methanol (CH3OH) is used as the liquid fuel which goes through droplet atomization, heating and evaporation. CO2 along with CH3OH is used as the sweep gas to increase the permeated oxygen. A constant liquid fuel flow rate of 5.5e−7 kg/s is used through the study. Simulations are conducted at a constant temperature of 1173 K. It is reported that the O2 flux increases as the thickness of the membrane decreased [37, 38]. However, there is a minimum value beyond which the membrane cannot structurally sustain the pressure difference applied to it. Therefore, a thickness of 1 mm for the BSCF ITM is used for the present study.

Grid independence test

Grid independence test is performed with four different grids ranging from 15,040 nodes to 45,480 nodes. They are designated as Grid 1, Grid 2, Grid 3, and Grid 4 with 15,040, 28,038, 37,840 and 45,480 nodes, respectively. Grids with more than 37,840 did not show any significant differences rather increased the computational time and effort. Therefore, an optimal grid of 37,840 nodes (Grid 3) was chosen for the present study. To show the grid independent behavior, the temperature profile along the outer wall of the reactor is shown in Fig. 2 for four different grids. The difference between results obtained by Grid 3 and Grid 4 is less than 2%. The solution was considered to be converged when the summation of the residuals in all grid points was less than 0.1%. This was ensured for all the governing equations.

Fig. 2
figure 2

Temperature along the top wall for four different grids computed

Full size image

ITM model validation

The validation for the chosen ITM model with experimental results is conducted by considering the experimental results of Behrouzifar et al. [29]. They reported experimental data from their investigation on oxygen separation from air utilizing BSCF membranes. Their experiments included different partial pressures of air and different conditions of temperature. The results were obtained for laminar flow at steady state conditions. The ITM model developed in the present study and UDF equations were validated against the experimental data of Behrouzifar et al. [29]. The pre-exponential coefficients (D v, k r, k f) and activation energies values are taken from Behrouzifar et al. [29] and are given in Table 1.

Table 1 D v, k f, k r values for present calculations
Full size table

Figure 3 shows the comparison of oxygen fluxes for the experimental data and the simulated results with increasing operating temperature for different thickness of BSCF membranes. The results indicate higher oxygen flux with membrane temperature and thinner membrane as in the experimental data. The experimental data agree well with the simulated data indicating that the BSCF model used, serves as a good prediction tool in our study.

Fig. 3
figure 3

Comparison of experimental (symbols) and numerical (solid lines) results of oxygen fluxes with increasing temperature for different thickness values of BSCF membranes

Full size image

Results and discussion

The simulation results of oxy-combustion of methanol (CH3OH) liquid fuel in an oxygen transport reactor (OTR), utilizing BSCF ion transport membrane for oxygen separation, are discussed in this section. Air is supplied through the feed side and methanol is injected in the CO2 (sweep gas) stream through the permeate side. Oxygen separation results for non-reactive and reactive cases are presented followed by a discussion of the effect of variation of feed and sweep flow rates on the characteristics of oxy-combustion of methanol liquid fuel in the OTR. Furthermore, the influence of increasing air flow rates in the feed side and carbon dioxide flow rates in the sweep side on temperature distributions, evaporation rates and species concentrations are presented and discussed.

Oxygen separation simulations for non-reactive and reactive cases

We start by discussing two sample simulation cases for non-reactive and reactive conditions in the OTR. Figure 4 presents the comparison of partial pressures of oxygen and the corresponding oxygen fluxes. Figure 4b compares the oxygen fluxes in non-reactive and reactive environments along the length of the ITM on the permeate side. For these cases the air/feed flow rate is 1e−3 kg/s and the CO2/sweep flow rate is 1e−5 kg/s. As stated earlier, the flow rate of fuel is retained constant at 5.5e−7 kg/s throughout the investigation. For the non-reactive case it is observed from Fig. 4b that the oxygen flux starts with a high value at the inlet, then it decreases monotonically as the partial pressure of O2 builds up. For the reactive case, the oxygen flux starts from a similar value as the non-reactive case, but instead of going down; it shoots up substantially reaching a maximum value, and then decreases till the exit of the reactor. This due to the combustion taking place resulting in the depletion of oxygen, and hence the flux driving-potential, proportional to the difference of partial pressure of oxygen over the membrane, increases. Once we pass the combustion zone, the permeated oxygen builds up again and hence the flux decreases.

Fig. 4
figure 4

Comparison of a partial pressure of O2, b O2 flux along the ITM length on the permeate side of the membrane for a constant feed, sweep, fuel flow rate of 1e−3, 1e−5 and 5.5e−7 kg/s, respectively

Full size image

To explain this phenomenon further, the contours of reaction rate, temperature, mass fraction of methanol and oxygen for the aforementioned reactive case is presented in Fig. 5. The legend at the bottom of each contour represents the variation in respective variables. The exponential increase in the oxygen flux in the near region of the OTR for the reactive case, shown in Fig. 4b, is due to the fact that the consumption of oxygen in the reaction, with methanol, decreases the partial pressure of oxygen in the permeate side, also seen as a small recess in Fig. 4a. It is well know that the O2 permeation depends on partial pressure gradient across an ITM. The reaction, as presented in Fig. 5a, of oxygen with methanol on the permeate side increases the partial pressure difference across the membrane, therefore, leading to increased oxygen permeation. Moreover, it is apparent from Eq. (17) that the flux of oxygen is also a function of D v , k r , k f which are in turn function of temperature. As the temperature (Fig. 5b) is increased due to reaction, the activation energy required for the oxygen permeation is decreased contributing to the increase in oxygen permeation. Finally, as we move along the OTR the oxygen flux decreases; although it is still higher across the length of the reactor for the reactive case compared to non-reactive case due to lower partial pressure of oxygen on permeate side for the reactive case. It can be also observed from Fig. 5c that the evaporation of liquid methanol is completed in the zone near to the inlet. On the hand, the oxygen contours, shown in Fig. 5d, display almost zero oxygen concentration in the inlet region of the OTR due to its complete consumption in the reaction zone. The O2/CH3OH ratio presented in Fig. 5e indicates the area with high ratio where the reaction will take place as justified by Fig. 5a indicating high values of reaction rates and Fig. 5b showing high flame temperature in and around the same zone.

Fig. 5
figure 5

Contours of a reaction rate, b temperature, c mass fraction of methanol, d mass fraction of O2, e O2/CH3OH ratio for a constant feed, sweep, fuel flow rate of 1e−3, 1e−5 and 5.5e−7 kg/s, respectively

Full size image

Figure 5: Contours of (a) reaction rate (b) temperature (c) mass fraction of methanol (d) mass fraction of O2 (e) O2/CH3OH ratio for a constant feed, sweep, fuel flow rate of 1e−3 kg/s, 1e−5 kg/s and 5.5e−7 kg/s, respectively.

In this section, the effect of feed flow rate on the oxygen permeation and other variables for the reactive cases are discussed. Keeping a constant fuel flow rate of 5.5e−7 kg/s and a constant sweep (CO2) flow rate of 1e−5 kg/s, we vary the feed (air) flow rate from 8e−4 kg/s to 6e−3 kg/s.

The effect of increasing the feed flow rate on the oxygen permeation for constant fuel and sweep flow rate is presented in Fig. 6. It must be mentioned that most of the published papers dealing with OTR have not treated the variation of feed flow rate effect including Ben-Mansour et al. [1, 2], Hong et al. [39] and Habib et al. [40]. The reason for this is due to the fact the variation of feed flow rate has very little effect on O2 permeation in the case of separation only. This conclusion has been verified experimentally and numerically. Wang et al. [18] has conducted experimental O2 permeation study in a tubular BSCF membrane and found that for a constant temperature, the O2 permeation flux is little affected by the feed flow rate. The numerical model studies of Hong et al. [39] and Ben-Mansour et al. [1] also showed similar behavior. Coming back to our present simulation it appears that there is some effect on the permeated oxygen flux. Based on our limited number of simulations it appears that the maximum permeation occurs at 3e−3 kg/s for the above mentioned fuel/CO2 flow rates and liquid OTR temperature of 1173 K. As we increase the feed flow rate the oxygen flux is reduced. This can be due to the fact that there is too much excess oxygen in the reactor after we reach the maximum flux. This excess oxygen decreases the potential of oxygen permeation, hence the lower value at a higher feed rate of 6e−3 kg/s. This hypothesis is indeed validated as we look at the temperature profiles and contours in the OTR (Figs. 7 and 8). Therefore, it is an optimum feed side flow rate for given fixed OTR operating conditions.

Fig. 6
figure 6

Effect of feed flow rate on the oxygen permeation for reactive cases

Full size image
Fig. 7
figure 7

Effect of feed flow rate on the maximum temperature obtained

Full size image
Fig. 8
figure 8

Contours of temperature with increasing air feed flow rates

Full size image

Figure 7 presents the variations in the maximum temperature obtained in the reaction with the rise in the feed flow rate, keeping the sweep and fuel flow rate constant. It is detected that the maximum temperature obtained in the reaction is slightly reduced with rise in the feed flow rate. It is exciting to observe that the maximum oxygen permeation feed rate, in Fig. 6, do not correspond to the maximum reaction temperature in Fig. 7. This can be explained by the fact that we have excess oxygen for that particular case leading to a leaner flame, hence lower maximum as well as average temperatures. These results are confirmed from the temperature contours presented in Fig. 8 where the case of 0.03 kg/s, which corresponds to highest oxygen permeation, have a leaner flame compared to the case of 0.0008 and 0.001 kg/s. Moreover, it is clear from these temperature contours that as the feed flow rate is increased the flame becomes leaner.

We now turn to the temperature field in the reaction zone along with the reaction rates. Figure 8 exhibits the temperature contours for the different feed rates simulated. It is important to indicate that the temperature contours are compared on the same color scale. If we define the central flame zone as the region with temperature higher than 1300 K, one can observe that as the feed flow rate is increased from 0.0008 to 0.006 kg/s the flame central zone is smaller indicating a decrease in reaction temperature. The oxygen mass fraction contours in Fig. 9 indicate that oxygen permeation is higher (yellow color covers more area in the reactor) for the 0.003 kg/s case compared to other cases. This agrees well with our hypothesis regarding the optimum feed flow rate. Furthermore, Fig. 9 indicates that the permeated oxygen in the entry region of the reactor is consumed by the combustion process. As we move downstream of the reaction zone, no reaction is taking place and the mass fraction of oxygen increases as a result.

Fig. 9
figure 9

Contours of oxygen mass fraction with increasing air feed flow rates

Full size image

Higher oxygen mass fraction concentrations are observed towards the end of the liquid fuel OTR due to the accumulation of permeated oxygen past the reaction zone. The excess oxygen permeated with increase in the feed flow rates causes a delay in the reaction and a decrease in the maximum reaction rates shown in Fig. 10.

Fig. 10
figure 10

Maximum reaction rates with increasing air feed flow rates

Full size image

To explain this delay, the contours of reaction rates with increasing feed flow rates are presented in Fig. 11. It is observed from these contours that the maximum reaction rate is shifted downstream as we increase the feed flow rates. Furthermore, the lower reaction rates in the case of 0.006 kg/s indicates that the reaction is shifted away from the stoichiometric region due to higher excess oxygen permeated, hence lower reaction rates are obtained resulting in leaner flames.

Fig. 11
figure 11

Contours of reaction rates with increasing air feed flow rates

Full size image

On the heat transfer aspect, there is a decrease in the maximum reaction temperatures along with the corresponding maximum reaction rates as shown in Figs. 7 and 10, respectively. This may be attributed to the fact that higher feed flow rates carry away the heat generated by advection (higher bulk motion of feed flow) and convection (higher velocity and temperature gradient at the membrane surface). This can be seen from the convection heat flux plot presented in the Fig. 12. The figure shows the convective heat flux, plotted lengthwise of the ITM feed side, for increasing feed flow rates. The figure indicates higher convection heat fluxes with higher feed flow rates, thereby reducing the temperatures as well as reaction rates.

Fig. 12
figure 12

Convective heat flux along the ITM with increasing air feed flow rates

Full size image

We end this section with Fig. 13, which shows the volume average devolatilization of methanol with increasing feed flow rate. The fuel (methanol) flow rate is kept constant for all the cases. It is observed that the devolatilization of methanol has increased slightly when the feed flow rate is augmented from 0.0008 to 0.001 kg/s and remains unchanged beyond this value. This indicates that there is no significant impact of feed flow rate on the evaporation of fuel in the sweep side.

Fig. 13
figure 13

Volume average devolatilization with increasing air feed flow rates

Full size image

We conclude this section by stating that for the present oxygen transport reactor and assuming all other operating parameters are fixed, the feed flow rate of 0.001 kg/s gives adequate oxygen permeation and minimum loss of convective heat loss to the feed side. It should be also noted that the maximum permeated oxygen flux occurs at a higher value of 0.003 kg/s; however, this flow rate results in much higher heat loss and lower reaction temperature. Hence, for the remaining of the parametric investigation a feed flow rate of 0.001 kg/s is chosen.

In this section, the effect of sweep flow rate variation on the oxygen permeation and other variables for the reactive cases are discussed keeping a constant fuel flow rate of 5.5e−7 kg/s and a constant feed (air) flow rate of 0.001 kg/s. Unlike variation in the feed flow rate, the change in the sweep flow rate will have a direct effect on the reaction rates and temperatures, as the sweep gas is in immediate contact with the fuel.

The effect of increasing sweep flow rates on the oxygen permeation for constant fuel and feed flow rates is presented in Fig. 14. It is observed that oxygen permeation flux increases steeply as the sweep flow rate is increased from 5e−6 to 1e−4 kg/s. Beyond the value of 1e−5 kg/s, the oxygen flux increases gradually till 3e−4 kg/s and then is decreases slightly as we further increase the sweep flow rate to 5e−4 kg/s. These results indicate that the purging effect of CO2 with increasing sweep flow rates reduces the partial pressure of oxygen, driving away the oxygen on the sweep side. The decrease in the partial pressure of O2 due to purging paves way to more oxygen permeation. These results are in line with the experimental results obtained by Ali et al. [38] and the numerical results presented by Ben-Mansour et al. [2]. Both studies indicated that increasing sweep flow rate leads to increasing oxygen permeation flux up to a limit in the case of separation only. For reactive cases, this is also the case. In addition with combustion, the consumption of oxygen in the sweep side also contributes to the increase in the rates of oxygen permeation up to a maximum beyond which we may start building excess oxygen and as a result reduction in the permeated flux.

Fig. 14
figure 14

Oxygen permeation with increasing sweep flow rates

Full size image

To understand this behavior better, we look at the maximum reactor temperature, presented in Fig. 15. It can be seen that the maximum temperature in the reactor zone increases as the amount of sweep flow rate is elevated from 5e−6 to 7e−5 kg/s. But further augmentation in the sweep flow rates reduces the maximum flame temperature obtained. This lowering of the maximum temperature can be attributed to the increase in the oxygen permeation, diluting the flame. To check this hypothesis, the corresponding maximum reaction rates are presented in Fig. 16. Indeed the maximum reaction rates are greatly reduced causing a decrease in the maximum temperature obtained in the reaction zone. However, the reduction in reaction rates started from a sweep rate of 4e−5 kg/s, while the maximum temperature decline started from 1e−5 kg/s. To well comprehend the overall reaction kinetics and thermodynamics of the OTR, we decided to look at the average values of the reaction rates.

Fig. 15
figure 15

Maximum temperatures with increasing sweep flow rates

Full size image
Fig. 16
figure 16

Maximum reaction rates with increasing sweep flow rates

Full size image

The volume average temperature (see Fig. 17) in the reactor follows the same trend of maximum temperature. Recall also that the large value of specific heat (C p) of CO2 contributes to the decrease in the volume averaged as well as the maximum temperature inside the reactor, as we increase the sweep (CO2) flow rates. On the contrary, the corresponding averaged reaction rates (see Fig. 18) increase with increase in the sweep flow rates. To understand this phenomenon, the reaction rate contours are presented in Fig. 19. In this case, there are two simultaneous competing effects. The sweeping effect increases the oxygen permeation rate and at the same time, the CO2 dilution effect which due to its large C p capacity reduces the maximum reaction and the corresponding maximum temperature. However, the increase in the average volume reaction rate can be attributed to the increase in the reaction zone as shown in reaction rates contours in Fig. 19.

Fig. 17
figure 17

Volume average temperatures with increasing sweep flow rates

Full size image
Fig. 18
figure 18

Volume average reaction rates with increasing sweep flow rates

Full size image
Fig. 19
figure 19

Reaction rate contours with increasing sweep flow rates

Full size image

The temperature contours are presented in Fig. 20 for increasing sweep flow rates. It is observed that the flame length increases with increase in the sweep flow rates. This is mainly due the increase in the velocity of the sweep gas/fuel mixture which travels longer distance before it completely reacts with the permeated oxygen, hence the flame stretching. These results are confirmed from the mass fraction contours of CH3OH shown in Fig. 21. These contours show that fuel is spread over a wider zone and with smaller concentration as we increase the sweep flow rates (recall we are keeping the same fuel flow rate for all cases). Though at higher sweep flow rates the maximum and the volume average temperature start to decrease from a sweep rate of 1e−4 kg/s, the bulk temperature at the outlet, shown in Fig. 22, do not follow the same trend. This is due to the fact that the increase in the sweep flow rates pushes the flame zone downstream, (see temperature contours of Fig. 20), and this keeps the bulk outlet temperature rising up to 3e−4 kg/s.

Fig. 20
figure 20

Temperature contours with increasing sweep flow rates

Full size image
Fig. 21
figure 21

CH3OH mass fraction contours with increasing sweep flow rates

Full size image
Fig. 22
figure 22

Mass weighted average temperature with increasing sweep flow rates

Full size image

Figure 23 shows the volume average devolatilization of methanol with increasing sweep flow rate. The fuel (methanol) is kept constant for all the cases. Figure 23 shows lower devolatilization of methanol at lower sweep flow rate of 5e−6 kg/s. However, it increases dramatically as the sweep flow rate is increased to 8e−6 kg/s. Beyond this value it decreases slightly and remains constant with further increase in the sweep flow rates.

Fig. 23
figure 23

Volume average devolatilization with increasing sweep flow rates

Full size image

From the above results and discussion it has been shown that there is an optimum sweep flow rate beyond which there is no significant effect on the oxygen permeation and devolatilization characteristics. Therefore, it is concluded that for the present oxygen transport reactor, sweep flow rate in the range of 7e−5 to 1e−4 kg/s gives adequate oxygen permeation along with satisfactory reaction rates. The results also indicate the feasibility of the liquid fuel combustion in oxygen transport reactors (OTRs). These OTRs can be utilized in combustors of gas turbines and boiler furnaces.

Conclusions

Oxy-combustion of methanol liquid fuel in a concentric parallel tube oxygen transport reactor (OTR) using BSCF ion transport membrane for oxygen separation has been investigated with the aid of a developed computational model. Validation of the model is performed against the available experimental results. The effect of feed flow rate and sweep flow rate on oxygen permeation has been evaluated. Subsequently, the effects of feed and sweep flow rates on temperature and reaction characteristics are presented. Increasing the feed flow rates beyond certain limits do not significantly affect the oxygen permeation characteristics, however, increases the convective and advective heat losses from the membrane casing lower performance of the OTR. It is also observed that increasing the sweep flow rates results in higher oxygen fluxes but with leaner flames. The optimal flow rates of 0.001 kg/s for air/feed flow rate and sweep flow rates in the range of 7e−5 to 1e−4 kg/s under the assumptions given herein for the present geometry model are suggested. The feasibility of using liquid fuels as potential fuel to be used in near future in oxygen transport reactors has been presented.