Introduction

The Landau damping is a physical phenomenon which is related to the resonant particles (the particles whose velocity is nearly equal to the wave phase velocity) [1, 2]. The resonant particles may include both trapped and un-trapped particles. The usual ion acoustic wave in electron-ion plasma suffers Landau damping due to these resonant particles [1,2,3]. However, the presence of charged dust grains in a plasma gives rise to very low-frequency new mode (~10–15 Hz), called dust acoustic wave (DAW) [4,5,6,7,8], where the inertia is provided by the charged and massive dust grains. In the linear theory, it has already been seen that this mode also suffers Landau damping due to the resonant wave–particle interactions [9, 10]. Another well known non-Landau damping mechanism in a dusty plasma is due to the dust charge variations in the presence of waves [11, 20]. Actually, dust grains immersed in a plasma can exhibit self-consistent charge variations in response to the surrounding plasma oscillations and thus become a time-dependent dynamical variable which causes an anomalous dissipation in a dusty plasma.

In the nonlinear theory, the linear electron Landau damping effects on ion acoustic solitary wave have been investigated in an electron-ion plasma neglecting the particle trapping effect under the assumption that the particle trapping time is much larger than the Landau damping time [1, 13]. It has been shown that the solitary wave amplitude decays with time due to the linear electron Landau damping [13]. Later, theoretical [14, 15] and experimental [16] results show similar behavior. The wave–particle interactions also cause the oscillations in the tail of the solitary waves in which the shape of the tail depends on the strength of the Landau damping [17]. Recent experimental observation also predicts the formation of ion acoustic shock wave due to the Landau damping induced dissipation [18]. However, no study of nonlinear DAW is carried out including Landau damping in a dusty plasma. In this paper, the effect of linear ion Landau damping on dust acoustic solitary wave has been investigated neglecting the particle trapping effect. The instantaneous dust charge variation effects are also incorporated.

The manuscript is organized in the following manner. Formulation of the problem including the physical assumptions and basic equations is described in Sect. 2. The Korteweg–de Vries (KdV) equation with linear damping is derived using the reductive perturbation technique in Sect. 3. The analytical solution and the effect of Landau damping on the solitary wave solution are investigated in Sect. 4. The results of the present investigation are summarized in Sect. 5.

Formulation of the problem and the basic equations

A fully ionized, un-magnetized plasma consisting of electrons, ions, and negatively charged dust grains are considered. The plasma is assumed to be in its equilibrium state at \(-\infty\), where electrostatic potential \(\phi =0\), electron number density \(n_{\text{e}}=n_{\text{e0}}\), ion density \(n_{\text{i}}=n_{\text{i}0}\), dust density \(n_{\text{d}}=n_{\text{d}0}\), and dust charge \(q_{\text{d}}=-z_{\text{d}e}\), so that the quasi-neutrality condition \(n_{\text{e}0}+z_{\text{d}}n_{\text{d}0}=n_{\text{i}0}\) is satisfied, where \(z_{\text{d}}\) is the number of electrons residing on the dust grains, \(n_{{ j }}\) is the number density of the \(j{\text{th }}\, (e=\text{ electron }, i=\text{ ion }\; \text{ and }\; d=\text{ dust } \text{ grain})\) species, and \(n_{\text{ j }0}\) be its equilibrium value.

The charge on the dust grain varies continuously in space (x) and time (t). The temperature of dust grain is very low compared to that of electrons \((T_{\text{e}})\) and ions (\(T_{\text{i}})\). Therefore, the dust grains are effectively cold with respect to the electrons and ions. The dust grains are moving with fluid velocity U. It is convenient to express all the variables in non-dimensional form before going to the details of the basic formalism of the problem. For this purpose, let us introduce the following normalization: \(\Phi =e\phi /T_{\text{i}}\), \(N=n_{\text{d}}/n_{\text{d}0}\), \(N_{\text{e}}=n_{\text{e}}/n_{\text{e}0}\), \(N_{\text{i}}=n_{\text{i}}/n_{\text{i}0}\), \(\bar{x}=x/\lambda _{\text{D}}\), \(\bar{t}=\omega _{\text{ pd }}t\), \(\bar{U}=U/C_{\text{ s }}\) and \(\bar{q_{\text{d}}}=q_{\text{d}}/z_{\text{ de }}=-1+\Delta Q\), and \(\Delta Q\) is the fluctuating dust charge. Here, \(\omega _{\text{ pd }}=(z_{\text{d}}^2e^2 n_{\text{d}0}/\epsilon _0 m_{\text{d}})^{1/2}\) is the dust plasma frequency, \(\lambda _{\text{D}}=(\epsilon _0 T_{\text{i}}/n_{\text{i}0}e^2)^{1/2}\) is the plasma Debye length, \(C_{\text{ s }}=(z_{\text{d}}T_{\text{i}}/m_{\text{d}})^{1/2}\) is the dust acoustic speed, \(\delta _{\text{i}}=n_{\text{i}0}/n_{\text{e}0}\), \(\sigma =T_{\text{i}}/T_{\text{e}}\), and \(z=z_{\text{ de }}^2/4\pi \epsilon _0 r_{\text{d}} T_{\text{e}}\) are the dimensionless dusty plasma parameters (the ratio of the electrostatic energy of a dust grain of radius \(r_{\text{d}}\) to the electron thermal energy). Hereafter, we will be using these new variables and remove all the bars for simplicity of notations.

We assume that \(\delta _{\text{i}}\left( m_{\text{i}}/m_{\text{d}}\right) ^{1/2} \gg \sigma ^{3/2} \left( m_{\text{e}}/m_{\text{i}}\right) ^{1/2}\), so that the electron Landau damping effect is neglected. The dust Landau damping effect is also neglected as the dust thermal velocity is much smaller than the wave phase velocity. Moreover, we are interested to study the low-frequency nonlinear DAW and, therefore, we neglect the inertia of the electrons compared to the dust grains. On this slow time scale, the electrons are in local thermodynamic equilibrium and their densities are modeled by the Boltzmann distribution: \(n_{\text{e}}=n_{\text{e}0}\exp (\sigma \Phi ).\)

The ions are treated kinetically, so that their number densities are given by

$$\begin{aligned} N_{\text{i}}=\int _{-\infty }^{+\infty } f {\text{d}}V. \end{aligned}$$
(1)

The velocity distribution function of ion f (normalized) satisfies the following Vlasov–Boltzmann equation:

$$\begin{aligned} M\,\frac{\partial f}{\partial t}+V\,\frac{\partial f}{\partial x}-\frac{\partial \Phi }{\partial x}\,\frac{\partial f}{\partial V}=0. \end{aligned}$$
(2)

Here, the parameter \(M=\left( z_{\text{d}} m_{\text{i}}/m_{\text{d}}\right) ^{1/2}\) represents the effect of finite ion inertia on propagation characteristics of DAW. The ion velocity V is normalized in units of ion thermal velocity \(V_{\text{ ti }}=\left( T_{\text{i}}/m_{\text{i}}\right) ^{1/2}\) and velocity distribution function f is normalized by \(V_{\text{ ti }}/n_{\text{ i0 }}\). It is to be noted that when the plasma is in thermodynamical equilibrium, the velocity distribution of the ion is given by the following Maxwellian distribution:

$$\begin{aligned} f^{(0)}=\frac{1}{\sqrt{2\pi }}\exp (-V^{2}/2) \end{aligned}$$
(3)

which is also the solution of Eq. (2) in the absence of external force \((\Phi =0)\).

Finally, the nonlinear propagation of low phase velocity (in comparison with the electron and ion thermal velocities) DAW is governed by the following normalized basic equations:

$$\begin{aligned} \frac{\partial N}{\partial t}+ \frac{\partial (N U)}{\partial x} = 0 \end{aligned}$$
(4)
$$\begin{aligned} \frac{\partial U}{\partial t}+ U \frac{\partial U }{\partial x} = -(\Delta Q-1)\frac{\partial \Phi }{\partial x} \end{aligned}$$
(5)
$$\begin{aligned} \frac{\partial ^2\Phi }{\partial x^2}=\left[ \frac{1}{\delta _{\text{i}}-1}\exp (\sigma \Phi )-\frac{\delta _{\text{i}}}{\delta _{\text{i}}-1} N_{\text{i}}-(\Delta Q-1)N \right] . \end{aligned}$$
(6)

The normalized dust grain charging equation becomes

$$\begin{aligned} \left( \frac{\omega_{\text{pd}}}{\nu _{\text{d}}}\right) \frac{{\text{d}}\Delta Q}{{\text{d}} t}=\frac{I_{\text{e}} +I_{\text{i}}}{\nu _{\text{d}} z_{\text{d}}e} \end{aligned}$$
(7)

where \(\nu _{\text{d}}=r_{\text{d}}\omega _{\text{ pi }}^2(1+z+\sigma )/\sqrt{2\pi }V_{\text {ti}}\) is the dust charging frequency and \(\omega _{\text{ pi }}\) is the ion plasma frequency. The expressions for electron current \((I_{\text{e}})\) and ion current \((I_{\text{i}})\) for negatively charged dust grains are given by

$$\begin{aligned} I_{\text{e}}=-\pi r_{\text{d}}^2 e \sqrt{\frac{8T_{\text{e}}}{\pi m_{\text{e}}}}n_{\text{e}0}\exp (\sigma \Phi )\exp [z(\Delta Q-1)] \end{aligned}$$
(8)

and

$$\begin{aligned} I_{\text{i}}=\pi r_{\text{d}}^2 e\sqrt{\frac{8T_{\text{i}}}{\pi m_{\text{i}}}}n_{\text{i}0}N_{\text{i}}\left[ 1-\frac{z}{\sigma }(\Delta Q-1)\right] . \end{aligned}$$
(9)

Korteweg–de Vries equation with Landau damping

To study the propagation characteristics of finite amplitude nonlinear DAW, the reductive perturbation technique is adopted. Accordingly, the stretched co-ordinates and power series expansion (in powers of \(\epsilon\)) of dependent variables are as follows:

$$\begin{aligned} \xi =\sqrt{\epsilon }(x-\Lambda t),\, \tau =\epsilon ^{3/2}\,t \end{aligned}$$
(10)
$$\begin{aligned} h=h^{(0)}+\epsilon \,h^{(1)}+\epsilon ^2 h^{(2)}+\cdots \end{aligned}$$
(11)

where \(\epsilon\) is the smallness parameter that indicates the magnitude of the rate of change and \(\Lambda\) is the normalized wave phase velocity. It is to be noted that \(h^{(0)}=1(0)\), \(h\equiv N_{{ j }}(\Phi , U)\), and \(h=f^{(0)}\) for \(h\equiv f\). To incorporate the effects of ion inertia on finite amplitude nonlinear DAW, the following scaling is assumed which is consistent with the perturbation:

$$\begin{aligned} M\sim O(\epsilon )\Rightarrow M=\mu \epsilon . \end{aligned}$$
(12)

Substituting Eqs. (10)–(12) in Eqs. (1)–(8) and then equating different powers of \(\epsilon\) on both sides of these equations, the following relations are obtained. In the lowest order of \(\epsilon\), Eqs. (1)—(8) reduce to

$$\begin{aligned} N_i^{(1)}=\int _{-\infty }^{+\infty } f^{(1)}{\text{d}}V,\, &\Lambda N^{(1)}=U^{(1)} \end{aligned}$$
(13)
$$\begin{aligned} \Lambda U^{(1)}=-\Phi ^{(1)},\, &\Delta Q^{(1)}=\frac{\sigma }{\delta _i-1}\Phi ^{(1)}-\frac{\delta _i}{\delta _i-1}N_i^{(1)}+N^{(1)}. \end{aligned}$$
(14)

The Vlasov–Boltzmann equation (2) for ions at the order of \(\epsilon ^{3/2}\) yields

$$\begin{aligned} V\frac{\partial f^{(1)}}{\partial \xi }+V f^{(0)}\,\frac{\partial \Phi ^{(1)}}{\partial \xi } = 0. \end{aligned}$$
(15)

This equation does not have unique solution [13]. However, the non-uniqueness can be removed by including a \(\partial f^{(1)}/\partial \tau\) term [13] in Eq. (15), and thus, we have the following equation:

$$\begin{aligned} \mu \,\epsilon ^2\,\frac{\partial f_\epsilon ^{(1)}}{\partial \tau }+V\,\frac{\partial f_\epsilon ^{(1)}}{\partial \xi }=-V f^{(0)}\frac{\partial \Phi ^{(1)}}{\partial \xi }. \end{aligned}$$
(16)

Then, \(f^{(1)}\) is uniquely determined from the solution of the Eq. (16) by taking \(f^{(1)}=\lim _{\epsilon \rightarrow 0} f_{\epsilon }^{(1)}\) [13]. Finally, we get

$$\begin{aligned} f^{(1)}=-f^{(0)}\Phi ^{(1)}. \end{aligned}$$
(17)

It is well known that the non-steady dust charge variations produce an anomalous dissipation which leads to collisionless, non-Landau wave damping in a dusty plasma [19,20,21,22]. However, for a typical laboratory dusty plasma [6], dust oscillation frequency \(\omega _{\text{ pd }}\approx 10^2\;{\text{ s }}^{-1}\) and dust charging frequency \(\nu _{\text{d}}\approx 10^8\;s^{-1}\) imply \(\omega _{\text{ p }d}/\nu _{\text{d}}\approx 10^{-6}\), and thus, the charging equation (7) can be approximated as

$$\begin{aligned} I_{\text{e}}+I_{\text{i}}\approx 0, \end{aligned}$$
(18)

so that the charge on the dust grains instantaneously reaches its equilibrium value, which is known as “adiabatic variation” of dust charge. In this adiabatic approximation, Eq. (18) together with Eqs. (8) and (9), at the order of \(\epsilon\) gives the following relation:

$$\begin{aligned} \Delta Q^{(1)}=\beta _{\text{d}}\left( N_i^{(1)}-\sigma \Phi ^{(1)}\right) ,\, &\beta _{\text{d}}=\frac{(z+\sigma )}{z\left( 1+z+\sigma \right) }. \end{aligned}$$
(19)

This equation together with Eqs. (13)–(15), (19) self-consistently determined the (normalized) phase velocity of DAW

$$\begin{aligned} \Lambda ^2=\frac{(\delta _{\text{i}}-1)}{(\sigma +\delta _{\text{i}})+\beta _{\text{d}}(1+\sigma )(\delta _{\text{i}}-1)}. \end{aligned}$$
(20)

In the absence of dust charge variations \((\beta _{\text{d}}=0)\), this Eq. (20) can be written in dimensional form, as

$$\begin{aligned} \omega ^2=\frac{k^2 C_{\text{ s }}^2(\delta _{\text{i}}-1)}{(\delta _{\text{i}}+\sigma )}, \end{aligned}$$

which is the phase velocity of the usual DAW in the long wavelength limit [4].

In the next higher order of \(\epsilon\), Eqs. (1), (2) and (4)–(6) yield the following relations:

$$\begin{aligned} \frac{\partial N^{(1)}}{\partial \tau }+\frac{\partial (N^{(1)} U^{(1)})}{\partial \xi }=\Lambda \frac{\partial N^{(2)}}{\partial \xi }-\frac{\partial U^{(2)}}{\partial \xi } \end{aligned}$$
(21)
$$\begin{aligned} \frac{\partial U^{(1)}}{\partial \tau }+ \Delta Q^{(1)}\frac{\partial \Phi ^{(1)}}{\partial \xi }+U^{(1)} \frac{\partial U^{(1)}}{\partial \xi }=\Lambda \frac{\partial U^{(2)}}{\partial \xi }+\frac{\partial \Phi ^{(2)}}{\partial \xi } \end{aligned}$$
(22)
$$\begin{aligned} \frac{\partial ^2\Phi ^{(1)}}{\partial \xi ^2}=\frac{\sigma }{\delta _i-1}\Phi ^{(2)}+\frac{\sigma ^2}{2(\delta _i-1)} \Phi ^{(1)^2}-\frac{\delta _i}{\delta _i-1}N_i^{(2)}-\Delta Q^{(1)}N^{(1)}-\Delta Q^{(2)}+N^{(2)} \end{aligned}$$
(23)
$$\begin{aligned} N_i^{(2)}=\int _{-\infty }^{+\infty } f^{(2)} {\text{d}}V. \end{aligned}$$
(24)

To get the unique solution for \(f^{(2)}\) of Eq. (2), proceeding as before, a term containing time derivative of \(f^{(2)}\) (as in the lowest order case) is included in the equation of order of \(\epsilon ^{5/2}\) of Eq. (2), and thus, we obtain

$$\begin{aligned} \mu \epsilon ^2\frac{\partial f_\epsilon ^{(2)}}{\partial \tau } + V\frac{\partial f_\epsilon ^{(2)}}{\partial \xi }= -\left[ \Lambda \mu f^{(0)}\frac{\partial \Phi ^{(1)}}{\partial \xi }+V f^{(0)}\frac{\partial \Phi ^{(2)}}{\partial \xi }- V f^{(0)}\Phi ^{(1)}\frac{\partial \Phi ^{(1)}}{\partial \xi }\right] . \end{aligned}$$
(25)

As before, \(f^{(2)}\) is uniquely determined from the solution of Eq. (25) by taking the limit \(f^{(2)}=\lim _{\epsilon \rightarrow 0} f_\epsilon ^{(2)}\) and thus finally using the relation (24), we obtain the following relation:

$$\begin{aligned} \frac{\partial N_{\text{i}}^{(2)}}{\partial \xi }= -\frac{\partial \Phi ^{(2)}}{\partial \xi }+ \Phi ^{(1)}\frac{\partial \Phi ^{(1)}}{\partial \xi }+ \left( \frac{\Lambda \mu }{\sqrt{2\pi }}\right) \wp \int _{-\infty }^{+\infty } \frac{\partial \Phi ^{(1)}}{\partial \acute{\xi }}\frac{d\acute{\xi }}{\xi - \acute{\xi }} \end{aligned}$$
(26)

where \(\wp\) represents Cauchy’s principal value. Note that in the derivation of the above relation (26), we use the properties of generalized functions [25]: \(1/(\eta -i0)=\wp (1/\eta )+i\pi \delta (\eta )\), \(\eta \wp (1/\eta )=1\), \(\eta \delta (\eta )=0\) and \(\delta (k\eta )=({\text{sgn}}(k)/k)\delta (\eta )\).

The Eq. (18) together with Eqs. (8) and (9) at the order of \(\epsilon ^2\) gives

$$\begin{aligned} \Delta Q^{(2)}=\beta _{\text{d}}\left( N_i^{(2)}- \sigma \Phi ^{(2)}-z\sigma \Delta Q^{(1)}\Phi ^{(1)}-\frac{\sigma ^2}{2} \Phi ^{(1)^2}-\frac{z^2}{2}\Delta Q^{(1)^2} -\frac{z}{\sigma +z}N_i^{(1)}\Delta Q^{(1)}\right) . \end{aligned}$$
(27)

Finally, the usual perturbation analysis (the elimination of all the second-order terms) yields the following modified form of Korteweg–de Vries (KdV) equation modified by Landau damping:

$$\begin{aligned} \frac{\partial \Phi ^{(1)}}{\partial \tau } - \alpha \Phi ^{(1)}\frac{\partial \Phi ^{(1)}}{\partial \xi }+\beta \frac{\partial ^3\Phi ^{(1)}}{\partial \xi ^3} +\gamma _L\wp \int _{-\infty }^{+\infty }\frac{\partial \Phi ^{(1)}}{\partial \acute{\xi }}\frac{d\acute{\xi }}{\xi - \acute{\xi }}=0 \end{aligned}$$
(28)

where

$$\begin{aligned} \alpha =\beta \left[ \frac{3}{\Lambda ^4}+\frac{\sigma ^2-\delta _{{ i }}}{\delta _{{ i }}-1} -\beta _{\text{d}}\left( \frac{3}{\Lambda ^2}(1+\sigma )+1-\frac{z^2 \beta _{\text{d}}^2}{(\sigma +z)^2}\left( (1+\sigma +z)^2+(1+\sigma )^2\right) \right) \right] , \end{aligned}$$
(29)
$$\begin{aligned} \beta =\frac{\Lambda ^3}{2} \end{aligned}$$
(30)

and

$$\begin{aligned} \gamma_{\text{L}}=\frac{\Lambda ^4 \mu }{2\sqrt{2\pi }}\left( \beta _{\text{d}} + \frac{\delta _{{i}}}{\delta _{{i}}-1}\right) . \end{aligned}$$
(31)

The variations of \(\gamma _{\text{L}}\) with ion-electron density ratio for different ion-electron temperature ratio are shown graphically in Fig. 3. Note that \(\mu =0\Rightarrow \gamma _{\text{L}}=0\) and then from Eq. (28), we recover the usual KdV equation for the finite amplitude nonlinear DAW. The term \(\beta _{\text{d}}\) present in the expression for \(\gamma _{\text{L}}\) is responsible for the instantaneous dust charge variations. It is also to be noted that one can easily obtain the regular Landau damping of DAW from Eq. (28) for \(\alpha =\beta =0\). Let us discuss it briefly: Taking the Fourier transform of Eq. (28) with \(\alpha =\beta =0\) with respect to \(\xi\) and \(\tau\) [according to the formula, \(\tilde{g}\left( \omega , k\right) =\int _{-\infty }^{\infty }\int _{-\infty }^{\infty } g\left( \xi , \tau \right) \exp \{i\left( k\xi -\omega \tau \right) \}{\text{d}}\xi {\text{d}}\tau\)] and then treating the integral as a convolution with the help of the result that the inverse transform of \([i {\text{sgn}}(k)] = -(1/\pi )\wp (1/\xi )\) [25], the following equation is obtained:

$$\begin{aligned} \omega =-i\pi k\gamma _{\text{L}}=-i k\mu \sqrt{\frac{\pi }{8}} \Lambda ^4\left( \beta _{\text{d}}+\frac{\delta _{\text{i}}}{\delta _{\text{i}}-1}\right) . \end{aligned}$$
(32)

This clearly shows that the wave becomes damped due to finite ion inertia effects as \(\mu \propto \left( z_{\text{d}} m_{\text{i}}/m_{\text{d}}\right) ^{1/2}\) with the damping decrement (normalized) \(\mid \gamma \mid =\pi \gamma _{\text{L}}\). More precisely, in the absence of dust charge variations \((\beta _{\text{d}}=0)\), we obtain the following Landau damping decrement (normalized):

$$\begin{aligned} \mid \gamma \mid =\pi \gamma _{\text{L}}(\beta _{\text{d}}=0)=\sqrt{\frac{\pi }{8}} \frac{\sqrt{z_{\text{d}}(\delta _{\text{i}}-1)}\,\,\delta _{\text{i}}}{\left( 1+\delta _{\text{i}} T_{\text{e}}/T_{\text{i}}\right) ^{3/2}}\left( \frac{T_{\text{e}}}{T_{\text{i}}}\right) ^{3/2}\sqrt{\frac{m_{\text{i}}}{m_{\text{d}}}} \end{aligned}$$
(33)

of DAW in usual dusty plasma [9]. These discussions clearly show that the term \(\gamma _{\text{L}}\) arises only due to the Landau damping, which is the consequence of the presence of \(\mu\) and the scaling (Eq. 12). This expression also shows that the dust charge variations enhance the Landau damping rate.

Landau damping effect on dust acoustic solitary wave

The KdV equation (28) without the Landau damping \((\gamma _{\text{L}}=0)\) represents a completely integrable Hamiltonian system which has an infinite set of conservation laws. We consider the following energy conservation equation:

$$\begin{aligned} \frac{1}{2}\frac{\partial }{\partial \tau }\int _{-\infty }^{+\infty }\Phi ^{(1)^2}(\xi ,\tau ){\text{d}}\xi =0. \end{aligned}$$
(34)

This shows that in the absence of Landau damping, the wave energy is conserved and possesses the following single soliton solution:

$$\begin{aligned} \Phi ^{(1)}(\xi ,\tau )=A\;\text{sech}^2\left[ \sqrt{\frac{\alpha A}{12\beta }}\left( \xi -\frac{\alpha }{3}A\tau \right) \right] \end{aligned}$$
(35)

where A is the amplitude of the solitary wave, \(3A/\alpha\) is the solitary wave velocity, and \(\left( 12\beta /A\alpha \right) ^{1/2}\) is the spatial width of the solitary wave.

However, in the presence of Landau damping \((\gamma _{\text L}\ne 0)\), the KdV equation (28) does not represent a completely integrable Hamiltonian system, and in this case, the above energy equation (34) becomes

$$\begin{aligned} \frac{1}{2}\frac{\partial }{\partial \tau }\int _{-\infty }^{+\infty }\Phi ^{(1)^2}(\xi ,\tau ){\text{d}}\xi =-\gamma _{\text{L}}\int _{-\infty }^{+\infty }\Phi ^{(1)}(\xi ,\tau ) \left[ \wp \int _{-\infty }^{+\infty }\frac{{\text{d}}\Phi ^{(1)}(\xi ,\tau )}{{\text{d}}\acute{\xi }}\frac{{\text{d}}\acute{\xi }}{\xi -\acute{\xi }}\right] {\text{d}}\xi . \end{aligned}$$
(36)

Now, following the procedures of Refs. [15, 23, 24], in the presence of Landau damping, a slow time-dependent form of the solution of Eq. (28) is considered

$$\begin{aligned} \Phi ^{(1)}(\xi ,\tau )=A(\tau )\;\text{sech}^2\left[ \sqrt{\frac{\alpha A(\tau )}{12\beta }}\left( \xi -\frac{\alpha A(\tau )}{3}\tau \right) \right] . \end{aligned}$$
(37)

Finally, substitution of Eq. (37) in Eq. (36) yields the following solution:

$$\begin{aligned} A(\tau )=A_0\,\left( 1+\frac{\tau }{\tau _0}\right) ^{-2} \end{aligned}$$
(38)

where

$$\begin{aligned} \tau _0^{-1}=\frac{6\gamma _{\text{L}}\zeta (3)}{\pi ^2}\sqrt{\frac{\alpha A_0}{3\beta }} \end{aligned}$$
(39)

where \(A_0=A(\tau =0)>0\) is the initial amplitude and \(\zeta (3)\) be the Riemann Zeta function [26] defined by

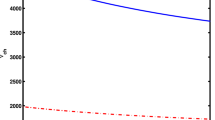
$$\zeta (3) = \frac{{\pi ^{2} }}{{24}}\wp \int_{{ - \infty }}^{{ + \infty }} {\text{d}} \xi \int_{{ - \infty }}^{{ + \infty }} {\frac{{\sec h^{2} \xi {\text{d}}\xi ^{\prime}}}{{\xi - \xi ^{\prime}}}} \frac{{\text{d}}}{{{\text{d}}\xi }}(\sec h^{2} \xi ).$$

The above solution (38) shows that the linear ion Landau damping causes the dust acoustic solitary wave amplitude \(A(\tau )\) to decay algebraically with time \((\tau )\) and the decay rate is proportional to \(\gamma _{\text{L}}\) (Landau damping). In the presence of Landau damping, the amplitude modulations with time \(\tau\) for different ion-electron density ratio \((\delta _{\text{i}})\) and temperature ratio \((\sigma )\) are shown in Figs. 1 and 2.

Fig. 1
figure 1

(Color online) Time variations of wave amplitude with \(\sigma (=T_{\text{i}}/T_{\text{e}})=1\) for different \(\delta _{\text{i}} (=n_{\text{i}0}/n_{\text{e}0})\)

Full size image
Fig. 2
figure 2

(Color online) Time variations of wave amplitude with \(\sigma =0.1\) for different \(\delta _{\text{i}}\)

Full size image
Fig. 3
figure 3

(Color online) Variations of damping rate \(\gamma _{\text{L}}\) with \(\delta _{\text{i}}\) for different \(\sigma\)

Full size image

Conclusions

In this paper, we have investigated the effects of ion Landau damping on nonlinear dust acoustic wave. It is shown that the nonlinear wave is governed by a modified form of KdV equation [see Eq. (28)]. In the presence of Landau damping, approximate analytical solutions reveal that the wave amplitude decays algebraically with time. To understand the feature, the wave amplitude modulations with time \(\tau\) [see Eqs. (38) and (39)] are shown graphically for different \(\sigma\) and \(\delta _{\text{i}}\) in Figs. 1 and 2 for \(K^+\) ion and electron plasma. Figures 1 and 2 show that wave amplitude decreases with time \(\tau\) for any fixed value of \(\delta _{\text{i}}\) and \(\sigma.\) However for any fixed time \(\tau,\) the amplitude increases with the increase of ion-electron temperature ratio (\(\sigma\)) and ion-electron density ratio (\(\delta _{\text{i}}\)). In addition, the Landau damping rate (\(\gamma _{\text{L}}\)) decreases with the increase of ion-electron temperature ratio (\(\sigma\)), as shown in Fig. 3.