Introduction

Plasma immersion ion implantation (PIII) [1, 2] has been shown to be an effective technique for semiconductor fabrication and material processing [3–6]. It emulates conventional ion-beam ion implantation (IBII) in a number of areas. For example, it has high sample throughput (high current density) and it is a paralleled processing technique in which the implantation time is independent of the wafer size.

The dynamic sheath model plays a very important role in PIII processes because it is used to predict process parameters and implantation results including the implant doses and energies. The optimum characteristics of plasma system can be determined from an appropriate and reasonable numerical analysis of the plasma-sheath dynamic. Unfortunately, accurate modeling and prediction of the ion implantation energy and dose in PIII is quite difficult because it is a complicated function of inter-related processing conditions such as plasma density, pulse duration, accelerating voltage, external magnetic field, ion mass, ion temperature, and ion charge state.

There has recently been an explosion of interest in the dynamic behavior of sheaths which is formed at an electrode biased with a pulsed negative voltage. This problem is of special interest in PIII technology, where ions are extracted from plasma, accelerated by a high potential drop in the sheath and injected into the surface layer of a material being treated.

In a simple model of PIII, the confined homogeneous plasma is brought in contiguity with a flat conducting electrode or target. A series of negative high-voltage pulses are applied to the electrode. As a result, electrons are repelled from the electrode and move back toward the plasma center leaving a positive ion sheath. This initial ion sheath, which is immediately formed after applying the negative voltage on the electrode, is called ion matrix sheath [7–9]. The matrix sheath is created on a time scale of the order of 1/ω p (where ω p is the electron plasma frequency). At a characteristic time scale of the order of 1/Ω p (where Ω p is the ion plasma frequency), the ions begin to move towards the electrode. Therefore, the sheath edge propagates into the plasma and a rarefactive ion distribution begins to propagate into the sheath. Thickness of the time-dependent collisionless sheath is given by [10];

$$d\left( t \right)\; = \;d_{0} \left( {\frac{2}{3}\varOmega_{\text{p}} t\; + \;1} \right)^{1/3} ,$$
(1)

where, \(d_{0} = \sqrt {2\varepsilon_{0} V_{T} /en_{0} }\) is the thickness of the ion matrix sheath, n 0 is the plasma density, V T is the applied negative voltage to the target, ɛ 0 is the free space permittivity and e is the unit of electric charge.

Navab Safa et al. [11] have investigated the sheath dynamics and implantation profiles during the PIII process on a long step shaped target in the presence of an external DC magnetic field and showed that the magnetic field inclination angle strongly affects the ion implanted dose and ion energy on the target surfaces. Minghao et al. [12] have analyzed the ion temperature and collision parameter effects on the plasma-sheath structure in the RF warm plasma-sheath. They have solved plasma fluid equations from plasma center to the wall (biased with a low-voltage sinusoidal source) and presented their results in time-averaged form. It has been examined [13, 14] the ion temperature and collision effects on the Bohm criteria in a multiply ionized and electronegative warm plasma sheath, respectively, and using these Bohm criterions it has been investigated [15, 16] the ion temperature and ion-neutral collision effects on the steady state plasma-sheath structure and sheath formation in warm magnetized plasmas.

In this paper, we will study the PIII process for different gas pressure to investigate the influence of ion-neutral collision on the dynamic behavior of a pulsed collisional magnetized sheath. Since the ion incident angle has a significant effect on the ion penetration at the target, we have used an external magnetic field in our model to be able to control the ion incident angle. Here, we use a fluid model to investigate the time evolution of a sheath expanding into the plasma. The model equations are solved through an implicit finite difference scheme.

After introduction, in “Fluid model and basic equations”, a collisional magnetized plasma is formulated and the proper initial and boundary conditions are nominated. In “Numerical results and discussion”, the numerical results and their explanation are presented. A summary and conclusions are presented in “Summary and conclusions”.

Fluid model and basic equations

The implantation geometry is schematically displayed in Fig. 1. A collisional magnetized plasma limited at one side by a conducting flat target is considered to discuss the formation of dynamic sheath. The position of the target is taken at x = 0. We assume at the moment t = 0, the plasma which is located at the x > 0 is filled with stationary singly charged ions and the charge neutrality condition n i  = n e  = n 0 is fulfilled there. At the moment t = 0+, the bias on the target is switched on from zero to a negative bias V T(t), drawing ions to the target and repelling electrons to the plasma. Under this configuration, the non-neutral plasma so-called plasma sheath is formed around the target.

Fig. 1
figure 1

A magnetized plasma-sheath as the simulation zone

Full size image

On the other hand, far from the plasma sheath, there is a cold (T i  = 0) plasma with electron temperature T e where the electric potential is V = 0. The fluid model is used to formulate the charged particles as electric fluids. The ion density and ion velocity distributions, as well as the electric potential distribution in the plasma-sheath evolve self-consistently in the fluid equations frame. The continuity and motion equations of the ions supplemented by the collisional term are:

$$\frac{{\partial n_{i} }}{\partial t} + \nabla \cdot \left( {n_{i} {\mathbf{v}}} \right) = 0,$$
(2)
$$mn_{i} \left( {\frac{\partial }{\partial t} + {\mathbf{v}} \cdot \nabla } \right){\mathbf{v}} = en_{i} \left( {{\mathbf{E}} + {\mathbf{v}} \times {\mathbf{B}}} \right) - mn_{i} \nu {\mathbf{v}} ,$$
(3)

where E = −∇V (with V as the electric potential) is the electric field, m, v and ν are the mass, velocity and collision frequency of ion, respectively.

Electrons in the electrostatic well of the target are in the thermal equilibrium, and their density n e obeys the Boltzmann relation

$$n_{\text{e}} \; = \;n_{0} { \exp }\left( {\frac{eV}{{k_{\text{B}} T_{\text{e}} }}} \right),$$
(4)

where k B is the constant of Boltzmann. Also, the electric potential and ion and electron densities satisfy the Poisson’s equation as follows:

$$\nabla^{2} V = - \frac{e}{{\varepsilon_{0} }}\left( {n_{i} - n_{\text{e}} } \right).$$
(5)

On the basis of the above equations and the ion-neutral collision frequency \(\nu = n_{\text{g}} \sigma_{\text{s}} \left( {v/c_{\text{s}} } \right)^{\beta } v\) (where \(n_{\text{g}} = P_{\text{g}} /k_{\text{B}} T_{\text{g}}\), P g and T g are the density, pressure and temperature of neutral gas, respectively, σ s is the ion-neutral collision cross section in the sound velocity c s and β so-called the collision power parameter is a real number between −1 and 0 that β = −1 introduces the constant collision frequency, while β = 0 presents the constant collision mean free path), one can describe the dynamic structure of plasma sheath around target.

For the sake of convenience, it is efficient to introduce some normalized parameters and variables,

$$N_{i} = \frac{{n_{i} }}{{n_{0} }} ,\quad N_{\text{e}} = \frac{{n_{\text{e}} }}{{n_{0} }} ,\quad {\mathbf{X}} = \frac{{\mathbf{x}}}{{\lambda_{\text{D}} }} ,\quad {\varvec{\Omega}}_{\text{c}} = \frac{{e{\mathbf{B}}}}{m}$$
$$\varOmega _{\text{p}} = \sqrt {\frac{{n_{0} e^{2} }}{{m\varepsilon_{0} }}} ,\quad \alpha = \frac{{\lambda_{\text{D}} }}{\lambda } = \lambda_{\text{D}} n_{\text{g}} \sigma_{\text{s}} ,\quad {\varvec{\Omega}} = \frac{{{\varvec{\Omega}}_{\text{c}} }}{{\varOmega _{\text{p}} }} ,\quad \tau =\varOmega _{\text{p}} t ,\quad \phi = \frac{eV}{{k_{\text{B}} T_{\text{e}} }}$$
$$\lambda_{D} = \sqrt {\frac{{\varepsilon_{0} k_{\text{B}} T_{\text{e}} }}{{n_{0} e^{2} }}} ,\quad c_{s} = \sqrt {\frac{{k_{\text{B}} T_{\text{e}} }}{m}} = \lambda_{\text{D}}\varOmega _{\text{p}} ,\quad u_{j} = \frac{{v_{j} }}{{c_{\text{s}} }} \left( {j = x, y, z} \right)$$

where Ω c is the ion cyclotron frequency and Ω is the ion cyclotron frequency to ion plasma frequency ratio. Indeed, Ω c introduces a vector paralleled to the magnetic field \({\mathbf{B}} = B_{0} \left( {\cos \theta_{0} {\hat{\mathbf{x}}} + \sin \theta_{0} {\hat{\mathbf{y}}}} \right)\) with the magnitude eB 0/m. τ is the normalized time by 1/Ω p, ϕ is the electric potential normalized by k B T e/e, α is the ion-neutral collision parameter, λ = 1/n g σ s is the mean free path of ion collision, u is the ion velocity normalized by the ion sound velocity c s, N i and N e are the ion and electron density, respectively, normalized by n 0, and X is the space coordinate normalized by Debye length λ D. Since the target is planar, \(\nabla \to \left( {\partial /\partial x} \right){\hat{\mathbf{x}}}\) and the normalized one-dimensional form of Eqs. (2)–(5) will be as follows:

$$\frac{{\partial N_{i} }}{\partial \tau } + \frac{{\partial \left( {N_{i} u_{x} } \right)}}{\partial X} = 0,$$
(6)
$$\left( {\frac{\partial }{\partial \tau } + u_{x} \frac{\partial }{\partial X}} \right){\mathbf{u}} = - \frac{\partial \phi }{\partial X}{\hat{\mathbf{x}}} + {\mathbf{u}} \times {\varvec{\Omega}} - \alpha u^{\beta + 1} {\mathbf{u}}$$
(7)
$$N_{\text{e}} = { \exp }\left( \phi \right)$$
(8)
$$\frac{{\partial^{2} \phi }}{{\partial X^{2} }} = N_{\text{e}} - N_{i} .$$
(9)

Using the definition \({\varvec{\Omega}} = eB_{0} \left( {\cos \theta_{0} {\hat{\mathbf{x}}} + \sin \theta_{0} {\hat{\mathbf{y}}}} \right)/m\varOmega _{\text{p}} =\varOmega _{0} \left( {\cos \theta_{0} {\hat{\mathbf{x}}} + \sin \theta_{0} {\hat{\mathbf{y}}}} \right)\), one can rewrite the vector Eq. (7) in the scalar form to find,

$$\left( {\frac{\partial }{\partial \tau } + u_{x} \frac{\partial }{\partial X}} \right)u_{x} = - \frac{\partial \phi }{\partial X} -\varOmega _{0} u_{z} \sin \theta_{0} - \alpha u^{\beta + 1} u_{x}$$
(10)
$$\left( {\frac{\partial }{\partial \tau } + u_{x} \frac{\partial }{\partial X}} \right)u_{y} =\varOmega _{0} u_{z} \cos \theta_{0} - \alpha u^{\beta + 1} u_{y}$$
(11)
$$\left( {\frac{\partial }{\partial \tau } + u_{x} \frac{\partial }{\partial X}} \right)u_{z} =\varOmega _{0} u_{x} \sin \theta_{0} -\varOmega _{0} u_{y} \cos \theta_{0} - \alpha u^{\beta + 1} u_{z} .$$
(12)

Equations (6) and (8)–(12) make a complete set of equations describing the dynamic structure of plasma sheath. We solve the equations in a region from plasma to target supplied by a negative high voltage \(V_{\text{T}} \left( t \right) = V_{\text{P}} \left[ {1 - \exp \left( { - t/t_{\text{r}} } \right)} \right]\) in which, V P and t r are the voltage amplitude and rise time of pulse, respectively.

In order to examine the dynamic structure of plasma sheath and investigate the influence of plasma parameters on the sheath structure, the complete set of equations are numerically solved using a second-order finite difference scheme in space and a first-order finite difference scheme in time. After discretization of equations in full implicit finite difference scheme, some linearization is required. In order to linearize the equations in time, we used Taylor’s expansion approximation; \(f\left( {t + \Delta t} \right) \approx f\left( t \right) + \left( {\partial f\left( t \right)/\partial t} \right)\Delta t\).

To solve the Eqs. (6) and (8)–(12), some proper initial and boundary conditions are necessary. The boundary conditions at the sheath edge and on the target for the time interval 0 < τ < τ p are:

$$\phi \left( {0, \tau } \right) = \phi_{T} \left( \tau \right), \phi \left( {L,\tau } \right) = 0, \, u_{x} \left( {L,\tau } \right) = u_{y} \left( {L,\tau } \right) = u_{z} \left( {L,\tau } \right) = 0, N_{i} \left( {L,\tau } \right) = 1 ,$$

where \(\tau_{p} =\varOmega _{\text{p}} t_{\text{p}}\) is the normalized simulation time or normalized pulse duration, \(\phi_{T} = eV_{T} /k_{\text{B}} T_{\text{e}}\) is the normalized voltage of target and L is the normalized length of the simulation area that introduces the location of a point in the plasma, sufficiently far from the sheath edge. Also, the initial conditions for the space interval 0 < X < L are:

$$\phi \left( {X,0} \right) = 0, u_{x} \left( {X,0} \right) = u_{y} \left( {X,0} \right) = u_{z} \left( {X,0} \right) = 0, N_{i} \left( {X,0} \right) = 1.$$

Numerical results and discussion

The normalized equations can now be solved assuming some constant parameters. Atomic nitrogen is used as the ion that should be implanted on the target surface. Nitrogen implantation of steel surfaces by PIII has shown to improve mechanical properties and corrosion performance [17, 18]. Nitrogen plasma density is assumed n o  = 5 × 1014 m−3 (\(\varOmega _{\text{p}} = 7.8843 \times 10^{6} {\text{Hz}}\)), electron temperature T e = 1 eV, magnetic field amplitude \(B_{0} = 0.5 {\text{T}}\) (\(\varOmega _{\text{c}} = 3.44 \times 10^{6} {\text{Hz}}\)) and the magnetic field deviation angle θ 0 = π/3. According to the assuming data, one can find \(\lambda_{\text{D}} = 332.85 \;\mu {\text{m}}\) and \(c_{\text{s}} = 2624.3 {\text{m}}/{\text{s}}\). We choose \(\sigma_{\text{s}} = 4 \times 10^{ - 19} {\text{m}}^{2}\) as the ion-neutral collision cross section and alter the gas pressure P g = k B T g n g and for the both values of collision power parameter β = 0 and −1 to examine their effect on time evolution of the sheath dynamic structure.

To study the dynamic structure of sheath, we have numerically solved the complete set of equations assuming \(\tau_{\text{r}} =\varOmega _{\text{p}} t_{\text{r}} = 0.1\tau_{\text{p}}\), \(\phi_{\text{p}} = eV_{\text{p}} /k_{\text{B}} T_{\text{e}} = - 10000\), \(\Delta \tau \; = \;\varOmega _{\text{p}} \Delta t\; = 4\; \times \;10^{ - 3}\) as the normalized time steps, n t = 40,000 as the total number of time steps, \(\Delta X\; = \;\Delta x/\lambda_{\text{D}} \; = \;0.5\) as the normalized space steps and n x  = 1400 as the total number of space steps. Using the time and space data, one can find the pulse duration \(t_{\text{p}} \; = \;n_{t} \Delta t\; = \;20.293\; \mu {\text{s}}\) (τ p = 160) and the simulation space \(L\lambda_{\text{D}} = n_{x} \Delta x = 2.33 \,{\text{cm}}\) (L = 700). The variable parameters are the gas pressure and collision power parameter which include the values P g = 0, 0.05 and \(0.1 \;{\text{Pa}}\) and β = 0 and −1, respectively. The simulation results are shown in Figs. 2, 3, 4 and 5.

Fig. 2
figure 2

Temporal variations of the ion current density J x normalized by \(J_{0} \; = \;en_{0} c_{\text{s}} \; = \;0.2099 \;{\text{A/m}}^{2}\) as a function of the gas pressure P g and collision power parameter β. The constant parameters in the simulation are; ϕ p = −10,000, Δτ = 4 × 10−3, n t = 40,000, ΔX = 0.5, n x = 1400, τ p = 160, \(1/\varOmega_{\text{p}} = 0.1268 \;\mu {\text{s}}\) and L = 700

Full size image
Fig. 3
figure 3

Temporal variations of the ion dose on the target normalized by \(n_{0} c_{\text{s}} = 1.3121 \times 10^{18} \;1/ {\text{m}}^{2} {\text{s}}\) as a function of the ion collision parameters. The constant parameters are the same as Fig. 2

Full size image
Fig. 4
figure 4

Temporal variations of the sheath width normalized by Debye length \(\lambda_{\text{D}} = 0.3328 \,{\text{mm}}\) as a function of ion collision parameters P g and β. The constant parameters are the same as Fig. 2

Full size image
Fig. 5
figure 5

Temporal variations of ion incident angle on the target as a function of ion collision parameters P g and β. The constant parameters are the same as Fig. 2

Full size image

Temporal variations of ion current density J x  = en i u x perpendicular to the target surface is shown in Fig. 2 as a function of gas pressure and collision power parameter. It can be seen that the ion current density on the target increases from zero, reaches to a maximum value, decreases and saturates to a constant value. This figure shows that the both of gas pressure and collision power parameter reduce the maximum and saturation values of ion current density. This is because the ion collision term in the ion motion Eq. (3) decelerates the ion velocity toward the target.

Figure 3 displays the temporal profile of ion dose on the target as a function of gas pressure and collision power parameter. Since the ion dose on the target is defined by \(D_{x} = \mathop \smallint \limits_{0}^{t} J_{x} {\text{d}}t\) and is directly related to J x , it has the same dependency on the ion collision parameters such as the ion current density. As it can be seen in Fig. 3, the both collision parameters P g and β, reduce the ion dose on the target. According to Fig. 3, one can find the necessary time to achieve the required dose for specified ion collision parameters.

We have defined the sheath edge as a point between target and plasma in which the normalized electric potential reduces to ϕ = −0.01. The distance between target and sheath edge is called the sheath width that has a critical role in PIII. Figure 4 exhibits temporal variations of sheath width normalized by Debye length \(\lambda_{\text{D}} = 0.3328 {\text{mm}}\) as a function of the ion collision parameters. It is clear that the sheath width is a descending function of the both collision parameters P g and β.

Ion incident angle is defined as the angle between ion velocity and normal vector on the target surface. It is then calculated via; \({\text{Arctan}}\left( {\sqrt {u_{y}^{2} + u_{z}^{2} } /u_{x} } \right)\). The vertical incident of the ion on the target increases the ion penetration while oblique incident of ion on the target grows up the sputtering of the target surface.

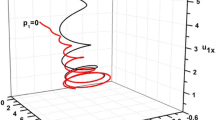
Temporal variations of ion incident angle are depicted in Fig. 5. This figure shows that the ion incident angle at the target surface increases from zero and after some fluctuations caused by the magnetic field is saturated to a constant value. In the absence of collision (P g = 0), the constant incident angle is approximated to the magnetic field deviation angle \(\theta_{0} = \pi /3 = 1.0472 \,{\text{rad}}\). It means the ion velocity on the target is paralleled to the external magnetic field. As a result, the magnetic force and fluctuations caused by it will be removed as soon as the ion velocity is constantly paralleled with the magnetic field. According to Fig. 5, the gas pressure reduces the saturated ion incident angle and diminishes the magnetic field effects.

Also, Fig. 5 shows that the ion incident angle is strongly reduced by increasing the collision power parameter from −1 (for constant collision frequency) to 0 (for constant collision mean free path). Indeed, further increasing the collision power parameter and the gas pressure reduces the ion incident angle. In other words, increasing the collision parameters turn the oblique incident to the perpendicular incident.

Time evolution of ion impact energy on the target surface defined by \(E_{k} = m_{i} \left( {v_{ix}^{ 2} + v_{iy}^{ 2} + v_{iz}^{ 2} } \right)/ 2 = k_{B} T_{e} \left( {u_{x}^{ 2} + u_{y}^{ 2} + u_{z}^{ 2} } \right)/ 2\) is displayed in Fig. 6 as a function of the ion collision parameters P g and β. This figure shows that the ion impact energy on the target surface increases from zero and is eventually saturated to a constant value by time. The saturation value of ion energy on the target is reduced by gas pressure and collision power parameter. As one can see, the ions never gain the full energy of bias voltage even in the absence of collision. Since ion transit time across the sheath is large (on the order of 1/Ω p ) and sheath expands during ion flight across the sheath, both the shape and magnitude of the potential barrier vary, so that the implanted ions do not get the full bias voltage. In other words, displacement current across the expanding sheath leads to an increase in the ion implanted current and causes a decrease in the implanted ion energy with respect to the stationary sheath with the same parameters [19, 20]. According to Fig. 6, one can anticipate the ion implanting energy for specified gas pressure and its proper collision model.

Fig. 6
figure 6

Temporal variations of ion impact energy on the target normalized by k B T e  = 1 eV as a function of the ion collision parameters P g and β. The constant parameters are the same as Fig. 2

Full size image

Summary and conclusions

In order to investigate the influence of the gas pressure and ion collision model on the dynamic behavior of plasma sheath in the PIII process, we have used the fluid model of plasma and numerically solved time-dependent equations of a pulsed magnetized plasma through an implicit finite difference scheme. Temporal variations of normalized current density, dose, incident angle and impact energy of ions on the target surface as well as sheath width were presented in the high-voltage sheath.

Calculations show that temporal profile of the ion current density and ion dose in the plasma-sheath decrease by increasing the gas pressure and collision power parameter. Sheath width is a descending function of the both collision parameters. Temporal profile of the ion incident angle on the target begins to increase from zero and after some fluctuations caused by magnetic field is saturated to a constant value. The constant value of incident angle is the same as the magnetic field deviation angle θ 0 = π/3 in the absence of collision. It means that the magnetic force and fluctuations arising from it will be removed over time. The collision parameters including gas pressure and collision power parameter strongly decrease the saturated ion incident angle.

Also, temporal profile of the ion impact energy on the target surface shows a growing up from zero and saturating to a constant value over time. The constant value is significantly reduced by gas pressure and collision power parameter. The profile shows that in the dynamic sheath, unlike the static sheath, the ions never gain the full energy of bias voltage. This is because the dynamic sheath expands during ion flight across the sheath and both the shape and magnitude of the potential barrier vary. Using the temporal profile of the ion impact energy one can anticipate the ion implanting energy for specified collision parameters.