Quasi monoenergetic electron bunch generation by frequency variation laser pulse in magnetized plasma

Abstract

The effect of the frequency variation of laser pulse in uniform magnetized plasma is considered in one-dimensional laser wakefield acceleration and carried out particle simulation. It is shown that wakefield amplitude is increased threefold for the negative Gaussian chirped laser pulse in the magnetized plasma. In our simulation, electrons with initial energy about 0.3 MeV with initial energy spread about 10 % were trapped, effectively compressed in longitudinal direction and accelerated to ultra-relativistic energy about 1.3 GeV with final energy spread about 6 %.

Introduction

High quality electron bunches accelerated by the laser-driven plasma wakes can be used for radiotherapy in medicine, ultrafast radiolysis in chemistry, fine structure imaging in biology and material science, and accelerator physics [1–4].

Laser-driven electron accelerators are capable of producing compact and high-energy electron sources in shorter distances than conventional RF accelerators due to the ultrahigh electric field.

This laser wakefield acceleration (LWFA) scheme is considered to be the most promising one among the various laser-plasma accelerators.

In laser wakefield acceleration, a short laser pulse propagates in an under dense plasma, and excites plasma waves [5, 6], which can trap and accelerate electrons to ultra-relativistic energies. Recently, significant experimental results came out showing quasi-monoenergetic bunches of relativistic electrons with up to GeV energy [7–12].

One of the most critical issues in LWFA process is related to how to enhance the wakefield amplitude and accelerated electrons energy. Although several techniques have been proposed to this end, including the use of microwave pulses [13–15] through changing pulse shape [16, 17], through using tapered plasma channel [18, 19] and chirped laser pulse [20, 21], and through external magnetic field [24–27], this paper explores the use of chirped laser pulse along with external magnetic field to excite wakefield. Previous investigations (see Ref. [20–23]) have already shown that a laser pulse with suitable chirp can drive stronger wakefield. The role of frequency chirps in the laser intensity profile and wakefield excitation has been explored experimentally [8, 28]. Moreover, experimental investigation showed that using an external magnetic field can improve the wakefield amplitude, particle trapping and acceleration [29].

Combination of an axial magnetic field and chirped laser pulse for electron acceleration, in vacuum, was investigated by Gupta and Suk [30]. They showed that the frequency variation plays an important role to enhance the electron energy in the presence of a static magnetic field in vacuum.

In this work, the effect of frequency variation of the circularly polarized laser pulse in magnetized plasma is investigated for 1-D laser wakefield excitation. Moreover, we examine acceleration of externally injected electron bunch in longitudinal electrostatic field in presence of the chirped laser pulse in magnetized plasma. This paper is organized as follows: In “Laser wakefield excitation in the magnetized plasma”, the equations which describe the generation of the wakefield by chirped laser pulse in magnetized plasma have been formulated. In “Chirped pulse laser wakefield excitation”, vector potential of the chirped laser pulse and numerical analysis of the longitudinal electrostatic wakefield’s excitation are described. In “Acceleration of an externally injected electron bunch”, electron bunch acceleration with frequency chirped laser pulse in the magnetized plasma is considered, and a discussion of the results is given in “Conclusion”.

Laser wakefield excitation in the magnetized plasma

A circularly polarized laser pulse with frequency chirped; $E=E_{0}exp\left[-{\left((z-z_0-v_{g}t)/{\mathit{\sigma }}_z\right)}^2\right]\times \left\{\widehat{x}\text{Cos}\left(k(z-z_0)-\mathit{\omega }t\right)+\widehat{y}\text{Sin}\left(k(z-z_0)-\mathit{\omega }t\right)\right\},$ is considered to propagate at positive z direction in homogeneous plasma. This plasma is placed in a constant external magnetic field ${\overrightarrow{B}}_0=\mathit{\sigma }{B}_0\widehat{z}$ where $\mathit{\sigma }=\pm 1$ recognizes direction of the field. The laser frequency will be assumed as a function of distance and time.

To describe the plasma electrons motion, we use the relativistic hydrodynamic equations and Maxwell equations for cold magnetized plasma as follows

$$\frac{\text{d}\overrightarrow{P}}{\text{d}t}=-e\left(\overrightarrow{E}+\frac{\overrightarrow{v}}{c}\times (\overrightarrow{B}+\mathit{\sigma }{\overrightarrow{B}}_0)\right),$$

(1)

$$\frac{\mathit{\partial }{n}_e}{\mathit{\partial }t}+\mathrm{\nabla }.(n_e\overrightarrow{v})=0,$$

(2)

$${\mathrm{\nabla }}^2\mathit{\varphi }=4\mathit{\pi }e(n_e-n_0),$$

(3)

$$\overrightarrow{E}=-\frac{1}{c}\frac{\mathit{\partial }\overrightarrow{A}}{\mathit{\partial }t}-\mathrm{\nabla }\mathit{\varphi },$$

(4)

$$\overrightarrow{B}=\mathrm{\nabla }\times \overrightarrow{A},$$

(5)

where $\overrightarrow{p}(=\mathit{\gamma }{m}_e\overrightarrow{v})$ is the plasma electrons momentum, $m_e$, $n_e$ and $\overrightarrow{v}$ are respectively the plasma electron’s mass, density and velocity. $\mathit{\gamma }={(1-v^2/\phantom{v^2{c}^2}{c}^2)}^{-1/\phantom{12}2}$ is the Lorenz relativistic factor, $\overrightarrow{A}$ is the vector potential of the laser pulse and $\mathit{\varphi }$ is the scalar potential of the generated electrostatic field.

Electron velocities may be considered to be slow and fast components $(\overrightarrow{v}={\overrightarrow{v}}_s+{\overrightarrow{v}}_f),$ where ${\overrightarrow{v}}_s$ (slow portion) oscillating at the plasma frequency $({\mathit{\omega }}_p={(4\mathit{\pi }{e}^2{n}_0/m_e)}^{1/2})$ and ${\overrightarrow{v}}_f$ (fast portion) oscillating at the laser frequency.

From Eqs. (1), (4) and (5), the equation for the velocity of the electron motion follows

$$\frac{\mathit{\partial }}{\mathit{\partial }t}\left[\mathit{\gamma }({\overrightarrow{v}}_s+{\overrightarrow{v}}_f)\right]+\left[({\overrightarrow{v}}_s+{\overrightarrow{v}}_f).\overrightarrow{\mathrm{\nabla }}(\mathit{\gamma }({\overrightarrow{v}}_s+{\overrightarrow{v}}_f))\right]=-\frac{e}{m_e}\left(-\frac{1}{c}\frac{\mathit{\partial }\overrightarrow{A}}{\mathit{\partial }t}-\mathrm{\nabla }\mathit{\varphi }+\frac{\overrightarrow{v}}{c}\times (\mathrm{\nabla }\times \overrightarrow{A}+\mathit{\sigma }{\overrightarrow{B}}_0)\right)$$

(6)

For dilute under dense plasma ${\mathit{\omega }}_p/\mathit{\omega }<<1,$ all of the axial and time dependencies of the laser pulse can be expressed as a function of a single variable $\mathit{\xi }=z-v_{g}t$, where $v_g$ is the group velocity of the laser pulse. In terms of this variable the electric field of the chirped laser pulse can be described by

$$E=E_0\text{Exp}\left[-{\left(\frac{\mathit{\xi }-{\mathit{\xi }}_0}{{\mathit{\sigma }}_z}\right)}^2\right]\left\{\widehat{x}sin\left(k\left(\mathit{\xi }-{\mathit{\xi }}_0\right)\right)+\widehat{y}cos\left(k\left(\mathit{\xi }-{\mathit{\xi }}_0\right)\right)\right\},$$

(7)

where $k=\mathit{\omega }(\mathit{\xi })/v_g$, $\mathit{\omega }(\mathit{\xi })$ and ${\mathit{\sigma }}_z$ are the wave number, the arbitrary frequency chirp function and the length of laser pulse, respectively. Then we write the general equation for the vector potential of this pulse as follows

$$A=A(\mathit{\xi })\left\{\widehat{x}\text{Sin}\left(k\left(\mathit{\xi }-{\mathit{\xi }}_0\right)\right)+\widehat{y}\text{Cos}\left(k\left(\mathit{\xi }-{\mathit{\xi }}_0\right)\right)\right\}$$

(8)

where $A(\mathit{\xi })$ is the vector potential envelop for the chirped laser pulse which is obtained in the next section.

The fast component of the plasma electrons velocity may be obtained from Eq. (6) as follows:

$$\frac{\mathit{\partial }(\mathit{\gamma }{\tilde{v}}_{xf})}{\mathit{\partial }\tilde{\mathit{\xi }}}=\frac{\mathit{\partial }{a}_x}{\mathit{\partial }\tilde{\mathit{\xi }}}+\mathit{\sigma }{\tilde{\mathit{\omega }}}_c{\tilde{v}}_{yf},$$

(9)

$$\frac{\mathit{\partial }(\mathit{\gamma }{\tilde{v}}_{yf})}{\mathit{\partial }\tilde{\mathit{\xi }}}=\frac{\mathit{\partial }{a}_y}{\mathit{\partial }\tilde{\mathit{\xi }}}-\mathit{\sigma }{\tilde{\mathit{\omega }}}_c{\tilde{v}}_{xf},$$

(10)

$$\frac{\mathit{\partial }(\mathit{\gamma }{\tilde{v}}_{zf})}{\mathit{\partial }\tilde{\mathit{\xi }}}=0,$$

(11)

where $\tilde{\mathit{\xi }}=k_p\mathit{\xi }$, ${\tilde{v}}_{if}=v_{if}/\phantom{v_{if}c}c(i=x,y,z)$ are the normalized velocity components, $\overrightarrow{a}=e\overrightarrow{A}/m_e{c}^2$ is the normalized vector potential of chirped laser pulse, and ${\tilde{\mathit{\omega }}}_c=e{B}_0/m_{e}c{\mathit{\omega }}_p$ is the normalized cyclotron frequency. Simultaneous solutions of Eqs. (9), (10), (11) give

$${\tilde{v}}_{xf}=\frac{a\tilde{\mathit{\omega }}(\mathit{\xi })}{\mathit{\sigma }{\tilde{\mathit{\omega }}}_c+\mathit{\gamma }\tilde{\mathit{\omega }}(\mathit{\xi })}\text{Sin}(\tilde{\mathit{\omega }}(\mathit{\xi })(\tilde{\mathit{\xi }}-{\tilde{\mathit{\xi }}}_0)),$$

(12)

$${\tilde{v}}_{yf}=-\frac{a\tilde{\mathit{\omega }}(\mathit{\xi })}{\mathit{\sigma }{\tilde{\mathit{\omega }}}_c+\mathit{\gamma }\tilde{\mathit{\omega }}(\mathit{\xi })}\text{Cos}(\tilde{\mathit{\omega }}(\mathit{\xi })(\tilde{\mathit{\xi }}-{\tilde{\mathit{\xi }}}_0)),$$

(13)

$${\tilde{v}}_{zf}=0,$$

(14)

where $\tilde{\mathit{\omega }}(\mathit{\xi })=\mathit{\omega }(\mathit{\xi })/{\mathit{\omega }}_p$ is the normalized laser pulse frequency. Obviously, electrons velocity is affected by the variation of laser pulse frequency and the variation of external magnetic field.

Equation (6) may also be used to obtain the governing equations for the evolution of the slow plasma electron velocities. We assumed that the laser pulse profile doesn’t change during the interaction. Using the quasi static approximation [6] this equation can be expressed as

$$-\frac{\mathit{\partial }(\mathit{\gamma }{\tilde{v}}_{xs})}{\mathit{\partial }\tilde{\mathit{\xi }}}+\frac{u_{zs}}{{\mathit{\beta }}_g}\frac{\mathit{\partial }(\mathit{\gamma }{\tilde{v}}_{xs})}{\mathit{\partial }\tilde{\mathit{\xi }}}+\frac{u_{zf}}{{\mathit{\beta }}_g}\frac{\mathit{\partial }(\mathit{\gamma }{\tilde{v}}_{xf})}{\mathit{\partial }\tilde{\mathit{\xi }}}=-\mathit{\sigma }{\tilde{\mathit{\omega }}}_c{\tilde{v}}_{ys},$$

(15)

$$-\frac{\mathit{\partial }(\mathit{\gamma }{\tilde{v}}_{ys})}{\mathit{\partial }\tilde{\mathit{\xi }}}+\frac{u_{zs}}{{\mathit{\beta }}_g}\frac{\mathit{\partial }(\mathit{\gamma }{\tilde{v}}_{ys})}{\mathit{\partial }\tilde{\mathit{\xi }}}+\frac{u_{zf}}{{\mathit{\beta }}_g}\frac{\mathit{\partial }(\mathit{\gamma }{\tilde{v}}_{yf})}{\mathit{\partial }\tilde{\mathit{\xi }}}=-\mathit{\sigma }{\tilde{\mathit{\omega }}}_c{\tilde{v}}_{xs},$$

(16)

$$-\frac{\mathit{\partial }(\mathit{\gamma }{\tilde{v}}_{zs})}{\mathit{\partial }\tilde{\mathit{\xi }}}+{\tilde{v}}_{zs}\frac{\mathit{\partial }(\mathit{\gamma }{\tilde{v}}_{zs})}{\mathit{\partial }\tilde{\mathit{\xi }}}=\frac{\mathit{\partial }\tilde{\mathit{\varphi }}}{\mathit{\partial }\tilde{\mathit{\xi }}}-{\tilde{v}}_{xf}\frac{\mathit{\partial }{a}_x}{\mathit{\partial }\tilde{\mathit{\xi }}}-{\tilde{v}}_{yf}\frac{\mathit{\partial }{a}_y}{\mathit{\partial }\tilde{\mathit{\xi }}},$$

(17)

where $\tilde{\mathit{\varphi }}=e\mathit{\varphi }/m_e{c}^2$ is the normalized scalar potential of the wakefield and ${\tilde{v}}_{is}=v_{is}/\phantom{v_{is}c}c(i=x,y,z)$ are the normalizes slow plasma electron velocities.

Equations (12–17) with the continuity equation and the Poisson equation are of the following

$$\frac{\mathit{\partial }\mathit{\gamma }}{\mathit{\partial }\tilde{\mathit{\xi }}}=\frac{{\tilde{v}}_{zs}}{{\mathit{\gamma }}^{3/2}+\frac{1}{\mathit{\gamma }}\left(1-\frac{1}{{\mathit{\gamma }}^2}\right)-{\tilde{v}}_{zs}^2}\frac{\mathit{\partial }{\tilde{v}}_{zs}}{\mathit{\partial }\tilde{\mathit{\xi }}},$$

(18)

$$\frac{\mathit{\partial }{\tilde{v}}_{zs}}{\mathit{\partial }\tilde{\mathit{\xi }}}=-\frac{1}{\mathit{\gamma }({\tilde{v}}_{zs}-{\mathit{\beta }}_g^{})}{\tilde{E}}_z-\frac{{\tilde{v}}_{zs}}{\mathit{\gamma }}\frac{\mathit{\partial }\mathit{\gamma }}{\mathit{\partial }\tilde{\mathit{\xi }}}-\frac{\tilde{\mathit{\omega }}(\mathit{\xi })}{2(\mathit{\sigma }{\tilde{\mathit{\omega }}}_c+\mathit{\gamma }\tilde{\mathit{\omega }}(\mathit{\xi }))({\tilde{v}}_{zs}-{\mathit{\beta }}_g^{})}\frac{\mathit{\partial }{a}^2}{\mathit{\partial }\tilde{\mathit{\xi }}},$$

(19)

$$\frac{\mathit{\partial }n}{\mathit{\partial }\tilde{\mathit{\xi }}}=-\frac{n}{({\tilde{v}}_{zs}-{\mathit{\beta }}_g^{})}\frac{\mathit{\partial }{\tilde{v}}_{zs}}{\mathit{\partial }\tilde{\mathit{\xi }}},$$

(20)

$$\frac{\mathit{\partial }{\tilde{E}}_z}{\mathit{\partial }\tilde{\mathit{\xi }}}=(1-n),$$

(21)

where $n=n_e/n_0$ is the normalized density of plasma electrons and ${\tilde{E}}_z(=-\mathit{\partial }\tilde{\mathit{\varphi }}/\mathit{\partial }\tilde{\mathit{\xi }})$ is the normalized wakefield.

The normalized group velocity of the left hand circularly polarized chirped laser pulse in the first order approximation, can be written as [31]

$${\mathit{\beta }}_g=\frac{2{[{\tilde{\mathit{\omega }}}^2(\mathit{\xi })-\tilde{\mathit{\omega }}(\mathit{\xi })/(\mathit{\gamma }\tilde{\mathit{\omega }}(\mathit{\xi })-\mathit{\sigma }{\tilde{\mathit{\omega }}}_c)]}^{1/\phantom{12}2}}{2\tilde{\mathit{\omega }}(\mathit{\xi })+\mathit{\sigma }{\tilde{\mathit{\omega }}}_c/{(\mathit{\gamma }\tilde{\mathit{\omega }}(\mathit{\xi })-\mathit{\sigma }{\tilde{\mathit{\omega }}}_c)}^2},$$

(22)

Equations (18–22) describe excitation of plasma waves in the presence of the axial magnetic field and frequency variation of the laser pulse. In the next section at first, we obtain profile of the vector potential of the laser pulse with Gaussian frequency variation and then solve simultaneously, Eqs. (18–21) by fourth order Runge–Kutta method.

Chirped pulse laser wakefield excitation

The vector potential component of the circularly polarized laser pulse is derived as

$$A_x(\mathit{\xi })=\underset{0}{\overset{\mathit{\xi }}{\int }}{E}_x({\mathit{\xi }}^{\prime })d{\mathit{\xi }}^{\prime },A_y(\mathit{\xi })=\underset{0}{\overset{\mathit{\xi }}{\int }}{E}_y({\mathit{\xi }}^{\prime })d{\mathit{\xi }}^{\prime }$$

(23)

Clearly, the profiles of x and y components are identical. Above equations cannot be solved analytically for an arbitrary chirped pulse. We find an equation for the pulse profile $A(\mathit{\xi })$ by fitting procedure and substituting in the general equation for the vector potential, Eq. (8). Obviously, changes in the chirp parameters can alter the pulse profile [21]. We consider the laser pulse as expressed by Eq. (7), and using Gaussian function for the chirp profile as [32] $\mathit{\omega }(\mathit{\xi })={\mathit{\omega }}_0+\mathrm{\Delta }\text{Exp}\left[-{(\mathit{\xi }-{\mathit{\xi }}_0)}^2/{\mathit{\sigma }}_z^2\right]$, in which ${\mathit{\omega }}_0+\mathrm{\Delta }$ is frequency at the center of the laser pulse, $\mathrm{\Delta }$ was called Gaussian chirp parameter and Gaussian chirp width set equal to the spatial duration of the laser pulse (Eq. 7).

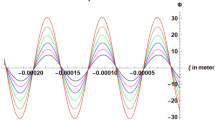
In Fig. 1, the normalized vector potential amplitude, $a(\tilde{\mathit{\xi }})=eA(\tilde{\mathit{\xi }})/m{c}^2$ amplitude is shown as a function of $k_p^{}\mathit{\xi }$, for the chirped laser pulse with amplitude $a_0=0.5$, duration of $k_p{\mathit{\sigma }}_z=2$, centered at $k_p{\mathit{\xi }}_0=-20$, and with normalized chirp parameter $\tilde{\mathrm{\Delta }}(=\mathrm{\Delta }/{\mathit{\omega }}_p)=-10$.

Fig. 1

The normalized vector potential amplitude in term of $k_p\mathit{\xi }$ for chirped laser pulse with $a_0=0.5$, $k_p{\mathit{\sigma }}_z=2$, $\tilde{\mathrm{\Delta }}=-10$ and $k_p{\mathit{\xi }}_0=-20$

Figure 2 shows envelop of the normalized vector potential of Gaussian chirped laser pulse and fitted curve on it. The equation of this curve can be expressed by inverse polynomial as

$$a(\mathit{\xi })=\frac{b}{1+b_1{\left(\mathit{\xi }-{\mathit{\xi }}_0\right)}^2+b_2{\left(\mathit{\xi }-{\mathit{\xi }}_0\right)}^4+b_3{\left(\mathit{\xi }-{\mathit{\xi }}_0\right)}^6},$$

(24)

where $b,b_1,b_2,b_3$ are fitting coefficients for Gaussian chirped pulse vector potential amplitude. We draw $b$, ${\tilde{b}}_1(=b_1/k_p^2)$, ${\tilde{b}}_2(=b_2/k_p^4)$ and ${\tilde{b}}_3(=b_3/k_p^6)$ for different chirp parameter $(-10<\tilde{\mathrm{\Delta }}<10)$ in Fig. 3, and fit nearest polynomials for their dependencies $b(\tilde{\mathrm{\Delta }})$, ${\tilde{b}}_1(\tilde{\mathrm{\Delta }})$, ${\tilde{b}}_2(\tilde{\mathrm{\Delta }})$ and ${\tilde{b}}_3(\tilde{\mathrm{\Delta }})$.

Fig. 2

Profile of normalized vector potential amplitude and fitted curve on it versus $k_p\mathit{\xi }$ for Gaussian chirped laser pulse with $a_0=0.5$, $k_p{\mathit{\sigma }}_z=2$, $\tilde{\mathrm{\Delta }}=-10$ and $k_p{\mathit{\xi }}_0=-20$

Fig. 3

Fitted curves for $b_{}$, $b_1/k_p^2$, $b_2/k_p^4$ and $b_3/k_p^6$ against $\mathrm{\Delta }/{\mathit{\omega }}_p$

$$b=0.46911-0.01789\tilde{\mathrm{\Delta }}+6.96026E^{-4}{\tilde{\mathrm{\Delta }}}^2-2.04859E^{-5}{\tilde{\mathrm{\Delta }}}^3$$

(25)

$${\tilde{b}}_1=0.25413-0.02632\tilde{\mathrm{\Delta }}+7.56068E^{-4}{\tilde{\mathrm{\Delta }}}^2+6.69191E^{-7}{\tilde{\mathrm{\Delta }}}^3$$

(26)

$${\tilde{b}}_2=0.0025-0.00194\tilde{\mathrm{\Delta }}+3.35897E^{-4}{\tilde{\mathrm{\Delta }}}^2-1.16643E^{-5}{\tilde{\mathrm{\Delta }}}^3$$

(27)

$${\tilde{b}}_3=0.00818-2.61135E^{-4}\tilde{\mathrm{\Delta }}+9.05002E^{-6}{\tilde{\mathrm{\Delta }}}^2-7.61634E^{-7}{\tilde{\mathrm{\Delta }}}^3$$

(28)

Substituting Eqs. (25–28) in (24) leads to a relation for pulse profile in term of $\mathit{\xi }$ and $\mathrm{\Delta }$. Then we obtain $a(\mathit{\xi },\mathrm{\Delta })$ for any Gaussian chirped parameter.

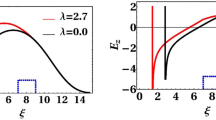
In order to analyze the generation of wakefield, we insert this pulse profile in Eq. (19) and solve numerically Eqs. (18–21) for different values of the chirp parameter. For a plasma with n _p  = 1.21 × 10¹⁸ cm⁻³ and a laser pulse with $\mathit{\omega }/{\mathit{\omega }}_p=30$, $a_0=0.5$, $k_p{\mathit{\sigma }}_z=2$ and $k_p{\mathit{\xi }}_0=-20$, the normalized longitudinal electric field of the wakefield and peak vector potential amplitude in terms of the different chirp parameters in unmagnetized plasma are shown in Fig. 4a. It is clear from this figure that the suitable negative Gaussian chirp parameter can increase the peak vector potential and wakefield amplitude. For this reason we consider negative Gaussian chirp parameter $\mathrm{\Delta }/{\mathit{\omega }}_p=-10$ in the following numerical results. In the negative Gaussian chirped laser pulse, frequency variation from the front part of the laser pulse to its center is decreasing $(\mathit{\partial }\mathit{\omega }(\mathit{\xi })/\mathit{\partial }\mathit{\xi }<0)$ and frequency variation from the center to the back of pulse is increasing $(\mathit{\partial }\mathit{\omega }(\mathit{\xi })/\mathit{\partial }\mathit{\xi }>0)$. In Fig. 4b, we have plotted the normalized frequency variation $\mathit{\omega }(\mathit{\xi })/{\mathit{\omega }}_p$ as a function of $k_p^{}\mathit{\xi }$, for the negative Gaussian chirped laser pulse with normalized chirp parameter $\tilde{\mathrm{\Delta }}(=\mathrm{\Delta }/{\mathit{\omega }}_p)=-10$.

Fig. 4

a The normalized wakefield amplitude versus the normalized Gaussian chirp parameter. b The normalized frequency variation in term of $k_p\mathit{\xi }$ for chirped laser pulse with $a_0=0.5$, $k_p{\mathit{\sigma }}_z=2$, $\tilde{\mathrm{\Delta }}=-10$ and $k_p{\mathit{\xi }}_0=-20$

Furthermore, Jha et al. [25] showed that a reversed external magnetic field ($\mathit{\sigma }=-1$) can increases the amplitude of the generated axial wakefield. We obtain the same results for the combined effect of the chirped pulse and axial magnetic field, then we consider only reversed magnetic field in this work. Normalized electrostatic field amplitude is shown as a function of $k_p\mathit{\xi }$ in Fig. 5, for three different cases, (1) Unchirped laser pulse in unmagnetized plasma ($\tilde{\mathrm{\Delta }}=0$ and ${\tilde{\mathit{\omega }}}_c=0$ in solid line), (2) Unchirped laser pulse in reversed external magnetic field ($\tilde{\mathrm{\Delta }}=0$ and ${\tilde{\mathit{\omega }}}_c=5$ in dotted line), (3) Chirped laser pulse without external magnetic field ($\tilde{\mathrm{\Delta }}=-10$ and ${\tilde{\mathit{\omega }}}_c=0$ in dashed line). It is seen that the normalized wakefield amplitude is about 0.35 for negative Gaussian chirped laser pulse in unmagnetized plasma which is doubled compared to unchirped laser pulse in unmagnetized plasma case. The normalized wakefield amplitude is about 0.18 for unchirped pulse in magnetized plasma which increases about %30 compared to unchirped laser pulse in unmagnetized plasma case.

Fig. 5

Normalized longitudinal electrostatic wakefield as a function of $k_p\mathit{\xi }$ for $a_0=0.5$, $k_p{\mathit{\sigma }}_z=2$ and $\tilde{\mathit{\omega }}=30$. $\tilde{\mathrm{\Delta }}=0$ and ${\tilde{\mathit{\omega }}}_c=0$ (solid line), $\tilde{\mathrm{\Delta }}=0$ and ${\tilde{\mathit{\omega }}}_c=5$ (dotted line), and $\tilde{\mathrm{\Delta }}=-10$ and ${\tilde{\mathit{\omega }}}_c=0$ (dashed line)

The normalized longitudinal electrostatic field versus $k_p\mathit{\xi }$ for negative Gaussian chirp and inverse magnetic field in plasma is shown in Fig. 6. As expected in this case the normalized wakefield amplitude increases about threefold and reaches to 0.45.

Fig. 6

Variation of normalized longitudinal electrostatic wakefield as a function of $k_p\mathit{\xi }$ for $a_0=0.5$, $k_p{\mathit{\sigma }}_z=2$ and $\tilde{\mathit{\omega }}=30$. $\tilde{\mathrm{\Delta }}=0$ and ${\tilde{\mathit{\omega }}}_c=0$ (solid line), $\tilde{\mathrm{\Delta }}=-10$ and ${\tilde{\mathit{\omega }}}_c=5$ with $\mathit{\sigma }=-1$ (dash dotted line)

In the next section we will investigate acceleration of an externally injected electron bunch in the wakefield of these explained cases.

Acceleration of an externally injected electron bunch

The relativistic momentum equation for an electron with charge $-e$ and rest mass $m_e$ is

$$\frac{\text{d}\overrightarrow{P}}{\text{d}t}=-e\left(\overrightarrow{E}+\frac{1}{c}\frac{\overrightarrow{P}}{m_e\mathit{\gamma }}\times \overrightarrow{B}\right),$$

(29)

where $\mathit{\gamma }$ is the relativistic factor, $\overrightarrow{E}$ and $\overrightarrow{B}$ are electric and magnetic fields associated to the generated wakefield, the interacting laser pulse and external magnetic field. The laser pulse magnetic field is related to the pulse electric field by $\mathrm{\nabla }\times \overrightarrow{E}=-(1/c)\mathit{\partial }\overrightarrow{B}/\mathit{\partial }t$.

We used the normalize variables such that

$$\tilde{p}=\frac{p}{m_{0}c},{\tilde{E}}_{zw}=\frac{e{E}_{zw}}{m_{e}c{\mathit{\omega }}_p},{\tilde{E}}_{ip}=\frac{e{E}_{ip}}{m_{e}c{\mathit{\omega }}_p}(i=x,y),\tilde{t}={\mathit{\omega }}_{p}t,{\tilde{\mathit{\omega }}}_c=\frac{e{B}_0}{m_{e}c{\mathit{\omega }}_p},$$

(30)

and decompose the Eq. (29) into the three components

$$\frac{\text{d}{\tilde{p}}_x}{\text{d}\tilde{t}}=-\left(\left(1-\frac{{\tilde{p}}_z}{\mathit{\gamma }}\right){\tilde{E}}_{xp}-\frac{{\tilde{p}}_y}{\mathit{\gamma }}{\tilde{\mathit{\omega }}}_c\right),$$

(31)

$$\frac{\text{d}{\tilde{p}}_y}{\text{d}\tilde{t}}=-\left(\left(1-\frac{{\tilde{p}}_z}{\mathit{\gamma }}\right){\tilde{E}}_{yp}-\frac{{\tilde{p}}_x}{\mathit{\gamma }}{\tilde{\mathit{\omega }}}_c\right),$$

(32)

$$\frac{d{\tilde{p}}_z}{d\tilde{t}}=\left({\tilde{E}}_{zw}+\frac{{\tilde{p}}_x}{\mathit{\gamma }}{\tilde{E}}_{xp}+\frac{{\tilde{p}}_y}{\mathit{\gamma }}{\tilde{E}}_{yp}\right),$$

(33)

with

$$\mathit{\gamma }=\sqrt{1+{\tilde{p}}_x^2+{\tilde{p}}_y^2+{\tilde{p}}_z^2}.$$

(34)

where E _zw is the normalized longitudinal electrostatic wakefield, E _xp and E _yp are the normalized laser pulse transverse electric fields.

These equations are governing electron momentum and energy. We solve them numerically by the fourth order Runge–Kutta method and the results are discussed as follows.

We performed one and a half dimensional simulation of an electron bunch with ${\mathit{\tau }}_b=70\text{fs}$, $r_b=20$ μm, and ${10}^5$ electrons. The injected electron bunch is distributed numerically by a random Gaussian distribution in both coordinates and velocities. The average initial energy was about 0.3 MeV with 10 % longitudinal energy spread and 1 mm mrad transverse emittance to be injected forward the laser pulse at $k_{p}z=-10$.

We assume a Gaussian chirped laser pulse with $a_0=0.5$, ${\mathit{\tau }}_l=30\text{fs}$, ${\mathit{\lambda }}_l=1$ μm, $w_0=100$ μm and the pulse chirp parameter is ${\tilde{\mathrm{\Delta }}}_w=-10$. The plasma wavelength is ${\mathit{\lambda }}_p=30$ μm which corresponds to $n_p=1.21\times {10}^{18}{\text{cm}}^{-3}$, embedded in a constant magnetic field ${\tilde{\mathit{\omega }}}_c^{}=5$.

In this simulation, with the assumption that $w_0>>{\mathit{\lambda }}_p$, the transverse wakefield effect is neglected but in this simulation, electrons transverse velocity and position are intended for the calculation of accelerated electron bunch divergence.

Initial energy is an effective parameter governing on electron acceleration. Figure 7 shows the final electrons energy via its initial energy. It is clear from this figure that the electron bunch with ${\mathit{\gamma }}_{\text{in}}=1.6$, can be accelerated to about ${\mathit{\gamma }}_{\text{out}}\approx 2,600$.

Fig. 7

Final energy of electron bunch via its initial energy

In Fig. 8, average energy of the accelerated electrons is shown in terms of axial coordinate k _p z. It can be seen that the final energy of the electrons is about 1.3 GeV (solid line) for the case of chirped laser pulse in magnetized plasma that is twice the electrons gain energy from generated wakefield by chirped pulse in unmagnetized plasma (dashed line) and fourfold the electrons gain energy from electrostatic field generated by unchirped laser pulse in unmagnetized plasma (dotted line).

Fig. 8

Average energy net of electron bunch as a function of $k_{p}z$ for $a_0=0.5$, $k_p{\mathit{\sigma }}_z=2$, $\tilde{\mathit{\omega }}=30$ and ${\mathit{\lambda }}_p=30$ μm. $\tilde{\mathrm{\Delta }}=0$ and ${\tilde{\mathit{\omega }}}_c=0$ (dotted line), $\tilde{\mathrm{\Delta }}=-10$ and ${\tilde{\mathit{\omega }}}_c=0$ (dashed line), $\tilde{\mathrm{\Delta }}=-10$ and ${\tilde{\mathit{\omega }}}_c=5$ with $\mathit{\sigma }=-1$ (solid line)

It is seen that the retained electrons energy is about 1.3 GeV in the case of generated wakefield by combined effect of chirped laser pulse and reversed external magnetic field in plasma.

The reversed external magnetic field enhances wakefield amplitude; moreover, it increases the phase velocity of the plasma wave (equal to group velocity of the laser pulse) and causes electrons to stay more in the acceleration region. Figure 9 shows group velocity of the negative Gaussian chirped laser pulse in the acceleration region for the presence (dotted line) and absence (solid line) of reversed external magnetic field. On the other hand, wakefield amplitude increases about threefold by negative Gaussian chirped laser pulse (see Fig. 6), since electrons gain more energy from the wake due to its larger amplitude. In other words, larger electrostatic field of the wake interacts in the larger distance (dephasing length) on the trapped electrons and these electrons gain energy about 1.3 GeV.

Fig. 9

Variation of the negative Gaussian chirped laser pulse group velocity in the acceleration region as a function of $k_p\mathit{\xi }$. ${\tilde{\mathit{\omega }}}_c=0$ (solid line), ${\tilde{\mathit{\omega }}}_c=5$ with $\mathit{\sigma }=-1$ (dotted line)

Energy distribution of electrons after acceleration is shown in Fig. 10. The final longitudinal energy spread is about 6 % that shows a decline of about 4 %.

Fig. 10

Energy distribution of the electron bunch after acceleration

Initial and final structures of electron bunch before and after acceleration are plotted in Fig. 11a and b, respectively.

Fig. 11

Electron bunch spatial distribution a before and b after acceleration

In this simulation about 96 % of the injected electrons is accelerated and the final transverse emittance of accelerated electrons is about $0.52\times {10}^{-3}$ mm mrad.

In a real experiment or 3D approach, scattering of electrons due to the transverse force of wakefield increases final electron bunch emittance and is close to the true value.

Conclusion

The effect of the Gaussian chirped laser pulse in uniform magnetized plasma is considered in one dimensional LWFA. Vector potential amplitude $a(\mathit{\xi },\mathrm{\Delta })$, of the Gaussian chirped laser pulse is obtained by fitting optimum polynomials as a function of Gaussian chirp parameter Δ. Equations governing laser wakefield excitation are solved numerically by fourth order Runge–Kutta method. It is shown that wakefield amplitude is increased threefold and electrons gain energy is grown more than four times for the negative Gaussian chirped laser pulse in the magnetized plasma compared with the case of unchirped laser pulse in unmagnetized plasma.

A simulation of the acceleration of the electron bunch with hundred thousands of electrons was carried out in the electrostatic field generated by a Gaussian chirped laser pulse in magnetized plasma. Results of this simulation indicate that electrons with initial kinetic energy about 0.3 MeV accelerated to final energy about 1.3 GeV. Further, the initial energy spread from about 10 % achieved to final energy spread about 6 %.

It may be noted that, the reversed external magnetic field enhances wakefield amplitude; moreover, it increases the phase velocity of the plasma wave (equal to group velocity of the laser pulse) (see Fig. 9), and causes electrons to stay more in the acceleration region, On the other hand, wakefield amplitude increases about threefold by negative Gaussian chirped laser pulse (see Fig. 6). In other words, larger electrostatic field of the wake interacts in the larger distance (dephasing length) on the trapped electrons and these electrons gain energy about 1.3 GeV (see Fig. 8).

Although this formalism for laser pulse and wakefield generation was studied in 1D geometry, electron bunch dynamic simulation was investigated in 3D space. However, the results are suitable for the real experiment for a large laser beam waist $(w_0>>{\mathit{\lambda }}_p,r_{\perp })$, where the transverse variation in the laser beam and wakefield is not substantial. Consider this issue that in most experiments of laser wakefield acceleration, the final energy of electron bunch has been reported up to GeV (see Ref. [7–12]); therefore, the results of this paper can be of interest to experimenters.