Optimal pricing and ordering policies for perishable products under advance-cash-credit payment scheme

Abstract

Recently, market globalization and competition have forced companies to find alternative means to boost sales and revenue. The use of the cash flow is increasingly becoming a viable alternative for managers to improve their company’s profitability in a supply chain. In today’s business transactions, a supplier usually asks a manufacturer to pay via the advance-cash-credit (ACC) payment scheme if the number of goods procured is high. Additionally, product perishability has been considered in an economic production quantity (EPQ) model since it is a real phenomenon. The present work develops an EPQ model for perishable products under the ACC payment scheme. The objective of the proposed model is to determine the optimal selling price and cycle time while maximizing profit under the ACC payment scheme using a discounted cash flow analysis. A nonlinear optimization algorithm is also proposed to solve the problem. In addition, some numerical examples are employed to illustrate the solution approach and show the concavity of the present value of the total annual profit in terms of both selling price and cycle time. The numerical results show that our proposal algorithm could be applied well to solve the problems. In addition, a sensitivity analysis is conducted to obtain some managerial insights. For example, if the impact of advance payment on procurement cost is relatively smaller than that of cash payment, then it is more profitable for the manufacturer to ask for a cash payment than to receive an advance payment and vice versa.

Introduction

Due to market globalization and competition, industry players try to find alternative means to boost sales and revenue. Three main flows of a supply chain management process: product flow, information flow, and financial flow are considered to obtain the new solutions for players. Among them, the financial flow is increasingly becoming the most viable alternative for managers to improve their company’s profitability in a supply chain. The concept of the advance-cash-credit (ACC) payment scheme that includes three payment methods: advance payment (prepayment), cash payment, and trade credit become common in today’s supply chain. Wherein advance payments are amounts paid for the business in advance before the goods and services are received; cash payment is amounts paid for the business at the time of placing an order. With the use of advance or cash payment, the customers could save money from taking some discounts from suppliers. In addition, on the use of advance payment, the manufacturers seek to pay suppliers all or fraction of procedure cost in advance to take advantages of lower interest rates in the present competitive market. In a different way, trade credit allows the players to delay paying the amount of purchasing cost in a fixed period and earn some interests from lending this amount of money. In practice, studies have found that in countries outside of the United States, trade credit accounts for approximately 20% of all investment financed externally (Cuñat and Garcia-Appendini, 2012). Specially, in the USA, trade credit is used by approximately 60% of small businesses, rendering it the second most popular financing option after that of banks and other financial institutions (FRS 2017).

According to the benefits of these three payment methods, suppliers, wholesalers, or retailers can offer/ask for the ACC payment to improve their own benefits. The ACC payment scheme is generally used in practical industry problems. For instance, a contractor often requests a 10–20% advance payment of the total cost when signing a contract to install a new roof or driveway. At the time of delivery of the materials, the customer pays cash to cover the contractor’s material cost. Later, the contractor allows the customer a credit payment to pay the remaining amount after satisfactory completion of the work. Therefore, an advanced model is needed. Generally, studies on this are always divided into two subcases: advance payment and trade credit. There is a vast amount of literature on inventory models under credit payments or permissible delay in payments. On the other hand, the literature focusing on cash and advance payments is limited. Specially, inventory models with ACC payment terms explored from the manufacturer’s perspective to derive the optimal solution for the manufacturer are rarely seen in the literature (see in “Literature review” section).

This paper is the first study which considers an EPQ model for deteriorated products under the ACC payment scheme (see Table 1). The objective is to determine the unit selling price and length of cycle time for maximizing the profit. In particular, a discounted cash flow (DCF) analysis is applied to maximize the present value of the total annual profit in this work. In practice, the DCF model is more frequently used in valuation because of the consistency in long-term value creation and the ability to capture all the elements that alter a company’s value in an inclusive manner. The theoretical part of this study determines the optimal inventory policy, and numerical examples are provided to gain managerial insight.

Table 1 A brief review of related literature

The rest of this paper is organized as follows: in “Literature review” section reviews the literature; in “Notation and assumptions” section describes the notations and assumptions; in “Model formulation” section defines the mathematical model for the three cases of the ACC payment scheme for upstream credit period by a supplier to a retailer, and in “Theoretical results and algorithm and Computational analysis” sections, respectively, present the theoretical and computational results with managerial insights into the later. Lastly, the conclusion and recommendation are presented in “Conclusion” section.

Literature review

Economic production quantity (EPQ) model for deteriorating items

Over decades, almost all researchers agree that inventory becomes an extensive study in order to optimize inventory management. The economic production quantity (EPQ) model is an extension of the economic order quantity (EOQ) model. This model was developed by Taft in (1918). The purpose of EPQ is to determine the optimal production as to minimize the total cost including the setup costs and inventory holding cost. It is considered to be one of the most popular inventory model used in industry. Some researchers have investigated and considered the practical usages of this model. Nowadays, the EPQ problems consideration such as demand type, product deterioration, production system reliability, and other uncertainties make even more complicated. One of captivating in recent years as consideration is product deteriorating. Deterioration is defined as damage, decay, evaporation, or loss of marginal value of goods, such as blood, vegetables, fruits, pharmaceuticals, chemicals, and photographic films.

First, an EPQ model for deteriorating items was established by Teng and Chang (2005). They provided the EPQ model when the demand rate depends not only the on-display stock level but also the selling price per unit for maximizing the profit. Furthermore, Huang (2007) modified Goyal’s model and proposed an EPQ model under supplier’s trade credit policy. Liao (2007) also derived a production model to determine the optimal ordering policies and bounds for the optimal cycle time under permissible delay in payments. Recently, many studies also combine EPQ model for product perishability under trade credit system such as Chen et al. (2014), Mahata (2014), Chakraborly et al. (2016), Shaikh et al. (2018), and Majumder et al. (2019).

Advance payment

The idea of advance payment was first introduced as the optimal cash deposit for customers to save time and money by Zhang (1996). However, until Taleizadeh et al. (2013) this concept was applied in the inventory model and named as advance payment. They considered an economic order quantity (EOQ) model with multiple advance payment under three conditions: no shortages, full back-ordering, and partial back-ordering. Taleizadeh (2014) extend Taleizadeh et al. (2013) to consider an advance-cash payment for an evaporating item. He also applied his model in a case study of a gas station. The station first pays a fraction of the purchasing cost in advance while taking an order, and then pays the remainder via cash on delivery. Recently, Taleizadeh (2017) and Diabat et al. (2017) considered advance payment in the lot-size model under different conditions of the inventory model.

Trade credit

For many businesses, trade credit is a fundamental tool for financing growth. In the beginning, Beranek (1967) emphasized the importance of credit terms when making lot-sizing decisions. A credit payment is often offered by a supplier to retailer in order to promote their commodities (Grubbstrorm 1980; Chung 2002; Teng 2002). Recently, Feng et al. (2013) proposed an algorithm to determine a retailer’s optimal cycle time and payment time. They also added the cash discount payment scheme and assumed that the retailer will provide a full trade credit to his/her good credit customer and request his/her bad credit customers to pay for the items as soon as receiving them. Majumder et al. (2015) studied an EPQ model under trade credit when demand is in decline and fuzzy. They derived an optimal cycle time to minimize the total average cost. Mahata (2015) considered a supply chain for deteriorating items with upstream and downstream trade credits. Recently, Chakraborly et al. (2016) considered an environment friendly economic production quantity (EPQ) model of a single item under trade credit. Their model involved selling price dependent demand and purchased raw material dependent credit period which are described by two sets of linguistic relations under fuzzy logic. A genetic algorithm used to solve the problem. Rajan and Uthayakumar (2017) developed an economic order quantity model to investigate the optimal replenishment policies for instantaneous deteriorating items under inflation and trade credit. Majumder et al. (2019) presented a multi-item EPQ model of deteriorating items under trade credit policy where items are substitute in nature, for example, bread and crackers, stocks and bonds, two different brands of soft drinks or water, etc. The change in a substitute product’s stock level could alter quantity demanded for another good. Panda et al. (2019) combined the three factors: price, stock, and trade credit in a two-warehouse inventory analysis.

The ACC payment scheme combined the benefits of the three payment methods: advance, cash, and trade credit is common in today’s business. However, to the best authors’ knowledge, only a few researchers have considered ACC payment in the literature review. For instances, Wu et al. (2018) studied another hybrid payment scheme of advance-cash-credit payment for perishable EOQ model with an expiration date, ad with an allowance for shortages. Li et al. (2019) developed an inventory model interfaced with marketing, operations, and finance in a supplier–retailer chain in which: (1) The demand curve is downward sloping, (2) the seller demands the buyer use an ACC payment for the total cost, and (3) for generality, shortages are allowed with a fixed market tolerance period. In a different way, this paper will consider an EPQ model for deteriorating items under ACC payment.

Discounted cash flow (DCF)

Discounted cash flow (DCF) analysis is an economic model studied by the classical financial mathematical tools. It is also commonly applied in many areas for example insurance, project management, and financial management. In practice, the DCF model more frequently used in valuation because of the consistency of long-term value creation and may capture all the elements that alter the company value in an inclusive way. For instance, if the annual compound interest rate is r per dollar per year, then $500 today is worth $e^r a year later. In vice versa, $500 a year from now is equivalent to $e^−r now. A study by Chung et al. (2014) proposed an inventory model for deteriorating items in the DCF approach under trade credit system. Another study, Wu et al. (2016) also used DCF analysis under downstream and partial trade credit.

Notation and assumptions

The following notations and assumptions are used for the mathematical model.

Notation

The notations pertain to three groups: parameters, decision variables, and functions.

Parameters

α :

Fraction of procurement cost to be paid in advance, $0 \le \alpha \le 1$

β :

Fraction of procurement cost to be paid at the time of delivery, $0 \le \beta \le 1$

τ :

Fraction of procurement cost granted a permissible delay from the supplier to the retailer, $0 \le \tau \le 1$ and $\alpha + \beta + \tau = 1$

µ :

Upstream credit period by the supplier to the retailer, $\mu \ge 0$

r :

Annual compound interest paid per dollar per year

A :

Procurement cost in dollars when placing an order at time − l

c :

Procurement cost per unit in dollars, c > 0

CC:

Present value of capital cost per cycle in dollars

h :

Holding cost excluding interest charge per unit per year in dollars, h > 0

HC:

Present value of holding cost excluding interest charge per cycle in dollars

l :

Length of time in years during which the prepayments are paid, l > 0

IC:

Interest charged by the supplier per dollar per year

IE:

Interest earned by the supplier per dollar per year

O :

Ordering cost in dollars per order, O > 0

OC:

Present value of ordering cost per cycle in dollars

Q :

Order quantity in units

SR:

Present value of sales revenue per cycle in dollars

PC:

Present value of procurement cost per cycle in dollars

t _p :

Time at which the production stops in a cycle

θ :

Deterioration rate

P :

Production Rate

Decision variables

p ^* :

Price per unit in dollars, p > c > 0

T* :

Length of cycle time in years

Functions

D(p):

Annual demand rate, D(p) = $ae^{ - \lambda p}$ with $a,$$\lambda > 0$

I(t):

Inventory level in units at time t

∏ (p, T):

Present value of total annual profit in dollar

Assumptions

To develop the mathematical model, the following assumptions are made.

• a. The demand function is D(p) = $ae^{ - \lambda p}$, where the demand increases as the price decreases.

• b. The production rate is $P > D(p)$.

• c. The deterioration rate is a constant.

• d. For simplicity, we assume that the retailer prepays $\alpha$ fraction of the procurement cost at time − l years when placing an order, pays another $\beta$ percentage of the procurement cost at time 0 upon receipt of all items, and receives an upstream credit period of µ years on the remaining τ portion of the procurement cost.

• e. Shortages are not allowed, and lead time is negligible.

• f. Time horizon is infinite.

Model formulation

In this section, a mathematical model is formulated to describe the EPQ model under advanced cash credit by a discounted cash flow analysis. We first explain the inventory model which is used in this model. The inventory level at time t is governed by the following differential equation. During [0, t_p], the inventory level is affected by production, demand, and deterioration so the initial condition is I₁(0) = 0 (Figs. 1, 2).

Fig. 1

EPQ inventory system

Fig. 2

Interest charged for advance and cash payments

$$\frac{{dI_{1} \left( t \right)}}{dt} = \left( {P - D\left( p \right)} \right) - \theta I_{1} \left( t \right)$$

(1)

$$I_{1} (t) = e^{\theta (t)} \int_{0}^{{t_{p} }} {(P - D(p))e^{u} {\text{d}}u,}$$

(2)

$$I_{1} \left( t \right) = \frac{P - D\left( p \right)}{\theta }\left( {1 - e^{ - \theta t} } \right) ,\quad 0 \le t \le t_{p}$$

(3)

Meanwhile, during [t_p, T], the inventory level is affected by demand and deterioration where I₂ (T) = 0.

$$\frac{{{\text{d}}I_{2} \left( t \right)}}{{{\text{d}}t}} = - D\left( p \right) - \theta I_{2} \left( t \right)$$

(4)

$$I_{2} (t) = e^{ - \theta (t)} \int_{{t_{p} }}^{T} {D(p)e^{u} {\text{d}}u,}$$

(5)

$$I_{2} \left( t \right) = \frac{D\left( p \right)}{\theta }\left( {{\text{e}}^{{ - \theta \left( {T - t} \right)}} - 1} \right),\quad t_{p} \le t \le T$$

(6)

Using the boundary condition I₁(t_p) = I₂ (t_p) (Please note that I(t) is a continuous function), we obtain that

$$t_{p} = \frac{1}{\theta }\ln \left\{ {1 + \frac{D(p)}{P}\left( {e^{\theta T} - 1} \right)} \right\}$$

(7)

The annual total relevant cost consists of the following elements:

• 1. Ordering Cost

  The retailer’s ordering time is l years prior to the time of delivery 0. Therefore, the present value of the ordering cost at time –l is

  $${\text{OC}} = O{\kern 1pt} {\kern 1pt} e^{rl}$$

  (8)

• 2. Sales Revenue

  The sales revenue is a fixed selling price per unit for each unit demanded. Hence, the present value of sales revenue is given by

  $${\text{SR}} = p\int_{0}^{{{\kern 1pt} T}} {D(p){\kern 1pt} e^{ - rt} {\text{d}}t}$$

  (9)

• 3. Procurement Cost

  The procurement cost is the cost which manufacturer has to pay for purchasing certain materials from supplier. In our model, we first calculate the procurement cost without considering the time value of money (the procurement cost at time t = -l):

  $$A = c\left( {\int_{{{\kern 1pt} 0}}^{{{\kern 1pt} t_{1} }} {I_{1} e^{ - rt} {\text{d}}t} + \int_{{{\kern 1pt} t_{1} }}^{T} {I_{2} e^{ - rt} {\text{d}}t} } \right)$$

  (10)

  Substitute Eqs. (3) and (6) into Eq. (10), the procedure cost at time − l is:

  $$A = c\left( {\int\limits_{0}^{{t_{p} }} {\frac{P - D(p)}{\theta }(1 - e^{ - \theta t} \, )e^{ - rt} {\text{d}}t} + \int\limits_{{t_{p} }}^{T} {\frac{D(p)}{\theta }(e^{\theta (T - t)} - 1)e^{ - rt} {\text{d}}t} } \right)$$

  (11)

  Then, we calculate the present value of procedure cost for final model. Under Advance-cash-credit payment, the payments for the procurement cost consist of three parts: (1) the advance payment at l years before time 0, (2) the cash payment at time 0, and (3) the credit payment at time µ. Therefore, the present value of procurement cost is given by

  $${\text{PC}} = \alpha {\kern 1pt} {\kern 1pt} A{\kern 1pt} {\kern 1pt} e^{rl} + \beta \;A + \tau {\kern 1pt} A{\kern 1pt} e^{ - r\mu } = A(\alpha {\kern 1pt} e^{rl} + \beta + \tau {\kern 1pt} e^{ - r\mu } )$$

  (12)

• 4. Holding Cost

  The present value of the holding cost excluding the interest charged per cycle time T is as follows:

  $$\begin{aligned} {\text{HC}} = & \,h\left( {\int\limits_{0}^{{t_{p} }} {I_{1} e^{ - rt} {\text{d}}t} + \int\limits_{{t_{p} }}^{T} {I_{2} e^{ - rt} {\text{d}}t} } \right) \\ = & \,h\left( {\int\limits_{0}^{{t_{p} }} {\frac{P - D(p)}{\theta }(1 - e^{ - \theta t} \, )e^{ - rt} {\text{d}}t} + \int_{{{\kern 1pt} 0}}^{{{\kern 1pt} t_{p} }} {\frac{D(p)}{\theta }(e^{\theta (T - t)} e^{ - rt} {\text{d}}t} } \right) \\ \end{aligned}$$

  (13)

• 5. Interest charged for both advance-cash payments

  $${\text{IC}}_{a} = {\kern 1pt} cD(p)TI_{c} {\kern 1pt} \left[ {\int_{{{\kern 1pt} - l}}^{{t_{p} }} {\alpha {\kern 1pt} {\kern 1pt} e^{ - rt} dt} + \int_{0}^{{t_{p} }} {\beta {\kern 1pt} {\kern 1pt} e^{ - rt} dt} } \right] + (\alpha + \beta ){\kern 1pt} cD(p)I_{c} {\kern 1pt} \int_{{{\kern 1pt} t_{p} }}^{{{\kern 1pt} T}} {(T - t){\kern 1pt} e^{ - rt} {\text{d}}t}$$

  (14)

  In case of credit payment with the upstream credit period $\mu$, we have three cases.

Case 1 $0 \le \mu \le t_{p} ,0 \le \mu \le \frac{1}{\theta }\ln \left\{ {1 + \frac{D(p)}{P}\left( {e^{\theta T} - 1} \right)} \right\}$

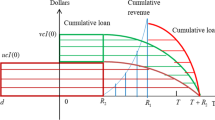
In this case, there is no interest earned for credit payment as shown in Fig. 3.

Fig. 3

Graphical representation of the case $0 \le \mu \le t_{p}$

The present value of interest charged for credit payment per cycle time T as shown in Fig. 3 is given by

$${\text{IC}}_{1} = \tau {\kern 1pt} {\kern 1pt} cD(p)I_{c} \left[ {\int_{{{\kern 1pt} \mu }}^{{{\kern 1pt} t_{p} }} {T{\kern 1pt} e^{ - rt} dt} + \int_{{{\kern 1pt} {\kern 1pt} t_{p} }}^{{{\kern 1pt} T}} {(T - t){\kern 1pt} e^{ - rt} {\text{d}}t} } \right]$$

(15)

Therefore, the present value of capital cost per cycle time T is as follows:

$$\begin{aligned} {\text{CC}} = & {\text{IC}}_{a} + {\text{IC}}_{1} \\ = & {\kern 1pt} cD(p)TI_{c} {\kern 1pt} \left[ {\int\limits_{ - l}^{{t_{p} }} {\alpha {\kern 1pt} {\kern 1pt} e^{ - rt} dt} + \int\limits_{0}^{{t_{p} }} {\beta {\kern 1pt} {\kern 1pt} e^{ - rt} dt} } \right] + (\alpha + \beta ){\kern 1pt} cD(p)I_{c} {\kern 1pt} \int\limits_{{t_{p} }}^{T} {(T - t){\kern 1pt} e^{ - rt} {\text{d}}t} \\ & \quad + \tau {\kern 1pt} {\kern 1pt} cD(p)I_{c} \left[ {\int\limits_{\mu }^{{t_{p} }} {T{\kern 1pt} e^{ - rt} {\text{d}}t} + \int\limits_{{t_{p} }}^{T} {(T - t){\kern 1pt} e^{ - rt} {\text{d}}t} } \right] \\ \end{aligned}$$

(16)

The present value of total annual profit is given by

$$\begin{aligned} \prod\nolimits_{1} {(p,T)} = & \frac{1}{T}({\text{SR}} - {\text{OC}} - {\text{PC}} - {\text{HC}} - {\text{CC}}) \\ = & \frac{1}{T}\left\{ {p\int_{0}^{T} {D(p){\kern 1pt} e^{ - rt} dt} } \right. \\ & \quad - Oe^{rl} - \left( {\alpha e^{rl} + \beta + \tau e^{ - r\mu } } \right)c\left( {\int\limits_{0}^{{t_{p} }} {\frac{P - D(p)}{\theta }(1 - e^{ - \theta t} \, )e^{ - rt} dt} + \int\limits_{{t_{p} }}^{T} {\frac{D(p)}{\theta }(e^{\theta (T - t)} - 1)e^{ - rt} {\text{d}}t} } \right) \\ & \quad - h\left( {\int\limits_{0}^{{t_{p} }} {\frac{P - D(p)}{\theta }\left( { 1- {\text{e}}^{{ - \theta {\text{t}}}} { )}e^{ - rt} {\text{d}}t} \right)} + \int\limits_{{t_{p} }}^{T} {\frac{D(p)}{\theta }\left( {e^{\theta (T - t)} - 1} \right)e^{ - rt} {\text{d}}t} } \right) \\ & \quad - {\kern 1pt} cD(p)TI_{c} {\kern 1pt} \left[ {\int\limits_{ - l}^{{t_{p} }} {\alpha {\kern 1pt} {\kern 1pt} e^{ - rt} {\text{d}}t} + \int\limits_{0}^{{t_{p} }} {\beta {\kern 1pt} {\kern 1pt} e^{ - rt} {\text{d}}t} } \right] - (\alpha + \beta ){\kern 1pt} cD(p)I_{c} \int\limits_{{t_{p} }}^{T} {(T - t){\kern 1pt} e^{ - rt} {\text{d}}t} \\ & \quad - \left. {\tau {\kern 1pt} {\kern 1pt} cD(p)I_{c} \left[ {\int\limits_{\mu }^{{t_{p} }} {T{\kern 1pt} e^{ - rt} {\text{d}}t} + \int\limits_{{t_{p} }}^{T} {(T - t){\kern 1pt} e^{ - rt} {\text{d}}t} } \right]} \right\} \\ \end{aligned}$$

(17)

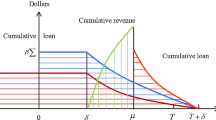
Case 2 $t_{p} \le \mu \le T,\quad \frac{1}{\theta }\ln \left\{ {1 + \frac{D(p)}{P}\left( {e^{\theta T} - 1} \right)} \right\} \le \mu \le T$

The present value of interest charged for credit payment per cycle time T as shown in Fig. 4 is given by

Fig. 4

Graphical representation of the case $t_{p} \le \mu \le T$

$${\text{IC}}_{2} = \tau cD(p)I_{c} \left[ {\int\limits_{\mu }^{T} {(T - t)\,e^{ - rt} {\text{d}}t} } \right]$$

(18)

The present value of interest earned for credit payment per cycle time T as shown in Fig. 4 is given by

$${\text{IE}}_{2} = \tau pD(p)I_{e} \left[ {\int\limits_{{t_{p} }}^{\mu } {(\mu - t)\,e^{ - rt} {\text{d}}t} } \right]$$

(19)

Therefore, the present value of capital cost per cycle time T is as follows:

$$\begin{aligned} {\text{CC}} = & \,{\text{IC}}_{a} + {\text{IC}}_{2} - {\text{IE}}_{2} \\ = & \,{\kern 1pt} cD(p)TI_{c} {\kern 1pt} \left[ {\int\limits_{ - l}^{{t_{p} }} {\alpha \,e^{ - rt} {\text{d}}t} + \int\limits_{)}^{{t_{p} }} {\beta {\kern 1pt} {\kern 1pt} e^{ - rt} {\text{d}}t} } \right] + (\alpha + \beta ){\kern 1pt} cD(p)I_{c} \int\limits_{{t_{p} }}^{T} {(T - t){\kern 1pt} e^{ - rt} {\text{d}}t} \\ & \quad + \tau {\kern 1pt} cD(p)I_{c} \left[ {\int\limits_{\mu }^{T} {(T - t){\kern 1pt} e^{ - rt} {\text{d}}t} } \right] - \tau pD(p)I_{e} \left[ {\int\limits_{{t_{p} }}^{\mu } {(\mu - t){\kern 1pt} e^{ - rt} {\text{d}}t} } \right] \\ \end{aligned}$$

(20)

The present value of total annual profit is given by

$$\begin{aligned} \prod\nolimits_{2} {(p,T)} = &\, \frac{1}{T}({\text{SR}} - {\text{OC}} - {\text{PC}} - {\text{HC}} - {\text{CC}}) \\ = &\, \frac{1}{T}\left\{ {p\int\limits_{0}^{T} {D(p){\kern 1pt} e^{ - rt} dt} - Oe^{rl} - \left( {\alpha {\kern 1pt} e^{rl} + \beta + \tau {\kern 1pt} e^{ - r\mu } } \right)} \right. \\ & \quad \times c\left( {\int\limits_{0}^{{t_{p} }} {\frac{P - D(p)}{\theta }\left( {1 - e^{ - \theta t} } \right)e^{ - rt} {\text{d}}t} + \int\limits_{{t_{p} }}^{T} {\frac{D(p)}{\theta }\left( {e^{\theta (T - t)} - 1} \right)e^{ - rt} {\text{d}}t} } \right) \\ & \quad - h\left( {\int\limits_{0}^{{t_{p} }} {\frac{P - D(p)}{\theta }\left( {1 - e^{ - \theta t} \, } \right)e^{ - rt} {\text{d}}t} + \int\limits_{{t_{p} }}^{T} {\frac{D(p)}{\theta }\left( {e^{\theta (T - t)} - 1} \right)e^{ - rt} {\text{d}}t} } \right) \\ & \quad - {\kern 1pt} cD(p)TI_{c} {\kern 1pt} \left[ {\int\limits_{ - l}^{{t_{p} }} {\alpha {\kern 1pt} {\kern 1pt} e^{ - rt} {\text{d}}t} + \int\limits_{0}^{{t_{p} }} {\beta {\kern 1pt} {\kern 1pt} e^{ - rt} {\text{d}}t} } \right] \\ & \quad - (\alpha + \beta ){\kern 1pt} cD(p)I_{c} {\kern 1pt} \int\limits_{{t_{p} }}^{T} {(T - t){\kern 1pt} e^{ - rt} {\text{d}}t} \\ & \quad - \tau {\kern 1pt} {\kern 1pt} cD(p)I_{c} \left[ {\int\limits_{\mu }^{T} {(T - t){\kern 1pt} e^{ - rt} {\text{d}}t} } \right]\left. { + \tau pD(p)I_{e} \left[ {\int\limits_{{t_{p} }}^{\mu } {(\mu - t){\kern 1pt} e^{ - rt} {\text{d}}t} } \right]} \right\} \\ \end{aligned}$$

(21)

Case 3 $\mu \ge T$

In this case, there is no interest charged for credit payment (see Fig. 5). However, the present value of interest earned for credit payment per cycle time T is given as

Fig. 5

Graphical representation of the case $T \le \mu$

$${\text{IE}}_{3} = \tau pD(p)I_{e} \left[ {\int\limits_{{t_{p} }}^{T} {(T - t){\kern 1pt} e^{ - rt} {\text{d}}t} + \int\limits_{T}^{\mu } {T{\kern 1pt} e^{ - rt} {\text{d}}t} } \right]$$

(22)

Therefore, the present value of capital cost per cycle time T is as follows:

$$\begin{aligned} {\text{CC}} = & {\text{IC}}_{a} - {\text{IE}}_{3} \\ = & {\kern 1pt} cD(p)TI_{c} {\kern 1pt} \left[ {\int\limits_{ - l}^{{t_{p} }} {\alpha {\kern 1pt} {\kern 1pt} e^{ - rt} {\text{d}}t} + \int\limits_{0}^{{t_{p} }} {\beta {\kern 1pt} {\kern 1pt} e^{ - rt} {\text{d}}t} } \right] + (\alpha + \beta ){\kern 1pt} cD(p)I_{c} \int\limits_{{t_{p} }}^{T} {(T - t){\kern 1pt} e^{ - rt} {\text{d}}t} \\ & \quad - \tau pD(p)I_{e} \left[ {\int_{{{\kern 1pt} {\kern 1pt} t_{p} }}^{T} {(T - t){\kern 1pt} e^{ - rt} {\text{d}}t} + \int_{T}^{\mu } {T{\kern 1pt} e^{ - rt} {\text{d}}t} } \right] \\ \end{aligned}$$

(23)

The present value of total annual profit is given by

$$\begin{aligned} \prod\nolimits_{3} {(p,T)} = & \frac{1}{T}({\text{SR}} - {\text{OC}} - {\text{PC}} - {\text{HC}} - {\text{CC}}) \\ = & \frac{1}{T}\left\{ {p\int\limits_{0}^{T} {D(p){\kern 1pt} e^{ - rt} {\text{d}}t} } \right. - Oe^{rl} - \left( {\alpha {\kern 1pt} e^{rl} + \beta + \tau {\kern 1pt} e^{ - r\mu } } \right) \\ & \quad \times c\left( {\int\limits_{0}^{{t_{p} }} {\frac{P - D(p)}{\theta }\left( {1 - e^{ - \theta t} \, } \right)e^{ - rt} {\text{d}}t} + \int\limits_{{t_{p} }}^{T} {\frac{D(p)}{\theta }\left( {e^{\theta (T - t)} - 1} \right)e^{ - rt} {\text{d}}t} } \right) \\ & \quad - h\left( {\int\limits_{0}^{{t_{p} }} {\frac{P - D(p)}{\theta }(1 - e^{ - \theta t} \, )e^{ - rt} {\text{d}}t} + \int\limits_{{t_{p} }}^{T} {\frac{D(p)}{\theta }\left( {e^{\theta (T - t)} - 1} \right)e^{ - rt} {\text{d}}t} } \right) \\ & \quad - {\kern 1pt} cD(p)TI_{c} {\kern 1pt} \left[ {\int\limits_{ - l}^{{t_{p} }} {\alpha {\kern 1pt} {\kern 1pt} e^{ - rt} {\text{d}}t} + \int\limits_{0}^{{t_{p} }} {\beta {\kern 1pt} {\kern 1pt} e^{ - rt} {\text{d}}t} } \right] \\ & \quad - (\alpha + \beta ){\kern 1pt} cD(p)I_{c} \int\limits_{{t_{p} }}^{T} {(T - t){\kern 1pt} e^{ - rt} {\text{d}}t} \\ & \quad + \left. {\tau {\kern 1pt} {\kern 1pt} pD(p)I_{e} \left[ {\int\limits_{{t_{p} }}^{T} {(T - t){\kern 1pt} e^{ - rt} dt} + \int\limits_{T}^{\mu } {T{\kern 1pt} e^{ - rt} {\text{d}}t} } \right]} \right\} \\ \end{aligned}$$

(24)

From the equations above, we can summarize the three cases as shown below:

$$\varPi \left( {p,T} \right) = \left\{ {\begin{array}{*{20}l} {\varPi_{1} \left( {p,T} \right),} \hfill & {when\;0 \le \mu \le \frac{1}{\theta }\ln \left\{ {1 + \frac{D(p)}{P}\left( {e^{\theta T} - 1} \right)} \right\}} \hfill \\ {\varPi_{2} \left( {p,T} \right),} \hfill & {when\;\frac{1}{\theta }\ln \left\{ {1 + \frac{D(p)}{P}\left( {e^{\theta T} - 1} \right)\mu \le T} \right\}} \hfill \\ {\varPi_{3} \left( {p,T} \right),} \hfill & {when\;\mu \ge T} \hfill \\ \end{array} } \right.$$

(25)

Theoretical results and algorithm

Theoretical results

Theorem 1

For any given selling price p, ∏₁(p, T), ∏₂(p, T), and ∏₃(p, T) are all concave functions of T (See “AppendixA” for proof).

The optimal value of T (T^*₁) is obtained when the first derivative of ∏₁ (p, T) with respect to T vanishes and the second derivative is less than zero. Similarly, we can also obtain the optimal length of cycle time T^*₂ and T^*₃. To show the optimality of the solution, Theorem 1 demonstrates that the annual total profit is concave in T. However, since ∏ (p, T) is a very complicated function due to the presence of the high-power exponential function, it is not analytically possible to show the validity of the closed form.

Theorem 2

∏₁(p, T), ∏₂(p, T), and ∏₃(p, T are all concave functions of p.

The optimal value of p (p^*₁) is obtained when the first derivative of ∏₁ (p, T) respect to p vanishes and the second derivative is less than zero. Similarly, we can also obtain p^*₂ and p^*₃. Theorem 2 demonstrates that the annual total profit is concave in p. However, as already mentioned, since ∏ (p, T) function is a very complicated function, it is not analytically possible to show the validity of the sufficient condition. We have developed an algorithm based on iteration to solve the problem.

Algorithm

In order to find the optimal values of p and T, the following algorithm is used.

Computational analysis

The purposes of computational analysis are as follows:

• 1. To show the optimal solutions of the problem

• 2. To discuss the influences of parameters on decisions and gain managerial insights by using sensitivity analysis.

Numerical examples

Example 1

The optimal selling price and cycle time for the maximum annual profit can be obtained by applying the methodology given in the preceding section.

For a perishable product, let the annual demand rate D(p) = $2000e^{ - 0.05p}$ and the degrading rate is constant, θ = 0.05, where P = 1500 units/year, r = 0.04 per dollar per year, O = $20 per order, l = 0.1 year, α = 0.3 year, β = 0.3 year, τ = 0.4 year, μ = 0.1 year, c = $10, IC= 0.05 per dollar per year, IE = 0.04 per dollar per year, and h = $1 per unit per year.

According to Algorithm 1, case 3 is the optimal solution. The optimal price for case 3 is $19.495, and the optimal cycle time is 0.0863117 years. In addition, the present value of the total profit is $\prod_{3}^{*} \left( {p^{*} ,T^{*} } \right)$ = $14256.89, and the dimensional graph of the present value of the total profit is presented in Figs. 6 and 7.

Fig. 6

Graph of $\prod_{3} \left( {p,T*} \right)$

Fig. 7

Graph of $\prod_{3} \left( {p*,T} \right)$

Figs. 6–7 show that the total annual profit is a strictly concave function of p and T, and thereby validate the optimal solution obtained from the proposed algorithm.

Example 2

In this example, we use the same data with Example 1. However, the values of α, τ, and β are modified to examine the effect of the three payment methods on the present value of the total profit and the decisions variables. We assume that the supplier asks manufacturer for advance payment is only 10% of procurement cost (α = 0.1); the fraction of procurement cost to be paid at the time of delivery others is β = 0.5, other τ = 0.4.

Applying Algorithm 1, case 3 is the optimal solution. The optimal price for case 3 is $20.045, and the optimal cycle time is 0.0864547 years. In addition, the present value of the total profit is $\prod_{3}^{*} \left( {p^{*} ,T^{*} } \right)$ = $14270.074, and the dimensional graph of the present value of the total profit is presented in Fig. 8 and Fig. 9. The results show that the profit, cycle time, and price all increase as the fraction of procurement cost granted by advance payment decreases. In this model, the discount when we prepay has not been taken into account. The result is reasonable because the less money manufacturers have to pay in advance, the more they can earn from lending this amount of money. However, in case of discount considering, the results may be different. We may consider that case in the future research.

Fig. 8

Graph of $\prod_{3} \left( {p,T*} \right)$

Fig. 9

Graph of $\prod_{3} \left( {p*,T} \right)$

Example 3

In this example, another product is considered, let the annual demand rate D(p) = $15000e^{ - 0.04p}$ and production rate P = 9500 units/year, O = $120 per order, c = $8, h = $2 per unit per year, and other parameters are kept as same as Example 1.

According to Algorithm 1, case 2 is the optimal solution. The optimal price for case 2 is $23.02, and the optimal cycle time is 0.157609 years. In addition, the present value of the total profit is $\prod_{2}^{*} \left( {p^{*} ,T^{*} } \right)$ = $13624.14, and the dimensional graph of the present value of the total profit is presented in Figs. 10 and 11. The result proves that our proposal method could be applied well in different kinds of product.

Fig. 10

Graph of $\prod_{3} \left( {p,T*} \right)$

Fig. 11

Graph of $\prod_{3} \left( {p*,T} \right)$

Sensitivity analysis

Here, we test the sensitivity of the optimal solution for different values of parameters (See Table 2).

Table 2 Sensitivity analysis for various inventory model parameters

Based on Table 1, the following results can be obtained.

• a. П* increases and p* and T* decrease as a increases. It indicates that the higher the number of potential customers, the higher is the present value of the total profit.

• b. П* and p* decrease and T* increases as λ increases. It shows that if the price in efficiency of demand increases, the cycle time also increases. Meanwhile, an increase of price elasticity could make the present value of the total profit decrease even the decrease of price. That means, under ACC payments, with the different kinds of product, the manager could choose a suitable pricing policy based on the price electricity. In addition, comparing to the number of potential customers a, the price in efficiency of demand has a larger effect on the total profit and the decisions λ.

• c. p* increases and П* and T* decrease as c increases. It implies that if the unit procurement cost is increased, then the price increases. On the other hand, a higher value of c results in a reduced value of the total profit and cycle time. It is reasonable because when the procurement increases, the selling price also increases in an effort to maintain the profit.

• d. p* increases and П* and T* decrease as h increases. Therefore, for higher holding cost, a reduced value of the total profit and cycle time is obtained. Specially, in practice, the holding cost for deteriorating items is really high. Therefore, managers should apply new technology to reduce the waste of energy and save cost of holding items.

• e. П*, p* and T* all increase as µ increases. It illustrates that when the supplier gives a longer credit period, the retailer will increase the cycle time and the selling price for the benefit of longer credit period.

• f. T* and П* decrease but p* increases as θ increase. It shows that for higher deterioration rate, the present value of the total profit and cycle time is reduced but the selling price is increased. Therefore, when the items start deteriorating, it is optimal to marginally increase the selling price to manage the profit. A potential marketing strategy (sale promotions, discount for early sale…) or a well transportation system is extremely important and necessary for deteriorating items manufacturers, specially, with the high deteriorated rate products.

• g. П*, p* and T* all increase as l increases. It shows that for a longer prepayment length, the unit selling price is higher and cycle time is longer. Moreover, the present value of the total profit increases.

• h. p* increases but T* and П* decreases as r increases. Therefore, for higher annual compound interest rate, the selling price will be higher. However, the cycle time and the present value of the total profit reduce. So that, in case of higher annual compound interest rate, manufacturer could ask the supplier for a longer length of trade credit period or lower fraction of procurement cost granted by advance-cash payment to reduce the effect of high interest.

• i. П*, p* and T* all decrease as P increases. Therefore, it is not advisable to increase the production rate without any prior information about the demand.

Conclusion

The present work develops an EPQ model for perishable products under ACC payment scheme. A retailer has to prepay a good-faith deposit when signing a contract, and then pay some cash at the time of receiving the products. The retailer then acquires a credit period for the remaining procurement cost. It is required to derive three different scenarios and analyze them under a discounted cash flow analysis to obtain the present values of total annual profit. The proposed algorithm develops solution procedures to support the decision maker to obtain the optimal selling price and cycle time. Through numerical analysis, the proposed algorithm is able to illustrate the solution procedures in many different cases. The computational results also present that if the impact of advance payment on procurement cost is relatively smaller than that of cash payment, then it is more profitable for the manufacturer to ask for an cash payment than to receive an advance payment and vice versa.

Moreover, the impact of parameters on the optimal solution is measured via a sensitivity analysis. The managerial implications could provide a proper scheme to determine the respective profitability. For instance, the result shows as the production cost c, holding cost h, production rate P, and interest r increase, the profit decreases. In that case, a higher price is necessary to compensate with the decrease in profit. In addition, manufacturer could reduce the cycle time to reduce the holding time and cost. In a different way, the profit could increase since the demand and trade credit period increase. To get a higher profit, manufacturer should ask a longer credit time from suppliers and also try to obtain a better marketing strategy to boost customers’ demand.

This research focuses on EPQ model for deteriorating items under ACC payment with several assumptions. It can be extended in other directions to catch up with the real case. For instance, the deteriorating rate is assumed to be constant in our model. However, in practice, this rate could be changed depended on kinds of products, outside weather, or stocking conditions. In addition, we do not consider shortage, downstream credit, or uncertain demand in the current research. Future work can consider a time-varying deterioration rate, including the downstream credit period by a retailer to customers, when shortage and backlog are allowed. Finally, future work can investigate this model for more general supply chain networks, for example, multi-echelon or assembly supply chains with several actual cases.

Appendix A: proof of Theorem 1

Case 1 $\mu \le t_{p}$

Proof

$$\begin{aligned} f_{1} (T) = & \,\left\{ {p\int_{0}^{{{\kern 1pt} T}} {D(p){\kern 1pt} e^{ - rt} dt} } \right. - Oe^{rl} - (\alpha {\kern 1pt} e^{rl} + \beta + \tau {\kern 1pt} e^{ - r\mu } ) \\ & \quad \times c\left( {\int_{{{\kern 1pt} 0}}^{{{\kern 1pt} t_{p} }} {\frac{P - D(p)}{\theta }(1 - e^{ - \theta t} \, )e^{ - rt} dt} + \int_{{{\kern 1pt} t_{p} }}^{T} {\frac{D(p)}{\theta }(e^{\theta (T - t)} - 1)e^{ - rt} dt} } \right) \\ & \quad - h\left( {\int_{{{\kern 1pt} 0}}^{{{\kern 1pt} t_{p} }} {\frac{P - D(p)}{\theta }(1 - e^{ - \theta t} \, )e^{ - rt} dt} + \int_{{{\kern 1pt} t_{p} }}^{T} {\frac{D(p)}{\theta }(e^{\theta (T - t)} - 1)e^{ - rt} dt} } \right) \\ & \quad - cD(p)TI_{c} {\kern 1pt} \left[ {\int_{{{\kern 1pt} - l}}^{{t_{p} }} {\alpha {\kern 1pt} {\kern 1pt} e^{ - rt} dt} + \int_{0}^{{t_{p} }} {\beta {\kern 1pt} {\kern 1pt} e^{ - rt} dt} } \right] - (\alpha + \beta ){\kern 1pt} cD(p)I_{c} {\kern 1pt} \int_{{{\kern 1pt} t_{p} }}^{{{\kern 1pt} T}} {(T - t){\kern 1pt} e^{ - rt} dt} \\ & \quad - \left. {\tau {\kern 1pt} {\kern 1pt} cD(p)I_{c} \left[ {\int_{{{\kern 1pt} \mu }}^{{{\kern 1pt} t_{p} }} {T{\kern 1pt} e^{ - rt} dt} + \int_{{{\kern 1pt} {\kern 1pt} t_{p} }}^{{{\kern 1pt} T}} {(T - t){\kern 1pt} e^{ - rt} dt} } \right]} \right\} \\ \end{aligned}$$

(26)

and

$$g_{1} (T) = T > 0.$$

Hence, $PTP_{1} (p,T) = f_{1} (T)/g_{1} (T)$. Taking the first- and second-order derivatives of $f_{1} (T)$ with respect to T, respectively, and simplifying terms, we get:

$$\begin{aligned} f_{1}^{{\prime }} (T) - p\,D(p)e^{ - rT} \frac{{c{\kern 1pt} {\kern 1pt} D(p)(e^{{T\theta - (r + \theta )t_{p} }} - e^{ - rT} )(\alpha \,e^{rl} + \beta + \tau \,e^{ - r\mu } )}}{r + \theta } \hfill \\ \quad - \frac{{h{\kern 1pt} {\kern 1pt} D(p)(e^{{T\theta - (r + \theta )t_{p} }} - e^{ - rT} )}}{r + \theta } - \frac{{c{\kern 1pt} {\kern 1pt} D(p)I_{c} }}{r}[\alpha (\,e^{rl} - e^{{ - rt_{p} }} ) + \beta (1 - e^{{ - rt_{p} }} )] \hfill \\ \quad - \frac{{c{\kern 1pt} {\kern 1pt} D(p)I_{c} (\alpha + \beta )}}{r}(e^{{ - r(T + t_{p} )}} )(e^{rT} - e^{{rt_{p} }} ) - \frac{{c{\kern 1pt} {\kern 1pt} D(p)I_{c} \tau }}{r}(e^{ - r\mu } )(e^{rT} - e^{ - rT} ) \hfill \\ \end{aligned}$$

(27)

and

$$\begin{aligned} f_{1}^{\prime \prime } (T) = & - p\,rD(p)e^{ - rT} - \frac{{c{\kern 1pt} {\kern 1pt} D(p)}}{r + \theta }\left( {e^{{T\theta - (r + \theta )t_{1} }} \theta + e^{ - rT} r} \right)\left( {\alpha \,e^{rl} + \beta + \tau \,e^{ - r\mu } {\kern 1pt} } \right) \\ & \quad - \frac{{h{\kern 1pt} {\kern 1pt} D(p)}}{r + \theta }\left( {e^{{T\theta - (r + \theta )t_{1} }} \theta + e^{ - rT} r} \right) - (\alpha + \beta ){\kern 1pt} cD(p)I_{c} e^{ - rT} {\kern 1pt} \\ & \quad - \tau {\kern 1pt} {\kern 1pt} cD(p)I_{c} \,e^{ - rT} < 0 \\ \end{aligned}$$

(28)

Case 2

$t_{p} \le \mu \le T$

Proof

$$\begin{aligned} f_{2} (T) = & \,\left\{ {p\int\limits_{0}^{T} {D(p){\kern 1pt} e^{ - rt} dt} } \right. - Oe^{rl} - (\alpha {\kern 1pt} e^{rl} + \beta + \tau {\kern 1pt} e^{ - r\mu } ) \\ & \quad \times c\left( {\int\limits_{0}^{{t_{p} }} {\frac{P - D(p)}{\theta }(1 - e^{ - \theta t} \, )e^{ - rt} {\text{d}}t} + \int\limits_{{t_{p} }}^{T} {\frac{D(p)}{\theta }(e^{\theta (T - t)} - 1)e^{ - rt} {\text{d}}t} } \right) \\ & \quad - h\left( {\int\limits_{0}^{{t_{p} }} {\frac{P - D(p)}{\theta }(1 - e^{ - \theta t} \, )e^{ - rt} {\text{d}}t} + \int\limits_{{t_{p} }}^{T} {\frac{D(p)}{\theta }(e^{\theta (T - t)} - 1)e^{ - rt} {\text{d}}t} } \right) \\ & \quad - cD(p)TI_{c} {\kern 1pt} \left[ {\int\limits_{ - l}^{{t_{p} }} {\alpha {\kern 1pt} {\kern 1pt} e^{ - rt} {\text{d}}t} + \int\limits_{0}^{{t_{p} }} {\beta {\kern 1pt} {\kern 1pt} e^{ - rt} {\text{d}}t} } \right] - (\alpha + \beta ){\kern 1pt} cD(p)I_{c} \int\limits_{{t_{p} }}^{T} {(T - t){\kern 1pt} e^{ - rt} {\text{d}}t} \\ & \quad - \tau {\kern 1pt} {\kern 1pt} cD(p)I_{c} \left[ {\int\limits_{\mu }^{T} {(T - t){\kern 1pt} e^{ - rt} {\text{d}}t} } \right]\left. { + \tau {\kern 1pt} {\kern 1pt} pD(p)I_{e} \left[ {\int\limits_{{t_{p} }}^{\mu } {(\mu - t){\kern 1pt} e^{ - rt} {\text{d}}t} } \right]} \right\} \\ \end{aligned}$$

(29)

and

$$g_{2} (T) = T > 0.$$

Hence, $PTP_{2} (p,T) = f_{2} (T)/g_{2} (T)$. Taking the first- and second-order derivatives of $f_{2} (T)$ with respect to T, respectively, and simplifying terms, we get:

$$\begin{aligned} f_{2}^{{\prime }} (T) = & \,prD(p)e^{ - rT} - \frac{{c{\kern 1pt} {\kern 1pt} D(p)\left( {e^{{T\theta - (r + \theta )t_{p} }} - e^{ - rT} } \right)\left( {\alpha \,e^{rl} + \beta + \tau \,e^{ - r\mu } } \right)}}{r + \theta } \\ = & - \frac{{h{\kern 1pt} {\kern 1pt} D(p)\left( {e^{{T\theta - (r + \theta )t_{p} }} - e^{ - rT} } \right)}}{r + \theta } - \frac{{c{\kern 1pt} {\kern 1pt} D(p)I_{c} }}{r}\left[ {\alpha \left( {e^{rl} - e^{{ - rt_{p} }} } \right) + \beta \left( {1 - e^{{ - rt_{p} }} } \right)} \right] \\ & \quad - \frac{{c{\kern 1pt} {\kern 1pt} D(p)I_{c} (\alpha + \beta )}}{r}\left( {e^{{ - r(T + t_{p} )}} } \right)\left( {e^{rT} - e^{{rt_{p} }} } \right) - \frac{{c{\kern 1pt} {\kern 1pt} D(p)I_{c} \tau }}{r}\left( {e^{ - r\mu } } \right)\left( {e^{rT} - e^{ - rT} } \right) \\ \end{aligned}$$

(30)

and

$$\begin{aligned} f_{2}^{\prime \prime } (T) = & - p\,rD(p)e^{ - rT} - \frac{{c{\kern 1pt} {\kern 1pt} D(p)}}{r + \theta }\left( {e^{{T\theta - (r + \theta )t_{p} }} \theta + e^{ - rT} r} \right){\kern 1pt} \left( {\alpha \,e^{rl} + \beta + \tau \,e^{ - r\mu } } \right) \\ & \quad - \frac{{h{\kern 1pt} {\kern 1pt} D(p)}}{r + \theta }\left( {e^{{T\theta - (r + \theta )t_{p} }} \theta + e^{ - rT} r} \right) - (\alpha + \beta ){\kern 1pt} cD(p)I_{c} e^{ - rT} \\ & \quad - \tau {\kern 1pt} {\kern 1pt} cD(p)I_{c} \,e^{ - rT} < 0 \\ \end{aligned}$$

(31)

Case 3

$$\mu \ge T$$

Proof

$$\begin{aligned} f_{3} (T) = & \,\left\{ {p\int_{{{\kern 1pt} 0}}^{{{\kern 1pt} T}} {D(p){\kern 1pt} e^{ - rt} {\text{d}}t} } \right. \\ & \quad - Oe^{rl} - \left( {\alpha {\kern 1pt} e^{rl} + \beta + \tau {\kern 1pt} e^{ - r\mu } } \right){\kern 1pt} c\left( {\int\limits_{0}^{{t_{p} }} {\frac{P - D(p)}{\theta }(1 - e^{ - \theta t} \, )e^{ - rt} {\text{d}}t} + \int\limits_{{t_{p} }}^{T} {\frac{D(p)}{\theta }(e^{\theta (T - t)} - 1)e^{ - rt} {\text{d}}t} } \right){\kern 1pt} \\ & \quad - h\left( {\int\limits_{0}^{{t_{p} }} {\frac{P - D(p)}{\theta }(1 - e^{ - \theta t} \, )e^{ - rt} {\text{d}}t} + \int\limits_{{t_{p} }}^{T} {\frac{D(p)}{\theta }(e^{\theta (T - t)} - 1)e^{ - rt} {\text{d}}t} } \right) \\ & \quad - cD(p)TI_{c} {\kern 1pt} \left[ {\int\limits_{ - l}^{{t_{p} }} {\alpha {\kern 1pt} {\kern 1pt} e^{ - rt} {\text{d}}t} + \int\limits_{0}^{{t_{p} }} {\beta {\kern 1pt} {\kern 1pt} e^{ - rt} {\text{d}}t} } \right] - (\alpha + \beta ){\kern 1pt} cD(p)I_{c} {\kern 1pt} \int\limits_{{t_{p} }}^{T} {(T - t){\kern 1pt} e^{ - rt} {\text{d}}t} \\ & \quad + \left. {\tau {\kern 1pt} {\kern 1pt} pD(p)I_{e} \left[ {\int\limits_{{t_{p} }}^{T} {(T - t){\kern 1pt} e^{ - rt} {\text{d}}t} + \int\limits_{T}^{\mu } {T{\kern 1pt} e^{ - rt} {\text{d}}t} } \right]} \right\} \\ \end{aligned}$$

(32)

and

$$g_{3} (T) = T > 0.$$

Hence, $PTP_{3} (p,T) = f_{3} (T)/g_{3} (T)$. Taking the first- and second-order derivatives of $f_{3} (T)$ with respect to T, respectively, and simplifying terms, we get:

$$\begin{aligned} f_{3}^{\prime } (T) = & p\,D(p)e^{ - rT} - \frac{{c{\kern 1pt} {\kern 1pt} D(p)\left( {e^{{T\theta - (r + \theta )t_{p} }} - e^{ - rT} } \right)\left( {\alpha \,e^{rl} + \beta + \tau \,e^{ - r\mu } } \right)}}{r + \theta } \\ & \quad - \frac{{h{\kern 1pt} {\kern 1pt} D(p)\left( {()} \right)}}{r + \theta } - \frac{{c{\kern 1pt} {\kern 1pt} D(p)I_{c} }}{r}\left[ {\alpha \left( {e^{rl} - e^{{ - rt_{p} }} } \right) + \beta \left( {1 - e^{{ - rt_{p} }} } \right)} \right] \\ & \quad - \frac{{c{\kern 1pt} {\kern 1pt} D(p)I_{c} (\alpha + \beta )}}{r}\left( {e^{{ - r(T + t_{p} )}} } \right)\left( {e^{rT} - e^{{rt_{p} }} } \right) - \frac{{pD(p)I_{e} \tau }}{r}\left( {e^{{ - rt_{p} }} - e^{ - r\mu } - rTe^{ - rT} } \right) \\ \end{aligned}$$

(33)

and

$$\begin{aligned} f_{3}^{\prime \prime } (T) = & - p\,rD(p)e^{ - rT} - \frac{{c{\kern 1pt} {\kern 1pt} D(p)}}{r + \theta }\left( {e^{{T\theta - (r + \theta )t_{p} }} \theta + e^{ - rT} r} \right)\left( {\alpha \,e^{rl} + \beta + \tau \,e^{ - r\mu } } \right) \\ & \quad - \frac{{h{\kern 1pt} {\kern 1pt} D(p)}}{r + \theta }\left( {e^{{T\theta - (r + \theta )t_{p} }} \theta + e^{ - rT} r} \right) - (\alpha + \beta ){\kern 1pt} cD(p)I_{c} e^{ - rT} \\ & \quad - \tau {\kern 1pt} {\kern 1pt} pD(p)I_{e} \,e^{ - rT} (rT - 1) < 0 \\ \end{aligned}$$

(34)