Abstract
Machines are a key element in the production system and their failure causes irreparable effects in terms of cost and time. In this paper, a new multi-objective mathematical model for dynamic cellular manufacturing system (DCMS) is provided with consideration of machine reliability and alternative process routes. In this dynamic model, we attempt to resolve the problem of integrated family (part/machine cell) formation as well as the operators’ assignment to the cells. The first objective minimizes the costs associated with the DCMS. The second objective optimizes the labor utilization and, finally, a minimum value of the variance of workload between different cells is obtained by the third objective function. Due to the NP-hard nature of the cellular manufacturing problem, the problem is initially validated by the GAMS software in small-sized problems, and then the model is solved by two well-known meta-heuristic methods including non-dominated sorting genetic algorithm and multi-objective particle swarm optimization in large-scaled problems. Finally, the results of the two algorithms are compared with respect to five different comparison metrics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Since 1970, increase in competitiveness among American industries have begun and adoption of new ideas such as just-in-time (JIT) and group technology (GT) have intensified. The GT philosophy is about division of a large system into smaller subsystems. This makes it simple to manage, because managing a subsystem is considerably easier than the entire large system (Sakhaii et al. 2016). Cellular manufacturing (CM) is one of the most important applications of GT, which takes advantage of the link between the flow-shop system (high rate of production) and job-shop systems (manufacturing flexibility and diversity of products). Cellular manufacturing system (CMS) enables us to produce various products with low waste (Niakan et al. 2016), so it is used in most major manufacturing centers with a relatively high diversity of products and also multipurpose facilities. As defined, CM means processing a set of similar parts on certain groups of machines or manufacturing processes (Mungwattana 2000). Designing of CMS consists of four steps. The first and foremost is solving a cell formation problem (CFP). At this stage, parts which have similarities in shape and configuration, and produced by the same or similarly required machines, are considered as a same family to process by a group of machines located in one cell. In the second step, facility layout is determined which involves cells layout at the level of workshop and also machines within each cell. The third step is about scheduling of the operation on each machine in the cells. Finally, the fourth step is allocation of resources in which resources such as tools, manpower and materials are assigned to machines and cells. Family formation for the parts and grouping the machines have some advantages such as reducing the setup times, material handling cost, work-in-process (WIP) inventories, throughput times, and production cost (Singh and Rajamani 2012). In the literature on this topic, various methods have been examined to solve CFP. These methods are included but not limited to procedure, cluster analysis, graph approach, mathematic programing and meta-heuristic approaches (Selim et al. 1998; Chan and Milner 1982; Tavakkoli-Moghaddam et al. 2005; Rabbani et al. 2015; Moradgholi et al. 2016). It should be noted that some companies create cells through machine assignment to a particular family group, but machines are not placed in a separate group, and so virtual cells are used. Examples for this case are presented in some researches such as Saad et al. (2002) and Kannan (1998). Hosseini et al. (2016) designed a bi-objective mathematical formulation to find the optimum routes for parts, the layout of machines and the assignment of cells to predefined locations. The presented model is solved by multi-choice goal programming (MCGP). Since CM is an NP-hard problem, a GA is used to tackle the model in large-sized problems.
From another point of view, according to the technological advancements and introduction of multi-function machines, few parts may have only one production route (Karim and Biswas 2015). Alternative process routes (APR) is defined as various processing programs for each part in which each operation of part can be processed with different costs and time on a variety of machines (Browne et al. 1984; Rabbani et al. 2016). Zhao and Wu (2000) presented a multi-objective CFP model by taking into account different routes for the production of parts. They aimed to optimize three conflicting objective functions simultaneously. Objective functions include minimization of the inter-/intra-cell movement, the workload variance in cells, and the exceptional elements. Jouzdani et al. (2014) utilized simulated annealing algorithm to solve a generalized cell formation problem, in which alternative routings and machine reliabilities were taken into considerations.
Nowadays, due to the increasingly competitive environment, companies need both flexibility and efficiency simultaneously. With regard to periodical changes in the level of products’ demand, the cell configuration in each period is not necessarily efficient for the next period. In a word, maybe cell reconfiguration differs from one period to the next one, which is known as the dynamic cellular manufacturing system (DCMS). Increase in the tendency to produce by make-to-order (MTO) systems and a high variety of products has changed the traditional static CMS to DCMS. An illustrative small-scaled example of DCMS for two periods is shown in Fig. 1.
Tavakkoli-Moghaddam et al. (2012) presented a DCMS model to identify the family cell parts and machine cell. The purpose was to minimize the inter-cell movement and other miscellaneous costs. Machine replication, cell’s size, sequence of operations, and reconfiguration are considered as constraints of the model. Mehdizadeh and Rahimi (2016) proposed an integrated mathematical model to tackle the dynamic cell formation problem by simultaneous consideration of inter-/intra-cell layout problems with machine duplication and operator assignment. The presented mathematical formulation consists of three main objectives in which the first one aims to minimize the inter-/intra-cell part movements, the second objective minimizes machine and operator costs, and the last one increases consecutive forward flow ratio. Rabbania et al. (2017) presented a new dynamic cell formation problem, where some new concepts such as lucky parts were introduced. Lucky parts are parts which are allowed to be produced in a specific period. Moreover, purchasing and selling of machines taking into account their book values were taken into consideration.
From another point of view, machine performance is frequently considered as a complete performance without any drawbacks and machine failure is usually neglected. However, machine failure can have an irreparable damage, because it can stop the production line and waste time. Chung et al. (2011) presented a multi-objective model of CMS with regard to machines failures and alternative process routes. They aimed to minimize the associated costs with cell production and also the machines failure cost. Hence, they used Tabu search algorithm to solve this model. Jabal Ameli et al. (2008) solved multi-objective DCMS model regarding machine reliability and multiple production routes, using ɛ - constraint method. On one hand, it seeks to minimize the costs associated with production, and on the other it reduces costs and waste of time caused by machine failure. Other examples of failure consideration in CMS are given in Aghajani et al. (2014).
Labor assignment as one of the CMS steps, despite its great importance in increasing the efficiency of production systems and workload balance of different cells, has received little attention. Aryanezhad et al. (2009) presented a new mathematical model to solve CFP and manpower allocation by considering the machines’ flexibility and alternative routes. In this model, each worker has a determined skill level, and improving the skill level is possible by expending training costs. Mehdizadeh et al. (2016) proposed a novel multi-objective mixed mathematical formulation, where cell formation and production planning problems are considered simultaneously. The paper aimed to decrease inter/intra-cell movement costs, setup costs, machine and reconfiguration costs, production planning costs, and worker hiring, firing, training, and salary costs. Azadeh et al. (2014) considered aspects of personality consistency and behavioral characteristics of individuals who are assigned to a same cell and presented a bi-objective mathematical model to minimize the inter-cell movement costs and the inconsistency of cell individuals according to their decision-making style. Rafiei and Ghods (2013) and Ghotboddini et al. (2011) presented a relatively similar multi-objective DCMS models. They solved the problem of grouping part/machine and machine/cell. In addition, they considered manpower allocation to cells with the aim of minimizing miscellaneous costs of production and maximizing the labor utilization, of considering who are allocated to the cells. Tavakkoli-Moghaddam et al. (2012) solved the multi-objective problem of CMS, using a scatter search algorithm, regarding alternative process routes for parts. The aims of the model include minimizing the fixed/variable cost of the machinery, maintenance and repair cost, inter-cell movement cost, maximizing the utilization of the machine, and minimizing workload variance of the different cells. Studies on the subject of CM are presented briefly in Table 1.
In this study, a new mathematical model, which is more comprehensive than previous models for multi-objective dynamic cellular manufacturing, is presented. This model contains many real-world factors such as cell workload balance, limitation of delivery time, and also negative effects of wasted time resulting from machine failure. The first objective of the proposed model is to minimize the miscellaneous expenses of the dynamic cellular manufacturing system such as fixed or variable costs, inter-/intra-cellular part movement costs, and machine reconfiguration costs, labor transfer between cells, delay in the date of parts delivery, and failure of the machines. The second and third objectives aim at minimizing the variance of workload on human resources and machinery in different cells as two main factors in the CMS efficiency.
The rest of the paper is organized as follows: In “Reliability in manufacturing systems”, we introduce the reliability in the production system. In “Problem description”, the description of the mathematical model and linearization of the proposed model are presented. The concept of a non-dominated solution is illustrated in “Methodology” and two proposed meta-heuristic algorithms are explained in detail. In “Numerical experiments”, we conduct a numerical experiment to compare the proposed meta-heuristic algorithms by presentation of a few test problems and using some comparison metrics. Finally, the study ends with conclusion remarks and future research.
Reliability in manufacturing systems
By definition, reliability is the probability that the machine, systems, device, vehicle, etc., perform the required duties under the operating conditions, for a specified period of time (Ebeling 1997). Jabal Ameli et al. (2008) stated that the reliability of the whole system cannot be considered as a function of the reliability of the individual members in the production system, because failure may occur when a machine is under operating condition, but in the production system all machines have idle time during the production period except bottleneck machines, and the previously considered functions cannot accurately estimate the reliability of the system. Therefore, it is better to evaluate the negative effects caused by the lack of reliability. These effects can be divided into two categories: first, cost-based effects; and second, time-based effects.
Cost-based effects
Machine reliability is defined as R = exp (λt), where λ and t stand for the machine failure rate and machine operation time, respectively. It should be mentioned that exp in this equation stands for exponential distribution. It is very common to assume this distribution for time intervals in which failures occur. Also, when time interval between failures follows exponential distribution, the number of failures will follow Poisson distribution (Walpole et al. 1993). Chung et al. (2011) said that any failure has pursuant expenses for machinery, such as repair and substitution costs. The usual way to deal with reliability in production systems is evaluation of the mean time between failures (MTBF). Its calculation formulation is shown in Eq. (1):
The cost estimation of the machine failure as a function of machine operation time (t) is calculable by Eq. (2):
where MTBF represents the mean time between failures, β denotes cost of machine failure each time and BR is the failure costs over the planning horizon.
Time-based effects
Another aspect is the machine’s failure during the manufacturing process, which may stop the production line, and subsequent delay may occur in completing the manufacturing operations. The downtime estimation of the machine failure as a function of machine operation time t is calculated by Eq. (3):
where MTTR represents the mean time to repair and Trep represents the total time of the machine downtime in the planning horizon.
Problem description
The model presented in this paper is multi-objective with regard to the real-world condition, and these objectives may be in conflict with each other. The first objective seeks to minimize the costs associated with DCMS (fixed or variable costs of machine, purchasing and selling costs of machinery between courses, parts and labor intercellular/intracellular transmission costs, delay costs of delivery time, and expenses arising from machine failure). The second one aims to increase labor utilization in different cells, such that the working pressure exerted on the human resources in different cells would not be much different. The third objective is to minimize the cells’ workload variance according to the number of allocated machines to each cell.
Problem assumptions
-
Each part has several operations, and each of these operations should be done respectively its number.
-
The operation time of the machines and manual labor are known and constant.
-
Fixed costs are specified for each machine and include all service costs.
-
Variable costs are specified for each machine and are dependent on the assigned workload.
-
Back order demand is not allowed and demand for each period should be provided in the same period.
-
Labor force is fixed for every period and hiring and firing is unauthorized.
-
Each machine can perform various operations, so machines are multipurpose.
-
Each part may have one or more routes for production and we are allowed to choose one and only one route among the existing routes.
-
The available time for every manpower is known and constant.
-
The demand for each part is specified and certain.
-
Delivery time and delay cost of each part are specified for each period.
-
The time capacity for each machine is constant and specified for each period.
-
The purchasing cost of each machine and selling them between periods are constant and known.
-
The maximum size of each cell space is specified.
-
Batch size for the part movement between machines and also the costs of inter- and intra-cellular movements are constant and specified (it is assumed that the inter-cell transfer cost is more than the intra-cell cost).
-
The cost of labor inter-cell transmission is constant and specified.
-
Number of machine failures have a Poisson distribution, and the MTBF and MTTR for each of the machines in each period are constant and specified.
Notations
- p :
-
Index for part types \( \left( {p = 1, \ldots P } \right) \)
- j p :
-
Index for operations belonging to part p \( \left( {j = 1, \ldots O_{p} } \right) \)
- c :
-
Index for manufacturing cells \( \left( {c = 1, \ldots C } \right) \)
- h :
-
Index for time periods \( (h = 1, \ldots H ) \)
- m :
-
Index for machine types \( \left( {m = 1, \ldots M } \right) \)
- P :
-
Number of part types
- O p :
-
Number of operations for part p
- C :
-
Number of cell types
- H :
-
Number of periods
- M :
-
Number of machine types
- L :
-
Total number of labors
- \( D_{ph} \) :
-
Demand for part p in period h
- ϑ ph :
-
If part p is planned to produce in period h, ϑph = 1; otherwise, it is zero
- UB :
-
Maximal cell size
- \( \gamma_{P}^{\text{inter}} \) :
-
Inter-cell movement cost per batch \( p \)
- \( \gamma_{P}^{\text{intra}} \) :
-
Intra-cell movement cost per batch p
- \( Del_{ph} \) :
-
Delivery time of part p in period h
- \( \varGamma_{p} \) :
-
Delay cost of part p for per unit time
- \( \varphi_{m} \) :
-
Marginal cost to purchase machine type m
- \( \omega_{m} \) :
-
Marginal revenue from selling machine type m
- α m :
-
Constant cost of machine type m in each period
- ρ h :
-
Constant cost of inter-cell labor moving in period h
- \( \delta_{m} \) :
-
Relocation cost of machine type m
- T mh :
-
Time capacity of machine type m in period h in regular time
- \( t_{{j_{p} m}} \) :
-
Processing time required to perform Operation j of part type p on machine type m
- \( t_{{j_{p} m}}^{\prime } \) :
-
Manual workload time required to perform Operation j of part type p on machine type m
- \( a_{{j_{p} m}} \) :
-
If operation j of part p can be done on machine type m, ajpm = 1; otherwise, it is zero
- BRm:
-
Cost of machine breakdown m
- MTBFm:
-
Mean time between failures on machine type m
- MTTRm:
-
Mean time to repair on machine type m
- β m :
-
Variable cost of machine type m for each unit time in regular time
- \( B_{P} \) :
-
Batch size for movements of part h
- WT:
-
Available time per worker
- \( X_{{j_{p} mch}} \) :
-
If operation j of part type p is done on machine type m in cell c in period h, \( X_{{j_{p} mch}} = 1 \); otherwise, it is zero
- N mch :
-
Number of machine type m allocated to cell c in period h
- K + mch :
-
Number of machine type m added in cell c in period h
- K − mch :
-
Number of machine type m removed from cell c in period h
- \( I^{ - }_{mh} \) :
-
Number of machine type m sold in period h
- \( I^{ + }_{mh} \) :
-
Number of machine type m purchased in period h
- L ch :
-
Number of labors that allocate cell c in period h
- LUh:
-
Labor utilization in period h
- LIh:
-
Reverse of labor utilization in period h
- RTph:
-
Completion time of the manufacturing part p in period h
- τ ph :
-
Bottleneck time for production part p in period h
- ℘ph:
-
Delay time from the date of delivery of part p in period h
- μ pch :
-
If there is at least one manufacturing operation of part p inside cell c in period h, μpch = 1; otherwise, it is zero
- OUh:
-
Utilization percent of all the machines in period h
- \( {\text{CU}}_{ch} \) :
-
Utilization percent of the machines’ cell c in period h
Mathematical model
s.t.
Equation (4) deals with minimization of the costs related to DCMS, including machines’ fixed costs (land, energy, maintenance), the cost of machine purchasing between the periods, the selling price of secondhand machines, the machines’ variable costs, the cost of intra- and inter-cell part movement (comprehensive explanation of how to calculate the fifth and sixth terms is presented by Safaei et al. (2008)], intercellular manpower transfer cost [costs of training and skilling the staff), machines relocation costs, expenses arising from machine failure, and cost of delay in delivery time. It should be noted that notation x denotes the smallest integer number larger than x. The second objective function considered in Eq. (5) deals with integration of the utilization of manpower in different cells. Utilization rate of manpower is defined as the total workload of the cell divided by the total available time of the manpower of that cell. This function seeks to maximize the minimum of manpower utilization rate between cells in different periods. For the third objective function, that is, Eq. (6), deals with minimization workload variance on machines in different cells. The percentage of machine utilization is defined as the total machine workload in terms of time divided by total machine’s available time in a period. In fact, this objective function seeks the uniformity of machine workload in different cells.
Equation (7) ensures that if there is demand for a part, its operation gets allocated only to one machine in one cell during a period, because according to Eq. (4), each part’s operation in a period cannot be done on more than one machine. Equation (8) shows that if there is lack of ability to perform an operation to produce a part on a machine, then that operation would not be performed in any cell and period. Equation (9) ensures that the total needed time for each kind of machines in each cell plus the wasted time caused by its failure would not be more than the total time capacity of the same kind. Equation (10) shows the balance of the number of machines in different periods with respect to purchases and selling at any period. Equation (11) determines the number of each cell’s machines by considering the machines’ relocation between each period. Equation (12) implies that the total labor allocated to different cells in each period is equal to the total number of labor. Equation (13) shows that the total number of machines allocated to each cell does not exceed the size of the cell. Equation (14) determines the entire manufacturing process time of each part, considering the failure of machinery and bottleneck machine in each period (Jabal Ameli et al. 2008). Equation (15) determines the operation time of the bottleneck machine for manufacturing each part during each period. Equation (16) and Eq. (17) are used to calculate the delay in delivery time. Equation (18) determines the machine utilization percentage in each cell and each period. Equation (19) specifies the utilization percentage of the total machines in each period. Equation (20) shows that the manual workload of each cell does not get bigger than the total manpower available capacity. Equation (21) determines the minimum utilization rate of manpower between different cells in each period. This equality is defined according to the objective function of Eq. (5).
Linearization of the proposed model
The proposed model in the previous subsection is a nonlinear model. Two of the three objective functions are transformed into the linear form as follows:
For the first objective function, replace Eq. (23) with Eq. (4).Then, the constraints of Eqs. (24)–(27) are added to the model. Moreover, Eq. (23) which is related to the objective function of Eq. (5) is nonlinear. Initially, we define a variable named LIch as follows:
Equation (5) is replaced by Eq. (35), and constraints are applied on Eqs. (30), (33), (34) and (36) instead of Eqs. (20) and (21).
Methodology
Two meta-heuristic algorithms, namely, non-dominated sorting genetic algorithm (NSGA-II) and multi-objective particle swarm optimization (MOPSO), are used for solving the proposed model. Since the proposed model is multi-objective, we initially refer to some concepts of multi-objective functions.
Non-dominated solution
On some issues related to the single-objective models, determining the best solution is easily possible and any solution that optimizes the objective function can be chosen as the best answer. However, there is more than one objective in some real-world issues. In these functions, existence of a single solution that optimizes all objectives may be unavailable. According to Ehrgott (2006), non-dominated points are mathematically defined as follows:
A feasible answer like \( \hat{x} \) is called non-dominated if there would be no answer such as x ∊ X, so that \( f\left( x \right) \le f\left( {\hat{x}} \right) \). In this algorithm, non-dominated answers are ranked as number 1, and ranking answers xi on generation t that are dominated by p t i of other answers can be calculated by the equity:
NSGA-II
NSGA-II is a population-based search method that is similar to the function of genes. A chromosome is a string of some genes. During each iteration of the algorithm, a new set of chromosomes is produced. During the reproduction process, genetic operators such as crossover operator and mutation operator apply to make the new chromosomes. Chromosomes that are produced in this way are called a child. Then, the children suitability is evaluated and more qualified chromosomes are chosen by a selection procedure and transferred to the next generation. In case of equality in a rank, we need another criterion to choose the answers. In this paper, we apply the notion of crowding distance. Boundary elements have an infinite crowding distance. For intermediate elements, crowding distance is determined by calculating the absolute value distance of the objective function from the adjacent elements that are normalized. In summary, the various stages of the NSGA-II algorithm are shown in Fig. 2.
MOPSO
Multi-objective particle swarm optimization (MOPSO) algorithm is one of the most important meta-heuristic algorithms that is usually used to optimize continuous nature problems (Azadeh et al. 2015). This algorithm is inspired by the social behavior of birds. In this system, a group of birds (those are called as particles) fly over the solution space. Each particle represents a potential solution to the mentioned problem. The position of each particle is influenced by the best position that the particle ever had (personal experience); one of the best positions found was chosen randomly from the non-dominated solutions archive and previous velocity of the particle. Thus, according to this factor, the new particle velocity is calculated (Figs. 3, 4, 5, and 6).
The particle’s specifications in the group can be stated as follows:
xi: The current location of the particle.
vi: The current velocity of the particle.
pi: The best position which has been found by the particle.
gi: The best position which has been found by the adjacent particles.
If the function of the mentioned problem would be function (f), then the amounts of xi, vi, pi and gi on any phase will be updated as follows:
where ω is inertia weight and usually reduces linearly during the iterations and r1, r2 are random numbers in the range of [0, 1]. c1, c2 are constant numbers and are known as acceleration coefficients; their amount is considered to be about 2.
Solution representation
We need to generate the initial population to use the proposed algorithm. According to the proposed model, initially it is sufficient to create the decision variables, XjPmch and Lch, at random, and then other decision variables are calculated through them.
In this section, we describe how chromosomes of solutions are represented. To create a feasible solution, XjPmch must be determined so that firstly it should be binary, and secondly Eqs. (7) and (8) would be established. These constraints state that if there is a demand for a part in a period, each of its manufacturing operations is performed only on a single machine and in a single cell. If there is possibility of any operation of any part on Q machine from M machine, since that operation can be performed in each of the cells, then Q × C different alternatives would exist to operate it. For each operation of each part in every period, create a random number in the interval of [0, 1]. Multiply the obtained number in Q × C and round it up. The final obtained number determines the cell and machine of the desired operation.
For example, if there are three cells for processing the parts, and there is the possibility for the performance of a part operation on three (2, 3, and 5) of six machines, then there will be nine different alternative operations for the part.
Lch To create a feasible solution, Lch must be determined so that firstly its amount would be an integer number, and secondly Eq. (12) would be established. For this purpose, we create C − 1 random number in the interval of \( \left[ {0,1} \right] \) in every period, then multiply the obtained numbers with L and round it up. The results are inserted in the table with \( \hat{L} \) ascending; the number of labor for each cell is calculated from the following equations:
Crossover operator
Three kinds of crossover, single-point, double-point, and uniform, are used for the algorithm NSGA-II and one of them will be chosen for each iteration at random. Initially, chromosomes of the parent in the form of two-dimensional (with the dimensions of C − 1 and H) and three-dimensional (with the dimensions of OP and P and H) are, respectively, by the number of arrays put in a row together and chromosomes are created in one dimension. Note that the number of chromosome cells for every new variable will be called length. In single-point crossover, we initially create random number in [1, length − 1]. Then, the two parent chromosomes of the cut points are combined to create two offspring; its example is presented in Fig. 7. The function of double-point crossover is similar to the single-point crossover with the exception that two random numbers are created in the range of [1, length − 1] and each parent chromosome from two corresponding points cute and then swap with each other. An example is presented in Fig. 8. In uniform crossover, we create a random chromosome which has same length as the parent chromosome. This chromosome determines which genes from the first parent and which one from the second parent are to be transferred to the offspring. Its function is shown in Fig. 9.
After obtaining the crossover, by reshaping we turn back chromosomes cells to their original dimensions.
Mutation operator
The same mutation is used in both algorithms and created based on the replacement of parent chromosome genes. The chromosome associated with the creation of Lch decision variables is two dimensional (C − 1 and H), and also the chromosome associated with the creation XjPmch decision variable has three dimensions (OP, P, and H). To create a mutation in the first chromosome, each time, two rows or two columns which are selected randomly replace each other (the sample of translocation in chromosome lines is shown in Fig. 10). For the second chromosome which is three dimensional, replace the corresponding plate to the two rows, two columns or two depths which are chosen randomly from each other (sample of translocation in chromosome columns is shown in Fig. 11). Since solution representation is based on real numbers between 0 and 1, all generated offsprings also will be in this range and an infeasible situation does not occur (Tables 2, 3).
Numerical experiments
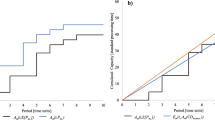
Two algorithms are coded in MATLAB R2013a software on a personal computer ASUS Core i7, 2.2 GHz with 4 GB RAM. 12 test problems are designed to verify the performance of this model; the 6 test problems of these are small sized and the others are large sized. The parameters of the test problem are shown in Tables 4, 5 and 6. This proposed model is validated by GAMS software in small sized of the problem that each objective function value calculated separately and other objective functions are calculated with regard to the obtained solution. Table 7 shows the result of GAMS software. The conflict of objectives can be seen in Table 7 and Fig. 12. The proposed model is NP hard; thus, GAMS software is unable to find the optimal solutions for large-scale problems and we use meta-heuristic approaches to solve it.
Parameter tuning
The good value of the input parameters of algorithms is calculated in large and small dimensions of the problem by the experiment design in Minitab software (TAGUCHI method). According to multi-objectiveness, the first front of the best solution (based on the second criterion) in each scenario is chosen for testing initially. Then, the amount of each function is divided by its maximum amount among different scenarios and the sum of three obtained amounts is considered as the scenario output. The results are shown in Tables 8, 9, 10, and 11.
Meta-heuristic algorithms comparison
In this section, we solve the presented test problem by the two algorithms of NSGA-ll and MOPSO, and then compare and analyze the results of the two methods by the five criteria including covered solution (x, y), spacing metric, diversification metric, quantity of non-dominated points, and space covered.
The quantity of non-dominated points that is discussed in more detail in “Methodology” represents the number of non-dominant points of each algorithm and is also briefly mentioned as QNDP in Tables 12 and 13.
Spacing metrics represents uniformity of the algorithm’s non-dominated answers in the Pareto space, which is briefly mentioned as SM in Tables 12 and 13. As much as the amount of these criteria is less, that algorithm will be more efficient. SM can be calculated from Eq. (44):
Diversification metrics indicates the dispersion and diffusion of the non-dominant solutions in the Pareto space, which is briefly mentioned as DM in Tables 12 and 13 and can be calculated from Eq. (45):
where xi represents the non-dominant solution (i) and yi represents the other non-dominant solution. In this equality, we obtain the farthest non-dominant answer for each archiving solution and then take the square root of the sum of them.
The space covered represents the amount of space that is covered by the non-dominant points in Pareto space and can be calculated from Eq. (39). It is briefly mentioned as CS in Tables 12 and 13.
where Z i f represents the objective function (f) for solution i of the archive.
The covered solution (x, y) is a criteria for comparing the quality of Pareto solutions obtained by x and y. In fact, the CS (x, y) criteria calculate the percentage of the Pareto front y which is dominated by Pareto front x.
Table 13 compares the algorithms NSGA-II and MOPSO (large sizes). The results of the comparison show that:
-
NSGA-II algorithm presents an archive with a larger number of non-dominated solutions in both small- and large-scaled problems.
-
NSGA-II has a greater average value of the spacing metric than MOPSO; in other words, non-dominated solution in MOPSO is more uniform on average.
-
The average of diversification metric and space covered obtained from the NSGA-II Pareto solution is more than that from MOPSO.
-
NSGA-II Pareto solution has a higher quality than MOPSO with respect to the CS metric and, as seen in Tables 14 and 15, on average, the percentage of MOPSO Pareto solution is dominated by NSGA-II Pareto solution.
Table 14 Coverage of two sets average values for small sizes Table 15 Coverage of two sets average values for large-sizes -
According to the computational time reported in Tables 12 and 13, the time needed to obtain a Pareto solution is less for MOPSO in almost all test problems.
Conclusion
In this work, an integrated multi-objective model was presented, in which grouping of parts/machines and allocation of manpower to cells were addressed simultaneously. In the mathematical model presented in this paper, real-world factors such as bad effects of failures including time-based and cost-based effects, cost of delay, human efficiency, and balancing workload in cells were considered in addition to factors of previous models. The objectives of the proposed model was to minimize the different costs of the DCMS, increase the manpower utilization, and also minimize the workload variance between cells. Two meta-heuristic algorithms, namely NSGA-II and MOPSO, were proposed for solving the problem. Also, a simple way to code the problem was introduced. To validate the proposed model, a small-sized problem was solved with GAMS software. To show the effectiveness of the proposed algorithm, several test instances were conducted and the results were compared with each other with respect to five comparison metrics (quantity of non-dominated points, spacing metrics, diversification metrics, space covered, and covered solution). As expected, due to the discrete nature of the problem, the results showed that the NSGA-II could discover more Pareto solutions than MOPSO and the solutions obtained by NSGA-II had more diversity than MOPSO. Also, it had more quality than MOPSO on average, but Pareto solution of algorithm MOPSO had more uniformity.
For future research, operators with different abilities and skills can be considered by the researcher. Also, the time value of money, determination of the machine layout, allocation of machinery and facilities, and solving the problems by other meta-heuristic methods are recommended for researchers who are interested in this particular subject.
References
Aghajani A, Ahmadi-Didehbani S, Zadahmad M, Seyedrezaei MH, Mohsenian O (2014) A multi-objective mathematical model for cellular manufacturing systems design with probabilistic demand and machine reliability analysis. Int J Manuf Technol. https://doi.org/10.1007/s00170-014-6084-0
Aramoon Bajestani M, Rabbani M, Rahimi-Vahed AR, Baharian Khoshkhou GA (2009) Multi-objective scatter search for a dynamic cell formation problem. Comput Oper Res 36:777–794
Aryanezhad MB, Deljoo V, Mirzapour Al-e-Hashem SMJ (2009) Dynamic cell formation and the worker assignment problem: a new model. Int J Adv Manuf Techol 41(3):329–342
Azadeh A, Rezaei-Malek M, Evazabadian F, Sheikhalishahi M (2014) Improved design of CMS by considering operators decision-making styles. International Journal of Production Research (ahead-of-print) 1–12
Azadeh A, Sangari MS, Sangari E, Fatehi S (2015) A particle swarm algorithm for optimising inspection policies in serial multistage production processes with uncertain inspection costs. Int J Comput Integr Manuf 28(7):766–780
Browne J, Dubois D, Rathmill K, Sethi SP, Stecke KE (1984) Classification of flexible manufacturing systems. FMS mag 2(2):114–117
Chan HM, Milner DA (1982) direct clustering algorithm for group formation in cellular manufacturing. J Manuf Syst 1(1):65–75
Chung SH, Wu TH, Chang CC (2011) An efficient tabu search algorithm to the cell formation problem with alternative routings and machine reliability considerations. Comput Ind Eng 60(1):7–15
Defersha FM, Chen M (2006) A comprehensive mathematical model for the design of cellular manufacturing system. Int J Prod Econ 103:767–783
Ebeling CE (1997) An introduction to reliability and maintainability engineering. McGraw-Hill, New York
Ehrgott M (2006) Multicriteria optimization. Springer, New York
Ghotboddini MM, Rabbani M, Rahimian H (2011) A comprehensive dynamic cell formation design: benders’ decomposition approach. Expert Syst Appl 38(3):2478–2488
Hosseini A, Paydar MM, Mahdavi I, Jouzdani J (2016) Cell forming and cell balancing of virtual cellular manufacturing systems with alternative processing routes using genetic algorithm. J Optim Ind Eng 9(20):41–51
Jabal Ameli MS, Barzinpour F, Arkat J (2008) Modelling the effects of machine breakdowns in the generalized cell formation problem. Int J Adv Manuf Technol 39:838–850
Jouzdani J, Barzinpour F, Shafia MA, Fathian M (2014) Applying simulated annealing to a generalized cell formation problem considering alternative routings and machine reliability. Asia-Pacific J Oper Res 31(04):1450021
Kannan VR (1998) Analysing the trade-off between efficiency and flexibility in cellular manufacturing system. Prod Plan Control 9(6):572–579
Karim R, Biswas SK (2015) Cell formation in a batch oriented production system using a local search heuristic with a genetic Aagorithm: an application of cellular manufacturing system. IOSR J Eng 5(4):28–41
Mehdizadeh E, Rahimi V (2016) An integrated mathematical model for solving dynamic cell formation problem considering operator assignment and inter/intra cell layouts. Appl Soft Comput 42:325–341
Mehdizadeh E, Niaki SVD, Rahimi V (2016) A vibration damping optimization algorithm for solving a new multi-objective dynamic cell formation problem with workers training. Comput Ind Eng 101:35–52
Moradgholi M, Paydar MM, Mahdavi I, Jouzdani J (2016) A genetic algorithm for a bi-objective mathematical model for dynamic virtual cell formation problem. J Ind Eng Int 12(3):343–359
Mungwattana A (2000) Design of cellular manufacturing systems for dynamic and uncertain production requirements with presence of routing flexibility (Doctoral dissertation, Virginia Tech)
Niakan F, Baboli A, Moyaux T, Botta-Genoulaz V (2016) A bi-objective model in sustainable dynamic cell formation problem with skill-based worker assignment. J Manuf Syst 38:46–62
Rabbani M, Farrokhi-Asl H, Rafiei H, Khaleghi R (2016) Using metaheuristic algorithms to solve a dynamic cell formation problem with consideration of intra-cell layout design. Intelligent Decision Technologies, vol. Preprint, no. Preprint, pp. 1–18
Rabbania M, Keyhanianb S, Manavizadehc N, Farrokhi-Asld H (2017) Integrated dynamic cell formation-production planning: a new mathematical model. Sci Iran 24(5):2550–2566
Rabbani M, Ramezankhani MJ, Farrokhi-Asl H, Farshbaf-Geranmayeh A (2015) Vehicle routing with time windows and customer selection for perishable goods. Int J Supply Operations Manage 2(2):700–719
Rafiei H, Ghods R (2013) A bi-objective mathematical model toward dynamic cell formation considering labor utilization. Appl Math Model 37:2308–2316
Ranjbar-Bourani M, Tavakkoli-Moghaddam R, Amoozad-Khalili H, Hashemian SM (2008) Applying scatter search algorithm based on TOPSIS to multi-objective cellular manufacturing system design. Int J Ind Eng (IJTE) 4870
Saad MS, Baykasoglu A, Gindy NNZ (2002) An integrated framework for reconfiguration of cellular manufacturing systems using virtual cells. Prod Plan Control 13(4):381–393
Safaei N, Saidi-Mehrabad M, Jabal-Ameli MS (2008) A hybrid simulated annealing for solving an extended model of dynamic cellular manufacturing system. Eur J Oper Res 185(2008):563–592
Sakhaii M, Tavakkoli-Moghaddam R, Bagheri M, Vatani B (2016) A robust optimization approach for an integrated dynamic cellular manufacturing system and production planning with unreliable machines. Appl Math Modell 40(1):169–191
Selim HM, Askin RG, Vakharia AJ (1998) cell formation group technology, review evaluation and direction for future research. Comput Ind Eng 34(1):3–20
Singh N, Rajamani D (2012) Cellular manufacturing systems: design, planning and control. Springer Science & Business Media, Berlin
Tavakkoli-Moghaddam R, Aryanezhad MB, Safaei N, Azaron A (2005) Solving a dynamic cell formation problem using meta-heuristics. Appl Math Comput 170:761–780
Tavakkoli-Moghaddam R, Ranjbar-Bourani M, Amin GR, Siadat A (2012) A cell formation problem considering machine utilization and alternative process routes by scatter search. J Intell Manuf 23(4):1127–1139
Walpole RE, Myers RH, Myers SL, Ye K (1993) Probability and statistics for engineers and scientists, vol 5. Macmillan, New York
Zhao C, Wu Z (2000) A genetic algorithm for manufacturing cell-formation whit multi routes and multiple objective. Int J Prod Res 38(2):385–395
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Rabbani, M., Farrokhi-Asl, H. & Ravanbakhsh, M. Dynamic cellular manufacturing system considering machine failure and workload balance. J Ind Eng Int 15, 25–40 (2019). https://doi.org/10.1007/s40092-018-0261-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40092-018-0261-y