A genetic algorithm for a bi-objective mathematical model for dynamic virtual cell formation problem

Abstract

Nowadays, with the increasing pressure of the competitive business environment and demand for diverse products, manufacturers are force to seek for solutions that reduce production costs and rise product quality. Cellular manufacturing system (CMS), as a means to this end, has been a point of attraction to both researchers and practitioners. Limitations of cell formation problem (CFP), as one of important topics in CMS, have led to the introduction of virtual CMS (VCMS). This research addresses a bi-objective dynamic virtual cell formation problem (DVCFP) with the objective of finding the optimal formation of cells, considering the material handling costs, fixed machine installation costs and variable production costs of machines and workforce. Furthermore, we consider different skills on different machines in workforce assignment in a multi-period planning horizon. The bi-objective model is transformed to a single-objective fuzzy goal programming model and to show its performance; numerical examples are solved using the LINGO software. In addition, genetic algorithm (GA) is customized to tackle large-scale instances of the problems to show the performance of the solution method.

Introduction

In current competitive business environment, customers demand diverse products with higher quality at lower costs. Therefore, manufacturers tend to reduce investment on tools, parts and area and increase their flexibility. With more efficient overall control techniques, companies and businesses use effective approaches in supply, manufacturing and distribution. Production costs constitute a significant share in the total costs incurred by a company. Conventional manufacturing systems (e.g., workshop or flowshop) are not flexible enough to respond to changes. As a result, cellular manufacturing (CM) as technique, stem from group technology (GT) has emerged as a promising manufacturing system. CM is described as a manufacturing procedure which produces part families within a cell of machines serviced by operators and/or robots functioning only within the cell. CMSs have some advantages, such as reduction in lead times, work-in-process inventories, setup times, etc. (Heragu 1994; Wemmerlov and Hyer 1989). However, the performance of CMS depends significantly on the stability of demand reGArding the volume and mix.

Dynamic cellular manufacturing system (DCMS) is one of the methods proposed for increasing the applicability of CMS when the demand for products fluctuates. In DCMS, to meet the demand in each period, the configuration of cells can be changed from one period to another (Rheault et al. 1995). However, the actual reconfiguration of cells may be time-consuming and costly. Furthermore, if these changes occur very frequently with stationary machines, the implementation of these systems is burdensome if not impossible (Thomalla 2000). In VCMS, unlike traditional cellular manufacturing, machines are not physically grouped into cells nor actually moved from their positions. Hence, some costs like assigning machines to cells or relocation of machines are not incurred. In VCMS, better controlling and planning of production is obtained by grouping of machines into virtual cells. VCMSs are capable of responding to demand fluctuations in a reasonable amount of time due to their high flexibility.

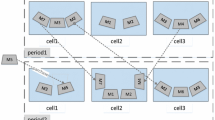
When a product mix or part demand level changes from a period to another, the configuration of cells may not be optimal anymore. In other words, the cells are reconfigured in the beginning of a period leading to a change in machine groups and parts families and work teams. Dynamic virtual cell formation (DVCF), unlike conventional dynamic manufacturing systems, can be utilized in this reGArd while reducing some costs, such as actual machine relocation costs. Figure 1 depicts an example of cellular reconfiguration in a dynamic environment. It is supposed that there are nine machines which are stationary for two periods. It can be easily seen that the manufacturing cells are virtual.

Fig. 1

Reconfiguration of virtual cells in a dynamic environment

Literature review

DCMS has been a point of attraction to both researchers and practitioners. Slomp et al. (2005) addressed the design of VCMS considering the limited availability of workers and worker skills. They presented a goal programming formulation, in which in the first stage, jobs and machines are grouped, and in the second step, workers are grouped to form a VCMS. Their objective was to assign the available capacity as efficiently as possible and also to make the VCMS as independent as possible. Nomden et al. (2006) reviewed the previous researches in the subject of VCMS. They addressed several definitions of virtual cells, offered by several researchers, and presented the potential problems for future researches. Mak et al. (2007) proposed a methodology for designing VCMS considering CFP and production scheduling problems. Their methodology included (1) a mathematical model for minimizing the total materials/components travelling distance subject to constraints, such as delivery due dates of products, capacities of resources, and critical tool limitations, and (2) an ant colony optimization method for solving cell formation and production scheduling. Liang et al. (2011) surveyed manufacturing resource modelling methods with a focus on resource element approach. They presented a function-clustering-degree concept addressing the trade-off between the granularity and quantity of virtual cells to verify the reconfiguration of manufacturing systems for solving virtual cell formation problem (VCFP). Mahdavi et al. (2011a) proposed an FGP-based approach to bi-objective mathematical model of CFP and production planning in a DVCMS. The objective of their research was to minimize the exceptional elements (EEs), holding and backorder costs in a cubic space of machine–part–worker incidence matrix. Rezazadeh et al. (2011) presented a mathematical model for DVCFP in which product mix/demand is variant in each period. The assumptions of their model were (1) considering operation sequence for the variety of processes as alternatives, (2) considering machines time capacity, maximum cell size and work capacity for each virtual cell. The objective of their proposed model was finding optimum number of virtual cells to minimize production, material transportation, inventory and manufacturing costs in each period. Nikoofarid and Aalaei (2012) designed a mathematical model for production planning in a dynamic virtual cellular manufacturing (DVCM) considering demand and part mix variation, machine capacity and as machine and worker availability as the main constraints. Han et al. (2014) addressed the problem of virtual cellular multi-period dynamic reconfiguration. They developed a model to incorporate the parameters of the problems, including product dynamic demand, machine capacity, operation sequence, balanced workload, alternative routings and batch setting. The objective of their mixed integer programming model is to minimize the total costs of operation, raw materials movements, inventory holding and process routes setup. Paydar and Saidi-Mehrabad (2015) developed a bi-objective possibilistic optimization mathematical model for formulating the integrated dynamic virtual cell formation and supply chain problem in a multi-echelon, multi-product and multi-period network. They developed a two-stage procedure, in which in the first stage, the proposed model is converted into an equivalent auxiliary crisp model, and in the second stage, a revised multi-choice goal programming approach is used for finding a compromise solution.

Although tremendous amount of research has already been conducted and published around CMS, the literature on DVCMS is still scarce. This paper is concentrated on DVCMS for processing multiple part types using multiple machine types and workers with different skills considering multiple candidate machine locations. We assume that several machines of any machine type are available for parts processing. In addition, we suppose that each worker is able to operate more than one machine in one cell.

In this paper, a DVCMS with several part types assigned to virtual cells to be processed by machines with different potential locations and cross-functional workers in a multi-period planning horizon is studied. In addition, more than one machine of each type may be available for part processing; i.e., duplicate machines are also considered. In this paper, unlike previous researches, we consider virtual cell of workers, machines (with candidate locations) and parts, simultaneously. The cost (number) of transportations between cells, as a major issue in DVCMS, is minimized. Furthermore, the number of exceptional elements is minimized as an objective function of the proposed model. The addressed problem is obviously NP-hard and considering dynamic conditions makes it even harder. Therefore, deterministic approaches may fail to efficiently solve real-world instances of the problem. Hence, metaheuristic approaches should be applied to obtain a satisfying solution in a reasonable amount of time. According to the literature and previously published researches (Mahdavi et al. 2009; Paydar and Saidi-Mehrabad 2013; Bootaki et al. 2014), genetic algorithm (GA) is capable of finding efficient solutions in the cell formation problems, and therefore, this algorithm is utilized for solving the proposed DVCMS mathematical problem. The main contributions of this paper to the literature on DVCMS are as follows:

• 1. Considering duplicate machines;

• 2. Simultaneous grouping of workers, machines and parts into virtual cells;

• 3. Proposing a bi-objective model that optimizes both:

  • (a) The exceptional and void elements, and;

  • (b) The total cost consisted of the fixed setup costs, the variable machine operation costs and the worker salary costs;

• 4. Developing a GA algorithm as a solution approach to the proposed model.

Problem description and formulation

In this section, the proposed mathematical model is formulated using a 4D machine–part–worker-location incidence matrix.

Sets

i :

index for part type (i = 1, 2 … , P);

m :

index for machine type (m = 1, 2 … , M);

w :

index for worker type (w = 1, 2, … , W);

k :

index for cell (k = 1, 2, … , C);

l :

index for location (l = 1, 2, … , L);

t :

index for time period (t = 1, 2, … , T).

Input parameters

r _mw :

1 if worker type w is capable of operating machine type m and 0 otherwise;

a _im :

1 if part type i can be processed on machine type m and 0 otherwise;

RW _wt :

available time for worker w in period t;

RM _mt :

available time for machine m in period t;

t _imw :

processing time of part i on machine type m with worker type w;

D _it :

demand of part i in period t;

SW _wt :

salary cost of worker type w in period t;

C _m :

fixed investment cost of machine type m;

α _m :

variable cost of machine type m.

Decision variables

X _imwklt :

1 if part type i is to be processed on machine type m in location l with worker type w in cell k in period t and 0 otherwise;

NW _wkt :

number of workers of type w allotted to cell k in period t;

Y _ml :

1if machine m is located in location l and 0 otherwise;

F _lkt :

1 if location l is assigned to cell k in period t and 0 otherwise;

Z _ikt :

1 if part i is processed in cell k in period t and 0 otherwise;

W _wkt :

1 if worker type w assigned to cell k in period t and 0 otherwise.

Mathematical model

Min Z ₁

$$= \sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{C} {\sum\limits_{l = 1}^{L} {\left( {\sum\limits_{i = 1}^{P} {\sum\limits_{m = 1}^{M} {\sum\limits_{w = 1}^{W} {Y_{ml} \times F_{lkt} \times Z_{ikt} \times W_{wkt} - \sum\limits_{i = 1}^{P} {\sum\limits_{m = 1}^{M} {\sum\limits_{w = 1}^{W} {Y_{ml} \times F_{lkt} \times Z_{ikt} \times W_{wkt} \times a_{im} \times r_{mw} } } } } } } } \right)}}}$$

(1-1)

$$+ \sum\limits_{t = 1}^{T} {\sum\limits_{i = 1}^{P} {\sum\limits_{m = 1}^{M} {\sum\limits_{l = 1}^{L} {\sum\limits_{k = 1}^{C} {\sum\limits_{w = 1}^{W} {a_{im} \times r_{mw} \left( {1 - Y_{ml} \times F_{lkt} \times Z_{ikt} \times W_{wkt} } \right).} } } } } }$$

(1-2)

Min Z ₂

$$= \sum\limits_{m = 1}^{M} {\sum\limits_{l = 1}^{L} {C_{m} \times Y_{ml} } }$$

(2-1)

$$+ \sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{C} {\sum\limits_{m = 1}^{M} {\alpha_{m} } } } \times D_{it} \times t_{imw} \times X_{imwklt}$$

(2-2)

$$+ \sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{C} {\sum\limits_{w = 1}^{W} {{\text{SW}}_{wt} \times {\text{NW}}_{wkt}}}}.$$

(2-3)

Subject to

$$X_{imwklt} \le Y_{ml} \quad \forall \; i,m,w,k,l,t.$$

(3)

$$X_{imwklt} \le F_{lkt} \quad \forall \; i,m,w,k,l,t.$$

(4)

$$X_{imwklt} \le W_{wkt} \quad \forall \; i,m,w,k,l,t.$$

(5)

$$X_{imwklt} \le Z_{ikt} \quad \forall i,m,w,k,l,t.$$

(6)

$$\sum\limits_{m = 1}^{M} {Y_{ml} } \le 1\quad \forall \; l.$$

(7)

$$\sum\limits_{k = 1}^{C} {F_{lkt} } = 1\quad \forall \; l,t.$$

(8)

$$\sum\limits_{k = 1}^{C} {Z_{ikt} } = 1\quad \forall \; i,t.$$

(9)

$${\text{NW}}_{wkt} \le A \times W_{wkt}\quad \forall \;k,w,t.$$

(10)

$$\sum\limits_{i = 1}^{P} {\sum\limits_{m = 1}^{M} \sum\limits_{l = 1}^{L} {D_{it} \times t_{imw} \times X_{imwklt} \le } } {\text{NW}}_{wkt} \times {\text{RW}}_{wt}\quad \forall \; w,k,t.$$

(11)

$$\sum\limits_{i = 1}^{P} {\sum\limits_{w = 1}^{W} {D_{it} \times t_{imw} \times X_{imwklt} \le } } Y_{ml} \times {\text{RM}}_{mt}\quad\forall \; m,l,k,t.$$

(12)

$$\sum\limits_{k = 1}^{C} {\sum\limits_{w = 1}^{W} {\sum\limits_{l = 1}^{L} {X_{imwklt} = a_{im} } } } \quad \forall \; i,m,t.$$

(13)

$$\sum\limits_{k = 1}^{K} {X_{imwklt} \le a_{im} } \times r_{mw} \quad \forall \; i,m,w,l,t.$$

(14)

$$Y_{ml} \in \left\{ {0,1} \right\}\quad \forall \; m,l.$$

(15)

$$F_{lkt} \in \left\{ {0,1} \right\}\quad \forall \; l,k,t.$$

(16)

$$W_{wkt} \in \left\{ {0,1} \right\}\quad \forall \; w,k,t.$$

(17)

$$Z_{ikt} \in \left\{{0,1} \right\} \quad \forall \; i,k,t.$$

(18)

$$X_{imwklt} \in \left\{ {0,1} \right\}\,\quad \forall \; i,m,w,l,k,t.$$

(19)

$${\text{NW}}_{wkt} \ge 0{\text{ and integer }}\quad \forall \; w,k,t.$$

(20)

The model has two objectives: in the first objective in (1-1), the goal is minimizing the number of exceptional elements, and in (1-2), the goal is to minimize the total number of voids; in the second objective, in (2-1), we minimize the fixed cost associated with machine investment and installation, and in (2-2), the variable cost of machines is minimized and (2-3) is to minimize the workers’ salary cost.

Constraint (3) ensures that if machine m is not assigned to location l, then certainly X _imwklt equals zero. Constraint (4) is to ensure that if location l is not assigned to cell k in period t, then certainly X _imwklt is equal to zero. Constraint (5) guarantees that if worker type w is not assigned to cell k in period t, then certainly X _imwklt is zero. Constraint (6) is for ensuring that if part type i is not assigned to cell k in period t, then certainly X _imwklt equals zero. Obviously, only one machine can be location in each location l. This is considered by Constraint (7). Each location l should be assigned to one cell k in each period; this fact is modeled by Constraint (8). Constraint (9) ensures that each part i is assigned to only one location l in each cell in the tth period. Constraint (10) determines the number of workers type w in all cells type k in the tth period where A is a large positive number.

Constraint (11) ensures that the sum of assigned time for workforce should not be more than available time. It is noticeable in this constraint that operations are performed only in cells to which the corresponding workers are assigned. This is because if NW _wkt  = 0, then no operations in that cell with worker type w can be performed and the left side of the constraint is equal to zero. Obviously, total assigned time to the machine m in the cell k in any period should not exceed the available time for machine m in cell k in each period. This fact is modeled by Constraint (12). Constraint (13) guarantees that each part is assigned to be processed on a machine in a period t with a worker w at a location l and in a cell k. Constraint (14) expresses the fact that each part could be manufactured in only one cell and by only one worker. Constraints (15)–(20) specify the allowed intervals and types of decision variables.

Linearization of the proposed model

The proposed model is obviously non-linear in the first part and the second part of the first objective function. Fortunately, most of the software have the ability to solve complex non-linear models; however, experiences show that solving such problems is usually time-consuming and results in local optima. Therefore, a linear model is practically more preferable and more convenient and efficient to solve. In addition, solving the model in small sizes utilizing fuzzy goal programming that the genetic algorithm method may be used for model verification. To linearize the model, some auxiliary variables and constraints are required to be defined and added to the original model. To linearize Eqs. (1-1) and (1-2), an auxiliary variable, Q _imwklt , is introduced as follows:

$$Q_{imwklt} = Y_{ml} \times F_{lkt} \times Z_{ikt} \times W_{wkt}.$$

Regarding Q _imwklt , the following constraints are also added to the model. It is easy to check that depending on the values of the binary variables, Y _ml , F _lkt , Z _ikt and W _wkt , the defined auxiliary variable, Q _imwklt , acts as the multiplication of the four binary variables.

$$Q_{imwklt} - Y_{ml} - F_{lkt} - Z_{ikt} - W_{wkt} + 3. 5\ge 0\quad \forall \; i,m,w,l,k,t.$$

(21)

$$3. 5\times Q_{imwklt} - Y_{ml} - F_{lkt} - Z_{ikt} - W_{wkt} \le 0\quad \forall \; i,m,w,l,k,t.$$

(22)

$$Q_{imwklt} \in \left\{ {0, 1} \right\}\quad \forall \; i,m,w,l,k,t.$$

(23)

Fuzzy goal programming-based approach

One of the most important differences between one-objective and multi-objective optimization is multi-objective optimization can solve multi-dimensional objective problems. One of the famous methods for solving multi-objective problems is goal programming (GP). However, the application of GP in real-world problems may face two important difficulties: the first is the mathematical expression of the decision maker’s imprecise aspiration levels for the goals and the second is the need to optimize all goals simultaneously. Fuzzy goal programming (FGP) is a mathematical decision-making mechanism to incorporate uncertainty and imprecision into the formulation. In practice, a high degree of fuzziness and uncertainty is included in the data set (Mahdavi et al. 2011b). The FGP has been tackled through different methods, such as probability distribution, penalty function, fuzzy numbers, preemptive FGP, interpolated membership function and the weighted additive model. Zimmermann first proposed fuzzy programming for solving the multi-objective linear programming problems (Zimmermann 1978). A number of researchers have extended the fuzzy set theory to the field of goal programming proposed by Narasimhan (1980). The fuzzy model of a generalized multi-objective multi-constrained optimization problem (Yang et al. 1991) can be expressed in what follows. Consider a problem with the following minimization objectives:

$$Z_{l} \left( X \right) \le g_{l}\quad l = 1, 2, \ldots,b$$

(24)

and subject to constraints:

$$d_{j} \left( X \right) \le D_{j}\quad j = 1, 2, \, \ldots,m,$$

(25)

where l is the index of goals, b represents the number of fuzzy-minimum goal constraints, g _l is the goal value (target value) for objective l given by the decision maker (DM), X is a k-dimensional decision vector, goal constraints are represented by Z _l (X) and finally, $G = \{ X|d_{j} (x) \le D_{j},\;j = 1, \ldots, m\}$ is the set of system constraints and defines the feasible space in which m represents the number of system constraints.

Let p _l denote the maximum tolerance limit for g _l determined by the DM. Thus, using the concept of fuzzy sets, the membership function of the objective functions can be defined as follows (Zimmermann 1978):

$$\left\{ {\mu_{{Z_{l} }} (X) = \left\{ {\begin{array}{*{20}l} 1 \\ {1 - \frac{{Z_{l} (X) - g_{l} }}{{p_{l} }}} \\ 0 \\ \end{array} \begin{array}{*{20}l} \quad {{\text{if}}\,Z_{l} (X) < g_{l} } \\ \quad{{\text{if}}\,g_{l} \le Z_{l} (X) \le g_{l} + p_{l} } \\ \quad {{\text{if}}\,Z_{l} (X) > g_{l} + p_{l} } \\ \end{array} } \right.} \right.$$

(26)

The term µ _zl (x) indicates the desirability of solution X in terms of the objective l. The corresponding graph of Eq. (26) is shown in Fig. 2.

Fig. 2

Membership function related to objectives

The α-level sets $Z_{l}^{\lambda } ,\quad \forall \; l \in \left\{ {1,2, \ldots ,b} \right\},\,\quad \forall \; \lambda \in \left[ {0,1} \right]$ are defined as:

$$Z_{l}^{\lambda } = \left\{ {\left. X \right|\mu_{{Z_{l} }} \left( X \right) \ge \lambda ,0 \le \lambda \le 1} \right\} , { }\;\;\; \, l = 1,2, \ldots b.$$

Then, the decision space is defined by intersecting the system constraints with the intersection of λ-level sets as follows:

$$Z^{*} = \left\{ {\bigcap\limits_{l = 1}^{b} {Z_{l}^{\lambda } } } \right\}\bigcap G,\quad 0\, \le \lambda \le 1.$$

According to the extension principle, the membership function of Z is defined as follows:

$$\mu_{Z} (X) = \mathop {\hbox{min} }\limits_{l = 1,2, \ldots m} \left\{ {\mu_{{Z_{l} }} (X)} \right\}.$$

Finally, the optimal solution, $Z^{*}$ $X^{*}$, must maximize μ _Z (X) by solving the following mathematical programming.

$$\begin{aligned} &{\text{Max }}Z^{*} \, = \,\,\lambda \hfill \\ &{\text{s}} . {\text{t}} .\hfill \\ \,\,\,\,\,&\lambda \le \mu_{{Z_{l} }} (X), \qquad l = 1,2, \ldots ,b \hfill \\&d_{j} (X) \le D_{j},\qquad j = 1,2, \ldots ,m \hfill \\ &0 \le \lambda \le 1 \hfill \\ \end{aligned}$$

(27)

The GA approach

GA is inspired by Darwin’s theory of evolution and genetic knowledge and is based on elitism. It simulates the genetic evolution of orGAnisms, and its generic usage is as an optimization method. The excellent books by Davis (1991) and Goldberg (1989) described many possible variants of GAs. GA is based on an analogy to the phenomenon of natural selection in biology. First, a chromosome structure is defined to represent the solutions to the problem. An initial solution population is generated either randomly or using a heuristic. Each chromosome is then improved through a selection/elitism mechanism. More specifically, members of the population are selected based on an evaluation function, called “fitness”, which associates a value to each member according to its objective function. The higher a member’s fitness value, the more likely it is to be selected. Thus, the less fit individuals are replaced by those with higher value. Genetic operators are then applied to the selected members to produce a new generation. This process is repeated until some stopping criteria are reached (Mahdavi et al. 2009). The main components of GA for implementation are:

• 1. The scheme for coding.

• 2. The initial population.

• 3. Adaptation function for evaluating the fitness of each member of the population.

• 4. Selection procedure.

• 5. The genetic operators used for combining the solution features for producing a new generation.

• 6. Certain control parameter values (e.g., population size, number of iterations, genetic operator probabilities, etc.).

The scheme for coding

For any implementation of GA, the first stage is to map solution characteristics into the format of a chromosome string. Each chromosome is made up of a sequence of genes from a certain alphabet. The alphabet can be a set of binary numbers, real numbers, integers, symbols, or matrices Goldberg (1989).

In genetic algorithms, each chromosome represents a feasible solution in the search space and is formed by a fixed number of genes. Usually, genes are represented using binary codes. In this paper, a four-component chromosome is used for solution representation.

The first component of the chromosome, formed according to the decision variable Y _ml , is a row vector in which the number of column represents the location and the value within the column determines the type of machine. For example, in Fig. 3, the first element of the vector is 2 meaning that a machine of type 2 is in located in the location 1.

Fig. 3

Example of chromosome Y _mi

The next component models the variable, Z _ikt , and is a matrix with P rows and T columns. The element in row p and column t of the matrix shows the number of the cell in which part p is processed in period t. For instance, in Fig. 4, the matrix with four rows and four columns determines the cell numbers for four parts in four periods. The number 3 in the first row and second column means that part number 1 in period 2 is processed in cell 3.

Fig. 4

Chromosome demonstration for variable Z _ikt

The variables F _lkt and w _wkt are represented using a similar matrix utilized to code the variable Z _ikt . The only difference is that rows in the matrices for F _lkt and w _wkt represent locations and workers, respectively. Figure 5 illustrates an example of the matrix for F _lkt with the element in the first row and the second column being equal to 3; showing that location 1 in period 2 is assigned to the cell number 2. Similarly, in Fig. 6, the matrix for variable w _wkt is formed by six workforces and four periods. The element in the first row and the first column specifics that worker 1 in period 1 is assigned to the cell 3.

Fig. 5

Chromosome representation for variable F _lkt

Fig. 6

Chromosome representation for variable w _wkt

The initial population

Another aspect of GA implementation is generating a set of initial solutions known as the initial population. The number of initial solutions to be included in the population is called population size. The population size is a key factor in a successful GA implementation. A small population size increases the speed of the algorithm; however, it may prevent the algorithm from converging to satisfying solutions. On the other hand, although a large population usually results in better solutions, it may significantly increase CPU time (Back et al. 1997)

Fitness function

In GA implementation, a fitness function is used to evaluate the chromosomes for reproduction. The purpose of the fitness function is to measure the quality of the candidate solutions in the population with respect to the objective and constraint functions of the model. The fitness function is calculated according to Eq. (27), where λ is the same $*$, and a penalty function is used in fitness function ($Z_{X}^{*}$) to satisfy the constraints.

$$Z_{X}^{*} = \hbox{min} \left( {\frac{{Z^{*}}}{{1 + {\text{penalty function}}}}} \right).$$

Selection rule

The roulette wheel selection procedure, as proposed by Goldberg (1989), is the selection strategy used in the proposed algorithm. The goal of the selection strategy is to allow the “fittest” individuals to be considered more often to reproduce children for the next generation. Each individual is assigned a probability of being selected based on its fitness value. Although individuals with higher fitness value have a higher selection probability, all individuals in the population should be given a chance to be selected. Hence, after ranking the individuals, the parents are selected randomly based on their fitness.

Genetic operators

Reproduction is carried out by applying crossover and mutation operators on the selected parents to produce offspring. The crossover and mutation operators for the proposed algorithm are discussed in what follows.

Uniform crossover

For every pair of randomly selected parents, a small proportion of randomly selected genes is exchanged. The crossover process is illustrated in Fig. 7. Individuals parent A and parent B produce offspring A and offspring B after applying the crossover. We define parent A as the direct parent of offspring A, and parent B as the direct parent of offspring B.

Fig. 7

Uniform crossover

Mutation operator

The conventional mutation operator randomly alters the value of the genes according to a small probability of mutation; thus, it is merely a random walk and does not guarantee a positive direction toward the optimal solution. The proposed heuristic mutation remedies this deficiency. In this scheme, an individual is randomly chosen from the population (Fig. 8).

Fig. 8

Proposed mutation

Parameters

The parameters required to run the algorithm are population size, number of generations, number of iterations, crossover and mutation probabilities. These parameters have a crucial role in the performance of the GAs. The number of generations is a function of the size of the problem at hand. As the solution space extends, the GA requires a larger number of generations to reach a satisfying convergence point. Population size may vary depending on the application. The number of iterations must be adjusted to allow the GA to complete the convergence process. The crossover operator has a significant effect on the performance of GA, and therefore, usually, a relatively large probability value is considered for this parameter. Mutation operator is basically used to maintain diversity in the population and is performed with a low probability.

Computational results

Solving the model with LINGO software

In this section, we present an example for which the branch and bound in the LINGO software and the genetic algorithm are utilized as solution methods. In addition, to evaluate the performance of the proposed model, a comparison of the outcomes is provided.

This example includes three cells, three parts, three machines, three workers, four locations and two periods in which all the presented hypothesis in “Problem description and formulation” are valid. Our goal is determining machine locations and cells and worker assignments.

Our data for the model include a _im which is a 2D variable to determine part–machine relations and is shown by the following matrix:

$$a_{im} = \begin{array}{*{20}c} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 1 & 0 & {0} \\ \end{array}$$

Another input is r _mw that determines the worker–machine assignments as shown as follows:

$$r_{mw} = \begin{array}{*{20}c} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 0 & 1 & 1 \\ \end{array}$$

Demand volume for each part in each period is given by:

$$D_{it} = \begin{array}{*{20}c} {30} & {100} \\ {70} & {80} \\ {90} & {60} \\ \end{array}$$

The time spent for processing each part on each machine by each worker is represented by a 3D matrix as follows (Table 1).

Table 1 Operation process times in example 1

The other input parameters for machines and workforces are depicted in Tables 2 and 3, respectively.

Table 2 Machines available times, machines fixed costs and machines variable costs in example 1

Table 3 Machines available times, workers hiring and number of available workers in example 1

FGP model of the problem is coded and solved using the LINGO Software run on a desktop PC equipped with an Intel^® Core™ i3 @ 3200 GHz and 4 GBs of RAM running Microsoft Windows™ 7 Ultimate. The results were obtained after 13 h and 54 min. In Table 4, parts, machines and locations assignments to cells in each period are presented. In the results, for example, in cell 3 in the first period, two machines of type 3, one machine of type 1 and one machine of type 2 are assigned.

Table 4 Output information of the proposed model related to assign machines and workers to each cell in each period using LINGO in example 1

In Table 5, assignments of machines to locations are presented. It should be noted that the locations of machines are determined in the first period and are fixed for all periods. For instance, the machine, M2, is assigned to location 1 for all periods.

Table 5 Output information related to assign each machine to the locations using LINGO in example 1

For more understanding of the results, the reconfigurations of this example are depicted in Fig. 9.

Fig. 9

Cell reconfiguration schema in each period for example 1

In Table 6, the obtained values for the FGP variables are presented. The optimized values of the first and second objective functions (Z ₁ and Z ₂) are 198 and 161,400, respectively.

Table 6 Obtained values for FGP variables

Solving example 1 using genetic algorithm (GA)

We coded the proposed GA solution method by MATLAB 2010 and applied the program to the same numerical example solved by the LINGO Software using the same desktop PC mentioned above and discussed in “Solving the model with LINGO software“. In the results, obtained after 330 s, λ was 0.77273 for which Fig. 10 illustrates the convergence in 24 iterations. In this figure, vertical and horizontal axes show λ and the number of iterations, respectively.

Fig. 10

Convergence of λ in example 1

Therefore, the obtained values translate into the matrix depicted in Table 7.

Table 7 In the interpretation of the results obtained from the proposed GA in example 1

For the parts, machines and workers, the best solution is derived from X _imwklt . The corresponding values are presented in Table 8.

Table 8 Output information of the proposed model related to assign the machines and workers to each cell in each period using the genetic algorithm in example 1

For more understanding of the solution, the reconfigurations of this example are given in Fig. 11.

Fig. 11

Cell reconfiguration schema in each period for example 1 in the MATLAB software

To illustrate the performance of the proposed method, the difference percentage GAP between the proposed GA and LINGO results is calculated which is shown in Table 9.

Table 9 GAP of between LINGO and GA

The performance GAP shows that the proposed GA outperforms LINGO Solver with a significant GAP.

Consideration of some examples with greater dimensions

For further investiGAtion, we considered the second example with the greater dimensions. It has three periods, five types of parts, three types of machines, four types of workers, three cells and eight locations. After entering input data to the model, the results were obtained as follows:

The model is solved in about 22 min (1327 s) and achieved the solution. λ is converged to 0.92646 and Fig. 12 depicts this convergence. The vertical axis depicts the value for λ and the horizontal axis represents the number of iterations. After 65 iterations, λ was converged to the aforementioned value.

Fig. 12

Convergence of λ in example 2

The obtained values for the variables are presented as follows (Tables 10, 11, 12).

Table 10 Output information related to assign each machine to the locations used genetic algorithm in example 2

Table 11 Output information of the proposed model related to the machines and workers to each cell in each period using the genetic algorithm in example 2

Table 12 Obtained values for GA variables in example 2

For more understanding, reconfigurations of this example are given in Fig. 13.

Fig. 13

Cell reconfiguration schema in each period for example 2 in the MATLAB software

Example 3: In this example, we considered a problem with ten parts, three workers, four machines, three cells, three periods and six locations. We ran the model, and after 6 h (21,560 s), the solution was found. At last, λ value was converged to 0.84897 after 138 iterations. Figure 14 depicts these values for iteration larger than 64. Vertical axis shows λ value, and horizontal axis depicts the iterations.

Fig. 14

Convergence of λ in example 3

Fig. 15

Cell reconfiguration schema in each period for example 3 in the MATLAB software

Output values for the variables are as follows (Tables 13, 14, 15).

Table 13 Output information related to assign each machine to the locations used genetic algorithm in example 3

Table 14 Output information of the proposed model related to assign machines and workers to each cell in each period using the genetic algorithm

Table 15 Obtained values for GA variables in example 3

Computational results for the proposed GA

To show the effectiveness of the proposed GA in solving the proposed model, first three small-sized examples which can be solved optimally using LINGO are presented. The results of solving these examples using the LINGO and the proposed GA are compared in Table 16. The relative differences between the objective values, achieved by the two methods, are shown as GAP in Table 16. According to this table, in the worst case, solution GAP between the proposed GA and the global optimum found by the LINGO software is 4.8 %. This shows that the proposed GA is capable of obtaining the near optimal solutions in a reasonable computational time. As shown in Table 16, the LINGO software has solved the third example in a time equal to 13:54:00 which is not a reasonable computational time for solving a small-sized example.

Table 16 Comparison of the proposed GA and LINGO for small-sized examples

To demonstrate the performance of the proposed GA in solving medium-sized examples, three test problems, in which LINGO fails to solve optimally, are designed and solved using the proposed GA. In a maximization problem, the LINGO software found a possible interval for optimum value of objective function ($Z^{*}$) that is limited by the Z ^bound and Z ^best values, where Z ^best ≤ $Z^{*}$ ≤ Z ^bound. Z ^best shows the best known feasible objective function value, and Z ^bound represents the upper bound of the objective function. Approaching to the current values for the best known solution and the bound, Z ^best is either the optimal solution, or very close to it. At such a point, the solver can be interrupted and report the current best solution with the aim of shortening additional computation time. Therefore, we limit runtime to 15 h to save computational effort and report the best solution obtained after 15 h. To validate the results found by GA, the solutions achieved by GA for three examples are compared with Z ^best obtained by LINGO after 15 h. These results are shown in Table 17. The GAP between the objective value of the proposed GA and Z ^best in the worst case is 6.2 %. This confirms that the proposed GA is able to obtain solutions to those examples effectively. In addition, computational time for those examples by GA is less than 40 min showing its superior efficiency. To evaluate the performance of the proposed GA in solving the large-sized examples, four random instances are solved by GA and LINGO, and the obtained results are shown in Table 18. LINGO solver is not capable of even finding feasible solutions for the last three test problems even after 15 h. However, GA has solved these examples in less than 6 h. Moreover, in the first example of Table 18, the solution obtained by GA is better than Z ^best, achieved by LINGO after 15 h.

Table 17 Comparison of the proposed GA and LINGO for medium-sized test examples

Table 18 Comparison of the proposed GA and LINGO for large-sized test examples

To further clarify the superiority of the proposed algorithm, a statistical test is conducted for each group of problems. More specifically, a paired t test is utilized to compare the objective function value and computational time of the proposed algorithm and those of LINGO solver. The results of the test are presented in Table 19. In this Table, μ _LINGO and μ _GA are the mean objective function value for LINGO and GA, respectively, and $\mu_{\text{LINGO}}^{\prime}$ and $\mu_{\text{GA}}^{\prime}$ are the mean computational time for LINGO and GA, respectively.

Table 19 Results of the test

Conclusions

In this paper, a bi-objective mathematical model for dynamic virtual cellular manufacturing system is developed which have several advantages toward the previous researches in the literature. One of the majors to another researches is introducing method to the assignment of workers alongside assignment of machines to locations in DVCMS which this mater concludes to complexity of the model. However, considering these features simultaneously causes to better planning and close to real-life situations. The most important features of this paper is as follows:

• 1. Developing the dimensions of cellular manufacturing problem, including machines, parts, workers and locations leading to a more realistic model.

• 2. Assigning workers, location to machines and parts to cells to operation processing in dynamic virtual cellular manufacturing system simultaneously.

• 3. Calculating the number of inter-cell transportations cost and exceptional elements in dynamic virtual cellular manufacturing system.

• 4. Calculating machine variable and fixed costs in each periods and also workforce hiring cost.

• 5. Forming virtual cells in each period.

Further researches on the proposed model may be attempted in future studies by incorporating the following issues:

• Developing a mathematical model with considering uncertainty with fuzzy parameters;

• Operation scheduling can be considered in virtual cellular manufacturing problem;

• Distances between each machine and transportation of materials can be added to the mathematical model.