Abstract
Tri-level optimization problems are optimization problems with three nested hierarchical structures, where in most cases conflicting objectives are set at each level of hierarchy. Such problems are common in management, engineering designs and in decision making situations in general, and are known to be strongly NP-hard. Existing solution methods lack universality in solving these types of problems. In this paper, we investigate a tri-level programming problem with quadratic fractional objective functions at each of the three levels. A solution algorithm has been proposed by applying fuzzy goal programming approach and by reformulating the fractional constraints to equivalent but non-fractional non-linear constraints. Based on the transformed formulation, an iterative procedure is developed that can yield a satisfactory solution to the tri-level problem. The numerical results on various illustrative examples demonstrated that the proposed algorithm is very much promising and it can also be used to solve larger-sized as well as n-level problems of similar structure.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Multi-level programming problem deals with an optimization problem with multiple decision makers who are organized in hierarchical levels. In this setting, at least one decision maker is located at each of the hierarchical decision making levels and each controls an independent decision vector for optimizing his/her own objective. In hierarchical (or multi-level) optimization, the constraint domain at each of the upper levels is implicitly determined by a series of optimization problems which must be solved in a predetermined sequence. In the real world, we often encounter situations where there are two or more decision makers in an organization with a hierarchical structure, and they make decisions in turn or at the same time so as to optimize their objective functions (Abo-Sinna and Baky 2006; Azad et al. 2006; Bialas and Karwan 1984; Sakawa et al. 2011).
When there are exactly three decision makers arranged in hierarchical order trying to optimize their own criteria functions, the resulting problem is called a tri-level programming problem. Mathematically, a tri-level programming problem with only one decision maker at each level can be formulated as (Woldemariam and Kassa 2015)
where \(X^{i} \subseteq {\mathbb{R}}^{n_{i}},\) \(\sum _{i=1}^{3}n_{i}=n.\) The set \(S = S^{1}\cap S^{2}\cap S^3\) is called the relaxed constraint set that every decision maker should select its decision variables from. We assume that S is non-empty and bounded. Moreover, we assume that each \(F_{i}:{\mathbb{R}}^{n_i}\rightarrow {\mathbb{R}}\) represents the objective function of the i-th level decision maker, \(i = 1,2,3.\)
Depending on the type of functions involved in the objectives and constraints of the problem, tri-level programming problems can be classified as linear and non-linear (Lee and Shih 2001). Among the non-linear tri-level programming problems, if some of the functions involved are ratio of two functions, we shall call them fractional tri-level programming problems.
In general, due to the nested structure of the optimization problems in each level, tri-level programming problems are complex in their nature. Several solution approaches for quadratic and quadratic fractional bi-level programming problems have been deeply investigated using various approaches so far (for instance see Bialas and Karwan 1982; Biswas and Bose 2011; Candler and Townsley 1982; Pal and Moitra 2003 and the references therein). Some of these approaches are classical or can fall in the category of extreme point search, transformation approach, descent or heuristic types. But the use of many of the approaches often lead to the NP-hard algorithm and might create ambiguity to choose an optimal solution if the lower problem is nonconvex, in particular. Due to the hierarchical nature of the problem and conflicting demands by the lower level decision makers, decision deadlock arise quite frequently in the process. To overcome such problems, a fuzzy programming approach to hierarchical decision problems has been introduced for bi-level problems by Lai (1996) and extended by Shih et al. (1983) and Shih and Lee (2000) using the concept of tolerance membership functions and multiple objective decision making. The main difficulty with a conventional fuzzy programming approach is that re-evaluation of the problem again and again by re-defining the elicited membership values of the objectives is involved to reach a satisfactory decision. To avoid such a computational burden, goal satisficing method in goal programming (Ignizio 1976) for minimizing the regrets of the DMs in case of a bi-level programming problem has been studied by Moitra and Pal (2002).
The main idea in fuzzy programming approach is to use the basic fuzziness and vague nature of such large hierarchical systems to make the complexity tractable. In Mohamed (1997), fuzzy goal programming technique is introduced to overcome the possibility of rejecting the solution again and again by decision makers at each level. This approach was also extended to solve multiobjective linear fractional programming problems (Pal et al. 2003), bi-level quadratic programming problems (Pal and Moitra 2003) and linear multi-level programming problems with single objective function in each of the levels (Pramanik and Roy 2007). Moreover, Osman et al. (2004) extended the fuzzy approach of Abo-Sinna (2001) for solving non-linear bi-level and tri-level multiobjective decision making under fuzziness by defining a membership function of each objective function and control variable of each decision maker to formulate a single level programming problem which is simpler to solve than the original problem. In this approach, the conventional single level programming has been formulated using the weighted sum technique with the weight is equal to reciprocal of the distance between the maximum and minimum value of each decision makers. However, there is a possibility that their fuzzy approach offers undesirable solution because of inconsistency among the fuzzy goals of the non-linear objective functions and linear fuzzy goals of the decision variables. So, small change of the decision variable may produce large change in the corresponding objective function and this may result in unstable solution (Ehrgott and Gandibleux 2002). In addition, if the number of levels increases the complexity of the problem increases. Thus, tri-level programming problem is more complex than a bi-level programming problem.
Using an inverse function transformation approach, Mishra and Ghosh (2006) proposed an interactive method to solve quadratic fractional bi-level problems. However, this method is computationally demanding as it involves additional steps at each iterations. Moreover, Lachhwani and Poonia (2012) proposed fuzzy goal programming approach for multi-level linear fractional programming problem by constructing a tolerance membership functions for the fuzzily described numerator and denominator part of the objective functions of all levels. To apply this method, decision makers need to change their tolerance value at each iterative step and this might cause a delay in arriving at a satisfactory solution, especially for large problems. Modifying this algorithm, Lachhwani and Nehra (2015) came up with an algorithm (and its MATLAB implementation) that can possibly solve linear fractional multi-level programming problems. In some other literature (such as Biswas and Bose 2011; Dalman 2016; Emam et al. 2015) a linearization technique, which is proposed in Ignizio (1976), is employed to transform the fractional membership functions to an approximate linear function one. Since this transformation contains only local behavior of the functions, there is a possibility that the algorithm may produce non-satisfactory solutions for the system.
In this paper, we especially focus on tri-level quadratic fractional programming problems with linear constraints. In such problems, we propose a new fuzzy approach to obtain a satisfactory (or near-optimal) solution by introducing a transformation that changes fractional quadratic fuzzy membership constraints into an equivalent non-fractional quadratic forms. The main advantage of the proposed approach is that the transformation will reduce the computational burden in the algorithm as compared to the previously proposed algorithms. Moreover, the current algorithm is shown to be convergent to a near-optimal solution of the problem. Therefore, one can continue executing the steps of the algorithm to find an approximate solution which is very close to the actual solution of the problem rather than stopping the procedure at a satisfactory solution.
The paper is organized as follows. In Sect. 2, fuzzy goal programming procedure is described. Section 3 presents solution concept of tri-level non-linear programming problem using fuzzy goal programming approach and the proposed algorithm is described. Illustrative examples are given in Sect. 4, while conclusive remarks are presented in Sect. 5.
The use of fuzzy goal programming
In multi-level programming procedure, even if the leader is assumed to take the first action, s/he has no direct influence on the decision of the others to get an optimal outcome as originally sought. This is because, in most of the cases, the objective functions of the decision makers at each level may conflict each other and the decision makers at all levels may not necessarily be cooperative to the leader. Therefore, to arrive at the optimal decision one has to check the response of others to choose her/his best decision vector. In this regard, one possible approach of taking the distribution of power in the hierarchies into account could be using fuzzy goal programming technique.
Goal programming is an optimization technique designed to handle decision making situations where a number of conditions characterized as goals are to be met as closely as possible. Mathematically, goal programming can be formulated as (Jones and Tamiz 2010)
subject to
where h represents the achievement function which measures lack of achievement, \(d_{q}^{+}\) is the positive deviational variable, \(d_{q}^{-}\) is the negative deviational variable and \(f_{q}(x)\) is the achieved value of the decision maker.
Definition 1
(Zimmermann 2001) Let f be a real-valued function whose domain is a set X and f is assumed to be bounded from below by \(\inf (f)\) and from above by \(\sup (f).\) The minimizing set is a fuzzy set M in X such that:
Definition 2
(Zimmermann 2001) Let f be a real-valued function and \(\tilde{C}(x)\) be a fuzzy constraint (solution space). If f(x) is bounded on \(\tilde{C},\) then the minimizing set over a fuzzy constraint \({\tilde{MC}}(f),\) is defined by its membership function
Fuzzy goal programming utilizes fuzzy set theory to deal with a level of imprecision in the goal programming model. This imprecision is normally related to the goal target values but could also be related to other aspects of the goal programme such as the priority structure. There are various possibilities for measuring the fuzziness around the target goals, each of which leads to a different fuzzy membership function. These functions model the drop in dissatisfaction from a state of total satisfaction (where the membership function takes the value 1) to a state of total dissatisfaction (where the membership function takes the value 0). There are many possible definitions of fuzzy membership functions; the algebraic structure of the most common linear fuzzy membership functions are outlined below (Jones and Tamiz 2010).
-
Algebraically positive deviations (right sided) penalized by the linear function:
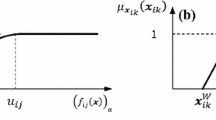
$$\mu [f_{q} (x)] = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if }}f_{q} (x) \le b_{q} } \hfill \\ {1 - \frac{{f_{q} (x) - b_{q} }}{{p_{{\max }} }},} \hfill & {{\text{if }}b_{q} \le f_{q} (x) \le b_{q} + p_{{\max }} } \hfill \\ {0,} \hfill & {{\text{if }}f_{q} (x) \ge b_{q} + p_{{\max }} } \hfill \\ \end{array} } \right.$$(4) -
Algebraically negative deviations (left sided) penalized by the linear function:
$$\mu [f_{q}(x)]= \left\{ \begin{array}{ll} 1, &{} \quad \text{if } f_{q}(x)\ge b_{q} \\ 1-\frac{b_{q}-f_{q}(x)}{p_{\max }}, &{} \quad \text{if } b_{q}-p_{\max }\le f_{q}(x)\le b_{q} \\ 0, &{} \quad \text{if } f_{q}(x)\le b_{q}-p_{\max } \end{array} \right.$$(5)where \(p_{\max }\) is the maximum difference between the target level \(b_{q}\) and the criterion in which the decision maker want to achieve.
Fuzzy goal programming approach to tri-level quadratic fractional programming problems
Consider a non-linear tri-level programming problem containing minimization type objective functions at each level. Suppose that DM\(_{i}\) denotes the decision maker at the ith-level \((i=1,2,3)\) and \(\text{DM}_{1},\) \(\text{DM}_{2}\) and \(\text{DM}_{3}\) control the decision vectors \(x\in X\subseteq {\mathbb{R}}^{n_{1}},\) \(y\in Y\subseteq {\mathbb{R}}^{n_{2}},\) and \(z\in Z\subseteq {\mathbb{R}}^{n_{3}},\) respectively, where \(n=n_{1}+n_{2}+n_{3},\) \(x = (x_{1},x_{2},x_{3}, \ldots , x_{n_{1}}), y = (y_{1},y_{2},y_{3}, \ldots , y_{n_{2}}), z = (z_{1},z_{2},z_{3},\ldots , z_{n_{3}})\) and \((x,y,z)\in {\mathbb{R}}^{n}.\) Let \(F_{1}, F_{2}\) and \(F_{3}\) be the non-linear objective functions of the first, second and third decision makers, respectively, controlling vector of decision variables x, y and z.
Mathematically, the quadratic fractional tri-level programming problem of minimization type can be formulated as, find \(X = (x, y, z)\) so as to solve
where
-
\(S=\{X = (x,y,z)\in {\mathbb{R}}^{n} | A_{1}x+A_{2}y+A_{3}z \{\le ,\ge ,=\}\, b,\ x, y, z \ge 0\}\) is the constraint set, and is assumed to be a non-empty, compact subset of \({\mathbb{R}}^n.\)
-
\(F_{i}(\bar{X})= \frac{f_{i1}(\bar{X})}{f_{i2}(\bar{X})} = \frac{\alpha _{i1}+C_{i1}\bar{X} + \frac{1}{2}\bar{X}^{T}D_{i1}\bar{X}}{\alpha _{i2}+C_{i2}\bar{X} + \frac{1}{2}\bar{X}^{T}D_{i2}\bar{X}},\) for all \(i=1,2,3.\)
-
\(f_{i2}(\bar{X}) = \alpha _{i2} + C_{i2}\bar{X} + \frac{1}{2}\bar{X}^{T}D_{i2}\bar{X} \, (i=1,2,3)\) is positive for all \(\bar{X} = (x,y,z) \in S,\)
-
\(C_{ij}\) and b \((i=1,2,3;j=1,2)\) are constant vectors,
-
\(D_{ij} (i=1,2,3;j=1,2)\) are constant symmetric matrices.
Now we need to solve problem (6) using fuzzy goal programming approach and find a satisfactory solution for all the decision makers in the hierarchy. In real life, different decision makers may or may not have conflicting objectives, and therefore they may or may not cooperate each other. Thus, we assume that if the objective functions of the decision makers (DMs) are conflicting to each other then they will be motivated to cooperate and if there is no conflict between each objective functions of the DMs then it is not necessary for them to cooperate.
Construction of membership functions
Assume that
and
Then \((x^{b_{1}},y^{b_{1}},z^{b_{1}}), (x^{b_{2}},y^{b_{2}},z^{b_{2}}),\) and \((x^{b_{3}},y^{b_{3}},z^{b_{3}})\) are absolutely acceptable optimal solutions to decision maker 1, 2 and 3, respectively; but the individual solution of one decision maker may not be satisfactory for the other decision makers. Therefore, the fuzzy goal concept can be expressed as: \(F_{i}(\bar{X})\preceq F_{i}^{b},\ i=1,2,3,\) where the relational symbol \(\preceq\) reads as “essentially less than or equal to”.
Now the corresponding membership function of the ith decision maker is algebraically formulated as
for \(i=1,2,3.\)
Formulation of the fuzzy goal programming approach for quadratic fractional tri-level programming problem
In the formulation of fuzzy goal programming problem, we use the concepts of membership functions at each level, and develop a new conventional programming problem for solving the tri-level non-linear programming problem.
The main goal for each of the decision makers in the hierarchy is to achieve a value which is not very far from their own ideal solution. That is equivalent to saying that they minimize the deviation \(d^-_i\) such that \(\mu _i[F_i(X)] + d^-_i =1\) for all \(i = 1,2,3,\) and for all \(X \in S.\)
Note that, since it is assumed that \(0 \le \mu _i[F_i(X)] \le 1\) for all \(X\in S\) and for all \(i = 1,2,3,\) we omitted the positive deviational parameter, i.e., \(d^+_i = 0\) for all \(i = 1,2,3.\)
The goal, that each decision maker to arrive at a solution near to its own aspiration value, is common for each of the decision makers in the hierarchy and can be checked by each one of them for its fulfillment at any order. Therefore, we can transform the tri-level programming problem in to a single objective and one-level optimization problem using a weighted sum technique. In this regard, considering the achievement of the goals at the same priority level, we consider the following single level fuzzy goal programming problem with only one objective:
where the weights \(w^1_i\) represent the relative importance of achieving the aspired levels of the respective fuzzy goals, in our case, we set \(w^1_{i}=F_{i}^{1}-F_{i}^{b}, i=1,2,3\) at the initial stage.
Problem (8) is a single objective problem with three more non-linear constraints corresponding to the satisfaction of the aspiration levels of the decision makers at each of the three levels. Because of the construction of the membership functions, the newly added constraints contain quadratic fractional functions. To make the solution procedure of the newly constructed conventional program (8) more efficient, we shall reformulate the following problem and show the equivalence between the two. For the construction of the new problem without a fractional formulation, we recall that \(F_i(X) = \frac{f_{i1}(X)}{f_{i2}(X)}, X \in S,\) where the numerator \(f_{i1}(X)\) and denominator \(f_{i2}(X)\) functions are quadratic with \(f_{i2}(X) > 0, \, \forall X \in S.\) Then we can formulate a single-level quadratic fuzzy goal programming problem,
Now we prove the equivalence between the conventional problems with fractional structure (8) and the quadratic programming problem with complementarity form (9) in the following theorem.
Theorem 1
\(\bar{X}=\bar{X}^{*}\) is an optimal solution for (8) if and only if it is an optimal solution for (9); and the values of achievement functions of both problems at the optimal points are equal.
Proof
Let \(\bar{X} =\bar{X}^{*}\) be an optimal solution of problem (8). Then from the constraint of the same problem it follows that
is satisfied for all \(i = 1,2,3\). When simplified, this equation becomes
But for quadratic fractional problems, since \(F_i(\bar{X}^{*}) = \frac{f_{i1}(\bar{X}^{*})}{f_{i2}(\bar{X}^{*})}\), we can set \(f_{i1}(\bar{X}^{*})t^{*}_i = \frac{f_{i1}(\bar{X}^{*})}{f_{i2}(\bar{X}^{*})}\), which yields \(t_{i}^{*}=\frac{1}{f_{i2}(\bar{X}^{*})}\) or \(t_{i}^{*}f_{i2}(\bar{X}^{*})=1\), \(i=1,2,3\).
Since the denominator functions are assumed to be always positive, i.e. \(f_{i2}(X) > 0, \, \forall X \in S\), the above argument also hold for the converse case as well.
Moreover, since the weight of problem (8) and (9) are the same and
the objective function of problem (8) is the same as the objective function of problem (9). \(\square\)
Therefore, solving the quadratic fuzzy goal programming problem with complementarity (9) is the same as solving the fractional type problem (8). Now, the single level problem we formulated in (8) may not be equivalent with the original tri-level programming problem. However, the optimal solution we obtained from problem (8) is a candidate solution of the original tri-level programming problem, given in equation (6). Through updating the weights for the deviational variables we may obtain new candidate solutions and we shall show that these candidate solutions are as good as or better than the previous ones. So, iteratively we will obtain a set of candidate solutions and from those candidate solutions we shall choose a satisfactory solution using the criteria developed.
To update the weights of the deviational variables, in the case when the current solution is not satisfactory, we apply the following procedure.
Assume that the solution obtained from problem (9) is \((x_{1},y_{1},z_{1})\). Then, if the first and second level DMs are satisfied with this solution, then we consider this solution as a satisfactory solution for all the DMs. Otherwise, we need to find a mechanism to update the current solution. To this end, suppose that the first level DM is not satisfied with the solution \((x_{1},y_{1},z_{1})\). Since \(F_{1}^{b}\le F_{1}(x_{1},y_{1},z_{1})\le F_{1}^{1}\) and \(F_{1}(x_{1},y_{1},z_{1})\) is not the best value, restrict the optimal value of the first level DM on the interval \([F_{1}^{b},F_{1}^{2}]\) where \(F_{1}^{2}=F_{1}(x_{1},y_{1},z_{1})\). Then define a new membership function on this interval. Similarly, the second level DM also updates its membership function, because its solution is dependent on the decision of the first level DM. Consequently, the following new problem is formulated in the second iteration:
where \(w^2_{i}=F_{i}^{2}-F_{i}^{b}, \, i=1,2\), \(w_{3}=F_{3}^{1}-F_{3}^{b}\), and
By solving this problem, we obtain a new solution, say \((x_{2},y_{2},z_{2})\) and then check whether the first level and second level DMs are satisfied with this solution. If not, continue to the next iteration by setting \(F_i^3 = F_i(x_2, y_2, y_3)\) for all \(i= 1,2,3\). Continuing the above procedure we may arrive at the kth iteration (\(k\ge 2\)), where the problem to be solved becomes
where \(w^k_{i}=F_{i}^{k}-F_{i}^{b}, \, i=1,2\), \(w_{3}=F_{3}^{1}-F_{3}^{b}\), and
with \(k=2,3,4,\ldots .\)
From the above formulation of the problem at the k-th iteration, we can observe that as the number of iterations increases, the weight \(w^k_{i}\) decreases proportionally. Consequently, the possible value of deviational variables that we take in each iteration controls the solution based on the corresponding weight.
Define the membership function for the interval \([F_i^b, F_i^k]\) by
for \(i=1,2,3\). Then, from the construction of the above iterative procedure, the following results can be formulated.
Theorem 2
If \([F_{i}^{b},F_{i}^{k+1}]\subseteq [F_{i}^{b},F_{i}^{k}],\) then \(\mu _{i}^{k+1}[F_{i}(X)]\le \mu _{i}^{k}[F_{i}(X)],\) for any \(X = (x,y,z)\in S\) and \(k=1,2,3,\ldots ,\) \(i=1,2,3.\)
Proof
Assume that \(\mu _{i}^{k}[F_{i}(x,y,z)] = \frac{F_{i}^{k} - F_{i}(x, y, z)}{F_{i}^{k} - F_{i}^{b}}\) and \([F_{i}^{b},F_{i}^{k+1}]\subset [F_{i}^{b},F_{i}^{k}]\) for each \(i= 1,2,3\) and \(k = 1,2,3,\ldots .\) Then, it follows that \(F_{i}^{k+1} \le F_{i}^{k}\) for each i and k.
Now, let \(w_{i}^{k+1}=F_{i}^{k+1}-F_{i}^{b}\) and \(w_{i}^{k}=F_{i}^{k}-F_{i}^{b}\). Then, we have that
This implies that \(\mu _{i}^{k}[F_{i}(X)]-\mu _{i}^{k+1}[F_{i}(X)]\ge 0\). Therefore, we can conclude that \(\mu _{i}^{k}[F_{i}(X)]\ge \mu _{i}^{k+1}[F_{i}(X)]\) for all \(X\in S\), \(i=1,2,3\), and \(k=1,2,3,\ldots .\) \(\square\)
Theorem 3
\(\mu _{i}^{k}[F_{i}(x_{k}, y_{k}, z_{k})] \le \mu _{i}^{k}[F_{i}(x_{k+1}, y_{k+1}, z_{k+1})]\) if and only if \(F_{i}(x_{k}, y_{k}, z_{k}) \ge F_{i}(x_{k+1}, y_{k+1}, z_{k+1}),\) for \(i = 1, 2,3\) and \(k = 1, 2, 3, \ldots .\)
[Hence, the deviational parameters \(d_i^-\) do not increase at consecutive iterations.]
Proof
From the definition of membership functions
where \(F_{i}^{k}=F_{i}(x_{k-1}, y_{k-1}, z_{k-1}), i = 1, 2, 3\). For \(k=1\) and \((x_{0}, y_{0}, z_{0}) = {{\mathrm{argmax}}}_{(x,y,z) \in S} F_{i}(x,y,z)\), the statement holds trivially.
Now, assume that \(\mu _{i}^{k}[F_{i}(x_{k},y_{k},z_{k})]\le \mu _{i}^{k}[F_{i}(x_{k+1},y_{k+1},z_{k+1})]\). Then,
After proper simplification, we obtain that \(F_{i}(x_{k},y_{k},z_{k})\ge F_{i}(x_{k+1},y_{k+1},z_{k+1})\), as \(F_i^k-F_i^b > 0\) for all i.
For the converse, suppose that \(F_{i}(x_{k},y_{k},z_{k})\ge F_{i}(x_{k+1},y_{k+1},z_{k+1})\). Then,
Since \(F_{i}^{k}> F_{i}^{b}\), for all \(k=1,2,3,\ldots ,i=1,2,3\), we have that (see Fig. 1).
Therefore, \(\mu _{i}^{k}[F_{i}(x_{k},y_{k},z_{k})]\le \mu _{i}^{k}[F_{i}(x_{k+1},y_{k+1},z_{k+1})]\). \(\square\)
From the construction of the above iterative procedure, since \(F_i^{k+1} \le F_i^k\) for \(i=1,2,3\) and for all k, the solution obtained in the \((k+1)\)th iteration is as good as or better than the solution obtained in the kth iteration.
The above iterative procedure should be stopped if \(F_i(x_k,y_k,z_k) = F_i^b\) for all \(i=1,2,3\), in which case the aspired ideal solution is achieved, or when the iteration produces no significant change in the value of the objective functions. To implement the second criteria, we assume that a tolerance value \(\epsilon > 0\) is given by the planners. Then, if \(\sum _{i=1}^3|F_{i}(x_{k+1}, y_{k+1}, z_{k+1}) - F_{i}(x_{k}, y_{k}, z_{k}) | \le \epsilon\), we shall say that the iteration does not produce a solution which has a significant change in the process. Therefore, this can be used as a stopping criteria.
The solution algorithm to solve quadratic fractional tri-level programming problems (6) is summarized as:

The proposed algorithm is designed to efficiently search a satisfactory solution for a quadratic fractional tri-level programming problem having a common constraint set S, which is assumed to be a closed and bounded (compact) set. However, the procedure can be extended to solve multi-level problems with any number of levels provided that the objectives at each stage are quadratic fractional functions. Moreover, if all the objectives are linear fractional functions, the procedure converts it to a linear optimization problem with complementarity at each iteration.
Illustrative examples
To demonstrate the feasibility of the proposed algorithm, we considered the following fractional tri-level programming problems and applied the transformation so that it can be used in the algorithm. In the implementation, we set the value of the tolerance to be \(\varepsilon =10^{-6}\) for all the examples.
Example 1
subject to
The minimum and maximum values of each of the three problems with respect to all the variables are found to be, \((F_1^b, F_2^b, F_3^b) =(4.8\times 10^{-7}, 0.1569, 0.0839)\) and \((F_1^1,F_2^1,F_3^1) = (2,1.2,1.2222)\), respectively. Using these values, the transformed fuzzy goal programming problem is found to be
Then using the above algorithm, we obtained after exactly two iterations, a satisfactory solution for the problem to be
with the corresponding near-optimal values
of first, second and third level decision makers, respectively.
Example 2
subject to
Solving this problem using the procedure described above, a satisfactory solution \((x^*,y^*,z^*)=(1.407947, 1.946424, 0.765045)\), with the corresponding near-optimal values \((f_{1}^*, f_{2}^*, f_{3}^*)=(0.250198, 0.067261, 0.745636)\), is obtained (again after only two iterations).
Example 3
The third example is a linear fractional tri-level problem taken from Lachhwani and Poonia (2012). Even though this problem is not quadratic, the purpose of including this example is to check the output of the current algorithm as compared to the previously obtained results.
subject to
After implementing the proposed algorithm on this problem, we obtained a satisfactory solution \(X^{*}=(x^*_{1},x^*_{2},y^*,z^*) =(2.3333, 0, 0, 0.3333)\) with the corresponding functional values of \((f_{1}, f_{2}, f_{3}) = (-5.0999, 0.3077, -0.9375)\). For this Example 3, iterative steps were required to arrive at the stopping criteria. In this case, the value of the membership functions at the solution point is calculated to check how close the solution is to the aspired goal. Therefore, for DM\(_{1}\) we have \(\mu _{1}(X^{*}) = 0.9999\), for DM\(_{2}\) \(\mu _{2}(X^{*}) = 0.460298\) and for DM\(_{2}\) \(\mu _{3}(X^{*}) = 0.9999\).
However, the result reported in Lachhwani and Poonia (2012) is \((f_{1},f_{2},f_{3})=(-3.42738,-1.642437, -0.751564)\) with satisfactory solution \(X^{*}=(1, 0, 0, 1)\). So, the solution using the current procedure made significant improvements in the values of the first and third decision makers (DM\(_{1}\) and DM\(_{3}\)) while the value of the second level decision maker (DM\(_{2}\)) has increased proportionally. Therefore, one has to weigh the significance of the criteria at each of the levels to consider the entire solution.
Example 4
The fourth example is a quadratic fractional tri-level problem with 11 variables.
subject to
After the problem is transformed and solved, we obtain the solution \((x^*,y^*,z^*) = (0, 0.6346, 0, 0, 0, 3.8316, 0, 0, 5.7761, 0, 1.3965)\)with the corresponding minimal functional values \((f_1^*, f_2^*, f_3^*) = (0.1521, 0.8346, 0.1963)\). Here as well, the algorithm arrived at the satisfactory solution after only two iterations. At this satisfactory solution, the deviational parameters are found to be \(d^- = (0.0144, 0.0152, 0.0079)\).
Conclusions
This study developed a transformation based algorithm to solve a tri-level quadratic fractional programming problems using fuzzy goal programming approach. First, a membership function was constructed to develop a fuzzy model for a general tri-level problem. Using the membership function and a weighted fuzzy goal programming approach, the original tri-level problem was reformulated into a conventional one-level optimization problem. Since the transformed one-level problem contains fractional functions, it was further transformed into an equivalent quadratic problem with complementarity form. This final optimization problem was solved using any available optimization algorithm to get a candidate solution for the original tri-level problem. Second, a method was developed to tighten the upper bounds which were used for the construction of the membership functions and to define weights for each deviational parameters. Applying this modification of the upper bounds at each iteration, a convergent iterative procedure was formulated. Finally, numerical examples are given to illustrate the performance of the proposed method. The computational results show that the current algorithm provides a practical way to solve tri-level quadratic fractional programming problems by arriving at a satisfactory solution after very few steps (not more than three steps in all the examples above). One of the most important features of the proposed approach is that the transformation will reduce the computational burden in the algorithm as compared to the previously proposed similar algorithms in the literature. In addition, the proposed algorithm is shown to be convergent to a nearly optimal solution of the problem. Moreover, this same algorithm can be used also to solve any m-level quadratic fractional programming problem, as the arguments do not depend on the number of levels of the hierarchy in the problem.
The procedures and computations involved in the proposed method are very simple and can be used to solve large-scale problems of the same structure within a reasonable time using available optimization resources for large-scale problems. Moreover, it can be seen from the construction of the algorithm that the method can also be used to solve linear fractional as well as quadratic tri-level problems.
References
Abo-Sinna MA (2001) A bilevel non-linear multi-objective decision making under fuzziness. J Oper Res Soc India 38(5):484–495
Abo-Sinna MA, Baky IA (2006) Interactive balance space approach for solving bilevel multi-objective programming problems. Adv Model Anal B 49(3–4):43–62
Azad AK, Sakawa M, Kato K, Katagiri H (2006) Interactive fuzzy programming for multi-level nonlinear integer programming problems through genetic algorithms. Asia Pac Manag Rev Int J 10(1):223–236
Bialas WF, Karwan MH (1982) On two-level optimization. IEEE Trans Autom Control 27(1):211–214
Bialas WF, Karwan MH (1984) Two level linear programming. Manag Sci 30(8):1004–1020
Biswas A, Bose K (2011) Fuzzy goal programming approach for quadratic fractional bilevel programming. In: Proceedings of the 2011 international conference on scientific computing (CSC 2011). CSREA Press, Las Vegas, pp 143–149
Candler W, Townsley R (1982) A linear two-level programming problem. Comput Oper Res 9(1):59–76
Dalman H (2016) An interactive fuzzy goal programming algorithm to solve decentralized bi-level multiobjective fractional programming problem. arXiv:https://arxiv.org/pdf/1606.00927.pdf
Ehrgott M, Gandibleux X (eds) (2002) Multiple criteria optimization: state of the art annotated bibliographic survey. International Series in Operations Research and Management Science, vol 52. Kluwer, Boston
Emam OE, Kholeif SA, Azzam SM (2015) A decomposition algorithm for solving stochastic multi-level large scale quadratic programming problems. Appl Math Inf Sci 9(4):1817–1822
Ignizio P (1976) Goal programming and extensions. Lexington DC, Lexington
Jones D, Tamiz M (2010) Practical goal programming. Springer, New York
Lachhwani K, Nehra S (2015) Modified FGP approach and MATLAB program for solving multi-level linear fractional programming problems. J Ind Eng Int 11:15–36. doi:10.1007/s40092-014-0084-4
Lachhwani K, Poonia MP (2012) Mathematical solution of multilevel fractional programming problem with fuzzy goal programming approach. J Ind Eng Int 8:16. http://www.jiei-tsb.com/content/8/1/16
Lai YJ (1996) Hierarchical optimization: a satisfactory solution. Fuzzy Sets Syst 77(3):321–335
Lee ES, Shih HS (2001) Fuzzy and multi-level decision making: an interactive computational approach. Springer, London
Mishra S, Ghosh A (2006) Interactive fuzzy programming approach to bilevel quadratic fractional programming problems. Ann Oper Res 143:251–263
Mohamed RH (1997) The relationship between goal programming and fuzzy programming problems. Fuzzy Sets Syst 89(2):215–222
Moitra BN, Pal BB (2002) A fuzzy goal programming approach for solving bilevel programming problems. In: Pal NR, Sugeno M (eds) Advances in soft computing-AFSS, vol 2275. Lecture notes in computer science. Springer, Berlin, pp 91–98
Osman MS, Abo-Sinna MA, Amer AH, Emam OE (2004) A multi-level non-linear multi-objective decision-making under fuzziness. Appl Math Comput 153(1):239–252
Pal BB, Moitra BN (2003) A fuzzy goal programming procedure for solving quadratic bilevel programming problems. Int J Intell Syst 18(5):529–540
Pal BB, Moitra BN, Maulik U (2003) A goal programming procedure for fuzzy multiobjective linear fractional programming problems. Fuzzy Sets Syst 139(2):395–405
Pramanik S, Roy TK (2007) Fuzzy goal programming approach to multi-level programming problem. Eur J Oper Res 176(2):1151–1166
Sakawa M, Katagiri H, Matsui T (2011) Stackelberg solutions to noncooperative two-level nonlinear programming problems through evolutionary multi-agent systems. In: Alkhateeb F (ed) Multi-agent systems—modeling, control, programming, simulations and applications. InTech, Faculty of Engineering, Hiroshima University, Japan. doi:10.5772/15628
Shih HS, Lee ES (2000) Compensatory fuzzy multiple decision making. Fuzzy Set Syst 114(1):71–87
Shih S, Lai J, Lee S (1983) Fuzzy approach for multi-level programming problems. Comput Oper Res 23(1):73–91
Woldemariam AT, Kassa SM (2015) Systematic evolutionary algorithm for general multilevel Stackelberg problems with bounded decision variables (SEAMSP). Ann Oper Res 229(1):771–790
Zimmermann H-J (2001) Fuzzy set theory – and its applications, 4th edn. Springer Science, New York
Acknowledgements
The authors thank the Swedish International Science Program (ISP), through the project at the Department of Mathematics, Addis Ababa University, for the partial support during the preparation of this research work.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kassa, S.M., Tsegay, T.H. An iterative method for tri-level quadratic fractional programming problems using fuzzy goal programming approach. J Ind Eng Int 14, 255–264 (2018). https://doi.org/10.1007/s40092-017-0224-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40092-017-0224-8