Introduction

Multi-level programming problem (MLPP) concerns with decentralized programming problems with multiple decision makers (DMs) in multi-level or hierarchical organizations, where decisions have interacted with each other. Multi-level organization or hierarchical organization has the following common characteristics: Interactive decision-making units exist within a predominantly hierarchical structure; the execution of decisions is sequential from higher level to lower level; each decision-making unit independently controls a set of decision variables and is interested in maximizing its own objective but is affected by the reaction of lower level DMs. So the decision deadlock arises frequently in the decision-making situations of multi-level organizations.

Numerous methods were suggested by researchers in literature (Anandilingam 1988, 1991; Lai 1996; Pramanik and Roy 2007; Shih et al. 1983; Shih and Lee 2000; Sinha 2003a, b) on MLPPs and also on multi-criteria decision-making problems (MCDM) and multi-objective programming problems with their applications like Zoraghi et al. (2013) presented a fuzzy multi-criteria decision making (MCDM) model by integrating both objective and subjective weights for evaluating service quality in hotel industries. Sadjadi et al. (2005) proposed a multi-objective linear fractional inventory model using fuzzy programming. Fattahi et al. (2006) proposed a Pareto approach to solve multi-objective job shop scheduling. Aryanezhad et al. (2011) considered the portfolio selection where fuzziness and randomness appear simultaneously in optimization process. Tohidi and Razavyan (2013) presented necessary and sufficient conditions to have unbounded feasible region and infinite optimal values for objective functions of multi-objective integer linear programming problems. Khalili-Damghani and Taghavifard (2011) proposed a multi-dimensional knapsack model for project capital budgeting problem in uncertain situation through fuzzy sets. Makul et al. (2008) presented the use of multiple objective linear programming approach for generating the common set of weights under the DEA framework. Each method appears to have some advantages as well as disadvantages. So, the issue of choosing a proper method in a given context is still a subject of active research. In context of such hierarchical problems, Fuzzy goal programming (FGP) approach seems to be more appropriate than other methodologies. The FGP introduced by Mohamed (1997) was extended to solve multi-objective linear fractional programming problems in Pal et al. (2003), bi-level programming problems in Moitra and Pal (2002), bi-level quadratic programming problems in Pal and Moitra (2003), and also extended to solve multi-level programming problems (MLPPs) with single objective function in each level in Pramanik and Roy (2007). In recent years, Aghdaghi and Jolai (2008) presented a goal programming approach and heuristic algorithm to solve vehicle routing problem with backhauls. Babeai et al. (2009) investigated the optimum portfolio for an investor using lexicographic goal programming approach. Ghosh and Roy (2013) formulated weighted goal programming as goal programming with logarithmic deviational variables. Lachhwani and Poonia (2012) proposed FGP approach for multi-level linear fractional programming problem. Lachhwani (2013) presented an alternate algorithm to solve multi-level multi-objective linear programming problems (ML-MOLPPs) which is simpler and requires less computational efforts than that of suggested by Baky (2010). Baky (2010) suggested two new techniques with FGP approach based on solution preferences by the decision maker at each level to solve new type of multi-level multi-objective linear programming (ML-MOLP) problems through the fuzzy goal programming (FGP) approach. Abo-Sinha and Baky (2007) presented interactive balance space approach for solving multi-level multi-objective programming problems. Baky (2009) proposed FGP algorithm for solving decentralized bi-level multi-objective programming (DBL-MOP) problems with a single decision maker at the upper level and multiple decision makers at the lower level. The main disadvantage of the FGP algorithms is that the possibility of rejecting the solution again and again by the upper level DMs and re-evaluation of the problem repeatedly, by redefining the tolerance values on decision variables, needed to reach the satisfactory decision frequently arises. To overcome such computational difficulties, we modified FGP approach for ML-LFPP in which solution preferences by decision maker at each level and sequential order of decision-making process in finding satisfactory solutions are not taken into account of proposed technique and we straightforwardly obtain compromise optimal solution of the problem with higher degree of membership function values. In this paper, we proposed modified FGP approach for multi-level linear fractional programming problem (ML-LFPP) in which solution preferences by decision maker at each level and sequential order of decision-making process in finding satisfactory solutions are not taken into account of proposed technique. Using modified technique, we straightforwardly obtain compromise optimal solution of the problem with higher degree of membership function values. This modified approach simplifies the solution procedure and reduces the computational efforts with it. Here, we also present coding of generalized MATLAB program based on proposed modified approach for solving ML-LFPPs which is the unique toward dealing with such complex mathematical problems with MATLAB. This software based program is useful and user can directly obtain compromise optimal solution of ML-LFPPs. The aim of this paper is to present modified FGP algorithm and generalized MATLAB program which is simple, efficient and requires less computational efforts for solving multi-level linear fractional programming problems (ML-LFPPs).

The paper is organized in following sections: MLPPs and related literature reviews are presented in introduction section. Formulation of ML-LFPP and related notations are discussed in next Sect. 2. Characterization of membership functions, solution approach based on FGP and formulation of FGP models are discussed in next section. Proposed MATLAB program and its functionality are discussed in Sect. 4. Numerical example on modified FGP technique and its comparison with solution technique suggested by Lachhwani and Poonia (2012) are discussed in numerical example Sect. 5. Concluding remarks are given in the last section. Coding of main function and recurresive simplex function are presented in appendices.

Formulation of ML-LFPPs

We consider a T-level maximization type multi-level linear fractional programming problem (ML-LFPP). Mathematically it can be defined as:

$$ \begin{gathered} \mathop {Max}\limits_{{\overline{{X_{1} }} }} Z_{1} (\overline{X} ) = \frac{{\overline{{C_{11} }} \;\overline{{X_{1} }} + \overline{{C_{12} }} \;\overline{{X_{2} }} + \cdots + \overline{{C_{1T} }} \;\overline{{X_{T} }} + \alpha_{1} }}{{\overline{{D_{11} }} \;\overline{{X_{1} }} + \overline{{D_{12} }} \;\overline{{X_{2} }} + \cdots + \overline{{D_{1T} }} \;\overline{{X_{T} }} + \beta_{1} }} = \frac{{N_{1} (\overline{X} )}}{{D_{1} (\overline{X} )}} \hfill \\ \mathop {Max}\limits_{{\overline{{X_{2} }} }} Z_{2} (\overline{X} ) = \frac{{\overline{{C_{21} }} \;\overline{{X_{1} }} + \overline{{C_{22} }} \;\overline{{X_{2} }} + \cdots + \overline{{C_{2T} }} \;\overline{{X_{T} }} + \alpha_{2} }}{{\overline{{D_{21} }} \;\overline{{X_{1} }} + \overline{{D_{22} }} \;\overline{{X_{2} }} + \cdots + \overline{{D_{2T} }} \;\overline{{X_{T} }} + \beta_{2} }} = \frac{{N_{2} (\overline{X} )}}{{D_{2} (\overline{X} )}} \hfill \\ \cdot \hfill \\ \cdot \hfill \\ \mathop {Max}\limits_{{\overline{{X_{T} }} }} Z_{T} (\overline{X} ) = \frac{{\overline{{C_{T1} }} \;\overline{{X_{1} }} + \overline{{C_{T2} }} \;\overline{{X_{2} }} + \cdots + \overline{{C_{TT} }} \;\overline{{X_{T} }} + \alpha_{T} }}{{\overline{{D_{T1} }} \;\overline{{X_{1} }} + \overline{{D_{T2} }} \;\overline{{X_{2} }} + \cdots + \overline{{D_{TT} }} \;\overline{{X_{T} }} + \beta_{T} }} = \frac{{N_{T} (\overline{X} )}}{{D_{T} (\overline{X} )}} \hfill \\ {\text{Subject to}},\;\;\;\;\;\overline{{A_{i1} }} \;\overline{{X_{1} }} + \overline{{A_{i2} }} \;\overline{{X_{2} }} + \cdots + \overline{{A_{iT} }} \;\overline{{X_{T} {\kern 1pt} }} ( \le , = , \ge ){\kern 1pt} {\kern 1pt} b_{i} \, \forall i = 1,2, \ldots ,m \hfill \\ {\text{and}}\;\;\;\;\;\;\;\;\;\;\;\;\;\overline{{X_{1} }} \ge 0,\,\overline{{X_{2} }} \ge 0,\, \ldots ,\overline{{X_{T} }} \ge 0. \hfill \\ \end{gathered} $$
(1)
$$ \begin{gathered} \overline{{X_{1} }} = \left\{ {X_{1}^{1} ,X_{1}^{2} , \ldots ,X_{1}^{{N_{1} }} } \right\}'\;{\text{decision variables under the control of first level DM}}. \hfill \\ \cdot \hfill \\ \cdot \hfill \\ \overline{{X_{T} }} = \left\{ {X_{T}^{1} ,X_{T}^{2} , \ldots ,X_{T}^{{N_{T} }} } \right\}'\;{\text{decision variable under the control of }}t{\text{ - level DM}} .\hfill \\ \end{gathered} $$

where \( ' \)denotes transposition, \( \overline{{A_{ij} }} \;i = 1,2, \ldots ,m, \, j = 1,2, \ldots ,T \) are m row vectors, each of dimension\( (1 \times N_{j} ) \). \( \overline{{{\text{A}}_{it} }} \;\overline{{X_{t} }} ,\;t = 1,2, \ldots ,T \) is a column vector of dimension \( (M \times 1) \).\( \overline{{C_{11} }} ,\overline{{C_{21} }} , \ldots ,\overline{{C_{T1} }} \) all are row vectors of dimension of \( (1 \times N_{1} ) \). Similarly \( \overline{{C_{1T} }} ,\overline{{C_{2T} }} , \ldots ,\overline{{C_{TT} }} \) and \( \overline{{D_{1T} }} ,\overline{{D_{2T} }} , \ldots ,\overline{{D_{TT} }} \) are row vectors of dimension of \( (1 \times N_{T} ) \). We take \( \overline{X} = \overline{{X_{1} }} \cup \overline{{X_{2} }} \cup \cdots . \cup \overline{{X_{T} }} \) and \( N = N_{1} + N_{2} + \cdots + N_{T} \). Here one DM is located on each level. Decision vector \( \overline{{X_{t} }} ,\;t = 1,2, \ldots ,T \) is control of tth level DM having \( N_{t} \) number of decision variables. Here, it is assumed that the denominator of objective functions is positive at each level for all the values of decision variables in the constraint region.

Modified FGP methodology for ML-LFPP

The proposed modified FGP procedure is based on finding the compromise optimal solution as described by Lachhwani (2013) for multi-level multi-objective linear programming (ML-MOLP) problems. Here, we need to express the definitions related to efficient solution and compromise optimal solution in context of MLPP as:

Definition 1

\( X^{*} \in S \) is an efficient solution to MLPP if and only if there exists no other \( X \in S \) such that \( Z_{t} \ge Z_{t}^{*} \) \( \forall t = 1,2, \ldots ,T \).

Definition 2

For a problem (1), a compromise optimal solution is an efficient solution selected by the decision maker (DM) as being the best solution where the selection is based on the DM’s explicit or implicit criteria.

Zeleny (1982) as well as most authors describes the act of finding a compromise optimal solution to problem as “……an effort or emulate the ideal solution as closely as possible”.

Our FGP model for determining compromise optimal (efficient) solution is based on the finding of the totality or subset of efficient solutions with the DM, then choosing one best solution on some explicit or implicit algorithm.

FGP formulation for ML-LFPP

To formulate the modified FGP models of ML-LFPP, the objective numerator \( f_{tN} (\overline{X} ) + \alpha_{t} ,\;\forall t = 1,2, \ldots ,T \), objective denominator \( f_{tD} (\overline{X} ) + \alpha_{t} ,\; \) \( \forall t = 1,2, \ldots ,T \) at each level and the decision vector \( \overline{{X_{t} }} , \) \( (t = 1,2,..,T - 1) \) would be transformed into fuzzy goals by assigning an aspiration level to each of them. Then, they are to be characterized by the associated membership functions by defining tolerance limits for the achievement of the aspired levels of the corresponding fuzzy goals. Here, decision vector \( \overline{{X_{t} }} \) of up to (T–1) levels is transformed into fuzzy goals in order to avoid decision deadlock situations.

Characterization of membership functions

To build membership functions, fuzzy goals and their aspiration levels should be determined first. Using the individual best solution without considering inference of decision variables on lower levels, we find the maximum and minimum values of all the numerator and denominator objective functions at each level solution and construct payoff matrices as:

$$ \left[ {\begin{array}{*{20}c} {\overline{{X_{t}^{{}} }} } & {\overline{{N_{t} }} } \\ {\overline{{X_{1}^{{}} }} } & {\overline{{N_{1} }} (\overline{{X_{1}^{{}} }} )} \\ {\overline{{X_{2}^{{}} }} } & {\overline{{N_{2} }} (\overline{{X_{2}^{{}} }} )} \\ . & . \\ . & . \\ {\overline{{X_{T}^{{}} }} } & {\overline{{N_{T} }} (\overline{{X_{T}^{{}} }} )} \\ \end{array} } \right] $$
(2)
$$ \left[ {\begin{array}{*{20}c} {\underline{{X_{t}^{{}} }} } & {\underline{{N_{t} }} } \\ {\underline{{X_{1}^{{}} }} } & {\underline{{N_{1} }} (\underline{{X_{1}^{{}} }} )} \\ {\underline{{X_{2}^{{}} }} } & {\underline{{N_{2} }} (\underline{{X_{2}^{{}} }} )} \\ . & . \\ . & . \\ {\underline{{X_{T}^{{}} }} } & {\underline{{N_{T} }} (\underline{{X_{T}^{{}} }} )} \\ \end{array} } \right] $$
(3)
$$ \left[ {\begin{array}{*{20}c} {\overline{{X_{t}^{{}} }} } & {\overline{{D_{t} }} } \\ {\overline{{X_{1}^{{}} }} } & {\overline{{D_{1} }} (\overline{{X_{1}^{{}} }} )} \\ {\overline{{X_{2}^{{}} }} } & {\overline{{D_{2} }} (\overline{{X_{2}^{{}} }} )} \\ . & . \\ . & . \\ {\overline{{X_{T}^{{}} }} } & {\overline{{D_{T} }} (\overline{{X_{T}^{{}} }} )} \\ \end{array} } \right] $$
(4)

and

$$ \left[ {\begin{array}{*{20}c} {\underline{{X_{t}^{{}} }} } & {\underline{{D_{t} }} } \\ {\underline{{X_{1}^{{}} }} } & {\underline{{D_{1} }} (\underline{{X_{1}^{{}} }} )} \\ {\underline{{X_{2}^{{}} }} } & {\underline{{D_{2} }} (\underline{{X_{2}^{{}} }} )} \\ . & . \\ . & . \\ {\underline{{X_{T}^{{}} }} } & {\underline{{D_{T} }} (\underline{{X_{T}^{{}} }} )} \\ \end{array} } \right] $$
(5)

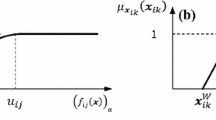
The maximum values of each row \( N_{t} (\overline{{X_{t}^{{}} }} ) \) and \( D_{t} (\overline{{X_{t}^{{}} }} ) \) \( \forall t = 1,2, \ldots ,T \) give upper and lower tolerance limit or aspired level of achievement for the membership function of tth level numerator and denominator objective function respectively. Similarly, the minimum values of each row \( N_{t} (\underline{{X_{t} }} ) \) and \( D_{t} (\underline{{X_{t} }} ) \) \( \forall t = 1,2, \ldots ,T \) give lower and upper tolerance limit or lowest acceptable level of achievement for the membership function of tth level numerator and denominator objective function respectively. Hence, linear membership functions for the defined fuzzy goals (as shown in Fig. 1a, b respectively) are:

Fig. 1
figure 1

a Membership functions of maximization type numerator objective functions. b Membership functions of maximization type denominator objective functions

Full size image
$$ \mu_{{Z_{t} }} (N_{t} (\overline{X} )) = \left\{ {\begin{array}{*{20}c} {1\quad{\text{ if }}N_{t} (\overline{X} ) \ge \overline{{N_{t} }} } \\ {\frac{{N_{t} (\overline{X} ) - \underline{{N_{t} }} }}{{\overline{{N_{t} }} - \underline{{N_{t} }} }}{\quad\text{ if }}\underline{{N_{t} }} \le N_{t} (\overline{X} ) \le \overline{{N_{t} }} } \\ {0{\quad\text{ if }}N_{t} (\overline{X} ) \le \underline{{N_{t} }} } \\ \end{array} } \right.\;\;\;\forall \, t = 1,2, \ldots ,T $$
(6)
$$ \mu_{{Z_{t} }} (D_{t} (\overline{X} )) = \left\{ {\begin{array}{*{20}c} {0{\quad\text{ if }}D_{t} (\overline{X} ) \ge \overline{{D_{t} }} } \\ {\frac{{\overline{{D_{t} }} - D_{t} (\overline{X} )}}{{\overline{{D_{t} }} - \underline{{D_{t} }} }}{\quad\text{ if }}\underline{{D_{t} }} \le D_{t} (\overline{X} ) \le \overline{{D_{t} }} } \\ {1{\quad\text{ if }}D_{t} (\overline{X} ) \le \underline{{D_{t} }} } \\ \end{array} } \right.\;\;\;\forall \, t = 1,2, \ldots ,T $$
(7)

Now, the linear membership functions for the decision vector \( X_{T} \)(\( t = 1,2, \ldots ,T - 1) \) (as shown in Fig. 2) are formulated in modified form as:

Fig. 2
figure 2

Membership function for \( \mu_{{X_{t} }} (X_{t} ) \) \( \forall t = 1,2, \ldots ,T - 1 \)

Full size image
Fig. 3
figure 3

Comparison of membership function values

Full size image
$$ \mu_{{X_{t} }} (X_{t} ) = \left\{ {\begin{array}{*{20}c} {1\quad {\text{ for}}\;X_{t} \ge \overline{{X_{t} }} } \\ {\frac{{X_{t} - \underline{{X_{t} }} }}{{\overline{{X_{t} }} - \underline{{X_{t} }} }}\quad {\text{ for}}\;\underline{{X_{t} }} \le X_{t} \le \overline{{X_{t} }} } \\ {0\quad {\text{ for}}\;X_{t} \le \underline{{X_{t} }} } \\ \end{array} } \right. $$
(8)

where \( \overline{{X_{t} }} \) and \( \underline{{X_{t} }} \) are taken as the values of the corresponding decision vectors at each level which yield the highest and lowest values of the numerator part of objective functions ((\( \overline{{N_{t} }} (\overline{X} ) \) and \( \underline{{N_{t} }} (\underline{X} ) \) \( \forall t = 1,2, \ldots ,T - 1) \) at each level respectively defined as:

$$ \overline{{N_{t} }} = \mathop {\text{Max}}\limits_{{\overline{{X_{t} }} \in X}} \left\{ {\overline{{N_{t} }} (\overline{{X_{t} }} ),\;\forall t = 1,2, \ldots ,T} \right\} $$
(9)
$$ \underline{{N_{t} }} = \mathop {\text{Min}}\limits_{{\underline{{X_{t} }} \in X}} \left\{ {\underline{{N_{t} }} (\underline{{X_{t} }} ),\;\forall t = 1,2, \ldots ,T} \right\} $$
(10)

Here, it is important to note that for simplicity of proposed technique and in order to avoid decision deadlock situation in the whole solution methodology, the solution preferences by the decision maker in terms of values of decision vector at each level with respect to the values of decision vector at lower levels are not considered. This results that large amount of computational tasks is reduced into limited simple calculation in modified FGP model formulation. Also, linear membership functions are considered because these are more suitable than nonlinear ones in context of complex ML-LFPPs and it further reduces computational difficulties in modified method.

FGP solution approach

In GP approach, decision policy for minimizing the regrets of the DMs for all the levels is taken into consideration. Then each DM should try to maximize his or her membership function by making them as close as possible to unity by minimizing its negative deviational variables. Therefore, in effect, we are simultaneously optimizing all the objective functions. So, for the defined membership functions in (6), (7) and (8), the flexible membership goals having the aspired level unity can be represented as:

$$ \mu_{t} (N_{t} ) + d_{t}^{N - } - d_{t}^{N + } = 1\quad \forall t = 1,2, \ldots ,T $$
(11)
$$ \mu_{t} (D_{t} ) + d_{t}^{D - } - d_{t}^{D + } = 1\quad \forall t = 1,2, \ldots ,T $$
(12)
$$ \mu_{{X_{t} }} (X_{t} ) + d_{t}^{ - } - d_{t}^{ + } = \overline{I} \quad \forall t = 1,2, \ldots ,T - 1 $$
(13)

where \( d_{t}^{N - } ,d_{t}^{D - } ,d_{t}^{N + } d_{t}^{D + } ( \ge 0) \) (\( \forall t = 1,2, \ldots ,T \)) and \( d_{t}^{ - } ,d_{t}^{ + } ( \ge 0)\;\forall t = 1,2, \ldots ,T - 1 \) represent the under and over deviational variables respectively from the aspired levels. \( \overline{I} \) is the column vector having all components equal to 1 and its dimension depends on \( X_{t} \). Thus ML-LFP problem (1) changes into:

$$ \hbox{min}\; \lambda = \sum\limits_{t = 1}^{T} {(d_{t}^{N - } + } d_{t}^{D - } ) + \sum\limits_{t = 1}^{T - 1} {d_{t}^{ - } } $$
(14)
$$ \begin{gathered} {\text{Subject to}},\;\;\;\;\;\;\;\;\mu_{t} (N_{t} ) + d_{t}^{N - } - d_{t}^{N + } = 1\quad \forall t = 1,2, \ldots ,T \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mu_{t} (D_{t} ) + d_{t}^{D - } - d_{t}^{D + } = 1\quad \forall t = 1,2, \ldots ,T \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mu_{{X_{t} }} (X_{t} ) + d_{t}^{ - } - d_{t}^{ + } = \overline{I} \;\quad \forall t = 1,2, \ldots ,T - 1\; \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\overline{{A_{i1} }} \;\overline{{X_{1} }} + \overline{{A_{i2} }} \;\overline{{X_{2} }} + \cdots + \overline{{A_{iT} }} \;\overline{{X_{T} {\kern 1pt} }} ( \le , = , \ge ){\kern 1pt} {\kern 1pt} b_{i} \quad \forall i = 1,2, \ldots ,m \hfill \\ {\text{and}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\overline{{X_{1} }} \ge 0,\,\overline{{X_{2} }} \ge 0,\, \ldots ,\overline{{X_{T} }} \ge 0. \hfill \\ \end{gathered} $$

In this FGP approach, only the sum of under deviational variables is required to be minimized to achieve the aspired level. It may be noted that when a membership goal is fully achieved, negative deviational variable becomes zero and when its achievement is zero, negative deviational variable becomes unity in the solution. Now if the most widely used and simplest version of GP (i.e. minsum GP) is introduced to formulate the model of the problem under consideration, the FGP model formulation becomes:

FGP model I

$$ \hbox{min}\, \lambda = \sum\limits_{t = 1}^{T} {(d_{t}^{N - } + } d_{t}^{D - } ) + \sum\limits_{t = 1}^{T - 1} {d_{t}^{ - } } $$
$$ \begin{gathered} {\text{Subject to}},\;\;\; - \overline{{N_{t} }} + N_{t} + d_{t}^{N - } (\overline{{N_{t} }} - \underline{{N_{t} }} ) \ge 0\;\quad \forall t = 1,2, \ldots ,T \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\underline{{D_{t} }} - D_{t} + d_{t}^{D - } (\overline{{D_{t} }} - \underline{{D_{t} }} ) \ge 0\;\quad \forall t = 1,2, \ldots ,T \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \overline{{X_{t} }} + X_{t} + d_{t}^{ - } (\overline{{X_{t} }} - \underline{{X_{t} }} ) \ge 0\quad \forall T = 1,2, \ldots ,T - 1 \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\overline{{{\text{A}}_{i1} }} \;\overline{{X_{1} }} + \overline{{{\text{A}}_{i2} }} \;\overline{{X_{2} }} + \cdots + \overline{{{\text{A}}_{iT} }} \;\overline{{X_{T} {\kern 1pt} }} ( \le , = , \ge ){\kern 1pt} {\kern 1pt} b_{i} \quad \forall i = 1,2, \ldots ,m \hfill \\ {\text{and}}\;\;\;\;\;\;\;\;\;\;\overline{{X_{1} }} \ge 0,\,\overline{{X_{2} }} \ge 0,\, \ldots ,\overline{{X_{T} }} \ge 0. \hfill \\ \end{gathered} $$

FGP model II

$$ \hbox{min}\, \lambda = \sum\limits_{t = 1}^T {({{\dot w}_t}d_t^{N -} +{{\ddot w}_t}} d_t^{D -}) + \sum\limits_{t = 1}^{T - 1} {d_t^-} $$
$$ \begin{gathered} {\text{Subject to}},\;\;\;\;\;\;\;\;\; - \overline{{N_{t} }} + N_{t} + d_{t}^{N - } (\overline{{N_{t} }} - \underline{{N_{t} }} ) \ge 0\;\quad \forall t = 1,2, \ldots ,T \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\underline{{D_{t} }} - D_{t} + d_{t}^{D - } (\overline{{D_{t} }} - \underline{{D_{t} }} ) \ge 0\;\quad \forall t = 1,2, \ldots ,T \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \overline{{X_{t} }} + X_{t} + d_{t}^{ - } (\overline{{X_{t} }} - \underline{{X_{t} }} ) \ge 0\;\quad \forall T = 1,2, \ldots ,T - 1 \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\overline{{{\text{A}}_{i1} }} \;\overline{{X_{1} }} + \overline{{{\text{A}}_{i2} }} \;\overline{{X_{2} }} + \cdots + \overline{{{\text{A}}_{iT} }} \;\overline{{X_{T} {\kern 1pt} }} ( \le , = , \ge ){\kern 1pt} {\kern 1pt} b_{i} \quad \forall i = 1,2, \ldots ,m \hfill \\ {\text{and}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\overline{{X_{1} }} \ge 0,\,\overline{{X_{2} }} \ge 0,\, \ldots ,\overline{{X_{T} }} \ge 0. \hfill \\ \end{gathered} $$

where \( \lambda \) (in FGP model II) represents the fuzzy achievement function consisting of the weighted under deviational variables and the numerical weights \( {\dot w_t},{\ddot w_t} > 0,\;(\forall t = 1, \ldots,T) \) represent the relative importance of achieving the aspired level of the respective fuzzy goals subject to the constraints in the decision-making situation. To assess the relative importance of the fuzzy goals properly, the weighted scheme suggested by Mohamed (1997) can be used to assign the values to \( {\dot w_t},{\ddot w_t} > 0,\;(\forall t = 1, \ldots,T) \). In the present formulation \( {\dot w_t},{\ddot w_t} > 0 \) can be determined as:

$$ \dot{w}_{t}^{{}} = \frac{1}{{\overline{{N_{t} }} - \underline{{N_{t} }} }}\;\;\forall t = 1, \ldots ,T $$
(15)
$$ {\ddot w_t} = \frac{1}{{\overline {D_t} - \underline {D_t}}}\;\;\forall t = 1, \ldots,T $$
(16)

MATLAB Program for ML-LFPPs based on modified FGP approach

Here, we discuss the coding and functionality of generalized MATLAB program for finding the compromise optimal solution of any ML-LFPPs based on proposed modified FGP approach. Using this program, the user needs to input data related to the problem and then user can directly obtain compromise optimal solution of ML-LFPP in single iteration with this program. To run this program, the two files are imported (used for main function and simplex function respectively and as shown in appendices) in the current MATLAB folder as:

  1. 1

    opt_pro.m

  2. 2

    simplex_function1.m

Then go to the MATLAB command prompt and type opt_pro to execute the program. The main coding of this program is partitioned into following two parts as:

  1. (a)

    Main function (MATLAB coding of main function is shown in appendices)

  2. (b)

    Simplex function (MATLAB coding of simplex function is shown in appendices)

The functionality of MATLAB program to obtain optimized values of decision variables and corresponding objective functions can be described in following stepwise algorithm as:

  • Step 1: In first step, main function takes input values from the user and converts them into suitable matrices. Then these matrices are passed to the simplex function as its input arguments in single matrix containing constraints as well as objective functions.

  • Step 2: For each level, the simplex function is called two times to compute minimized and maximized values of numerator and denominator objective functions.

  • Step 3: In this step, firstly the simplex function separates the constraints matrix and objective function matrix and then it computes the optimized solution based on the simplex method after some iteration. Then it provides these optimized solutions to the main function as its output argument in a single matrix containing values of decision variables and values of corresponding objective functions.

  • Step 4: So, in this way, repeating the step 2 and step 3, we get the maximum and minimum values for each objective function.

  • Step 5: Using these optimized values, the main function takes the decision variables up to (T-1) levels.

  • Step 6: Using these values of decision variables and values of numerator and denominator objectives, it constructs the type I, type II and type III constraints as defined in (6), (7) and (8).

  • Step 7: It recognizes all these constraints along with the initial constraints to construct a single constraint matrix.

  • Step 8: Then it constructs an objective function to minimize the sum of all the D variables (negative deviational variables) which are formulated during type I, II and III constraints.

  • Step 9: Now it again passes a matrix containing both the constraints as well as objective functions to the simplex function as its input argument.

  • Step 10: Now the simplex function decodes the input matrix to find the constraint matrix and objective function.

  • Step 11: Using the above constraints matrix and objective function, it computes the optimal solution using the usual simplex method. This optimized solution is then passed to the main function as its output argument.

  • Step 12: Now the main function, using these optimized values of main decision variables, computes the corresponding values of objective functions and displays them as output values.

Numerical Example

In this section, we illustrate the same numerical example considered in Lachhwani and Poonia (2012) in order to show efficiency of modified method over earlier technique as well as to demonstrate proposed MATLAB program on numerical example.

Illustration 1

$$ \begin{gathered} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathop {\text{Max}}\limits_{{x_{1} ,x_{2} }} Z_{1} = \frac{{7x_{1} + 3x_{2} - 4x_{3} + 2x_{4} }}{{x_{1} + x_{2} + x_{3} + 1}} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathop {\text{Max}}\limits_{{x_{3} }} Z_{2} = \frac{{x_{2} + 3x_{3} + 4x_{4} }}{{x_{1} + x_{2} + x_{3} + 2}} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathop {\text{Max}}\limits_{{x_{4} }} Z_{3} = \frac{{2x_{1} + x_{2} + x_{3} + x_{4} }}{{x_{1} + x_{2} + x_{3} + 3}} \hfill \\ {\text{Subject to}},\;\;\;\;\;\;x_{1} + x_{2} + x_{3} + x_{4} \le 5 \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x_{1} + x_{2} - x_{3} - x_{4} \le 2 \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x_{1} + x_{2} + x_{3} \ge 1 \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x_{1} - x_{2} + x_{3} + 2x_{4} \le 4 \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x_{1} + 2x_{3} + 2x_{4} \le 3 \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x_{4} \le 2 \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x_{1} ,\,x_{2} ,\;x_{3} ,\;x_{4} \ge 0 \hfill \\ \end{gathered} $$

Following the procedure, FGP model I and II can be described as:

FGP model I

$$ {\text{Minimize}}\;\;\lambda = (d_{1}^{N - } + d_{2}^{N - } + d_{3}^{N - } + d_{1}^{D - } + d_{2}^{D - } + d_{3}^{D - } ) + d_{1}^{ - } $$
$$ \begin{gathered} {\text{Subject to}},\;\;\;\;\;7x_{1} + 3x_{2} - 4x_{3} + 2x_{4} + 23d_{1}^{N - } \ge 17 \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x_{2} + 3x_{3} + 4x_{4} + 9.5d_{2}^{N - } \ge 9.5 \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2x_{1} + x_{2} + x_{3} + x_{4} + 4d_{3}^{N - } \ge 5 \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x_{1} + x_{2} + x_{3} - 4d_{1}^{D - } \ge 1 \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x_{1} + x_{2} + x_{3} - 4d_{2}^{D - } \ge 1 \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x_{1} + x_{2} + x_{3} - 4d_{3}^{D - } \ge 1 \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x_{1} + 2.3333d_{1}^{ - } \ge 2.3333 \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x_{1} ,\,x_{2} ,\;x_{3} ,\;x_{4} ,\,d_{1}^{N - } ,\,d_{2}^{N - } ,\,d_{3}^{N - } ,\,d_{1}^{D - } ,\,d_{2}^{D - } ,\,d_{3}^{D - } ,\,d_{1}^{ - } \ge 0 \hfill \\ \end{gathered} $$

Solving this programming problem, the compromise optimal solution obtained is: \( \lambda = 1.8596, \) \( x_{1} = 2.3333, \) \( x_{2} = 0, \) \( x_{3} = 0, \) \( x_{4} = 2.3750 \) with the values of objective functions as: \( Z_{1} = 5.0999 \), \( Z_{2} = 0.3076, \) \( Z_{3} = 0.9374 \). Also the achieved values of membership functions are \( \mu_{1} (N_{1} ) = 0.9999, \) \( \mu_{2} (N_{2} ) = 0.1403, \) \( \mu_{3} (N_{3} ) = 0.9999, \) \( \mu_{1} (D_{1} ) = 0.9999, \) \( \mu_{2} (D_{2} ) = 0.9999 \) and \( \mu_{3} (D_{3} ) = 0.9999 \). The same compromise optimal solution of this problem is obtained using FGP model II with the corresponding weights as defined in (15) and (16).

Note that the satisfactory solutions of the same problem using FGP technique proposed by Lachhwani and Poonia (2012) are: \( (x_{1} ,\,x_{2} ,\,x_{3} ,\,x_{4} ) = (0.4471,1.169105,0,1.2764) \) with \( (Z_{1} ,\,Z_{2} ,\,Z_{3} ) = (3.42738,1.642437,0.7515643) \) (For proposed method I) and \( (x_{1} ,\,x_{2} ,\,x_{3} ,\,x_{4} ) = (1,0,0,1) \) with \( (Z_{1} ,\,Z_{2} ,\,Z_{3} ) = (4.5,1.3333,0.75) \) (For proposed method II b). These satisfactory solutions of ML-LFPP are dependent on the tolerance values \( (p_{1}^{ - } ,p_{1}^{ + } ) \),\( (p_{1}^{ - } ,p_{1}^{ + } ) \) on the decision variables and type of FGP model used.

Table (Table 1) and graphs (Figs. 3, 4) show that the modified FGP technique yields better values of most of the membership functions and individual objective functions in comparison of FGP technique (method I and IIb) suggested by Lachhwani and Poonia (2012). It is clear that both the approaches are close to one another but the modified methodology is efficient and requires less computations than earlier technique in terms of considering the solution preferences by the decision maker at each level.

Table 1 Comparison of values between modified FGP approach and FGP technique by Lachhwani and Poonia (2012) for numerical example 1
Full size table
Fig. 4
figure 4

Comparison of objective function values

Full size image
Fig. 5
figure 5

Compromise optimal solution of ML-LFPP using proposed MATLAB program (trial version)

Full size image

Again, If we compare main advantages of proposed modified FGP methodology on different parameters as shown in table (Table 2) considering theoretical aspects of techniques and numerical example, it shows that the proposed modified technique has advantages of simplicity, efficiency, construction of MATLAB program, without decision deadlock situations, less computational efforts etc. than the technique suggested by Lachhwani and Poonia (2012) on each of these parameters.

Table 2 Comparison between modified FGP approach and FGP technique by Lachhwani and Poonia (2012) on general parameters
Full size table

Now, if we use the proposed MATLAB program on this numerical example and input the total no. of variables, total no. of constraints, numerator/denominator objective matrices, decision variables in matrix format for each stage etc. (as shown in Fig. 5). Then we get the compromise optimal solution \( (\lambda ,\,x_{1} ,\,x_{2} ,\,x_{3} ,\,x_{4} ) = (1.8596,\,2.3333,\,0,\,0,\,0.3333) \) which is the same as illustrated above with our proposed methodology. This validates our proposed MATLAB program.

Conclusions

This paper presents an improved FGP technique (in terms of achieving higher values of membership functions, simplicity, computational efforts etc.) as well as generalized MATLAB program to obtain compromise optimal solution of ML-LFPPs. The proposed technique is simple, efficient and requires less computational works than that of earlier techniques. Also the proposed MATLAB program is unique and latest for solving these complex mathematical problems. This software based program is useful and user can directly obtain compromise optimal solution of ML-LFPPs with it. However, the main demerit of this MATLAB program is that construction of its coding is difficult and complex which also depends on the complexity of the problem.

Certainly there are many points for future research in the areas of MLPPs, based on modified FGP approach and should be studied. Some of these areas are:

  1. (1)

    The proposed technique can be extended to more complex hierarchical programming problems like multi-level quadratic fractional programming problems (ML-QFPPs), multi-level multi-objective programming problems (ML-MOPPs) etc. and related computer programs can also be constructed in MATLAB or other programming platforms.

  2. (2)

    Further modifications can be carried out in recent techniques for ML-LFPPs in order to improve efficiency of solution algorithm.