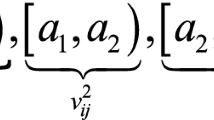Introduction

Globalization and its new approach of industrial out-sourcing, imposed an imperative role on freight transportation sector. In Porter’s value chain, logistics is one of the primary activities, and transportation is the main part of the logistics. This is the most visible aspect of supply chain that occupies one-third of the logistics costs (Tseng et al. 2005). In today’s competitive environment, logistics has been placed in the centre of attention by company managers. Responsiveness as one of the determinants of service quality, stands as a main driver for differentiation, and this will be evaluated by giving prompt services (Parasuraman et al. 1985). On the other hand, global warming and emission of greenhouse gases (GHGs) are presented as the challenges of the century. In actuality, the most important side effect of vehicle transportation is emission of GHGs, particularly carbon-di-oxide (Bektaş and Laporte 2011). GHGs are gases that trap heat in the atmosphere and transportation is responsible for 28 % of total emission in the US (EPA 2014).

As a result, decision-makers should deal with three problems including traditional objective of the VRP, strengthening the customers’ satisfaction influenced by service levels, and environmental concerns. Relevant to this issue, balancing between environmental and business concerns have been dealt with in a few researches. Additionally, there exist a number of studies which consider customers’ satisfaction level and economic objectives. Toro et al. (2016) have declared that presentation of trade-offs between environmental and economic concerns, in presence of customers’ satisfaction, have not been dealt yet. They have proposed this subject in their review paper as the future direction in the green VRP. Another review paper in the field of green VRP has been proposed by Lin et al. (2014). They have proposed exploring the trade-off between economic and environmental costs with soft time window constraints.

As in Toro et al. (2016), and to the best of authors’ knowledge, incorporating all three matters in one problem has been neglected. It could significantly help decision-makers select a solution that accounts not just for the economic orientation, but also for customer’s satisfaction with respect to the environmentally friendly aspects. Our purpose is to introduce a new vehicle routing problem variant, called Satisfactory-Green Vehicle Routing Problem (S-GVRP) where in addition to traditional objectives, both pollution and customer’s satisfaction have been taken into account.

In real-life transportation, time windows may be violated due to several reasons as given in Tang et al. (2009). They propose the idea of vehicle routing with fuzzy time windows. In their model, deviation of service time from the customer-specific time window against a decreasing customer’s satisfaction level is accepted. To solve this bi-objective problem they consider a two-stage algorithm in which defuzzification of the values of each satisfaction level (corresponding to time windows) must be calculated separately. It is notable that originally the concept of fuzzy die-time in vehicle routing and scheduling context is defined by Cheng et al. (1995). They believe the customers’ preferences for services can be classified into two kinds: the tolerable and desirable interval of service time. They propose fuzzy approach for handling both concepts simultaneously. Triangular fuzzy number for stating the grade of customer satisfaction is applied in their model.

The idea of semi-soft time windows is proposed by Qureshi et al. (2009). They consider one-tail soft time windows, where late arrival incurs penalty. Instead, in this research we control effects of time window violations by decreasing customer satisfaction or market share loss.

In the context of the VRP with stochastic travel times, Tavakkoli-Moghaddam et al. (2012) present a model considering driver’s working utility. In their model, driver’s satisfaction versus service time is illustrated by a fuzzy number. Similarly, Noori and Ghannadpour (2012) have applied the concept of hard/soft fuzzy time windows for locomotive assignment problem. They have used the concept of fuzzy approach to consider the different degrees of priority of trains for servicing.

Considering emission in vehicle routing problem have had a serious progressive elaboration from 2007, especially after the thesis of Palmer (2007). This integrates an emission model with the VRP for freight vehicles. Dekker et al. (2012) investigate the contribution of operations research to having a better environment. They discuss that efficiency of trade-offs between cost and environmental factors can be analysed by operations research. The amount of pollution emitted by a vehicle depends on several factors. Over the years, a wide range of emission and fuel consumption models have been presented. A comprehensive analysis of several vehicle emission models for road freight transportation is presented by Demir et al. (2011). In their research the ‘comprehensive modal emission model’ is exploited. Incorporating the fuel consumption and CO2 emissions into existing planning methods for vehicle routing was introduced by Bektaş and Laporte (2011). They offer some new integer programming formulations for the VRP, named pollution routing problem (PRP), that minimizes both operational cost, and carbon tax. Extending their model with independent objective function for emission level will be very useful, because emission tax is trivial in comparison with other costs. Moreover, considering heterogeneous fleet of vehicle instead of homogenous may lead to more reductions in energy consumption.

As it turns out, this research is mostly comparable with the PRP (Bektaş and Laporte 2011), and the work published by Tang et al. (2009). Table 1 shows a brief history of the PRP evolution over time. According to this table, it is obvious that in terms of the objective function, customer satisfaction has not been considered as a variant of the PRP yet. Moreover, considering heterogeneous fleet of vehicles and idle times lead to enrich the model. On the other hand, comparison of the proposed model with Tang’s is multifold: (1) they do not consider emission in their model; (2) since speed and idle time have considerable impact on customer satisfaction, unlike Tang’s work, such cases are considered in our model; (3) optimal route corresponding to a predefined service level has been achieved in a two-stage algorithm in Tang’s model. It is done by defuzzification of predefined service level, and sequentially the problem is solved in two stages. Conversely, in our work, using the PLF approach leads to only one stage optimization; (4) our proposed model is a linear model thanks to the PLF approach, while they have proposed a nonlinear programming problem. Nevertheless, as in Tang et al. (2009), we both conclude that increasing service level leads to increasing the cost and the shadow price for service level increases.

Table 1 A landscape of existing pollution routing problem models (PRPs)
Full size table

As a contribution to this new discussion, we introduce the S-GVRP as a mixed integer linear programming formulation. In this model, speed variable and service-level membership function have been transferred to linear equations. We overcome quadratic speed variable by discretization and nonlinear service-level membership function by exploiting piecewise linear functions modelled by special ordered sets of type two (SOS2) (Keha et al. 2004). Accordingly, we present a demonstration to illustrate some trade-offs between traditional, service level and environmental concerns. This issue is dealt with as managerial insights in “Discussion and managerial insights”. Finally, we report the results of computational experiments with MILP optimization on randomly generated instances.

Precisely, we could remark the contribution and special findings of this work as following: (1) by excluding service levels to existing models, proposed model could be considered as an extension of the PRP with heterogeneous fleet of vehicles; (2) customers’ satisfaction, emissions, and operational costs are optimized and discussed independently and simultaneously based on the well-known PRP models; (3) by trade-offs between total costs and average service levels, we find the best point wherein small added costs leads to notable improvements in customers’ service and carbon emissions; (4) we show that considering the idle time of vehicles usually could be useful for improving both environmental and customers’ service concerns; (5) finally, by numerical analysis, we propose some indicators, i.e., green less value (GLV), green ratio (GR), and carbon emission index (CEI) that could give an eco-warriors crucial information about the greenness of a routing programme.

The rest of this paper is organized as follows. “Problem description” provides a formal description of the problem and conceptual framework of the S-GVRP is presented. Innovative environmental factors are introduced in this section. “Model setup” describes the integer linear programming formulation of the S-GVRP. Computational experiments are provided in “Computational analysis”. Managerial insights are presented in this section, and the conclusions follow in “Conclusions”.

Problem description

The main issue in this paper is to optimize the routes, vehicles’ composition as well as finding the maximum speed of each segment for a heterogeneous fleet of vehicles. These are intended to meet the demands of a set of customers who are geographically dispersed. These patrons have predefined time windows. All the vehicles depart and return to the depot at most once daily. Each customer should be visited once and customers’ demands should not be distributed among the vehicles. The graph is a connected symmetric or asymmetric graph. The structural constraints of the problem depend on the capacity of each vehicle (Q K ), as well as the size and kind of vehicles that are available at the depot (|K| = k). Servicing at the interval of soft time windows leads to maximum customer satisfaction (supplier service level) and violating the hard time windows leads to infeasibility of the model and is impossible.

The S-GVRP is a new variant of the vehicle routing problem which is concerned about the level of customer satisfaction, total expenses and environmental aspects. The total expenses consist of the operational and environmental costs, as are depicted by Bektaş and Laporte (2011). The S-GVRP is looking for an appropriate approach for managerial insight and presents a four-time optimization to deal with this issue. First stage solves a bi-objective problem and afterwards evaluates the associated environmental aspects with some other factors. The bi-objective formulation is as follows:

Min ∑  Operational costs (Drivers’ wage, fuel, and Vehicles’ rent)

$$ + {\sum {\text{ Environmental costs }}}{\left({\text{taxes for carbon production}} \right)} $$
(1)
$$ {\text{Max}}\sum {\text{Average}}\,{\text{customers}}\,{\text{satisfaction}} $$
(2)

Aim of the S-GVRP

The main objective of the S-GVRP is to present a dashboard in which three pillars of economics, environment, and customer satisfaction are taken into account. As an extension of the well-known PRP, the model’s traditional objective is to minimize operational costs including emission tax (PC). Another objective is maximizing customers’ satisfaction (PS). As illustrated in conceptual framework (Fig. 1), non-dominated solutions between these two objectives are to be determined. This can be achieved by applying such methods like absolute priority. Thus, various service levels as the first priority transferred to the constraints. Subsequently, one can obtain a compromise solution [Named Best point (BP)] with applying global criterion method (Eqs. 3, 4, 5). Although, emission tax has been considered in operational cost, this cost is trivial in comparison to other costs (Bektaş and Laporte 2011). As a result, in another stage emission level is minimized independently subject to a predetermined amount of customers’ satisfaction (PE) (Eq. 6).

Fig. 1
figure 1

The conceptual framework of S-GVRP

Full size image
$$ \begin{aligned} {\text{P}}_{\text{S}} : \hfill \\ {\text{Max}}.\,\,\,{\text{SL}}(x) \hfill \\ s.t.\,\,\,\,\,\,\,\,\,x \in S \hfill \\ x^{*} ,{\text{SL}}^{*} \hfill \\ \end{aligned} $$
(3)
$$ \begin{aligned} {\text{P}}_{\text{C}} :\hfill \\ {\text{Min}} .\,\,\,C(x) \hfill \\ {\text{s}} . {\text{t}} .\,\,\,\,\,\,\,\,\,x \in S \hfill \\ x^{*} ,C^{*} \hfill \\ \end{aligned} $$
(4)
$$ \begin{aligned} {\text{P}}_{\text{COMP}} :\hfill \\ {\text{Min}} .\,\,\,\frac{C(x) - C*}{C*} + \frac{{{\text{SL}}* - {\text{SL}}(x)}}{{{\text{SL}}*}} \hfill \\ {\text{s}} . {\text{t}} .\,\,\,\,\,\,\,\,\,x \in S \hfill \\ C_{\text{BP}}^{*} ,{\text{SL}}_{\text{BP}}^{ *} \hfill \\ \end{aligned} $$
(5)
$$ \begin{aligned} {\text{P}}_{\text{E}} :\hfill \\ {\text{Min}} .\,\,\,{\text{EM}}(x) \hfill \\ {\text{s}} . {\text{t}} .\,\,\,\,\,\,\,\,\,x \in S \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,{\text{SL}} \ge {\text{SL}}_{\text{BP}}^{ *} \hfill \\ x^{*} ,{\text{EM}}_{\text{BP}}^{ *} \hfill \\ \end{aligned} $$
(6)

Consequently, for a specific satisfaction level, the optimal cost derives an amount of emission level, and mutually, optimal emission level derives an amount of cost. As it turns out, the difference between these amounts of costs as well as the ratio between these amounts of emissions can meaningfully help a decision-maker to measure greening of a decision. Therefore, the following three definitions are presented due to measuring the amount of greening for a decision based on the S-GVRP:

Definition 1

Green less value (GLV): in a particular transportation plan with a predefined average service level (SL), the GLV is the difference between two amounts of costs. One is derived by minimizing the problem of cost (PC). Another is derived by minimizing the problem of emission (PE), along with its relevant cost.

$$ {\text{GLV}}_{\text{SL}} = \, C_{\text{SL }} - C_{\text{SL}}^{ *} $$
(7)

Definition 2

Green ratio (GR): in a particular transportation plan with a predefined average service level (SL), the GR is the proportion between two amounts of carbon emissions. One is derived by minimizing the problem of emissions (PE). Another is derived by minimizing the problem of cost (PC), along with its relevant emissions.

$$ {\text{GR}}_{\text{SL}} = \frac{{{\text{EM}}_{\text{SL}}^{ *} }}{{{\text{EM}}_{\text{SL}} }} $$
(8)

Definition 3

Carbon emission index (CEI): in a particular transportation plan with a predefined service level this index demonstrates the proportion of emissions to the minimum of emissions at the minimal service level.

$$ {\text{CEI}}_{\text{SL}} = \frac{{{\text{EM}}_{\text{SL}} }}{{{\text{EM}}^{*} }} $$
(9)

The pareto front line between the objectives, and the measurements of the GLV and GR are the basis of the S-GVRP. Indeed, it significantly helps decision-makers to select a solution that not only accounts for the economic orientation, but also considers customers’ satisfaction with regard to the environmentally friendly aspects. The illustration of this matter will be presented in  “Computational analysis”.

Emission modelling

According to the comprehensive modal emission model, the emission of carbon is dependent on three modules each showing a component of energy consumer for vehicle traction: (1) speed module, (2) weight module, (3) engine module. Since the speed in our problem is assumed to be greater than 40 (km/h) the third module is not relevant to our case.

$$ p_{ij} = \psi_{ij} (w_{k} + f_{ij} )d_{ij} + \beta_{k} d_{ij} v_{ij}^{2} $$
(10)
$$ \psi_{ij} = a + g\sin \theta_{ij} + g\,C_{r} \cos \theta_{ij} $$
(11)
$$ \beta_{k} = 0.5C_{{d_{k} }} A_{k} \rho $$
(12)

In above formulations, p ij is the total amount of energy consumed on an arc (i,j). The first module, ψ ij (w k  + f ij ) d ij , is independent of speed and explains the road and load characteristics, and the second module, β k d ij v 2 ij , is a quadratic in the speed and explains the vehicle characteristics. Accordingly, the energy consumed in an arc is dependent on the kind of vehicle. f ij shows the flow of load in corresponding arc, and w k represents empty weight of the vehicle k. d ij is the distance of the arc and could be symmetric or asymmetric. ψ ij is an exogenous variable determined by the road slope characteristics (θ ij ), vehicle acceleration (a), and C r that is rolling resistance coefficient of the road. β k is another exogenous variable that depends on type of vehicle. \( C_{{d_{k} }} \) is the coefficient of aerodynamic drag of vehicle type k. Air density is considered as ρ, and the front area of vehicle type k is shown by A k .

The amount of consumed fuel in an arc is proportional to required energy and depends also on the vehicle drivetrain efficiency (ξ) and efficiency parameter for diesel engines (η). Therefore, regarding the fact that 1 l of gasoline provides 8.8 kWh of energy, the amount of consumed fuel could be calculated. All the measures are in international system of units (SI), but they need some conversions as given here. It is notable that 3,600,000 J is equal to 1 kWh. ξ ≈ 0.9 and η = 0.45 for diesel engine.

$$ F_{ij} = \frac{{P_{ij} }}{8.8 \times \varepsilon \times \eta }\, $$
(13)

In the meanwhile, emission carbon, according to Coe (2011), can be obtained considering the fact that 1 l of gasoline contains 2.32 kg of CO2.

Given the S-GVRP model, the acceleration and road slope is assumed to zero, so the fuel consumption and emission of carbon is dependent on both the total weighted load, namely TWL, (load multiplied by distance) and total square-speed distance, namely TSSD (km3/h2). These factors are dependent on decision variables of vehicle speed at each segment, routing plan and selection of mixed fleet of vehicles. This is notable that the idle time of each vehicle before or after servicing does not influence the problem of emission, i.e., (PE). For maintaining the problem in the form of MILP, the speed variable is discretized with r portions where R = {1, 2, 3 … r} and V = {v r ; r ∊ R}. Successively the model restricted as only one speed variable (v r ) assigned to a specific vehicle which is traversing a particular arc.

Satisfaction modelling

As described before, each customer defines soft and hard time windows characterized by a four-dimensional vector [EET i , e i , l i , ELTi]. The vector [e i , l i ] explains the soft time window that its violation causes customer dissatisfaction and vector [EET i , ELT i ] explains hard time window that its violation makes the problem infeasible. Of course, time windows may sometimes be violated for economic, operational or even [environmental causes] (Tang et al. 2009).

In view of the fact that the expression of satisfaction is an abstract concept, the fuzzy theory is an advantageous tool for explaining the subjective function of satisfaction level (Fig. 2).

Fig. 2
figure 2

Service-level function of fuzzy time windows

Full size image

The service-level function is a piecewise-linear-concave function with a shape of reversed rectangular, triangular or trapezoid that the function shape is subjected to tightness of the time between two adjacent points of vector. For the reason that our approach for the S-GVRP model is linear programming, we have to apply piecewise-linear representation. This method uses the MILP to represent a nonlinear function as a linear shape. For simplification, special ordered sets of type two (SOS2) is applied. This approach considers arrival time (a i ) as a convex combination of only two adjacent points, and sequentially uses the weighting values (m i ) that are obtained from the model to calculate the service level membership function, i.e., SL i= f(a i ).

SL i is a membership function over the set of U i  = {a i ; EET i  < a i  < ELT i } and B i is a fuzzy set. B i  = {(a i , SL i ); EET i  < a i  < ELT i }. For exploiting the PLFs based on the SOS2, the fuzzy set is shown as follows:

$$ B_{i} = \left\{ {(a_{i} ,m_{i2} + m_{i3} );{\text{EET}}_{i} < a_{i} < {\text{ELT}}_{i} } \right\}, $$
(14)

where

$$ a_{i} = {\text{EET}}_{i} \times m_{i1} + e_{i} \times m_{i2} + l_{i} \times m_{i3} + {\text{ELT}}_{i} \times m_{i4} $$
(15)
$$ m_{i1} + m_{i2} + m_{i3} + m_{i4} = 1\quad \quad \quad \quad \quad \quad \forall i \in N_{0} $$
(16)
$$ o_{i1} + o_{i2} + o_{i3} + o_{i4} = 1\quad \quad \quad \quad \quad \quad \forall i \in N_{0} $$
(17)
$$ m_{i1} \le o_{i1} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \forall i \in N_{0} $$
(18)
$$ m_{i2} \le o_{i1} + o_{i2} \quad \quad \quad \quad \quad \quad \quad \quad \quad \forall i \in N_{0} $$
(19)
$$ m_{i3} \le o_{i2} + o_{i3} \quad \quad \quad \quad \quad \quad \quad \quad \quad \forall i \in N_{0} $$
(20)
$$ m_{i4} \le o_{i3} + o_{i4} \quad \quad \quad \quad \quad \quad \quad \quad \quad \forall i \in N_{0} $$
(21)
$$ m_{iu} \ge 0\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \forall i \in N_{0} ,u = 1,{ 2},{ 3},{ 4} $$
(22)
$$ o_{iu} \in \left\{ {0, 1} \right\}\quad \quad \quad \quad \quad \quad \forall i \in N_{0} ,u = 1,{ 2},{ 3},{ 4} $$
(23)

In the model N is the set of all nodes and \( N_{0} = N\backslash \left\{ 1 \right\} \)c is the set of all customers. Moreover, m iu , o iu are internal (auxiliary) variables of the PLF.

As a result, for translating the ambiguous value of service level, these equalities and inequalities could be easily used along with the models of PC, PS, PE and PCOMP,etc. Consequently, we can easily replace the amount of service level (SL i ) with m i2 + m i3 in our models.

Model setup

The methodology of this research is mathematical modelling in field of operations research. This is subcategorized from analytical mathematical research and is to find the relations between the predefined concepts, and exploring the behaviour of the model under various conditions and restrictions.

Model notations

Sets:

N: Set of all nodes (N 0 for customers, \( N_{0} = N\backslash \left\{ 1 \right\} \))

K: Set of available vehicles in the depot (or rental vehicle company)

R: Set of speed levels

V: Set of discretized permitted speed V = {v r ; r ∊ R}

A: Set of all arcs in the network A = {(i, j); i, j ∊ N, i ≠ j}

Indices:

i, j, u: Indices of the nodes (customers or depot) i, j, u ∊ N = {1, …, n}, n = |N|

k: Index of vehicles k ∊ K = {1, …, k}, |K| = k

r: Index of speed level r ∊ R = {1, …, r}, |R| = r

Parameters:

C k : Capacity of vehicle type k (kg).

q i : Demand of customer i (kg)

ɛ: Lower average service level (lower bound)

[e i , l i ]: Soft time window for customer i (seconds)

[EET i , ELT i ]: Hard time window for customer i (seconds)

S i : Servicing time at the customer’s warehouse (seconds)

\( C_{{f_{k} }} \): Cost of fuel for every single unit of energy in joule (affected by vehicle’s efficiencies)

e k : Cost of taxes imposed on producing carbon (proportional to 1 J of energy for vehicle k)

d ij : Distance between node i to j (metre)

p: Drivers’ wage (for each second)

h k : Variable hiring cost of vehicle type k per second

fx k : Fixed hiring cost for vehicle type k

ψ ij : Weight module coefficient determined by the road characteristics (slope), vehicle acceleration and C r.

β k : Speed module coefficient determined by vehicle characteristics:\( C_{{d_{k} }} \), ρ and A k

w k : Empty weight of vehicle type k

M: Possible latest departure time from a customer to the depot

Decision variables:

x k ij : Binary variable determines if arc (i,j) is traversed by vehicle type k

z kr ij : Binary variable determines if arc (i,j) is traversed by vehicle type k at the speed v r ; r ∊ R

a i : Arrival time at customer i (seconds)

p k ij : Departure time from customer i to customer j via the vehicle type k

f k ij : Load flow quantity with vehicle type k in arc (i,j)

t k j : Elapsed time on a tour with vehicle type k.(latest customer served is j)

SL i : Satisfaction level of customer j (supplier service).

Mathematical formulation

The mixed integer linear programming for the S-GVRP is modelled as follows. The following formulation provided for PC with priority for a predefined service level (named ɛ). Similarly, optimization of PS can be formed by substituting the objective function to the summation of service levels. Also, for optimization of PE, cost-oriented functions, i.e., (26) and (27) must be omitted.

$$ {\text{Minimize}}\,C = \sum\limits_{(i,j) \in A,k \in K} {(C_{{f_{k} }} + e_{k} )\psi_{ij} d_{ij} \left( {w_{k} x_{ij}^{k} + f_{ij}^{k} } \right)} $$
(24)
$$ + \sum\limits_{(i,j) \in A,k \in K} {(C_{{f_{k} }} + e_{k} )} \beta_{k} d_{ij} (\sum\limits_{r \in R} {v_{r}^{2} } z_{ij}^{kr} ) $$
(25)
$$ + \sum\limits_{{j \in N_{0} ,k \in K}} {(p + h_{k} )t_{j}^{k} } $$
(26)
$$ + \sum\limits_{{j \in N_{0} ,k \in K}} {fx_{k} } x_{1j}^{k} $$
(27)

subject to

Constraints (15–23)

$$ \sum\limits_{{i \in N_{0} }} {\frac{{m_{i2} + m_{i3} }}{n - 1}} \ge \varepsilon $$
(28)
$$ \sum_{j \in N,k \in K} x_{ij}^{k} = 1\quad \quad \quad \quad \quad \quad \quad \quad \forall i \in N_{0} $$
(29)
$$ \sum_{i \in N,k \in K} x_{ij}^{k} = 1\quad \quad \quad \quad \quad \quad \quad \quad \quad \forall j \in N_{0} $$
(30)
$$ \sum\limits_{{i \in N_{0} }} {x_{i1}^{k} } \le 1\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \forall k \in K $$
(31)
$$ \sum\limits_{{j \in N_{0} }} {x_{1j}^{k} } \le 1\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \forall k \in K $$
(32)
$$ \sum\limits_{{j \in N_{0} }} {x_{ju}^{k} } - \sum\limits_{{i \in N_{0} }} {x_{ui}^{k} } = 0\quad \quad \quad \quad \quad \quad \quad \forall u \in N_{0} , \forall k \in K $$
(33)
$$ \sum\limits_{{j \in N_{0} ,k \in K}} {f_{ju}^{k} } - \sum\limits_{{i \in N_{0} ,k \in k}} {f_{ui}^{k} } = q_{u} \quad \quad \quad \quad \quad \forall u \in N_{0} $$
(34)
$$ q_{j} x_{ij}^{k} \le f_{ij}^{k} \le \left( {C_{k} - q_{i} } \right)x_{ij}^{k} \quad \quad \quad \quad \quad \forall \left( {i, j} \right) \in A, k \in K $$
(35)
$$ \sum_{r \in R} z_{ij}^{kr} = x_{ij}^{k} \quad \quad \quad \quad \quad \quad \quad \quad \forall \left( {i, j} \right) \in A, k \in K $$
(36)
$$ a_{j} \ge \sum\limits_{i \in N,k \in K,r \in R} {\frac{{d_{ij} }}{{v_{r} }}} z_{ij}^{kr} + \sum\limits_{i \in N,k \in K} {p_{ij}^{k} } \quad \quad \quad \quad \forall j \in N_{0} $$
(37)
$$ a_{i} + s_{i} \le \sum_{j \in N,k \in K} p_{ij}^{k} \quad \quad \quad \quad \quad \quad \quad \forall i \in N_{0} $$
(38)
$$ {\text{EET}}_{i} \le a_{i} \le {\text{ELT}}_{i} \quad \quad \quad \quad \quad \quad \quad \quad \quad \forall i \in N $$
(39)
$$ T_{j}^{k} \ge \sum\limits_{r \in R} {\frac{{d_{j1} }}{{v^{r} }}} z_{j1}^{kr} + p_{j1}^{k} \quad \quad \quad \quad \quad \quad \forall j \in N_{0} , \forall k \in K $$
(40)
$$ p_{ij}^{k} \le M \times x_{ij}^{k} \quad \quad \quad \quad \quad \quad \quad \quad \forall \left( {i, j} \right) \in A, k \in K $$
(41)
$$ x_{ij}^{k} \in \left\{ {0, 1} \right\}\quad \quad \quad \quad \quad \quad \quad \quad \quad \forall \left( {i, j} \right) \in A, k \in K $$
(42)
$$ z_{ij}^{kr} \in \left\{ {0, 1} \right\}\quad \quad \quad \quad \quad \quad \quad \quad \quad \forall \left( {i, j} \right) \in A, k \in K, r \in R $$
(43)
$$ a_{i} , p_{ij}^{k} , t_{i}^{k} , f_{ij}^{k} , SL_{i} \ge 0\quad \quad \quad \quad \quad \quad \forall i \in N, \forall j \in N, \forall k \in K $$
(44)

Model description

The first objective function (24) measures the cost incurred by the weight module. The unit cost of fuel and emission carbon multiplied by the total amount of fuel consumption over each leg of (i,j) explains this objective. The costs induced by the speed module in the form of fuel cost and emission carbon tax are described by the second component (25). The term (26) calculates the operational costs of drivers’ wage and variable and fixed cost of vehicles calculated by the last component (27). It is essential to note that the second objective of the model, i.e., maximizing the average service level is placed within the constraints due to deriving the Pareto front set, which can be obtained by frequently optimizing the model with various amounts of ɛ. Constraints (15–23) are the PLF constraints. Constraint (28) shows the assumed lower bound of average service level (ɛ). SL i is replaced by m i2 + m i3 according to the PLFs model. Constraints (29) and (30) are the degree constraints of the main VRP problem and guarantee that each customer is visited exactly one time. Constraints (31) and (32) guarantee that each vehicle can leave the depot and return to it at most for one time. In other words, any vehicle available in the depot can be exploited, but at most for one time. The constraints (33) control the continuity of each vehicle route by the flow equation. Constraints (34) model the balancing of flow goods of each node, while removing the sub-tours as well. Constraints (35) guarantee that the vehicle capacity is respected. Constraints (36) guarantee that only one vehicle’s speed value (v r ), which is corresponding to the r and (r ∊ R), could be considered by the vehicle type k that is traversing the arc (i,j). Constraints (37) make sure that if customer j follows customer i in the route, the arrival time to the customer j is equal to the departure time from customer i, PLFs the travel time between these two customers. The surplus value in these constraints equals the idle time for the vehicle that travelled the link before servicing the customer j (idle Bj ). The relation between arriving and departure time for the customers are described in constraints (38), and in case the slack variable were a non-zero variable, there would be an idle time for the vehicle after serving the customer i (idle Ai ). Hard time windows are imposed by constraints (39). Total elapsed time in a tour (on or off-road) is dependent on the visiting time of last customer in the route, and described by the constraints (40). The constraints (41) ensure that the departure time from i to j with the vehicle k has a non-zero value if the corresponding indicator variable is equal to one and the upper bound of the departure time is equal to the constant of M (the possible latest departure time), and finally, constraints (42–44) impose non-negativity and integrity on the variables.

Model solution

The model under study is a vehicle routing problem with fuzzy time windows that is defuzzed with employing the piecewise linear representation. The vehicle routing problem originally belonged to the NP-hard combinatorial optimization problem, thus its variants with more indices and constraints, undoubtedly, would be NP-hard as well. The optimal solution is generally obtained by using exact algorithm that can only tackle the problem of relatively small scale (Laporte 1992). Therefore, it is generally expected that the best solution cannot be found in an efficient time (Sheng et al. 2006; Javanshir and Najafi 2010; Yousefikhoshbakht and Khorram 2012). CPLEX Interactive Optimizer 12.4 with its default setting is used as the optimizer to solve the mixed integer linear programming models. In order to accelerate the solution process, the solver is allowed to run its branch-and-cut in a parallel mode. All the models are coded in Lingo 14 and subsequently are exported to the interactive optimizer environment of CPLEX commercial software via the mps format. All experiments are conducted using CPLEX 12.4 on a server with 2.27 GHz and 3 Gb RAM.

We have exploited two approaches to improve the efficiency of solution time: (1) we have reduced cardinality of the set of free-flow speed levels (V) by considering the intervals equal to 10 (km/h); (2) we have avoided using a big number. Instead, an upper bound for departure time is considered (M: possible latest departure time).

Computational analysis

As Wacker (1998) mentions, in analytical-mathematical studies, that develop relationships between narrowly defined concepts, there is not necessity or motivation to use external data to demonstrate or test the model. This type of research generally uses deterministic or simulated data to draw conclusions.

In this study, experiments were run with realistically generated data. One class of problem with 10 cities (except the depot) were generated and includes 30 instances, each one considered as the data of a day of a particular month. All experiments were performed for mixed fleet of vehicles (heterogeneous), and four types of vehicles considered accessible for renting. The classes of commercial trucks are the LDV and MDV that not only are consistent with urban transportation, but also the CMEM can be exploited efficiently.Footnote 1 In addition, all technical specifications are exactly extracted from the factories’ catalogues. The fixed and variable costs of the vehicles are an average quote in the UK obtained from the website of a commercial vehicle rental company. Since the fixed cost for renting is considered, there exists a capacity in the morning that decision-maker is about to increase the average vehicles’ utility ratio in order to reduce total costs.

Analyses were carried out for cases at which the parameters of x and y coordinates are for locations, and demands and time windows are initially generated randomly according to a discrete uniform distribution. The interval for x and y coordinates of the customer locations is in the range of [−40, +40] (km). This is a single-commodity distribution system and demands vary in the range of [300, 1200] (kg). The distributor is obligated to deliver the demands and for a particular customer, EET and ELT are randomly generated in [8:00, 14:30] interval. First an EET is selected and then that ELT is selected in the range of [EET + 0:40, EET + 2:00]. Subsequently, soft time window randomly selected within produced hard time window. The depot starts servicing at 7:00 and will be closed at 16:00. The unloading time is randomly selected among (10, 20, and 30) min. All the time are discretized at 10 min (Table 2).

Table 2 Randomly generated data for Instance No. 11
Full size table

Therefore, each customer upon his or her circumstances imposes time windows. All other parameters and values are given in Table 3. In the experiments we have used six points for speed variable discretization. The aim of this section is to demonstrate the application of theoretical framework presented in “Problem description”, and providing sensitive analyses and statistical inference for improving managerial insight and decision-making.

Table 3 Setting of vehicles and emission parameters
Full size table

Example analysing

For testing the model, we have selected randomly one of the instances to show its results. The information is presented in Table 2. In Table 4, the results are shown. As discussed in “Problem description”, total costs is a function of multiple factors; (1) total time (TT) elapsed in all tours (travelling, delivering, idling) that affects the cost of drivers and vehicles rental payments; (2) total weighted loads (TWL) that affects the cost of fuel and emission through the weight module of emission model; (3) total square-speed distance (TSSD) that affects the cost of fuel and emission through the speed module, and (4) fixed cost (FX) because of vehicle rental payments (Fig. 3c). Similarly, the measurement of the emission is dependent on two factors of TWL and TSSD. In this case, the least service level is about 50 %. Figure 3a illustrates that with increasing the average service level (SL), total costs increase as a roughly exponential shape of \(c = {c^* + (c_{\hbox{max} } - c^* )} \mathord{\left/ {\vphantom{{c^* + (c_{\hbox{max} } - c^* )} {e^{{\lambda (SL^* - SL)}} }}}\right. \kern-0pt} {e^{\lambda (SL^* - SL)}}. \) In these circumstances, the search space is over-restricted and alternative solutions reduced by lesser optimal routes. Figure 3a clearly illustrates that the emission’s function is a descending function, but fluctuates in the range of corresponding service levels. The optimized amount of emission at each point is obtained by optimizing the problem of emission respecting to the service-level constraint (Fig. 3b). Although this result could not be necessarily generalized to other cases, some statistical inferences are presented in the next section. Average utility ratio of the vehicles and total travelled distance areshown in Fig. 4, respectively, by r u and TD.

Table 4 S-GVRP results
Full size table
Fig. 3
figure 3

a, b, c Pareto optimal line for total costs and total emissions vs. average service levels

Full size image
Fig. 4
figure 4

Total distance and average utility ratio variances

Full size image

In the comparison between the cost components, the dominant part is the cost affected by total time (CTT) with 67 % share on the average, and the next ones are fixed cost, C TSSD and C TWD with 23, 6 and 4 % shares, respectively. It is notable that since the ratio of carbon tax by fuel cost per liter is 0.06/1.36 ≈ 5 %, and C TSSD + C TWD = 10 %, the emission tax represent only about 0.5 % of total costs. Therefore, as described in “Problem description”, evaluation of emission in another stage becomes crucial. At the best point (BP) service level improved up to 85 % with only 10 % of added cost. Emission at this point is 80 (kg), that is 13 (kg) lesser than the start point. The reason is decline in total weighted load and squared speed distance on account of changing the route and re-composition of the vehicles fleet. Although, the vehicles move more slowly, the average satisfaction levels improve and the total time with increasing the idle time, increases. Thus, emission and fuel consumption decrease (Figs. 3a, 8). For clarification purposes, consider that two points of (p1) and (p2) are so close and the delivery time is significantly different. When satisfaction level is minimal, the problem is optimized only in terms of the total cost, and consequently the speed increases to decrease total time, but when service promises are involved in the model, instead of departing from (p1) to other points and returning to (p2) in rush later, the vehicle must wait before (p2) primarily. This waiting time, off the road is showed by idle time variables (idle A and idle B ). Time sequencing and idle time’s table for current example is presented in Table 5. As specified in this table, sum of idle times for all the vehicles is equal to 9 h and 41 min. In this example, in charge of increased cost, the service level increases, and more surprisingly the amount of carbon emission decreased. Of course, because of spending much of time in idle mode, there exist another possible added cost in the form of fixed cost of renting extra vehicles that impacts the problem to avoid infeasibility.

Table 5 Time sequencing for the best point
Full size table

It is up to the managerial insight as to how to shift the best point (BP). He/she may select the point of 93 % (SL) that the total cost significantly increases from 499 £ to 567£ and emission decreases from 80 (kg) to the least, 66 (kg) approximately. Adding one vehicle leads to changes in the values. In addition, it is obvious that adding the vehicle to the fleet reduces average vehicle utilization. Total distance is globally decreased from 507 to 413 (km), but locally fluctuated in the range of service levels. Since distance is a variable that participates in both weight and speed module, and affects the spent time in the routes, this variable is an important component in all problems (Fig. 4).

As long as the speed is the only way for increasing the average of service level, the emission arises through raising the square of speed distance (Segment between 71 and 89 % in Table 4 and Fig. 6). Increasing the speed does not necessarily decrease the total time, because the idle time in almost all cases increases. In contrast, while the service level is increased by changing the routing plan and/or by reconfiguration of fleet of the vehicles (as in 70, 90, 93 and 97 % service levels), the total travelled distance changed and in this particular instance,TWL and TSSD decrease and lead to improving environmental aspects (Figs. 5, 6, 7, 8, 9).

Fig. 5
figure 5

The optimal routing and vehicles’ composition for average service level less than 69 %

Full size image
Fig. 6
figure 6

The optimal routing and vehicles’ composition for average service level between 70 and 89 %

Full size image
Fig. 7
figure 7

The optimal routing and vehicles’ composition for average service level between 90 and 92 %

Full size image
Fig. 8
figure 8

The optimal routing and vehicles’ composition for average service level between 93 and 96 %

Full size image
Fig. 9
figure 9

The optimal routing and vehicles’ composition for average service level between 97 and 99.7 %

Full size image

In order to measure the greening of each decision, we invoke to the environmental factors of the S-GVRP proposed in “Aim of the S-GVRP”. Accordingly, for the service level in the best point, GLV, GR and CEI are 90£, 56 %, and 2.08 respectively. This value could be obtained directly from Fig. 3 or can be calculated from Table 3 applying (7), (8), (9) equations, i.e., GLVBP = 589 − 499 = 90, GRBP = 44.9/80 = 56 % and CEIBP = 80/38.5 = 2.08.

Calculating these values for the start point, we have demonstrated 15 % improvement in GR and 0.34 reductions in CEI. To clarify these measures, assume the decision-maker thinks only about the environmental issue, and there are no restrictions on the costs. Comparing of EM* with EM and C * with C reflects that at the best point managerial insight is 15 % closer to the eco-friendly decision-maker in comparison with the start point with minimum service level. Some interesting managerial implication is that if the decision-maker wants to be greener and improve the GR from 56 to 100 % he or she should spend normally some amount of money named Green Less Value (GLV) that is equal to 90£ for this example. Similarly, for maximum service level the values, respectively, are as follows: 16£, 80 %, 1.82. Remarkably, the amount of GLV is significantly decreased and successively the GR is improved. Also, the absolute amount of produced carbon or CEI decreases. Last but not least, it should be considered that these results pertain to this particular example and could not be generalized to other instances. Statistical inferences are presented in next section for filling this gap to estimate the lower and upper bounds in the 95 percentile.

Eco-friendly decision-makers

An eco-worrier with an attitude towards green behaviours tries to improve his/her green credential. In actuality, most of the customers want to work with eco-friendly firms. Indeed, the role of customers in green supply chain has been recognized as an important research area (Kumar et al. 2013). Consequently, customer satisfaction can be evaluated both by prompt services and green product.

The S-GVRP presents a dashboard for decision-makers that not only cost, but also environment and customer satisfaction are taken into account. Green factors presented by the S-GVRP can significantly help decision-maker to find an appropriate decision. Based on the instance analysed in the previous section, we have presented a graph that the green ratio (GR), customer satisfaction and total costs have the same directions (Fig. 10). The solid line represents the GR ratio versus the cost. Similarly, the dashed line represents service level versus the cost.

Fig. 10
figure 10

A comparison of green ration, service level, and total costs

Full size image

The green ratio (GR) has been varied from 39 to 80 % along the GR line. Obviously, an economic decision-maker selects solution (1) with $455 cost, 41 % GR, and 50 % service level. On the other hand, an eco-friendly decision-maker selects the solution (2) with $576 cost, 80 % GR, and 99.7 % service level. As is illustrated in Fig. 10, he/she may choose a compromising solution, namely (BP), that represents $499 cost, 56 % GR, and 92 % service level.

Statistical inferences

Sensitive analyses around the values of the model and the green factors for a particular instance demonstrates that by adding little cost a noteworthy improvement in customer satisfaction and surprisingly a reduction in produced emission carbon is possible. Analysis on two scenarios of the best point and the maximum service level shows that the maximum point has more potential for this issue. In order to use statistical inference around these factors, estimation theory is imposed over 30-generated instances and the paired estimation is carried out for subtraction of GR at both the best and maximum points from the start point. The same procedure is done for CEI as well. The normality of data is initially assessed with third and fourth standardized moment, skewness and kurtosis. The results of interval estimation at the percentile of 95 are presented in Table 6.

Table 6 Confidence limits for cost and service variables and green factors
Full size table

The average of demands over 30 instances is equal to 7425 (kg) and the range of the service level for the best point is varying between 74 and 100 %. Adding 8.6 % to total costs will cause 87 % improvement for average of service levels.

Lower confidence limit (LSL) for green-ratio difference (ΔGR) shows that in the worst case the GR at the best point is equal to the start point, while at upper limit it reaches 9 % improvement. On the other hand, the index of carbon production difference (ΔCEI) in lower limit is negative near to zero, and shows becoming worse in production carbon, but it is so small, and in return, at the upper limit it is positive. For the best point the average of green less value is equal to 123£. The maximum service level will take place with adding up 32 % to total costs and obtaining significant improvement in both factors of GR and CEI. This amount of adding cost is approximately four times of the first scenario. In this scenario, average expenses for reaching the maximum possible greening will be occurred by the price of green less value equal to 62£. That is about half of the value for the former scenario. With increasing the average service levels up to possible maximum point, green factors at 95 % confidence level improves so that for the GR even at lower limit, 12 % increasing is showed. Presenting various graphs, and environmental factors the S-GVRP prepares an effective dashboard for the right decision-making.

Associated average computational times required to solve each point of an instance to optimality is 179.83 s for four time optimizations (PC, PS, PCOMP and PE). For creating the Pareto front lines the optimizations should be run several times for several service levels. However, solution time to optimality of PC for 10-node instances with 10 customers for the PRP is reported 3165 CPU seconds (316 s for each). Obviously, average solution time decreases four times for the proposed model, equalling 80 s.

Discussion and managerial insights

In today’s competitive environment, logistics has been placed at the centre of attention by company managers. In this regard, transportation is the most visible aspect of supply chain that occupies one-third of the logistics costs (Tseng et al. 2005). As a result, companies try to create competitive advantages by strengthening their transport fleet. On the other hand, customers expect prompt services and want to purchase green products. The reduction of vehicle emissions is a key concern for many companies. They try to take approaches for decreasing their carbon footprint and therefore improving their green credentials (Mallidis and Vlachos 2010). As it turns out, presenting an operational planning dashboard in which three pillars of economics, environment, and customer satisfaction seems to be essential.

As an extension of the well-known PRP, the S-GVRP is proposed in this paper. Accordingly, we describe a procedure to create some trade-offs between the problems which make managerial insight to make right and effective decisions. The S-GVRP presents a dashboard for decision-makers where not only the cost, but also environment and customer satisfaction are taken into account. Green factors presented by the S-GVRP can meaningfully help decision-makers to come to an appropriate decision. S-GVRP is based on the optimization of three problems of cost (PC), emission (PE), and satisfaction (PS), individually and simultaneously. Thus, several appropriate trade-offs between the objectives will help decision-makers make right decisions (“Aim of the S-GVRP”). In addition to generating pareto front line between the objectives, measuring GLV and GR as green performance indicators is followed in S-GVRP. Indeed, it significantly helps decision-makers to select a solution that not only accounts for the economic orientation, but also considers customers’ satisfaction with regard to the environmentally friendly aspects.

Consequently, based on computational analyses and statistical inferences (“Computational analysis”) we conclude that operational decisions can be significantly effective in a way that reduces transportation costs and improves the level of green ratio and customer satisfaction.

Conclusions

In this research, we have introduced a new mathematical model that three objectives of cost, pollution and customer satisfaction are explicitly considered and is named Satisfactory-Green Vehicle Routing Problem (S-GVRP). The model is addressed by mixed integer linear programming and solved to optimality. Subjective concept of customer satisfaction is presented by fuzzy intervals and exported to the MILP model through piecewise linear functions (PLFs). Mixed fleet of vehicles exponentially enlarges the scale of the problems. However, solution time is obtained efficiently by avoiding big numbers in the sequential constraints. Global criterion and absolute priority methods are applied at various stages of the problem, in order to obtain trade-offs between objectives. The S-GVRP creates some graphs and green factors. They can help decision-makers to select a solution based on the company’s circumstance or preferences. Both economic and eco-friendly decision-makers can apply the S-GVRP, and determine appropriate routes, the best mixed fleet, speed and idle time of the vehicles based on their preferences.

The numerical study demonstrates that the model can be applied effectively. We statistically estimated in 95 % percentile that improving average service level not only does not deteriorate the environmental factors, but also improves it at the best point, and specifically at the maximum of service level. In addition, environmental control policies like the carbon tax merely cannot be appropriate for motivating supply chains to respect the environmental aspects. The tax shares only about 0.5 % of total costs. This is also the conclusion of Bektaş and Laporte (2011) that show the emission costs such as carbon taxes can be easily dominated by fuel or labour costs. As a result, the S-GVRP can be construed as an effective dashboard for a right decision-making.

Promising area for future study can be the following: (1) extending the model over a long-term relation of the supplier-customer (e.g., VMI), instead of daily operational planning. The well-known problem of inventory routing problem (IRP) is an appropriate variant that meets this idea; (2) since the medium and large-scale problems cannot efficiently obtain exact solution, developing algorithmic approaches for the model is necessary; (3) applying fuzzy random theory for defining ambiguous and stochastic data of time windows are other capable areas for future research.