Introduction

During the last decade, growing attention has been paid to reverse logistics network design (RLND), which focuses on the backward network. RLN is utilized to pick up or collection, transportation and recycling of used products or end-of-life (EOL) goods by the consumers, such as electronic goods recycling (Hyunsoo et al. 2009), hazardous waste products recycling (Samanlioglu 2013), empty and aluminum soft-drink bottles recycling (Privé et al. 2006), paper recycling (Patia et al. 2008).

RLND generally refers to activities such as collection, inspection/separation, recovery, repair, recycling, remanufacturing or re-processing, disposal and re-distribution of the used products. Various researchers classified the reverse logistic process differently. Many logistic networks aim to decide on issues such as (1) locations for depots (2) allocation of customers to each established facilities, and (3) transportation networks connecting customers to facilities by vehicle routing. (4) Inventory management of goods on facilities. Nowadays, the combined two or more problem has been considered. The problem, which deals with combines the facility location problem (FLP) and the vehicle routing problem (VRP) decisions, is known in operations research context as the location-routing problem (LRP). According to Vidović et al. (2016) and Prodhon and Prins (2014), the LRPs can be classified based on the different aspects, such as single or multiple echelons, hierarchical structure, number of facilities, number and types of vehicles, homo-/heterogeneous fleet, (un) limited/(un)capacitated fleet, facility capacity, type of input data, nature of demand, planning horizon, time windows, number of objective functions, route structure, solution space, and solution method. In this paper, we have utilized a bi-objective capacitated location-routing problem with soft time window (LRPTW) and with four layers (e.g., collection and inspection centers, recycling centers, disposal centers and customers) in reverse logistics and heterogeneous vehicle fleet with capacity. Also, the turn of the customer is considered that it has not been seen, previously, in the literature. A predefined percent of demand from each customer is assumed as returned products, and a predefined value is determined as an average scrap fraction. The model determines which depots should be opened (or established) in all echelons and identifies the collection routes from the collection centers to the customers with considering the turn of customer in first echelon.

LRP deals with determining the location of facilities and the routes of the vehicles for serving the customers under some constraints, such as facility and vehicle capacities, route time, to minimize total cost including transportation costs, vehicle fixed costs, facility location fixed costs, recycling centers operating costs and penalty cost and to satisfy demands of all customers by minimizing total time as second objective function. Notably, these two objective functions are in conflict with each other. This means that an increase in one objective leads to a decrease in another one; therefore, optimizing the network involves a trade-off between these two objectives. Furthermore, a complete sensitivity analysis is presented to investigate this model from different perspectives.

So, the main contributions of this paper that differentiate our efforts from those already published on this issue can be summarized as follows: (1) We introduce a new formulation of the CLRPTW, in which vehicle routing is considered in first echelon and facilities location is considered for collection and inspection centers, recycling centers. (2) We support both collection and inspection processes in one facility for reducing cost. (3) Allow to trade off between two important objectives in this area, i.e., the total costs and the total network responsiveness by reducing maximum traveling time to offer different compromise efficient solutions to the decision makers. (4) We consider turn of the customer, the soft time window with penalty cost and the load of vehicles after leaving every node of customer in our LRP. (5) We propose exact solution in GAMS for solving small-size instances and metaheuristic solution methods, non-dominated sorting genetic algorithm II (NSGA-II), based on the new formulation, providing the means to solve large-size instances, and to compute tight gaps for small instances.

The remainder of this paper is organized as follows. The brief surveys’ literature on the CLRP and related problems are defined in “Literature review”. The problem definition and proposed bi-objective mathematical formulation are elaborated in “Problem description and mathematical formulation”, and the proposed algorithm is explained in “Multi-objective optimization”. Computational experiments are presented and analyzed in “Comparative methods”, and finally, the summary of conclusions is explained in “Computational experiments”.

Literature review

The first article where location and routing decisions were simultaneously studied dates back to 1968 and early 1980s. One of the first author group to analyze a LRP was Karp et al. (1972); few surveys on location-routing problems have been presented in the literature.

A good recent review on it can be found in Prodhon and Prins (2014), but several efforts have been published by Lopes et al. (2016), Laporte (1988), Gao et al. (2016), Zhalechian et al. (2016), Min et al. (1998). For detailed information about classification for the LRP; Laporte (1988) is the first researcher who classifies the LRP models. Min et al. (1998) proposed a classification for the LRP based on the solution methods, and the problem perspective, such as the number of depots, the presence of capacity, the form of the objective function, etc. Nagy and Salhi (Vidović et al. 2016), is based on the LRP models, solution approaches and application areas.

In this paper, we consider LRP with time window (LRPTW) in multi-echelon reverse logistic network which is a general case of the LRP by considering time window for vehicles while picking up demands of each customer. Some recent articles of LRPTW are Fazel Zarandi et al. (2013), Govindan et al. (2014). The terms multi-echelon or NE-echelon VRP/LRP are, in fact, first used in (Gonzalez Feliu et al. 2008). There are only a few papers on systems with more than two echelons in LRP/CLRP. Lee et al. (2010) study a three-echelon LRP with routing decisions on the first and third echelon. They consider capacitated facilities on levels 1–3 and fixed costs for opening facilities on levels 1 and 2. Two MIP models are developed. They consider the routing problems on echelons 1 and 3. A heuristic algorithm is presented by them. Contardo et al. (2012) introduced two algorithms to address the two-echelon CLRP (2E-CLRP). They proposed a branch-and-cut algorithm based on the new formulation, and a new adaptive large-neighborhood search (ALNS) meta-heuristic with the objective of finding good-quality solutions quickly. But there are many papers with two or more than two echelons in RLN. Krikke et al. (1999) designed a MILP model for a two-stage reverse logistics network of a copier manufacturer. In this model, the processing costs of returned products and inventory costs are considered in the objective function.

Travakkoli-Moghaddam et al. (2013) considered a single-sourcing network design problem for a three-level supply chain. Their model considered risk-pooling, the inventory existence at distribution centers (DCs) under demand uncertainty. Yousefikhoshbakht and Khorram (2012) presented a hybrid two-phase algorithm called sweep algorithm (SW) and ant colony system (ACS) for the classical VRP. At the first stage, the VRP is solved by the SW, and at the second stage, the ACS and 3-opt local search are used for improving the solutions.

Reverse logistics network design includes determining numbers, locations, and capacities of collection, recovery, and disposal centers, and the quantity of flow between them. Reverse logistics networks have special characteristics such as important role of collection/inspection centers that we consider in our LRP. Since return products have different qualities, they have different potentials for recovery activities, too. After testing in collection/inspection centers, return products are divided into recoverable and scrapped products to prevent excessive transportation and to ship the return products directly to proper facilities. Aras et al. (2008) develop a nonlinear model for determining the locations of collection centers in a simple reverse logistics network. The important point regarding their article is the capability of the presented model in determining the optimal buying price of used products with the objective of maximizing the total profit. They developed a heuristic approach based on tabu search to solve the model. Patia et al. (2008) proposed a mixed integer goal programming (MIGP) model to assist in proper design of a multi-product paper recycling logistics network. The model studies the interrelationship between multiple objectives of a recycled paper distribution network. The considered objectives are reduction in reverse logistics cost; product quality improvement through increased segregation at the source.

Within the literature reviewed, some works that considered a multiple objective approach for the LRP were found. Caballero et al. (2007) studied a capacitated LRP to locate a given number of incineration plants for solid animal waste in different cities. Five objectives must be minimized: (1) the total cost of the routes, (2) the total opening cost of selected plants, (3) a social rejection measure based on the number of inhabitants in the cities traversed by the routes, (4) an equity criterion (the maximum social rejection over the set of cities), and (5) another social rejection measure taking the distances between incineration plants and cities into account. They used an adaptative memory procedure (MOAMP) for the resolution of multi-objective combinatorial problems (MOCO). Lately, Hua-Li et al. (2012) presented a bi-level linear programming model for a bi-objective CLRP with a time window to rescue each customer, raised by emergency situations at the city level. Two objectives are considered. The first one is minimiztion of total cost and the second one is maximizing service level. A genetic algorithm is proposed to solve the problem.

Samanlioglu (2013) proposed a mathematical model for a three-objective (one economic and two social criteria) two-stage LRP, for an industrial hazardous waste management system in a region of Turkey. They considered recycling and disposal centers in their network. They used a lexicographic weighted formulation to obtain 16 different representative Pareto-optimal solutions.

Applications and numerous solution methods varying from exact to heuristic and metaheuristic approaches have been proposed to solve the LRP. Among many solution procedures, only a few of them are presented here, as follows. Berger et al. (2007) consider the uncapacitated LRP with route length constraints in their study, and they propose a branch-and-price algorithm to solve the problem. The heuristic proposed by Barreto et al. (2007) begins by clustering customers according to the capacity of the vehicles. Then, for each cluster, a TSP is solved—optimally for small clusters and heuristically, using the savings method and 3-opt, for large clusters. Finally, depot locations are found by treating each tour as a single customer. They considered integration of several hierarchical and non-hierarchical clustering methods in addition to several proximity measures to solve the General deterministic LRP. They compared the results of running their procedure on standard LRP datasets, and results were analyzed. Different metaheuristic approaches have also been proposed in the literature to solve larger LRPs. Prins et al. (2006) proposed a memetic algorithm with population management (MA|PM) to solve the LRP with capacitated routes and depots. MA|PM is a very recent form of memetic algorithm in which the diversity of a small population of solutions is controlled by accepting a new solution if its distance to the population exceeds a given threshold. Yu et al. (2010) implement a simulated annealing heuristic (SA) for the CLRP. Each solution is encoded as a list containing one sublist per depot. Each sublist begins with the index of the depot, followed by its routes separated by dummy zeros. The random moves performed are: relocations of a node, exchanges of two nodes, and 2-opt moves. The nodes involved can be customers, dummy zeros and, in relocations and exchanges, depot nodes. These nodes may belong to the same route, to two routes rooted at the same depot, or to routes from distinct depots. The 2-opt moves are restricted to nodes visited from the same depot. An iterative local search (ILS) by embedding it in a genetic algorithm (GA) is described by Derbel et al. (2012) to solve LRPs. The result GA-ILS is a kind of memetic algorithm in which the local search procedure is replaced by ILS. In another attempt to solve LRPs with metaheuristics, Rath and Gutjahr (2011) consider a three-objective warehouse location-routing problem (WLRP) to establish a supply system after a disaster. This WLRP is a kind of two-echelon LRP with plants, warehouses to be located, and customers. The aim is to minimize the strategic cost (total opening cost of warehouses), to minimize an operative cost (transportation costs from plants to depots and warehousing costs proportional to the throughput of each open warehouse) and to maximize a service measure (total demand satisfied). A metaheuristic based on the epsilon-constraint method is used to compute the Pareto frontier. Each single-objective problem is solved by a metaheuristic based on a mixed integer formulation. Constraints are generated on demand by a variable neighborhood search algorithm and stored in a constraint pool. Results are compared to those obtained by a direct resolution of the mixed integer program (on small instances) or by the classical NSGA-II metaheuristic (on larger instances). They indicate that the proposed solution method gives very good solutions.

Problem description and mathematical formulation

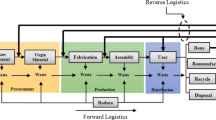
The reverse logistics network discussed in this paper is a multistage logistics network including customers, collection/inspection, recycling, and disposal centers with limited capacities. As shown in Fig. 1, returned products are collected from customer zones into collection/inspection centers and after inspection; they are divided into recoverable products and scrapped products. The recoverable products are carried to the recycling centers, and scrapped products are sent to the disposal centers. The authors implement a CLRPTW in a multi-echelon reverse logistics network. The location-routing problem (LRP) can be defined in this paper as follows. An applicative set of potential collection/inspection, and recycling centers locations and amount of return product of each customer is given. The LRP is to determine the location of facilities and the vehicle routes from facilities to customers to satisfy the objectives of the given problem. The objective of this location-routing problem in RLN is to choose the location and to determine the number of collection/inspection and recycling centers and to determine the quantity of flow between the network facilities.

Fig. 1
figure 1

Pareto diagram

Full size image

Problem assumption

  • All of the returned products from clients must be collected at the collection centers.

  • Each vehicle starts at a depot, visits a set of customers on a route, and returns to the same depot.

  • Each customer is served by one vehicle in exactly one turn and should be assigned to only one open collection/inspection centers.

  • Locations of customers and disposal centers are fixed and predefined.

  • The total returned products of clients on each route is less than or equal to the capacity of the vehicle assigned to that route.

  • The sum of the returned products of the customers assigned to each collection/inspection center must not exceed its corresponding capacity.

  • Recycling centers have limited capacity.

  • A single type of product is considered.

  • Soft time windows are considered.

  • Fleets of all vehicles are heterogeneous.

  • Routing problem is considered only for first echelon.

  • First echelon trip must begin/end at the same open collection/inspection centers.

  • A predefined percent of demand from each customer is assumed as returned products from the corresponding customer.

  • A predefined value is determined as an average scrap fraction.

Model parameters

The following notation is used in the formulation of the capacitated location-routing problem with time window in reverse logistic network design (CLRPTW-RLND) model.

Sets

I :

Set of the candidate points for hybrid collection/inspection centers, ∀i ∊ I

E :

Set of the candidate points for recovery centers, ∀e ∊ E

S :

Fixed set of points for disposal centers ∀s ∊ S

J :

Fixed set of points for customer centers, ∀j, k ∊ J

V :

Set of vehicle routes, ∀v ∊ V

N :

Set of turn of customer ∀n ∊ N

Parameters

d j :

Demand of customer zone j

ra j :

Rate of return percentage from customer zone j

θ :

Average scrap fraction

cas v :

Capacity of vehicle of type v

caf i :

Maximum capacity of hybrid collection/inspection center i

cat e :

Maximum capacity of recycling center e

g i :

Fixed cost of establishing hybrid collection/inspection center i

f e :

Fixed cost of establishing recovery center e

h v :

Fixed cost of using each vehicle that is operated in 1st-echelon for vehicles of type of v

ϕ e :

Recycling cost per unit of product at recycling center e

ct ij :

Transportation cost per unit of returned products from customer zone j to collection/inspection center i

cr ie :

Transportation cost per unit of recoverable products from hybrid collection/inspection center i to recovery center s

cd is :

Transportation cost per unit of scrapped products from hybrid collection/inspection center i to disposal center s

t ijv :

Travel time between node i and j with vehicle v

a j :

Earliest arrival time to customer j of the soft time window

b j :

Latest arrival time to customer j of the soft time window

ue j :

Lower bound of the soft time window for customer j

ul j :

Upper bound of the soft time window for customer j

pe:

Earliest penalty cost for hybrid collection/inspection center (penalty cost of one unit earliest)

pl:

Lateness penalty cost for hybrid collection/inspection center (penalty cost of one unit lateness)

Note: In this paper, we consider one of the time variants where the time constraint is ‘soft’, that is, it can be violated because of the model constraints; in other words, the classical vehicle routing problem with time windows (VRPTW) is an extension of the VRP where the service at each customer must take place within a given time interval (hard time window). The latter is often relaxed in practice (leading to soft time window) which enables early and late servicing with some penalty costs. A soft time window with non-negative boundaries (a j , b j ) is then defined for each node j. The time window at the depot (ue j , ul j ) can be thought of as the scheduling horizon of the problem.

Decision variable

q ijv :

Quantity of returned products shipped from beginning of route from hybrid collection/inspection center i to node j in vehicle route v (load remaining in vehicle v after leaving node j when Starting from collection/inspection center i)

q i1v :

Quantity of load of the vehicle v after leaving hybrid collection/inspection center i

p iev :

Quantity of recoverable products shipped from hybrid collection/inspection center i to recovery centers by vehicle v

o isv :

Quantity of scrapped products shipped from hybrid collection/inspection center i to disposal centers by vehicle v

qT i :

Total amount of return product collected to the hybrid collection/inspection center i

pT e :

Total amount of recoverable products shipped to the recovery center e

ot s :

Total amount of scrapped products shipped to the disposal center s

TCmax :

Maximum time for completion of the collecting return products

TF v :

Time for completion of the collection by vehicle v

w jv :

Starting time of the service to customer j by vehicle v

w e jv :

The amount of earliest time of the starting service to customer j by vehicle v

w l jv :

The amount of Latest time of the starting service to customer j by vehicle v

z ij :

Binary variable which is 1 if customer j is allocated to hybrid collection/inspection centers i and zero otherwise

Y i :

Binary variable which is1 if hybrid collection/inspection center is opened at location i and zero otherwise

Y e :

Binary variable which is 1if recovery center is opened at location e and zero otherwise

x ijnv :

Binary variable which is 1 if vehicle v goes from hybrid collection/inspection center i to customer j on turn of n and zero otherwise

R jkv :

Binary variable which is 1if customer k immediately precedes customer j by vehicle v and zero otherwise

c1 v , c2 v :

Binary variable which is1 if vehicle v is used in first and second level and zero otherwise

as iv :

Binary variable which is1if vehicle v is allocated to hybrid collection/inspection center i and zero otherwise

as ′ iev :

Binary variable which is1if goes from hybrid collection/inspection center i to recovery center e by vehicle v and zero otherwise

as ″isv :

Binary variable which is1if goes from hybrid collection/inspection center i to disposal center s by vehicle v and zero otherwise

In terms of the above notations, the capacitated location-routing problem with time window in reverse logistic network design (CLRPTW-RLND) can be formulated as follows:

Mathematical model

$$\begin{aligned} {\hbox{min} } {{f}}_{1} ({{x}}) = \sum\limits_{{{{i}} \in I}} {{{g}}_{{i}} } Y_{i} + \sum\limits_{{{{e}} \in {{E}}}} {{{f}}_{{e}} {{Y}}_{{e}} } + \sum\limits_{{{{v}} \in {{V}}}} {{{h}}_{{v}} } ({{c}}1_{{v}} + {{c}}2_{{v}} ) \hfill \\ + \sum\limits_{{{{i}} \in {{I}}}} {\sum\limits_{{{{j}} \in {{J}}}} {\sum\limits_{{{{v}} \in {{V}}}} {{\text {ct}}_{{ij}} } } } {{q}}_{{ijv}} + \sum\limits_{{{{i}} \in {{I}}}} {\sum\limits_{{{{e}} \in {{E}}}} {\sum\limits_{{{{v}} \in {{V}}}} ({\text {cr}_{{ie}} } } } + \varphi_{{e}} ){{p}}_{{iev}} \hfill \\ + \sum\limits_{{{{i}} \in {{I}}}} {\sum\limits_{{{{s}} \in {{S}}}} {\sum\limits_{{{{v}} \in {{V}}}} {\text {cd}_{{is}} } } } {{o}}_{{isv}} + \sum\limits_{{{{j}} \in {{J}}}} {\sum\limits_{{{{v}} \in {{V}}}} {({\text {pe}} \times {\text {we}}_{{jv}} } } + \text {pl} \times {\text {wl}}_{{jv}} ) \hfill \\ \end{aligned}$$
(1)
$${\hbox{min} } {{f}}_{2 } ({{x}})\; = \;{\text {TC}}_{\hbox{max} } \;{\text {s}}.{\text {t}}.$$
(2)
$$\sum\limits_{{{{i}} \in {{I}}}} {{{z}}_{{ij}} } = 1\, \quad \forall {{j}} \in {{J}}$$
(3)
$$\sum\limits_{{{{j}} \in {{J}}}} {{{z}}_{{ij}} } \le {{M}} . {{Y}}_{{i}} \;\quad \forall {{i}} \in {{I}}$$
(4)
$$\sum\limits_{{{{n}} \in {{N}}}} {\sum\limits_{{{{v}} \in {{V}}}} {{{x}}_{{ijnv}} } } = {{z}}_{{ij}} \;\quad \forall {{i}} \in {{I}},\;\;{{j}} \in {{J}}$$
(5)
$$\sum\limits_{{{{j}} \in {{J}}}} {{{x}}_{{ijnv}} } \le 1\;\quad \forall {{i}} \in {{I}},\;{{n}} \in {{N}},\;{{v}} \in {{V}}$$
(6)
$$\sum\limits_{{{{j}} \in {{J}}}} {{{x}}_{{ijnv}} } \; \le \;\sum\limits_{{{{j}} \in {{J}}}} {{{x}}_{{{{ijn}} - 1{{v}}}} } \;\quad \forall {{i}} \in {{I}},\;{{n}} \in {{N}},\;{{v}} \in {{V}}$$
(7)
$${{R}}_{{jkv}} \; = \;\sum\limits_{{{{i}} \in {{I}}}} {\sum\limits_{{{{n}} \in {{N}}}} {{{x}}_{{ijnv}} } } {{x}}{}_{{{{ikn}} + 1{{v}}}}\;\quad \forall {{j}},\;{{k}} \in {{J}},\;{{v}} \in {{V}}$$
(8)
$${{q}}_{{ikv}} \; \ge \;{{q}}_{{ijv}} \; + \;{\text {ra}}_{{k}} {{d}}_{{k}} - {{M}}(1 - {{R}}_{{jkv}} )\;\quad \forall {{i}} \in {{I}},\;{{j}},\;{{k}} \in {{J}},\;{{v}} \in {{V}}$$
(9)
$${{q}}_{{ikv}} \le {\text {cas}}_{{v}} \;\quad \forall {{i}} \in {{I}},\;{{k}} \in {{J}},\;{{v}} \in {{V}}$$
(10)
$${{q}}_{{{{i}}1{{v}}}} = 0\;\quad \forall {{i}} \in {{I}},\;{{v}} \in {{V}}$$
(11)
$$qt_{{i}} = \sum\limits_{{{{j}} \in {{J}}}} {\sum\limits_{{{{n}} \in {{N}}}} {\sum\limits_{{{{v}} \in {{V}}}} {{\text ra}_{{j}} {{d}}_{{j}} \times } {{x}}_{{ijnv}} } } \;\quad \forall {{i}} \in {{I}}$$
(12)
$$qt_{{i}} = \sum\limits_{{{{e}} \in {{E}}}} {\sum\limits_{{{{v}} \in {{V}}}} {{{p}}_{{iev}} } } + \sum\limits_{{{{s}} \in {{S}}}} {\sum\limits_{{{{v}} \in {{V}}}} {{{o}}_{{isv}} } } \;\quad \forall {{i}} \in {{I}}$$
(13)
$$(\theta ) {\text {qT}}_{{i}} = \sum\limits_{{{{e}} \in {{E}}}} {\sum\limits_{{{{v}} \in {{V}}}} {{{p}}_{{iev}} } } \;\quad \forall {{i}} \in {{I}}$$
(14)
$${\text {pT}}_{{e}} = \sum\limits_{{{{i}} \in {{I}}}} {\sum\limits_{{{{v}} \in {{V}}}} {{{p}}_{{iev}} } } \;\quad \forall {{e}} \in {{E}}$$
(15)
$${\text {OT}}_{{s}} = \sum\limits_{{{{i}} \in {{I}}}} {\sum\limits_{{{{v}} \in {{V}}}} {{{o}}_{{isv}} } } \;\quad \forall {{s}} \in {{S}}$$
(16)
$${\text {qt}}_{{i}} \le {\text {caf}}_{{i}} {{ Y}}_{{i}} \;\quad \forall {{i}} \in {{I}}$$
(17)
$${\text {PT}}_{{e}} \le {\text {cat}}_{{e }} {{Y}}_{{e}} \;\quad \forall {{e}} \in {{E}}$$
(18)
$$\sum\limits_{{{{i}} \in {{I}}}} {{\text {as}}_{{iv}} } \le {{c}}_{{v}} \;\quad \forall {{v}} \in {{V}}$$
(19)
$$\sum\limits_{{{{j}} \in {{J}}}} {\sum\limits_{{{{n}} \in {{N}}}} {{{x}}_{{ijnv}} } } \le {\text {BM}} \times as_{{iv}} \;\quad \forall {{i}} \in {{I}},{{v}} \in {{V}}$$
(20)
$$\sum\limits_{{{{e}} \in {{E}}}} {{\text {as}}_{{isv}}^{\prime } } + \sum\limits_{{{{s}} \in {{S}}}} {{\text {as}}_{{isv}}^{{^{\prime \prime } }} } \le {\text {as}}_{{iv}} \;\quad \forall {{i}} \in {{I}},{{v}} \in {{V}}$$
(21)
$${\text {cas}}_{{v}} \times {\text {as}}_{{isv}}^{{^{\prime \prime } }} \ge {{o}}_{{isv}} \;\quad \forall {{i}} \in {{I}},{{s}} \in {{S}},{{v}} \in {{V}}$$
(22)
$${\text {cas}}_{{v}} \times {\text {ca}}_{{iev}}^{\prime } \ge {{p}}_{{iev}} \;\quad \forall {{i}} \in {{I}},\;{{e}} \in {{E}},{{v}} \in {{V}}$$
(23)
$${\text {TC}}_{\hbox{max} } \ge {\text {TF}}_{{v}} \;\quad \forall {{v}} \in {{V}}$$
(24)
$${\text {TF}}_{{v}} = \sum\limits_{{{{i}} \in {{I}}}} {\sum\limits_{{{{j}} \in {{J}}}} {\sum\limits_{{{{n}} \in {{N}}}} {{{t}}_{{ijv}} } } } \times {{x}}_{{{{ijn}} = 1{{v}}}} + \sum\limits_{{{{j}},{{k}} \in {{J}}}} {{{R}}_{{jkv}} } \times {{t}}1_{{jkv}} \;\quad \forall {{v}} \in {{V}}$$
(25)
$${{w}}_{{jv}} \ge {\text {ue}}_{{j}} \sum\limits_{{{{i}} \in {{I}}}} {\sum\limits_{{{{n}} \in {{N}}}} {{{x}}_{{ijnv}} } } \;\quad \forall {{j}} \in {{J}},{{v}} \in {{V}}$$
(26)
$${{w}}_{{jv}} \le {\text {ul}}_{{j}} \sum\limits_{{{{i}} \in {{I}}}} {\sum\limits_{{{{n}} \in {{N}}}} {{{x}}_{{ijnv}} } } \;\quad \forall {{j}} \in {{J}},{{v}} \in {{V}}$$
(27)
$${{w}}_{{jv}}^{{e}} \ge {{a}}_{{j}} - {{w}}_{{jv}} - {{M}}\left( {1 - \sum\limits_{{{{i}} \in {{I}}}} {\sum\limits_{{{{n}} \in {{N}}}} {{{x}}_{{ijnv}} } } } \right)\;\quad \forall {{j}} \in {{J}},{{v}} \in {{V}}$$
(28)
$${{w}}_{{jv}}^{{l}} \ge {{w}}_{{jv}} - {{b}}_{{j}} - {{M}}\left( {1 - \sum\limits_{{{{i}} \in {{I}}}} {\sum\limits_{{{{n}} \in {{N}}}} {{{x}}_{{ijnv}} } } } \right)\;\quad \forall {{j}} \in {{J}},{{v}} \in {{V}}$$
(29)
$${{w}}_{{kv}} \ge {{w}}_{{jv}} + {{t}}1_{{jkv}} - {{M}}(1 - {{R}}_{{jkv}} )\;\quad \forall {{j}},\;{{k}} \in {{J}},\;{{v}} \in {{V}}$$
(30)
$$\begin{aligned} {{L}}_{{i,j,k,n,v}} = {{x}}_{{ijnv}} \times {{x}}_{{{{ikn}} + 1{{v}}}} \;\quad \forall {{i}} \in {{I}},\,{{j}},\;{{k}} \in {{J}},\;{{n}} \in {{N}},\;{{v}} \in {{V}} \hfill \\ \hfill \\ \end{aligned}$$
(31)
$$\begin{aligned} {{L}}_{{i,j,k,n,v}} \le {{x}}_{{ijnv}} \;\quad \forall {{i}} \in {{I}},\;{{j}},\;{{k}} \in {{J}},\;{{n}} \in {{N}},\;{{v}} \in {{V}} \hfill \\ \hfill \\ \end{aligned}$$
(32)
$$\begin{aligned} {{L}}_{{i,j,k,n,v}} \le {{x}}_{{{t{ikn}} + 1{{v}}}} \;\quad \forall {t{i}} \in {{I}},\;{t{j}},\;{{k}} \in {t{J}},\;{{n}} \in {{N}},\;{{v}} \in {{V}} \hfill \\ \hfill \\ \end{aligned}$$
(33)
$$\begin{aligned} {{L}}_{{i,j,k,n,v}} \ge {{x}}_{{ijnv}} + {{x}}_{{{{ikn}} + 1{{v}}}} - 1\;\quad \forall {{i}} \in {{I}},\;{{j}},\;{{k}} \in {{J}},\;{{n}} \in {{N}},\;{{v}} \in {{V}} \hfill \\ \hfill \\ \end{aligned}$$
(34)
$$\begin{aligned} {{z}}_{{ij}} ,\;{{Y}}_{{e}} ,\;{{Y}}_{{i}} ,\;{{x}}_{{ijnv}} ,\;{{R}}_{{jkv}} ,\;{{c}}_{{v}} ,\;{\text {as}}_{{iv}} \in \{ 0,\;1\} \;\quad \forall {{i}} \in {{I}},\;{{j}},\;{{k}} \in {{J}},\;e \in {{E}},\;{{n}} \in {{N}},\;{{v}} \in {{V}} \hfill \\ \hfill \\ \end{aligned}$$
(35)
$$\begin{aligned} {{q}}_{{ijv}} ,\;{{p}}_{{iev}} ,\;{{o}}_{{isv}} ,\;\text {qt}_{{i}} ,\;{\text {pt}_{{e}}} ,\;{\text {ot}_{{s}}} ,\;\text {tc}{}_{\hbox{max} },\text {TF}_{{v}} ,\;{{W}}_{{jv}} ,\,{{w}}_{{jv}}^{{l}} ,\;{{w}}_{{jv}}^{{e}} ,\;{{L}}_{{ijknv}} \ge 0\;\quad \forall {{i}} \in {{I}},\;{{j}},\;{{k}} \in {{J}},\;{{e}} \in {{E}},\,\;{{n}} \in {{N}},\;{{v}} \in {{V}} \hfill \\ \end{aligned}$$
(36)

Objective function (1) minimizes the total cost consisting of the sum of the fixed hybrid collection/inspection center location costs, the fixed recovery center location costs, the fixed costs of employing vehicles, variable transportation and processing costs and penalty cost, when arrival time for a node is not in the determined time window, in first echelon. Objective function (2) minimizes the maximum time of completion of the collecting return products. Constraint (3) ensures that each customer must be assigned to a collection/inspection center. Constraint (4) ensures that the customer can be assigned to hybrid collection/inspection center if and only if it is open. Constraints (5)–(8) are related to turn of the customer for collecting their return products. Constraint (9) calculates the vehicle load of each vehicle after finishing the service to each customer. Constraints (10) require that the capacity of each vehicle should be respected. Constraint (11) shows the initial load of each vehicle that is equal to zero. Constraint (12) ensures that the returned products of all customers are collected. Constraints (13)–(16) assure the flow balance at hybrid collection/inspection, recovery and disposal centers. Equations (17) and (18) are capacity constraints on hybrid collection/inspection and recovery centers, respectively. Constraint (19) ensures that each vehicle is allocated to one hybrid collection/inspection. Constraint (20) and (21) ensure that vehicle v is used in first and second level if it is allocated to hybrid collection/inspection center. Constraint (22) and (23) are related to capacity of vehicles in first and second level. Constraint (24) is related to total collected time. Constraint (25) calculates the collected time for each vehicle along a route. Equations (26)–(30) are related to time window Constraints. Constraints (31)–(34) are a set of constraints introduced to convert Constraints (8) to a linear form.

The Constraints (8) is in a nonlinear form; therefore, another binary variable along with a set of constraints is introduced to convert it to a linear form. The transformation equation (Eqs. 31–34) is added to the original constraints. The above equation means that the new variable (L i,j,k,n,v ) is also a binary one. Finally, Constraints (35) and (36) enforce the binary and non-negativity restrictions on decision variables.

Multi-objective optimization

Many real-world problems involve simultaneous optimization of several objective functions. Generally, optimization in terms of the number of objective functions and optimization criteria is divided into two categories of single-objective optimization problems and multi-objective optimization problems. A single-objective optimization algorithm is terminated upon obtaining an optimal or near-optimal solution. The purpose of solving a single-objective problem is to improve the unique performance index that should be the minimum or maximum. But in some cases, the problem may have more than one objective that is called multi-objective optimization problems. And because of the conflict between the objectives, usually by improving the value of one of the objectives, the other one becomes worse. So, it is natural to find a set of solutions depending on the non-dominance criterion, because it is difficult to find a single solution for a multi-objective problem. Solutions which dominate the others but do not dominate themselves, are called non-dominated solutions. When we have a globally optimal solution that is not dominated by any other solution in the feasible space, it is called Pareto optimal. The set of all Pareto-optimal solutions is also termed the Pareto-optimal set or efficient set. Their corresponding images in the objective space are called the Pareto-optimal frontier. There exists various algorithms such as heuristic and metaheuristic, for optimizing the multi-objective optimization problems.

Comparative methods

In this section, we have designed two solution methods, one of them is metaheuristic procedure based on the non-dominated sorting genetic algorithm II (NSGA-II) for small and large test problem, and the other is exact procedure based on the ɛ-Constraint Method. We try to evaluate the efficiency of the suggested a famous multi-objective evolutionary algorithms (EAs), namely NSGA-II with ɛ-Constraint Method. NSGA-II is coded using MATLAB software and run on a personal computer with 2.4 GHZ CPU Intel Core i7 Duo processor and 2.00-GB of RAM memory and ɛ-Constraint method is coded using GAMS software.

Procedure based on ɛ-constraint method

We solve the presented bi-objective model by the ɛ-constraint method in the GAMS software using Baron solver for the given small test problem. There is a conflict between two objectives. It means that the units of our two objectives are minimizing cost and time, respectively. Logically, if we incur more cost, we have less time and vice versa.

This method is based on optimizing one of the most preferred objective functions, and considering the other objectives as constraints. The authors provide some basic definitions to better understand the ɛ-Constraint Method. Without loss of generality, let us assume the following multi-objective minimization problem (MOMP) with m Objectives (Mavrotas 2009):

$$\begin{aligned} {\hbox{min}} \;({{f}}_{1} ({{x}}),\;{{f}}_{2} ({{x}}), \ldots ,{{f}}_{{m}} ({{x}})) \hfill {\text {s.t.}} \hfill \\ {{g}}({{x}}) \le 0,\;\;{{h}}({{x}}) = 0 \hfill \\ {{x}} \in {{s}}, \hfill \\ \end{aligned}$$
(37)

where x is the vector of decision variables and S is the feasible region. As we said, in this method, we optimize one of the objective functions using the other objective functions as constraints, as shown below:

$$\begin{aligned} {\hbox{min} } {{f}}_{1} ({{x}}) \hfill {\text {s.t.}} \hfill \\ {{f}}_{2} ({{x}}) \le {{e}}_{2} , \hfill \\ {{f}}_{3} ({{x}}) \le {{e}}_{3} , \ldots \hfill \\ {{f}}_{{n}} ({{x}}) \le {{e}}_{{n}} , \hfill \\ {{g}}({{x}}) \le 0,\;{{h}}(E) = 0, \hfill \\ {{x}} \in {{s}}. \hfill \\ \end{aligned}$$
(38)

By parametrical variation in the rRight hand side (RHS) of the constrained objective functions (e n ), we can obtain the efficient solutions of the problem and draw Pareto diagram (Fig. 1). One of the advantages of the ɛ-constraint in each run is to produce a different efficient solution, thus obtaining a more rich representation of the efficient set.

Procedure based on non-dominated sorting genetic algorithm II (NSGA-II)

NSGA-II is one of the most well-known multi-objective optimization evolutionary algorithms. It is basically a genetic algorithm with special characteristics in the selection phase. NSGA, for the first time, was introduced by Deb and Srinivas (1995), but because of some of the disadvantages, such as computational complexity, time-consuming and inadequacy of this edition, the second edition abbreviated NSGA-II was developed by Deb et al. (2002). The main features of this algorithm are: fast non-dominated sorting approach, fast crowded distance estimation procedure, simple crowded comparison operator and binary tournament selection operator (Tavakkoli-Moghaddam et al. 2012). Generally, the principal components of the NSGA-II procedure are summarized below.

Population initialization

An initial parent population p 0 of size number of population (n pop) is generated randomly based on the problem range and constraint. A series of genes that arrange sequentially is called chromosome. The number of genes in a chromosome is equal to the number of decision variables. Chromosome description is one of the most significant parts of the algorithm that is taken into account as the code form. In this paper, there-position is used for chromosome. The first position shows the allocation of customers to the hybrid collection/inspection centers and allocation of first level’s vehicles that is formed with a matrix dimensions I*(J + V) (the number of rows = number of hybrid collection/inspection center and the number of columns = number of customers + number of vehicle). The second part shows the allocation of recycling center to the hybrid collection/inspection centers and allocation of second level’s vehicles that is formed with a matrix dimensions I*(E + V). Finally, the third part shows the allocation of disposal centers to the hybrid collection/inspection centers and allocation of second level’s vehicles that is formed with a matrix dimensions I*(S + V). Moreover, Element of the matrix or each gene value (allele) of the chromosome is generated randomly of real values in the range (0, 1). Figure 2 depicts the structure of a chromosome.

Fig. 2
figure 2

Structure of a chromosome for algorithm NSGA-II

Full size image

Chromosome structure consists of three sections. Since most of the constraints and variables are related to each other sequentially, the following procedures are applied for constraint handling.

There are three types of variables: location, routing and allocation, and some continuous variables. Location variables are first stage. In other words, location decisions are selected randomly earlier according to capacity constraints. In this way, solutions will be generated feasibly. Also, allocation and routing decisions are made based on the previous location decisions. Therefore, nodes are assigned to previous stage nodes according to capacities and then, a random routing solution is selected. By this way, this part of solution is feasible. Finally, continuous variables are computed sequentially. In this way, if a variable such as time window be infeasible, then the objective function will be penalized.

Non-dominated sorting

Before selection is performed, every individual (chromosome) in the population is ranked based on the non-domination sorting procedure to create Pareto fronts. All non-dominated individuals are classified into one category in such a way that each individual of the population under evaluation obtains a rank equal to its non-domination level (1 is the best level, 2 is the next-best level, and so on), where the Front one consists of all solutions with the smallest rank, that are not dominated by any other solutions. The second front is made by all solutions that only dominated by solutions in front number one. A multi-objective model has n objective functions, solution x and y are placed in same front when do not dominate each other, a solution x dominate y when the following conditions are successful:

  • For all the objective functions, solution x is not worse than another solution y.

  • For at least one of the n objective functions, x is strictly better than y.

Crowding distance

Crowding distance proposes an estimate of the density of solutions surrounding a particular solution. The individuals in population at the first time are selected based on rank and the member with the lower rank is chosen, but if two solutions have the same rank, the remainder of the population is selected based on crowding distance between members. So, the member with the larger crowding distance is selected if they share an equal rank. The crowding distance used in the NSGA-II is computed by the following equation,

$$d_{i}^{j} = \sum\limits_{i = 1}^{n} {\frac{{f_{j}^{i + 1} - f_{j}^{i - 1} }}{{f_{j}^{\hbox{max} } - f_{j}^{\hbox{min} } }},}$$
(39)

where f min j and f max j are, respectively, the minimum and maximum values of the objective function j in the population, f i+1 j is the value of the objective function j of the (i + 1)-th solution and f i−1 j is the value of the objective function j of the (i − 1)-th solution.

Crossover

Crossover operator combines characteristics of parent chromosomes and generates new solutions called offspring (children) by changing some part of parent chromosomes. The idea behind crossover is that the new chromosome may be better than both of the parents if it takes the best characteristics from each of the parents with crossover rate p c that is usually consider 0.5 < p c < 1. There are several ways for crossover operator, including: one point crossover, partially mapped crossover (PMX), ordered crossover (OX), Cycle crossover (CX), and Arithmetic crossover. Generally, it chooses two parent chromosomes from a population based on the crowding selection operator described, with a crossover chance, crossover this parents to form new offspring through mating pairs of chromosomes. Next, a new population of offspring with a size of n is created. We can use the selection, the crossover, and the mutation operators to create a population consisting of the current and the new population of the size of (n pop + n). Proper crossover operator called arithmetic crossover is utilized in this paper, arithmetic crossover operator linearly combines two parent chromosome vectors to produce two new offspring according to the equations: (α is a random weighing factor chosen before each crossover operation). Figure 3 depicts the graphical representation of arithmetic crossover with α = 0.5.

Fig. 3
figure 3

shows a graphical representation of Arithmetic crossover with α = 0.5

Full size image
$$\begin{aligned} {{y}}_{{2{{i}}}} = \alpha_{{i}} {{x}}_{{2{{i}}}} + (1 - \alpha_{{i}} ){{x}}_{{1{{i}}}} \hfill \\ {{y}}_{{1{{i}}}} = \alpha_{{i}} {{x}}_{{1{{i}}}} + (1 - \alpha_{{i}} ){{x}}_{{2{{i}}}} \hfill \\ \end{aligned}$$
(40)

Mutation

Unary variation operator in genetic algorithm is named mutations. After generating the children from the crossover operator, mutations takes place. Mutations operator as well as the crossover operator creates a new space for searching in the algorithm. To enhance the diversity of a newly generated population, a mutation operator comes to the picture at the time of movement from the current population to the new population to explore new solution spaces. Using a mutation operator, a few genes of a candidate chromosome are randomly selected to change their values based on a predetermined mutation probability of pm. Mutation helps to prevent the population from stagnating at any local optima. Based on a permutation encoding, there are different mutation operators such as random resetting mutation, scramble mutation, flip bit, and uniform, inversion mutation, and mutation for decimal number, shift, and swap that can generate neighborhoods of a current solution. In this paper, we employ the mutation operator for decimal number in solution algorithm. In this case, in which the value of each gene replaced with one of the values in the range of L i (lower bound) to U i (upper bound) randomly. The mutation, in Eq. (35) is shown.

$$< {{x}}_{ 1} , \ldots ,{{ x}}_{{n}} >\,\rightarrow \; < {{x}}_{1}^{'} , \ldots ,\;{{x}}_{n}^{'}> ;\;{{x}}_{i} ,\;{{x}}_{i}^{'} \; \in \;[{{L}}_{{i}} ,{{U}}_{{i}} ]$$
(41)

Recombination and selection

In steps of the NSGA-II algorithm, there are two steps that the algorithm should do selection. First selection of individuals is carried out using a binary tournament selection operator. The binary tournament selection strategy repeatedly selects one parent regarding n from each pair of two randomly selected individuals until all n pop parents have been selected. These parent individuals are then paired randomly. As we said with crossover probability pc, each pair is recombined by the crossover operator to create two child individuals that is enter the offspring population; Otherwise the two parents undergoes a mutation by the mutation operator with mutation probability pm and then enter the offspring population so we have new generated solutions. Afterward, the current population and new generated solutions are combined together. Then sorting is performed using the value of the non-dominance and using the crowding distance. If two populations are from different fronts, the lowest front number is selected and if they are belong to the same front, the solution with the highest crowding distance is selected to form a mating pool. Finally, a population of an exact size of n pop is obtained using the sorting procedure. The new population is used to generate the next new offspring by repeating the above steps in order. This process is repeated until the stopping condition is met. The stopping criterion considered is a fixed number of iterations.

Computational experiments

This section presents a fair comparison between the two solution methods, to compare the numerical results generated by the proposed NSGA-II and ɛ-Constraint proposed here. For this target, 2 problem groups, plans one in small sizes, and other in medium and great sizes. First smaller sample problem solved by NSGA-II and resulted solutions compare by ɛ-constraint method with resulted solutions from model solving.

Parameter values

Parameters in these test problems have different values, but in a defined tolerance. Table 1 shows uniform distribution for parameters.

Table 1 Uniform distribution for different parameters in each test problem
Full size table

Parameter tuning

To evaluate the performance of the algorithm, we set the assigned value of the algorithm parameters. Parameter values have a very significant effect on the efficiency of the algorithm. If these values are not set truly, getting the proper result will become difficult. To tune the parameters of algorithms, we consider two different sets of problems, namely small sizes (i.e., problem numbers 1–10) and large sizes (i.e., problem number 10–20). To determine the values of parameters, we use the Taguchi methodology. In this section, each algorithm is run for different combinations of parameters and their levels. In the Taguchy methodology, we need an index to compare different combinations of parameters. The aim of this method for designing parameters was reaching a mean value of the objective function and reduces variation in the response variable. Table 2 shows the parameters and their levels for small and large sizes in the NSGA-II algorithm.

Table 2 Factors and their levels in the NSGA-II algorithm for small (S) and large (L) sizes
Full size table

Parameters are selected by trial and error and then best ones are selected.

Table 3 shows the default value for different parameters in each test problem. According to Table 3, different test problems are carried out in Tables 4 and 6.

Table 3 Default value for different parameters in each test problem
Full size table
Table 4 Comparison between the performances of ɛ-Constraint and the proposed NSGA-II (optimality and runtime) for small instances
Full size table

Comparison results of metaheuristic and exact solution methods

Ten samples were solved by NSGA-II and ɛ-Constraint in small sizes and were compared in the Table 4. In Table 4, first column represents problem number, second and third columns are customer index and hybrid collection/inspection centers index, respectively. And columns fourth and fifth show recovery centers and disposal centers indexes, respectively. And column sixth and seventh ones show vehicles index and turn of customer index, respectively. Columns eighth–thirteenth show the value of objective function 1 and objective function 2 with runtime which is resulted from running by ɛ-Constraint and NSGA-II. Finally, last columns show the amount of error or Gap (Eq. 36) between two methods.

Figure 4 shows that the exact time solution increases exponentially. Comparing the exact time and the time of solving meta-heuristic algorithm from Fig. 4 and Table 4, it can be seen that metaheuristic algorithm has reached optimal solution. This result makes the applicability of the algorithm clear.

Fig. 4
figure 4

Comparison of two methods to evaluate solutions based on time and sample

Full size image

The payoff Table 5 and Pareto Fig. 5 which obtains from running Gams software are given for Example 5. Pareto chart shows that with increasing time, total cost is decreasing and vice versa, so they are in conflict with each other. Also, amount of ɛ for Pareto chart is calculated by Eq. (42).

Table 5 Payoff table of problem 5
Full size table
Fig. 5
figure 5

The Pareto front chart of sample 5 in GAMS Software

Full size image
$$\varepsilon = 30055.120 + \frac{(49538.743 - 30055.120)}{5} \times counter$$
(42)

Figure 6 shows the optimization processes and solving time. From this figure, it can be said that time chart slope is decreasing. This leads us to the conclusion that metaheuristic algorithm is very applicable.

Fig. 6
figure 6

The descending trend of the relative optimality and runtime ratios

Full size image

10 instances or samples of large problems have been solved by NSGA-II algorithm and such as Table 4; the results are shown in Table 6.

Table 6 Objective function and runtime of the NSGA-II algorithm for large instances
Full size table

Figure 7 shows the Pareto front chart of sample 15 which is obtained from running Matlab software. Pareto chart shows that with increasing time, total cost is decreasing and vice versa, so they are in conflict with each other.

Fig. 7
figure 7

The Pareto chart of sample 15 in MATLAB software

Full size image

Conclusions

This paper has presented a new bi-objective location-routing problem (LRP) with attributes such as multi–level in a reverse logistics network, multiple depots, capacitated and heterogeneous fleets of vehicles, soft time windows, and penalty cost. Warning and threat on environment have forced the researchers to notice to the transportation and reverse logistics activities as collecting of expired products can have great effect on the environment seriously and think to application solutions.

The proposed RL network model included hybrid collection/inspection centers, recovery centers and disposal centers. We presented a new bi-objective mathematical programming (BOMP) for LRPTW in reverse logistic. Since this type of the problem was NP-hard, the Non-dominated Sorting Genetic Algorithm II (NSGA-II) was proposed to reach the Pareto frontier for the proposed problem in large sized problems.

At first, we solved problem with ɛ-Constraint method by GAMS software, but due to the complexity of the problem and available processing facilities, when the size of the instances increased for problems and for dimensions bigger than ten customers, metaheuristic method must, therefore, be applied. A number of test problems have been generated to evaluate the performance of the proposed algorithm (non-dominated sorting genetic algorithm II (NSGA-II)) in comparison with ɛ-Constraint. The result indicated that NSGA-II worked more efficiently than the ɛ-Constraint.

For further researches, we can suggest the following notes:

  • Authors may focus on handling uncertainties in traveling times and on exploring LRP in a closed-loop supply chain system.

  • The multi-periods LRP can be considered.

  • Robust optimization technique may be applied to develop model.

  • Inventory optimization can be considered through mathematical modeling.