Introduction

Supplier selection is turning to become one of the crucial decisions in operations management area for many companies. Nowadays that competition plays a major role in business, two factors, namely, cost reduction and increase in quality of products, are keys to success of a company. Attaining these two factors is heavily dependent on having appropriate suppliers. Therefore, selecting appropriate suppliers can increase the competitiveness of a business.

The main cost of a product is mostly dependent on the cost of raw material and component parts in most industries (Ghodsypour and O’Brien 2001). Under such a condition the raw material supply and its inventory control can play a key role in the efficiency and effectiveness of a business and have a direct impact on cost reduction, profitability and its flexibility. Regarding supplier selection, there are two general situations:

Single sourcing A situation in which there is no constraint and a single supplier of an item is able to satisfy all requirements of the buyer.

Multiple sourcing In this situation there are many suppliers of a required item, but no single suitable supplier can satisfy all requirements of the buyer. Thus, the buyer must choose “an appropriate set of suitable supplies” to work with (Ghodsypour and O’Brien 1998).

Considering many factors such as variations in price, terms and conditions, quality, quantity, transportation costs and distances, etc. of each supplier, the multiple sourcing situations usually involves taking complex decisions.

While there is a paucity of research that takes into account different aspects of this complex decision situation, only a limited number of mathematical models have been proposed for such decisions. Many of the proposed models consider “net price” as the main factor, a few of them consider “the total costs of logistics”.

The present study investigates the issue of multiple sourcing and proposes mathematical models based on considering factors such as net price, transportation costs, inventory costs and shrinkage problems.

The rest of this paper is organized as follows. In “Background” section literature review is presented. In “The situation” section, the case study is described. The mathematical formulating of problem is presented in “Formulating the models” section. Data collection and parameters are described in “Parameters of model” section. Computational result is presented in “Model runs and results” section and finally, some concluding remarks are given in “Discussion and conclusion” section.

Background

Supplier selection literature may generally be divided into two areas: First, descriptive, survey type approaches and, second, quantitative modeling methods. In the first area, the researches of Dickson (1966) and Weber et al. (1991) should be mentioned as the most comprehensive ones. Dickson has identified and summarized a number of criteria that purchasing managers consider for supplier selection. In his view, the most important criteria are quality, delivery, and the performance history of the supplier. Weber et al. (1991) in a review of 74 articles on supplier selection criteria, found that the most important factor is net price, yet, they suggested that supplier selection is dependent on a multitude of factors with different priorities, depending on the particular purchasing situation.

In the second area, which is more relevant to this article, a few number of fine research attempts should be mentioned here.

Benton (1991) applied Lagrange relaxation to develop a non-linear program for supplier selection under various conditions including multiple suppliers, multiple items, resource limitations and quantity discount. Ghodsypour and O’Brien (1997) suggested integrated analytical hierarchy process (AHP) with mixed integer programming to develop a decision support system (DSS). Their objective was to reduce the number of suppliers. Ghodsypour and O’Brien (1998) also developed a model to take into account both qualitative and quantitative factors. This approach was based on the integration of AHP and linear programming model. In a further development Ghodsypour and O’Brien (2001) presented a mixed integer non-linear programming model to solve the multiple sourcing problems. Their model takes the total cost of logistics into consideration. Kumar et al. (2004) advised a fuzzy goal programming approach to solve the vendor selection problem in case of multiple objectives. Chen et al. (2006) presented a fuzzy decision making approach to solve the supplier selection problem. They proposed linguistic values to evaluate the ratings for a number of quantitative and qualitative factors including quality, price, flexibility, and delivery performance. Their model shown to be very good tool for supplier selection decision making situation. Basnet and Leung (2005) investigated the problem of supplier selection considering the lot-sizing. Amid et al. (2006) represented multi objective linear programming model to supplier selection. Lin and Chang (2008) propose mixed-integer programming and fuzzy TOPSIS approach to solve the supplier selection problem. Aissaouia et al. (2007) have extended previous survey papers by presenting a literature review that covers the entire purchasing process and covers internet-based procurement environments. In the mentioned work they have focused especially on the final selection stage that consists of determining the best mixture of vendors and allocating orders among them so as to satisfy different purchasing requirements. Also, they have concentrate mainly on works that employ operations research and computational models. Farzipoor saen (2007) has considered widespread application of manufacturing philosophies such as just-in-time (JIT), emphasis has shifted to the simultaneous consideration of cardinal and ordinal data in supplier selection process and proposed an innovative method, which is based on imprecise data envelopment analysis (IDEA) to selected the best suppliers in the presence of both cardinal and ordinal data. Ustun and Aktar Demirtas (2008) have recommended an integrated approach of analytic network process (ANP) and multi-objective mixed integer linear programming (MOMILP) for supplier selection problem. Their approach considers both tangible and intangible factors in choosing the best suppliers and defines the optimum quantities among selected suppliers to maximize the total value of purchasing (TVP), and to minimize the total cost and total defect rate and to balance the total cost among periods. Soukhakian et al. (2007) developed a model based on the Ghodsypour and O’Brien (2001) model. The contribution of the developed model is compared with basic the basic model which consider limitations such as integer number of orders and minimum assigned order quantity to each supplier. Due to the complexity of model and its non-linearity, the model is solved by genetic algorithm. Rabieh et al. (2008) developed a new model based on the Ghodsypour and O’Brien (2001) model for a real case of the agglomeration unit of Isfahan Steel Company. In this model assume that some suppliers of iron concentrate in have to cover the inventory in turn during each ordering cycle (T), while other suppliers of iron ore deliver their shipments simultaneously. In end, the non-linear model is solved by LINGO 8 software. Jafarnezhad et al. (2009) introduced a fuzzy decision making approach for supplier selection problem in case of single sourcing. In this research, the fuzzy TOPSIS method was developed for ranking and selecting suppliers. At the end, a numerical example was introduced for showing performance of the developed method. Wu and Blackhurst (2009) presented a supplier selection and evaluation method based on an extension of data envelopment analysis (DEA) that can efficiently evaluate suppliers. Kuo and Lin (2012) introduced an integrated approach of analytic network process (ANP) and data envelopment analysis (DEA) in solving supplier selection problem. Their model also considered green indicators due to environmental protections issues. Finally, Mendoza and Ventura (2012) presented two mixed integer nonlinear programming models to select the best suppliers and determine order quantities. Their research integrated the issues of inventory management and supplier selection. Rao et al. (2013) developed a new approach to design a multi-echelon, multi-facility, and multi-product supply chain in uncertain environment in fuzzy form. In this research, a mixed integer programming was formulated at strategic level and a non-linear programming model was presented in tactical level. In the tactical level, inventory control of raw material of suppliers was considered (Table 1).

Table 1 The features of other reviewed quantitative researches and our research
Full size table

The situation

The agglomeration unit of Isfahan Steel works—one of the largest steel manufacturing firms in the ME region located in central Iran—is the case studied in this research. The main task of this unit is to agglomerate different kinds of raw materials in specific proportions. Most of the raw materials come from different quarries and plants scattered all over the country. The materials are bought and transported to the works mainly via railroads and sometimes by trucks in distances even up to 1300 km. The functional and financial importance of each required raw materials for agglomeration unit found to be different in nature. So, as the first step, a classification of inventory items should have been curried out prior to actual modeling. The following three popular classification methods, so called selective inventory control techniques, are usually applied for grouping inventory items:

  • ABC analysis, classifies items in terms of annual financial requirement.

  • VED analysis, classifies items in terms of their functional importance (Vital, Essential, Desirable).

  • FNS analysis, classifies items in terms of their movement speed (Fast, Normal, Slow; Nair 2002).

Using ABC and VED methods, the inventory items of agglomeration plant were analyzed, and iron ore and iron concentrate were found to be the most important raw materials respectively. Thus, modeling in this study was focused around the purchasing and supply of these two items.

Iron concentrate is a supplementary material which is very similar to iron ore in appearance and should be mixed with iron ore in agglomeration process. Since it contains more Fe; its price is much higher than iron ore. However, to obtain a desired and consistent quality of the agglomeration process output, a right percentage of these two materials should be mixed together each time. The needed iron ore and concentrate for agglomeration plant is purchased from five different suppliers, none of which has the sufficient capacity to supply the whole annual requirements. Furthermore, there are some quality variations in their products and each supplier has its own supply characteristics.

The developed models in this study take into account such variations, and are formulated in a way to obtain a right combination of the raw materials in one hand, and minimize the total inventory costs in the other.

Formulating the models

Defining model parameters and variables

Before describing the model, the pertaining parameters and variables are defined as follows:

Decision variables

  • Q: Ordered quantity to all suppliers in each period.

  • Q i : Ordered quantity to ith supplier in each period.

  • X i : Percentage of Q assigned to ith supplier.

    $$ Y_{i} = \left\{ \begin{aligned} 1\quad {\text{if}}\;X_{i} > 0 \hfill \\ 0\quad {\text{if}}\;X_{i} = 0 \hfill \\ \end{aligned} \right. $$

Parameters

  • D: Annual iron ore and concentrate demand (in term of tons).

  • T: The length of each period.

  • T i : Part of the period in which the lot of ith supplier (Q i ) is used.

  • n: Number of suppliers

  • C i : Annual capacity of the ith supplier to supply raw material.

  • C ti : Transportation cost for ith supplier per unit of raw material.

  • r: Inventory holding cost rate.

  • A i : Ordering cost of ith supplier’s raw material.

  • P i : Selling price of ith supplier’s raw material.

  • h i : Percentage of moisture in the item of the ith supplier.

  • \( D^{\prime } \): Speed of material consumption.

  • \( P^{{^{\prime } }} \): Speed of receiving materials.

  • SS: Safety stock.

  • SS i : Safety stock of the ith supplier’s item.

  • $$ \beta_{i} = (P_{i} + C_{ti} )\quad {\text{and}}\quad \alpha_{i} = \left( {1 - \frac{{D_{i}^{\prime } }}{{P_{i}^{\prime } }}} \right) $$

Other parameters and variables will be described later.

The basic assumptions

  • Constant annual demand (D)

  • Infinite raw materials storage space

  • Stable prices over the year

  • Gradual receiving and consumption of raw materials

  • Stable safety-stock levels

  • Stock-out is not allowed.

Graphical explanation of models

The basic model

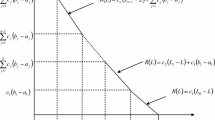
The basic model is built following the approach and assumptions of Ghodsypour and O’Brien (2001) model. This model assumes instant, in-simultaneous order receives from different suppliers and gradual consumption of the materials. Figure 1 shows the behavior of inventory levels of an item under the assumptions of this model.

Fig. 1
figure 1

Inventory behavior in the basic model

Full size image

In Fig. 1, total order cycle (T) is equal to the sum of order cycles of every supplier (T i ) and at the time one supplier’s inventory is used up, the next supplier’s shipment would arrive in.

In general, this model is applicable to situations where, the quality specification of receiving items from different sources is identical. And no mixing of different items is required.

The new models

Because of the need for mixing iron ore and concentrating on the agglomeration process, the basic model couldn’t be applied for the current situation. Furthermore, the inventory supply is not instantaneous, but placed orders are shipped gradually. So, the basic model had to be manipulated to fit the situation correctly. Two slightly different possibilities were considered as shown in Figs. 2 and 3.

Fig. 2
figure 2

Inventory behavior in Model A

Full size image
Fig. 3
figure 3

Inventory behavior in Model B

Full size image
Model A

The two supplier of iron concentrate in Model A (Q 4 and Q 5) have to cover the inventory in turn during each ordering cycle (T), while the three suppliers of iron ore deliver their shipments simultaneously.

Model B

In Model B all suppliers send their shipments simultaneously, therefore, they are under less pressure to keep up with a tight delivery schedule.

Comparing with The basic model, at the first glance, one may expect a rise in average inventory in Models A and B, which leads to an increase in total annual carrying costs as a result. But, as we will see later, the inherent flexibility of the new models paves the way for formulating more effective ordering policies. This would prevent such increase in costs to materialize in practice.

Obviously, Models A and B were formulated for different purchasing behaviors. The formulation process of both models is very similar to each other. The slight differences actually are in formulating the carrying cost in objective function and in the quality constraints of the models. So, we skip from presenting such details here, and continue our model formulation only for Model A.

Formulating the objective function

Because of the objective function of this model is formed from inventory related costs such as the purchasing price, transportation costs, carrying and ordering costs, shrinkage cost, it is a minimizing type objective function. The shrinkage cost is mainly related to the evaporation of raw materials moisture during the agglomeration process. Since the iron ore quarries are located in both dray and wet areas of the country, the water content of their stones differ significantly, and should be taken into account as a part of the total annual purchasing cost.

Annual purchasing cost (APC)

Since ordering quantity (Q) should be shared by n = 5 suppliers, we have the following:

$$ Q = \sum\limits_{i = 1}^{n} {Q_{i} } \quad Q_{i} = X_{i} Q\quad T_{i} = X_{i} T\quad 0 \le X_{i} \le 1 \, \quad \sum\limits_{i = 1}^{n} {X_{i} = 1} \quad i = 1,2, \ldots ,n $$

Since annual purchasing from ith supplier is X i D and its price is P i , APC is:

$$ {\text{APC}} = \sum\limits_{i = 1}^{n} {X_{i} P_{i} D\quad i = 1,2, \ldots ,n} $$

Annual transportation cost (ATC)

ATC is computed by multiplying annual purchasing quantity, and transportation tariff, for ith supplier, thus:

$$ {\text{ATC}} = \sum\limits_{i = 1}^{n} {X_{i} C_{ti} D} \quad i = 1,2, \ldots ,n $$

Annual weight reduction cost (AWRC)

As we mentioned earlier, the moisture content of receiving shipments from each supplier is significantly different. Therefore, the weight reduction of materials due to evaporation in agglomeration process should be taken into account. The data for this is obtainable from Isfahan Steel works daily Lab Reports. Let h i be the average moisture fraction of ith supplier, then, AWRC is computed as:

$$ {\text{AWRC}} = \sum\limits_{i = 1}^{n} {X_{i} D(h_{i} )(P_{i} + C_{ti} )} = \sum\limits_{i = 1}^{n} {X_{i} Dh_{i} (P_{i} + C_{ti} )} $$

The above formula considers the fact that the evaporated moisture is actually bought and paid for its transportation.

To avoid unnecessary repetition, let \( \beta_{i} \) be equal to \( (P_{i} + C_{ti} ) \)1. Hence:

$$ {\text{AWRC}} = \sum\limits_{i = 1}^{n} {X_{i} Dh_{i} \beta_{i} } \quad i = 1,2, \ldots ,5 $$

And, the sum of forgoing three costs is:

$$ {\text{APC}} + {\text{ATIC}} + {\text{AWRC}} = \sum\limits_{i = 1}^{n} {X_{i} } D(1 + h_{i} )(P_{i} + C_{ti} ) = \sum\limits_{i = 1}^{n} {X_{i} } D(1 + h_{i} )\beta_{i} $$

Therefore, it is inferred that the unit cost of ith supplier’s material in agglomeration process is equal to \( (1 + h_{i} )\beta_{i} \). We will apply this formula to compute annual holding (carrying) cost.

Annual holding cost (AHC)

Referring to different behavior of inventory levels in Models A and B, especially in regard with iron concentrate, obviously, the formulation of AHC differs slightly. To save us time, we proceed with formulating AHC for Model A only.

Average inventory in gradual receipt of shipments is equal to: \( \frac{Q}{2}\left( {1 - \frac{{D^{\prime } }}{{P^{\prime } }}} \right) + {\text{SS}} \), or in general is \( \frac{Q}{2}\left( {1 - \frac{{D_{i}^{\prime } }}{{P_{i}^{\prime } }}} \right) + {\text{SS}}_{i} \), so, the average holding cost in T i would be:

$$ \left( {X_{i} \frac{Q}{2}\left( {1 - \frac{{D_{i}^{\prime } }}{{P_{i}^{\prime } }}} \right) + {\text{SS}}_{i} } \right)rp_{i} $$

In order to avoid unnecessary repetitions, let \( \left( {1 - \frac{{D_{i}^{\prime } }}{{P_{i}^{\prime } }}} \right) \) be equal to \( \alpha_{i} \). Since SS is a constant value, it will be omitted in differentiation process any way. Thus, Total Holding Cost per Period (THCP) is formulated as follows:

$$ {\text{THCP}} = X_{1} \frac{Q}{2}\alpha_{1} r(1 + h_{1} )\beta_{1} T_{1} + X_{2} \frac{Q}{2}\alpha_{2} r(1 + h_{2} )\beta_{2} T_{2} + \cdots + X_{n} \frac{Q}{2}\alpha_{n} r(1 + h_{n} )\beta_{n} T_{n} $$

In Model A, for those suppliers that we have on hand inventory during the whole order cycle, \( \,\,T_{i} = T \), \( i = 1,2, \ldots ,m \), and for those vendors that we have on hand inventory just during a part of cycle, \( T_{i} = \frac{{X_{i} }}{{\sum\nolimits_{i = m + 1}^{n} {X_{i} } }}T \), \( i = m + 1, \ldots ,n \). Now, we know that \( T = \frac{Q}{D} \), and considering the shape of the model, and the fact that n = 5, we have:

$$ T_{1} = T_{2} = T_{3} = T = \frac{Q}{D},\quad T_{4} = \frac{{X_{4} }}{{X_{4} + X_{5} }}\frac{Q}{D},\quad T_{5} = \frac{{X_{5} }}{{X_{4} + X_{5} }}\frac{Q}{D} $$

(Here the flexibility and adoptability of the new models become clearer, as when the model, for any reason, does not allow purchase from supplier 4, for instance, then, we have: \( X_{4} \) = 0, T 4 = 0, and T 5 = T).

However, the detailed computation of THCP is:

$$ \begin{aligned} {\text{THCP}} & = X_{1} \frac{Q}{2}\alpha_{1} r(1 + h_{1} )\beta_{1} \frac{Q}{D} + X_{2} \frac{Q}{2}\alpha_{2} r(1 + h_{2} )\beta_{2} \frac{Q}{D} + X_{3} \frac{Q}{2}\alpha_{3} r(1 + h_{3} )\beta_{3} \frac{Q}{D} \\ & \quad + X_{4} \frac{Q}{2}\alpha_{4} r(1 + h_{4} )\beta_{4} \frac{{X_{4} }}{{X_{4} + X_{5} }}\frac{Q}{D} + X_{5} \frac{Q}{2}\alpha_{5} r(1 + h_{5} )\beta_{5} \frac{{X_{5} }}{{X_{4} + X_{5} }}\frac{Q}{D} \\ \end{aligned} $$

or

$$ {\text{THCP}} = \sum\limits_{i = 1}^{3} {X_{i} Q^{2} } \frac{{\alpha_{i} r(1 + h_{i} )\beta_{i} }}{2D} + \frac{{X_{4}^{2} }}{{X_{4} + X_{5} }}Q^{2} \frac{{\alpha_{4} r(1 + h_{4} )\beta_{4} }}{2D} + \frac{{X_{5}^{2} }}{{X_{4} + X_{5} }}Q^{2} \frac{{\alpha_{5} r(1 + h_{5} )\beta_{5} }}{2D} $$

Still, the shorter form for THCP is

$$ {\text{THCP}} = \frac{{rQ^{2} }}{2D}\left( {\sum\limits_{i = 1}^{3} {X_{i} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right) + \frac{{rQ^{2} }}{2D}\frac{1}{{\sum\nolimits_{i = 4}^{5} {x_{i} } }}\left( {\sum\limits_{i = 4}^{5} {X_{i}^{2} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right) $$

The Annual Holding Cost (AHC) is computed by multiplying THCP and the number of order cycles per year, or

$$ {\text{AHC}} = ({\text{THCP}}) \times \frac{1}{T} = \frac{{({\text{THCP}})D}}{Q} $$

And with suitable substitutions, we have

$$ {\text{AHC}} = \frac{{rQ^{2} }}{2D}\left( {\sum\limits_{i = 1}^{3} {X_{i} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right)\frac{D}{Q} + \frac{{rQ^{2} }}{2D}\frac{1}{{\sum\nolimits_{i = 4}^{5} {x_{i} } }}\left( {\sum\limits_{i = 4}^{5} {X_{i}^{2} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right)\frac{D}{Q} $$

or, simply

$$ {\text{AHC}} = \frac{rQ}{2}\left( {\sum\limits_{i = 1}^{3} {X_{i} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right) + \frac{rQ}{2}\frac{1}{{\sum\nolimits_{i = 4}^{5} {x_{i} } }}\left( {\sum\limits_{i = 4}^{5} {X_{i}^{2} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right) $$

Also holding cost of Model B is:

$$ {\text{AHC}} = \frac{rQ}{2}\left( {\sum\limits_{i = 1}^{5} {X_{i} } \alpha_{i} (1 + h_{i} )\beta_{i} } \right) $$

Annual ordering cost (AOC)

Due to the fact that the required raw materials are ordered and purchased from n suppliers, the Ordering Cost each Period (OCP) is:

$$ {\text{OCP}} = \sum\limits_{i = 1}^{n} {A_{i} Y_{i} } ,\quad i = 1,2, \ldots ,5 $$

where \(Y_{i} = \left\{ \begin{aligned} 1\quad {\text{if}}\;X_{i} > 0 \hfill \\ 0{\kern 1pt} \quad {\text{if}}\;X_{i} = 0 \hfill \\ \end{aligned} \right.\quad i = 1,2, \ldots ,5 \)

AOC is obtained from multiplication of OCP by the number of periods per year:

$$ {\text{AOC}} = ({\text{OCP}}) \times \frac{1}{T} \Rightarrow {\text{AOC}} = \left( {\sum\limits_{i = 1}^{n} {A_{i} Y_{i} } } \right)\frac{1}{T} = \left( {\sum\limits_{i = 1}^{n} {A_{i} Y_{i} } } \right)\frac{D}{Q} $$

Having formulated the annual costs of purchased materials and AHC and AOC, the Total Annual Costs (TAC) is simply computed by adding up all these costs:

$$ \begin{aligned} {\text{TAC}} & = {\text{APC}} + {\text{ATC}} + {\text{AWRC}} + {\text{AHC}} + {\text{AOC}} \\ {\text{TAC}} & = \sum\limits_{i = 1}^{5} {X_{i} P_{i} D} + \sum\limits_{i = 1}^{5} {X_{i} C_{ti} D + \frac{rQ}{2}\left( {\sum\limits_{i = 1}^{3} {X_{i} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right) + \frac{1}{{\sum\limits_{i = 4}^{5} {x_{i} } }}} \\ & \quad \times \frac{rQ}{2}\left( {\sum\limits_{i = 4}^{5} {X_{i}^{2} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right) + \frac{D}{Q}\left( {\sum\limits_{i = 1}^{5} {A_{i} Y_{i} } } \right) + \sum\limits_{i = 1}^{n} {h_{i} \beta_{i} X_{i} D} \\ \end{aligned} $$

Manipulating the above equation a bit and considering that \( \beta_{i} = P_{i} + C_{ti} \), a simpler from of TAC will be:

$$ \begin{aligned} {\text{TAC}} & = \sum\limits_{i = 1}^{5} {X_{i} D(1 + h_{i} )\beta_{i} + } \frac{rQ}{2}\left( {\sum\limits_{i = 1}^{3} {X_{i} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right) + \frac{1}{{\sum\limits_{i = 4}^{5} {x_{i} } }} \\ & \quad \times \frac{rQ}{2}\left( {\sum\limits_{i = 4}^{5} {X_{i}^{2} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right) + \frac{D}{Q}\left( {\sum\limits_{i = 1}^{5} {A_{i} Y_{i} } } \right) \\ \end{aligned} $$

As usual, we differentiate the above equation in respect to Q to obtain the optimum order quantities. Doing so, we have:

$$ ({\text{TAC)}}^{\prime } = \frac{r}{2}\left( {\sum\limits_{i = 1}^{3} {X_{i} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right) + \frac{r}{2} \times \frac{1}{{\sum\nolimits_{i = 4}^{5} {X_{i} } }}\left( {\sum\limits_{i = 4}^{5} {X_{i}^{2} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right) - \frac{D}{{Q^{2} }}\left( {\sum\limits_{i = 1}^{5} {A_{i} Y_{i} } } \right) $$

Finally, omitting Q, the objective function for Model A is:

$$ {\text{TAC}} = \sum\limits_{i = 1}^{5} {X_{i} D(1 + h_{i} )\beta_{i} + \sqrt {2Dr\left( {\sum\limits_{i = 1}^{3} {X_{i} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right) + \frac{1}{{\sum\nolimits_{i = 4}^{5} {X_{i} } }}\left( {\sum\limits_{i = 4}^{5} {X_{i}^{2} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right)} \times } \sqrt {\sum\limits_{i = 1}^{5} {A_{i} Y_{i} } } $$

And the optimum order quantity, Q *, is:

$$ Q^{*} = \sqrt {\frac{{2D\left( {\sum\nolimits_{i = 1}^{n} {A_{i} Y_{i} } } \right)}}{{r\left( {\sum\nolimits_{i = 1}^{m} {X_{i} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right) + \frac{1}{{\sum\nolimits_{i = m + 1}^{n} {X_{i} } }}\left( {\sum\nolimits_{i = 1}^{n} {X_{i}^{2} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right)}}} $$

the objective function for Model B after omitting Q is:

$$ {\text{Min}}\,{\text{TAC}} = \sum\limits_{i = 1}^{5} {X_{i} D(1 + h_{i} )\beta_{i} + \sqrt {2Dr\left( {\sum\limits_{i = 1}^{5} {X_{i} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right)\left( {\sum\limits_{i = 1}^{5} {A_{i} Y_{i} } } \right)} } $$

And the optimum order quantity, Q*, is:

$$ Q^{*} = \sqrt {\frac{{2D\left( {\sum\nolimits_{i = 1}^{n} {A_{i} Y_{i} } } \right)}}{{r\left( {\sum\nolimits_{i = 1}^{n} {X_{i} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right)}}} $$

The model constraints

The constraints of this model actually pertains to the buyer’s annual demand and quality of receiving materials, on one hand, and the suppliers’ allocable capacity, on the other. In the following section, we present formulation of these constraints, as they were introduced to the model:

Demand constraint

Assuring D is the Isfahan works, annual demand for iron ore and iron concentrate, as we mentioned earlier, n = 5 vendors can satisfy D at the present time. Therefore, we have:

$$ \sum\limits_{i = 1}^{n} {X_{i} D = D\quad i = 1,2, \ldots ,5} $$

Omitting D from both sides of equation, then we have:

$$ \sum\limits_{i = 1}^{n} {X_{i} = 1} \quad i = 1,2, \ldots ,5 $$

Fe quality constraint

In practice, to get a quality agglomeration process output with a prescribed Fe content, a calculated mix of input materials, based on their Fe content is used. In this case we have:

$$ \sum\limits_{i = 1}^{5} {X_{i} Dq_{{{\text{Fe}}i}} \ge q_{\text{aFe}} D} $$

And, omitting D from both sides, we have:

$$ \sum\limits_{i = 1}^{5} {X_{i} q_{{{\text{Fe}}i}} \ge q_{\text{aFe}} } $$

where \( q_{\text{aFe}} \) is the minimum acceptable percent of Fe in the input mix, and \( q_{{{\text{Fe}}i}} \) is the percent of Fe content in the ith supplier’s material.

Due to the assumptions of Model A, which requires breaking the order cycle into two parts, we should divide the Fe quality constraint into two parts as well, and introduce it to the model as follows:

$$ \begin{aligned} & (X_{1} Dq_{{{\text{Fe}}1}} + X_{2} Dq_{{{\text{Fe}}2}} + X_{3} Dq_{{{\text{Fe}}3}} + (1 - X_{1} + X_{2} + X_{3} ))Dq_{{{\text{Fe}}4}} ) \ge Dq_{\text{aFe}} \\ & (X_{1} Dq_{{{\text{Fe}}1}} + X_{2} Dq_{{{\text{Fe}}2}} + X_{3} Dq_{{{\text{Fe}}3}} + (1 - X_{1} + X_{2} + X_{3} ))Dq_{{{\text{Fe}}5}} ) \ge Dq_{\text{aFe}} \\ & \sum\limits_{i = 1}^{5} {DX_{i} q_{{{\text{Fe}}i}} - 10^{20} Y_{4} D - 10^{20} Y_{5} D \ge Dq_{\text{afe}} } \\ \end{aligned} $$

Knowing that:

$$ \begin{aligned} & X_{4} \le (1 - (X_{1} + X_{2} + X_{3} )) \\ & X_{5} \le (1 - (X_{1} + X_{2} + X_{3} )) \\ \end{aligned} $$

And omitting D from both sides, we have:

$$ \begin{aligned} & (X_{1} q_{{{\text{Fe}}1}} + X_{2} q_{{{\text{Fe}}2}} + X_{3} q_{{{\text{Fe}}3}} + (1 - X_{1} + X_{2} + X_{3} ))q_{{{\text{Fe}}4}} ) \ge q_{\text{afe}} \\ & (X_{1} q_{{{\text{Fe}}1}} + X_{2} q_{{{\text{Fe}}2}} + X_{3} q_{{{\text{Fe}}3}} + (1 - X_{1} + X_{2} + X_{3} ))q_{{{\text{Fe}}5}} ) \ge q_{\text{afe}} \\ & \sum\limits_{i = 1}^{5} {X_{i} q_{{{\text{Fe}}i}} - 10^{20} Y_{4} - 10^{20} Y_{5} \ge q_{\text{afe}} } \\ & X_{4} \le (1 - (X_{1} + X_{2} + X_{3} )) \\ & X_{5} \le (1 - (X_{1} + X_{2} + X_{3} )) \\ \end{aligned} $$

Additionally the number \( 10^{20} \) that represented is a very large number in the model.

Quality Constraint for Model B is:

$$ \sum\limits_{i = 1}^{5} {X_{i} q_{{{\text{Fe}}i}} \ge q_{\text{aFe}} } $$

Capacity constraint

This constraint stems from the fact that the ith supplier can satisfy only a fraction of the annual buyer’s needs, C i , each year. Thus: \( X_{i} D \le C_{i} \).

Finally, we have to make sure that Y i has an integer value of 0 or 1. To introduce this constraint to model, and knowing that X i is always equal or less than 1, then we have:

$$ \begin{aligned} & X_{i} \le Y_{i} \quad i = 1,2, \ldots ,n \\ & X_{i} \ge \varepsilon Y_{i} \\ \end{aligned} $$

where, ε is a little bit greater than 0.

Instead, in above constraint formulas, where ever we have X i , we can multiply it by Y i .

Fe quality constraint

Model A formulation

Now, we summarize Model A formulation as follows:

$$ \begin{aligned} & {\text{Min}}\,{\text{TAC}} = \sum\limits_{i = 1}^{n} {X_{i} D(1 + h_{i} )\beta_{i} } + \frac{rQ}{2}\left( {\sum\limits_{i = 1}^{m} {X_{i} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right) + \frac{1}{{\sum\nolimits_{i = m + 1}^{n} {X_{i} } }} \\ & \quad \times \frac{rQ}{2}\left( {\sum\limits_{i = m + 1}^{n} {X_{i}^{2} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right) + \frac{D}{Q}\left( {\sum\limits_{i = 1}^{n} {A_{i} Y_{i} } } \right) \\ & \sum\limits_{i = 1}^{n} {X_{i} } = 1\quad i = 1,2, \ldots ,m, \ldots m + 1, \ldots n \\ & \left( {\sum\limits_{i = 1}^{m} {X_{i} q_{{{\text{Fe}}i}} } + \left( {1 - \left( {\sum\limits_{i = 1}^{m} {X_{i} } } \right)} \right)q_{{{\text{Fe}}(m + 1)}} } \right) \ge q_{\text{aFe}} Y_{m + 1} \\ & \left( {\sum\limits_{i = 1}^{m} {X_{i} q_{{{\text{Fe}}i}} } + \left( {1 - \left( {\sum\limits_{i = 1}^{m} {X_{i} } } \right)} \right)q_{{{\text{Fe}}(m + 2)}} } \right) \ge q_{\text{aFe}} Y_{m + 2} \\ & \vdots \quad \quad \quad \quad \quad \quad \quad \vdots \quad \quad \quad \quad \quad \quad \quad \quad \quad \vdots \\ & \left( {\sum\limits_{i = 1}^{m} {X_{i} q_{{{\text{Fe}}i}} } + \left( {1 - \left( {\sum\limits_{i = 1}^{m} {X_{i} } } \right)} \right)q_{{{\text{Fe}}(n)}} } \right) \ge q_{\text{aFe}} y_{n} \\ & \sum\limits_{i = 1}^{n} {X_{i} q_{{{\text{Fe}}i}} - 10^{20} } \sum\limits_{i = m + 1}^{n} {Y_{i} \ge q_{\text{aFe}} } \\ & 0 \le X_{m + 1} \le \left( {1 - \left( {\sum\limits_{i = 1}^{m} {X_{i} } } \right)} \right) \\ & 0 \le X_{m + 2} \le \left( {1 - \left( {\sum\limits_{i = 1}^{m} {X_{i} } } \right)} \right) \\ & \quad \quad \quad \vdots \quad \quad \quad \quad \vdots \\ & 0\,\le\,X_{n}\,\le\,\left( {1 - \left( {\sum\limits_{i = 1}^{m} {X_{i} } } \right)} \right) \\ & X_{i} D\,\le\,C_{i} \quad i = 1,2, \ldots ,n \\ & Q_{i} = X_{i} Q \\ & X_{i}\,\le\,Y_{i} \\ & X_{i}\,\ge\,\varepsilon Y_{i} \\ & Q = \sum\limits_{i = 1}^{n} {Q_{i} } \\ & X_{i}\,\ge\,0,Y_{i} = 0,1,\quad i = 1, 2, \ldots ,m, \ldots ,n \\ \end{aligned} $$

Model B formulation

We summarize Model B formulation as follows:

$$ \begin{aligned} & {\text{Min}}\,{\text{TAC}} = \sum\limits_{i = 1}^{n} {X_{i} D(1 + h_{i} )\beta_{i} + \frac{rQ}{2}\left( {\sum\limits_{i = 1}^{n} {X_{i} \alpha_{i} (1 + h_{i} )\beta_{i} } } \right) + } \frac{D}{Q}\left( {\sum\limits_{i = 1}^{n} {A_{i} Y_{i} } } \right) \\ & \sum\limits_{i = 1}^{n} {X_{i} } = 1\quad i = 1,2, \ldots ,n \\ & \sum\limits_{i = 1}^{n} {X_{i} q_{{{\text{Fe}}i}} } \ge q_{\text{aFe}} \quad i = 1,2, \ldots ,n \\ & X_{i} D \le C_{i} \quad i = 1,2, \ldots ,n \\ & Q_{i} = X_{i} Q \\ & X_{i} \le Y_{i} \\ & X_{i} \ge \varepsilon Y_{i} \\ & Q = \sum\limits_{i = 1}^{n} {Q_{i} } \\ & X_{i} \ge 0,Y_{i} = 0,1,\quad i = 1,2, \ldots ,m \ldots ,n \\ \end{aligned} $$

Parameters of model

It should be considered that the model was tested for two time periods (two successive years). Some of the parameters are the same for two time period and others are different thus they are represented separately (Tables 2, 3).

Table 2 Common parameters for two successive years
Full size table
Table 3 Different parameters for two successive years
Full size table

Model runs and results

In order to run the formulated models and compare its results with actual performance, we had to compute model parameters from Company’s records. This was done carefully using data of two consecutive financial years. We employed the global option of Lingo Version 8 for running the models. The results are summarized in Table 4.

Table 4 Model A results
Full size table

Take notice of the fact that the model has chosen three of the suppliers for the first year and only two of them in the second year. Exactly, the same results obtained when running Model B too. Obtaining the same results from Models A and B is rather exceptional, and relates only to this studied situation, and stems from the fact that both models rejected buying iron concentrate from a particular vendor. Models are based on important criteria such as cost, quality and capacity.

Actually, Isfahan Steel Co. on a regular basis, has been buying raw materials form all five suppliers during those 2 years. A comparison of the model results with the actual cost performance of the Company is made in Table 5.

Table 5 Comparing the model results with actual data
Full size table

Discussion and conclusion

Examining the results presented in Tables 4 and 5, reducing cost by 10.9 and 7.1 %, increasing company’s annual profit, attract any top manager’s attention. One might argue that real world mangers of large processing firms like Isfahan Steel Company keep purchasing from different sources to ensure a continuous and reliable stream of supplies. However, it turned out to be a very expensive way to get such assurances. The responsible managers of the said company had not been aware of the tremendous differences that a wrong suppliers selection decisions could create. Furthermore, one of the real potential values of mathematical modeling is reminding the mangers of alternative ways of doing their daily affairs.

However, some points should be mentioned about the new models and the present study:

  1. 1.

    The models determine the percentages of iron ore and iron concentrate to be mixed in agglomeration process. This is done by considering the minimum Fe contents required for specified output quality of the process, \( q_{\text{afe}} \), and other constraints, and objective function. The models recommended a mix of 88.73472 % iron ore and 11.26528 %, concentrate for the first year and 99.49174 % iron ore, 0.005082592 % concentrate for the second year.

  2. 2.

    A sensitivity analysis of the models was assumed by changing capacity and quality constraints’ parameters, the number of placed orders in a year, D/Q. The results of the sensitivity analysis revealed that even in the most pessimistic conditions, the models would result in total costs reduction.

    One of the interesting findings of the sensitivity analysis of the model was that if the second iron ore supplier had no capacity limitations, and could supply the Company’s whole annual needs, a substantial costs reduction could happened. Based on this finding, we recommended the management helping that particular supplier to invest in increasing its capacity through a joint venture project.

  3. 3.

    The non-linear assumption of these models makes them closer to the real world managerial problems. Most of the relationships in socio-economic systems are non-linear in nature. Yet, Model B is flexible enough to be changed to a linear model simply by assuming D/Q as constant. As a result, the new models are applicable to a fairly large area of operations management special problems.

  4. 4.

    The new models are not just a simple inventory model. As we have seen, the models can handle a multi-criteria situation comprising cost and quality and help us select appropriate suppliers. They also can present a purchasing schedule to tell us when and how much to buy from each vendor. At the same time, the models can suggest an optimum consumption mix of the materials.

In summary, the new models presented in this article have notable advantages and improvements over the previously introduced ones, such as Ghodsypour and O’Brien model (2001), with a considerable number of real world special applications.