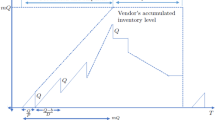
Abstract
Lead time is one of the major limits that affect planning at every stage of the supply chain system. In this paper, we study a continuous review inventory model. This paper investigates the ordering cost reductions are dependent on lead time. This study addressed two-echelon supply chain problem consisting of a single vendor and a single buyer. The main contribution of this study is that the integrated total cost of the single vendor and the single buyer integrated system is analyzed by adopting two different (linear and logarithmic) types ordering cost reductions act dependent on lead time. In both cases, we develop effective solution procedures for finding the optimal solution and then illustrative numerical examples are given to illustrate the results. The solution procedure is to determine the optimal solutions of order quantity, ordering cost, lead time and the number of deliveries from the single vendor and the single buyer in one production run, so that the integrated total cost incurred has the minimum value. Ordering cost reduction is the main aspect of the proposed model. A numerical example is given to validate the model. Numerical example solved by using Matlab software. The mathematical model is solved analytically by minimizing the integrated total cost. Furthermore, the sensitivity analysis is included and the numerical examples are given to illustrate the results. The results obtained in this paper are illustrated with the help of numerical examples. The sensitivity of the proposed model has been checked with respect to the various major parameters of the system. Results reveal that the proposed integrated inventory model is more applicable for the supply chain manufacturing system. For each case, an algorithm procedure of finding the optimal solution is developed. Finally, the graphical representation is presented to illustrate the proposed model and also include the computer flowchart in each model.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Operations Research (OR) is a term which stands for an approach to problem solving characterized by a system orientation, an interdisciplinary philosophy, a focus on the qualification of the relevant aspects of the situation into a model and the manipulation of this model through the use of mathematical, statistical and computer methodologies to develop decisions, plans and policies. As the Operations Management (OM ) and Supply Chain Management (SCM) field has developed, a better importance on services has appeared. Inventory is important role in the Operations Research. The inventory system is taking an important part of cost controlling in business and organization.
VelMurugan and Uthayakumar (2015) discussed the definition of inventory; inventory consists of usable but idle resources which are materials and goods. The amount of material, a company has in stock at a specific time is known as inventory or in terms of money it can be defined as the total capital investment over all the materials stocked in the company at any specific time. Inventory may be in the form of, raw material inventory, in process inventory, finished goods inventory, etc. Inventory management is a key component in any production environment. This has been recognized not only in the chemical engineering literature but also in the operations research and industrial engineering domains. Inventory Control (IC) is the supervision of supply, storage and accessibility of items to ensure an adequate supply without excessive oversupply.
Inventory is an important part of our manufacturing, distribution and retail infrastructure where demand plays an important role in choosing the best inventory policy. To meet the needs of customers timely, businesses must maintain higher inventory levels to avoid shortages. However, high inventory levels are often associated with high inventory costs, many companies strive to reduce production or lead time cycle, and thus have a corresponding reduction in inventory. Continuous review is the main aspect of the inventory system. In this system the record of the inventory level is checked continuously until a specified point is reached where a new order is placed. This system is also called fixed order quantity system.
The integrated inventory management system is a common practice in the global markets and provides economic advantages for both the vendor and the buyer. In recent years, most integrated inventory management systems have focused on the integration between vendor and buyer. Once the form a strategic alliance to minimize their own cost or maximize their own profit, then trading parties can collaborate and share information to achieve improved benefits. Nowadays, companies can no longer compete solely as individual entities in the constantly changing business world. Globalization of market and increased competition force organizations to rely on effective supply chains to improve their overall performance.
The goal of many research efforts related to the SCM is to present models to reduce operational costs. The SCM has enabled numerous firms to enjoy advantages by integrating all activities associated with the raw material supplier, finished goods manufacturer, retailers, wholesalers, buyers/consumers etc. who are responsible for converting the raw material into a finished good and make them available to customers to satisfy their demand in time at least possible cost. Successful SCM requires a change from managing distinct function to integrating activities into key supply chain processes. Integration between two different business entities is an important way to gain competitive advantages as it lowers supply chain cost. The benefits of a properly managed supply include reduced costs, faster product delivery, greater efficiency and low costs for both the business and its customer. In the increasingly fierce competitive environment in today’s global markets, the supply chain coordination is becoming a key component. If no coordination exists, the supply chain members act independently to maximize their own profits or minimize the costs.
Lead Time (LT) is the time that elapses between the placing of an order (either a purchase order or a production order issued to the shop or the factory floor) and actually receiving the goods ordered. If a supplier (an external firm or an internal department or plant) cannot supply the required goods on demand, then the client firm must keep an inventory of the needed goods. The longer the lead time, the larger the quantity of goods the firm must carry in inventory. In general, the time of order receiving, order handling, order processing, manufacturing, assembly, distribution and delivery time to the customer includes in a lead time. Since the customer perspective is very important. LT has been counted until products or goods arrive to the customer. Hence the lead time measurement can be done from the customer points of view. The customers can be varies by different meanings. For instance, suppliers deliver components or parts to the main manufacturer where manufacturer is the customer from supplier’s perspective. LT can be also measured from the manufacturer points of view. Manufacturer also measures the lead from starting of the processing, fabrication and assembly up-to ready the product for shipment. This can be said as internal lead time. Whereas the external lead time can define by includes shipping, logistics and distribution time.
In most deterministic and probabilistic inventory models, lead-time is viewed as a prescribed constant or a stochastic variable, which, therefore, is not subject to control. But in many practical situations, LT can be reduced at an added cost; in other words, it is controllable. By shortening the lead-time, we can lower the safety stock, reduce the loss caused by stockout, improve the service level to the customer, and, therefore, increase the competitiveness in business. Through the Japanese experience of using Just - In - Time (JIT) production, the advantages and benefits associated with the efforts to control the lead-time can be clearly perceived. On the other hand, lead time can be reduced by an additional crashing cost, so as to improve customer service level, and to reduce safety stocks; In other words, lead time is controllable. The Japanese experience of using JIT production proved that the reimbursement connected with lead time control is obvious. Therefore, reducing lead time is both essential and advantageous.
Inventory models incorporating lead time as a decision variable were developed by several researchers. Liao and Shyu (1991) presented a probabilistic model in which the order quantity was predetermined and lead-time was a unique decision variable. Later, Ben-Daya and Raouf (1994) extended Liao and Shyu’s (1991) model by considering both lead-time and the order quantity as decision variables where shortages were neglected. Ouyang et al. (1996) allowed shortages and extended Ben-Daya and Raouf’s (1994) model by adding the stockout cost. In addition, the total amount of stockout was considered a mixture of backorders and lost sales during the stockout period. Moon and Choi (1998) and Hariga and Ben-Daya (1999) improved the model of Ouyang et al. (1996) by simultaneously optimizing the order quantity, the reorder point and lead-time. Ouyang et al. (1999) incorporated ordering cost reduction into the model of Moon and Choi (1998), where the ordering cost can be reduced by capital investment.
LT plays an important role and has been a topic of interest for many authors in inventory management [see, for example, Das (1975), Foote et al. (1988) and Magson (1979)]. In most of the early literature dealing with inventory problems, in both deterministic and probabilistic models, lead time is viewed as a prescribed constant or a stochastic variable, which, therefore, is not subject to control [see, e.g., Naddor (1966), Silver and Peterson (1985)]. In 1983, Monden (1983) studied the Toyota production system and pointed out that shortening lead time is a crux of elevating productivity.
The successful Japanese experiences using JIT production show that the advantages and benefits associated with efforts to control the lead time can be clearly perceived. In fact, lead time usually consists of the following components: order preparation, order transit, supplier lead time, delivery time and setup time (Tersine 1982). In numerous realistic situations, lead time can be reduced at an added crashing cost; in other words, it is controllable. By limitation the lead time, we can lower the safety stock, decrease the pasting caused by stockout, improve the examination level to the purchaser and enlarge the spirited ability in business. Inventory models considering lead time as a decision variable have been developed by several researchers recently. Initially, Liao and Shyu (1991) presented an inventory model in which lead time is a unique decision variable and the order quantity is predetermined. Ben-Daya and Raouf (1994) extended Liao and Shyu’s (1991) model to permit both the lead time and the order quantity as decision variables. In 1996, Ouyang et al. (1996) generalized Ben-Daya and Raouf’s (1994) model by allowing shortages with partial backorders. Later, Moon and Choi (1998) and Hariga and Ben-Daya (1999) modified Ouyang et al.’s (1996) model to consider the reorder point as another decision variable. In addition, based on the Ouyang et al.’s (1996) model, Pan and Hsiao (2005) further have discussed the inventory problem of backorder price discount.
Ordering Cost (OC) is the costs of ordering a new batch of raw materials. These include cost of placing a purchase order, costs of inspection of received batches, documentation costs, etc. Ordering costs vary inversely with carrying costs. It means that the more orders a business places with its suppliers, the higher will be the ordering costs. However, more orders mean smaller average inventory levels and hence lower carrying costs. It is important for a business to minimize the sum of these costs which it does by applying the economic order quantity model. All the aforementioned integrated vendor–buyer inventory systems treat the ordering cost and/or lead time as constants. However, in the practical market, ordering cost and lead time can be controlled and reduced in various ways. For example, lead time can be reduced at an added crashing cost; ordering cost reduction can be attained through worker training, procedural changes, and specialized equipment acquisitions; in other words, the lead time is controllable, and the ordering cost can be reduced through further investment. It has been a trend by shortening the lead time and reducing ordering cost; we can lower the safety stock, reduce the stockout loss, and improve the service level to the customer.
In modern production management, controllable lead time and ordering cost reduction are keys to business success and have attracted considerable research attention. Ordering quantity, service level and business competitiveness can be shown to possibly be influenced directly or indirectly via lead-time and/or ordering cost control. Most of the integrated inventory models treat the ordering cost and/or lead time as constants. However, in some practical situations, lead time and ordering cost can be controlled and reduced in various ways. OC reduction can be attained through worker training, procedural changes, and specialized equipment acquisition. Through the Japanese experience of using JIT production, the advantages associated with efforts to reduce the order cost can be clearly perceived. On the other hand, lead time can be reduced by an additional crashing cost, so as to improve customer service level, and to reduce safety stocks; In other words, lead time is controllable. The Japanese experience of using JIT production proved that the reimbursement connected with lead time control is obvious. Therefore, reducing lead time is both essential and advantageous.
Initially, Porteus (1986) investigated the impact of capital investment in reducing ordering cost on the classical Economic Order Quantity (EOQ) model for the first time. Ouyang et al. (1999) discussed lead time and ordering cost reductions in continuous review inventory systems with partial backorders. Later, Chang et al. (2006) presented lead time and ordering cost reduction problem in the single-vendor single-buyer integrated inventory model. They considered that buyer lead time can be shortened at an extra crashing cost which depends on the lead time length to be reduced and the ordering lot size, as well buyer ordering cost can be reduced through further investment. The main important single factor which influences the decision on re-order quantity is the total of carrying cost and ordering cost. Carrying cost increase with increase in re-order quantity while ordering cost decreases with increase order quantity. Thus, carrying cost and ordering cost move in opposite directions. Material manager, in deciding the re-order quantity, endeavours to keep the total of carrying cost and ordering cost at the minimum.
In this direction, several authors has encouraged to examine setup/ordering cost reduction [e.g. Keller and Noori (1988), Nasri et al. (1990), Kim et al. (1992), Paknejad et al. (1995)]. As stated in Tersine (1994), lead time usually comprises several components, such as setup time, process time, wait time, move time and queue time. In many practical situations, lead time can be reduced using an added crashing cost. In other words, lead time is controllable. The Japanese experience of using JIT production showed that the benefits associated with lead time control are clear. Therefore, reducing lead time is both necessary and beneficial.
In the proposed model, the optimum inventory control policy in a single vendor and a single-buyer integrated inventory model with ordering cost reduction dependent on lead time. In addition, the proposed model includes an appropriate method to contain upstream members to believe the best policy. The contribution of this paper can be considered as the major aspects: the mathematical model as well as structure and concept of ordering cost is dependent on lead time. Here, the proposed model considers the two case (i) linear function case and (ii) logarithmic function case.
Specially, we modify Pan and Yang (2002) model to include the cases of the linear and logarithmic relationship between lead time and ordering cost reductions. The objective of this paper is to find out an optimal inventory strategy that can minimize the value of the integrated total cost for the single vendor and the single buyer. An algorithm is developed to determine the optimal strategy and numerical examples are taken to illustrate the solution procedure in linear case as well as logarithmic case. Finally, the graphical representation is presented to illustrate the model. Furthermore, the sensitivity analysis is incorporated and the numerical examples are given to illustrate the results.
This paper is organized as follows. In the next section “Literature review”, contains the literature review and “Notations and assumptions” section, we describe the notation and assumptions used throughout this study. We mathematical model is developed to optimize the integrated total cost for the single vendor and the single buyer where the lead time dependent on ordering cost is presented in section “Mathematical moder”. Two numerical examples are provided to illustrate the proposed models in “Numerical examples” section. In “Sensitivity analysis in linear case and logarithmic case” section, sensitivity analysis of the parameters is provided in linear case as well as logarithmic case. Managerial insights are also included in “Managerial insights” section. “Conclusion” section summarizes the paper and discusses future directions.
Literature Review
A business viewpoint for institutional buying and vendor relationship management, or supply chain management, is a necessary functional position within any association. Organizations, large and small, have some form of a purchasing function. Even a sole-proprietor is accountable for purchasing the needed goods and services to keep their industry running. So when we consider the importance of a well-defined, well-engineered supply chain management function, the implications, organizationally, are widespread and certainly worth noting.
By tradition, inventory problems for the vendor and the buyer are treated independently. In the past, Economic Order Quantity (EOQ) and Economic Production Quantity (EPQ) was treated independently from the viewpoints of the buyer or the vendor. In most cases, the optimal solution for one player was non-optimal to the other player. In today’s competitive markets, close cooperation between the vendor and the buyer is necessary to reduce the joint inventory cost and the response time of the vendor–buyer system. The successful experiences of National Semiconductor, Wal-Mart, and Procter and Gamble have demonstrated that integrating the supply chain has significantly influenced the company’s performance and market share (Simchi-Levi et al. 2000). Other studies (Weng 1995; Li et al. 1996; Yang and Wee 2000; Chen et al. 2001) show that an integrated approach results in improved performance and increased profitability to all players in the supply chain.
Most inventory models considered to date assume just one facility (e.g., a buyer or a vendor) managing its inventory policy to minimize its own cost or maximize its own profit. This one-sided-optimal-strategy is not suitable for global markets. The issue of JIT has recently received great attention. Most JIT research has focused on the integration between vendor and buyer. Once a long-term relationship between both facilities has been developed, both parties can cooperate and share information to achieve improved benefits.
The integration between vendor and buyer for improving the performance of inventory control has received a great deal of attention and the integrated approach has been examined for years. In 1986, Banerjee (1986) assumed that the vendor manufactures at a finite rate and considered a joint economic-lot-size model in which a vendor produces to order for a buyer on a lot-for-lot basis. Goyal (1976) is among the first who analyzed an integrated inventory model for a single-buyer single- buyer system. The framework he proposed has encouraged many researchers to present various types of integrated inventory system. Banerjee (1986) modified Goyal’s (1976) model and presented a joint economic lot size model where a vendor produces for a buyer to order on a lot for lot basis. Goyal (1988) further generalized Banerjee’s (1986) model relaxing the assumption of the lot for lot policy of the vendor and suggested that the vendor’s economic production quantity should be a positive integer multiple of the buyer’s purchase quantity.
Ha and Kim (1997) further generalized Goyal’s (1988) model and presented an integrated lot splitting model of facilitating multiple shipment in small lots. Hill (1999) proposed a more general batching and shipping policy involving the successive shipment size of the first \(m\) shipments increases by a fixed factor and remaining shipments would be equal sixed. In a recently study, Pan and Yang (2002) generalized Goyal’s (1988) model by considering lead time as a decision variable and obtained a lower joint total expected cost and shorter lead time. Yang and Pan (2004) considered variable lead time and quantity improvement investment with normal distributional demand in the model proposed in Pan and Yang (2002), Ouyang et al. (2004) extend Pan and Yang (2002) and developed a single-vendor single-buyer integrated production inventory model under the assumption that the lead time is stochastic and lead time is decision variable.
Goyal and Gupta (1989), Monden (1983), Lu (1995), Hill (1999) investigated an unequal shipment policy for the joint single-vendor single-buyer inventory problem and concluded that an optimal policy for this problem is to use shipment sizes that increase by a fixed factor in the beginning and then remaining constant after a well-specified number of shipments. Ouyang et al. (1996) extended the Ben-Daya and Raouf’s (1994) model in which shortages were allowed and the total amount of stockouts was considered as a mixture of back orders and lost sales. Hsiao and Lin (2005) investigated an economic order quantity model on Stackelberg game in supply chain; that is, a distribution channel system containing one supplier and a single retailer such that the supplier in the channel holds monopolistic status, in which he not only owns cost information about the retailer but also has the decision making right of the lead time.
Recently, some researchers investigated on the integrated vendor–buyer inventory problems with quantity discount. Weng and Wong (1993) considered the optimal pricing and replenishment policy for a general all-unit quantity discount system with multiple buyers and constant demand. Weng (1995) discussed both all-unit and incremental quantity discount policies with price-sensitive demand. On the other hand, Munson and Rosenblatt (2001) proposed a three-level supply chain system with quantity discount and a fixed demand rate. They showed that quantity discount can effectively decrease each party’s cost. Li and Liu (2006) developed a supplier–buyer supply chain system with quantity discount and probabilistic customer demand. Qin et al. (2007) Established a supply chain system consisting of a supplier and a buyer with volume discounts and price-sensitive demand. More research papers dealing with the quantity discount problem in a supply chain system can be found in Parlar and Wang (1994), Li and Huang (1995), Hofmann (2000), Yang (2004), Tsai (2007), Sheen and Tsao (2007), Burke et al. (2008), etc., and the references therein. Lin (2008) has developed minimax distribution free procedure with backorder price discount.
Taleizadeh et al. (2013) have presented joint single-vendor and single-buyer supply chain problem with stochastic problem and fuzzy lead-time. Taleizadeh et al. (2012) have proposed Multiproduct multiple-buyer single-vendor supply chain problem with stochastic demand, variable lead-time, and multi-chance constraint. Taleizadeh et al. (2011) have formulated Multiple-buyer multiple-vendor multi-product multi-constraint supply chain problem with stochastic demand and variable lead-time: A harmony search algorithm. Taleizadeh et al. (2010) proposed A particle swarm optimization approach for constraint joint single buyer-single vendor inventory problem with changeable lead time and (r, Q) policy in supply chain. Lin (2009) have considered a buyer-vendor EOQ model with changeable lead-time in supply chain. Yang et al. (2007) have developed global optimal policy for vendor–buyer integrated system with just in environment. Viswanathan (1998) have considered optimal strategy for the integrated vendor–buyer inventory model. Lin and Ho (2011) have considered integrated inventory model with quantity discount and price-sensitive demand.
LT is very important things in inventory system and supply chain system. Traditional inventory models assumed that lead time is a constant or random variable which is not a controllable factor. However, in practice, lead time could be shortened by paying an additional crashing cost; in other words, it is controllable. Stated that this crashing cost could be expenditures on equipment improvement, information technology, order expedite, or special shipping and handling. By shortening lead time, buyers can lower the safety stock, reduce the out-of-stock loss, and improve the customer service level. Thus, in present supply chain and inventory management system, controllable lead time is a key to business achievement and has attracted considerable research attention.
LT as a quantitative performance index is an important specification for each facility in a supply chain. Researchers have investigated the lead time in several states. The lead time is more significant when demand is uncertain and effect of demand uncertainty can be decreased with effective lead time management. Therefore, two opinions exist about lead time. In the first lead time is a parameter and in the second lead time is variable. If lead time is considered as variable, the models try to select the best value to minimize the cost and delivery time. Nielson and Michna (2016) developed an approach for designing order size dependent lead time models for use in inventory and supply chain management. Heydari et al. (2009) presented a study of lead time variation impact on supply chain performance. Lead time is the duration between placing an order and receiving it. This duration is due to production, transportation, batch processing, etc., which may be long and stochastic. Long and stochastic lead times can interrupt the production process and inventory planning and also decrease service level (Louly and Dolgui 2013). In real cases, a supply chain may encounter long and stochastic lead times because of the competitive condition of today’s global trades. A Change in the production process, transportation, and inspection procedures leads to fluctuations in lead times and, consequently, unexpected shortages/surplus in inventory systems (Sajadieh et al. 2009).
As stated by Tersine (1982), lead time usually consists of more than one component such as order preparation, order transition, supplier lead time, delivery time and setup time components. Considering this fact lead time can be reduced by decreasing the time of these components with crashing cost, that is to say the lead time is controllable. Many researchers utilize controllable lead time in supply chain design problem to reduce the customers waiting time and increase the service level. Lee et al. (2007) proposed the continuous review inventory system with backorder discount and variable lead time, where capital investment leads to reduce the ordering cost and lead time can be shortened at an extra crashing cost. Their objective is to simultaneously optimize the order quantity, ordering cost, back-order discount and lead time. Ouyang and Chang (2002) proposed a model deals with lead time and set-up cost reductions on the modified lot size reorder point. In the proposed model lead time can be shortened at an extra crashing cost the model objective is to optimize the lot size, reorder point, set-up cost and lead time. Pan and Hsiao (2001) proposed an integrated inventory model with controllable lead time and backorder discount in which lead time crashing cost is a function of reduced lead time and orders quantities.
Li et al. (2012) investigated on a supply chain consisting of a vendor and a buyer with controllable lead time. They considered two scenarios such as complete information and incomplete information about buyer. Arkan and Hejazi (2012) proposed a coordination mechanism based on a credit period in a two echelon supply chain with one buyer and one supplier that both lead time and ordering cost can be reduced at an added cost. Jha and Shanker (2013) presented an integrated production-inventory model where a vendor produces an item and supplies it to a set of buyers. The buyer level demand is assumed to be independent normally distributed and lead time of every buyer can be reduced at an added crash cost. Yi and Sarker (2013) also used controllable lead time in a buyer–vendor system.
Most of researches in the area of lead time reduction assume that lead time is composed of n mutually dependent deterministic components where each component can be shortened by a crashing cost (Ben-Daya and Raouf 1994; Hayya et al. 2011; Pan et al. 2002). Usually, it is considered that lead time crash cost depends on the amount of lead time to be shortened. Lead time reduction falls in the field of selecting between regular and expedited shipping services which in turn is related to what transportation mode is used. Li (2013) have provided a model for designing a logistics network in which regular shipping services with long uncertain lead time could be replaced with more expensive expedited shipping services in negligible lead time.
Heydari (2014) presented lead time variation control using reliable shipment equipment: an incentive scheme for supply chain coordination. Heydari et al. (2016) developed lead time aggression: A three echelon supply chain model. Vijayashree and Uthayakumar (2015) have considered an integrated inventory model with controllable lead time involving investment for quality improvement in supply chain system. Vijayashree and Uthayakumar (2016) have presented inventory models involving lead time crashing cost as an exponential function. Vijayashree and Uthayakumar (2016) have developed an integrated vendor and buyer inventory model with investment for quality improvement and setup cost reduction. Jamshidi et al. (2015) presented flexible supply chain optimization with controllable lead time and shipping option. Heydari and Norouzinasab (2016) have developed coordination of pricing, ordering and lead time decisions in a manufacturing supply chain. Zhu (2015) have presented integration of capacity, pricing and lead time decisions in a decentralized supply chain.
Vijayashree and Uthayakumar (2014) have presented a two stage supply chain model with selling price dependent demand and investment for quality improvement. Vijayashree and Uthayakumar (2013) have discussed vendor–buyer integrated inventory model with quality improvement and negative exponential lead time crashing cost. Vijayashree and Uthayakumar (2015) have developed two-echelon supply chain inventory model with controllable lead time. Lin (2009) discussed an integrated vendor–buyer inventory model with backorder price discount and effective investment to reduce ordering cost. Vijayashree and Uthayakumar (2014) developed an integrated inventory model with controllable lead time and setup cost reduction for defective and non-defective items. Vijayashree and Uthayakumar (2015) have developed an EOQ model for time deteriorating items with infinite and finite production rate with shortage and complete backlogging. Vijayashree and Uthayakumar (2016) have considered an optimizing integrated inventory model with investment for quality improvement and Setup cost reduction. Hemapriya and Uthayakumar (2016) have developed ordering cost dependent lead time in integrated inventory model.
Pan and Yang (2002) have developed the study of an integrated inventory model with controllable lead time. In practices, the lead time and ordering cost reductions may be related closely; the reduction of lead time may accompany the reduction of ordering cost and vice versa. For example, the implementation of electronic data interchange can be reduced both the lead time and ordering cost simultaneously [see Silver and Peterson (1985), Ouyang et al. (2005), Chen et al. (2001)]. Therefore, it is more reasonable to assume that lead time and ordering cost reductions are dependent and their functional relationship may be as linear, logarithmic, exponential and the like. In the above papers (Liao and Shyu 1991; Ben-Daya and Raouf 1994; Ouyang et al. 1996; Moon and Chois 1998; Hariga and Ben-Daya 1999), which focus on deriving the benefits from lead time reduction, the ordering cost is treated as s fixed constant.
Recently, Ouyang et al. (1999) investigated the influence of ordering cost reduction on modified continuous review inventory systems involving variable lead time with partial backorders. Subsequently, Ouyang and Chang (2002) proposed a modified lot-size reorder-point inventory model with imperfect production processes to study the effects of reducing lead time and set-up cost. The optimal policies derived in these two articles are buyer focused, and the lead time and ordering/set-up cost reduction were assumed to act independently. However, an independent relationship between lead time and ordering/set-up cost is just one possibility. In some practices, lead time and ordering/set-up cost reduction might be closely related. A lead time reduction could accompany a reduction in the ordering/set-up cost, and vice versa. For example, Electronic Data Interchange (EDI) technology could simultaneously reduce both the lead time and the ordering/set-up cost. To date, little research has been done on establishing the relationship between lead times and ordering cost reduction. To provide insight and analytical tractability, as in Chiu (1998) and Chen et al. (2001), this study employed a linear function to formulate the above relationship. Pan and Yang (2002) have considered the ordering cost is fixed.
Therefore, the innovation of the proposed model ordering cost reducing lead time is both necessary and beneficial. Many researchers to reduce the ordering cost and setup cost reduction using logarithmic as well as power function, so the proposed model we have considered the ordering cost reduction dependent on lead time. An optimal solution procedure is developed by incorporating two types of investment functions such as (i) Linear case and (ii) Logarithmic case to reduce the ordering cost reduction in each mathematical model.
To the best of our knowledge, the author has developed a single vendor and single-buyer integrated inventory model with ordering cost reduction dependent on lead time. The contribution of this study is developed an effective iterative solution procedure to determine the optimal policy for a single vendor and single-buyer integrated inventory model with ordering cost reduction dependent on lead time in a supply chain system. In this study, we investigate two-echelon supply chain inventory problem consisting of a single vendor and a single buyer with controllable lead time. The purpose of this paper is to sturdy the effect of lead time reduction on continuous review inventory system with ordering cost reduction. And we consider the case where the lead time and ordering cost reductions with linear function case, and then consider the logarithmic function case relationship.
An algorithm is developed to optimize the integrated total cost for the buyer and the vendor. In addition, numerical examples and a sensitivity analysis are given to illustrate the results of the model. Furthermore, an iterative procedure is proposed to find the optimal solution. A solution procedure is developed to find the optimal solution and numerical solution is presented to illustrate the proposed model. The solution procedure is furnished to determine the optimal solution and the sensitivity analysis has been carried out to illustrate the behaviours of the proposed model. A graphical representation of the linear as well as logarithmic algorithm is represented by a flowchart.
Notations and assumptions
To develop the proposed model, we adopt the following notations and assumptions which are similar to those used in Pang and Yang (2002). Besides, additional notations and assumptions will be given out when required.
Notations
The notations are divided into two subsection variables and parameters are used to develop the model.
Variables
- \(Q\) :
-
Order quantity for the buyer
- \(L\) :
-
Length of lead time for the buyer
- \(A\) :
-
Buyer’s ordering cost per order \(0 \le A \le A_{0}\)
- \(m\) :
-
The number of lots in which the product is delivered from the vendor to the buyer in one production cycle, a positive integer.
Parameters
To develop the proposed model, the following parameters are used
- \(D\) :
-
Average demand per unit time on the buyer
- \(P\) :
-
Production rate of the vendor \(\left( {P > D} \right)\)
- \(S\) :
-
Vendor’s setup cost per setup
- \(c_{\text{v}}\) :
-
Unit production cost paid by the vendor \(\left( {c_{\text{v}} < c_{\text{b}} } \right)\)
- \(c_{\text{b}}\) :
-
Unit purchase cost paid by the buyer
- \(r\) :
-
Annual inventory holding cost per dollar invested in stocks
- \(R\) :
-
Reorder point of the buyer
- \(A_{0}\) :
-
Original ordering cost (before any investment is made)
- \({\text{ITC}}\) :
-
Integrated total cost for the single vendor and the single buyer.
Assumptions
To develop the model, we adopt the following assumptions.
-
1.
There is single-vendor and single-buyer for a single product in this model.
-
2.
The buyer orders a lot of size \(Q\) and the vendor manufactures \(mQ\) with a finite production rate \(P\) \(\left( {P > D} \right)\) at one setup but ship in quantity \(Q\) to the buyer over \(m\) times. The vendor incurs a set up cost \(S\) for each production run and the buyer incurs an ordering cost \(A\) for each order of quantity \(Q\).
-
3.
The demand \(X\) during lead time \(L\) follows a normal distribution with mean \(\mu L\) and standard deviation \(\sigma \sqrt L\).
-
4.
The inventory is continuously reviewed. The buyer places the order when the on hand inventory reaches the reorder point \(R\).
-
5.
The reorder point (ROP) equals the sum of the expected demand during lead time and the safety stock. The reorder point \(R\) = the expected demand during lead time +safety stock, that is \(R = DL + k\sigma \sqrt L\) where \(k\) is safety factor.
-
6.
The lead time \(L\) consists of \(n\) mutually independent components. The \(i\)th component has a normal duration \(b_{i}\), minimum duration \(a_{i}\), and crashing cost per unit time \(c_{i}\). For convenience, we rearrange \(c_{i}\) such that \(c_{1} < c_{2} < c_{3} < \cdots < c_{n}\).
-
7.
The components of lead time are crashed one at a time starting from the first component because it has the minimum unit crashing cost and then the second component, and so on.
-
8.
Let \(L_{0} = \sum\nolimits_{i = 1}^{n} {b_{i} } ,\) and \(L_{i}\) be the length of lead time with components \(1,2,3, \ldots ,i\) crashed to their minimum duration, then \(L_{i}\) can be expressed as \(L_{i} = L_{0} - \sum\nolimits_{j = 1}^{n} {\left( {b_{j} - a_{j} } \right)} ,\quad i = 1,2, \ldots ,n;\) and the lead time crashing cost per cycle \(R\left( L \right)\) is given by \(R\left( L \right) = c_{i} \left( {L_{i - 1} - L} \right) + \sum\nolimits_{j = 1}^{i - 1} {c_{j} } \left( {b_{j} - a_{j} } \right),\quad L \in \left[ {L_{i} ,L{}_{i - 1}} \right]\).
In addition, the length of lead time is equal for all shipping cycles, and the lead time crashing costs occur in each shipping cycle. The relationship between lead time and crashing cost is shown in Fig. 1. Liao and Shyu (1991), Li et al. (2012), Yang and Pan (2004), Pan and Yang (2002), Vijayashree and Uthayakumar (2014, 2016).
-
9.
The reduction of lead time \(L\) accompanies a reduce of ordering cost \(A\) and \(A\) is a firmly, concave function of \(L\), i.e., \(A^{{\prime }} \left( L \right) > 0\) and \(A^{{\prime \prime }} \left( L \right) < 0\) (Ouyang et al. 2005; Chen et al. 2001).
-
10.
If extra costs incurred by the vendor will be fully transferred to the buyer if shortened lead time is required (Pan and Yang 2002).
Mathematical model
Under the assumptions (1–5), described above, Pan and Yang (2002), the integrated total cost, which is composed of buyer and vendor ordering cost, inventory holding cost and lead time crashing cost, is expressed by
In the following two subsections, we consider the situation where shortening lead accompanies a decrease of ordering cost. Specifically, we consider the cases that the relationships between ordering cost and time is linear function and logarithmic function in two subsections.
Linear function case
In this subsection, we assume that lead time and ordering cost reductions act dependently with the following relationship (Chen et al. 2001; Chiu 1998; Ouyang et al. 2004).
where \(\omega > 0\) is a constant scaling parameter to describe the linear relationship between percentages of reduction in lead time and ordering cost. Chen et al. (2001), Chiu (1998), Ouyang et al. (2004) utilized relationship (2) to formulate the inventory problems by treating \(Q,\,L\) as a decision variable. In this paper, in addition to \(Q,\,L\) and \(m\) is also considered to be a decision variable.
By considering relationship (2), the ordering cost \(A\) can be written as a linear function of \(L\), that is
where \(x = \left( {1 - \frac{1}{\omega }} \right)A_{0}\) and \(y = \frac{{A_{0} }}{{\omega L_{0} }}\)
Using (3) into (1), our problem is
for, \(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\).
To solve the nonlinear problem and try to solve the optimal solution of \({\text{ITC}}\left( {Q,L,m} \right)\). For a fixed \(m\), we take the first order partial derivatives of \({\text{ITC}}\left( {Q,L,m} \right)\) with respect to \(Q\) and \(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\), respectively, and obtain
By examining the second-order sufficient conditions (SOSC) for a minimum value, it can be verified that \({\text{ITC}}\left( {Q,L,m} \right)\) is not a convex function of \(\left( {Q,\,L} \right)\). However, for a fixed \(\left( {Q,\,m} \right)\), \({\text{ITC}}\left( {Q,L,m} \right)\) is concave in \(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\), because
Hence for a fixed \(\left( {Q,\,L,\,m} \right)\), the minimum total integrated cost per unit time will occur at the end points of the interval \(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\), \(i = 1,2, \ldots ,n\).
On the other hand, for given \(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\), the minimum value of (4) will occur at the point \(Q\) satisfying the Eq. (5), equal to zero, we obtain the resulting solution is given below
For a fixed \(m\) and \(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\), by solving Eq. (8), we obtain the values of \(Q\)(denote the value by \(Q^{*}\)). The following proposition asserts that, for fixed \(m\) and \(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\), the point \(Q^{*}\) is the optimal solution such that the integrated total cost has minimum value.
Proposition 1
For a fixed \(m\) and \(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\), the integrated total cost \({\text{ITC}}\left( {Q,L,m} \right)\) is positive definite at point \(Q^{*}\)
Next, to examine the effect of \(m\) on the integrated total cost per unit time, we take the first and second order partial derivatives of \({\text{ITC}}\left( {Q,L,m} \right)\) with respect to \(m\) and obtain
and
Therefore, \(ITC\left( {Q,\,L,\,m} \right)\) is convex in \(m\), for a fixed \(Q\) and \(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\). As a result, the search for the optimal derivatives, \(m^{*}\), is reduce to find a local minimum.
From Eq. (8) requires knowledge of the value of others; we can prove the convergence of the procedure by adopting a graphical technique similar to that used in Hadley and Whitin (1963). Further, based on the convexity behaviour of the objective function with respect to the decision variable, the following linear function case algorithm is designed to find the optimal values for order quantity, lead time, ordering cost and the number of deliveries in one production cycle. Linear function case algorithm describes the computer flowchart shown in Fig. (2).
Algorithm for Linear Function Case
-
Set 1 Set \(m = 1\)
-
Set 2 For each \(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\) perform (2.1)–(2.2),\(i = 1,2, \ldots ,n\).
-
Step 3. Find \(\min_{i = 1,2,3, \ldots n} {\text{ITC}}\left( {Q_{i}^{*} ,\theta_{i}^{*} ,L_{i} ,m} \right)\). Let \({\text{ITC}}\left( {Q_{m}^{*} ,\theta_{m}^{*} ,L_{m} ,m} \right) =\)
-
\(\min_{i = 1,2,3, \ldots n} {\text{ITC}}\left( {Q_{i}^{*} ,\theta_{i}^{*} ,L_{i} ,m} \right)\), then \(\left( {Q_{m}^{*} ,\,\,\theta_{m}^{*} ,\,L_{m} } \right)\) is the optimal solution for a fixed \(m\).
-
Step 4. Set \(m = m + 1\) and repeat steps (2)–(3) to get \({\text{ITC}}\left( {Q_{m}^{*} ,L_{m} ,m} \right)\).
-
Step 5. If \({\text{ITC}}\left( {Q_{m}^{*} ,L_{m} ,m} \right) \le {\text{ITC}}\left( {Q_{m - 1}^{*} ,L_{m - 1} ,m - 1} \right)\); go to step 4, otherwise go to step 6.
-
Step 6. Set \({\text{ITC}}\left( {Q^{*} ,m^{*} ,L^{*} } \right) = {\text{IITC}}\left( {Q_{m - 1}^{*} ,L_{m - 1} ,m - 1} \right)\), then \(\left( {Q^{*} ,\,L^{*} ,\,m^{*} } \right)\) is the optimal solution. The optimal ordering cost \(A\left( L \right) = x + yL\)(for linear case) follow.
Logarithmic function case
In this subsection, we assume that the lead time and ordering cost reductions act dependently with the following relationship (Chen et al. 2001)
where \(\delta < 0\) is a constant scaling parameter to describe the logarithmic relationship between percentages of reductions in lead time and ordering cost. In this case, the ordering cost \(A\) can be written as
where \(a = A_{0} + \tau A_{0} \ln L_{0}\) and \(b = - \delta A_{0}\)
Using (13) into (1), our problem is
\(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\).
To solve the nonlinear problem and try to solve the optimal solution of \({\text{ITC}}\left( {Q,L,m} \right)\). For a fixed \(m\), we take the first order partial derivatives of \({\text{ITC}}\left( {Q,L,m} \right)\) with respect to \(Q\) and \(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\), respectively, and obtain
By examining the second-order sufficient conditions (SOSC) for a minimum value, it can be verified that \({\text{ITC}}\left( {Q,L,m} \right)\) is not a convex function of \(\left( {Q,\,L} \right)\). However, for a fixed \(\left( {Q,\,m} \right)\), \({\text{ITC}}\left( {Q,L,m} \right)\) is concave in \(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\), because
Hence for a fixed \(\left( {Q,\,L,\,m} \right)\), the minimum total integrated cost per unit time will occur at the end points of the interval \(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\), \(i = 1,2, \ldots ,n\).
On the other hand, for given \(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\),the minimum value of (14) will occur at the point \(Q\) satisfying the Eq. (15), equal to zero, we obtain the resulting solution is given below,
For a fixed \(m\) and \(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\), by solving Eq. (18), we obtain the values of \(Q\) (denote the value by \(Q^{*}\)). The following proposition asserts that, for fixed \(m\) and \(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\), the point \(Q^{*}\) is the optimal solution such that the integrated total cost has minimum value.
Proposition 1
For a fixed \(m\) and \(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\), the integrated total cost \({\text{ITC}}\left( {Q,L,m} \right)\) is positive definite at point \(Q^{*}\)
Next, to examine the effect of \(m\) on the integrated total cost per unit time, we take the first and second order partial derivatives of \({\text{ITC}}\left( {Q,L,m} \right)\) with respect to \(m\) and obtain loagrithmic function case
and
Therefore, \({\text{ITC}}\left( {Q,L,m} \right)\) is convex in \(m\), for a fixed \(Q\) and \(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\). As a result, the search for the optimal derivatives, \(m^{*}\), is reduce to find a local minimum.
From Eq. (18) requires knowledge of the value of others; we can prove the convergence of the procedure by adopting a graphical technique similar to that used in Hadley and Whitin (1963). Further, based on the convexity behaviour of the objective function with respect to the decision variable, the following logarithmic function case algorithm is designed to find the optimal values for order quantity, lead time, and the number of deliveries in one production cycle. Loagrithmic function case algortithm describes the computer flowchart shown in Fig. (3).
Algorithm for Logarithmic Function Case
-
Set 1 Set \(m = 1\)
-
Set 2 For each \(L \in \left[ {L_{i} ,\,L{}_{i - 1}} \right]\) perform (2.1)–(2.2),\(i = 1,2, \ldots ,n\).
-
Step 3. Let \({\text{ITC}}\left( {Q_{m}^{*} ,L_{m} ,m} \right)\) = minimum of \({\text{ITC}}\left( {Q_{i}^{*} ,L_{i} ,m} \right)\), then \(\left( {Q_{m}^{*} ,\,\,L_{m} } \right)\) is the optimal solution for a fixed \(m\).
-
Step 4. Set \(m = m + 1\) and repeat steps (2)–(3) to get \({\text{ITC}}\left( {Q_{m}^{*} ,L_{m} ,m} \right)\).
-
Step 5. If \({\text{ITC}}\left( {Q_{m}^{*} ,L_{m} ,m} \right) \le {\text{ITC}}\left( {Q_{m - 1}^{*} ,L_{m - 1} ,m - 1} \right)\); go to step 4, otherwise go to step 6.
-
Step 6. Set \({\text{ITC}}\left( {Q^{*} ,m^{*} ,L^{*} } \right) = {\text{IITC}}\left( {Q_{m - 1}^{*} ,L_{m - 1} ,m - 1} \right)\), then \(\left( {Q^{*} ,\,L^{*} ,\,m^{*} } \right)\) is the optimal solution. The optimal ordering cost \(A\left( L \right) = a + b\ln L\)(for logarithmic case).
Numerical examples
To illustrate the above solution procedure, let us consider an inventory system with the data used in Pan and Yang (2002) \(D = 1000\,{\text{units/year}},\) \(P = 3200\,{\text{units/year,}}\) \(k = 2.33,\) \(c_{\text{v}} = 20/{\text{units}},\) \(r = 0.2,\) \(A_{\text{o}} = \$ 25/{\text{order}},\) \(S = \$ 400/{\text{setup}},\) \(c_{\text{b}} = 25/{\text{units}},\) \(\sigma = 7\,{\text{units}}/{\text{week}}\) and lead time has three components with data shown in Table 1 and summarized lead time data shown in Table 2.
Example 1 (Linear case)
We consider the case that the relationship between lead time and ordering cost is linear. We solve the case when \(\omega = 5.00\).
Applying the algorithm in subsection, the results of the solution procedures are summarized in Table 3.
A graphical representation is presented to show the convexity of \({\text{ITC}}\left( {Q^{*} ,L^{*} ,m} \right)\) in Fig. 4 and the graphical representation of the integrated total cost for different number of deliveries \(m\) is shown in Fig. 5.
The optimal solutions from Table 4, can be read off as lead time \(L^{*} = 6\,{\text{weeks}},\) order quantity \(Q^{*} = 110\,{\text{units}}\), ordering cost \(A^{*} = 23.75\) number of deliveries \(m^{*} = 5\) and the corresponding integrated total cost \({\text{ITC}}^{*} = 2104\). Plotted the optimal solution for ordering cost dependent on lead time in Fig. 6.
Example 2 (Logarithmic case)
We consider the case that the relationship between lead time and ordering cost is linear. We solve the case when \(\delta = - 0.5\).
Applying the algorithm in subsection, the results of the solution procedures are summarized in Table 5.
A graphical representation is presented to show the convexity of \({\text{ITC}}\left( {Q^{*} ,L^{*} ,m} \right)\) in Fig. 7 and the graphical representation of the integrated total cost for different number of deliveries \(m\) is shown in Fig. 8.
The optimal solutions from Table 6, can be read off as lead time \(L^{*} = 6\,\,{\text{weeks}},\) order quantity \(Q^{*} = 109\,{\text{units}}\), number of deliveries \(m^{*} = 5\) and the corresponding integrated total cost \({\text{ITC}}^{*} = 2083\). Plotted the optimal solution for ordering cost dependent on lead time in Fig. 9.
Sensitivity analysis in linear case and logarithmic case
We now study the effects of changes in the system parameters demand, production rate, vendor’s setup cost, purchase cost and production cost on the optimal order quantity \(Q,\) lead time \(L\), ordering cost \(A\) and the total number of deliveries \(m\) in order to minimize the integrated total cost \({\text{ITC}}\) of the given example.
Effect of demand \(D\) on the optimal solution (linear case)
To study how various demand \(D\) affect the optimal solution of the model, the demand sensitivity analysis is performed by changing the values of parameter \(D\) by +50, +25, −50, −25% and keeping the remaining parameters unchanged. The results of the demand analysis are shown in Table 7 and the corresponding curve representing of the minimum integrated total cost is plotted in Fig. 10 as well.
Effect of production rate on the optimal solution (linear case)
To study how various production rate \(P\) affect the optimal solution of the model, the demand sensitivity analysis is performed by changing the values of parameter \(P\) by +50, +25, −50, −25% and keeping the remaining parameters unchanged. The results of the production rate analysis are shown in Table 8 and the corresponding curve representing of the minimum integrated total cost is plotted in Fig. 11 as well.
Effect of setup cost \(S\) on the optimal solution (linear case)
To study how various setup cost \(S\) affect the optimal solution of the model, the demand sensitivity analysis is performed by changing the values of parameter \(S\) by +50, +25, −50, −25% and keeping the remaining parameters unchanged. The results of the setup cost analysis are shown in Table 9 and the corresponding curve representing of the minimum integrated total cost is plotted in Fig. 12 as well.
Effect of purchase cost \(c_{\text{b}}\) and production cost \(c_{\text{v}}\) on the optimal solution (linear case)
To study how various purchase cost \(c_{\text{b}}\) and production cost \(c_{\text{v}}\) affect the optimal solution of the model, the demand sensitivity analysis is performed by changing the values of parameter \(c_{\text{b}} \;{\text{and}}\;c_{\text{v}}\) by +50, +25, −50, −25% and keeping the remaining parameters unchanged. The results of the purchase cost \(c_{\text{b}}\) and production cost \(c_{\text{v}}\) rate analysis are shown in Table 10 and the corresponding curve representing of the minimum integrated total cost is plotted in Fig. 13 as well.
Effect of demand \(D\) on the optimal solution (logarithmic case)
To study how various demand \(D\) affect the optimal solution of the model, the demand sensitivity analysis is performed by changing the values of parameter \(D\) by +50, +25, −50, −25% and keeping the remaining parameters unchanged. The results of the demand analysis are shown in Table 11 and the corresponding curve representing of the minimum integrated total cost is plotted in Fig. 14 as well.
Effect of production rate \(P\) on the optimal solution (logarithmic case)
To study how various production rate \(P\) affect the optimal solution of the model, the demand sensitivity analysis is performed by changing the values of parameter \(P\) by +50, +25, −50, −25% and keeping the remaining parameters unchanged. The results of the production rate analysis are shown in Table 12 and the corresponding curve representing of the minimum integrated total cost is plotted in Fig. 15 as well.
Effect of setup cost \(S\) on the optimal solution (logarithmic case)
To study how various setup cost \(S\) affect the optimal solution of the model, the demand sensitivity analysis is performed by changing the values of parameter \(S\) by +50, +25, −50, −25% and keeping the remaining parameters unchanged. The results of the setup cost analysis are shown in Table 13 and the corresponding curve representing of the minimum integrated total cost is plotted in Fig. 16 as well.
Effect of purchase cost \(c_{\text{b}}\) and production cost \(c_{\text{v}}\) on the optimal solution (logarithmic case)
To study how various purchase cost \(c_{\text{b}}\) and production cost \(c_{\text{v}}\) affect the optimal solution of the model, the demand sensitivity analysis is performed by changing the values of parameter \(c_{\text{b}} \;{\text{and}}\;c_{\text{v}}\) by +50, +25, −50, −25% and keeping the remaining parameters unchanged. The results of the purchase cost \(c_{\text{b}}\) and production cost \(c_{\text{v}}\) rate analysis are shown in Table 14 and the corresponding curve representing of the minimum integrated total cost is plotted in Fig. 17 as well.
Managerial insights
The following attractive comments are made regards managerial insights in linear case as well as logarithmic case
-
When tabulating (7)–(14) the optimal values for linear function case as well as logarithmic function case the increment and decrement of various parameters in demand, production rate, setup cost, purchase cost and production cost we could be able to suggest that the integrated total cost of the 6th weeks is lesser than all the other weeks.
-
When tabulating (7)–(14) the optimal values for linear function case as well as logarithmic function case the increment and decrement of various parameters in demand, production rate, setup cost, purchase cost and production cost we could be able to suggest that the order quantity of the 6th weeks is lesser than all the other weeks.
-
When tabulating (7)–(14) the optimal values for linear function case as well as logarithmic function case the decrease the number of delivers and ordering cost in various parameters in demand, production rate, setup cost, purchase cost and production cost we could be able to suggest that the integrated total cost.
-
The proposed model can be used in industries such as aircraft, healthcare, automobiles, computers, textiles, footwear, printers, refrigerators, mobile phones, televisions, air conditioners, washing machines, tyres and bulky products such as printed circuit boards, etc.
-
The proposed integrated inventory model is useful particularly for Just-in-time (JIT) inventory systems where the vendor and the buyer form a strategic alliance for profit sharing.
-
The proposed integrated inventory model is more valid for the supply chain manufacturing system and vendor and buyer management.
Conclusion
In conclusion, we formulated a single vendor and the single buyer integrated inventory model with ordering cost reduction dependent on lead time. Lead time is an imperative factor in any inventory management organization. By shortening the lead time, we can lower the safety stock, reduce the pasting caused by stockout, get better buyer service level and increase the opposition’s ability in business. In many sensible situations, lead time can be reduced by an additional crashing cost. That is, lead time is controllable. In this paper, the lead crashing cost \(R\left( L \right)\) as the previous researches on lead time reduction [see, examples Hariga and Ben-Daya (1999), Liao and Shyu (1991), Moon and Chois (1998), Ouyang et al. (1999, 2004, 2005), Pan and Yang (2002), Vijayashree and Uthayakumar (2014, 2016)] is assumed to be a piecewise linear function.
Pan and Yang (2002) have considered the ordering cost is fixed. So, the proposed model, we have reduced the ordering cost, using the relationship between lead time and ordering cost reduction is linear and logarithmic case function. A mathematical model is employed in this study for optimizing the order quantity, lead time, ordering cost and number of deliveries in one production cycle.
An algorithm to find the optimal solutions is developed. The mathematical modelling is developed by incorporating two types of cases. The aim of our model is to reduce the ordering cost. Here the ordering cost dependent on lead time. The algorithm with the help of the software Matlab 2008 is furnished to determine the optimal solution. A graphical representation of the linear and logarithmic algorithm is represented by a flowchart.
Numerical examples are provided to illustrate the models and sensitivity analysis has been carried out to analyze the behavior of the key parameters on order quantity, lead time, ordering cost, number of deliveries from the vendor to the buyer in one production run and the integrated total cost of the proposed models.
Finally, some numerical examples are presented to illustrate the models. In future research on this, would be motivated to deal with different constraints like ordering constraints, inventory constraints etc. The model can be extended to the single-buyer, multiple-vendor and multiple-buyer, single-vendor and multiple-buyer multiple-vendor systems.
Another possible extension of this work can be done by assuming a discrete investment to reduce the vendor’s setup cost instead of continuous investment. Another possible research topic is to evaluate the impact of various types of imperfect production systems and inspection policies on integrated inventory models.
References
Arkan A, Hejazi SR (2012) Coordinating orders in a two echelon supply chain with controllable lead time and ordering cost using the credit period. Comput Ind Eng 62:56–69
Banerjee A (1986) A joint economic-lot-size model for purchaser and vendor. Decis Sci 17:292–311
Ben-Daya M, Raouf A (1994) Inventory models involving lead time as decision variable. J Oper Res Soc 45:579–582
Burke GJ, Carrillo J, Vakharia AJ (2008) Heuristics for sourcing from multiple suppliers with alternative quantity discounts. Eur J Oper Res 186:317–329
Chang HC, Ouyang LY, Wu KS, Ho CH (2006) Integrated vendor buyer cooperative inventory models with controllable lead time and ordering cost reduction. Eur J Oper Res 170:481–495
Chen CK, Chang HC, Ouyang LY (2001a) A continuous review inventory model with ordering cost dependent on lead time. Inf Manag Sci 12:1–13
Chen F, Federgruen A, Zheng YS (2001b) Coordination mechanisms for a distribution system with one supplier and multiple retailers. Manag Sci 47:693–708
Chiu PP (1998) Economic production quantity models involving lead time as a decision variable. Master Thesis: National Taiwan University of Science and Technology
Das C (1975) Approximate solution to the (Q, r) inventory model for gamma lead time demand. Manag Sci 22:273–282
Foote B, Kebriaei N, Kumin H (1988) Heuristic policies for inventory ordering problems with long and randomly varying lead time. J Oper Manag 7:115–124
Goyal SK (1976) An integrated inventory model for a single supplier-single customer problem. Int J Prod Res 15:107–111
Goyal SK (1988) A joint economic-lot-size model for purchaser and vendor: a comment. Decis Sci 19:236–241
Goyal SK, Gupta YP (1989) Integrated inventory models: the vendor–buyer coordination. Eur J Oper Res 41:261–269
Ha D, Kim SL (1997) Implementation of JIT purchasing: an integrated approach. Prod Plann Control 8:152–157
Hadley G, Whitin T (1963) Analysis of inventory systems. Prentice-Hall, New Jersey
Hariga M, Ben-Daya M (1999) Some stochastic inventory models with deterministic variable lead time. Eur J Oper Res 113:42–51
Hayya JC, Harrison TP, He XJ (2011) The impact of stochastic lead time reduction on inventory cost under order crossover. Eur J Oper Res 211:274–281
Hemapriya S, Uthayakumar R (2016) Ordering cost dependent lead time in integrated inventory model. Commun Appl Anal 20:411–439
Heydari J (2014) Lead time variation control using reliable shipment equipment: an incentive scheme for supply chain coordination. Transp Res Part E 63:44–58
Heydari J, Norouzinasb Y (2016) Coordination of pricing, ordering, and lead time decisions in a manufacturing supply chain. J Ind Syst Eng 9:1–16
Heydari J, Kazemzadeh RB, Kamal Chaharsooghi S (2009) A study of lead time variation impact on supply chain performance. Int J Adv Manuf Technol 401:1206–1215
Heydari J, Mahmoodi M, Taleizadeh AA (2016) Lead time aggregation: a three-echelon supply chain model. Transp Res Part E 89:215–233
Hill RM (1999) The optimal production and shipment policy for the single-vendor single-buyer integrated production-inventory problem. Int J Prod Res 37:2463–2475
Hofmann C (2000) Supplier’s pricing policy in a just-in-time environment. Comput Oper Res 27:1357–1373
Hsiao JM, Lin C (2005) A buyer-vendor EOQ model with changeable lead time in supply chain. Int J Adv Manuf Technol 26:917–921
Jamshidi R, Fatemi Ghomi SMT, Karimi B (2015) Flexible supply chain optimization with controllable lead time and shipping option. Appl Soft Comput 30:26–35
Jha JK, Shanker K (2013) Single-vendor multi-buyer integrated production inventory model with controllable lead time and service level constraints. Appl Math Model 37:1753–1767
Keller G, Noori H (1988) Justifying new technology acquisition through its impact on the cost of running an inventory policy. IIE Trans 20:284–291
Kim KL, Hayya JC, Hong JD (1992) Setup reduction in economic production quantity model. Decis Sci 23:500–508
Lee WC, Wu JW, Lei CL (2007) Computational algorithmic procedure for optimal inventory policy involving ordering cost reduction and back-order discounts when lead time demand is controllable. Appl Math Comput 189:186–200
Li X (2013) An integrated modeling framework for design of logistics networks with expedited shipment services. Transp Res E Log Transp Rev 56:46–63
Li SX, Huang Z (1995) Managing buyer–seller system cooperation with quantity discount considerations. Comput Oper Res 22:947–958
Li J, Liu L (2006) Supply chain coordination with quantity discount policy. Int J Prod Econ 101:89–98
Li SX, Huang Z, Ashley A (1996) Inventory channel coordination and bargaining in a manufacturer retailer system. Ann Oper Res 68:47–60
Li Y, Xu X, Zhao X, Yeung JHY, Ye F (2012) Supply chain coordination with controllable lead time and asymmetric information. Eur J Oper Res 217:108–119
Liao CJ, Shyu CH (1991) An analytical determination of lead time with normal demand. Int J Oper Prod Manag 11:72–78
Lin YJ (2008) Minimax distribution free procedure with backorder price discount. Int J Prod Econ 111:118–128
Lin YJ (2009) An integrated vendor–buyer inventory model with backorder price discount and effective investment to reduce ordering cost. Comput Ind Eng 56:1597–1606
Lin YJ, Ho CH (2011) Integrated inventory model with quantity discount and price-sensitive demand. Top 19:177–188
Louly MA, Dolgui A (2013) Optimal MRP parameters for a single item inventory with random replenishment lead time, POQ policy and service level constraint. Int J Prod Econ 143:35–40
Lu L (1995) A one-vendor multi-buyer integrated inventory model. Eur J Oper Res 81:312–323
Magson D (1979) Stock control when the lead time cannot be considered constant. J Oper Res 30:317–322
Monden Y (1983) Toyota production system. Institute of Industrial Engineers, Norcross
Moon I, Chois S (1998) A note on lead time and distributional assumptions in continuous review inventory models. Comput Oper Res 25:1007–1012
Munson CL, Rosenblatt MJ (2001) Coordinating a three-level supply chain with quantity discount. IIE Trans 33:371–384
Naddor N (1966) Inventory systems. Wiley, New York
Nasri F, Affisco JF, Paknejad MJ (1990) Setup cost reduction in an inventory model with finite-range stochastic lead times. Int J Prod Res 28:199–212
Nielson P, Michna Z (2016) An approach for designing order size dependent lead time models for use in inventory and supply chain management. Smart Innov Syst Technol 56:15–25
Ouyang LY, Chang HC (2002) Lot size reorder point inventory model with controllable lead time and set-up cost. Int J Syst Sci 33:635–642
Ouyang LY, Yeh NC, Wu WS (1996) Mixture inventory model with backorders and lost sales for variable lead time. J Oper Res Soc 47:829–832
Ouyang LY, Chen CK, Chang HC (1999) Lead time and ordering cost reductions in continuous review inventory systems with partial backorders. Int J Oper Res Soc 50:1272–1279
Ouyang LY, Wu KS, Ho CH (2004) Integrated vendor–buyer cooperative models with stochastic demand in controllable lead time. Int J Prod Econ 92:255–266
Ouyang LY, Chuang BR, Lin YJ (2005) The inter-dependent reductions of lead time and ordering cost in periodic review inventory model with backorder price discount. Inf Manag 18:195–208
Paknejad MJ, Nasri F, Affisco JF (1995) Defective units in a continuous review (s, Q) system. Int J Prod Res 33:2767–2777
Pan CHJ, Hsiao YC (2001) Inventory models with back-order discounts and variable lead time. Int J Syst Sci 32:925–929
Pan JCH, Hsiao YC (2005) Integrated inventory models with controllable lead time and backorder discount considerations. Int J Prod Econ 93–94:387–397
Pan CHJ, Yang JS (2002) A study of an integrated inventory with controllable lead time. Int J Prod Res 40:1263–1273
Pan JCH, Hsiao YC, Lee CJ (2002) Inventory models with fixed and variable lead time crash costs considerations. J Oper Res Soc 53:1048–1053
Parlar M, Wang Q (1994) Discounting decisions in a supplier–buyer relationship with a linear buyer’s demand. IIE Trans 26:34–41
Porteus EL (1986) Investing in new parameter values in the discounted EOQ model. Naval Res Logist 33:39–48
Qin Y, Tang H, Guo C (2007) Channel coordination and volume discounts with price-sensitive demand. Int J Prod Econ 105:43–53
Sajadieh MS, Jokar MRA, Modarres M (2009) Developing a coordinated vendor–buyer model in two-stage supply chains with stochastic lead times. Comput Oper Res 36:2484–2489
Sheen GJ, Tsao YC (2007) Channel coordination, trade credit and quantity discounts for freight cost. Transp Res E 43:112–128
Silver EA, Peterson R (1985) Decision system for inventory management and production planning. Wiley, New York
Simchi-Levi D, Kaminsky P, Simchi-Levi E (2000) Designing and managing the supply chain. McGraw-Hill Companies, Singapore
Taleizadeh AA, Akhavan Niaki ST, Shafi N, Meibodi RG, Jabbrazadeh A (2010) A particle swarm optimization approach for constraint joint single buyer-single vendor inventory problem with changeable lead time and (r, Q) policy in supply chain. Int J Adv Manuf Technol 51:1209–1223
Taleizadeh AA, Niaki STA, Barzinpour F (2011) Multiple-buyer multiple-vendor multi-product multi-constraint supply chain problem with stochastic demand and variable lead-time: a harmony search algorithm. Appl Math Comput 217:9234–9253
Taleizadeh AA, Akhavan Niaki ST, Makui A (2012) Multiproduct multiple-buyer single-vendor supply chain problem with stochastic demand, variable lead-time, and multi-chance constraint. Exp Syst Appl 39:5338–5348
Taleizadeh AA, Akhavan Niaki ST, Wee HM (2013) Joint single vendor–single buyer supply chain problem with stochastic demand and fuzzy lead-time. Knowl Based Syst 48:1–9
Tersine RJ (1982) Principles of inventory and materials management. North Holland, New York
Tersine RJ (1994) Principles of inventory and materials management. Prentice Hall, Englewood Cliffs
Tsai JF (2007) An optimization approach for supply chain management models with quantity discount policy. Eur J Oper Res 177:982–994
Velmurugan C, Uthayakumar R (2015) A study on inventory modeling through matrices. Int J Appl Comput Math 1:203–217
Vijayashree M, Uthayakumar R (2013) Vendor-buyer integrated inventory model with quality improvement and negative exponential lead time crashing cost. Int J Inf Manag Sci 24:307–327
Vijayashree M, Uthayakumar R (2014a) A two-stage supply chain model with selling price dependent demand and investment for quality improvements. Asia Pac J Math 1:182–196
Vijayashree M, Uthayakumar R (2014b) An integrated inventory model with controllable lead time and setup cost for defective and non-defective items. Int J Supply Oper Manag 1:190–215
Vijayashree M, Uthayakumar R (2015a) An EOQ model for time deteriorating items with infinite & finite production rate with shortage and complete backlogging. Oper Res Appl Int J 3:31–50
Vijayashree M, Uthayakumar R (2015b) Integrated inventory model with controllable lead time involving investment for quality improvement in supply chain system. Int J Supply Oper Manag 2:617–639
Vijayashree M, Uthayakumar R (2015c) Two-echelon supply chain inventory model with controllable lead time. Int J Syst Assur Eng Manag. doi:10.1007/s13198-015-0346-6
Vijayashree M, Uthayakumar R (2016a) An integrated vendor and buyer inventory model with investment for quality improvement and setup cost reduction. Oper Res Appl Int J 3:1–14
Vijayashree M, Uthayakumar R (2016b) An optimizing integrated inventory model with investment for quality improvement and Setup cost reduction. Int J Inf Technol Control Autom 6:1–13
Vijayashree M, Uthayakumar R (2016c) Inventory models involving lead time crashing cost as an exponential function. Int J Manag Value Supply Chains 7:29–39
Viswanathan M (1998) Optimal strategy for the integrated vendor-buyer inventory model. Eur J Oper Res 105:38–42
Weng ZK (1995) Modeling quantity discounts under general price-sensitive demand functions: optimal policies and relationships. Eur J Oper Res 86:300–314
Weng ZK, Wong RT (1993) General models for the supplier’s all-unit quantity discount policy. Nav Res Logist 40:971–991
Yang PC (2004) Pricing strategy for deteriorating items using quantity discount when demand is price sensitive. Eur J Oper Res 157:389–397
Yang JS, Pan CHJ (2004) Just-in-time purchasing: an integrated inventory model involving deterministic variable lead time and quality improvement investment. Int J Prod Res 42:853–863
Yang PC, Wee HM (2000) Economic ordering policy of deteriorated item for vendor and buyer: an integrated approach. Prod Plann Control 11:474–480
Yang PC, Wee HM, Yang HJ (2007) Global optimal policy for vendor–buyer integrated inventory system within just in time environment. J Global Optim 37:505–511
Yi H, Sarker BR (2013) An operational policy for an integrated inventory system under consignment stock policy with controllable lead time and buyers’ space limitation. Comput Oper Res 40:2632–2645
Zhu SX (2015) Integration of capacity, pricing and lead-time decisions in a decentralized supply chain. Int J Prod Econ 164:14–23
Acknowledgements
The authors are thankful to the anonymous reviewers and the editor for their perceptive and beneficial comments and encouraging suggestions, which have led to a most important development in the earlier revised version of the paper. The authors greatly appreciate the anonymous referees for their valuable comments and suggestions on an earlier version of the revised paper. First author research work is supported by DST INSPIRE Fellowship, Ministry of Science and Technology, Government of India under the Grant No. DST/INSPIRE Fellowship/2011/413A dated 09.09.2016 and UGC–SAP, Department of Mathematics, The Gandhigram Rural Institute—Deemed University, Gandhigram—624302, Tamilnadu, India.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Vijayashree, M., Uthayakumar, R. A single-vendor and a single-buyer integrated inventory model with ordering cost reduction dependent on lead time. J Ind Eng Int 13, 393–416 (2017). https://doi.org/10.1007/s40092-017-0193-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40092-017-0193-y
Keywords
- Operations research
- Inventory model
- Continuous review system
- Ordering cost reduction
- Lead time crashing cost