Abstract
In many applications, ranking of decision making units (DMUs) is a problematic technical task procedure to decision makers in data envelopment analysis (DEA), especially when there are extremely efficient DMUs. In such cases, many DEA models may usually get the same efficiency score for different DMUs. Hence, there is a growing interest in ranking techniques yet. The main purpose of this paper is to overcome the lack of infeasibility and unboundedness in some DEA ranking methods. The proposed method is for ranking extreme efficient DMUs in DEA based on exploiting the leave-one out and minimizing distance between DMU under evaluation and virtual DMU.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Data envelopment analysis (DEA) was initiated by Charnes et al. (1978) as a method to assess relative efficiency of homogeneous decision making units with multiple inputs and multiple outputs. Then, Banker et al. (1984) extended basic DEA models under returns to scale. As regards, the most models of DEA are introduced the more than one efficient DMU in evaluating the relative efficiency DMUs, thus the investigating rank of efficient DMUs is an interesting research topic. A DMU is called extremely efficient if it cannot be represented as a linear combination (with nonnegative coefficients) of the remaining DMUs (Cooper et al. 2007). In data envelopment analysis, there are several methods for ranking of the extreme efficient DMUs, e.g. AP (Andersen and Petersen 1993) method, MAJ (Mehrabian et al. 1999) method. Andersen and Petersen proposed a new procedure to rank efficient DMUs. The AP method exhibits the rank of a given DMU by removing it from the reference set and by computing its super efficiency score. However, the AP model may be infeasible in some cases. It is proved that super efficient DEA models are infeasible (see Thrall 1996, Cooper et al. 2007, Seiford and Zhu 1999, Charnes et al. 1989). Mehrabian et al. (Charnes et al. 1978) suggested as MAJ model for complete ranking efficient DMUs, but their approach lacks infeasibility in some cases, too. To overcome the drawbacks of the AP (Andersen and Petersen 1993) and MAJ (Mehrabian et al. 1999) models, Jahanshahloo et al. (2004a) presented a method to rank the extremely efficient DMUs in DEA models with constant and variable returns to scale using L 1-norm. The proposed model is a nonlinear programming form which has the computational complexity in solving. A complex treatment was applied in Jahanshahloo et al. (2004a) to convert the nonlinear model into a linear one which provides an approximately optimal solution. Wu and Yan (2010) have also used an effective transformation to convert the nonlinear model in Jahanshahloo et al. (2004a) into a linear model. Also Jahanshahloo et al. (2004b) have applied gradient line for ranking efficient units. Rezai Balf et al. (2012) applied Tchebycheff norm (L 1-norm) introduced in (Briec 1998; Tavares et al. 2001) for complete ranking efficient units. Amirteimoori et al. (2005) introduced a method for ranking of extreme efficient DMUs, based on distance. Hashimoto (1999) proposed a super efficiency DEA model with assurance region in order to rank the DMUs completely. Torgesen et al. (1996) suggested a method for ranking efficient units, by their importance as benchmarks for the inefficient units. Sexton et al. (1986) investigated a ranking method for DMUs based on a cross-efficiency ratio matrix. The cross-efficiency ranking method computes the efficiency score of each DMU that determines a set of optimal weights using linear programs corresponding to each DMU. Then by taking the average of scores of given DMU is obtained the rank of that DMU. Liu and Peng (2008) determined one common set of weights for ranking efficient DMUs, that DMUs are ranked according to the efficiency score weighted by the common set of weights. Bal et al. (2008) suggested a DEA model for ranking of DMUs based on defining the coefficient of variation for input–output weights. Khodabakhshi and Aryavash (2012) proposed a method to rank the efficient DMUs. According to their method, first the minimum and maximum efficiency values of each DMU are computed under the assumption that the sum of efficiency values of all DMUs is equal to unity. Then, the rank of each DMU is determined in proportion to a combination of its minimum and maximum efficiency values. Shetty and Pakkala (2010) suggested a method for ranking efficient units, which is created the average of the corresponding inputs and outputs of all DMUs. Early, Jahanshahloo and Firoozi Shahmirzadi (2013) modified the model which was proposed by Bal et al. (2008). They introduced two new models for ranking efficient DMUs based on L 1-norm and using mean of input–output weights. For our new method it does not need any additional constraints.
In this paper, we suggest a new method for ranking extreme efficient DMUs. The rest of the paper is organized as follows. In “DEA models and ranking models review”, we review the concept of DEA framework. We review some ranking methods in “The proposed ranking model for efficient DMUs”, “Extension to variable returns to scale” proposes the new model for ranking efficient units. “Illustrated examples” includes some numerical examples. The last section concludes the study.
DEA model and ranking model review
DEA model review
DEA is a methodology for assessing the relative efficiency of decision making units (DMUs) where each DMU has multiple inputs used to secure multiple outputs.
It is assumed in DEA that there are \(n\) DMUs and for each DMU j \((j = 1, \ldots ,n)\) is considered a column vector of inputs \((X_{j} )\) to produce a column vector of outputs \((Y_{j} )\), where \(X_{j} = (x_{1j} ,x_{2j} , \ldots ,x_{mj} )^{T}\) and \(Y_{j} = (y_{1j} ,y_{2j} , \ldots ,y_{sj} )^{T}\). Here, the superscript \((T)\) indicates a vector transpose. It is also assumed that \(X_{j} \ge 0, Y_{j} \ge 0, X_{j} \ne 0,\) and \(Y_{j} \ne 0\) for every \(j = 1, \ldots ,n\).
The following input-oriented CCR model [see (Cooper et al. 2007)] in the envelopment form with constant Returns to Scale measures the level of DEA efficiency \((\theta )\) of the \(k\)th DMU \((X_{k} ,Y_{k} )\):
Here, \(\lambda = (\lambda_{1} , \ldots ,\lambda_{n} )^{T}\) is a column vector of unknown variables used for components of the input and output vectors by a combination. \(\theta^{*}\) represents the efficiency score of DMU k in (1), where the superscript (*) indicates optimality.
DMU k is relatively efficient if and only if on optimality, the objective of (1) equals to one and all the slacks are zero.
Similarly, the output-oriented CCR model, corresponding to (1), is formulated as follows:
Here, \(1/\phi^{*}\) intends the DEA efficiency score in the output-oriented model.
Also, the following input-oriented BCC model [see Banker et al. (1984)] in the envelopment form with variable Returns to Scale measures the level of DEA efficiency \((\theta )\) of the \(k\)th DMU \((X_{k} ,Y_{k} )\):
DMU k is relative efficient if and only if on optimality, the objective of (3) equals to one and all the slacks are zero.
Similarly, the output-oriented BCC model, corresponding to (3) which obtains from (2) by adding constraint,
Moreover, the following additive model is based on input and output slacks which accounts the possible input decreases as well as output increases simultaneously.
DMU k is relative efficient if and only if on optimality, the objective of (4) equals to zero.
Ranking models
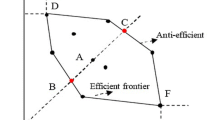
In this subsection we review the some ranking models in data envelopment analysis. The first ranking model proposed by Anderson and Peterson (1993) which is the supper efficiency model. In the AP model DMU under evaluation is excluded from reference set and by using other units, the rank of given DMU is obtained.
The AP model using the CRS super-efficiency model is as follows:
The main drawbacks of this model are infeasibility and instability for some DMUs. It is said that a model is stable if a DMU under evaluation is efficient, it is remains efficient after perturbation on data.
The second ranking model under investigation proposed by Mehrabian et al. (1999) to solve infeasibility of AP models in some cases. The following model is MAJ model:
The third ranking model proposed by Jahanshahloo et al. (2004a), that their proposed method to rank the extremely efficient DMUs in DEA models with constant and variable Returns to Scale using the omitted DMU under evaluation from production possibility set and applying L 1-norm. It is shown that the proposed method is able to overcome the existing difficulties in the AP (Andersen and Petersen 1993) and MAJ (Mehrabian et al. 1999) models. On the other hand, the proposed model is the form of nonlinear programming which is difficult to be solved. The model of Jahanshahloo et al. (2004a) is presented as follows:
The fourth ranking model proposed by Rezai Balf et al. (2012) which applies for ranking extreme efficient units using the leave-one-out idea and \(L_{\infty }\)-norm. The proposed model is always feasible and so, it is able to remove the existing difficulties in some methods, such as Andersen and Petersen (1993). The model of Rezai Balf et al. (2012) is formulated as follows:
The proposed ranking model for efficient DMUs
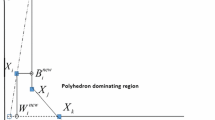
In this section, we suppose that the DMUk is extreme efficient. By excluding the DMUk from the CCR production possibly set, it is obtained a new efficiency frontier. In order to gain the ranking score of DMUk by exploiting the new efficiency frontier, we suggest a new model by by using the leave-one out idea and minimizing distance between DMU under evaluation and virtual DMU. The proposed model is as follows:
where \(\alpha = (\alpha_{1} , \ldots ,\alpha_{m} )\), \(\beta = (\beta_{1} , \ldots ,\beta_{s} )\) and \(\lambda = (\lambda_{1} , \ldots ,\lambda_{k - 1} ,\lambda_{k + 1} , \ldots ,\lambda_{n} )\) are the variables of the model (9).
Theorem 1
The model (9) is feasible and bounded.
Proof
For \(p \ne k\) we set \(\lambda_{p} = 1, \lambda_{j} = 0, j = 1, \ldots ,n, j \ne k,p; \alpha_{i} = \text{min} \{ x_{ik} - xip\} , i = 1, \ldots ,m; \beta_{r} = min\{ y_{rp} - y_{rk} \} , r = 1, \ldots ,s.\)
Obviously, it can be seen that \((\lambda ,\alpha ,\beta )\) according to above selection is a feasible solution of the model (9). Moreover, the objective function of model (9) is bounded below zero, because the variables of model are nonnegative. Also, the target function is zero when \(\alpha_{i} = 0\) and \(\beta_{r} = 0\) for all \(i, r\) \(\square\).
Extension to variable returns to scale
In this section, the proposed model in previous section is extended to variable Returns to Scale model. For this purpose, the model (9) is reformulated by adjoining the following convexity constraint to the model:
So, in order to get the ranking score under variable returns to Scale assumption is solved the following model:
Theorem 2
The model (10) is feasible and bounded.
Proof
The proof of this theorem is similar to the proof of Theorem 1.
Illustrated examples
In this section, we employ the above DEA model (6) and (7) on the two data sets which they are introduced here, with the assumption of constant returns to scale.
Example 1
As can be seen from Table 1, the data set consists of 19 DMUs with 2 inputs and 2 outputs. The data originally are used by Rezai Balf et al. (2012). Table 2 reports the results of ranking for 6 extremely efficient DMUs \((D_{1} ,D_{2} ,D_{5} ,D_{9} ,D_{15} ,D_{19} )\) in model (7) with constant Returns to Scale and the proposed method is compared with Ap, MAJ, \(L_{1}\) and \(L_{\infty }\). The results imply that the model proposed in this paper provides a easy tool for ranking extremely efficient DMUs. The value of inputs and outputs.
Example 2
(Empirical example). We employ DEA model (10) on the empirical example used in Zhu (1998), with the assumption of variable Returns to Scale. The data set in Table 3 provides 13 open coastal Chinese cities and five Chinese special economic zones in 1989. Two inputs and three outputs were chosen to characterize the technology of those cities/zones. Two inputs include Investment in fixed assets by state-owned enterprises, Foreign funds actually used. Three outputs include Total industrial output value, Total value of retail sales and Handling capacity of coastal ports. Table 4 reports the results of ranking for 10 extremely efficient DMUs \((D_{1} ,D_{2} ,D_{5} ,D_{6} ,D_{7} ,D_{9} ,D_{10} ,D_{11} ,D_{13} ,D_{16} )\) in model (10) with variable returns to scale and the proposed method are compared with other methods.
Conclusion
Many DEA researches are proposed on ranking of efficient decision making units, but they have a problem, e.g. the AP model may be infeasible in some cases. In the present paper, we proposed a model for ranking extreme efficient DMUs in DEA by exploiting the leave-one out and minimizing distance between DMU under evaluation and virtual DMU. The proposed model is linear form and always feasible and bounded. Therefore, it is able to rank all extreme efficient DMUs in the DEA methods with constraint and variable Returns to Scale and so, eliminate the existing difficulties in some methods. In addition, it can be easily used when the number of inputs and outputs is much larger than the number of DMUs. Illustrative examples are included to show good ranking results by the proposed method.
References
Amirteimoori A, Jahanshahloo GR, Kordrostami S (2005) Ranking of decision making units in data envelopment analysis: a distance-based approach. Appl Math Comput 171:122–135
Andersen P, Petersen NC (1993) A procedure for ranking efficient units in data envelopment analysis. Manag Sci 39:1261–1264
Bal H, Horkcu H, Celebioglu S (2008) A new method based on the dispersion of weights in data envelopment analysis. J Comput Ind Eng 54:502–512
Banker RD, Charnes A, Cooper WW (1984) Some methods for estimating technical and scale inefficiencies in data envelopment analysis. Manag Sci 30(9):1078–1092
Briec W (1998) Hölder distance function and measurement of technical efficiency. J Prod Anal 11:111–131
Charnes A, Cooper WW, Rhodes E (1978) Measuring the efficiency of decision making units. Eur J Oper Res 2(6):429–444
Charnes A, Cooper WW, Li S (1989) Using DEA to evaluate relative efficiencies in the economic performance of Chinese-key cities. Soc Econ Plan Sci 23:325–344
Cooper WW, Seiford LM, Tone K (2007) Data envelopment analysis: a comprehensive text with models, applications, references and DEA-solver Software, Second Edition. Springer
Hashimato A (1999) A ranked voting system using a DEA/AR exclusion model: a note. Eur J Oper Res 97:600–604
Jahanshahloo GR, Firoozi Shahmirzadi P (2013) New methods for ranking decision making units based on the dispersion of weights and Norm 1 in data envelopment analysis. Comput Ind Eng 65:187–193
Jahanshahloo GR, Hosseinzadeh Lotfi F, Shoja N, Tohidi G, Razavian S (2004a) Ranking by using L 1-norm in data envelopment analysis. Appl Math Comput 153:215–224
Jahanshahloo GR, Sanei M, Hosseinzadeh Lotfi F, Shoja N (2004b) Using the gradient line for ranking DMUs in DEA. Appl Math Comput 151:209–219
Khodabakhshia M, Aryavash K (2012) Ranking all units in data envelopment analysis. Appl Math Lett 25:2066–2070
Liu FF, Peng HH (2008) Ranking of units on the DEA frontier with common weights. Comput Oper Res 35:1624–1637
Mehrabian S, Alirezaee MR, Jahanshahloo GR (1999) A complete efficiency ranking of decision making units in data envelopment analysis. Comput Optim Appl 14:261–266
Rezai Balf F, Zhiani Rezai H, Jahanshahloo GR, Hosseinzadeh Lotfi F (2012) Ranking efficient DMUs using the Tchebycheff norm. Appl Math Model 36:46–56
Seiford LM, Zhu J (1999) Infeasibility of super-efficiency data envelopment analysis models. INFOR 37(2):174–187
Sexton TR, Silkman RH, Hogan AJ (1986) Data envelopment analysis: critique and extensions. In: Silkman RH (ed) Measuring efficiency: an assessment of data envelopment analysis. Jossey-Bass, San Francisco, pp 73–105
Shetty U, Pakkala TPM (2010) Ranking efficient DMUs based on single virtual DMU in DEA. Oper Res Soc 47(1):20–72
Tavares G, Antunes CH (2001) A Tchebycheff DEA Model. Rutcor Research Report
Thrall RM (1996) Duality, classification and slacks in DEA. Ann Oper Res 66:109–138
Torgersen AM, Forsund FR, Kittelsen SAC (1996) Slack-adjusted efficiency measures and ranking of efficient units. J Prod Anal 7:379–398
Wu J, Yan H (2010) An effective transformation in ranking using L 1-norm in data envelopment analysis. Appl Math Comput 217:4061–4064
Zhu J (1998) Data envelopment analysis vs. principal component analysis: an illustrative study of economic performance of Chinese cities. Eur J Oper Res 111:50–61
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ziari, S., Raissi, S. Ranking efficient DMUs using minimizing distance in DEA. J Ind Eng Int 12, 237–242 (2016). https://doi.org/10.1007/s40092-016-0141-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40092-016-0141-2