Abstract
The focus of this study is to investigate the seismic behavior of outrigger-braced building considering the soil–structure interaction based on finding the best location of outrigger and belt truss system. For this purpose, a central outrigger-braced frame of a steel tall building is considered. A layered soil deposit underlied this frame and the resulting soil–structure system is subjected to seismic excitation. To analyze this system, direct method is employed in OpenSees. Also, elastic and in-elastic analyses are both considered and a comparison is made between current results and the results related to the system with fixed base. The best location of outrigger–belt truss system is determined by considering the maximum roof displacement, base moment and base shear with and without soil–structure interaction. It is shown that considering SSI affects the location of outrigger–belt truss system. Elastic analysis of both systems, namely with fixed base and with soil–structure interaction, showed that locating the belt truss at higher stories caused lower amounts of roof displacement.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In tall buildings, the most important criterion is lateral forces such as earthquake and wind which may have significant effects on design. Therefore, if horizontal loadings are to be efficiently resisted, the appropriate structural form in a tall building should be determined (Kamgar and Saadatpour 2012). There are different structural forms of tall buildings and numerous researches have been carried out about the approximate and exact methods of investigating the behavior, deflection, vibration, optimal design and control of such buildings (Rahgozar et al. 2015; Alavi et al. 2018; Khatibinia et al. 2018; Kamgar et al. 2018). An effective technique to resist lateral loading in tall building is to use an outrigger-braced system. This system is comprised of a central core (braced frame or shear wall) which connects to the peripheral columns by horizontal outrigger braces or deep girders (Rahgozar et al. 2014; Malekinejad et al. 2016). In tall steel buildings, braced frames are used as lateral load resisting systems. There are several studies about optimum design of steel frame structure (Gholizadeh and Ebadijalal 2018; Gholizadeh and Poorhoseini 2015, 2016; Gholizadeh and Shahrezaei 2015). Adding outrigger in a high-rise steel-braced frame increases the stiffness of structure by incorporating stiff outrigger at different position. Determining the best location of outrigger and belt truss system is one of the most important challenges in outrigger-braced system, with the objective to decrease lateral displacement at top of the building, base moment and base shear (Wu and Li 2003; Gerasimidis et al. 2009).
Nonlinear static pushover analysis was used to find the best location of outrigger in a two-dimensional high-rise steel building by Patil and Sangle (2016). In this study, the position of outriggers along a high-rise building can significantly influence the seismic performance such as base shear, storey displacement, and inter-storey drift ratio. Kamgar and Rahgozar (2017) located a flexible outrigger–belt truss system optimally based on maximizing the strain energy of system; Continuum approach model has been used for a system consisting of framed tube, shear core, belt truss and outrigger. The effect of outrigger and shear core system was considered as a rotational spring, placed where belt truss and outrigger system was located. Three types of lateral loading, i.e., uniformly, triangularly distributed loads along the structure’s height and concentrated load at the top of the structure, were applied and best location was calculated for outrigger and belt truss system.
In previous researches, all of the structures have fixed-base conditions; whereas, in this study, the goal is to locate outrigger–belt truss system optimally in tall buildings, considering soil–structure interaction (SSI). Investigation of SSI shows that the dynamic response of a structure on soft soil is considerably different from the one supported on a fixed base (Chopra and Gutierrez 1974). Dynamic analysis of SSI has been focused in the field of structural analysis over the last 40 years. Modal characteristics of a frame structure considering dynamic soil–structure interaction is computed by finite-element perfectly matched layers model (Papadopoulos et al. 2018). Bilotta et al. (2015) evaluated the seismic vulnerability of a tall building in Italy by considering finite-element analysis of pile–soil kinematic to determine the foundation input motion. It was concluded that the effects of inertial interaction result in an increase of the structural period of vibration; the increased structural period also causes more reduction in spectral acceleration. Kamgar et al. (2019) studied a 40-storey shear building to find the optimum parameters of tuned mass damper system considering soil–structure interaction effect.
Lu et al. (2003) carried out a three-dimensional finite-element analysis of a tall building by considering dynamic SSI. In this analysis, the effects of different parameters like soil property, the rigidity of structure and buried depth on dynamic characteristics and seismic response were discussed. A three-dimensional non-linear finite-element direct approach was adopted by Amorosi et al. (2017) to analyze the SSI behavior of a 1/4-scale nuclear power plant containment structure at the Lotung site. The nonlinear nature of soil and initial stiffness varied with depth were taken into account in this model. Moreover, Tabatabaiefar et al. (2013) evaluated the effects of dynamic SSI on seismic behavior and lateral structural response of mid-rise moment-resisting building frames using finite difference method (FDM). Three types of mid-rise structures with three soil types under two different boundary conditions were considered. Liang et al. (2018) used a 3D model of a single-degree-of-freedom oscillator on embedded hemispherical foundation to evaluate the effects of dynamic characteristics of the site on dynamic SSI. The effect of SSI on change of damping ratio of a structure subjected to earthquake was studied by Cruz and Miranda (2017). Bolisetti et al. (2018) evaluated the effect of linear and nonlinear SSI analysis on safety of nuclear structures. Karabork et al. (2014) studied the effect of SSI on responses of base-isolated and fixed-base structures. Bagheripour et al. (2010) evaluated SSI problems using wavelet theory and infinite elements. Effects of soil–structure interaction on adjacent building were investigated by Rahgozar (2015). In this study, finite-element method has been used to evaluate the effects of soil–structure interaction on dynamics response of different types of buildings constructed in Kerman. O’Riordan et al. (2018) have applied a performance-based design to two different projects, one in San Francisco and one in Mexico City considering soil–structure interaction and compared the results with currently existing very limited code-based guidance for performance-base design of foundations.
In this paper, outrigger and belt truss system is located optimally in tall buildings by considering SSI. For this purpose, a central braced frame of a steel tall building with outrigger has been considered. A layered soil deposit underlied this frame and the resulting soil–structure system is subjected to seismic excitation. For the aim of analyzing this system, direct method is employed in OpenSees. Also, elastic and in-elastic analyses are both considered and a comparison is made between current results and the results obtained from the system with a fixed base. The best location of the outrigger and belt truss system is determined by considering the maximum roof displacement, base shear and base moment in both models with and without SSI.
Soil–structure interaction
In analyzing structures, particularly in case of dynamic loading such as seismic excitation, it is important to consider SSI, because seismic loading affects the soil around the structure. When the base of a structure is rigid, it is assumed that the structure is founded on solid rock. Rigidity of solid rock causes free field motion to be very close to rock; therefore, free field motion can be directly applied to the structure. For structures built on soft soil, base motion is completely different from free field motion. Preliminary studies of SSI have showed that there are mainly two types of SSI effects, inertial and kinematic interactions. The presence of soil layer on solid rock, excavation and implementation of rigid foundation into the site can modify the motion and cause horizontal displacement and rocking component of fixed base. This may change the acceleration of stories, which varies over the building’s height. Geometric averaging of input seismic motion is called kinematic interaction. Moreover, it is also required to consider inertial interaction. The inertial loads applied to the structure causes an overturning moment and a transverse shear which results in soil deformation which, in turn, modifies the base motion again (Wolf 1985).
There are two main methods to consider SSI effect, namely direct and substructure methods. In the substructure method, the entire soil-structured system is partitioned into two main substructures: the truncated region of the soil and the structure. At first, the unbounded soil is analyzed independently and the displacement–force relationship for nodes in the interface of soil and structure is determined as dynamic-stiffness coefficient of soil and is replaced by a spring–dashpot system. Then, the structure which was supported on this spring–dashpot system was analyzed. This approach is valid until the superposition law is accredited. In direct approach, the entire structure–soil system is modeled together by considering transmitting or absorbing boundaries at the truncated region of the soil and the whole system was analyzed in a single step. This method is able to consider the non-linear nature of the problem related to soft soil conditions (Wolf 1985). Direct approach has been employed in the present study, using OpenSess software.
Numerical model
Modeling of tall building
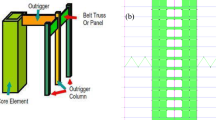
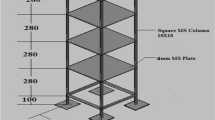
This study evaluates a 30-storey tall building with outrigger and belt truss system. A central outrigger-braced frame of this building is modeled for dynamic analysis of seismic load on a layered soil. The plane of the building and the configuration of the central outrigger-braced system are shown in Fig. 1.
The building is analyzed and designed for static and earthquake loading using SAP 2000 program and LRFD method based on AISC 360-10. The dead and live loads are taken to be 500 and 300 (N/m2), respectively. The height of each storey is 3.2 (m). All beam–column and connections are considered rigid and hinge connection is considered for all the outrigger–belt truss connections. Young modulus of elasticity and yield stress considered to be 2 × 1011 (N/m2) and 248 × 106 (N/m2), respectively. The properties of 2D central outrigger-braced frame which is modeled in OpenSees are shown in Table 1.
Soil characteristics
The underlied soil is comprised of three 10-m-thick sand layers. The percentage of density (Dr) is the lowest for the top most layer and increases with the increase of depth. The topmost layer consists of a 10-m sand (Dr = 45%), the middle one is considered to be a 10-m medium sand (Dr = 70%) and finally the layer underneath the middle layer is comprised of a 10-m dense sand (Dr = 85%). The main soil properties, including poison’s ratio and critical damping ratio, are considered to be 0.35 and 10%, respectively. The other parameters for each layer of soil are given in Table 2. The soil domain in the analysis is 100-m wide and constant cross plane thickness is 6 m which is equal to centerline distances of adjacent frames under plain strain condition, as assumed.
In Table 2, ρ indicates saturated soil mass density, Gr is reference low-strain shear modulus determined at a reference mean effective confining pressure, Br indicates reference bulk modulus determined at a reference mean effective confining pressure, and \(\phi\) represents friction angle at peak shear strength in degrees. \(\gamma_{ \rm{max} }\) represents octahedral shear strain where maximum shear strength is reached, determined at a reference mean effective confining pressure. P’r represents reference mean effective confining pressure, based on which, Gr, Br and \(\gamma_{\rm{max} }\) have been defined. d represents positive constant which defines variations G and B, which are both functions of the instantaneous effective confinement p′. ϕ PT is phase transformation angle in degrees. Contract1 is a non-negative constant which defines the rate of shear-induced volume decrease (contraction) or pore pressure build-up; dilate1and dilate2 are non-negative constants defining the rate of shear-induced volume increase (dilation). Liqufac1, liqufac2, and liqufac3 are parameters, which control the mechanisms of liquefaction-induced perfectly plastic shear strain accumulation, i.e., cyclic mobility. Finally, e indicates initial void ratio.
Finite-element model of SSI system
OpenSees is particularly designed for the analysis of soil and structural systems subjected to seismic loading which is an open-source finite-element software. OpenSees has been used to model the structure and the soil underlied, as it is capable of considering different geotechnical features and analyzing SSI. Figure 2 shows SSI system configuration in OpenSees. For modeling and analysis of structures in OpenSees, the properties of the materials and type of the elements must be defined.
Material property and type of elements
For the elastic analysis, the behavior of steel used in the cross section of beams and columns is considered to be elastic and elastic beam column is adopted for modeling all the elements. For the in-elastic analysis, the steel is modeled using Giuffre–Menegotto–Pinto model. Figure 3 shows stress–strain behavior of this material. Also, displacement beam column element is utilized for modeling all the beams and columns which are distributed plasticity, displacement-base element and capable of predicting highly nonlinear inelastic material behavior.
Stress–strain relationship of steel (Mazzoni et al. 2006)
A series of material properties are required to define the constitutive behavior of the soil. These properties corresponded to the particular constitutive model selected in the analysis. In this study, constitutive soil model is pressure-dependent multi-yield material. Pressure-dependent multi-yield material, which is an elastic–plastic material, is used for simulating the essential response characteristics of pressure sensitive soil materials under general loading conditions. These characteristics include shear-induced volume contraction or dilation and non-flow liquefaction (cyclic mobility), typically exhibited in sands or silts through monotonic or cyclic loadings. In this model, a set of Drucker–Prager nested yield surfaces, with a common apex and different sizes, form the hardening zone as shown in Fig. 4 (Zhang et al. 2008). For both the elastic and in-elastic analyses, soil behavior is linear elastic during the application of gravity load; but the soil properties are updated in in-elastic analysis after applying gravity and the stress–strain response is considered to be elastic–plastic in dynamic loading phase. This remains elastic for the elastic SSI analysis.
Pressure-dependent soil material model: (a) yield surface configuration in principal effective stress space, and (b) schematic of constitutive model response (Zhang et al. 2008)
For the case of multiple layers, one material object is generated for each layer, using the material properties defined in Table 2. With the exception of a few global properties, each layer is given a separate set of properties. The soil is considered to be dry and there is no groundwater. Therefore, the soil is modeled in two dimensions with two degrees-of-freedom using the plane strain formulation of the quad element. Finally, four-node quad elements are used to model the soil and counterclockwise pattern is used for their connectivity. The soil elements should be finer in the vicinity of the structure. Therefore, in this study, in soil element generation, the size of the soil elements is considered to be finnier in the vicinity of the structure in comparison to the other elements of soil domain.
Boundary condition
Modeling the domain boundaries of truncated soil is one of the most important issues in SSI analysis. Characteristics of these infinite boundaries should be defined in such a way that the boundaries can absorb all the outgoing waves and reflect no waves back into computational domain. For this purpose, this study adopted the standard viscous boundary, introduced by Lysmer and Kuhlemeyer (1969). Dashpots are positioned tangential and normal to the boundaries of a finite model (Fig. 2) and their characteristics can be described using Eq. 1.
In Eq. 1, Cn and Cs indicate normal and shear damping’s, Vp, Vs are dilatational and shear wave velocity of propagation, respectively; G is low strain shear modulus; ρ and \(\vartheta\) are the mass density and Poisson ratio of soil, respectively; and a and b are dimensionless parameters to be determined. Viscous boundary is defined by zero length elements based on material properties, as defined in Eq. 1 (Lysmer and Kuhlemeyer 1969). The constants a and b are determined based on following equations:
where \(\vartheta\) is the Poisson ratio of the soil.
Dynamic analysis
In this paper, the time history for acceleration of El Centro is considered to locate outrigger and belt truss system optimally. The position of outrigger and belt truss system changed from the first to the top storey by applying seismic loading each time to determine the maximum value of base shear, base moment and roof displacement and the best location is determined based on minimization of the parameters.
Seismic response of structure
The fundamental frequency and the seismic responses such as maximum roof displacement, overturning moment and base shear of two systems (fixed base and SSI) without outrigger, are calculated and shown in Tables 3 and 4. The maximum internal column shears at the base of the structure are considered as the base shear. In addition, the overturning moment is equal to sum of moments in stories.
According to Table 3, in elastic analysis, fundamental frequency is lower in SSI system than fixed base, because of the presence of soil in dynamic models, rendering a more flexible system. By comparing the maximum roof displacements, this factor is increased about 13% relative to the system with fixed base. In fact, consideration of SSI, whose function is to result in foundation motion, caused an increase in lateral deflection at the top the structure. This is especially important in high-rise buildings, since it can affect the distance between the two adjacent structures, as well as increasing P–Δ effect. Moreover, elastic analysis showed that consideration of SSI led to increases in the overturning moment and base shear.
As shown in Table 4, for in-elastic analysis, by considering the SSI effects, the fundamental frequency has been decreased and the maximum roof displacement increased and like elastic analysis, base shear and overturning moment are larger in SSI system than those in a system with fixed base.
Determining best location of outrigger and belt truss system
In the following sections, outrigger–belt truss system was located optimally based on maximum roof displacement, base shear and overturning moment. For this purpose, outrigger and belt truss system location is changed from the first to the last storey and each time the mentioned parameters are calculated. The best location is imputed to a height which brings about the minimum amount of the above mentioned parameters. Therefore, the best location of belt truss is determined for four different cases: elastic structure supported on a fixed base (El FB), elastic soil–structure system (El SSI), in-elastic structure supported on a fixed-base (In-El FB), and in-elastic soil–structure system (In-El SSI).
Overturning moment
To locate belt truss optimally based on this criterion, changes of overturning amount are calculated relative to belt truss location and are depicted in Fig. 5. As shown in this figure, elastic analysis for both systems (SSI and fixed base) brings about larger overturning moment than that brought by in-inelastic analysis. For both analyses, the changing pattern of overturning moment along the height of building is almost the same in both systems (fixed base and SSI).
The best locations of outrigger and belt truss system are calculated along the structure’s height based on overturning moment for the different cases mentioned above and are shown in Table 5. Moreover, for every case, the amount of base moment reduction when the outrigger is placed in the best location relative to the system without outrigger and belt truss system is shown. As it is shown in Table 5, considering SSI effect makes lower heights better candidates for best location of outrigger–belt truss system.
Base shear
Base shear can be an effective factor in determining the best outrigger–belt truss location. Changes in the amount of base shear can be recognized in Fig. 6. It can be observed in this figure that the same as overturning moment parameter, elastic analysis results in larger value for base shear in relation to in-elastic analysis. Moreover, elastic analysis reveals that consideration of SSI significantly increased the amount of base shear. The best location of outrigger–belt truss system along the height based on base shear and reduction in base shear, is calculated and shown in Table 6. As it is shown in Table 6, the best location of outrigger and belt truss system for elastic analysis is equal for both systems (fixed base and SSI system); but for in-elastic analysis, considering SSI causes variation in best location and shifts it to the lower height of the structure.
Maximum roof displacement
Maximum roof displacement is one of the most important criteria for locating outrigger–belt truss system optimally. To consider this criterion, changes of roof displacement along the structure’s height, in which the belt truss is located, are shown in Fig. 7. As illustrated in this figure, in-elastic analysis for both cases (fixed base and SSI) caused larger values for roof displacement than those obtained in the elastic analysis. In comparison to the system with fixed base, consideration of SSI caused larger roof displacement in both elastic and in-elastic analyses for most of the heights of belt truss placement. In elastic analysis of both systems, namely with fixed base and with SSI, locating the belt truss at higher stories causes lower amounts of roof displacement. The exact height of best location of belt truss based on roof displacement is determined and reduction of roof displacement in comparison with the system without outrigger can be seen in Table 7. As it is shown in Table 7, considering SSI causes variation in best location and shifts it to upper height of the structure.
Conclusion
In the present paper, SSI was investigated for tall buildings with the objective of finding best location of outrigger and belt truss system. In this process, outrigger–belt truss was located optimally based on a few decisive parameters, applied once to an SSI system and once to a system with fixed base. For both systems, two types of analysis, namely elastic and in-elastic analyses, were performed. Comparison of the results revealed that elastic analysis predicted larger values of overturning moment and base shear for both systems (i.e., SSI and fixed base system) than the values obtained in in-elastic analysis. Conversely, the amount of roof displacement increased in the in-elastic analysis. It can be concluded that SSI model in both types of analysis can predict larger values for roof displacement. Since the presence of soil in the model increased lateral displacement, it can be concluded that in the designing tall buildings, locating the belt truss optimally with the objective of decreasing lateral displacement is of primary importance. Furthermore, base shear and moment as additional parameters can be minimized; it was shown how considering SSI affects the best location of belt truss. Also, in elastic analysis for both systems, namely with fixed base and with SSI, locating the belt truss at higher stories caused lower values of roof displacement.
References
Alavi A, Rahgozar P, Rahgozar R (2018) Minimum-weight design of high-rise structures subjected to flexural vibration at a desired natural frequency. Struct Design Tall Spec Build 27(15):e1515
Amorosi A, Boldini D, di Lernia A (2017) Dynamic soil-structure interaction: a three-dimensional numerical approach and its application to the Lotung case study. Comput Geotech 90:34–54
Bagheripour MH, Rahgozar R, Malekinejad M (2010) Efficient analysis of SSI problems using infinite elements and wavelet theory. Geomech Eng 2(4):229–252
Bilotta E, Sanctis LD, Di Laora R, D’Onofrio A, Silvestri F (2015) Importance of seismic site response and soil–structure interaction in dynamic behaviour of a tall building. Géotechnique 65(5):391–400
Bolisetti C, Whittaker AS, Coleman JL (2018) Linear and nonlinear soil-structure interaction analysis of buildings and safety-related nuclear structures. Soil Dyn Earthq Eng 107:218–233
Chopra AK, Gutierrez JA (1974) Earthquake response analysis of multistorey buildings including foundation interaction. Earthq Eng Struct Dyn 3(1):65–77
Cruz C, Miranda E (2017) Evaluation of soil-structure interaction effects on the damping ratios of buildings subjected to earthquakes. Soil Dyn Earthq Eng 100:183–195
Gerasimidis S, Efthymiou E, Baniotopoulos CC (2009) Optimum outrigger locations of high rise steel buildings for wind loading, vol 5. EACWE, Florence, pp 1–10
Gholizadeh S, Ebadijalal M (2018) Performance based discrete topology optimization of steel braced frames by a new metaheuristic. Adv Eng Softw 123:77–92
Gholizadeh S, Poorhoseini H (2015) Optimum design of steel frame structures by a modified dolphin echolocation algorithm. Struct Eng Mech 55(3):535–554
Gholizadeh S, Poorhoseini H (2016) Seismic layout optimization of steel braced frames by an improved dolphin echolocation algorithm. Struct Multidiscip Optim 54(4):1011–1029
Gholizadeh S, Shahrezaei AM (2015) Optimal placement of steel plate shear walls for steel frames by bat algorithm. Struct Design Tall Spec Build 24(1):1–18
Kamgar R, Rahgozar R (2017) Determination of optimum location for flexible outrigger systems in tall buildings with constant cross section consisting of framed tube, shear core, belt truss and outrigger system using energy method. Int J Steel Struct 17(1):1–8
Kamgar R, Saadatpour MM (2012) A simple mathematical model for free vibration analysis of combined system consisting of framed tube, shear core, belt truss and outrigger system with geometrical discontinuities. Appl Math Model 36(10):4918–4930
Kamgar R, Samea P, Khatibinia M (2018) Optimizing parameters of tuned mass damper subjected to critical earthquake. Struct Design Tall Spec Build 27(7):e1460
Kamgar R, Khatibinia M, Khatibinia M (2019) Optimization criteria for design of tuned mass dampers including soil-structure interaction effect. Int J Optim Civil Eng 9(2):213–232
Karabork T, Deneme IO, Bilgehan RP (2014) A comparison of the effect of SSI on base isolation systems and fixed-base structures for soft soil. Geomech Eng 7(1):87–103
Khatibinia M, Gholami H, Kamgar R (2018) Optimal design of tuned mass dampers subjected to continuous stationary critical excitation. Int J Dyn Control 6(3):1094–1104
Liang J, Han B, Fu J, Liu R (2018) Influence of site dynamic characteristics on dynamic soil-structure interaction: comparison between 3D model and 2D models. Soil Dyn Earthq Eng 108:79–95
Lu X, Chen B, Li P, Chen Y (2003) Numerical analysis of tall buildings considering dynamic soil-structure interaction. J Asian Archit Build Eng 2(1):1–8
Lysmer J, Kuhlemeyer RL (1969) Finite dynamic model for infinite media. J Eng Mech Div 95(4):859–878
Malekinejad M, Rahgozar R, Malekinejad A, Rahgozar P (2016) A continuous–discrete approach for evaluation of natural frequencies and mode shapes of high-rise buildings. Int J Adv Struct Eng 8(3):269–280
Mazzoni S, McKenna F, Scott MH, Fenves GL (2006) OpenSees command language manual. Pacific Earthquake Engineering Research (PEER) Center, University of California, Berkeley
O’Riordan NJ, Almufti I, Lee J, Ellison K, Motamed R (2018) Site response analysis for dynamic soil-structure interaction and performance-based design. Proc Inst Civil Eng Geotech Eng 12:1–33
Papadopoulos M, Van Beeumen R, François S, Degrande G, Lombaert G (2018) Modal characteristics of structures considering dynamic soil-structure interaction effects. Soil Dyn Earthq Eng 105:114–118
Patil DM, Sangle KK (2016) Seismic behaviour of outrigger braced systems in high rise 2-D steel buildings. Structures 8:1–16
Rahgozar P (2015) Effects of soil-structure on adjacent buildings. M.Sc. thesis, Department of Civil Engineering, Shahid Bahonar University of Kerman, Kerman, Iran
Rahgozar R, Ahmadi AR, Ghelichi M, Goudarz Y, Malekinejad M, Rahgozar P (2014) Parametric stress distribution and displacement functions for tall buildings under lateral loads. Struct Design Tall Spec Build 23(1):22–41
Rahgozar R, Mahmoudzadeh Z, Malekinejad M, Rahgozar P (2015) Dynamic analysis of combined system of framed tube and shear walls by Galerkin method using Bspline functions. Struct Design Tall Spec Build 24(8):591–606
Tabatabaiefar R, Hamid S, Fatahi B, Samali B (2013) Lateral seismic response of building frames considering dynamic soil-structure interaction effects. Struct Eng Mech 45(3):311–321
Wolf J (1985) Dynamic soil-structure interaction. Prentice Hall Inc, Upper Saddle River
Wu JR, Li QS (2003) Structrual performance of multi-outrigger braced tall buildings. Struct Design Tall Spec Build 12:155–176
Zhang Y, Conte JP, Yang Zh, Elgamal A, Bielak J, Acero G (2008) Two-dimensional nonlinear earthquake response analysis of a bridge-foundation-ground system. Earthq Spectra 24(2):343–386
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Tavakoli, R., Kamgar, R. & Rahgozar, R. Seismic performance of outrigger–belt truss system considering soil–structure interaction. Int J Adv Struct Eng 11, 45–54 (2019). https://doi.org/10.1007/s40091-019-0215-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40091-019-0215-7