Introduction

Combined systems of framed tube, shear core and outrigger-belt truss are regularly used in modern multi-storey and tall buildings (Smith and Coull 1996; Taranath 1988; Halis Gunel and Emer Ilgin 2007; Paulino 2010). The major function of such a structure is to provide resistance against lateral loads arising from wind or earthquake. For assessing these lateral loads and performing related structural design operations, fundamental frequencies of the structure are generally required. In addition, the fundamental frequencies are often used in practice as a guide in assessing the validity of the structural layout during preliminary design stages. Many researchers have studied fundamental frequencies of tall buildings (Hamdan and Jubran 1991; Li and Choo 1995, 1996; Kuang and Chau 1998, 1999; Aksogan et al. 2003; Lee 2007; Kaviani et al. 2008; Rahgozar and Sharifi 2009; Ghasemzadeh and Rahmani Samani 2010; Rahgozar et al. 2010, 2011; Mahjoub et al. 2011; Malekinejad and Rahgozar 2011, 2012a, b; Jahanshahi et al. 2012; Kamgar and Rahgozar 2013). Natural frequencies of the combined system can be evaluated by conducting free vibration analysis. This analysis may be carried out through various approaches. The discrete Finite Element Method (FEM), for example, can be employed for this purpose, though FEM analysis may involve considerable data preparation effort and computing time. Continuous approaches can also be adopted for free vibration analysis of combined system of framed tube, shear core and outrigger-belt truss. An established approach for doing this is based on the assumption that discrete systems of spandrel beams connecting the columns may be replaced by a continuum model of equivalent stiffness. It can be seen that an important advantage of the continuous approach is that it enables the free vibration characteristic of combined system to be expressed with parameters which are related to structural properties. However, there are difficulties in using the continuous approach to calculate natural frequencies of such combined systems. The major difficulty is that a closed form solution to governing equation of motion is not obtainable. To overcome this mathematical difficulty, techniques based on Galerkin method of weighted residuals and Ritz-Galerkin have been proposed for approximate solution of the equation (Li and Choo 1995). These techniques enable the eigenvalue equations for structural free vibrations to be converted to a set of linear equations for which standard solutions exist. Nevertheless, it is difficult to estimate the inherent errors of the continuous approach arising from the approximation process in evaluating natural frequencies, especially higher frequencies, of the combined system. The continuous–discrete approach developed in this paper overcomes the above-mentioned shortcomings and combines the advantages of both discrete and continuous approaches. At present, computers are widely used in all scientific fields. Nevertheless, straightforward approaches, which can be carried out by hand, for estimating natural frequencies of structures are still very useful to practicing engineers involved in design of civil engineering structures. Such an approach may be used either for rapid assessment of structural behavior in the preliminary design or for checking the correctness of computational results in the final design.

In this paper, the approximate free vibration analysis of combined system of framed tube, shear core and outrigger-belt truss based on continuum–discrete approach is investigated. Framed tube system is modeled as cantilever beam with lumped mass at each storey level. This modeling decreases tall buildings’ number of degrees of freedom. Effect of outrigger-belt truss and shear core is modeled as rotational spring at outrigger-belt truss location. Then, stiffness and mass matrices are formed and the resulting eigenvalue problem is solved to obtain natural frequencies and the corresponding mode shapes. Results calculated by the proposed method are compared with those obtained from detailed FE model.

Continuous–discrete model for structural analysis

A lot of computer software for structural analysis is now available. Most of this software is based on the conventional finite element method. However, it is well known that the accuracy of structural analysis is largely dependent on the idealization of the structures and that the errors involved in it are much greater than those caused by the numerical methods. Therefore, it is not always worthwhile to employ a full finite element analysis which would require a lot of computer storage and large amounts of computer time. Simplified methods, which are computationally more efficient, seem to be more practical for engineering purposes. This is particularly the case in design offices where only microcomputers are available. In fact, even with large mainframe computers, simplified methods, which are much faster, should be more suitable for rapid interactive design. To reduce the computational effort required in the analysis of tall building structures, various simplifications by means of simplifying assumptions have been attempted.

In this section, a simplified approximate method is proposed for free vibration analysis of combined system of framed tube, shear core and outrigger-belt truss in high-rise buildings.

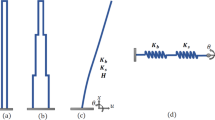
The framed tube system’s structure is modeled as cantilever beam with mass of each storey being lumped at that floor’s position (Fig. 1). In this model using Kwan’s method, framed tube structure is modeled based on continuum approach as a cantilever beam with box section which has constant thickness along the height of the structure. Then, using stiffness method, stiffness matrix for equivalent model is calculated. Mass matrix of equivalent model can be calculated considering degrees of freedom for each storey. Effect of shear core and outrigger-belt truss on framed tube is considered as rotational spring at outrigger-belt truss location. Bending stiffness of outrigger-belt truss system is calculated and inserted in stiffness matrix of the equivalent structure. Then, using calculated stiffness and mass matrices, a generalized eigenvalue problem is formed to compute natural frequencies and the corresponding mode shapes.

Fig. 1
figure 1

Combined system: a actual structure, b equivalent structure

Full size image

The following assumptions are adopted in this paper for structural analysis: (1) Material model is linear elastic, (2) Plan of the structure is symmetric about x and y axes along the height of the structure, (3) Outriggers are rigidly attached to the core and pin connected with the columns, (4) Sectional properties of the core, columns, beams and outriggers are uniform throughout the height, and finally (5) Roofs are considered as rigid diaphragms.

The following computational steps are implemented to create a realistic model of the structure:

  1. 1.

    Calculation of the bending stiffness for outrigger-belt trusses and the equivalent parameters of framed tube system are based on Kwan’s method (Kwan 1994).

  2. 2.

    Computation of structure’s mass matrix as stated in Sect. 2.1.

  3. 3.

    Calculation of the equivalent stiffness for rotational spring at outrigger-belt truss location.

  4. 4.

    Determination of structure’s stiffness matrix using stiffness method and applying effect of outrigger-belt truss system by inserting the equivalent stiffness of rotational spring into stiffness matrix of the structure.

  5. 5.

    Formation of the corresponding eigenvalue problem.

  6. 6.

    Solving the eigenvalue problem and calculating natural frequencies and corresponding mode shapes.

Determination of mass matrix

Since floor layout is uniform throughout the building, the mass of each storey is the same (i.e., \( m_{1} = m_{2} = \cdots = m_{n} = m \)) and rotational inertias are also the same (i.e., \( J_{1} = J_{2} = \cdots = J_{n} = J \)). The mass matrix M t is a diagonal matrix containing the storey mass (floor mass and half mass of upper and lower storey) as well as the rotational inertia, as follows:

$$ {\text{M}}_{\text{t}} = diag\left[ {\begin{array}{*{20}c} {M_{1} } & {M_{2} } & \ldots & {M_{3n} } \\ \end{array} } \right] $$
(1)

where

$$ M_{i} (i = 1 , { 2, } \ldots , {\text{ 3n}}) = \left\{ {\begin{array}{lll} {m \quad {\text{ for }}i < n + 1} \\ {(i - n)\quad m{\text{ for }}n + 1 \le i \le 2n} \\ {J\quad {\text{ for 2}}n + 1 \le i \le 3n} \\ \end{array} } \right. $$
(2)

where m is the lumped mass value at different locations throughout the structural height, n is the number of the lumped masses, i is the number corresponding to degree of freedom and J is the rotational inertia for each storey which calculated as follows:

$$ J = \frac{{ml^{2} }}{12} $$
(3)

where l is plan framed tube’s length which is parallel to vibrating direction.

Calculation of bending stiffness for outrigger-belt trusses

The equivalent stiffness value, K r, of the rotational spring replacing the outrigger-belt truss system can be obtained by inverting the outrigger-belt truss rotation (Malekinejad and Rahgozar 2011):

$$ K_{\text{r}} = \left[ {\frac{2C}{{d^{2} EA_{c}^{{\prime }} }} + \frac{d}{{12EI_{oe} }}} \right]^{ - 1} $$
(4)

Here, C is the outrigger-belt truss location as measured from structure’s base, d is the center to center distance between exterior columns, E is the modulus of elasticity, \( A^{\prime}_{c} \) is the area of exterior columns that are perpendicular to the direction of vibration, and \( EI_{oe} \) is the effective flexural stiffness for outrigger-belt truss.

Determination of structure’s stiffness matrix

Lumped masses of the equivalent structure have two translational and one rotational degrees of freedom (see Fig. 2).

Fig. 2
figure 2

Translational and rotational degrees of freedom

Full size image

It is well known that the key step in forming the stiffness matrix of a structure is derivation of the forces at nodes of the equivalent structure as subjected to a unit rotation or displacement at an arbitrary level (see Fig. 3).

Fig. 3
figure 3

Applying unit rotation or displacement at degrees of freedom

Full size image

Stiffness matrix entries can be calculated after applying unit displacements and computing forces at every degree of freedom. Stiffness of the equivalent spring should then be added to the rotational stiffness value of the storey where outrigger-belt truss is located. Therefore, the 3n × 3n stiffness matrix K t is a diagonal matrix as follows:

$$ {\text{K}}_{\text{t}} = \left[ {\begin{array}{*{20}c} {{\text{K}}_{\text{A}} } & {{\text{K}}_{\text{B}} } & {{\text{K}}_{\text{C}} } \\ {{\text{K}}_{\text{B}} } & {{\text{K}}_{\text{D}} } & {{\text{K}}_{\text{B}} } \\ {{\text{K}}_{\text{E}} } & {{\text{K}}_{\text{B}} } & {{\text{K}}_{\text{F}} } \\ \end{array} } \right] $$
(5)

where (n × n) matrix \( {\text{K}}_{\text{A}} \) is:

$$ {\text{K}}_{\text{A}} = \left[ {\begin{array}{*{20}c} {2K_{b} } & { - K_{b} } & 0 & 0 & \ldots & 0 \\ { - K_{b} } & {2K_{b} } & { - K_{b} } & 0 & \ldots & 0 \\ 0 & { - K_{b} } & {2K_{b} } & 0 & \ldots & 0 \\ 0 & 0 & 0 & {K_{b} } & \vdots & 0 \\ \vdots & \vdots & \vdots & \ldots & \ddots & 0 \\ 0 & 0 & 0 & \ldots & 0 & {K_{b} } \\ \end{array} } \right] $$
(6)

\( {\text{K}}_{\text{B}} \) is (n × n) zero matrix, and \( {\text{K}}_{\text{C}} \) is (n × n) matrix as:

$$ {\text{K}}_{\text{C}} = \left[ {\begin{array}{*{20}c} 0 & {K_{m1} } & 0 & 0 & 0 & \cdots & 0 \\ { - K_{m1} } & 0 & {K_{m1} } & 0 & 0 & \cdots & 0 \\ 0 & { - K_{m1} } & 0 & {K_{m1} } & 0 & \cdots & 0 \\ 0 & 0 & 0 & 0 & { - K_{m1} } & \vdots & 0 \\ 0 & 0 & 0 & 0 & 0 & \ddots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & { - K_{m1} } \\ \end{array} } \right] $$
(7)

and (n × n) matrix \( {\text{K}}_{\text{D}} \) is:

$$ {\text{K}}_{\text{D}} = \left[ {\begin{array}{*{20}c} {2K_{a} } & { - K_{a} } & 0 & \ldots & 0 \\ { - K_{a} } & {2K_{a} } & { - K_{a} } & \ldots & 0 \\ 0 & { - K_{a} } & {2K_{a} } & \ldots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & {K_{a} } \\ \end{array} } \right] $$
(8)

and (n × n) matrix \( {\text{K}}_{\text{E}} \) is:

$$ {\text{K}}_{\text{E}} = \left[ {\begin{array}{*{20}c} 0 & { - K_{m1} } & 0 & \cdots & 0 \\ {K_{m1} } & 0 & { - K_{m1} } & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & {K_{m1} } & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & { - K_{m1} } \\ \end{array} } \right] $$
(9)

and (n × n) matrix \( {\text{K}}_{\text{F}} \) is:

$$ {\text{K}}_{\text{F}} = \left[ {\begin{array}{*{20}c} {2K_{m2} } & {K_{m3} } & 0 & 0 & \cdots & 0 \\ {K_{m3} } & {2K_{m2} } & {K_{m3} } & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & {K_{m3} } & {2K_{m2} + K_{r} } & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & {K_{m2} } \\ \end{array} } \right] $$
(10)

where K a , K b , K m1 , K m2 and K m3 are:

$$ K_{b} = \frac{{12EI_{t} }}{{h^{3} }} $$
(11)
$$ K_{m1} = \frac{{6EI_{t} }}{{h^{2} }} $$
(12)
$$ K_{m2} = \frac{{4EI_{t} }}{h} $$
(13)
$$ K_{m3} = \frac{{2EI_{t} }}{h} $$
(14)

where E, h and I t, respectively, are modulus of elasticity, storey’s height and moment inertia for the equivalent structure’s plan of the framed tube and shear core (see Fig. 4). I t can be calculated as follows:

$$ I_{t} = I_{F} + I_{C} $$
(15)

where I F is moment of inertia for the equivalent framed tube system which is modeled by Kwan’s method; and I C is shear core’s moment of inertia.Also, K a is:

$$ K_{a} = \frac{{EA_{t} }}{h} $$
(16)

where A t is the cross-sectional area of the equivalent framed tube and shear core’s plan which is:

$$ A_{t} = A_{F} + A_{C} $$
(17)

where A F is the cross-sectional area of equivalent framed tube’s plan and A C is the cross-sectional area of shear core’s plan.

Fig. 4
figure 4

Equivalent modeling of framed tube and shear core systems

Full size image

As shown in Fig. 4, framed tube system is modeled as a hollow cantilever beam based on Kwan’s method, and shear core is also modeled as hollow cantilever beam placed at the centre of the equivalent framed tube cantilever beam. Equivalent properties of framed tube can be calculated from the following equations (Kwan 1994):

$$ t_{e} = \frac{{A_{\text{Column}} }}{S} $$
(18)

where t e , A Column, S are equivalent thickness of framed tube system, cross-sectional area of an exterior column and central distance between exterior columns, respectively. Equivalent modulus elasticity is same as the actual modulus elasticity for the framed tube structure. Also, equivalent shear modulus of framed tube structure can be obtained as (Kwan 1994):

$$ G_{e} = \frac{h}{{St_{e} \left( {\alpha + \beta } \right)}} $$
(19)

where α and β are:

$$ \alpha = \frac{{\left( {h - l_{\text{Beam}} } \right)^{3} }}{{12EI_{\text{Col}} }} + \left( {\frac{h}{S}} \right)^{2} \frac{{\left( {S - l_{\text{Col}} } \right)^{3} }}{{12EI_{\text{Beam}} }} $$
(20)
$$ \beta = \frac{{\left( {h - l_{Beam} } \right)}}{{GA_{Col} }} + \left( {\frac{h}{S}} \right)^{2} \frac{{\left( {S - l_{Col} } \right)}}{{GA_{Col} }} $$
(21)

In Eqs. (19–21) A Col , I Col , l Col , A Beam , I Beam and l Beam are the cross-sectional area, moment of inertia and length of columns and beams, respectively. G is the shear modulus of the actual framed tube structure.

General equation of motion and solving the eigenvalue problem

After obtaining both mass and stiffness matrices, free vibration analysis of the combined system of framed tube, shear core and outrigger-belt truss for the case of no damping can be conducted by solving the following generalized eigenvalue equation (Chopra 2000):

$$ \left| {{\text{K}}_{\text{t}} - \omega_{i}^{2} {\text{M}}_{\text{t}} } \right| = 0 $$
(22)

where M t and K t are the lumped mass matrix and consistent stiffness matrix of the equivalent structural system, respectively. \( \omega_{i} \) is the circular frequency of the ith mode of the system.

Verification of methodology

In this section, to verify the methodology adopted in continuous–discrete approach, four numerical examples were solved by the proposed method. The results are compared with the ones obtained from computer analyses.

For this purpose 55- and 65-storey tall buildings, with framed tube system or combined system of framed tube, shear core and an outrigger-belt truss are considered with structural properties listed in Table 1.

Table 1 Structural properties of the 55- and 65-storey tall buildings
Full size table

Outrigger-belt trusses are located at 1/4, 1/2 and 3/4 height of the structure. All columns and outrigger-belt truss members have same size of 0.8 × 0.8 m. Density of concrete is \( \rho_{c} = 2400{\text{ kg/m}}^{ 3} \) and modulus elasticity of concrete is \( E = 20{\text{ GPa}} \). Thickness of slab is \( t_{Slab} = 0.3{\text{ m}} \).

Natural frequencies and corresponding mode shapes of the 55- and 65-storey buildings are obtained by the proposed method and compared with SAP 2000 computer analysis results (SAP 2000 Advanced 12.0.0, Computers and Structures, Berkeley, CA, USA) (see Tables 2, 3 and Figs. 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22).

Table 2 Comparison of natural frequencies of the 55- and 65-storey framed tube tall buildings
Full size table
Table 3 Comparison of natural frequencies of the 55- and 65-storey tall buildings with combined system
Full size table
Fig. 5
figure 5

First mode of the free vibration analysis for 55-storey framed tube tall building with 15 % relative error in frequency

Full size image
Fig. 6
figure 6

Second mode of the free vibration analysis for 55-storey framed tube tall building with 1 % relative error in frequency

Full size image
Fig. 7
figure 7

Third mode of the free vibration analysis for 55-storey framed tube tall building with 0.9 % relative error in frequency

Full size image
Fig. 8
figure 8

First mode of the free vibration analysis for 65-storey framed tube tall building with 6 % relative error in frequency

Full size image
Fig. 9
figure 9

Second mode of the free vibration analysis for 65-storey framed tube tall building with 6 % relative error in frequency

Full size image
Fig. 10
figure 10

Third mode of the free vibration analysis for 65-storey framed tube tall building with 8 % relative error in frequency

Full size image
Fig. 11
figure 11

First mode of the free vibration analysis for 55-storey tall building with combined system (C = 42 m) with 15 % relative error in frequency

Full size image
Fig. 12
figure 12

Second mode of the free vibration analysis for 55-storey tall building with combined system (C = 42 m) with 11 % relative error in frequency

Full size image
Fig. 13
figure 13

Third mode of the free vibration analysis for 55-storey tall building with combined system (C = 42 m) with 4 % relative error in frequency

Full size image
Fig. 14
figure 14

First mode of the free vibration analysis for 65-storey tall building with combined system (C = 48 m) with 1 % relative error in frequency

Full size image
Fig. 15
figure 15

Second mode of the free vibration analysis for 65-storey tall building with combined system (C = 48 m) with 8 % relative error in frequency

Full size image
Fig. 16
figure 16

Third mode of the free vibration analysis for 65-storey tall building with combined system (C = 48 m) with 12 % relative error in frequency

Full size image
Fig. 17
figure 17

First mode of the free vibration analysis for 55-storey tall building with combined system (C = 81 m) with 16 % relative error in frequency

Full size image
Fig. 18
figure 18

Second mode of the free vibration analysis for 55-storey tall building with combined system (C = 81 m) with 10 % relative error in frequency

Full size image
Fig. 19
figure 19

Third mode of the free vibration analysis for 55-storey tall building with combined system (C = 81 m) with 3 % relative error in frequency

Full size image
Fig. 20
figure 20

First mode of the free vibration analysis for 65-storey tall building with combined system (C = 96 m) with 4 % relative error in frequency

Full size image
Fig. 21
figure 21

Second mode of the free vibration analysis for 65-storey tall building with combined system (C = 96 m) with 6 % relative error in frequency

Full size image
Fig. 22
figure 22

Third mode of the free vibration analysis for 65-storey tall building with combined system (C = 96 m) with 10 % relative error in frequency

Full size image

Discussion and conclusion

In this paper, an approximate approach to free vibration analysis of combined system of framed tube, shear core and outrigger-belt truss based on continuum–discrete approach was investigated. Framed tube system based on Kwan’s method was modeled as cantilever beam with lumped mass model for each storey level. This modeling can decrease tall buildings’ number of degrees of freedom. Also axial and bending stiffness of actual structure can be considered in this model as well. Effect of outrigger-belt truss and shear core was modeled as rotational spring at outrigger-belt truss location. Equivalent stiffness of this spring depends on height of the outrigger-belt truss from base of the structure and outrigger-belt truss members’ size. Then, stiffness and mass matrices were formed and finally eigenvalue problem was solved for obtaining natural frequencies and corresponding mode shapes. Results calculated by the proposed method were compared with those obtained from computer analysis. Differences were within acceptable ranges (errors of 55- and 65-storey for framed tube system were about 0.9–14.9 and 6.2–8.7 % and for combined system were about 2.1–16.3 and 1.1–12.1 %, respectively). Sources of errors are neglecting the shear effects in equivalent structure, modeling of framed tube and shear core as cantilever hallow beams, modeling effect of shear core and outrigger-belt truss on framed tube as rotational spring with equivalent stiffness and neglecting shear lag effects in approximate analysis. It should be noted that average value of error for the first mode of the framed tube system or combined system in 55-storey building was higher than those of the 65-storey building because tall buildings with different height to diameter of circumference ratio have different behavior. Buildings with lower height to diameter ratio exhibit shear behavior and buildings with higher height to diameter ratio have bending behavior. Proposed method has further errors in buildings with lower height to diameter ratio because of neglecting the shear effects in the proposed method. The approximate proposed method which is concise and easy to use is valuable to engineers involved in the preliminary structural design of tall buildings employing combined system of framed tube, shear core and outrigger-belt truss structures.