Introduction

Tall buildings are a logical and economical solution for the settlement of the population, jobs, departments, etc. in a small area of land, which can help the town planners, besides its appearance and glory. However, for many cosmopolitans, high-rise buildings are the only response to the continuous growth of population concentration. The purpose of constructing high-rise buildings is to use more area to meet the needs of different citizens. This is a way to save on land use and share prices to users, thus avoiding the unnecessary land use, coping with its scarcity, and expanding urban levels. The conventional analysis of tall structures is often time-consuming and costly due to having high degrees of freedom. The designers of this kind of buildings require a proper and reasonable design for their design and it is necessary to be able to analyze the static and dynamic characteristics of the structure quickly and accurately. Additionally, the effect of each variable in assumed structural system should be determined and finally, the first appropriate design should be recommended. Considering the importance of framed tube structures in high-rise buildings as a system resistant to lateral loads, it is necessary to have a simple but precise method for analyzing these structures.

There are different forms of tall buildings and numerous researches have been carried out about the approximate and exact methods of investigating the behaviour, deflection, vibration, optimal design and control of such buildings. Coull and Bose (1975) presented a method based on the theory of elasticity. In this method, the structure is equivalent to orthotopic planes, and the equations and equilibrium relations are satisfied in the equivalent structure. Coull and Ahmed (1978) presented a method in calculation of stories displacement in the framed tube. Kwan (1994) presented equations for determining the stress in columns and obtaining the lateral displacement of the framed tube structure using equivalence orthotropic planes, energy relations and the theory of elasticity. Connor and Pouangare (1991) recommended the five-stringer model, in which the structure is equalled with beams and vertical planes and by calculating the shear and moment rigidity of members, the formulas for stresses in the column are proceeded. One of the other methods for improving the behavior of the framed tube is adding internal tubed frames to the original structure. In this case, the stress distribution and displacement will be appreciably reduced. Other methods for analyzing framed-tube are presented by researchers such as Paulino (2010), Mahjub et al. (2011), Kamgar and Rahgozar (2013), Rahgozar et al. (2014), Malekinejad and Rahgozar (2014), Mohammadnejad (2015), Rahgozar et al. (2015), Khajuai Rad et al. (2017). A parametric dimensionless formula has been developed for flexural stiffness of high-rise buildings with the objective of optimization problem by Alavi et al. (2017). Kamgar and Rahgozar (2019) introduced a method to reduce the static roof displacement and axial forces in the columns of tall buildings. Tavakoli et al. (2019) considered a direct method for high-rise structures with elastic and inelastic analysis with fixed-base system. Davari and Rahgozar (2019) conducted their research on the static analysis of high-rise buildings without shear lag effect, too. Davari et al. (2019) explained the Euler–Bernoulli and the Timoshenk’s beam theory to analyse the tall buildings, which it concluded that the Timoshenko theory is more accurate than the Euler–Bernoulli. In this paper, a simple approximation method has been proposed for static analysis of a tall structure with a framed tube system with symmetrical plan and fixed profile in height using a Timoshenko beam model with regard to shear and flexural hardening and regardless of the shear lag effects (Herrmann 1955). Finally, a revised formula for the shape factor of the high-rise buildings is proposed to minimize the error between ETABS modeling and the Timoshenko’s theory.

Method

In this study, the framed tube was equalized with four orthotropic orthogonal planes with a hollow box section, the structure of the framed tube was subjected under a uniform load and triangular distributed loading, and static analysis was performed. Davari et al. presented the Euler–Bernoulli’s theory and the Timoshenko’s beam theory to calculate the displacement of the stories.

Uniform distributed loading

Equations 1 and 2 show the displacement of the structure at the distance of x from the bottom of the structure for the Euler–Bernoulli and the Timoshenko theories, respectively.

$$\omega (x) = \frac{q}{EI}\left( {\frac{{L^{2} x^{2} }}{4} - \frac{{Lx^{3} }}{6} + \frac{{x^{4} }}{24}} \right)$$
(1)
$$\omega (x) = \frac{q}{EI}\left( {\frac{{L^{2} x^{2} }}{4} - \frac{{Lx^{3} }}{6} + \frac{{x^{4} }}{24}} \right) + \frac{{qlx - qx^{2} /2}}{kAG}$$
(2)

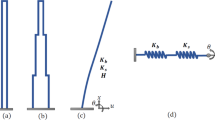
In the above equations, q is the uniform loading pattern, L is the height of the structure and x is the distance from the bottom of the structure (see Fig. 1). Moreover, the parameters E, G, I, k and A are Young’s modulus of the material, shear modulus of the material, moment of the inertia, shape factor and area of the section, respectively.

Fig. 1
figure 1

Analysis model of structure under uniform distributed loading pattern

Full size image

Triangular distributed loading

When the structure is subjected to a triangular loading pattern in accordance with Fig. 2, the angle of rotation of the different points at the height of the structure is equal to \(\varphi\) and the lateral displacement is equal to \(\omega\).

Fig. 2
figure 2

Analysis model of structure subjected to triangular loading pattern

Full size image

In this loading pattern, \(M_{x}\) can be written as:

$$M_{x} = \frac{{cL^{2} x}}{2} - \frac{{cL^{3} }}{3} - \frac{{cx^{3} }}{6}.$$
(3)

Using Eq. 3, it will be concluded:

$$\begin{aligned} EI\frac{{{\text{d}}^{2} \omega }}{{{\text{d}}x^{2} }} & = \frac{{cL^{2} x}}{2} - \frac{{cL^{3} }}{3} - \frac{{cx^{3} }}{6} \\ \varphi (x) & = \frac{{{\text{d}}\omega }}{{{\text{d}}x}} = \frac{c}{EI}\left( {\frac{{L^{2} x^{2} }}{4} - \frac{{L^{3} x}}{3} - \frac{{x^{4} }}{24}} \right) + c_{1} . \\ \end{aligned}$$
(4)

By applying boundary condition on Eq. 4, the constant will be:

$$\varphi \, (0) = 0 \, \Rightarrow \, c_{1} = 0.$$
(5)

So:

$$\varphi (x) = \frac{c}{EI}\left( {\frac{{L^{2} x^{2} }}{4} - \frac{{L^{3} x}}{3} - \frac{{x^{4} }}{24}} \right).$$
(6)

Using Eq. 6, \(\omega (x)\) will be calculated in Eq. 7:

$$\begin{aligned} \omega (x) & = \int {\varphi (x){\text{d}}x} \\ & = \frac{c}{EI}\left( {\frac{{L^{2} x^{3} }}{12} - \frac{{L^{3} x^{2} }}{6} - \frac{{x^{5} }}{120}} \right) + c_{1} . \\ \end{aligned}$$
(7)

By applying another boundary condition, the constant of integration will be obtained:

$$\omega \, (0) = 0 \, \Rightarrow \, c_{1} = 0.$$
(8)

Overall, the displacement formula will proceed in Eq. 9:

$$\omega (x) = \frac{c}{EI}\left( {\frac{{L^{2} x^{3} }}{12} - \frac{{L^{3} x^{2} }}{6} - \frac{{x^{5} }}{120}} \right).$$
(9)

In the following, two examples are presented to examine the proposed method and compare the results of the numerical investigation with two others theories. Each of these structures has been analyzed and studied with ETABS modeling, proposed method and Euler–Bernoulli’s theory under a uniform static load pattern.

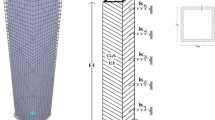
Concrete framed-tube with symmetric plan

The structure of a 40-storey concrete frame with a symmetrical plan has been used and statically analyzed (Fig. 3) (Kwan 1994). The overall dimensions of the structure are 35 m × 30 m. The distance between the columns is 2.5 m and the height of each storey is 3 m. In this structure, dimensions of all beams and columns are 0.8 × 0.8 m and Young’s modulus and shear modulus of the materials are 200 GPa and 8 GPa, respectively. In addition, a uniform loading pattern (120 kN/m) is applied to the structure for calculating the deformation of the structure.

Fig. 3
figure 3

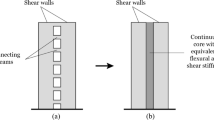
Framed-tube system: a actual structure, b equivalent structure (Khajouyi Rad et al. 2017)

Full size image

For numerical analysis, we considered the values of some parameters given for a Timoshenko beam in a uniformly loading pattern, as the following (Table 1). As it is obvious from Fig. 1b, the a and b are the half of the length and the width of the plan of the high-rise building. The parameter t is the equivalent thickness of the plan of the structure which will be calculated based on the formula that presented in Table 1. Ac and the S are the column area section and the distances between them. k and I are the shape factor and the section modulus of the box section. Δb and Δc are the deflection induced by bending and the shear, respectively. Q is defined as lateral loading pattern, too. Moreover, all parameters are described in Hutchinson research (Hutchinson 2001). The mentioned parameters will be equal to Table 1.

Table 1 Parameters of equivalent structure
Full size table

Results

To compare the results of above methods, including ETABS modeling, Euler–Bernoulli and Timoshenko methods, once a 40-storey concrete structure with symmetric plan and then an 80-storey like the previous one had been modeled in ETABS and the displacement at top of the structure have been compared. Figure 4 shows the displacement of stories for the three proposed methods of a 40-storey building.

Fig. 4
figure 4

Comparison of displacement obtained by three proposed methods for a 40-storey concrete building

Full size image

Based on mean square displacement (MSD) by the ETABS modeling compared to Bernoulli method is about 82%, and it was 45% with the Timoshenko method. Figure 5 shows the stories displacement for the three proposed methods for a 80-storey building. The MSD of Bernoulli’s method and the ETABS is 54%, which is about 31% for the proposed method with ETABS modeling.

Fig. 5
figure 5

Comparison of displacement obtained by three presented methods for an 80-storey concrete building

Full size image

As can be seen from Eq. 2, the value of displacement is related to the three main parameters of k, G and A, which can be evaluated by changing some geometric characteristics of the structure. Doing so, the structure is firstly modeled in both concrete and steel structures, and the parameter G, which represents the shear modulus, and is investigated by changing the height of the stories. In addition, changes have been made to the dimensions of the architectural plan to obtain the parameters k and A, which represent the shape factor and area of the plan, respectively. The height of the floors structures was considered in five different conditions including 3, 3.5, 4, 4.5 and 5 m to study the shear modulus. The plan dimensions in the values of 25 × 30 m, 30 × 35 m, 35 × 40 m and 40 × 45 m have been changed to examine the shape factor and area of the plan. The results of concrete structure are presented in Tables 2 and 3, and the results of the steel structure, have been represented in Tables 4 and 5. Figures 6, 7, 8 and 9 represent the area effect and height of the stories in concrete and steel structure, respectively.

Table 2 Lateral displacements calculated in different area of concrete structure
Full size table
Table 3 Lateral displacements calculated in concrete structure with different heights of the stories
Full size table
Table 4 Lateral displacements calculated in different area of steel structure
Full size table
Table 5 Lateral displacements calculated in different areas of steel structure
Full size table
Fig. 6
figure 6

Displacement of proposed method and FEM for 40-storey concrete structure with different areas in plan

Full size image
Fig. 7
figure 7

Displacement of proposed method and FEM for 40-storey concrete structure with varying storey’s height

Full size image
Fig. 8
figure 8

Displacement of proposed method and FEM for the 40-storey steel structure with different areas in plan

Full size image
Fig. 9
figure 9

Displacement of proposed method and FEM for a 40-storey building with varying storey height

Full size image

As can be seen from Figs. 7 and 9, it could be concluded that with the change in the height of the stories, there is not much difference between the displacements obtained from the two methods for the highest point of the structure. Moreover, on the other hand, this variation in height changes the modulus parameter shear, G, so it can be concluded that the shear-modulus changes do not affect the difference in the results of the two methods. Based on Figs. 6 and 8, it could be stated that by changing the dimensions of the plan, there is a greater difference between the displacements obtained from the two methods for the highest point of the structure relative to the changes in the shear modulus in the previous state. Additionally, the area of each floor, A, changes the coefficient of the parameter k, so it could be concluded that area variations have a greater effect on the difference in the results of the two methods. By varying the values of the parameters a and b, we can obtain an equation for parameter k, which gives us a more precise amount of displacement in the theoretical method. For this purpose, various amounts of k have been checked in the formulation of the proposed method to achieve the nearly displacement, which is obtained from ETABS modeling, then this procedure is repeated for all of the models. Therefore, a series of numbers obtained by it for parameter k, the relation formula with a and b will be developed by solving this function. The Eq. 10 shows the k formula that is based on Hutchinson research (Alavi et al. 2017) for the rectangular cross section. The parameter C4 in Eq. 11 is also revised like Eq. 10. In fact, calculation of the displacement for the tall structures is simplified by these changes.

$$k = - \frac{0.0034(1 + \upsilon )}{{\left[ {0.0715\frac{{C_{4} }}{{a^{5} b}} + \upsilon \times 0.3948\left( {1 - \frac{{b^{2} }}{{a^{2} }}} \right)} \right]}}$$
(10)
$$C_{4} = \frac{4}{45}a^{3} b\left( { - 12a^{2} - 15\upsilon a^{2} + 5\upsilon b^{2} } \right)$$
(11)

To investigate the accuracy of the proposed equation, a 20 × 25 m planar concrete structure was modeled in ETABS software and the output results were obtained. On the other hand, we extracted the same output from the theoretical method with k value obtained from the formula presented above. According to the results, obtained k value had an acceptable accuracy. Table 6 indicates the results of the ETABS modelling, proposed method by k = \(\frac{5}{6}\) and the proposed method by Eq. 10.

Table 6 Comparison of results for shape factor and displacement
Full size table

Conclusion

  • Proposed model for the analysis of tall structures with symmetrical plan produced acceptable results, particularly in the initial design stage.

  • Although numerical methods and commercial software were more accurately able to model tall structures, the analytical approach presented in the proposed method provided the ability to determine the parameters affecting structure behavior and their sensitivity analysis in the structure response.

  • Proposed method was less costly compared to the numerical methods such as finite element, and required less computing procedures. This issue becomes more important in the case of high-rise structures with a large number of elements.

  • New coefficients for the shape factor equation induced better accuracy for the displacement of the framed-tube structures.

  • Besides the accuracy of the shape factor equation for the framed-tube structures, the time-consuming analysis could be reduced significantly.

  • The results of the analysis with shear effect is considerable because Timoshenko beam theory adapted vigorously on the ETABS modeling results.