Abstract
Composite one-way concrete slabs with profiled steel decking as permanent formwork are commonly used in the construction industry. The steel decking supports the wet concrete of a cast in situ reinforced or post-tensioned concrete slab and, after the concrete sets, acts as external reinforcement. In this type of slab, longitudinal shear failure between the concrete and the steel decking is the most common type of failure at the ultimate load stage. Design codes require the experimental evaluation of the ultimate load capacity and longitudinal shear strength of each type of steel decking using full-scale tests on simple-span slabs. There is also no procedure in current design codes to evaluate the ultimate load capacity and longitudinal shear strength of continuous composite slabs and this is often assessed experimentally by full-scale tests. This paper presents the results of three full-scale tests up to failure on continuous composite concrete slabs cast with trapezoidal steel decking profile (KF70) that is widely used in Australia. Slab specimens were tested in four-point bending at each span with shear spans of span/4. The longitudinal shear failure of each slab is evaluated and the measured mid-span deflection, the end slip and the mid-span steel and concrete strains are also presented and discussed. Redistribution of bending moment in each slab is presented and discussed. A finite element model is proposed and verified by experimental data using interface element to model the bond properties between steel decking and concrete slab and investigate the ultimate strength of continuous composite concrete slabs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Composite slabs consisting primarily of cold-formed profiled steel decking and structural concrete are increasingly used in steel-framed buildings worldwide. In this system, the steel decking is normally continuous over two-spans between the supporting steel beams and during construction the concrete is poured to form a continuous one-way composite slab.
The steel decking has two main roles in this type of floor system; firstly, it serves as permanent formwork supporting the wet concrete during construction. Secondly, it acts as external reinforcement for the slab, carrying the tension induced by positive bending moment throughout the life of the structure. If the strength provided by the steel decking is not adequate, additional reinforcement might be included in the concrete slab, as shown in Fig. 1 (Johnson 2004; Oehlers and Bradford 1995).
The composite action between the steel decking and the hardened concrete is dependent on the transmission of horizontal shear stresses acting on the interface between the concrete slab and the steel decking (Abdullah and Easterling 2009; Bradford 2010; Ferrer et al. 2006; Gholamhoseini et al. 2014a). Composite action and the transmission of horizontal shear stresses at the concrete–steel interface are necessary for the steel decking to perform its role as the tension reinforcement for the system. The composite action between the concrete and the steel decking is achieved, not only by chemical bonding between the decking and the concrete, but also by mechanical interlock between the concrete and the embossments on the profiled steel decking. Further composite action can be attained by attaching shear studs or similar shear devices.
Ultimate strength of composite concrete slabs
There are two methods presented in Eurocode 4 (EN 2004) to evaluate the ultimate capacity of simple-span composite slabs, known as the ‘‘m–k’’ and ‘‘partial shear connection’’ methods.
The m–k method to evaluate the design resistance against longitudinal shear is mainly based on the numerous experimental works of Porter and Ekberg (1975, 1976) and essentially needs some tests to determine the empirical values of m and k for a certain type of steel decking.
In the partial shear connection method, the flexural capacity of the composite slab at full shear connection stage is calculated by simple plastic analysis of the section and by employing rectangular stress blocks for the concrete and profiled steel decking. Due to interface slip occurrence, to evaluate the ultimate longitudinal shear stress between steel decking and concrete slab, full-scale tests are also required in this method to determine the degree of shear connection.
As stated earlier, the steel decking is usually supplied in two-span lengths and negative reinforcement is provided on top of the supports during construction. This makes the composite slab normally continuous. Despite several studies reported in recent years on the serviceability behaviour of simple-span and continuous reinforced and steel fibre-reinforced composite slabs (Abas et al. 2013; Ackermann and Schnell 2008; Al-Deen et al. 2011; Al-Deen and Ranzi 2015; Bednar et al. 2013; Gholamhoseini et al. 2012, 2013a, b, 2014b, 2016; Gholamhoseini 2016; Gilbert et al. 2012; Kim and Jeong 2006, 2009; Lin et al. 2014a, b; Marciukaitis et al. 2006; Marimuthu et al. 2007; Mansour et al. 2015; Mirza and Uy 2012; Petkevicius and Valivonis 2010; Ranzi et al. 2013a, b), limited information is available in the literature on the assessment of their ultimate strength. For this, current codes do not present a procedure to evaluate the ultimate load capacity and longitudinal shear strength of continuous composite slabs and this is often assessed by full-scale tests. Hence, practising engineers often assume that the composite slab is simply supported and carry out the design accordingly.
This paper presents the results of three full-scale tests up to failure on continuous composite concrete slabs cast with using trapezoidal steel decking profile (KF70) that is widely used in Australia. Slab specimens were tested in four-point bending at each span with shear spans of span/4. The longitudinal shear failure of each slab is evaluated and the measured mid-span deflection (from first loading to ultimate and into the post-peak range), the end slip and the mid-span steel and concrete strains and the redistribution of bending moments are also presented and discussed. A finite element model is proposed and verified by experimental data using interface element to model the bond properties between steel decking and concrete slab and investigate the ultimate strength of continuous composite concrete slabs.
Experimental study
Overview
The short-term behaviour of three composite slabs cast on commonly used KF70 trapezoidal decking profile manufactured by Fielders Australia Pty Ltd (2008) has been studied. The shape, dimensions and section properties of the profile are shown in Fig. 2. The thickness of the steel sheeting was 0.75 mm.
Each slab was 6900 mm long, with a cross section 150 mm deep and 1200 mm wide, and contained no bottom reinforcement (other than the external steel decking). The decking was formed from 0.75 mm thick grade G500 steel with a Z275 coating produced according to (Standards Australia 2011). The composite slabs were cast with the profiled steel decking as permanent formwork and the concrete was then cured for 7 days under wet hessian. For each specimen, the steel decking was completely supported on the laboratory floor during casting of the concrete to minimise initial stress or deformation in the steel decking and the deck was cleaned thoroughly before placing concrete.
It should be highlighted that the test specimens were part of a separate study on the long-term behaviour of continuous composite concrete slabs and were cracked on the interior support in that test. The complete results of that study have been reported elsewhere (Gholamhoseini et al. 2013a).
Each specimen was continuous over the interior support and simply supported on a roller at each of the two exterior supports with a 100 mm overhang at each end. The centre–centre distance between the each exterior roller support and interior pin support was 3350 mm. Longitudinal and transverse reinforcements were provided in the top of the slabs in the negative moment region over the interior support, as shown in Fig. 3.
The first digit in the designation of each slab is the specimen number (1–3), and the following letter “C” indicates geometry of the slab and stands for “continuous”. The next two numbers indicate the type of decking (where 70 means KF70 decking).
Test setup and instrumentation
The test method for all tested slabs was the same. Each slab was tested with shear span of \(L_{\text{s}} { = }{{L^{\prime}} \mathord{\left/ {\vphantom {{L^{\prime}} 4}} \right. \kern-0pt} 4} = 8 40{\text{ mm}}\). Two load cells were placed underneath each support to measure the support reaction and its variation at any time. The deflection at the mid-spans and the end slip at both exterior supports were measured by LVDTs (linear variable displacement transducers). The strains in the concrete and in the steel decking were measured at selected sections on the top and bottom surfaces of slabs using 60 mm long surface-mounted strain gauges. The strain in the longitudinal reinforcement at the interior support was measured by embedded strain gauges.
The applied load and the reactions at each support were also recorded continuously throughout the tests. The applied load was measured by a load cell placed under the actuator. A schematic view of the experimental setup and the measured parameters is shown in Fig. 3.
The load was applied in a displacement control manner at a rate of 0.3 mm/min. The deformation was applied at a slow rate throughout the test to examine the complete load–deflection response, including in the post-peak unloading range. Failure was considered to have occurred when one of the spans had deflected excessively and hence, the load had dropped significantly.
Material properties
The mean compressive strength fcm and modulus of elasticity Ec of the concrete at the age of testing were determined from tests on six standard 100 mm diameter cylinder companion specimens and were 47.9 and 33,050 MPa, respectively. At the time of testing each slab, tests were also conducted on 100 mm × 100 mm × 500 mm prisms to determine the flexural tensile strength of concrete. The mean concrete flexural tensile strength fct.f (modulus of rupture) was 4.68 MPa.
The complete stress–strain curve, elastic modulus Es and yield stress fyp of the steel decking were also measured from tests on three coupons cut from the sheet of decking. The yield stress fyp and the elastic modulus Es of the steel decking were 532 MPa and 203 GPa, respectively. Similarly, from tests on three samples of the reinforcing bars, the average values were fy = 495 MPa and Es = 205 GPa, respectively.
Discussion of test results
The mid-span deflection versus applied load for each slab is shown in Fig. 4. Without exception, the widest crack occurred at the interior support and in the vicinity of one of the applied loads. After the peak load had been reached, wide cracks at the top surface of the interior support (as shown in Fig. 5) and below the applied line loads eventually divided the concrete. This was typically associated with excessive end slip as exemplified in Fig. 6. Significant post-slip strength was observed in all three slabs.
The longitudinal shear failure mode determines the post-slip strength and behaviour of composite slabs. According to the Eurocode 4 definition of ductility, the longitudinal shear behaviour is considered to be ductile if the failure load exceeds the load causing a recorded end slip of 0.1 mm by more than 10% and hence, all slabs failed in a ductile manner.
Graphs of end slip S versus applied load are shown in Fig. 7. The measured load causing an end slip of 0.1 mm P(0.1 mm), the peak load capacity Pmax and the applied load at the end of the test for each slab are summarised in Table 1. Also given in Table 1 are the deflection at peak load, the deflection at the end of the test; the maximum end slip (at the end of the test); the strain in steel decking at mid-span and the strain in the compressive concrete at mid-span at the peak load.
The mid-span deflections in the slabs at the peak load were highly variable, and ranged from (L′/71) for the eastern span to (L′/176) for the western span of slab 2-C-70, respectively. Graphs of major measured parameters are shown in Figs. 8, 9, 10.
The maximum value of the strain in the steel decking at mid-span at the peak load was measured at the eastern span of slab 2-C-70 and was εsm(max) = 1290 με. The steel yield strain is εyp = fyp/Es = 2620 με and therefore, the maximum steel strain was only 49% of the yield strain. Clearly, the loss of longitudinal shear stress in all slabs prevented the steel decking from yielding and the full plastic flexural capacity could not be reached.
Figure 11 shows slab 1-C-70 after reaching its peak load and just before termination of the test. The different deflections in either of spans, due to different levels of slip in each span, are quite visible. The cracking patterns in slabs at the end of the test are shown in Figs. 12, 13, 14.
Bending moments redistribution
The bending moment distribution over the length of each slab was calculated from the support reactions (measured by load cells). The bending moment values for the failed span of the slabs 1-C-70, 2-C-70 and 3-C-70 versus the total load are shown in Figs. 15, 16 and 17, respectively. Also shown in Figs. 18, 19 and 20 is the ratio of negative–positive moment for each slab versus the total load.
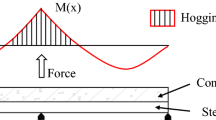
The total load in each figure is the applied load P plus the slab self-weight (3.6 kN/m) and the self-weight of the spreader beams and all packing plates used in the test and measured at the start of the test (i.e. P + 30.84 kN). The dashed straight lines in the figures represent the bending moments calculated by assuming constant stiffness along the slab and linear elastic behaviour of materials. The sagging (positive) moments are the values directly under the applied concentrated load and were calculated from statics using the measured reaction at the exterior support at the end of the slab. The hogging (negative) moment at the interior support was also calculated using the measured reaction at the exterior support of the failed span.
As stated earlier, all three slabs were cracked at mid-support under self-weight and the various sustained loading histories, prior to the commencement of these short-term load tests (Gholamhoseini et al. 2013b). Therefore, both the mid-span and mid-support moments increased linearly with load until the onset of slip. The negative moment was carried largely by the steel reinforcement in the concrete tensile zone at the top of the slab.
In slab 3-C-70, a further sudden change in the moment distribution occurred when a sudden bond slip at the steel concrete interface occurred when the total load reached 169.2 kN. At this point, the load dropped suddenly to 144.6 kN and the positive moment dropped suddenly from 26.7 to 21.2 kNm. However, the negative moment remained essentially constant as 30.8 kNm, as can be seen in Fig. 17. The drop-off in load at this point was almost totally associated with the sudden drop in positive moment. This drop-off in load was not evident in the other two slabs.
A further sudden change in the moment distribution occurred in all slabs when positive moment cracking eventually initiated bond slip at the steel concrete interface when the total load reached to about 240 kN. At this point, there was a significant drop in total load and also in the ratio of negative–positive moment as can be seen in Figs. 15, 16 and 17, respectively.
Finite element analysis
General structural modelling
The general purpose nonlinear finite element software ATENA 3D version 4.2.7 was used in the present study to investigate the ultimate strength of the composite concrete slabs tested in the laboratory. ATENA 3D programme is specifically designed for 3D nonlinear finite element analysis of solids with rigorous constitutive relationships to model the behaviour of reinforced concrete structures including concrete cracking, concrete crushing and reinforcement yielding (ATENA Program Documentation 2009).
A three-dimensional (3D) finite element model was developed to account for the material and geometric nonlinearities in the composite slabs and to investigate the ultimate strength of the continuous composite concrete slabs tested in the laboratory. The material properties for steel decking and concrete slabs were similar to the values stated earlier.
The Newton–Raphson iterative solution method was chosen. The mid-span deflection of each slab versus the total load was monitored in the analysis. Four monitoring points at the location of the applied line loads and two monitoring points at mid-span were defined to monitor the amount of total load and mid-span deflection, respectively. All of the monitoring points were defined on the top surface of each slab.
Steel plates with 50 mm thickness and 100 mm width were modelled at the load application points to simulate the steel profiles used in the laboratory experiments and to prevent high stress concentrations at these locations. The partial connection allowing slip to occur between the steel decking and concrete was considered.
The concrete slab, steel plates and steel decking were modelled with three-dimensional solid linear tetrahedral elements with three translation degrees of freedom per node. Linear tetrahedral elements contain four nodes compared to the ten nodes in quadratic elements and require less computational effort and time to run the analysis. The global element size was limited to 50 mm. Similar to the experimental study, in each analysis, the load was applied in a displacement control manner. The finite element model for the analysis of the slabs is shown in Fig. 21.
Material modelling
Steel plates
Steel plates at the load application points were modelled as a linear elastic material using “CC3D Elastic Isotropic” material type with Es = 200 GPa.
Steel decking
In the present study, steel decking was modelled as an elastic–fully plastic material without strain hardening using “CC3D Bilinear Steel Von Mises” material type. A bilinear stress–strain relationship, as shown in Fig. 22, was used for steel decking in both tension and compression. The Von Mises yield criterion was used in the nonlinear analysis to treat the plasticity of the steel material.
Reinforcing bar
The reinforcing bars over the interior support were modelled using “CC reinforcement” material type with elastic–fully plastic behaviour without strain hardening. There are two ways that a reinforcing bar can be modelled in ATENA; either as smeared or as discrete bar element. In smeared element modelling, the reinforcement is spread along the macroelement by assigning a reinforcement ratio, whereas in discrete bar element modelling, the reinforcing bar is modelled as one-dimensional line element with the assigned bar diameter.
The contact between the reinforcing bar and the surrounding concrete macroelement can be assigned either as perfect bond or as specified bond–slip relationship. In this study, the reinforcement bars were modelled as discrete bars with perfect bond to concrete.
Concrete slab
Concrete slab was modelled using “CC3D Nonlinear Cementitious 2” material type. This material type has the capability to consider concrete cracking; crushing and plastic behaviour. The material properties in the different stress states are presented below.
Tension before cracking
The behaviour of concrete in tension before cracking was assumed to be linear elastic, i.e., σ = Ecɛ; where σ is the tensile stress in concrete, Ec is the initial elastic modulus of concrete and ɛ is the strain in concrete.
Tension after cracking
A fictitious model based on a crack-opening law and fracture energy (shown in Fig. 23) was used in combination with the crack band theory for modelling concrete tension after cracking and is given by:
where w is the crack opening, wc is the crack opening at the complete release of stress, \(c_{1} = 3,\,\,c_{2} = 6.93,\,\,w_{\text{c}} = 5.14\frac{{G_{\text{f}} }}{{f_{\text{t}} }}\) and Gf is the fracture energy needed to create a unit area of stress-free crack and here taken as 30 N/m in the numerical model.
Compression before peak stress
The stress–strain curve for concrete in compression is given in Fig. 24. The formula recommended by CEB-FIP Model Code 1990 (Comite Euro-International du Beton 1993) was adopted for the ascending branch of the concrete stress–strain law in compression and is given by:
where \(\sigma\) is the concrete compressive stress; x is normalised strain; \(\varepsilon_{\text{c}}\) is strain at peak stress; Ec is the initial elastic modulus and Ec1 is the secant elastic modulus at the peak stress, respectively. Shape parameter k may have any positive value greater than or equal 1 (e.g. k = 1 linear, k = 2 parabolic).
Compression after peak stress
The softening law in compression is linearly descending. In this study, a fictitious compression model based on dissipated energy was used. The model is based on the assumption that compression failure is localised in a plane normal to the direction of compressive principal stress. All post-peak compressive displacements and energy dissipation are localised in this plane. It is assumed that this displacement is independent of the size of the structure. This hypothesis is supported by experiments conducted by Van Mier (1986). The strain is calculated from the following expression:
where wd is the plastic displacement at the end of the softening curve taken as 0.5 mm, \(\varepsilon_{\text{d}}\) is the limiting compressive strain and \(L'_{\text{d}}\) is band size, respectively.
Steel decking–concrete slab contact
The “CC3D Interface” material type in ATENA 3D was used to model contact between steel decking and concrete slab. The interface material is based on Mohr–Coulomb criterion with tension cut off. The constitutive relation for a general two-dimensional case is given in terms of tractions on the interface planes and relative sliding and opening displacements as (ATENA Program Documentation 2009):
The initial failure surface corresponds to Mohr–Coulomb condition with ellipsoid in tension regime. After stresses violate this condition, this surface collapses to a residual surface which corresponds to dry friction. The frictional properties of the interface material model in ATENA 3D are defined by shear cohesion c and the friction coefficient ϕ. The maximum shear stress is limited by the linear relation τ = c − ϕσ where σ is the interface compressive stress. In tension, the failure criterion is replaced by an ellipsoid which intersects the normal stress axis at the value of ft with a vertical tangent (as shown in Fig. 25) and intersects the shear axis at the value of c (i.e. cohesion) with the tangent at this point equivalent to ϕ (also shown in Fig. 25).
The coefficients K n and K t in Eq. 4 denote the initial elastic normal and shear rigidities, respectively. There are two additional rigidity values that need to be specified in the ATENA 3D input. They are denoted in Fig. 26 as Kn(min) and Kt(min). These values are used only for numerical purposes after the failure of the element to preserve the positive definiteness of the global system of equations. Theoretically, after the interface failure the interface rigidity should be zero, which would mean that the global rigidity will become indefinite. These minimal rigidities are recommended to be about 0.001 times the initial rigidities.
The assumed values of K n = 1000 MN/m3 and K t = 60 MN/m3 showed the best agreement between the finite element model and the test results as shown in Fig. 27. Of course, these values are deemed to be a function of material properties and rigidities of the steel decking and concrete slab. Vertical and transverse separation at the steel–concrete interface was assumed to be negligible. This was achieved by assigning a very large value for the initial elastic normal rigidity K n in the model. The material properties for steel decking and concrete slabs were similar to the values summarised in Sect. 3.3. The cohesion stress value of 0.1 MPa and tensile stress value of 0.5 MPa were selected for the interface element properties, respectively.
Finite element analysis results
A summary of the comparison between the test results and the numerical results obtained from the partial interaction analyses is presented in Fig. 27. The average measured ultimate load capacity of the three slabs was Pu = 207.1 kN and the result obtained from finite element modelling was Pu = 234.0 kN. In lieu of the expense involved with full-scale testing, the good agreement between the finite element modelling and the test results obtained in the study suggests that far less expensive numerical modelling can be used to verify the performance of continuous composite slabs.
Conclusions
The results of short-term testing up to failure of three continuous composite slabs constructed using a profiled steel decking section that is widely used in construction industry in Australia have been presented and discussed. The slabs were tested in symmetric four-point bending in each span with shear span of L′/4. For all slabs, the maximum flexural capacity was controlled by yielding of the reinforcement at the interior support with significant slip at the concrete–steel interface in the shear span, well before the fully plastic moment of the composite cross section could be reached. All slabs satisfied the ductility provisions given in Eurocode 4.
The slabs were then modelled in a finite element programme to investigate the behaviour of the slabs throughout the full range of loading and the results were compared with test results. Interface elements were used to model the bond properties between steel decking and concrete slab. Currently, the design standards do not present guidance for the design of continuous composite slabs, and full-scale testing is needed. In lieu of the expense involved with full-scale testing, the good agreement between the finite element modelling and the test results obtained in the study suggests that far less expensive numerical modelling can be used to verify the performance of continuous composite slabs.
References
Abas FM, Gilbert RI, Foster SJ, Bradford MA (2013) Strength and serviceability of continuous composite slabs with deep trapezoidal steel decking and steel fibre reinforced concrete. Eng Struct J 49:866–875
Abdullah R, Easterling WS (2009) New evaluation and modeling procedure for horizontal shear bond in composite slabs. J Constr Steel Res V65(4):891–899
Ackermann FP, Schnell J (2008) Steel fibre reinforced continuous composite slabs. In: Proceedings of the 6th International Conference on composite construction, Tabernash, Colorado
Al-Deen S, Ranzi G (2015) Effects of non-uniform shrinkage on the long-term behaviour of composite steel–concrete slabs. Int J Steel Struct V15(2):415–432
Al-Deen S, Ranzi G, Vrcelj Z (2011) Full-scale long-term and ultimate experiments of simply-supported composite beams with steel deck. J Constr Steel Res V67(10):1658–1676
ATENA Program Documentation (2009) Part 1: ATENA theory manual, CERVENKA Consulting
Bednar J, Frantisek W, Vodicka J, Kohoutkova A (2013) Experiments on membrane action of composite floors with steel fibre reinforced concrete slab exposed to fire. Fire Saf J 59:111–121
Bradford MA (2010) Generic modelling of composite steel–concrete slabs subjected to shrinkage, creep and thermal strains including partial interaction. J Eng Struct 32:1459–1465
Comite Euro-International du Beton (1993) CEB-FIP Model Code 1990. Thomas Telford Ltd., London
EN (2004) 1994-1-1 Eurocode 4 design of composite steel and concrete structures-Part 1.1: general rules. European Committee for Standardization (CEN), Brussels, Belgium
Ferrer M, Marimon F, Crisinel M (2006) Designing cold-formed steel sheets for composite slabs: an experimentally validated FEM approach to slip failure mechanics. Thin-Walled Struct J 44:1261–1271
Fielders Australia Pty Ltd (2008) Specifying fielders: KingFlor composite steel formwork system design manual
Gholamhoseini A (2016) Modified creep and shrinkage prediction model B3 for serviceability analysis of composite slabs. Int J Adv Struct Eng (IJASE) V8(1):87–101
Gholamhoseini A, Gilbert RI, Bradford MA, Chang ZT (2012) Long-term deformation of composite concrete slabs. Concr Aust 38:25–32
Gholamhoseini A, Gilbert RI, Bradford MA (2013) Time-dependent deflection of continuous composite concrete slabs. The Concrete Institute of Australia’s 26th Biennial National Conference, Gold Coast, Australia
Gholamhoseini A, Gilbert RI, Bradford MA (2013b) Time-dependent deflection of continuous composite concrete slabs.In: The Concrete Institute of Australia’s 26th Biennial National Conference. Gold Coast, Australia
Gholamhoseini A, Gilbert RI, Bradford MA, Chang ZT (2014a) Longitudinal shear stress and bond–slip relationships in composite concrete slabs. Eng Struct J 69:37–48
Gholamhoseini A, Gilbert RI, Bradford MA, Chang ZT (2014b) Time-dependent deflection of composite concrete slabs. Am Concr Inst ACI Struct J V111(4):765–776
Gholamhoseini A, Khanlou A, MacRae G, Scott A, Hicks S, Leon R (2016) An experimental study on strength and serviceability of reinforced and steel fibre reinforced concrete (SFRC) continuous composite slabs. J Eng Struct 114:171–180
Gilbert RI, Bradford MA, Gholamhoseini A, Chang ZT (2012) Effects of shrinkage on the long-term stresses and deformations of composite concrete slabs. J Eng Struct 40:9–19
Johnson RP (2004) Composite structures of steel and concrete, 3rd edn. Blackwell Scientific Publishing, Oxford
Kim HY, Jeong YJ (2006) Experimental investigation on behaviour of steel–concrete composite bridge decks with perfobond ribs. J Constr Steel Res 62:463–471
Kim HY, Jeong YJ (2009) Steel–concrete composite bridge deck slab with perofiled sheeting. J Constr Steel Res 65:1751–1762
Lin W, Yoda T, Taniguchi N (2014a) Application of SFRC in steel–concrete composite beams subjected to hogging moment. J Constr Steel Res 101:175–183
Lin W, Yoda T, Taniguchi N, Kasano H, He J (2014b) Mechanical performance of steel–concrete composite beams subjected to a hogging moment, J Struct Eng, V140, pp. 04013031/1-04013031/11
Mansour FR, Abu Bakar S, Ibrahim IS, Marsono AK, Marabi B (2015) Flexural performance of a precast concrete slab with steel fiber concrete topping. J Constr Build Mater 75:112–120
Marciukaitis G, Jonaitis B, Valivonis J (2006) Analysis of deflections of composite slabs with profiled sheeting up to the ultimate moment. J Constr Steel Res V62:820–830
Marimuthu V, Seetharaman S, Jayachandran SA, Chellappan A, Bandyopadhyay TK, Dutta D (2007) Experimental studies on composite deck slabs to determine the shear-bond characteristic (m–k) values of the embossed profiled sheet. J Constr Steel Res 63:791–803
Mirza O, Uy B (2012) Experimental study of short- and long-term behaviour of composite steel–concrete slab. J Concr Aust V38(4):41–49
Oehlers DJ, Bradford MA (1995) Composite steel and concrete structural members: fundamental behaviour. Pergamon Press, Oxford
Petkevicius M, Valivonis J (2010) Analysis of bending capacity of composite steel–concrete slabs with steel fiber reinforced concrete. In: Proceedings of the 10th International Conference “Modern building materials, structures and techniques”. Vilnius, Lithuania, pp 744–751
Porter M, Ekberg C (1975) Design recommendations for steel deck floor slabs. Proceedings of 3rd International Specialty Conference on cold-formed steel structures, University of Missouri-Rolla, MO, pp 761–791
Porter M, Ekberg C (1976) Design recommendations for steel deck floor slabs. ASCE J Struct Div 102:2121–2136
Ranzi G, Leoni G, Zandonini R (2013a) State of the art on the time dependent behaviour of composite steel–concrete structures. J Constr Steel Res 80:252–263
Ranzi G, Al-Deen S, Hollingum G, Hone T, Gowripalan S, Uy B (2013b) An experimental study on the ultimate behaviour of simply-supported post-tensioned composite slabs. J Constr Steel Res 89:293–306
Standards Australia (2011) Continuous hot-dip metallic coated steel sheet and strip-coatings of zinc and zinc alloyed with aluminium and magnesium. AS 1397-2011, Sydney
Van Mier JGM (1986) Multi-axial strain-softening of concrete. Part I: fracture. Mater Struct J V19(3):179–190
Acknowledgements
The experimental work reported in this paper was undertaken with the steel decking material supplied from decking manufacturer Fielders Australia Pty Limited. This support is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that he has no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to urisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Gholamhoseini, A. Experimental and finite element study of ultimate strength of continuous composite concrete slabs with steel decking. Int J Adv Struct Eng 10, 85–97 (2018). https://doi.org/10.1007/s40091-018-0183-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40091-018-0183-3