Abstract
An effective form-finding method for form-fixed spatial network structures is presented in this paper. The adaptive form-finding method is introduced along with the example of designing an ellipsoidal network dome with bar length variations being as small as possible. A typical spherical geodesic network is selected as an initial state, having bar lengths in a limit group number. Next, this network is transformed into the ellipsoidal shape as desired by applying compressions on bars according to the bar length variations caused by transformation. Afterwards, the dynamic relaxation method is employed to explicitly integrate the node positions by applying residual forces. During the form-finding process, the boundary condition of constraining nodes on the ellipsoid surface is innovatively considered as reactions on the normal direction of the surface at node positions, which are balanced with the components of the nodal forces in a reverse direction induced by compressions on bars. The node positions are also corrected according to the fixed-form condition in each explicit iteration step. In the serial results of time history, the optimal solution is found from a time history of states by properly choosing convergence criteria, and the presented form-finding procedure is proved to be applicable for form-fixed problems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Since the 1960s, the form finding process, also called the shape finding process, has been used to find the certain structural state of desired geometry, an equilibrium state, or both of them, with specified boundary conditions. Currently, the process has been progressively adopted for structural-engineering applications, such as buildings and bridges (Allahdadian and Boroomand 2010; Huang and Xie 2008; Neves et al. 1995; Stromberg et al. 2010; Zordan et al. 2010; Briseghella et al. 2010, 2013a, b; Zordan et al. 2014), and it is widely applied in the architectural design of structures that transfer their loads almost purely using their shapes, or vice versa (Adriaenssens et al. 2014; Basso and Del Grosso 2011; Fenu et al. 2015; Briseghella et al. 2016). Such structures mainly include unstrained grid-shells (components in compression), cable nets or membranes (components in tension) and tensegrity structures (components both in compression and tension) (Barnes 1977; Topping and Ivanyi 2007; Tran and Lee 2010; Koohestani 2013). Those structures are considered to be designed not only in a highly efficient manner from the structural point of view but also in an aesthetically pleasing manner (Lucerga and Armisén 2012). Some form finding methods have been developed through decades of practices (Nouri-Baranger 2004). The existing well-known methods can be categorized in the following main families:
-
Stiffness matrix methods are based on using the standard elastic and geometric stiffness matrices that were adapted from structural analysis. These methods account for the material properties in computation, which may lead to difficulty in operations of matrices and control of (stable) convergence.
-
Geometric stiffness methods are material independent, with only a geometric stiffness. However, these methods are applied in their linear form and produce results that are not constructionally practicable (Barnes 1977); thus, they can serve only as a preliminary result.
-
Force density methods. Because the ratio of force to length is a central unit in mathematics, force density methods can be considered as subtypes under the category of geometric stiffness methods. Similar to geometric stiffness methods, additional iterations are necessary for uniform or geodesic networks or shape-dependent loading, making the method non-linear (Barnes 1977; Haber and Abel 1982; Tan 1989; Lewis 2008; Koohestani 2014). Recently, the so-called thrust network analysis derived from the force density method has been used to find the shape of a discrete membrane restrained to a given geometric limitation (Block 2009; Marmo and Rosati 2017).
-
Dynamic equilibrium or relaxation methods that solve the problem of dynamic equilibrium to arrive at a steady-state solution are equivalent to the static solution of static equilibrium. As adapted from explicit time series integration, the time step parameters are required to control stability and convergence (Barnes 1977; Lewis 1989; Baraff and Witkin 1998). The main advantage of the dynamic relaxation method is that no assembled structural stiffness matrix is required; hence, it is suitable for highly nonlinear problems (Topping and Ivanyi 2007). The iterations in dynamic relaxation methods simulate the physical evolutionary process of the structures with feasible geometric configurations. Furthermore, with the development of the computer technique, the time and resource consumption in iterations and results storage has been significantly reduced. Such dynamic relaxation methods are becoming more popular (Olsson 2012; Bagrianski and Halpern 2014) and will be the basis for developing the method to be presented in this paper.
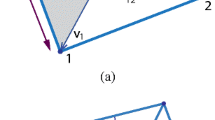
Similar categorizations can be found in other works with different names (Topping and Ivanyi 2007; Basso and Del Grosso 2011; Veenendaal and Block 2012). In applying these methods, the general shapes or forms of structures are unknown in advance, the so called free-form structures (Liu and Shimoda 2014). By fixing boundary conditions, where the forces ended (transferred to constraints/supports), the final optimal forms will be found through continuous force paths (Fig. 1). In the phase of considering boundary conditions in the form-finding method or finite element method, typically, the degrees of freedom (DOFs) in a Cartesian coordinates system will be separated into the following two groups: interior ones (free to move) and exterior ones (fixed). Correspondingly, the mass matrix, stiffness matrix, displacement vectors, force vectors and so on, will be divided into sub-matrices and sub-vectors to solve the static system equations.

(Reproduced with permission from Veenendaal and Block 2012)
Typical form-finding of a saddle
In the case that the general network form is known or fixed, for example, finding a network in the shape of the desired ellipsoidal dome, as shown in Fig. 2, the “form” to find is the position of the joints/nodes in the network, while the “form” surface of network is already fixed. If the typical form-finding method is applied, then the nodal supports should be movable in the surface with changing supports directions that are normal to the surface, that is, the boundary conditions change at every iteration step. This situation could make it difficult to correctly describe the boundary conditions in the Cartesian coordinate system (with the exception of specific desired shapes, e.g., a cylinder shape could be described in a cylindrical coordinates system, a spherical shape could be described in a spherical coordinates system, and so on; otherwise, stiffness matrices in the corresponding surface coordinates must be developed). Moreover, the calculation matrices will be very complicated and might cause singularity problems in the matrix operations.
In this case, the dynamic relaxation method will be applied, thus avoiding inverse of stiffness matrices of complicated and varied geometries; the typical method needs to be adapted to easily update the position-dependent boundary conditions. Therefore, the objective of this paper is to, based on the dynamic relaxation method, construct an adaptive form finding method for a bar network on a form-fixed surface with boundary conditions updated in each time step.
Objective and framework
To demonstrate the framework of the presenting method, the example of designing an ellipsoid shaped geodesic network dome is employed. The lengths of semi-principal axes of the ellipsoid are a = 15 m, b = 11 m, and c = 12 m (height). The target is to obtain a geodesic network dome in this desired ellipsoidal shape, having bars with as few length variations as possible, and each bar length should be approximately 3 m, for the purpose of economy and convenience of construction.
Geodesic network
As is known to architectural designers, the typical geodesic network in the form of a sphere or half sphere, besides the aesthetical aspect, the length of all bars (or called struts, beams, edges) of the network are in groups of limited number, according to the frequency of the network, as shown in Table 1. The “frequency” here, is defined by the subdivisions of one basic triangular face of an icosahedron. The higher the frequency, the more triangles there are in the geodesic dome. In icosahedron-based geodesic domes, the flat bottoms are available from half-sphere of even frequencies, whereas no flat bottoms are available from those of odd frequencies. Thus, the geodesic domes could be fabricated in a few types of nodes (also called joints, hubs, vertices) and bars and then assembled on-site with a lower cost of construction.
Based on the characteristics of the geodesic network, the design target is considered to have similar distribution of bars of a geodesic dome at a frequency of 6 V with a spherical radium of 15 m, where bar lengths in nine groups vary from 2.439 to 3.429 m. Thus, this network (designated as initial state or zero state in the following content) is transformed to an ellipsoidal geodesic network by scaling in x, y, and z directions with factors of 15/15, 11/15, and 12/15, respectively (designated as first state). The next step is to find a new node position on the current ellipsoidal surface that allows the bar lengths to “return” to the corresponding lengths of the geodesic network before transformation. To achieve this goal, the adaptive form-finding procedure is conducted, as presented in the following section.
Form-finding procedure
In the first state, bars are given pre-compressions calculated from the changing lengths while being transformed from the initial state, F1 = EA(L1 − L0)/L0. It can be predicted that, after releasing the bar forces, the network form will expand along the surface to cover more surface than a half-dome in the end; thus, the “over-design” part will be cut off properly to fit the target network.
In the form-finding procedure, the pre-compressions in bars are the only loadings considered on the network structure. Regarding the nodal forces induced by releasing the pre-compressed bars, their components in the directions of surface normal at the nodes should be balanced with the reaction forces from the surface constraining boundary conditions. The residual forces of the nodal forces and the reaction forces, therefore, are the components of the nodal forces in the tangent plane of the surface at nodes and can be calculated according to the nodal forces and the positions of the nodes. In this manner, for any state of the network, the boundary conditions are considered in the calculation of the residual forces without recognizing the degrees of freedom that are fixed or not fixed. Moreover, the operations on vectors and matrices are unified for different geometries.
As the dynamic relaxation method is applied, the network undergoes a structural dynamic process, where the explicit integration of time-dependent variables will be performed to obtain the evolutionary node positions over a given time duration until the convergence criteria are met. As ideally expected, in the end of an iteration, if all nodes are to be at stable positions, then the network in that state will have more or less the same bar length groups as those in the initial state. However, due to the inconstant curvatures of the desired ellipsoidal surface, the primary radii varying in the quarter part, the bars obviously will not have the same length as those in the spherical dome. The general objective of this form-finding is to find a state of the structure with the most averaged bar length variations, where the forces in bars will be the most balanced. Therefore, the bar length or force will be the main criterion for convergence. The framework of this procedure is summarized and shown in the following flowchart (Fig. 3). The detailed procedure and relative formulations are discussed in the next section.
Procedure and formulations
Geometry state
In each step of the calculation, the items are mainly calculated based on the geometric state of the network. Generally, a bar-node matrix C is used to describe the topology of a network of bars and nodes (Schek 1974). For a network with m bars and n nodes in three-dimensional space, a bar-node matrix C is constructed, where the entries of the i-th row and j-th column of the m × n matrix C are as follows:
The n × 3 nodal coordinate vectors x is as follows:
The coordinate difference vectors (bar directions in rows) u can be written as a function of C and coordinate vectors x as follows:
where \(\overline{{\mathbf{u}}}\), \(\overline{{\mathbf{v}}}\) and \(\overline{{\mathbf{w}}}\) are vectors, each containing m coordinate differences in the corresponding Cartesian direction. With coordinate difference vectors, the bar lengths L are as follows:
where the function diag() returns the diagonal matrix from the vector or the diagonal elements from the matrix. Therefore, L is an m × m matrix that contains only diagonal elements that are bar lengths.
The masses of the structure are considered to be lumped at the nodes. The lumped mass matrix can be written as follows:
where ml is the mass per unit length of bars or is expressed in material density and bar section area ml = ρA.
The problem with form-finding is, in principle, a geometric one, i.e., material independent (Barnes 1999). After convergence, the forces on bars with m desired stiffnesses EA do not disturb the state of equilibrium (Gründig et al. 2000). In this procedure, the bar stiffnesses EA are considered as constant for all bars and are applied directly to all steps of the calculation of forces on beams, expressed as follows:
where L0 is calculated via Eqs. (2)–(4) with coordinates x0 of the geodesic dome of a unit sphere; and I is an identity matrix. Thus, the force-to-length ratios, also called force densities or tension coefficients (Veenendaal and Block 2012), are given by the following:
The resulting forces on nodes are as follows:
Thus, the secant stiffness matrix can be written as follows:
Boundary conditions/constraints update
The boundary conditions are updated through achieving the equilibrium of forces, as introduced above. In the design example, the nodes are constrained on an ellipsoidal surface, where movements in the normal directions of the surface are fixed, whereas movements in the tangent planes are free. The ellipsoidal surface function in the Cartesian coordinates system can be written as follows:
where [x, y, z] is an arbitrary point on the surface. Thus, the normal direction vector of the ellipsoidal surface at point [x, y, z] is as follows:
or, expressed as vectors as follows:
The normal vectors can be normalized as follows:
where the expression of ||n|| returns the second order norm of each row in n. The projections of nodal forces P on normal \(\widetilde{{\mathbf{n}}}\) are given by the following:
Because the reaction forces at nodes are balanced with Ppn, the reaction forces are − Ppn. The resulting residual forces are as follows:
Explicit integration
The relaxation of the bar forces initiates the structural dynamic time history process. The state variables of a new step will be explicitly integrated from the current state according to the governing ordinary differential equations. Typically, the integration implementation uses either the explicit classic 4th order Runge–Kutta Method (Baraff and Witkin 1998) or the Central Finite Difference Method (Barnes 1999). Here, a simple conditionally stable explicit method based on the Modified Trapezoidal Rule Method (Pezeshk and Camp 1995) is used.
The structural equation of motion at step time of t can be expressed as follows:
where the subscript of t denotes the present variable calculated based on the geometric state at time of t. The mass matrix is constant over time; the external forces Pe are the reaction forces; the displacement induced internal forces Kx are the nodal forces resulting from the bar forces. Therefore, Eq. (16) can be rewritten as follows:
The integration using the Modified Trapezoidal Rule Method is accomplished as follows:
Considering the constraints again here, the resulting coordinates xt+Δt, will position outside from the ellipsoid surface because the nodal accelerations cause the displacements and velocities on the tangent directions of previous positions xt. Therefore, the coordinates will be projected back to the constraint of the ellipsoid surface, and the velocities will be updated by removing the component on newly normal directions \({\tilde{\mathbf{n}}}_{t + \Delta t}\) updated via Eqs. (12) and (13). The updated coordinates and velocities will be used for updating other state variables and for integration in the next iteration.
where k is the absolute minimum root of the surface constraint function as follows:
The condition of stability of the integration is to satisfy the maximum time step length (Pezeshk and Camp 1995) as follows:
where L is the minimum length of bars; ρ is the material density of bars. In this case, for example, all the bars are made of structural steel, and all the bars are longer than 2 m. Thus, the time step in the length of Δt = 1 × 10−5 s < 2 × 2 × (7850/2 × 1011)1/2 s ≈ 8 × 10−4 s is satisfied.
Convergence criteria
To solve the convergence of form-finding problem, the following criteria (or some of them) are usually adopted (Veenendaal and Block 2012) as follows:
-
(1)
small variations in the displacements between successive iterations (\(\left\| {{\mathbf{x}}_{t + \Delta t} - {\mathbf{x}}_{t} } \right\| < {\varvec{\upvarepsilon}}\));
-
(2)
small variations of the bar forces (or bar lengths) between successive iterations (\(\left\| {{\mathbf{F}}_{t + \Delta t} - {\mathbf{F}}_{t} } \right\| < {\varvec{\upvarepsilon}}\));
-
(3)
small values of the residual forces (\(\left\| {{\mathbf{R}}_{t} - {\mathbf{P}}_{t} } \right\| < {\varvec{\upvarepsilon}}\));
-
(4)
small values of the kinetic energy \(\left( {\left\| {\frac{1}{2}{\mathbf{M}}\text{diag} \left( {\left\| {{\mathbf{v}}_{t} } \right\|} \right)^{2} } \right\| < {\varvec{\upvarepsilon}}} \right)\);
-
(5)
maximum number of iterations (or maximum time duration) reached.
The dynamic relaxation process may not have a numerical convergence that allows the structure to achieve a still or rest state because no damping is introduced, as the equation of motion Eq. (16) represents an undamped structure system to simplify the calculation. However, with a preset maximum number of iterations, the calculation will “converge”, even if no damping exists in the system.
After the calculation converged, the optimal (best) solution of the network will be selected according to the convergence criteria that the calculation achieved. Recalling the objective description of the design example, the state of minimum residual forces of the entire calculation duration will be selected as the optimal solution. The maximum acceptable errors have been decided according to not only numerical considerations but also structural design ones. If no numerical convergence is achieved in the relevant time durations (converged according to criterion 5), the state of minimum residual forces may not be at the end of the time history; as a result, the state variables must be evaluated if the network is desired. Otherwise, the time duration must be extended for another new calculation, or the almost-target state from current calculation is used as the initial state for the new calculation.
Solutions and evaluation
Optimal solution
As the state of the dome network fixed on the ellipsoidal surface of a = 15 m, b = 11 m, and c = 12 m, through the procedure presented above and considering all the five convergence criteria, the time history results, with time step length Δt = 1 × 10−5 s and time duration of 500Δt (500 iteration steps), of the state variables maximum displacements, maximum residual forces, maximum bar length variations, average bar length variations, and standard deviation of bar length variations are shown in Figs. 4, 5, 6, 7 and 8. The state variables are calculated and compared between some the representative states over the time history. The selected states are shown in Table 2.
It is observed that in this calculation, no numerical convergence was achieved; nevertheless, the maximum residual force met the minimum value at the 181st step during the dynamic process. In the same step, the variation of the bar length reaches the point having minimum values of the average and standard deviation at the same time. Thus, the present procedure is proved to be applicable.
Therefore, the 181st state is considered to be the optimal solution to the network structure (Fig. 9). Thus, the final network can be the part above the ground level by cutting off either directly at the ground level or at the horizontal bars closest to the ground level. Here, as shown in Fig. 9, if the part above the bands that connect the centres of lower pentagons is kept as the final solution to the design goal, then the possible design would be as shown in Fig. 10.
Discussion
In the procedure presented above, some key parameters should be noted, such as the initial state and the control of explicit integration and convergence. Avoiding lengthy parametric analyses, some discussions are introduced as follows.
Initial forces or impact pulse applied on bars will obviously affect the final state at end of time duration and the speed of dynamic evolution process. The induced higher accelerations on nodes will cause the nodes to oscillate at higher amplitudes. Therefore, the intermediate state will be missed in the time history records. In the present example, the initial bar forces (pre-compressions) are obtained from a spherical geodesic dome (as original bar lengths). If this radium of the geodesic dome is chosen with a large difference between the target ellipsoid semi-principal axes, then the initial bar forces and the forces calculated during dynamic relaxation will be higher and induce time states with lower resolution. Thus, the initial geometry is suggested to be as closer to the target as possible.
In the explicit integration, as stated above, the studies on the explicit dynamic process revealed the time step length effect on the stability of integration. If the procedure is calculated in a material-independent manner, then the time step also must be less than the dimension unit of the structure elements to ensure the explicit integration remains stable.
The convergence criteria chosen for the form-finding procedure are also important. In the example case presented, the target is to minimize length variations, which leads to the state of minimum residual force. The other convergence criteria (except the criterion 5) have reached 0-state at the initial state and obviously are not applicable in this case. Finally, with the state of optimal solution found, the form-finding method and criterion chosen are proved to be effectively applicable.
Conclusions
The adaptive form-finding method presented in this paper is a simple and effective procedure for computational design of spatial network structures with a fixed form. According to the limitation of the research, the following conclusions can be drawn:
-
(1)
The dynamic relaxation method is applicable in form-finding process of form-fixed spatial network structure, which avoids the inverse operations on complicated stiffness matrices in each step;
-
(2)
During form-finding process, the boundary conditions can be applied as reaction forces through force equilibrium to avoid varying operations on vectors and matrices, especially for cases of time-dependent varying boundary conditions;
-
(3)
In spatial form-fixed problem, the coordinates and velocities integrated from accelerations could be positioned out of the constraint form. In order to keep solution feasible, it is necessary to update the coordinates and velocities after each explicit integration;
-
(4)
It is noticed that the choosing of initial state will affect a lot the states obtained in the time duration. It is better to choose the initial state closer as much as possible to the target state; the time step length is important for the stability of explicit integration, and for finding accurately the optimal solution; the convergence criteria chosen for time step iteration influence the target state characteristics. Therefore, the convergence criteria need to be chosen properly, especially in undamped systems.
References
Adriaenssens S, Block P, Veenendaal D, Williams C (2014) Shell structures for architecture: form finding and optimization. Routledge, London
Allahdadian S, Boroomand B (2010) Design and retrofitting of structures under transient dynamic loads by a topology optimization scheme. In: Proceedings of the 3rd International Conference on Seismic Retrofitting, Iranian North-West Retrofitting Center (Iranian Retrofitting Researchers Ins.), Tabriz, Iran, pp 1–9
Bagrianski S, Halpern AB (2014) Form-finding of compressive structures using prescriptive dynamic relaxation. Comput Struct 132:65–74
Baraff D, Witkin A (1998) Large steps in cloth animation. SIGGRAPH 98 Computer Graphics Proceedings, Orlando, FL, USA
Barnes MR (1977) Form-finding and analysis of tension space structures by dynamic relaxation, PhD thesis, City University London, UK
Barnes MR (1999) Form finding and analysis of tension structures by dynamic relaxation. Int J Space Struct 14:89–104
Basso P, Del Grosso A (2011). Form-finding methods for structural frameworks: a review. In: Proceedings of the International Association of Shells and Spatial Structures, London
Block P (2009). Thrust network analysis: exploring three-dimensional equilibrium. PhD thesis, Massachussets Institute of Technology, MA, USA
Briseghella B, Lan C, Zordan T (2010) Optimized design for soil-pile interaction and abutment size of integral abutment bridges. Large Structures and Infrastructures for Environmentally Constrained and Urbanised Areas
Briseghella B, Fenu L, Feng Y, Mazzarolo E, Zordan T (2013a) Topology optimization of bridges supported by a concrete shell. Struct Eng Int 23(3):285–294
Briseghella B, Fenu L, Lan C, Mazzarolo E, Zordan T (2013b) Application of topological optimization to bridge design. J Bridge Eng. https://doi.org/10.1061/(ASCE)BE.1943-5592.0000416
Briseghella B, Fenu L, Feng Y, Lan C, Mazzarolo E, Zordan T (2016) Optimization indexes to identify the optimal design solution. J Bridge Eng 21(3):04015067-1–04015067-12
Fenu L, Briseghella B, Zordan T (2015) Curved shell-supported footbridges. IABSE Conference, Geneva 2015: structural engineering: providing solutions to global challenges—report, pp 394–401
Gründig L, Moncrieff E, Singer P, Ströbel D (2000) A history of the principal developments and applications of the force density method in Germany 1970–1999. In: Proceedings of IASS-IACM 2000 Fourth International Colloquium on Computation of Shell & Spatial Structures, Chania-Crete, Greece
Haber RB, Abel JF (1982) Initial equilibrium solution methods for cable reinforced membranes. Part I—formulations. Comput Methods Appl Mech Eng 30:263–284
Huang X, Xie Y (2008) Topology optimization of nonlinear structures under displacement loading. Eng Struct 30(7):2057–2068
Koohestani K (2013) A computational framework for the form-finding and design of tensegrity structures. Mech Res Commun 54:41–49
Koohestani K (2014) Nonlinear force density method for the form-finding of minimal surface membrane structures. Commun Nonlinear Sci Numer Simul 19(6):2071–2087
Lewis WJ (1989) The efficiency of numerical methods for the analysis of prestressed nets and pin-jointed frame structures. Comput Struct 33:791–800
Lewis WJ (2008) Computational form-finding methods for fabric structures. In: Proceedings of the ICE—Engineering and Computational Mechanics, vol 161, pp 139–149
Liu Y, Shimoda M (2014) A non-parametric solution to shape identification problem of free-form shells for desired deformation mode. Comput Struct 144:1–11
Lucerga JJJ, Armisén JM (2012) An iterative form-finding method for antifunicular shapes in spatial arch bridges. Comput Struct 108–109:42–60
Marmo F, Rosati L (2017) Reformulation and extension of the thrust network analysis. Comput Struct 182:104–118
Neves M, Rodrigues H, Guedes J (1995) Generalized topology design of structures with a buckling load criterion. Struct Multidiscip Optim 10(2):71–78
Nouri-Baranger T (2004) Computational methods for tension-loaded structures. Arch Comput Methods Eng 11:143–186
Olsson J (2012) Form finding and size optimization—implementation of beam elements and size optimization in real time form finding using dynamic relaxation, Master’s thesis, Chalmers University of Technology, Gothenburg, Sweden
Pezeshk S, Camp CV (1995) An explicit time integration technique for dynamic analyses. Int J Numer Methods Eng 38:2265–2281
Schek HJ (1974) The force density method for form finding and computation of general networks. Comput Methods Appl Mech Eng 3:115–134
Stromberg LL, Beghini A, Baker WF, Paulino GH (2010) Application of layout and topology optimization using pattern gradation for the conceptual design of buildings. Struct Multidiscip Optim 43(2):165–180
Tan KY (1989) The computer design of tensile membrane structures, PhD thesis, University of Queensland, Brisbane, Australia
Topping BHV, Ivanyi P (2007) Computer aided design of cable membrane structures. Saxe-Coburg Publications, Kippen
Tran HC, Lee J (2010) Advanced form-finding of tensegrity structures. Comput Struct 88(3–4):237–246
Veenendaal D, Block P (2012) An overview and comparison of structural form finding methods for general networks. Int J Solids Struct 49:3741–3753
Zordan T, Briseghella B, Mazzarolo E (2010) Bridge structural optimization through step-by-step evolutionary process. Struct Eng Int 20(1):72–78
Zordan T, Mazzarolo E, Briseghella B, Chen BC, Feng Y, Siviero E, Fenu L (2014) Optimization of Calatrava bridge in Venice. Bridge maintenance, safety, management and life extension. In: Proceedings of the 7th International Conference of Bridge Maintenance, Safety and Management, IABMAS 2014
Funding
National Natural Science Foundation of China (51508103) and Department of Education of Fujian Province (CN) (JA15074) by Junqing XUE, National Natural Science Foundation of China (51778148) and Recruitment Program of Global Experts Foundation (TM2012-27) by Bruno Briseghella, and National Natural Science Foundation of China (51508053) by Xi Tu.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to urisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lan, C., Tu, X., Xue, J. et al. Adaptive form-finding method for form-fixed spatial network structures. Int J Adv Struct Eng 10, 99–109 (2018). https://doi.org/10.1007/s40091-018-0179-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40091-018-0179-z