Introduction

The field of atomic and molecular acoustics relates the macroscopic parameters of sound waves and their properties of the propagating medium. And so, the studies of velocity and adsorption in sound give detail about the properties of gases, liquids such as in much different dispersion. The dependence temperature and concentration dependence of acoustic studies pave some significant observations of intermolecular interaction in liquid medium and solutions, since the liquid mixtures were found applications in the area of medical, technology, agriculture, fertilizers, restorations of food and related industries [1, 2]. In recent times, the ultrasonic analysis found wide applications in determining the physicomechanical (solids), physicochemical and bio-physical behavior of variety of liquid mixtures [3, 4]. The acoustical with thermodynamic properties evaluated in the in liquids mixtures, which are not obtained by any other methods which may be useful mainly in automobiles like combustion, petrol and diesel. Further, confirming the existence of specific interaction, the authors try to relate the values from experimental findings with those predicted molecular models and to know the molecular insight. This comparison gives fruitful information about the mixtures to test the validity of many empirical theories for the mixtures of binary, ternary [5, 6], tertiary and sometimes pentenary [4]. The thermodynamic dependence of fluids is more useful for sustaining the properties (density, viscosity) at high temperatures with more mechanical operations worldwide like train engine working continuously more than 100 h. The race car and high-speed motors run many revolutions per minute (tribology). It creates more temperature, absorbing heat from components of mixtures and remove the heat frequently by nanofluids. In recent time’s nano-lubricants, nano-coolant plays a vital role for high-speed mechanical operations.

The cohesive and adhesive properties of liquids indicate the nature of suspended solid particles and also indicate the intermediate properties of gas and solids. So, the liquid possesses the intermediate physical properties of solid and gasses, collectively called as condensed matter. The idea behind the liquid is considered as disordered solid and as condensed gas and so the pair potential parameter is accountable [7, 8].

Based on the molecular structure, Eyring proposed that the idea of condensed matter behavior and Hilderbrand commented and refused to consider a solid [9]. The molecular movement sometimes favors a condensed state, but the thermal energy agitates and destroys the actual structure. The concluding analysis is based on the molecular theories like perturbation, spherical particle, etc. [10]. And so, the acceptable partition function cannot be obtained due to many structures of particles other than sphere.

The nature of the molecules can be studied in liquids and liquid mixtures with statistical analysis from the standard references. Besides the available models, some new models can be proposed. However, the aim is to investigate the interaction, catalytic activity, molecular–kinetic nature for the assumed systems; it is much important to select and apply one model among those existing models. If the available models are not suitable to validate the experimental results, we can propose new model suitable for experiment with valid assumption. Evaluating ultrasonic velocity values computed from various models in liquid mixtures are compared and validate with suitable following model [11]. These models are Kudriatsav theory (KT), Jouyban–Acree model (JAM), Floty theory (FT), Ramasamy–Anbanantham model (RAM), Glinkski model (GM), Mc. Alister model (Mc-AM), time average model (TAM), Tavlorides groups (TG), Urick model (UM), Kuster and Toksoz model and modified Urick model (MUM). Also, the percentage deviation, standard percentage error and Chi-squared test are computed [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31].

While making the solution and for calculation of the percentage composition of the constituent of liquid mixtures [32,33,34], to find the strength of molecular interactions of liquid mixtures, through the non-rectilinear behavior of ultrasonic velocity. To obtain the additional information about the nature and strength of interaction of molecule, other parameters related to ultrasonic velocity can be used. The important features of ultrasonic velocity in experiment and the relevant experimental model are non-invariant, precision, rapidly and easy automation. Several researchers reported on ultrasonic velocity with models used for computing ultrasonic velocity [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31].

Experimental

The Analar Grade chemicals are purified with normal procedures [32, 33]. And proper mixtures are prepared with mole fractions and the experimental ultrasonic velocities are measured with ultrasonic interferometer of any made, with an accuracy of ΔU ± 10−2 ms−1. The density of liquid mixtures was determined with densitometer and the viscosity of the samples was measured with Ostwald’s viscometer with the accuracy of Δρ = ± 10−6 cm−3 and Δη = ± 0.001 kg m−3, respectively [34]. Further, it is completely free from air and bubbles (complete solutions). The particle sizes can be determined with laser diffractions/any other conventional methods suitable to the nature of solutions.

Theories/models

Kudriavtsev theory (U KT)

Kudriavtsev theory [12] gives the velocity theoretically UKT, through the following relation:

$$ U_{\text{KT}}^{2} \, = \;X_{\text{A}} \left( {\frac{{M_{\text{A}} }}{{\overline{M} }}} \right)U_{\text{A}}^{2} + X_{\text{B}} \left( {\frac{{M_{\text{B}} }}{{\overline{M} }}} \right)U_{\text{B}}^{2} + 5.5 \times 10^{8} L , $$
(1)

where MA, MB, and M represent the mol. wts. of components A and B, the effective molecular weight Meff = (XAMA + XBMB), L represents the heat capacity of the mixture in cal/g.

Jouyban–Acree model (U JA)

Jouyban–Acree and his groups [13, 14] recently correlated viscosity; density is further extended to velocity by the units of Mehdi Hasan [15]. According to his assumption, the velocity due to JA model is given by j:

$$ \ln U_{\text{JA}} \,\, = X_{1} \ln U_{1} + X_{2} \ln U_{2} + (X_{1} X_{2} /T)\{ A_{0} + A_{1} (X_{1} - X_{2} ) + A_{1} (X_{1} - X_{2} )^{2} \} . $$
(2)

Here, U1 and U2 are velocities of pure liquids 1 and 2. X1 and X2 are the mole fractions of 1 and 2 correspondingly.

Flory’s theory (U FT)

A significant method from surface tension of mixtures is the Flory based on statistics [16]. Patterson and Rastogi proposed the model with reduced parameters [17]. The values of ultrasonic velocity from surface tension, temperature, pressure, volume with their reduced parameters through Auerbeck relation [35]

To calculate the characteristic surface tension [5],

$$ \sigma *\,\, = \,\,K^{1/3} P*^{2/3} T*^{1/3} , $$
(3)

where, K, P* and T* are the Boltzmann constant, pressure and temperature of corresponding characteristics nature of fluids. Here

$$ P*\,\, = \,\frac{{\alpha TV^{2} }}{{k_{\text{T}} }}, $$
(4)

where ‘α’ is the thermal expansion coefficient and ‘kT’ is the isothermal compressibility,

$$ \alpha \,\, = \,\,\frac{{75.6 \times 10^{ - 3} }}{{T\frac{1}{9}u_{\text{m}}^{{\frac{1}{2}}} \rho_{m}^{{\frac{1}{2}}} }}, $$
(5)
$$ k_{\text{T}} \,\, = \,\frac{{1.71 \times 10^{ - 3} }}{{T^{{\frac{4}{9}}} \rho_{\text{m}}^{{\frac{4}{3}}} u_{\text{m}}^{2} }}. $$
(6)

The reduced volume V through ‘α’ is from the following expression:

$$ V\,\, = \,\,\left[ {1 + \left( {\frac{\alpha T}{3(1 + \alpha T)}} \right)} \right]^{3} . $$
(7)

The characteristic temperature T* is given as:

$$ T* = T\left( {\frac{{V^{{\frac{4}{3}}} }}{{V^{{\frac{1}{3}}} - 1}}} \right). $$
(8)

where the characteristic and reduced parameters are used to compute the surface tension of binary liquid mixtures:

$$ V_{\text{m}}^{*} \,\, = \,x_{1} \,V_{1}^{*} + x_{2} V_{2}^{*} , $$
(9)
$$ V_{\text{m}} \,\, = \frac{{V_{\text{m}} }}{{\{ x_{1} V_{1}^{*} + x_{2} V_{2}^{*} \} }}, $$
(10)
$$ P*\,\, = \,\psi_{1} P_{1}^{*} + \psi_{2} P_{2}^{*} - \psi_{1} \theta_{2} X_{12} , $$
(11)
$$ T*\,\, = \,\frac{P*}{{\left[ {\frac{{\psi_{1} P_{1}^{*} }}{{T_{1}^{*} }} + \frac{{\psi_{2} P_{2}^{*} }}{{T_{2}^{*} }}} \right]}}. $$
(12)

where ψ is the segment fraction, θ2 is the site fraction, and X12 is the interaction parameters:

$$ \psi_{1} \,\, = \,\frac{{x_{1} V_{1}^{*} }}{{x_{1} V_{1}^{*} + x_{2} V_{2}^{*} }}, $$
(13)
$$ \psi_{2} \,\, = \,1 - \psi_{1} , $$
(14)
$$ \theta_{2} \,\, = \frac{{\psi_{2} }}{{\left[ {\psi_{2} + \psi_{1} \left( {\frac{{V_{2}^{*} }}{{V_{1}^{*} }}} \right)^{1/3} } \right]}}, $$
(15)
$$ X_{12} \,\, = \,P_{1}^{*} \left[ {1 - \left( {\frac{{V_{2}^{*} }}{{V_{1}^{*} }}} \right)^{{\frac{1}{6}}} \left( {\frac{{P_{2}^{*} }}{{P_{1}^{*} }}} \right)^{{\frac{1}{2}}} } \right]^{2} \,. $$
(16)

The ‘reduced surface tension’ is given by Priogogonie and Saraga [36]:

$$ \sigma (V)\,\, = \,MV^{{ - \frac{5}{3}}} \, - \frac{{V^{{\frac{1}{3}}} - 1}}{{V^{2} }}\ln \left[ {\frac{{V^{{\frac{1}{3}}} - 0.5}}{{V^{{\frac{1}{3}}} - 1}}} \right], $$
(17)

where M is the fraction of nearest neighbors, the molecule moving from the bulk to the surface. And the surface tension (σ) of a mixture is

$$ \sigma_{\text{m}} \,\, = \,\sigma *\sigma (V). $$
(18)

The surface tension from Flory theory has been used to evaluate ultrasonic velocity of mixture, with the help of familiar Auerback relation [16, 35]:

$$ u_{\text{m}} \,\, = \,\,\left( {\frac{{\sigma_{\text{m}} }}{{6.3 \times 10^{ - 4} \rho_{\text{m}} }}} \right)^{2/3} . $$
(19)

Ramasamy and Anbanantham model (URAM)

Ramasamy and Anbananthan [18] proposed the theory based on the idea of impedance parameter with the mole fraction of components. With equilibrium condition:

$$ A + B \leftrightarrow AB $$
(20)

and the constant of association Kas is

$$ K_{\text{as}} \,\, = \,\frac{[AB]}{[A][B]}, $$
(21)

where [A] is the amount of solvent and [B] is the amount of solute in the liquid mixture.

By applying the linearity condition,

$$ U_{\text{obs}} \,\, = \,X_{\text{A}} U_{\text{A}} + X_{\text{AB}} U_{\text{AB}} , $$
(22)

where XA, XAB, UA and UAB are the mole fraction of component A, and associative AB, ultrasonic velocity of component A and associate AB and observed ultrasonic velocity, respectively, and sometimes with non-equilibrium condition. With the existence of non-associated component, the above expression becomes:

$$ U_{\text{RA}} \,\, = \,[X_{\text{A}} U_{\text{A}} + X_{\text{B}} U_{\text{B}} + X_{\text{AB}} U_{\text{AB}} ], $$
(23)

where XB and UB are the mole fractions of component B and ultrasonic velocity of B (non-associated component).

$$ K_{\text{as}} \,\, = \,\frac{[AB]}{{(C_{\text{A}} - [AB])\;(C_{\text{B}} - [AB])}}, $$
(24)

where CA and CB are initial molar concentrations of the components. The value of Kas computes the equilibrium value of [AB] for every composition of the mixture as well as [a] = CA− [AB] and [B] = CB − [AB].

$$ K_{\text{as}} \,\, = \,\frac{{a_{\text{AB}} }}{{(a_{\text{A}} - a_{\text{AB}} )\;(a_{\text{B}} - a_{\text{AB}} )}} $$
(25)

where aA, aB and aAB are the additivity of components A, B and associate AB with equimolar which may be equal to

$$ a^{\prime}_{\text{A}} \,\, = \,a_{\text{A}} - a_{\text{AB}} \,\;{\text{and}}\;\;a^{\prime}_{B} \,\, = \,a_{\text{B}} - a_{\text{AB}} , $$

where a′A and a′B are the activities of [A] and [B] in equimolar quantities.

From Eq. (25), Kas is

$$ K_{\text{as}} \,\, = \,\frac{{a_{\text{AB}} }}{{a_{\text{A}} a_{\text{B}} - a_{\text{A}} a_{\text{AB}} - a_{\text{B}} a_{\text{AB}} + a_{\text{AB}}^{2} }}\;\;\; = \frac{{a_{\text{AB}} }}{{a^{\prime}_{\text{A}} \cdot a^{\prime}_{\text{B}} }}. $$
(26)

At now, consider if any value of ultrasonic velocity in the hypothetical pure component AB, UAB, it is possible to equate the ultrasonic velocity calculated using Eq. (26) with the experiment.

$$ S\,\, = \,\sum {(U_{\text{obs}} - U_{\text{cal}} )^{2} } , $$
(27)

where Uobs and Ucal are the observed and calculated equilibrium properties, respectively.

The low values of S can be obtained theoretically by a pair of fitted parameters. But, we found that for some Kas and UAB, the values of S are high and varied rapidly, and for others, it is low and changes occur slowly when changing the fitted parameters. In these types, the value of UAB is not much lower/higher than the lowest/highest observed ultrasonic velocity of the system. Quantitatively, it should be accepted with reasonable parameters Kas and UAB which has the physical meaning and which reproduces satisfactorily experimental properties.

Glinkski model (U GM)

On analyzing the ultrasonic velocity values from Ramaswamy and Anbananthan model, Glinski [19] suggested the additive function with the volume fraction, ϕ of the components, the extracted form by Natta and Baccaredda model [20] as:

$$ U_{\text{GL}} \,\, = \,\frac{{U_{\text{A}} U_{\text{B}} U_{\text{AB}} }}{{\phi_{\text{A}} U_{\text{A}} U_{\text{AB}} + \phi_{\text{B}} U_{\text{A}} U_{\text{A}} B_{\phi } + \phi_{\text{AB}} U_{\text{A}} U_{\text{B}} ,}} $$
(28)

where UGL is the theoretical ultrasonic velocity of binary liquid mixtures, ϕA and ϕB are the volume fractions of components A and B and UA, UB and UAB are the ultrasonic velocity of components A, B and AB. The numerical procedure, computation and calculation of constant are same as described before. In addition to this, model which was already mentioned was further developed and elaborated by many researchers [21, 22, 37].

McAllister 3-body model (U McA-3)

McAllister assumed in the study of the viscosity of a mixture of molecules type (1) and (2). And he proposed that the total free energy of activation will be dependent on (ΔGii, ΔGij or ΔSijk) of individual interactions, with their fraction and the total occurrences (\( x_{i}^{3} ,\;x_{i}^{2} x_{j} ,\;x_{j}^{2} ,\;x_{i} x_{j}^{2} \;\;or\;\;x_{i} x_{j} x_{k} ) \). Hence

$$ \Delta G*\,\, = \,x_{1}^{2} \Delta G_{1}^{*} \, + x_{1}^{2} x_{2} \Delta G_{121}^{*} + 2x_{1}^{2} x_{2} \Delta G_{112}^{*} + x_{1} x_{2}^{2} \Delta G_{212}^{*} + 2x_{1} x_{2}^{2} \Delta G_{123}^{*} + x_{2}^{3} \Delta G_{2}^{*} . $$
(29)

In another way

$$ \Delta G_{{}}^{*} \,\, = \,x_{1}^{3} \Delta G_{1}^{*} \, + 3x_{1}^{2} x_{2} \Delta G_{12}^{*} + 3x_{1} x_{2}^{2} \Delta G_{12}^{*} + x_{2} \Delta G_{2}^{*} . $$
(30)

Now, applying Eq. (30) for each set of possible interactions (i.e., 111, 121, … , and 222) and then taking logarithms of equations obtained and removing free energy terms,

$$ \begin{aligned} \ln u\,\, = \,x_{1}^{3} \ln u_{1} + 3x_{1}^{2} x_{2} \ln u_{12} + 3x_{1} x_{2} \ln u_{21} + x_{2}^{3} \ln u_{2} - \ln [x_{1} + x_{2} M_{2} /M_{1} ] \hfill \\ + 3x_{1}^{2} x_{2} \ln [(2 + M_{2} /M_{1} )/3] + 3x_{1} x_{2}^{2} \ln [(1 + 2M_{2} /M_{1} )/3] + x_{2}^{3} \ln [M_{2} /M_{1} ], \hfill \\ \end{aligned} $$
(31)

where,

$$ M_{12} \,\, = \,\,\frac{{2M_{1} + M_{2} }}{3}, $$
(32)

and

$$ M_{21} \,\, = \,\,\frac{{2M_{2} + M_{2} }}{3}. $$
(33)

McAllister 4-body model (U MCA-4)

If the molecular size is somewhat more differed, the 4 body system seems to be 3 body systems. Further, considering different interactions, the occurrence of free energy is the sum of all activations energy.

$$ \Delta G*\,\, = \,\mathop x\nolimits_{1}^{4} \,\Delta \mathop G\nolimits_{1}^{*} + 4\mathop x\nolimits_{1}^{3} x2\Delta \mathop G\nolimits_{2221}^{*} + 6x_{1}^{2} x_{2}^{2} \Delta G_{2221}^{*} 4x_{1} \mathop x\nolimits_{2}^{3} \Delta \mathop G\nolimits_{2221}^{*} + \mathop x\nolimits_{2}^{3} \Delta \mathop G\nolimits_{2}^{*} . $$
(34)

By the techniques entirely similar to method in (34), it becomes

$$ \begin{aligned} \ln u_{\text{mix}} \,\, = \,x_{1}^{4} \ln u_{1} + 4x_{1}^{3} x_{2} \Delta \ln u_{1112} + 6x_{1}^{2} x_{2} \ln u_{1122} + 4x_{1} x_{2}^{2} \ln u_{222} + x_{2}^{4} \ln u_{2} \hfill \\ - \ln (x_{1} + x_{2} M_{2} /M_{1} ) + 4x_{1}^{3} x_{2} \ln [(3 + M_{2} /M_{1} )/4] + 6x_{1}^{2} x_{2}^{2} \ln [(1 + M_{2} /M_{1} )/2] \hfill \\ + 4x_{1} x_{2}^{3} \ln [(1 + 3M_{2} /M_{1} )/4] + x_{2}^{4} \ln (M_{2} /M_{1} ), \hfill \\ \end{aligned} $$
(35)

where all the notations having the usual meaning.

Time average model (U tAvg)

In time average model, the reflection with refraction effects is neglected.

$$ \phi \,\, = \,\,(t* - t_{\text{c}} )/(t_{\text{d}} - t_{\text{c}} ). $$
(36)

Tavlarides and co-workers model (U TM)

Tavlarides and their co-workers proposed this model, and here the effects of reflection and refraction phenomenon are accountable. The coefficients gd and gc depend on the ratio γ and subsequently the model produces branches depending on phase continuity [23, 24],

$$ \phi \,\, = \,\,\frac{{t* - t_{\text{c}} }}{{g_{\text{d}} t_{\text{d}} - g_{\text{c}} t_{\text{c}} }}, $$
(37)
$$ \gamma \,\, = \,\frac{{{\text{speed}}\,{\text{of}}\;{\text{sound}}\;{\text{in}}\;{\text{dispersed}}\;{\text{space}}}}{{{\text{speed}}\,{\text{of}}\;{\text{sound}}\;{\text{in}}\;{\text{continous}}\;{\text{space}}}}, $$
(38)

for γ ≥ 1

$$ g_{\text{c}} \,\, = \,1 + \frac{1}{{r^{3} }}[1 - (1 - \gamma^{2} )^{3/2} ] - \frac{3}{{5\gamma^{3} }}[1 - (1 - \gamma^{2} )^{5/2} ] - \frac{2}{5}\gamma^{2} ,$$
(39)
$$ g_{\text{d}} \,\, = \,\frac{1}{{\gamma^{2} }}[1 - (1 - \gamma^{2} )^{3/2} ], $$
(40)

for γ ≤ 1

$$ g_{\text{c}} \,\, = \,1 + \frac{2}{{5\gamma^{3} }}\, - \gamma^{2} \left[ {1 - \left( {1 - \frac{1}{{\gamma^{2} }}} \right)^{3/2} } \right] + \frac{3}{5}\gamma^{2} \left[ {1 - \left( {\frac{1}{{\gamma^{2} }}} \right)^{5/2} } \right] - \left( {1 - \frac{1}{{\gamma^{2} }}} \right)^{3/2} , $$
(41)
$$ g_{\text{d}} \,\, = \,\,\frac{1}{{\gamma^{2} }}. $$
(42)

Urick model (U Ur)

In this Urick model, the particles are assumed to be very small compared to the sound wavelength and so the effect of scattering and the velocity of sound can be omitted [25]. Density and compressibility values are found averages weighted by the phase concentration:

$$ u\,\, = \,\frac{1}{{\sqrt {\rho *k_{\text{m}} } }}, $$
(43)
$$ \frac{{\rho_{\text{c}} - \rho *}}{{\rho_{\text{c}} + 2\rho *}} = \phi \frac{{\rho_{\text{c}} - \rho_{\text{d}} }}{{\rho_{\text{c}} + 2\rho_{\text{d}} }}, $$
(44)
$$ k_{\text{m}} \,\, = \,\phi k_{\text{d}} + (1 - \phi )k_{\text{c}} . $$
(45)

Kuster and Toksoz model (U KUT)

In this model, the dispersed solid with spherical and the phase is non-viscous fluid. With the same above assumption of particle size with wavelength of sound, multiple scattering effects are negligible and so it gives two branches [26]:

$$ U\, = \,\frac{1}{{\sqrt {\rho_{\text{m}} *k_{\text{m}} } }}, , $$
(46)
$$ \frac{{\rho_{\text{c}} - \rho *}}{{\rho_{\text{c}} + 2\rho *}}\,\, = \,\phi \,\frac{{\rho_{\text{c}} - \rho_{\text{d}} }}{{\rho_{c} + 2\rho_{\text{d}} }}, $$
(47)
$$ k_{\text{m}} \, = \phi k_{\text{d}} \, + (1 - \phi )k_{\text{c}} . $$
(48)

Modified Urick model (U MUr)

In this model, they account the scattering by thermal means, but applying the long wavelength limit with the two branches from phase continuity [27,28,29,30].

From Urick equation, \( u\,\, = \,\frac{1}{{\sqrt {\rho_{\text{m}} k_{\text{m}} } }} \), after substituting pm and km, wee obtain

$$ u\,\, = \,\frac{1}{{\sqrt {(\phi \rho_{\text{d}} + (1 - \phi )\rho_{\text{c}} )(\phi k_{\text{d}} + (1 - \phi )k_{\text{c}} } }}. $$
(49)

In general, the speed of sound in the continuous phase is

$$ u_{\text{c}} \,\, = \,\frac{1}{{\sqrt {\rho_{\text{c}} k_{\text{c}} } }}. $$
(50)

Squaring and dividing Eqs. (50) by (49), and making a series, algebraic transformation is

$$ \begin{aligned} \frac{{u_{\text{c}}^{2} }}{{u^{2} }}\,\, & = \frac{{(\phi \rho_{\text{d}} + 1 - \phi )\rho_{\text{c}} )(\phi k_{\text{d}} + (1 - \phi )k_{\text{c}} )}}{{\rho_{\text{c}} k_{\text{c}} }} \\ \, & = \,\frac{{((\rho_{\text{d}} - \rho_{\text{c}} )\phi \rho_{\text{c}} )(k_{\text{d}} - k_{\text{c}} )\phi + k_{c} )}}{{\rho_{\text{c}} k_{\text{c}} }}\, \\ & = \,\frac{{\rho_{\text{c}} k_{\text{c}} + (k_{\text{c}} (\rho_{\text{d}} - \rho_{\text{c}} ) + \rho_{\text{c}} (k_{\text{d}} - k_{\text{c}} ))\phi + (\rho_{\text{d}} - \rho_{c} )(k_{\text{d}} - k_{\text{c}} )\phi_{2} }}{{\rho_{\text{c}} k_{\text{c}} }}\, \\ & = \,1 + \left( {\frac{{\rho_{\text{d}} - \rho_{\text{c}} }}{{\rho_{\text{c}} }} + \frac{{k_{\text{d}} - k_{\text{c}} }}{{k_{\text{c}} }}} \right)\phi + \left( {\frac{{\rho_{\text{d}} - \rho_{\text{c}} }}{{\rho_{\text{c}} }}} \right)\,\left( {\frac{{k_{\text{d}} - k_{\text{c}} }}{{k_{\text{c}} }}} \right)\phi^{2} . \\ \end{aligned} $$

Hence,

$$ \frac{1}{{u^{2} }}\,\, = \,\frac{1}{{u_{\text{c}}^{2} }}\,\left( {1 + \left( {\frac{{k_{\text{d}} - k_{\text{c}} }}{{k_{\text{c}} }} + \frac{{\rho_{\text{d}} - \rho_{\text{c}} }}{{\rho_{\text{c}} }}} \right)\phi + \left( {\frac{{k_{\text{d}} - k_{\text{c}} }}{{k_{\text{c}} }}} \right)\left( {\frac{{\rho_{\text{d}} - \rho_{\text{c}} }}{{\rho_{\text{c}} }}} \right)\phi^{2} } \right). $$
(51)

Or in simple (introducing α1 and δ1 as coefficients in front of ϕ and ϕ2 terms);

$$ \frac{1}{{u_{2} }}\,\, = \frac{1}{{u_{c}^{2} }}\,(1 + \alpha_{1} \phi + \delta_{1} \phi^{{_{2} }} ). $$
(52)

The other form of modified Urick Eq. (55) is

$$ \frac{1}{{u_{2} }}\,\, = \frac{1}{{u_{c}^{2} }}\,(1 + \alpha \phi + \delta \phi^{{_{2} }} ). $$
(53)
$$ \begin{aligned} \alpha \,\, &= \,\,\left( {\frac{{k_{\text{d}} - k_{\text{c}} }}{{k_{\text{c}} }} + \theta + \frac{{\rho_{\text{d}} - \rho_{\text{c}} }}{{\rho_{\text{c}} }}} \right) \hfill \\ \delta \,\, &= \,\,\left( {\frac{{k_{\text{d}} - k_{\text{c}} }}{{k_{\text{c}} }} + \theta } \right){\kern 1pt} {\kern 1pt} \left( {\frac{{\rho_{\text{d}} - \rho_{\text{c}} }}{{\rho_{\text{c}} }}} \right) + \frac{{2(\rho_{\text{d}} - \rho_{\text{c}} )^{2} }}{{3\rho_{\text{c}}^{2} }} \hfill \\ \theta \,\,& = \,(\mu - 1)\frac{{\rho_{\text{d}} C_{{^{\text{pd}} }} }}{{\rho_{\text{c}} C_{\text{pc}} }}R^{2} \;\;{\text{and}}\;\;R\,\, = \,\,\left( {\frac{{\beta_{\text{d}} }}{{\rho_{\text{d}} C_{\text{pd}} }} - \frac{{\beta_{\text{c}} }}{{\rho_{\text{c}} C_{pc} }}} \right)/\frac{{\beta_{\text{c}} }}{{\rho_{\text{c}} C_{\text{pc}} }}. \hfill \\ \end{aligned} $$

Validations

Among the all above models, the validations of some models were illustrated as follows, the time-average model, which equivalent to the sound propagation through a the medium is considered as layer by layer, (ii) In this modified time-average model by Taylaries and co-workers [23, 24], (iii) Urick model [25], (iv) model of Kuster and Toksoz [26] and (v) modified Urick model [27, 28].

Meng and his co-workers studied the above models for water with oil at temperatures 25 °C, 40 °C and 55 °C [29]. For the comparison of models (i)–(iv), model (i) based on the time-average approach is not a sufficient model to describe the behavior of oil–water mixtures studied here. Because in this model there is no consideration of any scattering effects, it is slightly concentrated with high dispersion media (droplets). The models (iii) and (iv) seem to match the experimental data most closely. The phase inversions of oil and water occur at the content values of 30–70% and that inversion causes due to the thermodynamic conditions. The application of model (v) is considering scattering by thermal energy of thermal with β, specific heat capacities, Cp and Cv, for both continuous and non-continuous medium.

The effect of specific heat capacities for hydrocarbons of petrochemicals like crude oil and water in this experiments reports is generally a mixture of many hydrocarbons and the properties are similar [30, 31, 38, 39]. From the model (v), the view of θ depends on the magnitude of factor (μ − 1), mostly which is small in case of fluids for water and very large molecules of hydrocarbons. The effect of temperature and the changes in Cp, μwater = 1, μoil = 1 become μwater > 1 and μoil > 0.

The Ramasamy and Anbanantham model [18] was corrected by Glinski [19] and tested by Natta and Baccaredda [40] to predict direct and the related associational behavior of liquid mixtures. The quantities analyzed were refractive index, molar volume, viscosity, free length, free volume, internal pressure, compressibility and many [35,36,37, 40, 41]. The results are fitted with the adjustable parameters. The values of Kas, UA and B are the fitted parameters. On changing the parameters, the equilibrium concentrations of individual components [A], [B] and [AB] change and the ultrasonic velocity can be computed. The difference in experiment and theory values for ultrasonic velocity is used to obtain the sum of squares of deviation. The values of ultrasonic velocity in pure associate can be treated as a fitted one with the values of Kas.

Values of (α) and Ks are needed in the PFP model obtained from the equations which have been tested already in many cases [36, 37, 41,42,43]. The advantage of the Flory theory over others is that the essential parameters required in this theory can be precisely determined using the physical parameters of pure liquids [44]; the average percentage deviations of the ultrasonic velocity obtained by the Flory statistical theory for both the mixtures have been discussed [45]. The ultrasonic velocities of both the mixtures were also analyzed in terms of the Flory statistical theory using Eq. (19). The APD of the comparison of ultrasonic velocity are reported in et al. [46] and it is found good agreement between the experimental and calculated values of u with a minimum APD of − 0.81 for the THF + 1-P mixture and a maximum APD of − 5.15 for the THF + 2-P mixture [46]. It may be concluded that the statistical mechanical theory can be used as a powerful tool to evaluate the excess functions directly from the ultrasonic velocity and density data.

This is common the deviations in any parameter (ultrasonic velocity) can be mentioned by Redlich–Kishter polynomial equation [47] for correlating the experimental data as:

$$ y\,\, = \,x_{i} (1 - x_{i} )\sum\limits_{i = o}^{p} {A_{i} (2x_{i} - 1)^{i} } , $$
(54)

where ‘y’ shows deviation in ultrasonic velocity, xi is the mole fraction and Ai is the coefficient of ith component, respectively. The coefficient values can be computed through multiple regression analysis (least square) and are summarized along with the standard deviations.

The reduced Redlich–Kister excess properties are expressed as:

$$ Q_{y.\exp } ,(x_{1} )\,\, = \,Y^{E} /(x_{1} (1 - x_{1} )), $$
(55)

where YE denotes any excess values (excess ultrasonic velocity). The reduced Redlich–Kister (RR–K) functions give much better insight information of the non-ideality. i.e., RRK excess property is more sensitive than direct excess property occurring at low concentrations [48, 49]. The liquid mixtures having specific interactions like association at low concentrations with different size of molecules (clusters). And in the RRK- polynomials remove the effect of excess functions and gives specific reduced functions in (55) characterizing the velocity and other property and also gives evidence to the existence of important interactions [48, 49].

Combined nearly ideal binary solvent/Redlich–kister equation (CNIBS/R-K) is

$$ \ln \;X_{\text{m}} \,\, = \,fc\ln Xc + fw\ln Xw + fcfw\varSigma w(fc - fw). $$
(56)

The solubility behavior of liquid mixtures with organic solvent is from i = 0 to i = 3 [50]. And it is also able to describe the multiple solubility maximum and solubility at various temperatures [51]. The miscibility and solubility are the key factors while designing the drugs in mixed solvents [52].

McAllister coefficient a, b and c were calculated using the least square procedure. With the variation in mole fractions, the values of speed of sound obtained from all the models decrease in trend at all temperatures.

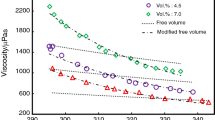
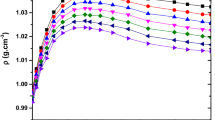
The observations leading to the associated components parameters provide better agreement over the non-associated components’ parameters. It means that larger deviation values in PFP model can be explained as the model was developed for non-electrolyte γ-meric spherical chain molecules and the system under investigation has interacting and associating properties, Even though the formula used for this computation of α and βT is also empirical in general. The molecular function and complex functions lead to positive deviations in speed of sound, whereas negative deviations are due to molecular dissociation. The sign and magnitude of deviations in sound depend on the relative strength of the two opposite effects. The less smoothness in deviations is due to the interaction between the existing component molecules. Isentropic compressibility shows increasing trend with the increase in mole fraction, and the density and ultrasonic velocity show other behavior [46].

The recently developed Juoyban–Acree model is applied successfully to the mixture of ortho, meta, para cresols and 1,4 dioxane, aniline and pyridine; these correlations in all six systems further fitted with Redlich–Kister Polynomials. From the analysis, Juoyban–Acree model is fitted better over than other studied models [53]. The spectroscopic analysis such as FTIR and UV–Visible absorption study can support to confirm the acoustical results obtained from various derived and theoretical parameters. And it is applicable to some alcohols and electrolytes [54,55,56,57].

Conclusions

Here, the author taken twelve no of theory/model of ultrasonic velocities for various liquid mixtures and are validated with experimental observations. The trends in observation of any one model suggest highly suitable with particular mixtures, either ideal, non-ideal and strength with magnitude of interactions of confirmed. Overall, further it is stated that all the models used in this present investigation successfully agree well with the experimental values and findings, and its shows that the liquids should have poor associating properties. In future, a general equation is fit to explain the liquid property more reliable and acceptable for associate and non-associated parameters of many fluids at nano and all ranges.