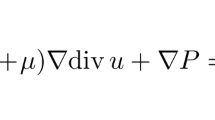Global well-posedness of the two-dimensional stochastic viscous nonlinear wave equations

Abstract

We study well-posedness of viscous nonlinear wave equations (vNLW) on the two-dimensional torus with a stochastic forcing. In particular, we prove pathwise global well-posedness of the stochastic defocusing vNLW with an additive stochastic forcing $D^\alpha \xi$, where $\alpha < \frac{1}{2}$ and $\xi$ denotes the space–time white noise.

1 Introduction

1.1 Viscous nonlinear wave equations

In this paper, we consider the following nonlinear wave equation (NLW) on the two-dimensional torus $\mathbb {T}^2 = (\mathbb {R}/\mathbb {Z})^2$, augmented by viscous effects:

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t^2 u + (1-\Delta ) u + D \partial _tu + |u|^{p-1}u = D^\alpha \xi \\ (u, \partial _tu)|_{t=0} = (u_0, u_1), \end{array}\right. } \end{aligned}$$

(1.1)

where $p > 1$, $D = |\nabla | = \sqrt{-\Delta }$, $\alpha < \frac{1}{2}$, and $\xi$ denotes the (Gaussian) space–time white noise on $\mathbb {R}_+ \times \mathbb {T}^2$. Our main goal in this paper is to prove pathwise global well-posedness of (1.1) in $C(\mathbb {R}_+; H^s (\mathbb {T}^2))$ for some $\alpha \le \alpha _p$ and $s \ge s_p$, where $H^s(\mathbb {T}^2)$ is the $L^2$-based Sobolev space on $\mathbb {T}^2$ with regularity s (see Sect. 2 for more details).

In [21], Kuan–Čanić proposed the following viscous NLW on $\mathbb {R}^2$:

$$\begin{aligned} \partial _t^2 u - \Delta u + 2\mu D \partial _tu = F(u), \end{aligned}$$

(1.2)

where $\mu > 0$ and F(u) is a general external forcing. This equation typically shows up in fluid–structure interaction problems, such as the interaction between a stretched membrane and a viscous fluid. The viscosity term $2\mu D \partial _tu$ in (1.2) comes from the Dirichlet–Neumann operator typically arising in fluid–structure interaction problems in three dimensions. See [21, 23] for the derivation of (1.2). It is easy to see that, when $\mu \ge 1$, the Eq. (1.2) is purely parabolic (see [23, 26]). On the other hand, when $0< \mu < 1$, the viscous NLW (1.2) exhibits an interesting mixture of dispersive effects and parabolic smoothing. Since the precise value of $0< \mu < 1$ does not play an important role, we simply set $\mu = \frac{1}{2}$. In addition, we consider a defocusing power-type nonlinearity of the form

$$\begin{aligned} F(u) = -|u|^{p-1}u, \end{aligned}$$

for positive real numbers $p > 1$. This power-type nonlinearity has been studied extensively for nonlinear dispersive equations (see, for example, [40]). With $\mu = \frac{1}{2}$ and $F(u) = -|u|^{p-1}u$, the general form of vNLW (1.2) becomes the following version of vNLW:

$$\begin{aligned} \partial _t^2 u - \Delta u + D \partial _tu + |u|^{p-1}u = 0 \end{aligned}$$

(1.3)

We now consider the analytical aspects of vNLW (1.3). Note that as in the case of the usual NLW:

$$\begin{aligned} \partial _t^2 u - \Delta u + |u|^{p-1}u = 0, \end{aligned}$$

the viscous NLW (1.3) on $\mathbb {R}^2$ enjoys the following scaling symmetry: $u(t,x) \mapsto u_\lambda (t, x):= \lambda ^{\frac{2}{p-1}} u(\lambda t, \lambda x)$. Namely, if u is a solution to (1.3), then $u_\lambda$ is also a solution to (1.3) for any $\lambda > 0$ with rescaled initial data. This scaling symmetry induces the scaling critical Sobolev regularity $s_{\text {scaling}}$ on $\mathbb {R}^2$ given by

$$\begin{aligned} s_{\text {scaling}} = 1 - \frac{2}{p-1} \end{aligned}$$

such that under this scaling symmetry, the homogeneous Sobolev norm on $\mathbb {R}^2$ remains invariant. While there is no scaling symmetry on $\mathbb {T}^2$, the scaling critical regularity $s_{\text {scaling}}$ still plays an important role in studying nonlinear partial differential equations in the periodic setting, especially for dispersive equations. Namely, in both periodic and non-periodic settings, a dispersive equation is usually well-posed in $H^s$ for $s > s_{\text {scaling}}$ and is usually ill-posed in $H^s$ for $s < s_{\text {scaling}}$. On the one hand, there is a good local well-posedness theory for dispersive equations above the scaling regularities (see [3, 31, 38] for the references therein). Moreover, we show in this paper that vNLW (1.3) is locally well-posed in $H^s(\mathbb {T}^2)$ for all $s \ge s_{\text {crit}}$ (with a strict inequality when $p = 3$), where $s_{\text {crit}}$ is defined by

$$\begin{aligned} s_{\text {crit}}:= \max (s_{\text {scaling}}, 0) = \max \bigg ( 1-\frac{2}{p-1}, 0 \bigg ), \end{aligned}$$

(1.4)

for a given $p > 1$. See “Appendix A”. Here, the second regularity restriction 0 is required to make sense of powers of u. On the other hand, many dispersive equations are known to be ill-posed below the scaling critical regularity. Among these ill-posedness results, many of them are in the form of norm inflation (see [6, 8,9,10, 13, 20, 31, 33, 36, 37, 41]), which is a stronger notion of ill-posedness. In [21], Kuan–Čanić proved norm inflation for vNLW (1.3) in $\mathcal {H}^s(\mathbb {R}^d)$ for $0< s < s_{\text {scaling}}$ and any odd integers $p \ge 3$. Moreover, they pointed out that the viscous term has the potential to slow down the growth of the $H^s$ norm, i.e. to slow down the speed of the norm inflation. For details, see [21]. Also, it is of interest to see if norm inflation for vNLW holds in negative Sobolev spaces. See [12].

Let us now turn our attention to the viscous NLW with a stochastic forcing. In [22], Kuan–Čanić studied the stochastic viscous wave equation with a multiplicative noise on $\mathbb {R}^d$, $d = 1, 2$:

$$\begin{aligned} \partial _t^2 u - \Delta u + D \partial _tu = f(u) \xi , \end{aligned}$$

where f is Lipschitz and $\xi$ is the (Gaussian) space–time white noise on $\mathbb {R}_+ \times \mathbb {R}^2$. In [26], Oh and the author studied (the renormalized version of) SvNLW (1.1) with $\alpha = \frac{1}{2}$. When $\alpha = \frac{1}{2}$, the solution is not a function but is only a distribution and thus a renormalization on the nonlinearity is required to give a proper meaning to the dynamics (which in particular forces us to consider $|u|^{p-1}u$ only for $p \in 2 \mathbb {N}+ 1$ or $u^k$ for an integer $k \ge 2$). See [26] for details. In the cubic case, we proved pathwise global well-posedness. For an odd integer $p \ge 5$, we also used an invariant measure argument to prove almost sure global well-posedness with suitable random initial data.¹ In this paper, our goal is to investigate further well-posedness of SvNLW (1.1) with an additive forcing $D^\alpha \xi$ and, in particular, prove pathwise global well-posedness for any $p > 1$, where the range of $\alpha < \frac{1}{2}$ depends on the degree $p >1$ of the nonlinearity.

1.2 SvNLW with an additive stochastic forcing

We say that u is a solution to SvNLW (1.1) if u satisfies the following Duhamel formulation of (1.1):

$$\begin{aligned} u(t) = V(t) (u_0, u_1) - \int _0^t S(t-t') \big ( |u|^{p-1} u \big ) (t') dt' + \Psi . \end{aligned}$$

(1.5)

Here, V(t) is the linear propagator defined by

$$\begin{aligned} V(t) (u_0, u_1)= & {} e^{-\frac{D}{2} t} \bigg ( \cos (t[[ D ]]) + \frac{D}{2[[ D ]]} \sin (t [[ D ]]) \bigg ) u_0\nonumber \\{} & {} + e^{-\frac{D}{2}t} \frac{\sin (t[[ D ]])}{[[ D ]]} u_1 \end{aligned}$$

(1.6)

and S(t) is defined by

$$\begin{aligned} S(t) = e^{-\frac{D}{2}t} \frac{\sin (t [[ D ]])}{[[ D ]]}, \end{aligned}$$

(1.7)

where

$$\begin{aligned}{}[[ D ]] = \sqrt{1-\tfrac{3}{4}\Delta }, \end{aligned}$$

and $\Psi$ denotes the stochastic convolution defined by

$$\begin{aligned} \Psi := \Psi _\alpha = \int _0^t S(t-t') D^\alpha \xi (dt'). \end{aligned}$$

(1.8)

A standard argument shows that $\Psi$ belongs to $C(\mathbb {R}_+; W^{\frac{1}{2} - \alpha - \varepsilon , \infty } (\mathbb {T}^2))$ almost surely, where $\varepsilon > 0$ can be arbitrarily small; see Lemma 2.5 below. In particular, when $\alpha < \frac{1}{2}$, $\Psi$ is a well-defined function on $\mathbb {R}_+ \times \mathbb {T}^2$.

We first state a local well-posedness result for SvNLW (1.1).

Theorem 1.1

Let $p > 1$ and $\alpha < \frac{1}{2}$. Define q, r, and $\sigma$ as follows.

• (i) When $1< p < 2$, set $q = 2+\delta$, $r = \frac{4+2\delta }{1+\delta }$, and $\sigma = 0$, for some sufficiently small $\delta > 0$.

• (ii) When $p \ge 2$, set $q = p + \delta$, $r = 2p$, and $\sigma = 1 - \frac{1}{p+\delta } - \frac{1}{p}$ for some arbitrary $\delta > 0$.

Let $s \ge \sigma$. Then, SvNLW (1.1) is pathwise locally well-posed in $\mathcal {H}^s(\mathbb {T}^2)$. More precisely, given any $(u_0, u_1) \in \mathcal {H}^s(\mathbb {T}^2)$, there exists $T = T_\omega (u_0, u_1)$ (which is positive almost surely) and a unique solution u to (1.1) with $(u, \partial _tu)|_{t=0} = (u_0, u_1)$ in the class

$$\begin{aligned} \Psi + C([0,T]; H^\sigma (\mathbb {T}^2)) \cap L^q([0,T]; L^r(\mathbb {T}^2)). \end{aligned}$$

We present the proof of Theorem 1.1 in Sect. 3. The proof of Theorem 1.1 is based on the following first order expansion [5, 11, 28]:

$$\begin{aligned} u = v + \Psi , \end{aligned}$$

(1.9)

where the residual term v satisfies the following equation:

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t^2 v + (1-\Delta ) v + D\partial _tv + |v + \Psi |^{p-1}(v + \Psi ) = 0 \\ (v, \partial _tv) |_{t=0} = (u_0, u_1). \end{array}\right. } \end{aligned}$$

(1.10)

See Proposition 3.1 for the pathwise local well-posedness result at the level of the residual term v using the homogeneous Strichartz estimates for the viscous wave equation (Lemma 2.8).

The main idea of the proof of pathwise local well-posedness of SvNLW (1.1) comes from [23]. Note that the nonlinearity $|u|^{p-1}u$ in SvNLW (1.1) is not necessarily algebraic for general $p>1$, which creates a difficulty for obtaining the difference estimate when applying the contraction argument. To deal with this issue, we apply the idea from Oh–Okamoto–Pocovnicu [32] using the fundamental theorem of calculus.

Remark 1.2

• (i) Using the same argument, the proof of Theorem 1.1 works for both the defocusing case (with the nonlinearity $|u|^{p-1}u$) and the focusing case (with the nonlinearity $-|u|^{p-1}u$, i.e. with the negative sign). The proof of Theorem 1.1 also works for SvNLW with nonlinearity $u^k$, where $k \ge 2$ is an integer. In fact, a simple argument based on Sobolev’s inequality can be applied to prove local well-posedness of SvNLW with nonlinearity $u^k$ in the class $\Psi + C([0,T]; \mathcal {H}^s(\mathbb {T}^2))$ for $s \ge 1$. See, for example, Proposition 3.1 in [26].

• (ii) As it is written in Theorem 1.1, we point out that the regularity of initial data can be lowered to the subcritical case, i.e. $s \ge s_{\text {crit}}$ (with a strict inequality when $p = 3$), where $s_{\text {crit}}$ is the critical regularity as defined in (1.4) (note that $s_{\text {crit}} \le \sigma$ with $\sigma$ defined in Theorem 1.1). See Theorem A.6 and Remark A.7 for details.

• (iii) One can also directly prove local well-posedness of (1.1) for $u \in L^q ([0, T]; L^r (\mathbb {T}^2))$ for some appropriate $q, r \ge 2$. Specifically, in the Duhamel formulation (1.5), the linear term $V(t) (u_0, u_1)$ can be estimated by the Strichartz estimate (Lemma 2.8), the nonlinear perturbation term $\int _0^t S(t - t') (|u|^{p-1} u) (t') dt'$ can be estimated by the Schauder estimate (Lemma 2.7) along with Young’s convolution inequality, and the stochastic convolution $\Psi$ can also be bounded in $L^q ([0, T]; L^r (\mathbb {T}^2))$ (Lemma 2.5). This approach yields a stronger uniqueness result since the solution does not depend on any specific structure such as (1.9). Nevertheless, this paper is meant to be a continuation of the work in [26], and so we choose to study (1.1) from a dispersive point of view. Due to the assumption that the initial data lies in the Sobolev space $\mathcal {H}^s (\mathbb {T}^2)$ for some $s \ge 0$, it is more natural to construct the solution in $C([0, T]; H^s (\mathbb {T}^2))$ for $T > 0$. The Strichartz spaces $L^q ([0, T]; L^r (\mathbb {T}^2))$ can be viewed as “helper” spaces that allow us to show local well-posedness for rough initial data (i.e. with $s \ge 0$ as small as possible).

We now turn our attention to pathwise global well-posedness of SvNLW (1.1), and we restrict our attention to the defocusing case. Our pathwise global well-posedness result reads as follows.

Theorem 1.3

Let $p > 1$ and $\alpha < \min (\frac{1}{2}, \frac{2}{p-1} - \frac{1}{2})$. Let $\sigma = \max (0, 1 - \frac{1}{p+\delta } - \frac{1}{p})$ for some arbitrary $\delta > 0$ and let $s \ge \sigma$. Then, SvNLW (1.1) is pathwise globally well-posed in $\mathcal {H}^s(\mathbb {T}^2)$. More precisely, given any $(u_0, u_1) \in \mathcal {H}^s(\mathbb {T}^s)$, there exists a unique global-in-time solution u to (1.1) with $(u, \partial _tu)|_{t=0} = (u_0, u_1)$ in the class

$$\begin{aligned} \Psi + C(\mathbb {R}_+; H^\sigma (\mathbb {T}^2)). \end{aligned}$$

In Theorem 1.3, the uniqueness holds in the following sense. For any $t_0 \in \mathbb {R}_+$, there exists a time interval $I(t_0) \ni t_0$ such that the solution u to (1.1) is unique in

$$\begin{aligned} \Psi + C(I(t_0); H^\sigma (\mathbb {T}^2)) \cap L^q(I(t_0); L^r(\mathbb {T}^2)), \end{aligned}$$

where $q,r \ge 2$ are as in Theorem 1.1.

As stated in Theorem 1.3, when $1 < p \le 3$, we have the condition $\alpha < \frac{1}{2}$; when $p > 3$, we have the condition $\alpha < \frac{2}{p-1} - \frac{1}{2}$. As $p \rightarrow \infty$, the condition for $\alpha$ becomes $\alpha \le -\frac{1}{2}$. Note that when $1< p < 5$, we can prove pathwise global well-posedness of SvNLW (1.1) with the space–time white noise (i.e. $\alpha = 0$).

We prove Theorem 1.3 by studying (1.10) for the residual term v in Sect. 4. From the proof of Theorem 1.1, we see that pathwise global well-posedness follows once we control the $\mathcal {H}^1$-norm of $\vec v(t):= (v(t), \partial _tv (t))$. For this purpose, we study the evolution of the energy

$$\begin{aligned} E(\vec v) = \frac{1}{2} \int _{\mathbb {T}^2} (v^2 + |\nabla v|^2) dx + \frac{1}{2} \int _{\mathbb {T}^2} (\partial _tv)^2 dx + \frac{1}{p+1} \int _{\mathbb {T}^2} |v|^{p+1} dx, \qquad \end{aligned}$$

(1.11)

which is conserved under the (deterministic) usual NLW:

$$\begin{aligned} \partial _t^2 u + (1-\Delta )u + |u|^{p-1}u = 0. \end{aligned}$$

Note that for our problem, we proceed with the first order expansion (1.9), where the residual term $v = \Psi - u$ only satisfies (1.10). In this case, the energy $E(\vec v)$ is not conserved under the Eq. (1.10) because of the perturbative term $|v+\Psi |^{p-1}(v+\Psi ) - |v|^{p-1}v$. For our problem, we first follow the globalization argument by Burq–Tzvetkov [7] and establish an exponential growth bound on $E(\vec v)$, which works in the sub-cubic case $1 < p \le 3$. For the super-cubic case $p > 3$, this argument no longer works due to the high homogeneity of the non-linearity. When $3 < p \le 5$, we use an integration by parts trick introduced by Oh–Pocovnicu [34]. In the super-quintic case $p > 5$, we use a trick involving the Taylor expansion, where the idea comes from Latocca [24].

One important prerequisite for studying the evolution of the energy $E(\vec v)$ is that the local-in-time solution $\vec v$ lies in $\mathcal {H}^1(\mathbb {T}^2)$, which is not guaranteed by the pathwise local well-posedness result (Theorem 1.1) as it is written. Nonetheless, due to the dissipative nature of the equation, we show that $\vec v(t)$ indeed belongs to $\mathcal {H}^1(\mathbb {T}^2)$ for any $t > 0$ by using the Schauder estimate (Lemma 2.7) along with Theorem 1.1. See Sect. 4 for details.

We conclude our introduction by stating several remarks.

Remark 1.4

• (i) We point out that Theorem 1.1 and 1.3 also hold if we have $-\Delta$ instead of $1-\Delta$ in (1.1) by using an essentially identical proof.

• (ii) In Oh [26] and the author studied SvNLW (1.1) with $\alpha = \frac{1}{2}$. In this case, due to $\alpha = \frac{1}{2}$, the stochastic term $\Psi$ defined in (1.8) turns out to be merely a distribution, so that we studied a renormalized version of (1.1) and proved pathwise global well-posedness in the cubic case. Because of the singular nature of the stochastic convolution in this setting, the standard Gronwall argument does not work, and so we used a Yudovich-type argument to bound the corresponding energy. In the same paper, we also proved almost sure global well-posedness of (1.1) with $p \in 2\mathbb {N}+1$ and with random initial data, using the formal invariance of the Gibbs measure. However, the argument only works for $\alpha = \frac{1}{2}$, so it does not apply to our problem with $\alpha < \frac{1}{2}$ in this paper. Instead, in this paper, we establish pathwise global well-posedness of SvNLW (1.1).

(iii) We can also consider the vNLW with randomized initial data:

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t^2 u + (1 - \Delta ) u + D \partial _tu + |u|^{p-1} u = 0 \\ (u, \partial _tu) |_{t = 0} = (u_0^\omega , u_1^\omega ). \end{array}\right. } \end{aligned}$$

(1.12)

Here, the randomization $(u_0^\omega , u_1^\omega )$ of the initial data $(u_0, u_1)$ is defined by

$$\begin{aligned} (u_0^\omega , u_1^\omega ) := \bigg ( \sum _{n \in \mathbb {Z}^2} g_{n, 0} (\omega ) \widehat{u_0} (n) e^{in \cdot x}, \sum _{n \in \mathbb {Z}^2} g_{n, 1} (\omega ) \widehat{u_1} (n) e^{in \cdot x} \bigg ), \end{aligned}$$

(1.13)

where for $j = 0, 1$, $\widehat{u_j} (-n) = \overline{\widehat{u_j} (n)}$ for all $n \in \mathbb {Z}^2$ and $\{g_{n, j}\}_{n \in \mathbb {Z}^2}$ is a sequence of mean zero complex-valued random variables such that $g_{-n, j} = \overline{g_{n, j}}$ for all $n \in \mathbb {Z}^2$. Moreover, we assume that $g_{0, j}$ is real-valued for $j = 0, 1$, $\{ g_{0, j}, \Re g_{n, j}, \Im g_{n, j} \}_{n \in \mathcal {I}, j = 0, 1}$ are independent with $\mathcal {I}= (\mathbb {Z}_+ \times \{0\}) \cup (\mathbb {Z}\times \mathbb {Z}_+)$, and there exists a constant $c > 0$ such that on the probability distributions $\mu _{n, j}$ of $g_{n, j}$, we have

$$\begin{aligned} \int e^{\gamma \cdot x} d\mu _{n, j} (x) \le e^{c |\gamma |^2}, \quad j = 0, 1 \end{aligned}$$

(1.14)

for all $\gamma \in \mathbb {R}^2$ when $n \in \mathbb {Z}^2 {\setminus } \{0\}$ and all $\gamma \in \mathbb {R}$ when $n = 0$. Note that (1.14) is satisfied for standard complex-valued Gaussian random variables, standard Bernoulli random variables, and any random variables with compactly supported distributions.

The randomization (1.13) allows us to consider almost sure global well-posedness of (1.12) for $(u_0, u_1)$ living in negative Sobolev spaces. For almost sure local well-posedness, we consider the following first order expansion similar to (1.9):

$$\begin{aligned} u = v + z, \end{aligned}$$

where z is the solution of the linear viscous wave equation with initial data $(u_0^\omega , u_1^\omega )$:

$$\begin{aligned} z(t) = z^\omega (t) := V(t) (u_0^\omega , u_1^\omega ) \end{aligned}$$

with V(t) defined as in (1.6). By using the Schauder estimate (Lemma 2.7), we can establish similar (but stronger) probabilistic Strichartz estimates for z and $\langle \nabla \rangle ^{-1} \partial _tz$ as in [34, 35]. This enables us to prove almost sure local well-posedness of (1.12) using a similar argument as for proving Theorem 1.1, as long as $(u_0, u_1) \in \mathcal {H}^s (\mathbb {T}^2)$ with $s > - \frac{1}{p}$. On the other hand, the proof for almost sure global well-posedness of (1.12) is much simpler than that for Theorem 1.3, since z(t) is smooth for $t > 0$ thanks to the parabolic smoothing. We omit details since this is not the main focus in this paper.

2 Preliminary lemmas

In this section, we discuss some notations and lemmas that are necessary for proving our well-posedness results.

We use $A \lesssim B$ to denote $A \le CB$ for some constant $C>0$, and we write $A \sim B$ if $A \lesssim B$ and $B \lesssim A$. Also, we use $a+$ (and $a-$) to denote $a+\varepsilon$ (and $a-\varepsilon$, respectively) for arbitrarily small $\varepsilon > 0$. In addition, we use short-hand notations to work with space–time function spaces. For example, $C_T H_x^s = C([0,T]; H^s(\mathbb {T}^d))$.

2.1 Sobolev spaces and Besov spaces

Let $s \in \mathbb {R}$. We denote $H^s(\mathbb {T}^d)$ as the $L^2$-based Sobolev space with the norm:

$$\begin{aligned} \Vert u \Vert _{H^s(\mathbb {T}^d)} = \Vert \langle n \rangle ^s \widehat{u} (n) \Vert _{\ell _n^2(\mathbb {Z}^d)}, \end{aligned}$$

where $\widehat{u} (n)$ is the Fourier coefficient of u and $\langle \cdot \rangle = (1 + |\cdot |)^{\frac{1}{2}}$. We then define $\mathcal {H}^s(\mathbb {T}^d)$ as

$$\begin{aligned} \mathcal {H}^s(\mathbb {T}^d) = H^s(\mathbb {T}^d) \times H^{s-1}(\mathbb {T}^d). \end{aligned}$$

Also, we denote $W^{s,p}(\mathbb {T}^d)$ as the $L^p$-based Sobolev space with the norm:

$$\begin{aligned} \Vert u \Vert _{W^{s,p}(\mathbb {T}^d)} = \big \Vert \mathcal {F}^{-1} ( \langle n \rangle ^s \widehat{u} (n) ) \big \Vert _{L^p(\mathbb {T}^d)}, \end{aligned}$$

where $\mathcal {F}^{-1}$ denotes the inverse Fourier transform on $\mathbb {T}^d$. When $p=2$, we have $H^s(\mathbb {T}^d) = W^{s,2}(\mathbb {T}^d)$.

Let $\varphi : \mathbb {R}\rightarrow [0,1]$ be a bump function such that $\varphi \in C_c([-\tfrac{8}{5}, \tfrac{8}{5}])$ and $\varphi \equiv 1$ on $[-\tfrac{5}{4}, \tfrac{5}{4}]$. For $\xi \in \mathbb {R}^d$, we define $\varphi _0(\xi ) = \varphi (|\xi |)$ and

$$\begin{aligned} \varphi _j(\xi ) = \varphi \big ( \tfrac{|\xi |}{2^j} \big ) - \varphi \big ( \tfrac{|\xi |}{2^{j-1}} \big ) \end{aligned}$$

for $j \in \mathbb {Z}_+$. Note that

$$\begin{aligned} \sum _{j \in \mathbb {Z}_{\ge 0}} \varphi _j(\xi ) = 1 \end{aligned}$$

(2.1)

for any $\xi \in \mathbb {R}^d$. For $j \in \mathbb {Z}_{\ge 0}$, we define the Littlewood-Paley projector $\textbf{P}_j$ as

$$\begin{aligned} \textbf{P}_j u = \mathcal {F}^{-1} (\varphi _j \widehat{u}). \end{aligned}$$

Due to (2.1), we have

$$\begin{aligned} u = \sum _{j=0}^\infty \textbf{P}_j u. \end{aligned}$$

(2.2)

We also recall the definition of Besov spaces $B_{p,q}^s (\mathbb {T}^d)$ equipped with the norm:

$$\begin{aligned} \Vert u \Vert _{B_{p,q}^s(\mathbb {T}^d)} = \big \Vert 2^{sj} \Vert \textbf{P}_j u \Vert _{L_x^p(\mathbb {T}^d)} \big \Vert _{\ell _j^q(\mathbb {Z}_{\ge 0})}. \end{aligned}$$

Note that $H^s(\mathbb {T}^d) = B_{2,2}^s(\mathbb {T}^d)$.

We then recall the definition of paraproducts introduced by Bony [4]. For details, see [1, 16]. For given functions u and v on $\mathbb {T}^d$ of regularities $s_1$ and $s_2$, respectively. By (2.2), we can write the product uv as

The term (and the term ) is called the paraproduct of v by u (and the paraproduct of u by v, respectively), and it is well defined as a distribution of regularity $\min (s_2, s_1+s_2)$ (and $\min (s_1, s_1+s_2)$, respectively). The term is called the resonant product of u and v, and it is well defined in general only if $s_1+s_2 > 0$.

With these definitions in hand, we recall some basic properties of Besov spaces.

Lemma 2.1

(i) Let $s_1,s_2 \in \mathbb {R}$ and $1 \le p, p_1, p_2, q \le \infty$ which satisfies $\frac{1}{p} = \frac{1}{p_1} + \frac{1}{p_2}$. Then, we have

(2.3)

When $s_1 + s_2 > 0$, we have

(2.4)

(ii) Let $s_1 < s_2$ and $1\le p,q \le \infty$. Then, we have

$$\begin{aligned} \Vert u \Vert _{B_{p,q}^{s_1}(\mathbb {T}^d)} \lesssim \Vert u \Vert _{W^{s_2,p}(\mathbb {T}^d)}. \end{aligned}$$

(2.5)

In particular, when $q = \infty$, we have

$$\begin{aligned} \Vert u \Vert _{B_{p,\infty }^{s_1}(\mathbb {T}^d)} \lesssim \Vert u \Vert _{W^{s_1,p}(\mathbb {T}^d)}. \end{aligned}$$

(2.6)

See [1, 30] for the proofs of (2.3) and (2.4) in the $\mathbb {R}^d$ setting, which can be easily extended to the $\mathbb {T}^d$ setting. The embedding (2.5) follows from the $L^p$ boundedness of $\textbf{P}_j$ and the $\ell ^q$-summability of $\big \{ 2^{(s_1-s_2)j} \big \}_{j \in \mathbb {Z}_{\ge 0}}$, and the embedding (2.6) follows easily from the $L^p$ boundedness of $\textbf{P}_j$.

Using (2.3) and (2.4), we get the following product estimate.

Corollary 2.2

Let $s > 0$, $1 \le p,q \le \infty$ and $1 \le p_1,p_2,q_1,q_2 \le \infty$ satisfying

$$\begin{aligned} \frac{1}{p_1} + \frac{1}{q_1} = \frac{1}{p_2} + \frac{1}{q_2} = \frac{1}{p}. \end{aligned}$$

Then,

$$\begin{aligned} \Vert uv \Vert _{B_{p,q}^s(\mathbb {T}^d)} \lesssim \Vert u \Vert _{B_{p_1,q}^s(\mathbb {T}^d)} \Vert v \Vert _{L^{q_1}(\mathbb {T}^d)} + \Vert u \Vert _{L^{p_2}(\mathbb {T}^d)} \Vert v \Vert _{B_{q_2,q}^s(\mathbb {T}^d)}. \end{aligned}$$

Next, we recall the following chain rule estimates.

Lemma 2.3

Let u be a smooth function on $\mathbb {T}^d$, $s \in (0,1)$, $r \ge 2$. Let F denote the function $F(u) = |u|^{r-1}u$ or $F(u) = |u|^r$.

(i) Let $1< p, p_1 < \infty$ and $1 < p_2 \le \infty$ satisfying $\frac{1}{p} = \frac{1}{p_1} + \frac{1}{p_2}$. Then, we have

$$\begin{aligned} \Vert F(u) \Vert _{W^{s,p}(\mathbb {T}^d)} \lesssim \Vert u \Vert _{W^{s, p_1}(\mathbb {T}^d)} \big \Vert |u|^{r-1} \big \Vert _{L^{p_2}(\mathbb {T}^d)}. \end{aligned}$$

(2.7)

(ii) Let $1 \le p,q \le \infty$ and $1 \le p_1,p_2 \le \infty$ satisfying $\frac{1}{p} = \frac{1}{p_1} + \frac{1}{p_2}$. Then, we have

$$\begin{aligned} \Vert F(u) \Vert _{B_{p,q}^s(\mathbb {T}^d)} \lesssim \Vert u \Vert _{B_{p_1,q}^s(\mathbb {T}^d)} \big \Vert |u|^{r-1} \big \Vert _{L^{p_2}(\mathbb {T}^d)}. \end{aligned}$$

(2.8)

The estimate (2.7) follows immediately from the fractional chain rule on $\mathbb {T}^d$ in [14]. For the proof of (2.8), see, for example, Lemma 3.5 in [24] in the $\mathbb {R}^d$ setting, which can be easily extended to the $\mathbb {T}^d$ setting.

Lastly, we recall the following Gagliardo-Nirenberg interpolation inequality.

Lemma 2.4

Let $p_1, p_2 \in (1,\infty )$ and $s_1,s_2 > 0$. Let $p > 1$ and $\theta \in (0,1)$ satisfying

$$\begin{aligned} -\frac{s_1}{d} + \frac{1}{p} = (1-\theta )\bigg ( \frac{1}{p_1} - \frac{s_2}{d} \bigg ) + \frac{\theta }{p_2} \quad \text {and} \quad s_1 \le (1-\theta )s_2. \end{aligned}$$

Then, for $u \in W^{s_2,p_1}(\mathbb {T}^d) \cap L^{p_2}(\mathbb {T}^d)$, we have

$$\begin{aligned} \Vert u \Vert _{W^{s_1,p}(\mathbb {T}^d)} \lesssim \Vert u \Vert _{W^{s_2,p_1}(\mathbb {T}^d)}^{1-\theta } \Vert u \Vert _{L^{p_2}(\mathbb {T}^d)}^\theta . \end{aligned}$$

This inequality follows from a direct application of Sobolev’s inequality on $\mathbb {T}^d$ (see [2]) and then interpolation.

2.2 On the stochastic term

In this subsection, we discuss the regularity properties of the stochastic term $\Psi$ defined in (1.8). Given $N \in \mathbb {N}$, we denote $\Psi _N = \pi _N \Psi$ as the truncated stochastic convolution, where $\pi _N$ is the frequency cutoff onto the spatial frequencies $\{|n| \le N\}$. Then, we have the following regularity result for $\Psi$.

Lemma 2.5

For any $\varepsilon > 0$ and $T > 0$, $\Psi _N$ converges to $\Psi$ in $C([0,T];W^{1-2\alpha -\varepsilon ,\infty }(\mathbb {T}^2))$ almost surely. In particular, we have

$$\begin{aligned} \Psi \in C([0,T];W^{\frac{1}{2}-\alpha -\varepsilon ,\infty }(\mathbb {T}^2)) \end{aligned}$$

almost surely.

The proof of Lemma 2.5 follows from a straightforward modification of the proof in [18, Lemma 3.1], and so we omit details. See also [17, Proposition 2.1].

Remark 2.6

One can use an integration by parts to write

$$\begin{aligned} \widehat{\Psi }(t, n) = -\int _0^t B_n(t') \frac{d}{ds} \Big |_{s=t'} \Big ( e^{- \frac{|n|}{2}(t-s)} \frac{\sin ((t-s)[[ n ]] )}{[[ n ]]} |n|^\alpha \Big ) dt' \end{aligned}$$

almost surely, which allows us to compute that

$$\begin{aligned} \partial _t\widehat{\Psi }(t, n)&= \int _0^t \bigg ( -\frac{|n|}{2 [[ n ]]} e^{-\frac{|n|}{2} (t-t')} \sin ((t-t')[[ n ]]) \\&\quad + e^{-\frac{|n|}{2} (t-t')} \cos ((t-t')[[ n ]]) \bigg ) |n|^\alpha dB_n(t') \end{aligned}$$

almost surely. Using a similar argument as in [18, Lemma 3.1] or [17, Proposition 2.1], we have $\partial _t\Psi \in C([0,T]; W^{-\frac{1}{2} - \alpha -, \infty } (\mathbb {T}^2))$ almost surely. This will be useful in the proof of pathwise global well-posedness of SvNLW (1.1) in Sect. 4.2.

2.3 Linear estimates

In this subsection, we show some relevant linear estimates and the Strichartz estimates that are used to prove our well-posedness results.

Let

$$\begin{aligned} P(t) = e^{-\frac{D}{2} t} \end{aligned}$$

be the Poisson kernel with a parameter $\frac{t}{2}$, which appears in the viscous wave linear propagator V(t) defined in (1.6). We first recall the following Schauder-type estimate for the Poisson kernel P(t). For a proof, see Lemma 2.3 in [26].

Lemma 2.7

Let $1 \le p \le q \le \infty$ and $\beta \ge 0$. Then, we have

$$\begin{aligned} \Vert D^\beta P(t) \phi \Vert _{L^q(\mathbb {T}^d)} \lesssim t^{-\beta -d(\frac{1}{p}-\frac{1}{q})} \Vert \phi \Vert _{L^p(\mathbb {T}^d)} \end{aligned}$$

for any $0 < t \le 1$.

Next, we turn our attention to the Strichartz estimates for the homogeneous linear viscous wave equation on $\mathbb {T}^d$. We recall that the linear propagator V(t) is defined in (1.6).

Lemma 2.8

Given $s \ge 0$, suppose that $2 < q \le \infty$, $2 \le r \le \infty$ satisfy the following scaling condition:

$$\begin{aligned} \frac{1}{q} + \frac{d}{r} = \frac{d}{2} - s. \end{aligned}$$

(2.9)

Then, we have

$$\begin{aligned} \Vert V(t) (\phi _0, \phi _1) \Vert _{C ([0,T]; \mathcal {H}^{s-1}(\mathbb {T}^d))} \lesssim \Vert (\phi _0, \phi _1) \Vert _{\mathcal {H}^s(\mathbb {T}^d)} \end{aligned}$$

(2.10)

and

$$\begin{aligned} \Vert V(t) (\phi _0, \phi _1) \Vert _{L^q ([0,T]; L_x^r(\mathbb {T}^d))} \lesssim \Vert (\phi _0, \phi _1) \Vert _{\mathcal {H}^s(\mathbb {T}^d)} \end{aligned}$$

(2.11)

for all $0 < T \le 1$.

Proof

The bound (2.10) can be immediately seen from the definition of the $\mathcal {H}^s$-norm and the fact that $e^{-\frac{|n|}{2} t} \le 1$, $|\cos (t [[ n ]])| \le 1$, and $|\sin (t [[ n ]])| \le 1$.

To prove (2.11), we use the $TT^*$ method. We first consider the case when $s = 0$. Let

$$\begin{aligned} V_1(t) = e^{-\frac{D}{2}t} \cos (t[[ D ]]), \quad V_2(t) = e^{-\frac{D}{2}t} \frac{D}{2[[ D ]]} \sin (t[[ D ]]), \end{aligned}$$

so that

$$\begin{aligned} V(t)(\phi _0, \phi _1) = V_1(t) \phi _0 + V_2(t) \phi _0 + S(t) \phi _1. \end{aligned}$$

Let $L: L^2(\mathbb {T}^d) \rightarrow L_T^q L_x^r(\mathbb {T}^d)$ be the linear operator given by $L \phi = V_1(t) \phi$. Note that $L^*$ is the linear operator given by

$$\begin{aligned} L^* f = \int _0^T V_1(t') f(t') dt' \end{aligned}$$

for any space–time Schwartz function f. By Minkowski’s integral inequality, the Schauder estimate (Lemma 2.7) twice, the scaling condition (2.9), and the Hardy-Littlewood-Sobolev inequality, we have

$$\begin{aligned} \Vert LL^* f \Vert _{L_T^q L_x^r}&\le \bigg \Vert \int _0^T \big \Vert e^{-\frac{D}{2} (t+t')} \cos (t [[ D ]]) \cos (t' [[ D ]]) f(t') \big \Vert _{L_x^r} dt' \bigg \Vert _{L_T^q} \\&\lesssim \bigg \Vert \int _0^T \frac{1}{|t-t'|^{2(\frac{1}{2} - \frac{1}{r})}} \big \Vert e^{-\frac{D}{4} (t+t')} \cos (t [[ D ]]) \cos (t' [[ D ]]) f(t') \big \Vert _{L_x^2} dt' \bigg \Vert _{L_T^q} \\&\lesssim \bigg \Vert \int _0^T \frac{1}{|t-t'|^{2(\frac{1}{r'} - \frac{1}{r})}} \Vert f(t') \Vert _{L_x^{r'}} dt' \bigg \Vert _{L_T^q} \\&= \bigg \Vert \int _0^\infty \frac{1}{|t-t'|^{2/q}} \Vert \textbf{1}_{[0,T]}f(t') \Vert _{L_x^{r'}} dt' \bigg \Vert _{L_T^q} \\&\lesssim \Vert f \Vert _{L_T^{q'}\! L_x^{r'}}. \end{aligned}$$

Thus, by a standard duality argument, we obtain

$$\begin{aligned} \Vert V_1(t) \phi _0 \Vert _{L_T^q L_x^r(\mathbb {T}^d)} \lesssim \Vert \phi _0 \Vert _{L^2(\mathbb {T}^d)}. \end{aligned}$$

By using similar arguments, we obtain

$$\begin{aligned} \Vert V_2(t) \phi _0 \Vert _{L_T^q L_x^r(\mathbb {T}^d)} \lesssim \Vert \phi _0 \Vert _{L^2}, \quad \Vert S(t) \phi _1 \Vert _{L_T^q L_x^r} \lesssim \Vert \phi _0 \Vert _{H^{-1}(\mathbb {T}^d)}, \end{aligned}$$

so that we have

$$\begin{aligned} \Vert V(t) (\phi _0, \phi _1) \Vert _{L_T^q L_x^r(\mathbb {T}^d)} \lesssim \Vert (\phi _0, \phi _1) \Vert _{\mathcal {H}^0(\mathbb {T}^d)}. \end{aligned}$$

(2.12)

When $s > 0$, by Sobolev’s inequality, the scaling condition (2.9), and (2.12), we obtain

$$\begin{aligned} \Vert V(t) (\phi _0, \phi _1) \Vert _{L_T^q L_x^r}&\lesssim \Vert V(t) (\langle \nabla \rangle ^s \phi _0, \langle \nabla \rangle ^s \phi _1) \Vert _{L_T^q L_x^{1/(\frac{s}{d} + \frac{1}{r})}} \\&= \Vert V(t) (\langle \nabla \rangle ^s \phi _0, \langle \nabla \rangle ^s \phi _1) \Vert _{L_T^q L_x^{d / (\frac{d}{2} - \frac{1}{q})}} \\&\lesssim \Vert (\langle \nabla \rangle ^s \phi _0, \langle \nabla \rangle ^s \phi _1) \Vert _{\mathcal {H}^0} \\&= \Vert (\phi _0, \phi _1) \Vert _{\mathcal {H}^s}, \end{aligned}$$

as desired. $\square$

Remark 2.9

• (i) Compared to the Strichartz estimates for the usual linear wave equations [15, 17, 19, 25], the Strichartz estimates for the homogeneous linear viscous wave equation on $\mathbb {T}^d$ hold for a larger class of pairs (q, r), thanks to the parabolic smoothing effect.

• (ii) In Kuan–Čanić [21] proved the Strichartz estimates for the homogeneous linear viscous wave equation on $\mathbb {R}^d$. They used the method from Keel–Tao [19], so that their result requires (q, r) to be $\sigma$-admissible for some $\sigma > 0$, i.e. $(q,r,\sigma ) \ne (2,\infty ,1)$ and

  $$\begin{aligned} \frac{2}{q} + \frac{2\sigma }{r} \le \sigma . \end{aligned}$$

  We point out that the $TT^*$ method we use in the proof also works on $\mathbb {R}^d$ and does not have this $\sigma$-admissible restriction on q and r. However, our proof works only for $s \ge 0$.

We complete this subsection by establishing the following inhomogeneous linear estimates.

Lemma 2.10

Let $p \ge 2$ and let S(t) be as in (1.7). Then, given $\delta > 0$, we have

$$\begin{aligned} \bigg \Vert \int _0^t S(t-t') F(t') dt' \bigg \Vert _{L^{p+\delta } ([0,T]; L_x^{2p}(\mathbb {T}^2))} \lesssim \Vert F \Vert _{L^1 ([0,T]; L^2(\mathbb {T}^2))} \end{aligned}$$

(2.13)

for any $0 < T \le 1$.

Proof

We let

$$\begin{aligned} s = 1 - \frac{1}{p + \delta } - \frac{2}{2p} = 1 - \frac{1}{p + \delta } - \frac{1}{p}, \end{aligned}$$

so that $(p+\delta , 2p, s)$ satisfies the scaling condition in Lemma 2.8. By Minkowski’s integral inequality and Lemma 2.8, we obtain

$$\begin{aligned} \bigg \Vert \int _0^t S(t-t') F(t') dt' \bigg \Vert _{L_T^{p+\delta } L_x^{2p}}&\lesssim \int _0^T \Vert \textbf{1}_{[0,t]}(t') S(t-t')F(t') \Vert _{L_T^{p+\delta } L_x^{2p}} dt' \\&\lesssim \int _0^T \Vert F(t') \Vert _{H_x^{s-1}} dt' \\&\le \Vert F \Vert _{L_T^1 L_x^2}, \end{aligned}$$

so that (2.13) follows. $\square$

Lemma 2.11

Let S(t) be as in (1.7). Then, given $s \le 1$, we have

$$\begin{aligned} \bigg \Vert \int _0^t S(t-t') F(t') dt' \bigg \Vert _{C([0,T]; H_x^s(\mathbb {T}^2))} \lesssim \Vert F \Vert _{L^1 ([0,T]; L_x^2(\mathbb {T}^2))}, \end{aligned}$$

(2.14)

$$\begin{aligned} \bigg \Vert \partial _t\int _0^t S(t-t') F(t') dt' \bigg \Vert _{C([0,T]; H_x^{s-1}(\mathbb {T}^2))} \lesssim \Vert F \Vert _{L^1 ([0,T]; L_x^2(\mathbb {T}^2))} \end{aligned}$$

(2.15)

for any $0 < T \le 1$.

Proof

The estimate (2.14) follows from (1.7) and Minkowski’s integral inequality. The estimate (2.15) follows similarlly by noting that

$$\begin{aligned} \partial _t\int _0^t S(t-t') F(t') dt' = \int _0^t \partial _tS(t-t') F(t') dt', \end{aligned}$$

where

$$\begin{aligned} \partial _tS(t) = e^{-\frac{D}{2} t} \bigg ( \cos (t [[ D ]]) - \frac{D}{2 [[ D ]]} \sin (t [[ D ]]) \bigg ). \end{aligned}$$

$\square$

3 Local well-posedness of SvNLW

In this section, we prove Theorem 1.1, pathwise local well-posedness for SvNLW (1.1). As mentioned in Sect. 1.2, we consider the following vNLW:

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t^2 v + (1-\Delta ) v + D\partial _tv + F(v+\Psi ) = 0 \\ (v, \partial _tv)|_{t=0} = (u_0, u_1) \end{array}\right. } \end{aligned}$$

(3.1)

for given initial data $(u_0, u_1) \in \mathcal {H}^s(\mathbb {T}^2)$, $F(u) = |u|^{p-1}u$, and $\Psi$ is the stochastic convolution defined in (1.8). By Lemma 2.5, we can fix a good $\omega \in \Omega$ such that $\Psi = \Psi (\omega ) \in C([0,T]; W^{\frac{1}{2} - \alpha - \varepsilon , \infty }(\mathbb {T}^2))$ for $\alpha < \frac{1}{2}$ and sufficiently small $\varepsilon > 0$, so that (3.1) becomes a deterministic equation. Then, we have the following pathwise local well-posedness of (3.1).

Proposition 3.1

Let $p > 1$ and $\alpha < \frac{1}{2}$. Define q, r, and $\sigma$ as follows.

• (i) When $1< p < 2$, set $q = 2+\delta$, $r = \frac{4+2\delta }{1+\delta }$, and $\sigma = 0$, for some sufficiently small $\delta > 0$.

• (ii) When $p \ge 2$, set $q = p+\delta$, $r = 2p$, and $\sigma = 1 - \frac{1}{p+\delta } - \frac{1}{p}$, for some arbitrary $\delta > 0$.

Let $s \ge \sigma$. Then, (3.1) is pathwise locally well-posed in $\mathcal {H}^s(\mathbb {T}^2)$. More precisely, given any $(u_0, u_1) \in \mathcal {H}^s(\mathbb {T}^2)$, there exists $0 < T = T_\omega (u_0, u_1) \le 1$ and a unique solution $\vec v = (v, \partial _tv)$ to (3.1) in the class

$$\begin{aligned} (v, \partial _tv) \in C([0,T]; \mathcal {H}^\sigma (\mathbb {T}^2)) \quad \text {and} \quad v \in L^q([0,T]; L^r(\mathbb {T}^2)). \end{aligned}$$

Note that Theorem 1.1 follows immediately from Proposition 3.1. The main idea of the proof of Proposition 3.1 comes from [23].

Proof

We first consider the case when $p \ge 2$. We write (3.1) in the Duhamel formulation:

$$\begin{aligned} v(t) = \Gamma (v):= V(t)(u_0,u_1) - \int _0^t S(t-t') F(v+\Psi )(t') dt', \end{aligned}$$

(3.2)

where V(t) and S(t) are as defined in (1.6) and (1.7), respectively. Let $\vec \Gamma (v) = (\Gamma (v), \partial _t\Gamma (v))$ and $\vec v = (v, \partial _tv)$. Given $0 < T \le 1$, we define the space $\mathcal {X}(T)$ as

$$\begin{aligned} \mathcal {X}^\sigma (T) = \mathcal {X}_1^\sigma (T) \times \mathcal {X}_2^\sigma (T), \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&\mathcal {X}_1^\sigma (T):= C([0,T]; H^\sigma (\mathbb {T}^2)) \cap L^{p+\delta }([0,T]; L^{2p}(\mathbb {T}^2)), \\&\mathcal {X}_2^\sigma (T):= C([0,T]; H^{\sigma -1} (\mathbb {T}^2)). \end{aligned} \end{aligned}$$

Here, $\delta > 0$ is arbitrary and $\sigma = 1 - \frac{1}{p+\delta } - \frac{1}{p}$. Note that this choice of $\sigma$ along with the $L_T^{p+\delta } L_x^{2p}$ norm satisfies the scaling condition in Lemma 2.8. Our goal is to show that $\vec \Gamma$ is a contraction on a ball in $\mathcal {X}^\sigma (T)$ for some $0 < T \le 1$.

By (3.2), Lemma 2.8, (1.6), Lemmas 2.10 and 2.11, and Sobolev’s inequality with the fact that $|\mathbb {T}^2| = 1$, we have

$$\begin{aligned} \begin{aligned} \Vert \vec \Gamma (v) \Vert _{\mathcal {X}^\sigma (T)}&\lesssim \Vert (u_0, u_1) \Vert _{\mathcal {H}^\sigma } + \big \Vert |v + \Psi |^p \big \Vert _{L_T^1 L_x^2} \\&\lesssim \Vert (u_0, u_1) \Vert _{\mathcal {H}^s} + T^\theta \Big ( \Vert v \Vert _{L_T^{p+\delta } L_x^{2p}}^p + \Vert \Psi \Vert _{L_T^{p+\delta } L_x^{2p}}^p \Big ) \\&\lesssim \Vert (u_0, u_1) \Vert _{\mathcal {H}^s} + T^\theta \Big ( \Vert \vec v \Vert _{\mathcal {X}^\sigma (T)}^p + \Vert \Psi \Vert _{C_T W_x^{\frac{1}{2} - \alpha - \varepsilon , \infty }}^p \Big ) \end{aligned} \end{aligned}$$

(3.3)

for some $\theta > 0$ and sufficiently small $\varepsilon > 0$.

For the difference estimate, we use the idea from Oh–Okamoto–Pocovnicu [32]. Noticing that $F'(u) = p|u|^{p-1}$, we use (3.2), Lemmas 2.8, 2.10 and 2.11, the fundamental theorem of calculus, Minkowski’s integral inequality, Hölder’s inequality, and Sobolev’s inequality to obtain

$$\begin{aligned} \Vert \vec \Gamma (v) - \vec \Gamma (w) \Vert _{\mathcal {X}^\sigma (T)}\lesssim & {} \Vert F(v+\Psi ) - F(w+\Psi ) \Vert _{L_T^1 L_x^2} \nonumber \\= & {} \bigg \Vert \int _0^1 F'(w+\Psi +\tau (v-w)) (v-w) d\tau \bigg \Vert _{L_T^1 L_x^2} \nonumber \\\lesssim & {} \int _0^1 \Vert w + \Psi + \tau (v-w) \Vert _{L_T^p L_x^{2p}}^{p-1} \Vert v-w \Vert _{L_T^p L_x^{2p}} d\tau \nonumber \\\lesssim & {} T^\theta \Big ( \Vert v \Vert _{L_T^{p+\delta } L_x^{2p}}^{p-1} + \Vert w \Vert _{L_T^{p+\delta } L_x^{2p}}^{p-1} + \Vert \Psi \Vert _{L_T^{p+\delta } L_x^{2p}}^{p-1} \Big ) \Vert v-w \Vert _{L_T^{p+\delta } L_x^{2p}} \nonumber \\\lesssim & {} T^\theta \Big ( \Vert \vec v \Vert _{\mathcal {X}^\sigma (T)}^{p-1} + \Vert \vec w \Vert _{\mathcal {X}^\sigma (T)}^{p-1} + \Vert \Psi \Vert _{C_T W_x^{\frac{1}{2} - \alpha - \varepsilon , \infty }}^{p-1} \Big ) \Vert \vec v - \vec w \Vert _{\mathcal {X}^\sigma (T)} \nonumber \\ \end{aligned}$$

(3.4)

for some $\theta > 0$ and sufficiently small $\varepsilon > 0$.

Thus, by choosing $T = T_\omega ( \Vert (u_0,u_1) \Vert _{\mathcal {H}^s} ) > 0$ small enough, we obtain that $\vec \Gamma$ is a contraction on the ball $B_R \subset \mathcal {X}^\sigma (T)$ of radius $R \sim 1 + \Vert (u_0,u_1) \Vert _{\mathcal {H}^s}$. Note that at this point, the uniqueness of the solution v only holds in the ball $B_R$, but we can use a standard continuity argument to extend the uniqueness of v to the entire $\mathcal {X}^\sigma (T)$.

For the case when $1< p < 2$, we may have $p + \delta < 2$, so that Lemma 2.8 may not work for the $L_T^{p+\delta } L_x^{2p}$ norm. Instead, we consider the $L_T^q L_x^r$ norm with $q = 2+\delta$ and $r = \frac{4+2\delta }{1+\delta }$, where $\delta > 0$ is small enough so that r is close enough to 4. We also set $\sigma = 0$, so that that this choice of $\sigma$ along with this $L_T^q L_x^r$ norm satisfies the scaling condition in Lemma 2.8. Note that we also need to modify the definition of $\mathcal {X}_1^\sigma (T)$ using this $L_T^q L_x^r$ norm. We then modify (3.3) as follows. By (3.2), Lemma 2.8, (1.6), Lemmas 2.10 and 2.11, and Sobolev’s inequality, we have

$$\begin{aligned} \Vert \vec \Gamma (v) \Vert _{\mathcal {X}^0(T)}&\lesssim \Vert (u_0, u_1) \Vert _{\mathcal {H}^0} + \big \Vert |v + \Psi |^p \big \Vert _{L_T^1 L_x^2} \\&\lesssim \Vert (u_0, u_1) \Vert _{\mathcal {H}^s} + T^\theta \Big ( \Vert v \Vert _{L_T^{2+\delta } L_x^{2p}}^p + \Vert \Psi \Vert _{L_T^{p+\delta } L_x^{2p}}^p \Big ) \\&\lesssim \Vert (u_0, u_1) \Vert _{\mathcal {H}^s} + T^\theta \Big ( \Vert \vec v \Vert _{\mathcal {X}^0(T)}^p + \Vert \Psi \Vert _{C_T W_x^{\frac{1}{2} - \alpha - \varepsilon , \infty }}^p \Big ) \end{aligned}$$

for some $\theta > 0$. Here, we can ensure that $2p \le r = \frac{4+2\delta }{1+\delta }$ for any $1< p < 2$ by choosing $\delta = \delta (p) > 0$ small enough. A similar modification can be applied to (3.4) to obtain a difference estimate, which then allows us to close the contraction argument. $\square$

Remark 3.2

We point out that the local well-posedness result of vNLW (3.1) can be improved using the inhomogeneous Strichartz estimates. In particular, we can show that (3.1) is locally well-posed in $\mathcal {H}^s(\mathbb {T}^2)$ as long as $s \ge s_{\text {crit}}$ (with a strict inequality when $p=3$), where $s_{\text {crit}}$ is the critical regularity as defined in (1.4). For details, see Theorem A.6 and Remark A.7.

4 Global well-posedness of SvNLW

In this section, we aim to prove Theorem 1.3, i.e. pathwise global well-posedness of SvNLW (1.1). As mentioned in Sect. 1.2, we prove Theorem 1.3 by studying the Eq. (1.10) for v with $(v, \partial _tv)|_{t=0} = (u_0, u_1)$, for given initial data $(u_0, u_1) \in \mathcal {H}^s (\mathbb {T}^2)$ of (1.1).

Fix an arbitrary $T \ge 1$. In view of Proposition 3.1, in order to show well-posedness of (3.1) on [0, T], it suffices to show that the $\mathcal {H}^\sigma$-norm of the solution $\vec v(t) = (v(t), \partial _tv(t))$ to (3.1) remains finite on [0, T], where $\sigma$ is as defined in Proposition 3.1. This will allow us to iteratively apply the pathwise local well-posedness result in Proposition 3.1.

In fact, we show that the solution $\vec v(t)$ belongs to $\mathcal {H}^1(\mathbb {T}^2)$. Let $0 < t \le 1$. From Lemma 2.7, we have

$$\begin{aligned} \Vert V(t)(u_0, u_1) \Vert _{\mathcal {H}^1} \lesssim ( 1 + t^{-1+\sigma } ) \Vert (u_0,u_1) \Vert _{\mathcal {H}^\sigma }. \end{aligned}$$

(4.1)

Then, let $0 < T_0 \le 1$ be the local existence time as in the proof of Proposition 3.1. Thus, given $s \ge \sigma ,$ by (3.2), (4.1), Lemma 2.11, Hölder’s inequality, and Sobolev’s inequality, we have that for $0 < t \le T_0$,

$$\begin{aligned} \begin{aligned} \Vert \vec v (t) \Vert _{\mathcal {H}^1}&\lesssim (1+t^{-1+\sigma }) \Vert (u_0,u_1) \Vert _{\mathcal {H}^\sigma } + \Vert (v + \Psi )^p \Vert _{L_{T_0}^1 L_x^2} \\&\lesssim (1+t^{-1+\sigma }) \Vert (u_0,u_1) \Vert _{\mathcal {H}^s} + T_0^\theta \Big ( \Vert v \Vert _{L_{T_0}^q L_x^r}^p + \Vert \Psi \Vert _{C_{T_0} W_x^{\frac{1}{2} - \alpha - \varepsilon , \infty }}^p \Big ), \end{aligned} \end{aligned}$$

(4.2)

where $\delta > 0$, $\varepsilon > 0$ are sufficiently small, $\theta > 0$, and q, r are as defined in the statement of Proposition 3.1. Here, due to Lemma 2.5, we can fix a good $\omega \in \Omega$ such that $\Psi = \Psi (\omega ) \in C([0,T_0]; W^{\frac{1}{2} - \alpha - \varepsilon , \infty }(\mathbb {T}^2))$ for $\alpha < \frac{1}{2}$ and sufficiently small $\varepsilon > 0$, so that we know from (4.2) that $\Vert \vec v (t) \Vert _{\mathcal {H}^1} < \infty$. A standard argument then shows that $\vec v \in C((0, T_0]; \mathcal {H}^1(\mathbb {T}^2))$. Thus, our main goal is to control the $\mathcal {H}^1$-norm of $\vec v (t)$ on [0, T] by bounding the energy $E(\vec v)$ defined in (1.11).

For the following computation, we need to work with the smooth solution $(v_N, \partial _tv_N)$ to the truncated equation with initial data $(\pi _N v_0, \pi _N v_1)$, where $\pi _N$ is the frequency truncation onto the frequencies $\{ |n| \le N \}$. After establishing an upper bound for $E(\vec v(t))$ with the implicit constant independent of N, we can take $N \rightarrow \infty$ by using Proposition 3.1 (specifically, the continuous dependence of a solution on the initial data). Here, we omit details and work with $(v, \partial _tv)$ instead for simplicity. See, for example, [34] for a standard argument.

4.1 Case $1 < p \le 3$

In this case, we follow the globalization argument by Burq–Tzvetkov [7]. For simplicity of notation, we set $E(t) = E(\vec v(t))$.

Given $T > 0$, we fix $0 < t \le T$. By (1.11) and (1.10), we have

$$\begin{aligned} \begin{aligned} \partial _tE(t)&= \int _{\mathbb {T}^2} \partial _tv \big ( \partial _t^2 v + (1-\Delta ) v + |v|^{p-1}v \big ) dx \\&\le -\int _{\mathbb {T}^2} \partial _tv\big ( |v + \Psi |^{p-1}(v + \Psi ) - |v|^{p-1}v \big ) dx. \end{aligned} \end{aligned}$$

(4.3)

Let $F(u) = |u|^{p-1}u$, so that we can compute $F'(u) = p|u|^{p-1}$. Thus, by the fundamental theorem of calculus, we have

$$\begin{aligned} \begin{aligned} |v + \Psi |^{p-1}(v + \Psi ) - |v|^{p-1}v&= F(v+\Psi ) - F(v) \\&= \Psi \int _0^1 F'(v + \tau \Psi ) d\tau \\&\lesssim |\Psi | |v|^{p-1} + |\Psi |^p. \end{aligned} \end{aligned}$$

(4.4)

Combining (4.3) and (4.4) and then applying the Cauchy-Schwartz inequality, we obtain

$$\begin{aligned} \begin{aligned} \partial _tE(t)&\lesssim \Vert \Psi \Vert _{L_x^\infty } \int _{\mathbb {T}^2} |\partial _tv| |v|^{p-1} dx + \int _{\mathbb {T}^2} |\partial _tv| |\Psi |^p dx \\&\le \Vert \Psi \Vert _{L_x^\infty } \bigg ( \int _{\mathbb {T}^2} (\partial _tv)^2 dx \bigg )^{\frac{1}{2}} \bigg ( \int _{\mathbb {T}^2} |v|^{2(p-1)} dx \bigg )^{\frac{1}{2}} \\&\quad + \Vert \Psi \Vert _{L_x^\infty }^{2p} \bigg ( \int _{\mathbb {T}^2} (\partial _tv)^2 dx \bigg )^{\frac{1}{2}} \\&\le C(\Psi ) E(t), \end{aligned} \end{aligned}$$

(4.5)

as long as $2(p-1) \le p+1$, or equivalently, $p \le 3$. By Gronwall’s inequality on (4.5), we get

$$\begin{aligned} E(t) \lesssim e^{C(\Psi ) t} \end{aligned}$$

for any $0 < t \le T$.

4.2 Case $3 < p \le 5$

In this case, we follow the idea introduced by Oh–Pocovnicu [34]. See also [27, 29, 39] for similar arguments. In this setting, we let $\alpha < \frac{2}{p-1} - \frac{1}{2}$, the reason of which will become clear in the following steps.

By (1.11), (1.10), and Taylor’s theorem, we have

$$\begin{aligned} \partial _tE(t)= & {} \int _{\mathbb {T}^2} \partial _tv \big ( \partial _t^2 v + (1-\Delta ) v + |v|^{p-1}v \big ) dx \nonumber \\= & {} -\int _{\mathbb {T}^2} \partial _tv \big ( |v + \Psi |^{p-1} (v + \Psi ) - |v|^{p-1} v \big ) dx - \int _{\mathbb {T}^2} \big ( D^{\frac{1}{2}} \partial _tv \big )^2 dx \nonumber \\\le & {} -p \int _{\mathbb {T}^2} \partial _tv \cdot |v|^{p-1} \Psi dx - \frac{p(p-1)}{2} \int _{\mathbb {T}^2} \partial _tv \cdot |v + \theta \Psi |^{p-3} (v + \theta \Psi ) \Psi ^2 dx \nonumber \\=: & {} A_1 + A_2, \end{aligned}$$

(4.6)

where $\theta \in (0,1)$. To estimate $A_2$, by the Cauchy-Schwartz inequality and Cauchy’s inequality, we have

$$\begin{aligned} |A_2|\lesssim & {} \int _{\mathbb {T}^2} |\partial _tv| \big ( |v|^{p-2} \Psi ^2 + \Psi ^p \big ) dx \nonumber \\\lesssim & {} \bigg ( \int _{\mathbb {T}^2} (\partial _tv)^2 dx \bigg )^{1/2} \bigg ( \Vert \Psi \Vert _{L_x^{\infty }}^4 \int _{\mathbb {T}^2} |v|^{2(p-2)} dx + \Vert \Psi \Vert _{L_x^{2p}}^{2p} \bigg )^{1/2} \nonumber \\\lesssim & {} (1 + \Vert \Psi \Vert _{L_x^{\infty }}^4) E(t) + \Vert \Psi \Vert _{L_x^{2p}}^p, \end{aligned}$$

(4.7)

where in the last inequality, we need $2(p-2) \le p+1$, which is equivalent to $p \le 5$. To estimate $A_1$, for $0 < t_1 \le t_2 \le T$, by integration by parts and Young’s inequality, we have

$$\begin{aligned} \int _{t_1}^{t_2} A_1 dt'= & {} - \int _{t_1}^{t_2} \int _{\mathbb {T}^2} \partial _t(|v|^{p-1}v) \Psi dx dt' \nonumber \\= & {} - \int _{\mathbb {T}^2} |v(t_2)|^{p-1} v(t_2) \Psi (t_2) dx + \int _{\mathbb {T}^2} |v(t_1)|^{p-1} v(t_1) \Psi (t_1) dx \nonumber \\{} & {} + \int _{t_1}^{t_2} \int _{\mathbb {T}^2} |v|^{p-1} v (\partial _t\Psi ) dx dt' \nonumber \\\lesssim & {} \varepsilon \Vert v(t_2) \Vert _{L_x^{p+1}}^{p+1} + \frac{1}{\varepsilon } \Vert \Psi (t_2) \Vert _{L_x^{p+1}}^{p+1} + \Vert v(t_1) \Vert _{L_x^{p+1}}^{p+1} + \Vert \Psi (t_1) \Vert _{L_x^{p+1}}^{p+1} \nonumber \\{} & {} + \int _{t_1}^{t_2} \int _{\mathbb {T}^2} |v|^{p-1} v (\partial _t\Psi ) dx dt', \end{aligned}$$

(4.8)

where $0< \varepsilon < 1$. We see in Remark 2.6 that $\partial _t\Psi \in C([0,T]; W^{-\frac{1}{2} - \alpha -, \infty } (\mathbb {T}^2))$. By duality, Hölder’s inequality, Lemma 2.3 (i), and Lemma 2.4, we obtain

$$\begin{aligned}{} & {} \int _{t_1}^{t_2} \int _{\mathbb {T}^2} |v|^{p-1} v (\partial _t\Psi ) dx dt' \nonumber \\{} & {} \quad = \int _{t_1}^{t_2} \int _{\mathbb {T}^2} \langle \nabla \rangle ^{\frac{1}{2}+\alpha +} (|v|^{p-1}v) \langle \nabla \rangle ^{-\frac{1}{2}-\alpha -} (\partial _t\Psi ) dx dt' \nonumber \\{} & {} \quad \lesssim \int _{t_1}^{t_2} \Vert v \Vert _{L_x^{p+1}}^{p-1} \big \Vert \langle \nabla \rangle ^{\frac{1}{2}+\alpha +} v(t')\big \Vert _{L_x^{\frac{p+1}{2}}} \big \Vert \langle \nabla \rangle ^{-\frac{1}{2}-\alpha -} (\partial _t\Psi )(t') \big \Vert _{L_x^\infty } dt' \nonumber \\{} & {} \quad \lesssim \Vert \partial _t\Psi \Vert _{C_TW_x^{-\frac{1}{2} - \alpha -, \infty }} \int _{t_1}^{t_2} E(t')^{\frac{p-1}{p+1}} \Vert \langle \nabla \rangle v \Vert _{L_x^2}^{\frac{2}{p-1}} \Vert v \Vert _{L_x^{p+1}}^{\frac{p-3}{p-1}} dt' \nonumber \\{} & {} \quad \lesssim \Vert \partial _t\Psi \Vert _{C_TW_x^{-\frac{1}{2} - \alpha -, \infty }} \int _{t_1}^{t_2} E(t') dt', \end{aligned}$$

(4.9)

where we require that

$$\begin{aligned} \frac{1}{2} + \alpha + = \frac{2}{p-1}, \end{aligned}$$

which is equivalent to $\alpha < \frac{2}{p-1} - \frac{1}{2}$. By combining (4.6), (4.7), (4.8), and (4.9), we have

$$\begin{aligned} E(t_2) \le (1+ C_1(\Psi )) \int _{t_1}^{t_2} E(t') dt' + C_2(\Psi , v(t_1)). \end{aligned}$$

By Gronwall’s inequality, we get

$$\begin{aligned} E(t) \lesssim e^{C(\Psi ) t} \end{aligned}$$

for any $0 < t \le T$.

4.3 Case $p > 5$

In this case, we follow the idea by Latocca [24]. In this setting, we also let $\alpha < \frac{2}{p-1} - \frac{1}{2}$.

We need the following lemma to close the energy estimates in the Gronwall argument. We define $\beta _p:= \lceil \frac{p-3}{2} \rceil$, $F(u):= |u|^{p-1}u$, and $s_p:= \frac{p-3}{p-1}$.

Lemma 4.1

For any $0 < t \le T$ and every integer $1 \le k \le \beta _p$, we have

$$\begin{aligned}&\bigg | \int _{\mathbb {T}^2} F^{(k-1)}(v(t)) \Psi (t)^{k-1} \partial _t\Psi (t) dx \bigg | \\&\quad \lesssim g\big ( \Vert \Psi \Vert _{L^\infty ([0,T]; X)}, \Vert \langle \nabla \rangle ^{-1} \partial _t\Psi \Vert _{L^\infty ([0,T]; Y)} \big ) (1+E(t)), \end{aligned}$$

where g is a polynomial with positive coefficients, and

$$\begin{aligned} X:= L^\infty (\mathbb {T}^2) \cap B_{\frac{p+1}{2},1}^{1-s_p} (\mathbb {T}^2) \quad \text {and} \quad Y:= L^\infty (\mathbb {T}^2) \cap B_{\infty ,1}^{s_p} (\mathbb {T}^2).\end{aligned}$$

Note that given $\alpha < \frac{2}{p-1} - \frac{1}{2}$, by Lemma 2.5, Remark 2.6, and Lemma 2.1 (ii), we have

$$\begin{aligned} g\big ( \Vert \Psi \Vert _{L^\infty ([0,T]; X)}, \Vert \langle \nabla \rangle ^{-1} \partial _t\Psi \Vert _{L^\infty ([0,T]; Y)} \big ) < \infty \end{aligned}$$

almost surely.

Let us first assume Lemma 4.1 and work on the energy bound. As in the case when $p > 3$, we can compute that for $0 < t \le T$,

$$\begin{aligned} \partial _tE(t) \le -\int _{\mathbb {T}^2} \partial _tv (F(v + \Psi ) - F(v)) dx. \end{aligned}$$

(4.10)

For our convenience we compute that for $k \in \mathbb {Z}_+$,

$$\begin{aligned} F^{(k)} (u) = {\left\{ \begin{array}{ll} C_{p,k} |u|^{p-k-1}u &{} \text {for}\quad k~\hbox {even}, \\ C_{p,k} |u|^{p-k} &{} \text {for}\quad k~\hbox {odd}. \end{array}\right. } \end{aligned}$$

By Taylor’s formula at the point v(t, x) with integral remainder up to the order $\beta _p = \lceil \frac{p-3}{2} \rceil$, we have

$$\begin{aligned} F(v + \Psi ) - F(v) = \sum _{k=1}^{\beta _p} \frac{1}{k!} F^{(k)}(v) \Psi ^k + \int _v^{v+\Psi } \frac{F^{(\beta _p + 1)}(\tau )}{\beta _p!} (v+\Psi -\tau )^{\beta _p} d\tau . \end{aligned}$$

Let $0 < t_1 \le t_2 \le T$. By integrating (4.10) from $t_1$ to $t_2$, we can write

$$\begin{aligned} E(t_2) \le E(t_1) + \sum _{k=1}^{\beta _p} C_k I_k + C_p R, \end{aligned}$$

(4.11)

where

$$\begin{aligned} I_k:= & {} -\int _{t_1}^{t_2} \int _{\mathbb {T}^2} \partial _tv F^{(k)}(v) \Psi ^k dx dt' \quad \text {for} \quad 1 \le k \le \beta _p,\\ R:= & {} -\int _{t_1}^{t_2} \int _{\mathbb {T}^2} \int _v^{v+\Psi } \partial _tv F^{(\beta _p+1)}(\tau ) (v+\Psi -\tau )^{\beta _p} d\tau dx dt'. \end{aligned}$$

We first estimate R. Note that for $\tau \in [v, v+\Psi ]$, we have

$$\begin{aligned} |F^{(\beta _p+1)}(\tau )| \lesssim |v|^{p-\beta _p-1} + |\Psi |^{p-\beta _p-1}. \end{aligned}$$

Thus, by Hölder’s inequality and Young’s inequality, we have

$$\begin{aligned} R\lesssim & {} \int _{t_1}^{t_2} \int _{\mathbb {T}^2} \partial _tv (|v|^{p-\beta _p-1} |\Psi |^{\beta _p+1} + |\Psi |^p) dx dt' \nonumber \\\lesssim & {} \int _{t_1}^{t_2} \Vert \partial _tv(t') \Vert _{L_x^2} \Vert v(t') \Vert _{L_x^{p+1}}^{p-\beta _p-1} \Vert \Psi (t') \Vert _{L_x^{r_p(\beta _p+1)}}^{\beta _p+1} dt' \nonumber \\{} & {} + \int _{t_1}^{t_2} \Vert \partial _tv(t') \Vert _{L_x^2}^2 dt' + \Vert \Psi \Vert _{L_T^{2p} L_x^{2p}}^{2p} \nonumber \\{} & {} \le \Vert \Psi \Vert _{L_T^{2p} L_x^{2p}}^{2p} + \bigg ( 1 + \Vert \Psi \Vert _{L_T^\infty L_x^{r_p(\beta _p+1)}}^{\beta _p+1} \bigg ) \nonumber \\{} & {} \times \int _{t_1}^{t_2} \max \bigg \{ E(t'), E(t')^{\frac{1}{2} + \frac{p-\beta _p-1}{p+1}} \bigg \} dt', \end{aligned}$$

(4.12)

where $r_p$ satisfies $\tfrac{1}{2} + \tfrac{p-\beta _p-1}{p+1} + \frac{1}{r_p} = 1$. Since $\beta _p = \lceil \frac{p-3}{2} \rceil \ge \frac{p-3}{2}$, we have $\frac{p-\beta _p-1}{p+1} \le \frac{1}{2}$, so that

$$\begin{aligned} R \lesssim \Vert \Psi \Vert _{L_T^{2p} L_x^{2p}}^{2p} + \bigg ( 1 + \Vert \Psi \Vert _{L_T^\infty L_x^{r_p(\beta _p+1)}}^{\beta _p+1} \bigg ) \int _{t_1}^{t_2} (1+E(t')) dt'. \end{aligned}$$

We now estimate $I_k$. By Fubini’s theorem and integration by parts in time, we have

$$\begin{aligned} |I_k|= & {} \bigg | -\int _{\mathbb {T}^2} \int _{t_1}^{t_2} \partial _t(F^{(k-1)}(v)) \Psi ^k dt' dx \bigg | \nonumber \\\le & {} \bigg | \int _{\mathbb {T}^2} F^{(k-1)}(v(t_2)) \Psi ^k(t_2) dx \bigg | + \bigg | \int _{\mathbb {T}^2} F^{(k-1)}(v(t_1)) \Psi ^k(t_1) dx \bigg | \nonumber \\{} & {} + \bigg | k \int _{\mathbb {T}^2} \int _{t_1}^{t_2} F^{(k-1)}(v(t')) \Psi (t')^{k-1} \partial _t\Psi (t') dt' dx \bigg | \nonumber \\\lesssim & {} \int _{\mathbb {T}^2} |v(t_2)|^{p-k+1} |\Psi (t_2)|^k + |v(t_1)|^{p-k+1} |\Psi (t_1)|^k dx \nonumber \\{} & {} + \bigg | \int _{t_1}^{t_2} \int _{\mathbb {T}^2} F^{(k-1)}(v(t')) \Psi (t')^{k-1} \partial _t\Psi (t') dx dt' \bigg | \nonumber \\= & {} J_k + K_k. \end{aligned}$$

(4.13)

To handle $J_k$, by Hölder’s inequality and Young’s inequality, we obtain

$$\begin{aligned} \begin{aligned} J_k&\le E(t_2)^{\frac{p-k+1}{p+1}} \Vert \Psi (t_2) \Vert _{L_x^{p+1}}^k + E(t_1)^{\frac{p-k+1}{p+1}} \Vert \Psi (t_1) \Vert _{L_x^{p+1}}^k \\&\le \varepsilon E(t_2) + C_1 E(t_1) + C_2 \Vert \Psi \Vert _{L_T^\infty L_x^{p+1}}^{p+1}, \end{aligned} \end{aligned}$$

(4.14)

where $0< \varepsilon < 1$. To deal with $K_k$, by Lemma 4.1,

$$\begin{aligned} K_k \lesssim g\big ( \Vert \Psi \Vert _{L^\infty ([0,T]; X)}, \Vert \langle \nabla \rangle ^{-1} \partial _t\Psi \Vert _{L^\infty ([0,T]; Y)} \big ) \bigg ( 1+\int _{t_1}^{t_2} E(t') dt' \bigg ). \end{aligned}$$

(4.15)

By combining (4.11), (4.12), (4.13), (4.14), (4.15), we obtain

$$\begin{aligned} E(t_2)&\lesssim \bigg ( 1+\Vert \Psi \Vert _{L_T^\infty L_x^{r_p(\beta _p+1)}}^{\beta _p+1} + g\big ( \Vert \Psi \Vert _{L^\infty ([0,T]; X)}, \Vert \langle \nabla \rangle ^{-1} \partial _t\Psi \Vert _{L^\infty ([0,T]; Y)} \big ) \bigg ) \\&\, \times \bigg ( 1+\int _{t_1}^{t_2} E(t') dt' \bigg ) + \Vert \Psi \Vert _{L_T^{2p} L_x^{2p}}^{2p} + \Vert \Psi \Vert _{L_T^\infty L_x^{p+1}}^{p+1} + E(t_1). \end{aligned}$$

We can then use Gronwall’s inequality to get the desired bound.

We now provide the proof of Lemma 4.1.

Proof of Lemma 4.1

Recall that $s_p = \frac{p-3}{p-1}$. We first consider the case when $k \ge 2$. By the Fourier–Plancherel theorem, we have

$$\begin{aligned}{} & {} \bigg | \int _{\mathbb {T}^2} F^{(k-1)}(v(t)) \Psi (t)^{k-1} \partial _t\Psi (t) dx \bigg | \nonumber \\{} & {} \quad = \bigg | \sum _{j'=-1}^1 \sum _{j \ge 0} \int _{\mathbb {T}^2} \textbf{P}_j (F^{(k-1)}(v(t)) \Psi (t)^{k-1}) \textbf{P}_{j+j'} (\partial _t\Psi (t)) dx \bigg |\nonumber \\{} & {} \quad \lesssim \sum _{j > 2} \int _{\mathbb {T}^2} |\textbf{P}_j (F^{(k-1)}(v(t)) \Psi (t)^{k-1})| |\textbf{P}_j (\partial _t\Psi (t))| dx \nonumber \\{} & {} \qquad + \sum _{j = 0}^2 \int _{\mathbb {T}^2} |\textbf{P}_j (F^{(k-1)}(v(t)) \Psi (t)^{k-1})| |\textbf{P}_j (\partial _t\Psi (t))| dx \nonumber \\{} & {} \quad =: I_1 + I_2. \end{aligned}$$

(4.16)

Let $r_k:= \frac{(k-1)(p+1)}{k}$. To estimate $I_2$, by Hölder’s inequality, Bernstein’s inequality, and Young’s inequality, we have

$$\begin{aligned} \begin{aligned} I_2&\lesssim \Vert \Psi (t) \Vert _{L_x^{r_k}}^{k-1} \Vert v(t) \Vert _{L_x^{p+1}}^{p-k+1} \sum _{j=0}^2 \Vert \textbf{P}_j \partial _t\Psi (t) \Vert _{L_x^\infty } \\&\lesssim \Vert \Psi (t) \Vert _{L_x^{r_k}}^{k-1} \Vert \langle \nabla \rangle ^{-1} \partial _t\Psi (t) \Vert _{L_x^\infty } E(t)^{\frac{p-k+1}{p+1}} \\&\lesssim E(t) + \Vert \Psi \Vert _{L_T^\infty L_x^{r_k}}^{r_k} \Vert \langle \nabla \rangle ^{-1} \partial _t\Psi \Vert _{L_T^\infty L_x^\infty }^{\frac{p+1}{k}}. \end{aligned} \end{aligned}$$

It remains to estimate $I_1$. By Hölder’s inequality, Bernstein’s inequality, and then Hölder’s inequality for series,

$$\begin{aligned} I_1&\lesssim \sum _{j > 2} 2^{j(1-s_p)} \Vert \textbf{P}_j (F^{(k-1)}(v(t)) \Psi (t)^{k-1}) \Vert _{L_x^1} 2^{j s_p} \Vert \textbf{P}_j (\langle \nabla \rangle ^{-1}\partial _t\Psi (t)) \Vert _{L_x^\infty } \\&\le \Vert F^{(k-1)}(v(t)) \Psi (t)^{k-1} \Vert _{B_{1,\infty }^{1-s_p}} \Vert \langle \nabla \rangle ^{-1}\partial _t\Psi \Vert _{B_{\infty ,1}^{s_p}}. \end{aligned}$$

Then, by Corollary 2.2, we have

$$\begin{aligned} \Vert F^{(k-1)}(v(t)) \Psi (t)^{k-1} \Vert _{B_{1,\infty }^{1-s_p}}\lesssim & {} \Vert F^{(k-1)} (v(t)) \Vert _{B_{\frac{p+1}{p+2-k}, \infty }^{1-s_p}} \Vert \Psi (t)^{k-1} \Vert _{L^{\frac{p+1}{k-1}}} \nonumber \\{} & {} + \Vert |v(t)|^{p-k+1} \Vert _{L^{\frac{p+1}{p-k+1}}} \Vert \Psi (t)^{k-1} \Vert _{B_{p_k,\infty }^{1-s_p}} \nonumber \\\lesssim & {} \Vert F^{(k-1)} (v(t)) \Vert _{B_{\frac{p+1}{p+2-k}, \infty }^{1-s_p}} \Vert \Psi (t) \Vert _{L^{p+1}}^{k-1} \nonumber \\{} & {} + E(t)^{\frac{p-k+1}{p+1}} \Vert \Psi (t)^{k-1} \Vert _{B_{p_k,\infty }^{1-s_p}}, \end{aligned}$$

(4.17)

where $p_k$ satisfies $\frac{1}{p_k} + \frac{p-k+1}{p+1} = 1$. By Lemma 2.3 (ii), we have

$$\begin{aligned} \begin{aligned} \Vert \Psi (t)^{k-1} \Vert _{B_{p_k,\infty }^{1-s_p}}&\lesssim \Vert \Psi (t) \Vert _{B_{p_k,\infty }^{1-s_p}} \Vert \Psi (t) \Vert _{L^\infty }^{k-2} \\&\le \Vert \Psi (t) \Vert _{B_{\frac{p+1}{2},\infty }^{1-s_p}} \Vert \Psi (t) \Vert _{L^\infty }^{k-2}. \end{aligned} \end{aligned}$$

(4.18)

By Lemma 2.3 (ii), Lemma 2.1 (ii), and Lemma 2.4, we have

$$\begin{aligned} \Vert F^{(k-1)} (v(t)) \Vert _{B_{\frac{p+1}{p+2-k}, \infty }^{1-s_p}}&\lesssim \Vert v(t) \Vert _{B_{\frac{p+1}{2}, \infty }^{1-s_p}} \big \Vert |v(t)|^{p-k} \big \Vert _{L^{\frac{p+1}{p-k}}} \\&\lesssim \Vert v(t) \Vert _{W^{1-s_p, \frac{p+1}{2}}} E(t)^{\frac{p-k}{p+1}} \\&\lesssim \Vert \langle \nabla \rangle v(t) \Vert _{L^2}^{1-\beta } \Vert v(t) \Vert _{L^{p+1}}^\beta E(t)^{\frac{p-k}{p+1}}, \end{aligned}$$

where $\beta \in [0,s_p]$ satisfies $\frac{2}{p+1} = \frac{1-s_p}{2} + \frac{\beta }{p+1}$, and so $\beta = \frac{p-3}{p-1} = s_p$. Thus, we obtain

$$\begin{aligned} \Vert F^{(k-1)} (v(t)) \Vert _{B_{\frac{p+1}{p+2-k}, \infty }^{1-s_p}}\lesssim & {} E(t)^{\frac{1-\beta }{2} + \frac{\beta }{p+1} + \frac{p-k}{p+1}} = E(t)^{\frac{2}{p+1} + \frac{p-k}{p+1}} \nonumber \\\lesssim & {} 1 + E(t). \end{aligned}$$

(4.19)

By combining (4.17), (4.18), and (4.19), we obtain the desired bound for $I_1$.

For the case when $k=1$, after (4.16), we have the estimate $I_2 \lesssim E(t) + \Vert \langle \nabla \rangle ^{-1} \partial _t\Psi \Vert _{L_T^\infty L_x^\infty }^{p+1}$. For the term $I_1$, by the estimate in (4.19), we have

$$\begin{aligned} I_1 \lesssim \Vert F(v(t)) \Vert _{B_{1,\infty }^{1-s_p}} \Vert \langle \nabla \rangle ^{-1} \partial _t\Psi \Vert _{B_{\infty ,1}^{s_p}} \lesssim \Vert \langle \nabla \rangle ^{-1} \partial _t\Psi \Vert _{B_{\infty ,1}^{s_p}} (1+E(t)), \end{aligned}$$

as desired. $\square$

Appendix A: On local well-posedness of subcritical vNLW

In this appendix, we aim to show that the deterministic viscous NLW is locally well-posed in $\mathcal {H}^s(\mathbb {T}^2)$ with $s \ge s_{\text {crit}}$, where we recall that $s_{\text {crit}}$ is defined by

$$\begin{aligned} s_{\text {crit}}:= \max \bigg ( 1-\frac{2}{p-1}, 0 \bigg ). \end{aligned}$$

(A.1)

More precisely, we prove local well-posedness of the following subcritical vNLW:

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t^2 u + (1-\Delta ) u + D \partial _tu \pm |u|^{p-1}u = 0 \\ (u, \partial _tu)|_{t=0} = (u_0, u_1), \end{array}\right. } \end{aligned}$$

(A.2)

where $(u_0, u_1) \in \mathcal {H}^s(\mathbb {T}^2)$ and $s \ge s_{\text {crit}}$ (with a strict inequality when $p = 3$). To achieve this, we will need the inhomogeneous Strichartz estimates for the linear viscous wave equation on $\mathbb {T}^2$.

1.1 A.1 The inhomogeneous Strichartz estimates

In this subsection, we prove the Strichartz estimates for the inhomogeneous linear viscous wave equation on $\mathbb {T}^d$. To achieve this, we first establish the following estimate for the linear operator S(t) defined in (1.7).

Lemma A.1

Let $1 \le p \le 2 \le q \le \infty$. Then, we have

$$\begin{aligned} \Vert S(t) \phi \Vert _{L^q(\mathbb {T}^d)} \lesssim t^{1-d(\frac{1}{p} - \frac{1}{q})} \Vert \phi \Vert _{L^p(\mathbb {T}^d)} \end{aligned}$$

for any $0 < t \le 1$

Proof

By (1.7) and applying the Schauder estimate (Lemma 2.7) twice, we obtain

$$\begin{aligned} \Vert S(t) \phi \Vert _{L^q(\mathbb {T}^d)}&= \bigg \Vert e^{-\frac{D}{4}t} \frac{\sin (t[[ D ]])}{[[ D ]]} e^{-\frac{D}{4}t} \phi \bigg \Vert _{L^q(\mathbb {T}^d)} \\&\lesssim t^{-d(\frac{1}{2} - \frac{1}{q})} \bigg \Vert \frac{\sin (t[[ D ]])}{[[ D ]]} e^{-\frac{D}{4}t} \phi \bigg \Vert _{L^2(\mathbb {T}^d)} \\&\le t^{1-d(\frac{1}{2} - \frac{1}{q})} \big \Vert e^{-\frac{D}{4}t} \phi \big \Vert _{L^2(\mathbb {T}^d)} \\&\lesssim t^{1-d(\frac{1}{p} - \frac{1}{q})} \Vert \phi \Vert _{L^p(\mathbb {T}^d)}, \end{aligned}$$

as desired. $\square$

We now establish the Strichartz estimates for the inhomogeneous linear viscous wave equation on $\mathbb {T}^d$. We say that u is a solution to the following inhomogeneous linear viscous wave equation:

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t^2 u + (1 - \Delta ) u + D \partial _tu = f \\ (u, \partial _tu) |_{t=0} = (\phi _0, \phi _1), \end{array}\right. } \end{aligned}$$

(A.3)

if u satisfies the following Duhamel formulation:

$$\begin{aligned} u(t) = V(t)(\phi _0, \phi _1) + \int _0^t S(t-t') f(t') dt', \end{aligned}$$

where V(t) and S(t) are as defined in (1.6) and (1.7), respectively.

Lemma A.2

Given $s \ge 0$, suppose that $1< \widetilde{q} \le 2< q < \infty$, $1 \le \widetilde{r} \le 2 \le r \le \infty$ satisfy the following scaling condition:

$$\begin{aligned} \frac{1}{q} + \frac{d}{r} = \frac{d}{2}-s = \frac{1}{\widetilde{q}} + \frac{d}{\widetilde{r}} - 2. \end{aligned}$$

(A.4)

Then, a solution u to the inhomogeneous linear viscous wave Eq. (A.3) satisfies the following inequality:

$$\begin{aligned} \Vert (u, \partial _tu) \Vert _{C_T \mathcal {H}^s_x (\mathbb {T}^d)} + \Vert u \Vert _{L_T^q L_x^r (\mathbb {T}^d)} \lesssim \Vert (\phi _0, \phi _1) \Vert _{\mathcal {H}^s (\mathbb {T}^d)} + \Vert f \Vert _{L_T^{\widetilde{q}} L_x^{\widetilde{r}} (\mathbb {T}^d)}, \end{aligned}$$

(A.5)

for all $0 < T \le 1$.

Proof

By (1.6), we have

$$\begin{aligned} \big \Vert \big (V(t)(\phi _0,\phi _1), \partial _tV(t)(\phi _0,\phi _1)\big ) \big \Vert _{C_T \mathcal {H}^s_x (\mathbb {T}^d)} \lesssim \Vert (\phi _0, \phi _1) \Vert _{\mathcal {H}^s (\mathbb {T}^d)}. \end{aligned}$$

(A.6)

By Lemma 2.8, we have

$$\begin{aligned} \Vert V(t)(\phi _0, \phi _1) \Vert _{L_T^q L_x^r (\mathbb {T}^d)} \lesssim \Vert (\phi _0, \phi _1) \Vert _{\mathcal {H}^s (\mathbb {T}^d)}. \end{aligned}$$

(A.7)

We then use Lemma 3.5 in [21] (which is in the $\mathbb {R}^d$ setting, but the proof also works in the $\mathbb {T}^d$ setting with Lemma A.1 in hand) to obtain

$$\begin{aligned} \bigg \Vert \int _0^t S(t-t') f(t') dt' \bigg \Vert _{L_T^q L_x^r (\mathbb {T}^d)} \lesssim \Vert f \Vert _{L_T^{\widetilde{q}} L_x^{\widetilde{r}} (\mathbb {T}^d)}. \end{aligned}$$

(A.8)

It remains to show

$$\begin{aligned} \bigg \Vert \int _0^t S(t-t') f(t') dt' \bigg \Vert _{C_T H_x^s (\mathbb {T}^d)} \lesssim \Vert f \Vert _{L_T^{\widetilde{q}} L_x^{\widetilde{r}} (\mathbb {T}^d)} \end{aligned}$$

(A.9)

and

$$\begin{aligned} \bigg \Vert \partial _t\int _0^t S(t-t') f(t') dt' \bigg \Vert _{C_T H_x^{s-1} (\mathbb {T}^d)} \lesssim \Vert f \Vert _{L_T^{\widetilde{q}} L_x^{\widetilde{r}} (\mathbb {T}^d)}, \end{aligned}$$

(A.10)

so that (A.5) follows from (A.6), (A.7), (A.8), (A.9), and (A.10).

To show that the inequality (A.9) holds, we use the Littlewood-Paley decomposition as in Lemma 3.6 in [21]. In view of the proof of Lemma 3.6 in [21], we know that it suffices to show (A.9) for all f such that $\widehat{f}$ is supported in $\{ n \in \mathbb {Z}^d: 2^{j-1} \le |n| \le 2^{j+1} \}$ for all $j \in \mathbb {Z}_+$ (the case for $\{ n \in \mathbb {Z}^d: 0 \le |n| \le 2\}$ follows in a similar manner) with the underlying constant independent of j. Fix $0< t < T$. By Minkowski’s integral inequality, Hölder’s inequality in n, Hausdorff-Young inequality, Hölder’s inequality in $t'$ (along with the fact that the number of lattice points inside a ball of radius R in $\mathbb {R}^d$ is $O(R^d)$), and a change of variable, we have

$$\begin{aligned}&\bigg \Vert \int _0^t S(t-t') f(t') dt' \bigg \Vert _{C_T H_x^s} \\&\quad \lesssim \int _0^t \bigg ( \sum _{n \in \mathbb {Z}^2 } |n|^{2s} \bigg | e^{-\frac{|n|}{2} (t-t')} \frac{\sin ((t-t') [[ n ]])}{[[ n ]]} \widehat{f} (t', n) \bigg |^2 \bigg )^{1/2} dt' \\&\quad \lesssim 2^{(j+1)s} \int _0^t (t-t') e^{2^{j-2}(t-t')} \bigg ( \sum _{n \in \mathbb {Z}^2} \big |\widehat{f} (t', n)\big |^2 \bigg )^{1/2} dt' \\&\quad \lesssim 2^{(j+1)s} \int _0^t (t-t') e^{2^{j-2}(t-t')} \big ( 2^{(j+1)d} \big )^{\frac{\widetilde{r}' - 2}{2\widetilde{r} '}} \big \Vert \widehat{f} (t', n) \big \Vert _{\ell _n^{\widetilde{r} '}} dt' \\&\quad \lesssim 2^{(j+1) (s + \frac{d}{\widetilde{r}} - \frac{d}{2})} \bigg ( \int _0^t \Big | (t-t') e^{2^{j-2}(t-t')} \Big |^{\widetilde{q} '} dt' \bigg )^{1/\widetilde{q} '} \Vert f \Vert _{L_T^{\widetilde{q}} L_x^{\widetilde{r}}} \\&\quad \lesssim 2^{(j+1) (s + \frac{d}{\widetilde{r}} - \frac{d}{2} + \frac{1}{\widetilde{q}} - 2)} \Vert f \Vert _{L_T^{\widetilde{q}} L_x^{\widetilde{r}}}. \end{aligned}$$

By using the second equality in the scaling condition (A.4), we obtain the desired inequality with the underlying constant independent of j, and so the inequality (A.9) follows. The inequality (A.10) follows in a similar manner. $\square$

Remark A.3

As in the case of the homogeneous Strichartz estimates (Lemma 2.8), the Strichartz estimates for the inhomogeneous linear viscous wave equation on $\mathbb {T}^d$ also hold for a larger class of pairs (q, r) and $(\widetilde{q}, \widetilde{r})$ compared to the Strichartz estimates for the usual linear wave equations [15, 17, 19, 25]. Again, this is due to the parabolic smoothing effect. Note that this is also true on $\mathbb {R}^d$ (see [21]).

We complete this subsection by making the following observation. Recall that we are considering the viscous NLW on $\mathbb {T}^2$ with nonlinearity $|u|^{p-1}u$ for $p>1$. Suppose that we can find pairs (q, r) and $(\widetilde{q}, \widetilde{r})$ satisfying the scaling condition (A.4) such that

$$\begin{aligned} q > p \widetilde{q} \quad \text {and} \quad r \ge p \widetilde{r}. \end{aligned}$$

Then, by Hölder’s inequality and the fact that $|\mathbb {T}^2| = 1$, we have

$$\begin{aligned} \big \Vert |u|^{p-1}u \big \Vert _{L_T^{\widetilde{q}} L_x^{\widetilde{r}}} \le T^{\frac{1}{\widetilde{q}} - \frac{p}{q}} \Vert u \Vert ^p_{L_T^q L_x^r}. \end{aligned}$$

Note that the power of T is positive when $q > p \widetilde{q}$. The following lemma shows that there exist such pairs (q, r) and $(\widetilde{q}, \widetilde{r})$.

Lemma A.4

Let $s_{\text {crit}}$ be as defined in (A.1). Given $s_{\text {crit}}< s < 1$, there exist $1< \widetilde{q} \le 2< q < \infty$, $1 \le \widetilde{r} \le 2 \le r \le \infty$ satisfying the scaling condition (A.4) such that

$$\begin{aligned} q > p \widetilde{q} \quad \text {and} \quad r \ge p \widetilde{r}. \end{aligned}$$

(A.11)

Proof

In view of Lemma 3.3 in [17], given $0< s < 1$, we have

$$\begin{aligned} \min \bigg ( \frac{q}{\widetilde{q}}, \frac{r}{\widetilde{r}} \bigg ) \le \frac{3-s}{1-s}, \end{aligned}$$

and the equality holds by taking, for example,

$$\begin{aligned} (q, r) = \bigg ( \frac{3-s}{1-s}\delta , \frac{2}{1-s-\frac{1-s}{(3-s)\delta }} \bigg ) \quad \text {and} \quad (\widetilde{q}, \widetilde{r}) = \bigg ( \delta , \frac{2}{3-s-\frac{1}{\delta }} \bigg ), \end{aligned}$$

(A.12)

where $\delta = \delta (s) > 1$ is sufficiently close to 1. Moreover, we note that $\frac{3-s}{1-s} > p$ if and only if $s > 1 - \frac{2}{p-1}$. Thus, as long as $s_{\text {crit}}< s < 1$, there exist pairs (q, r) and $(\widetilde{q}, \widetilde{r})$ that satisfy (A.11). $\square$

Remark A.5

In the case when $p > 3$ and $s = s_{\text {crit}} = 1 - \frac{2}{p-1} > 0$, we have

$$\begin{aligned} \min \bigg ( \frac{q}{\widetilde{q}}, \frac{r}{\widetilde{r}} \bigg ) \le \frac{3-s}{1-s} = p, \end{aligned}$$

so that we can only find pairs (q, r) and $(\widetilde{q}, \widetilde{r})$ that satisfy $q = p \widetilde{q}$ and $r = p \widetilde{r}$ instead of $q > p \widetilde{q}$ and $r \ge p \widetilde{r}$. Such pairs do exist. One can take, for example, (q, r) and $(\widetilde{q}, \widetilde{r})$ as in (A.12).

In the case when $1 < p \le 3$ and $s = s_{\text {crit}} = 0$, there does not exist any pair $(\widetilde{q}, \widetilde{r})$ that satisfies $1 < \widetilde{q} \le 2$, $1 \le \widetilde{r} \le 2$, and the scaling condition (A.4) (with $d = 2$) simultaneously. In this case, the inhomogeneous Strichartz estimates (Lemma A.2) no longer applies, so that an alternative approach is needed to deal with this case.

1.2 A.2: Local well-posedness of subcritical vNLW

In this subsection, we prove the following theorem for the local well-posedness result of vNLW (A.2).

Theorem A.6

Let $p > 1$ and let $s_{\text {crit}}$ be as in (A.1). Then, (A.2) is locally well-posed in $\mathcal {H}^s(\mathbb {T}^2)$ for

(i) $p \ne 3$: $s \ge s_{\text {crit}}$    or    (ii) $p = 3$: $s > s_{\text {crit}}$.

More precisely, given any $(u_0, u_1) \in \mathcal {H}^s(\mathbb {T}^2)$, there exists $0 < T = T(u_0, u_1) \le 1$ and a unique solution $\vec u = (u, \partial _tu)$ to (A.2) in the class

$$\begin{aligned} (u, \partial _tu) \in C([0,T]; \mathcal {H}^s (\mathbb {T}^2)) \quad \text {and} \quad u \in L^q([0,T]; L^r(\mathbb {T}^2)), \end{aligned}$$

for some suitable $q,r \ge 2$.

Proof

For the proof, we only consider the case $s < 1$. We first consider the case $s > s_{\text {crit}}$. We write (A.2) in the Duhamel formulation:

$$\begin{aligned} u(t) = \Gamma (u):= V(t)(u_0,u_1) - \int _0^t S(t-t') F(u)(t') dt', \end{aligned}$$

(A.13)

where $F(u) = |u|^{p-1}u$, V(t) is as defined in (1.6), and S(t) is as defined in (1.7). Let $\vec \Gamma (u) = (\Gamma (u), \partial _t\Gamma (u))$ and $\vec u = (u, \partial _tu)$.

Let (q, r) and $(\widetilde{q}, \widetilde{r})$ be as given in Lemma A.4, which guarantees that $q > p\widetilde{q}$ and $r \ge p\widetilde{r}$. Given $0 < T \le 1$, we define the space $\mathcal {Y}(T)$ as

$$\begin{aligned} \mathcal {Y}^s(T) = \mathcal {Y}_1^s(T) \times \mathcal {Y}_2^s(T), \end{aligned}$$

where

$$\begin{aligned}&\mathcal {Y}_1^s(T) := C([0,T]; H^s (\mathbb {T}^2)) \cap L^{q}([0,T]; L^{r}(\mathbb {T}^2)), \\&\mathcal {Y}_2^s(T) := C([0,T]; H^{s-1} (\mathbb {T}^2)). \end{aligned}$$

Our goal is to show that $\vec \Gamma$ is a contraction on a ball in $\mathcal {Y}^s(T)$ for some $0 < T \le 1$.

By (A.13), Lemma A.2, and Hölder’s inequality, we have

$$\begin{aligned} \begin{aligned} \Vert \vec \Gamma (u) \Vert _{\mathcal {Y}^s(T)}&\lesssim \Vert (u_0, u_1) \Vert _{\mathcal {H}^s} + \big \Vert |u|^p \big \Vert _{L_T^{\widetilde{q}} L_x^{\widetilde{r}}} \\&\lesssim \Vert (u_0, u_1) \Vert _{\mathcal {H}^s} + T^\theta \Vert u \Vert _{L_T^q L_x^r}^p \\&\lesssim \Vert (u_0, u_1) \Vert _{\mathcal {H}^s} + T^\theta \Vert \vec u \Vert _{\mathcal {Y}^s(T)}^p \end{aligned} \end{aligned}$$

(A.14)

for some $\theta > 0$.

For the difference estimate, we use the idea from Oh–Okamoto–Pocovnicu [32]. Noticing that $F'(u) = p|u|^{p-1}$, we use (A.13), Lemma A.2, the fundamental theorem of calculus, Minkowski’s integral inequality, and Hölder’s inequality to obtain

$$\begin{aligned} \Vert \vec \Gamma (u) - \vec \Gamma (v) \Vert _{\mathcal {Y}^s(T)}&\lesssim \Vert F(u) - F(v) \Vert _{L_T^{\widetilde{q}} L_x^{\widetilde{r}}} \\&= \bigg \Vert \int _0^1 F'(v+\tau (u-v)) (u-v) d\tau \bigg \Vert _{L_T^{\widetilde{q}} L_x^{\widetilde{r}}} \\&\lesssim \int _0^1 \Vert v + \tau (u-v) \Vert _{L_T^{p\widetilde{q}} L_x^{p\widetilde{r}}}^{p-1} \Vert u-v \Vert _{L_T^{p\widetilde{q}} L_x^{p\widetilde{r}}} d\tau \\&\lesssim T^\theta \Big ( \Vert u \Vert _{L^q_T L_x^r}^{p-1} + \Vert v \Vert _{L^q_T L_x^r}^{p-1} \Big ) \Vert u-v \Vert _{L^q_T L_x^r} \\&\lesssim T^\theta \Big ( \Vert \vec u \Vert _{\mathcal {Y}^s(T)}^{p-1} + \Vert \vec v \Vert _{\mathcal {Y}^s(T)}^{p-1} \Big ) \Vert \vec u - \vec v \Vert _{\mathcal {Y}^s(T)}. \end{aligned}$$

for some $\theta > 0$.

Thus, by choosing $T = T ( \Vert (u_0,u_1) \Vert _{\mathcal {H}^s} ) > 0$ small enough, we obtain that $\vec \Gamma$ is a contraction on the ball $B_R \subset \mathcal {Y}^s(T)$ of radius $R \sim 1 + \Vert (u_0,u_1) \Vert _{\mathcal {H}^s}$.

In the case when $p > 3$ and $s = s_{\text {crit}} = 1 - \frac{2}{p-1} > 0$, we can only find pairs (q, r) and $(\widetilde{q}, \widetilde{r})$ that satisfy $q = p \widetilde{q}$ and $r = p \widetilde{r}$ (see Remark A.5). In this case, we modify the argument as follows. By (A.13), Lemma A.2, and Hölder’s inequality, we obtain

$$\begin{aligned} \Vert \Gamma (u) \Vert _{L_T^q L_x^r}&\lesssim \Vert V(t) (u_0, u_1) \Vert _{L_T^q L_x^r} + \big \Vert |u|^p \big \Vert _{L_T^{\widetilde{q}} L_x^{\widetilde{r}}} \\&\lesssim \Vert V(t) (u_0, u_1) \Vert _{L_T^q L_x^r} + \Vert u \Vert _{L_T^{q} L_x^{r}}^p \end{aligned}$$

for some $\theta > 0$ and sufficiently small $\varepsilon > 0$. A difference estimate on $\Gamma (u) - \Gamma (v)$ also holds by a similar computation. By the dominated convergence theorem, we have $\Vert u \Vert _{L_T^{q} L_x^{r}}^p \rightarrow 0$ as $T \rightarrow 0$. Thus, we can choose $T = T(u_0, u_1) > 0$ sufficiently small such that $\Vert V(t) (u_0, u_1) \Vert _{L_T^q L_x^r} \le \frac{1}{2} \eta \ll 1$, so that we can show that $\Gamma$ is a contraction on the ball of radius $\eta$ in $L_T^q L_x^r$. Moreover, (A.14) gives

$$\begin{aligned} \Vert \vec u \Vert _{C_T \mathcal {H}_x^s} = \Vert \vec \Gamma (u) \Vert _{C_T \mathcal {H}_x^s} \lesssim \Vert (u_0, u_1) \Vert _{\mathcal {H}^s} + \Vert u \Vert _{L_T^{q} L_x^{r}}^p < \infty , \end{aligned}$$

so that $\vec u = (u, \partial _tu) \in C_T \mathcal {H}_x^s$.

Lastly, we consider the case when $1< p < 3$ and $s = s_{\text {crit}} = 0$. Note that $s = 0$ along with the $L_T^3 L_x^3$ norm satisfies the scaling condition (2.9) in Lemma 2.8. By (A.13), Minkowski’s integral inequality, Lemma 2.8, Sobolev’s inequality, and Hölder’s inequality, we obtain

$$\begin{aligned} \Vert \Gamma (u) \Vert _{L_T^3 L_x^3}&\lesssim \Vert V(t) (u_0, u_1) \Vert _{L_T^3 L_x^3} + \int _0^T \big \Vert \textbf{1}_{[0,t]} (t') S(t-t') \big (|u|^{p-1}u \big ) (t') \big \Vert _{L_T^3 L_x^3} dt' \\&\lesssim \Vert (u_0, u_1) \Vert _{\mathcal {H}^0} + \int _0^T \big \Vert \big ( |u|^{p-1} u \big ) (t') \big \Vert _{H_x^{-1}} dt' \\&\lesssim \Vert (u_0, u_1) \Vert _{\mathcal {H}^0} + \big \Vert |u|^p \big \Vert _{L_T^1 L_x^{1+}} \\&\lesssim \Vert (u_0, u_1) \Vert _{\mathcal {H}^0} + T^\theta \Vert u \Vert _{L_T^3 L_x^3} \end{aligned}$$

for some $\theta > 0$. Also, by (1.6) and (1.7), we easily obtain

$$\begin{aligned} \Vert \vec \Gamma (u) \Vert _{C_T \mathcal {H}^0_x} \lesssim \Vert (u_0, u_1) \Vert _{\mathcal {H}^0} + T^\theta \Vert u \Vert _{L_T^3 L_x^3}. \end{aligned}$$

Similar difference estimates also hold, so that we can conclude using the standard contraction argument. This finishes the proof. $\square$

We finish this appendix by stating several remarks.

Remark A.7

• (i) At this point, we do not know how to prove local well-posedness for the cubic vNLW (with $p = 3$) in $L^2(\mathbb {T}^2)$, i.e. with $s = s_{\text {crit}} = 0$. It would be of interest to investigate if spaces of functions of bounded p-variation (i.e. $U^p$- and $V^p$-spaces) such as those in [3, 32] can be applied to handle the cubic case.

• (ii) A slight modification of the proof of Theorem A.6 yields local well-posedness of SvNLW (1.1) in $\mathcal {H}^s(\mathbb {T}^2)$ for all $s \ge s_{\text {crit}}$ (with a strict inequality when $p = 3$), which improves the local well-posedness result for SvNLW (1.1) in Theorem 1.1.

• (iii) One can compare the local well-posedness result for vNLW (A.2) in Theorem A.6 with the local well-posedness result for the usual NLW (see Remark 1.4 in [17]):

  $$\begin{aligned} \partial _t^2 u - \Delta u \pm |u|^{p-1}u = 0. \end{aligned}$$

  Note that vNLW enjoys a better local well-posedness result than does the usual NLW, thanks to the parabolic smoothing effect.

• (iv) Note that the global well-posedness result of SvNLW (1.1) in Theorem 1.3 easily gives global well-posedness of vNLW (A.2) in the class $\mathcal {H}^s(\mathbb {T}^2)$ for $s \ge \max (0, 1 - \frac{1}{p+\delta } - \frac{1}{p})$, where $\delta > 0$ is arbitrary. However, at this point, we do not know how to prove global well-posedness of vNLW (A.2) in $\mathcal {H}^s(\mathbb {T}^2)$ for $s_{\text {crit}} \le s < \max (0, 1 - \frac{1}{p+\delta } - \frac{1}{p})$. The main difficulty for this range of s is showing $\vec v(t) \in \mathcal {H}^1(\mathbb {T}^2)$ for all small enough $t > 0$, which is needed to guarantee the finiteness of the energy $E(\vec v)$ defined in (1.11).