Abstract
We study the stochastic cubic nonlinear wave equation (SNLW) with an additive noise on the three-dimensional torus \({\mathbb {T}}^3\). In particular, we prove local well-posedness of the (renormalized) SNLW when the noise is almost a space-time white noise. In recent years, the paracontrolled calculus has played a crucial role in the well-posedness study of singular SNLW on \({\mathbb {T}}^3\) by Gubinelli et al. (Paracontrolled approach to the three-dimensional stochastic nonlinear wave equation with quadratic nonlinearity, 2018, arXiv:1811.07808 [math.AP]), Oh et al. (Focusing \(\Phi ^4_3\)-model with a Hartree-type nonlinearity, 2020. arXiv:2009.03251 [math.PR]), and Bringmann (Invariant Gibbs measures for the three-dimensional wave equation with a Hartree nonlinearity II: Dynamics, 2020, arXiv:2009.04616 [math.AP]). Our approach, however, does not rely on the paracontrolled calculus. We instead proceed with the second order expansion and study the resulting equation for the residual term, using multilinear dispersive smoothing.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Singular stochastic nonlinear wave equation
In this paper, we study the following Cauchy problem for the stochastic nonlinear wave equation (SNLW) with a cubic nonlinearity on the three dimensional torus \({\mathbb {T}}^3=({\mathbb {R}}/(2\pi {\mathbb {Z}}))^3\), driven by an additive noise:
where \(\xi (x, t)\) denotes a (Gaussian) space-time white noise on \({\mathbb {T}}^3\times {\mathbb {R}}\) with the space-time covariance given by
and \(\phi \) is a bounded operator on \(L^2({\mathbb {T}}^3)\). Our main goal is to present a concise proof of local well-posedness of (1.1), when \(\phi \) is the Bessel potential of order \(\alpha \):
for any \(\alpha > 0\). Namely, we consider (1.1) with an “almost” space-time white noise.
Given \(\alpha \in {\mathbb {R}}\), let \(\phi = \phi _\alpha \) be as in (1.2). Then, a standard computation shows that the stochastic convolution:

belongs almost surely to \(C({\mathbb {R}}; W^{s, \infty }({\mathbb {T}}^3))\) for any \(s < \alpha - \frac{1}{2}\). See Lemma 3.1 below. Here, we adopted Hairer’s convention to denote stochastic terms by trees; the vertex  in
in  corresponds to the random noise \(\phi \xi = \langle \nabla \rangle ^{-\alpha } \xi \), while the edge denotes the Duhamel integral operator:
corresponds to the random noise \(\phi \xi = \langle \nabla \rangle ^{-\alpha } \xi \), while the edge denotes the Duhamel integral operator:
corresponding to the forward fundamental solution to the linear wave equation. Note that when \(\alpha > \frac{1}{2}\), the stochastic convolution  is a function of positive (spatial) regularity \(\alpha - \frac{1}{2}-\varepsilon \).Footnote 1 Then, by proceeding with the first order expansion:
is a function of positive (spatial) regularity \(\alpha - \frac{1}{2}-\varepsilon \).Footnote 1 Then, by proceeding with the first order expansion:

and studying the equation for the residual term  , we can show that (1.1) is locally well-posed, when \(\alpha > \frac{1}{2}\). See [13, 58] in the case of the deterministic cubic nonlinear wave equation (NLW):
, we can show that (1.1) is locally well-posed, when \(\alpha > \frac{1}{2}\). See [13, 58] in the case of the deterministic cubic nonlinear wave equation (NLW):
with random initial data. Furthermore, by controlling the growth of the \({\mathcal {H}}^1\)-norm of the residual term v via a Gronwall-type argument, we can prove global well-posedness of (1.1), when \(\alpha > \frac{1}{2}\).Footnote 2 See [13].
When \(\alpha \le \frac{1}{2}\), solutions to (1.1) are expected to be merely distributions of negative regularity \(\alpha -\frac{1}{2} -\varepsilon \), inheriting the regularity of the stochastic convolution, and thus we need to consider the renormalized version of (1.1), which formally reads
where the formal expression \(u^3- \infty \cdot u \) denotes the renormalization of the cubic power \(u^3\). In the range \(\frac{1}{4} < \alpha \le \frac{1}{2}\), a straightforward computation with the second order expansion:

yields local well-posedness of the renormalized SNLW (1.6) (in the sense of Theorem 1.1 below). Here, the second order process  is defined by
is defined by

where  denotes the renormalized version of
denotes the renormalized version of  . See [51] for this argument in the context of the deterministic renormalized cubic NLW (1.5) with random initial data.
. See [51] for this argument in the context of the deterministic renormalized cubic NLW (1.5) with random initial data.
We state our main result.
Theorem 1.1
Let \(0 < \alpha \le \frac{1}{2}\). Given \( s > \frac{1}{2}\), let \((u_0, u_1) \in {\mathcal {H}}^{s}({\mathbb {T}}^3) = H^s({\mathbb {T}}^3)\times H^{s-1}({\mathbb {T}}^3)\). Then, there exists a unique local-in-time solution to the renormalized cubic SNLW (1.6) with \((u, \partial _tu)|_{t = 0} = (u_0, u_1)\).
More precisely, given \(N \in {\mathbb {N}}\), let \( \xi _N = \pi _N \xi \), where \(\pi _N\) is the frequency projector onto the spatial frequencies \(\{|n|\le N\}\) defined in (1.13) below. Then, there exists a sequence of time-dependent constants \(\{\sigma _N(t)\}_{N\in {\mathbb {N}}}\) tending to \(\infty \) (see (1.16) below) such that, given small \(\varepsilon = \varepsilon (s) > 0\), the solution \(u_N\) to the following truncated renormalized SNLW:
converges to a non-trivialFootnote 3 stochastic process \(u \in C([-T, T]; H^{\alpha -\frac{1}{2} -\varepsilon } ({\mathbb {T}}^3))\) almost surely, where \(T = T(\omega )\) is an almost surely positive stopping time.
Stochastic nonlinear wave equations have been studied extensively in various settings; see [15, Chapter 13] for the references therein. In particular, over the last few years, we have witnessed a rapid progress in the theoretical understanding of nonlinear wave equations with singular stochastic forcing and/or rough random initial data; see [12, 19, 20, 25,26,27, 45, 47,48,49,50,51, 53,54,57, 66]. In [26], Gubinelli, Koch, and the first author studied the quadratic SNLW on \({\mathbb {T}}^3\):
By adapting the paracontrolled calculus [24], originally introduced by Gubinelli, Imkeller, and Perkowski in the study of stochastic parabolic PDEs, to the dispersive setting, the authors of [26] reduced (1.8) into a system of two unknowns. This system was then shown to be locally well-posed by exploiting the following two ingredients: (i) multilinear dispersive smoothing coming from a multilinear interaction of random waves (see also [12, 45]) and (ii) novel random operators (the so-called paracontrolled operators) which incorporate the paracontrolled structure in their definition. These random operators are used to replace commutators which are standard in the parabolic paracontrolled approach [14, 40].
More recently, Okamoto, Tolomeo, and the first author [48] and Bringmann [12] independently studied the following SNLW with a cubic Hartree-type nonlinearity:Footnote 4
where V is the kernel of the Bessel potential \(\langle \nabla \rangle ^{-\beta }\) of order \(\beta > 0\).Footnote 5 In [48], the authors proved local well-posedness for \(\beta > 1\) by viewing the nonlinearity as the nested bilinear interactions and utilizing the paracontrolled operators introduced in [26]. In [12], Bringmann went much further and proved local well-posedness of (1.9) for any \(\beta > 0\). The main strategy in [12] is to extend the paracontrolled approach in [26] to the cubic setting. The main task is then to study regularity properties of various random operators and random distributions. This was done by an intricate combination of deterministic analysis, stochastic analysis, counting arguments, the random matrix/tensor approach by Bourgain [9, 10] and Deng, Nahmod, and Yue [18], and the physical space approach via the (bilinear) Strichartz estimates due to Klainerman and Tataru [36], analogous to the random data Cauchy theory for the nonlinear Schrödinger equations on \({\mathbb {R}}^d\) as in [2,3,4].
From the scaling point of view, the cubic SNLW (1.6) with a slightly smoothed space-time white noise (i.e. small \(\alpha >0\)) is essentially the same as the Hartree SNLW (1.9) with small \(\beta > 0\). Hence, Theorem 1.1 is expected to hold in view of Bringmann’s recent result [12]. The main point of this paper is that we present a concise proof of Theorem 1.1without using the paracontrolled calculus. In the next subsection, we outline our strategy.
Due to the time reversibility of the equation, we only consider positive times in the remaining part of the paper.
Remark 1.2
The equations (1.1) and (1.6) indeed correspond to the stochastic nonlinear Klein–Gordon equations. The same results with inessential modifications also hold for the stochastic nonlinear wave equation, where we replace the linear part in (1.1) and (1.6) by \(\partial _t^2 u- \Delta u\). In the following, we simply refer to (1.1) and (1.6) as the stochastic nonlinear wave equations.
Remark 1.3
Our argument also applies to the deterministic (renormalized) cubic NLW on \({\mathbb {T}}^3\) with random initial data of the form:
where the series \(\{ g_n \}_{n \in {\mathbb {Z}}^3}\) and \(\{ h_n \}_{n \in {\mathbb {Z}}^3}\) are two families of independent standard complex-valued Gaussian random variables conditioned that \(g_n=\overline{g_{-n}}\), \(h_n=\overline{h_{-n}}\), \(n \in {\mathbb {Z}}^3\). In particular, Theorem 1.1 provides an improvement of the main result (almost sure local well-posedness) in [51] from \(\alpha > \frac{1}{4}\) to \(\alpha > 0\).
Remark 1.4
-
(i)
The first part of the statement in Theorem 1.1 is merely a formal statement in view of the divergent behavior \(\sigma _N (t) \rightarrow \infty \) for \(t\ne 0\). In the next subsection, we provide a precise meaning to what it means to be a solution to (1.6) and also make the uniqueness statement more precise. See Remark 1.9.
-
(ii)
In the case of the defocusing cubic SNLW with damping:
$$\begin{aligned} \partial _t^2 u + \partial _tu + (1 - \Delta ) u + u^3 = \langle \nabla \rangle ^{-\alpha } \xi , \end{aligned}$$a combination of our argument with that in [47] yield the following triviality result. Consider the following truncated (unrenormalized) SNLW with damping:
$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t^2 u_N + \partial _tu_N + (1- \Delta ) u_N + u_N^3 = \langle \nabla \rangle ^{-\alpha } \xi _N\\ (u_N, \partial _tu_N)|_{t = 0} = (u_0, u_1), \end{array}\right. } \end{aligned}$$where \(\xi _N = \pi _N \xi \). As we remove the regularization (i.e. take \(N\rightarrow \infty \)), the solution \(u_N\) converges in probability to the trivial function \(u_\infty \equiv 0\) for any (smooth) initial data \((u_0, u_1)\). See [47] for details.
Remark 1.5
-
(i)
In our proof, we use the Fourier restriction norm method (i.e. the \(X^{s, b}\)-spaces defined in (2.8)), following [12, 57]. While it may be possible to give a proof of Theorem 1.1 based only on the physical-side spaces (such as the Strichartz spaces) as in [25,26,27], we do not pursue this direction since our main goal is to present a concise proof of Theorem 1.1 by adapting various estimates in [12] to our current setting. Note that the use of the physical-side spaces would allow us to take the initial data \((u_0, u_1)\) in the critical space \({\mathcal {H}}^\frac{1}{2}({\mathbb {T}}^3)\) (for the cubic NLW on \({\mathbb {T}}^3\)). See for example [25]. One may equally use the Fourier restriction norm method adapted to the space of functions of bounded p-variation and its pre-dual, introduced and developed by Tataru, Koch, and their collaborators [28, 31, 37], which would also allow us to take the initial data \((u_0, u_1)\) in the critical space \({\mathcal {H}}^\frac{1}{2}({\mathbb {T}}^3)\). See for example [3, 46] in the context of the nonlinear Schrödinger equations with random initial data. Since our main focus is to handle rough noises (and not about rough deterministic initial data), we do not pursue this direction.
-
(ii)
On \({\mathbb {T}}^3\), the Bessel potential \(\phi _\alpha = \langle \nabla \rangle ^{-\alpha }\) is Hilbert–Schmidt from \(L^2({\mathbb {T}}^3)\) to \(H^s({\mathbb {T}}^3)\) for \(s < \alpha - \frac{3}{2}\). It would be of interest to extend Theorem 1.1 to a general Hilbert–Schmidt operator \(\phi \), say from \(L^2({\mathbb {T}}^3)\) to \(H^{\alpha - \frac{3}{2}}({\mathbb {T}}^3)\) as in [16, 44, 52].Footnote 6 Note that our argument uses the independence of the Fourier coefficients of the stochastic convolution
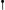 but that such independence will be lost for a general Hilbert–Schmidt operator \(\phi \).
but that such independence will be lost for a general Hilbert–Schmidt operator \(\phi \).
Remark 1.6
-
(i)
When \(\alpha = 0\), SNLW (1.6) with damping
$$\begin{aligned} \partial _t^2 u + \partial _tu + (1 - \Delta ) u + u^3 - \infty \cdot u = \xi \end{aligned}$$(1.10)corresponds to the so-called canonical stochastic quantization equationFootnote 7 for the Gibbs measure given by the \(\Phi ^4_3\)-measure on u and the white noise measure on \(\partial _tu\). See [60]. In this case (i.e. when \(\alpha = 0\)), our approach and the more sophisticated approach of Bringmann [12] for (1.9) with \(\beta > 0\) completely break down. This is a very challenging problem, for which one would certainly need to use the paracontrolled approach in [12, 26, 48] and combine with the techniques in [18].
-
(ii)
As mentioned above, when \(\alpha > \frac{1}{2}\), the globalization argument by Burq and Tzvetkov [13] yields global well-posedness of SNLW (1.1) with \(\phi \) as in (1.2). When \(\alpha = 0\), we expect that (a suitable adaptation of) Bourgain’s invariant measure argument would yield almost sure global well-posedness once we could prove local well-posedness of (1.10) (but this is a very challenging problem). It would be of interest to investigate the issue of global well-posedness of (1.6) for \(0 < \alpha \le \frac{1}{2}\). See [27, 66] for the global well-posedness results on SNLW with an additive space-time white noise in the two-dimensional case.
1.2 Outline of the proof
Let us now describe the strategy to prove Theorem 1.1. Let W denote a cylindrical Wiener process on \(L^2({\mathbb {T}}^3)\):Footnote 8
where \(e_n(x) = e^{ i n \cdot x}\) and \(\{ B_n \}_{n \in {\mathbb {Z}}^3}\) is defined by \(B_n(t) = \langle \xi , {\mathbf {1}}_{[0, t]} \cdot e_n \rangle _{ x, t}\). Here, \(\langle \cdot , \cdot \rangle _{x, t}\) denotes the duality pairing on \({\mathbb {T}}^3\times {\mathbb {R}}\). As a result, we see that \(\{ B_n \}_{n \in {\mathbb {Z}}^3}\) is a family of mutually independent complex-valued Brownian motions conditioned so that \(B_{-n} = \overline{B_n}\), \(n \in {\mathbb {Z}}^3\). In particular, \(B_0\) is a standard real-valued Brownian motion. Note that we have, for any \(n \in {\mathbb {Z}}^2\),
With this notation, we can formally write the stochastic convolution  in (1.3) as
in (1.3) as

where \(\langle \nabla \rangle = \sqrt{1-\Delta }\) and \(\langle n \rangle = \sqrt{1 + |n|^2}\). We indeed construct the stochastic convolution  in (1.11) as the limit of the truncated stochastic convolution
in (1.11) as the limit of the truncated stochastic convolution  defined by
defined by

for \(N \in {\mathbb {N}}\), where \(\pi _N\) denotes the (spatial) frequency projector defined by
A standard computation shows that the sequence  is almost surely Cauchy inFootnote 9\(C([0,T];W^{\alpha - \frac{1}{2} - ,\infty }({\mathbb {T}}^3))\) and thus converges almost surely to some limit, which we denote by
is almost surely Cauchy inFootnote 9\(C([0,T];W^{\alpha - \frac{1}{2} - ,\infty }({\mathbb {T}}^3))\) and thus converges almost surely to some limit, which we denote by  , in the same space. See Lemma 3.1 below.
, in the same space. See Lemma 3.1 below.
We then define the Wick powers  and
and  by
by

and the second order process  by
by

where \({\mathcal {I}}\) denotes the Duhamel integral operator in (1.4). Here, \(\sigma _N(t)\) is defined byFootnote 10

We point out that a standard argument shows that  and
and  converge almost surely to
converge almost surely to  in \(C([0,T];W^{2\alpha -1 - ,\infty }({\mathbb {T}}^3))\) and to
in \(C([0,T];W^{2\alpha -1 - ,\infty }({\mathbb {T}}^3))\) and to  in \(C([0,T];W^{3\alpha -\frac{3}{2} - ,\infty }({\mathbb {T}}^3))\), respectively, but that we do not need these regularity properties of the Wick powers
in \(C([0,T];W^{3\alpha -\frac{3}{2} - ,\infty }({\mathbb {T}}^3))\), respectively, but that we do not need these regularity properties of the Wick powers  and
and  in this paper.
in this paper.
As for the second order process  in (1.15), if we proceed with a “parabolic thinking”,Footnote 11 then we expect that
in (1.15), if we proceed with a “parabolic thinking”,Footnote 11 then we expect that  has regularityFootnote 12\(3\alpha - \frac{1}{2} - = (3\alpha - \frac{3}{2} -) + 1\), which is negative for \(\alpha \le \frac{1}{6}\). In the dispersive setting, however, we can exhibit multilinear smoothing by exploiting multilinear dispersion coming from an interaction of (random) waves. In fact, by adapting the argument in [12] to our current problem, we can show an extra \(\sim \frac{1}{2}\)-smoothing for
has regularityFootnote 12\(3\alpha - \frac{1}{2} - = (3\alpha - \frac{3}{2} -) + 1\), which is negative for \(\alpha \le \frac{1}{6}\). In the dispersive setting, however, we can exhibit multilinear smoothing by exploiting multilinear dispersion coming from an interaction of (random) waves. In fact, by adapting the argument in [12] to our current problem, we can show an extra \(\sim \frac{1}{2}\)-smoothing for  , uniformly in \(N \in {\mathbb {N}}\), and for the limit
, uniformly in \(N \in {\mathbb {N}}\), and for the limit  and thus they have positive regularity. See Lemma 3.1. As in [12, 26], such multilinear smoothing plays a fundamental role in our analysis.
and thus they have positive regularity. See Lemma 3.1. As in [12, 26], such multilinear smoothing plays a fundamental role in our analysis.
Let us now start with the truncated renormalized SNLW (1.7) and obtain the limiting formulation of our problem. By proceeding with the second order expansion:

we rewrite (1.7) as

where we used (1.14). The main problem in studying singular stochastic PDEs lies in making sense of various products. In this formal discussion, let us apply the following “rules”:
-
A product of functions of regularities \(s_1\) and \(s_2\) is defined if \(s_1 + s_2 > 0\). When \(s_1 > 0\) and \(s_1 \ge s_2\), the resulting product has regularity \(s_2\).
-
A product of stochastic objects (not depending on the unknown) is always well defined, possibly with a renormalization. The product of stochastic objects of regularities \(s_1\) and \(s_2\) has regularity \(\min ( s_1, s_2, s_1 + s_2)\).
We postulate that the unknown v has regularity \(\frac{1}{2}+\),Footnote 13 which is subcritical with respect to the standard scaling heuristics for the three-dimensional cubic NLW. In order to close the Picard iteration argument, we need all the terms on the right-hand side of (1.18) to have regularity \(-\frac{1}{2}+\). With the aforementioned regularities of the stochastic terms  ,
,  , and
, and  and applying the rules above, we can handle the products on the right-hand side of (1.18), giving regularity \(-\frac{1}{2}+\), except for the following terms (for small \(\alpha >0\)):
and applying the rules above, we can handle the products on the right-hand side of (1.18), giving regularity \(-\frac{1}{2}+\), except for the following terms (for small \(\alpha >0\)):

As for the first term  , we first use stochastic analysis to make sense of
, we first use stochastic analysis to make sense of  with regularity \(\alpha -\frac{1}{2} -\), uniformly in \(N \in {\mathbb {N}}\), (see Lemma 3.3) and then interpret the product as
with regularity \(\alpha -\frac{1}{2} -\), uniformly in \(N \in {\mathbb {N}}\), (see Lemma 3.3) and then interpret the product as

Note that the right-hand side is well defined since the sum of the regularities is positive: \((\alpha -\frac{1}{2} -) + (\frac{1}{2} +) > 0\). The last product  in (1.19) makes sense but the resulting regularity is \(2\alpha - 1-\), smaller than the required regularity \( -\frac{1}{2}+\), when \(\alpha \) is close to 0. As for the second term in (1.19), it depends on the unknown \(v_N\) and thus the product does not make sense (at this point) since the sum of regularities is negative (when \(\alpha > 0\) is small).
in (1.19) makes sense but the resulting regularity is \(2\alpha - 1-\), smaller than the required regularity \( -\frac{1}{2}+\), when \(\alpha \) is close to 0. As for the second term in (1.19), it depends on the unknown \(v_N\) and thus the product does not make sense (at this point) since the sum of regularities is negative (when \(\alpha > 0\) is small).
As we see below, by studying the last two terms in (1.19) under the Duhamel integral operator \({\mathcal {I}}\), we can indeed give a meaning to them and exhibit extra \((\frac{1}{2}+)\)-smoothing with the resulting regularity \(\frac{1}{2}+\) (under \({\mathcal {I}}\)), which allows us to close the argument. By writing (1.18) with initial data \((u_0, u_1)\) in the Duhamel formulation, we have

where \(S(t) (u_0, u_1) = \cos (t\langle \nabla \rangle ) u_0 + \frac{\sin (t\langle \nabla \rangle )}{\langle \nabla \rangle }u_1\) denotes the (deterministic) linear solution. Here,  denotes the random operator defined by
denotes the random operator defined by

and (as the notation suggests), the last term in (1.20) is defined by

(without a renormalization). By exploiting random multilinear dispersion, we show that
-
the random operator
 maps functions of regularity \(\frac{1}{2}+\) to those of regularity \(\frac{1}{2}+\) (measured in the \(X^{s, b}\)-spaces) with the operator norm uniformly bounded in \(N \in {\mathbb {N}}\) and
maps functions of regularity \(\frac{1}{2}+\) to those of regularity \(\frac{1}{2}+\) (measured in the \(X^{s, b}\)-spaces) with the operator norm uniformly bounded in \(N \in {\mathbb {N}}\) and  converges to some limit, denoted by
converges to some limit, denoted by 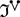 , as \(N \rightarrow \infty \). We study the random operator
, as \(N \rightarrow \infty \). We study the random operator  via the random matrix approach [9, 10, 12, 18, 59].Footnote 14 See Lemma 3.5.
via the random matrix approach [9, 10, 12, 18, 59].Footnote 14 See Lemma 3.5. -
the third order process
 has regularity \(\frac{1}{2} +\) (measured in the \(X^{s, b}\)-spaces) with the norm uniformly bounded in \(N \in {\mathbb {N}}\) and
has regularity \(\frac{1}{2} +\) (measured in the \(X^{s, b}\)-spaces) with the norm uniformly bounded in \(N \in {\mathbb {N}}\) and  converges to some limit, denoted by
converges to some limit, denoted by  , as \(N \rightarrow \infty \). See Lemma 3.4.
, as \(N \rightarrow \infty \). See Lemma 3.4.
We deduce these claims as corollaries to Bringmann’s work [12]. In [12], the smoothing coming from the potential \(V = \langle \nabla \rangle ^{-\beta }\) in the Hartree nonlinearity \((V*u^2)u\) played an important role. In our problem, this is replaced by the smoothing \(\langle \nabla \rangle ^{-\alpha }\) on the noise and we reduce our problem to that in [12], essentially by the following simple observation:
for any \(\gamma \ge 0\).
Remark 1.7
In the following, we also set

By carrying out analysis analogous to (but more involved than) that for  studied in Lemma 3.3 below, we can show that
studied in Lemma 3.3 below, we can show that  forms a Cauchy sequence in \(C([0,T];W^{\alpha - \frac{1}{2} - ,\infty }({\mathbb {T}}^3))\) almost surely, thus converging to some limit
forms a Cauchy sequence in \(C([0,T];W^{\alpha - \frac{1}{2} - ,\infty }({\mathbb {T}}^3))\) almost surely, thus converging to some limit  . In this paper, however, we proceed with space-time analysis as in [12]. Namely, we study
. In this paper, however, we proceed with space-time analysis as in [12]. Namely, we study  in the \(X^{s, b}\)-spaces and show that it converges to some limit denoted by
in the \(X^{s, b}\)-spaces and show that it converges to some limit denoted by  . See Lemma 3.4.
. See Lemma 3.4.
Putting everything together, we can take \(N \rightarrow \infty \) in (1.20) and obtain the following limiting equation for  :
:

By the Fourier restriction norm method with the Strichartz estimates, we can then prove local well-posedness of (1.25) in the deterministic manner. Namely, given the following enhanced data set

of appropriate regularities (depicted by stochastic analysis), there exists a unique local-in-time solution v to (1.25), continuously depending on the enhanced data set \(\Xi \). See Proposition 3.7 for a precise statement.
This local well-posedness result together with the convergence of  and
and  then yields the convergence of
then yields the convergence of  in (1.17) to the limiting process
in (1.17) to the limiting process

where v is the solution to (1.25).
Remark 1.8
In terms of regularity counting, the sum of the regularities in  is positive. In the parabolic setting, one may then proceed with a product estimate. In the current dispersive setting, however, integrability of functions plays an important role and thus we need to proceed with care. See Lemmas 2.7 and 3.6.
is positive. In the parabolic setting, one may then proceed with a product estimate. In the current dispersive setting, however, integrability of functions plays an important role and thus we need to proceed with care. See Lemmas 2.7 and 3.6.
Remark 1.9
(i) By the use of stochastic analysis, the stochastic terms  ,
, ,
,  ,
,  ,
,  , and
, and  in the enhanced data set are defined as the unique limits of their truncated versions. Furthermore, by deterministic analysis, we prove that a solution v to (1.25) is pathwise unique in an appropriate class. Therefore, under the decomposition
in the enhanced data set are defined as the unique limits of their truncated versions. Furthermore, by deterministic analysis, we prove that a solution v to (1.25) is pathwise unique in an appropriate class. Therefore, under the decomposition  , the uniqueness of u refers to (a) the uniqueness of
, the uniqueness of u refers to (a) the uniqueness of  and
and  as the limits of
as the limits of  and
and  and (b) the uniqueness of v as a solution to (1.25).
and (b) the uniqueness of v as a solution to (1.25).
(ii) In this paper, we work with the frequency projector \(\pi _N\) with a sharp cutoff function on the frequency side. It is also possible to work with smooth mollifiers \(\eta _{\delta }(x) = \delta ^{-3}\eta (\delta ^{-1}x)\), where \(\eta \in C^\infty ({\mathbb {R}}^3 ; [0, 1])\) is a smooth, non-negative, even function with \(\int \eta dx = 1\) and \({{\,\mathrm{supp}\,}}\eta \subset (-\pi , \pi ]^3\simeq {\mathbb {T}}^3\). In this case, working with
we can show that a solution \(u_\delta \) to (1.27) converges in probability to some limit u in \( C([-T_\omega , T_\omega ]; H^{\alpha -\frac{1}{2} -\varepsilon } ({\mathbb {T}}^3))\) as \(\delta \rightarrow 0\). Furthermore, the limit \(u_\delta \) is independent of the choice of a mollification kernel \(\eta \) and agrees with the limiting process u constructed in Theorem 1.1. This is the second meaning of the uniqueness of the limiting process u.
Remark 1.10
-
(i)
From the “scaling” point of view, our problem for \(0 < \alpha \ll 1\) is more difficult than the quadratic SNLW (1.8) considered in [26], where the paracontrolled calculus played an essential role. On the other hand, for the proof of Theorem 1.1, we do not need to use the paracontrolled ansatz for the remainder terms
 thanks to the smoothing on the noise and the use of space-time estimates, which allows us to place v in the subcritical regularity \(\frac{1}{2} + \).
thanks to the smoothing on the noise and the use of space-time estimates, which allows us to place v in the subcritical regularity \(\frac{1}{2} + \).Our approach to (1.6) and Bringmann’s approach in [12] crucially exploit various multilinear smoothing, gaining \(\sim \frac{1}{2}\)-derivative. When \(\alpha = 0\) (or \(\beta = 0\) in the Hartree SNLW (1.9)), such multilinear smoothing seems to give (at best) \(\frac{1}{2}\)-smoothing and thus the arguments in this paper and in [12] break down in the \(\alpha = 0\) case.
-
(ii)
In [26], Gubinelli, Koch, and the first author studied the quadratic SNLW on \({\mathbb {T}}^3\) with an additive space-time white noise (i.e. \(\alpha = 0\)):
$$\begin{aligned} \partial _t^2 u + (1 - \Delta ) u + u^2 = \xi . \end{aligned}$$(1.28)With the Wick renormalization and the second order expansion
 , where
, where  , the remainder term
, the remainder term  satisfies
satisfies  (1.29)
(1.29)As observed in [26], the main issue in studying (1.29) comes from the regularity \(\frac{1}{2} - \) of v, which is inherited from the regularity \(-\frac{1}{2} - \) of
 . As a result, the product
. As a result, the product 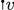 in (1.29) is not well defined since the sum of the regularities of
in (1.29) is not well defined since the sum of the regularities of  and v is negative. As in (1.21), it is tempting to directly define the random operator
and v is negative. As in (1.21), it is tempting to directly define the random operator 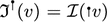 , using the random matrix estimates. However, there is an issue in handling the “high \(\times \) high \(\rightarrow \) low” interaction and thus the random matrix approach alone is not sufficient to close the argument. In [26], this issue was overcome by a paracontrolled ansatz and an iteration of the Duhamel formulation. We point out that the use of the paracontrolled ansatz in [26] led to the following paracontrolled operator
, using the random matrix estimates. However, there is an issue in handling the “high \(\times \) high \(\rightarrow \) low” interaction and thus the random matrix approach alone is not sufficient to close the argument. In [26], this issue was overcome by a paracontrolled ansatz and an iteration of the Duhamel formulation. We point out that the use of the paracontrolled ansatz in [26] led to the following paracontrolled operator  , which avoids the undesirable high \(\times \) high \(\rightarrow \) low interaction. Instead of the paracontrolled calculus, one may use the random averaging operator from [17] together with an iteration of the Duhamel formulation. We, however, point out that due to the problematic high \(\times \) high interaction, the random averaging operator as introduced in [17] alone (without iterating the Duhamel formulation) does not seem to be sufficient to study the quadratic SNLW (1.28).
, which avoids the undesirable high \(\times \) high \(\rightarrow \) low interaction. Instead of the paracontrolled calculus, one may use the random averaging operator from [17] together with an iteration of the Duhamel formulation. We, however, point out that due to the problematic high \(\times \) high interaction, the random averaging operator as introduced in [17] alone (without iterating the Duhamel formulation) does not seem to be sufficient to study the quadratic SNLW (1.28).
Organization of the paper In Sect. 2, we go over the basic definitions and lemmas from deterministic and stochastic analysis. In Sect. 3, we first state the almost sure regularity and convergence properties of (the truncated versions of) the stochastic objects in the enhanced data set \(\Xi \) in (1.26). Then, we present the proof of our main result (Theorem 1.1). In Sect. 4, we establish the almost sure regularity and convergence properties of the stochastic objects in the enhanced data set. In Appendix A, we recall the counting lemmas from [12] which play a crucial role in Sect. 4. In Appendices B and C, we provide the basic definitions and lemmas on multiple stochastic integrals and (random) tensors, respectively.
2 Notations and basic lemmas
We write \( A \lesssim B \) to denote an estimate of the form \( A \le CB \). Similarly, we write \( A \sim B \) to denote \( A \lesssim B \) and \( B \lesssim A \) and use \( A \ll B \) when we have \(A \le c B\) for small \(c > 0\). We also use \( a+ \) (and \( a- \)) to mean \( a + \varepsilon \) (and \( a-\varepsilon \), respectively) for arbitrarily small \( \varepsilon >0 \).
When we work with space-time function spaces, we use short-hand notations such as \(C_T H^s_x = C([0, T]; H^s({\mathbb {T}}^3))\).
When there is no confusion, we simply use \(\widehat{u}\) or \({\mathcal {F}}(u)\) to denote the spatial, temporal, or space-time Fourier transform of u, depending on the context. We also use \({\mathcal {F}}_x\), \({\mathcal {F}}_t\), and \({\mathcal {F}}_{x, t}\) to denote the spatial, temporal, and space-time Fourier transforms, respectively.
We use the following short-hand notation: \(n_{ij} = n_i + n_j\), etc. For example, \(n_{123} = n_1 + n_2 + n_3\).
2.1 Sobolev spaces and Besov spaces
Let \(s \in {\mathbb {R}}\) and \(1 \le p \le \infty \). We define the \(L^2\)-based Sobolev space \(H^s({\mathbb {T}}^3)\) by the norm:
and set \({\mathcal {H}}^s({\mathbb {T}}^3)\) to be
We also define the \(L^p\)-based Sobolev space \(W^{s, p}({\mathbb {T}}^3)\) by the norm:
When \(p = 2\), we have \(H^s({\mathbb {T}}^3) = W^{s, 2}({\mathbb {T}}^3)\).
Let \(\phi :{\mathbb {R}}\rightarrow [0, 1]\) be a smooth bump function supported on \(\big [-\frac{8}{5}, \frac{8}{5}\big ]\) and \(\phi \equiv 1\) on \(\big [-\frac{5}{4}, \frac{5}{4}\big ]\). For \(\xi \in {\mathbb {R}}^3\), we set \(\phi _0(\xi ) = \phi (|\xi |)\) and
for \(j \in {\mathbb {N}}\). Note that we have
for any \(\xi \in {\mathbb {R}}^3\). Then, for \(j \in {\mathbb {N}}_0 := {\mathbb {N}}\cup \{0\}\), we define the Littlewood-Paley projector \({\mathbf {P}}_j\) as the Fourier multiplier operator with a symbol \(\phi _j\). Thanks to (2.1), we have
Next, we recall the following paraproduct decomposition due to Bony [6]. See [1, 24] for further details. Let f and g be functions on \({\mathbb {T}}^3\) of regularities \(s_1\) and \(s_2\), respectively. Using (2.2), we write the product fg as

The first term  (and the third term
(and the third term  ) is called the paraproduct of g by f (the paraproduct of f by g, respectively) and it is always well defined as a distribution of regularity \(\min (s_2, s_1+ s_2)\). On the other hand, the resonant product
) is called the paraproduct of g by f (the paraproduct of f by g, respectively) and it is always well defined as a distribution of regularity \(\min (s_2, s_1+ s_2)\). On the other hand, the resonant product  is well defined in general only if \(s_1 + s_2 > 0\).
is well defined in general only if \(s_1 + s_2 > 0\).
We briefly recall the basic properties of the Besov spaces \(B^s_{p, q}({\mathbb {T}}^3)\) defined by the norm:
Note that \(H^s({\mathbb {T}}^3) = B^s_{2,2}({\mathbb {T}}^3)\).
Lemma 2.1
-
(i)
(paraproduct and resonant product estimates) Let \(s_1, s_2 \in {\mathbb {R}}\) and \(1 \le p, p_1, p_2, q \le \infty \) such that \(\frac{1}{p} = \frac{1}{p_1} + \frac{1}{p_2}\). Then, we have
 (2.4)
(2.4)When \(s_1 < 0\), we have
 (2.5)
(2.5)When \(s_1 + s_2 > 0\), we have
 (2.6)
(2.6) -
(ii)
Let \(s_1 < s_2 \) and \(1\le p, q \le \infty \). Then, we have
$$\begin{aligned} \Vert u \Vert _{B^{s_1}_{p,q}}&\lesssim \Vert u \Vert _{W^{s_2, p}}. \end{aligned}$$(2.7)
The product estimates (2.4), (2.5), and (2.6) follow easily from the definition (2.3) of the paraproduct and the resonant product. See [1, 39] for details of the proofs in the non-periodic case (which can be easily extended to the current periodic setting). The embedding (2.7) follows from the \(\ell ^{q}\)-summability of \(\big \{2^{(s_1 - s_2)j}\big \}_{j \in {\mathbb {N}}_0}\) for \(s_1 < s_2\) and the uniform boundedness of the Littlewood-Paley projector \({\mathbf {P}}_j\).
We also recall the following product estimate from [25].
Lemma 2.2
Let \(0\le s\le 1\). Let \(1<p,q,r<\infty \) such that \(s \ge 3\big (\frac{1}{p}+\frac{1}{q}-\frac{1}{r}\big )\). Then, we have
Note that while Lemma 2.2 was shown only for \(s = 3\big (\frac{1}{p}+\frac{1}{q}-\frac{1}{r}\big )\) in [25], the general case \(s \ge 3\big (\frac{1}{p}+\frac{1}{q}-\frac{1}{r}\big )\) follows the embedding \(L^{r_1}({\mathbb {T}}^3) \subset L^{r_2}({\mathbb {T}}^3)\), \(r_1 \ge r_2\).
2.2 Fourier restriction norm method and Strichartz estimates
We first recall the so-called \(X^{s, b}\)-spaces, also known as the hyperbolic Sobolev spaces, due to Klainerman-Machedon [34] and Bourgain [7], defined by the norm:
For \( b > \frac{1}{2}\), we have \(X^{s, b} \subset C({\mathbb {R}}; H^s({\mathbb {T}}^3))\). Given an interval \(I \subset {\mathbb {R}}\), we define the local-in-time version \(X^{s, b}(I)\) as a restriction norm:
When \(I = [0, T]\), we set \(X^{s, b}_T = X^{s, b}(I)\).
Next, we recall the Strichartz estimates for the linear wave/Klein–Gordon equation. Given \(0 \le s \le 1\), we say that a pair (q, r) is s-admissible if \(2 < q \le \infty \), \(2 \le r < \infty \),
Then, we have the following Strichartz estimates.
Lemma 2.3
Given \(0 \le s \le 1\), let (q, r) be s-admissible. Then, we have
for any \(0 < T \le 1\).
See Ginibre–Velo [23], Lindblad–Sogge [38], and Keel–Tao [32] for the Strichartz estimates on \({\mathbb {R}}^d\). See also [33]. The Strichartz estimates (2.10) on \({\mathbb {T}}^3\) in Lemma 2.3 follows from those on \({\mathbb {R}}^3\) and the finite speed of propagation.
When \(b > \frac{1}{2}\), the \(X^{s, b}\)-spaces enjoy the transference principle. In particular, as a corollary to Lemma 2.3, we obtain the following space-time estimate. See [35, 64] for the proof.
Lemma 2.4
Let \(0 < T \le 1\). Given \(0 \le s \le 1\), let (q, r) be s-admissible. Then, for \(b > \frac{1}{2}\), we have
We also state the nonhomogeneous linear estimate. See [22].
Lemma 2.5
Let \( - \frac{1}{2} < b' \le 0 \le b \le b'+1\). Then, for \(0 < T \le 1\), we have
In the following, we briefly go over the main trilinear estimate for the basic local well-posedness of the cubic NLW (1.5) in \({\mathcal {H}}^{\frac{1}{2}+\varepsilon }({\mathbb {T}}^3)\).
Lemma 2.6
Fix small \(\delta _1, \delta _2 > 0\) with \(4\delta _2 \le \delta _1\). Then, we have
for any \(0 < T\le 1\).
Proof
Recall that \((q, r) = (4, 4)\) is \(\frac{1}{2}\)-admissible. Then, in view of Lemma 2.4, interpolating
with small \(\delta _0 > 0\), we obtain
Moreover, noting that \(\big (\frac{12}{3-2\delta _1},\frac{12}{3-2\delta _1}\big )\) is \(\big (\frac{1}{2} + \frac{2}{3} \delta _1\big )\)-admissible, we obtain from Lemma 2.4 that
for any \(\delta _2 > 0\).
Hence, from Lemma 2.5, duality, Hölder’s inequality, (2.13), and (2.14), we obtain
provided that \(0 < 4\delta _2 \le \delta _1 \ll 1\). This proves (2.11). \(\square \)
We conclude this part by establishing the following trilinear estimate, which will be used to control the term  in (1.25). See Proposition 8.6 in [12] for an analogous trilinear estimate.
in (1.25). See Proposition 8.6 in [12] for an analogous trilinear estimate.
Lemma 2.7
Let \(\delta _1, \delta _2 > 0\) be sufficiently small such that \(8 \delta _2 \le \delta _1\). Then, we have
for any \(0 < T \le 1\).
Proof
By applying the Littlewood-Paley decompositions, we have
For simplicity of notation, we set \(N_1 = 2^{j_1}\), \(N_{23} = 2^{j_{23}}\), and \(N_{123} = 2^{j_{123}}\), denoting the dyadic frequency sizes of \(n_1\) (for \(u_1\)), \(n_{23}\) (for \(u_2u_3\)), and \(n_{123}\) (for \(u_1 u_2 u_3\)), respectively. We set \(v_k = {\mathbf {P}}_{j_k} u_k\). In view of \(n_{123} = n_1 + n_{23}\), we separately estimate the contributions from (i) \(N_{123} \sim \max (N_1, N_{23})\) and (ii) \(N_{123} \ll \max (N_1, N_{23})\).
Case 1: \(N_{123} \sim \max (N_1, N_{23})\).
By Hölder’s inequality and the \(L^4\)-Strichartz estimate (2.12), we have
This is summable in dyadic \(N_1, N_{23}, N_{123}\ge 1\), yielding (2.15) in this case.
Case 2: \(N_{123} \ll \max (N_1, N_{23})\).
In this case, we further apply the Littlewood-Paley decompositions for \(u_2\) and \(u_3\) and write
Without loss of generality, assume \(N_3 \ge N_2\), where \(N_k = 2^{j_k}\), \(k = 2, 3\). Then, we have
By duality and (2.13) (with \(\delta _1 = 4\delta _2\)), we have
Then, from (2.17), (2.14), and (2.16) with \(8 \delta _2 \le \delta _1\), we have
This is summable in dyadic \(N_1, N_2, N_3, N_{23}, N_{123}\ge 1\), yielding (2.15) in this case. \(\square \)
2.3 On discrete convolutions
Next, we recall the following basic lemma on a discrete convolution.
Lemma 2.8
-
(i)
Let \(d \ge 1\) and \(\alpha , \beta \in {\mathbb {R}}\) satisfy
$$\begin{aligned} \alpha + \beta > d \quad \text {and}\quad \alpha , \beta < d. \end{aligned}$$Then, we have
$$\begin{aligned} \sum _{n = n_1 + n_2} \frac{1}{\langle n_1 \rangle ^\alpha \langle n_2 \rangle ^\beta } \lesssim \langle n \rangle ^{d - \alpha - \beta } \end{aligned}$$for any \(n \in {\mathbb {Z}}^d\).
-
(ii)
Let \(d \ge 1\) and \(\alpha , \beta \in {\mathbb {R}}\) satisfy \(\alpha + \beta > d\). Then, we have
$$\begin{aligned} \sum _{\begin{array}{c} n = n_1 + n_2\\ |n_1|\sim |n_2| \end{array}} \frac{1}{\langle n_1 \rangle ^\alpha \langle n_2 \rangle ^\beta } \lesssim \langle n \rangle ^{d - \alpha - \beta }\end{aligned}$$for any \(n \in {\mathbb {Z}}^d\).
Namely, in the resonant case (ii), we do not have the restriction \(\alpha , \beta < d\). Lemma 2.8 follows from elementary computations. See, for example, Lemmas 4.1 and 4.2 in [41] for the proof.
2.4 Tools from stochastic analysis
We conclude this section by recalling useful lemmas from stochastic analysis. See [5, 43, 62] for basic definitions. See also Appendix B for basic definitions and properties for multiple stochastic integrals.
Let \((H, B, \mu )\) be an abstract Wiener space. Namely, \(\mu \) is a Gaussian measure on a separable Banach space B with \(H \subset B\) as its Cameron-Martin space. Given a complete orthonormal system \(\{e_j \}_{ j \in {\mathbb {N}}} \subset B^*\) of \(H^* = H\), we define a polynomial chaos of order k to be an element of the form \(\prod _{j = 1}^\infty H_{k_j}(\langle x, e_j \rangle )\), where \(x \in B\), \(k_j \ne 0\) for only finitely many j’s, \(k= \sum _{j = 1}^\infty k_j\), \(H_{k_j}\) is the Hermite polynomial of degree \(k_j\), and  denotes the B–\(B^*\) duality pairing. We then denote the closure of polynomial chaoses of order k under \(L^2(B, \mu )\) by \({\mathcal {H}}_k\). The elements in \({\mathcal {H}}_k\) are called homogeneous Wiener chaoses of order k. We also set
denotes the B–\(B^*\) duality pairing. We then denote the closure of polynomial chaoses of order k under \(L^2(B, \mu )\) by \({\mathcal {H}}_k\). The elements in \({\mathcal {H}}_k\) are called homogeneous Wiener chaoses of order k. We also set
for \(k \in {\mathbb {N}}\).
Let \(L = \Delta -x \cdot \nabla \) be the Ornstein-Uhlenbeck operator.Footnote 15 Then, it is known that any element in \({\mathcal {H}}_k\) is an eigenfunction of L with eigenvalue \(-k\). Then, as a consequence of the hypercontractivity of the Ornstein-Uhlenbeck semigroup \(U(t) = e^{tL}\) due to Nelson [42], we have the following Wiener chaos estimate [63, Theorem I.22]. See also [65, Proposition 2.4].
Lemma 2.9
Let \(k \in {\mathbb {N}}\). Then, we have
for any \(p \ge 2\) and any \(X \in {\mathcal {H}}_{\le k}\).
The following lemma will be used in studying regularities of stochastic objects. We say that a stochastic process \(X:{\mathbb {R}}_+ \rightarrow {\mathcal {D}}'({\mathbb {T}}^d)\) is spatially homogeneous if \(\{X(\cdot , t)\}_{t\in {\mathbb {R}}_+}\) and \(\{X(x_0 +\cdot \,, t)\}_{t\in {\mathbb {R}}_+}\) have the same law for any \(x_0 \in {\mathbb {T}}^d\). Given \(h \in {\mathbb {R}}\), we define the difference operator \(\delta _h\) by setting
Lemma 2.10
Let \(\{ X_N \}_{N \in {\mathbb {N}}}\) and X be spatially homogeneous stochastic processes \(:{\mathbb {R}}_+ \rightarrow {\mathcal {D}}'({\mathbb {T}}^d)\). Suppose that there exists \(k \in {\mathbb {N}}\) such that \(X_N(t)\) and X(t) belong to \({\mathcal {H}}_{\le k}\) for each \(t \in {\mathbb {R}}_+\).
-
(i)
Let \(t \in {\mathbb {R}}_+\). If there exists \(s_0 \in {\mathbb {R}}\) such that
$$\begin{aligned} {\mathbb {E}}\big [ |\widehat{X}(n, t)|^2\big ]\lesssim \langle n \rangle ^{ - d - 2s_0} \end{aligned}$$(2.18)for any \(n \in {\mathbb {Z}}^d\), then we have \(X(t) \in W^{s, \infty }({\mathbb {T}}^d)\), \(s < s_0\), almost surely.
-
(ii)
Suppose that \(X_N\), \(N \in {\mathbb {N}}\), satisfies (2.18). Furthermore, if there exists \(\gamma > 0\) such that
$$\begin{aligned} {\mathbb {E}}\big [ |\widehat{X}_N(n, t) - \widehat{X}_M(n, t)|^2\big ]\lesssim N^{-\gamma } \langle n \rangle ^{ - d - 2s_0} \end{aligned}$$for any \(n \in {\mathbb {Z}}^d\) and \(M \ge N \ge 1\), then \(X_N(t)\) is a Cauchy sequence in \(W^{s, \infty }({\mathbb {T}}^d)\), \(s < s_0\), almost surely, thus converging to some limit in \(W^{s, \infty }({\mathbb {T}}^d)\).
-
(iii)
Let \(T > 0\) and suppose that (i) holds on [0, T]. If there exists \(\sigma \in (0, 1)\) such that
$$\begin{aligned} {\mathbb {E}}\big [ |\delta _h \widehat{X}(n, t)|^2\big ] \lesssim \langle n \rangle ^{ - d - 2s_0+ \sigma } |h|^\sigma \end{aligned}$$for any \(n \in {\mathbb {Z}}^d\), \(t \in [0, T]\), and \(h \in [-1, 1]\),Footnote 16 then we have \(X \in C([0, T]; W^{s, \infty }({\mathbb {T}}^d))\), \(s < s_0 - \frac{\sigma }{2}\), almost surely.
-
(iv)
Let \(T > 0\) and suppose that (ii) holds on [0, T]. Furthermore, if there exists \(\gamma > 0\) such that
$$\begin{aligned} {\mathbb {E}}\big [ |\delta _h \widehat{X}_N(n, t) - \delta _h \widehat{X}_M(n, t)|^2\big ] \lesssim N^{-\gamma }\langle n \rangle ^{ - d - 2s_0+ \sigma } |h|^\sigma \end{aligned}$$
for any \(n \in {\mathbb {Z}}^d\), \(t \in [0, T]\), \(h \in [-1, 1]\), and \(M\ge N \ge 1\), then \(X_N\) is a Cauchy sequence in \(C([0, T]; W^{s, \infty }({\mathbb {T}}^d))\), \(s < s_0 - \frac{\sigma }{2}\), almost surely, thus converging to some process in \(C([0, T]; W^{s, \infty }({\mathbb {T}}^d))\).
Lemma 2.10 follows from a straightforward application of the Wiener chaos estimate (Lemma 2.9). For the proof, see Proposition 3.6 in [41] and Appendix in [50]. As compared to Proposition 3.6 in [41], we made small adjustments. In studying the time regularity, we made the following modifications: \(\langle n \rangle ^{ - d - 2s_0+ 2\sigma }\mapsto \langle n \rangle ^{ - d - 2s_0+ \sigma }\) and \(s< s_0 - \sigma \mapsto s < s_0 - \frac{\sigma }{2}\) so that it is suitable for studying the wave equation. Moreover, while the result in [41] is stated in terms of the Besov-Hölder space \({\mathcal {C}}^s({\mathbb {T}}^d) = B^s_{\infty , \infty }({\mathbb {T}}^d)\), Lemma 2.10 handles the \(L^\infty \)-based Sobolev space \(W^{s, \infty }({\mathbb {T}}^3)\). Note that the required modification of the proof is straightforward since \(W^{s, \infty }({\mathbb {T}}^d)\) and \(B^s_{\infty , \infty }({\mathbb {T}}^d)\) differ only logarithmically:
for any \(\varepsilon > 0\). For the proof of the almost sure convergence claims, see [50].
3 Local well-posedness of SNLW, \(\alpha > 0\)
In this section, we present the proof of local well-posedness of (1.25) (Theorem 1.1). In Sect. 3.1, we first state the regularity and convergence properties of the stochastic objects in the enhanced data set \(\Xi \) in (1.26). In Sect. 3.2, we then present a deterministic local well-posedness result by viewing elements in the enhanced data set as given (deterministic) distributions and a given (deterministic) operator with prescribed regularity properties.
3.1 On the stochastic terms
In this subsection, we state the regularity and convergence properties of the stochastic objects in (1.26) whose proofs are presented in Sect. 4.
Lemma 3.1
Let \(\alpha >0\) and \(T > 0\).
-
(i)
For any \(s< \alpha - \frac{1}{2} \),
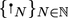 defined in (1.12) is a Cauchy sequence in \(C([0,T];W^{s,\infty }({\mathbb {T}}^3))\), almost surely. In particular, denoting the limit by
defined in (1.12) is a Cauchy sequence in \(C([0,T];W^{s,\infty }({\mathbb {T}}^3))\), almost surely. In particular, denoting the limit by  (formally given by (1.11)), we have
(formally given by (1.11)), we have 
for any \(\varepsilon >0\), almost surely.
-
(ii)
Let \(0 < \alpha \le \frac{1}{2}\). Then, for any \(s< \alpha \),
 defined in (1.15) is a Cauchy sequence in \(C([0,T];W^{s,\infty }({\mathbb {T}}^3))\) almost surely. In particular, denoting the limit by
defined in (1.15) is a Cauchy sequence in \(C([0,T];W^{s,\infty }({\mathbb {T}}^3))\) almost surely. In particular, denoting the limit by  , we have
, we have 
for any \(\varepsilon >0\), almost surely.
Remark 3.2
-
(i)
As mentioned in Sect. 1, a parabolic thinking gives regularity \(3\alpha - \frac{1}{2}-\) for
 . Lemma 3.1 (ii) states that, when \(\alpha > 0\) is small, we indeed gain about \(\frac{1}{2}\)-regularity by exploiting multilinear dispersion as in the quadratic case studied in [26]. We point out that our proof is based on an adaptation of Bringmann’s analysis on the corresponding term in the Hartree case [12] and thus the regularities we obtain in Lemma 3.1 (ii) as well as Lemmas 3.3, 3.4, and 3.5 may not be sharp (especially for large \(\alpha >0\); see, for example, a crude bound (4.9)). They are, however, sufficient for our purpose.
. Lemma 3.1 (ii) states that, when \(\alpha > 0\) is small, we indeed gain about \(\frac{1}{2}\)-regularity by exploiting multilinear dispersion as in the quadratic case studied in [26]. We point out that our proof is based on an adaptation of Bringmann’s analysis on the corresponding term in the Hartree case [12] and thus the regularities we obtain in Lemma 3.1 (ii) as well as Lemmas 3.3, 3.4, and 3.5 may not be sharp (especially for large \(\alpha >0\); see, for example, a crude bound (4.9)). They are, however, sufficient for our purpose. -
(ii)
In this section, we only state almost sure convergence but the same argument also yields convergence in \(L^p(\Omega )\) with an exponential tail estimate (as in [12, 27, 48]). Our goal is, however, to prove local well-posedness and thus the almost sure convergence suffices for our purpose.
Lemma 3.3
Let \(0 < \alpha \le \frac{1}{2}\) and \(T >0\). Let  and
and  be as in (1.12) and (1.15). Then, for any \(s< \alpha - \frac{1}{2} \),
be as in (1.12) and (1.15). Then, for any \(s< \alpha - \frac{1}{2} \),  is a Cauchy sequence in \(C([0,T];W^{s,\infty }({\mathbb {T}}^3))\) almost surely. In particular, denoting the limit by
is a Cauchy sequence in \(C([0,T];W^{s,\infty }({\mathbb {T}}^3))\) almost surely. In particular, denoting the limit by  , we have
, we have

for any \(\varepsilon >0\), almost surely.
Lemma 3.4
Let \(\alpha > 0\), \(T > 0\), and \(b > \frac{1}{2}\) be sufficiently close to \(\frac{1}{2}\).
-
(i)
For any \(s < \alpha + \frac{1}{2}\),
 defined in (1.22) is a Cauchy sequence in \(X^{s, b}([0, T])\). In particular, denoting the limit by
defined in (1.22) is a Cauchy sequence in \(X^{s, b}([0, T])\). In particular, denoting the limit by  , we have
, we have 
for any \(\varepsilon > 0\), almost surely.
-
(ii)
For any \(s < \alpha + \frac{1}{2}\),
 defined in (1.24) is a Cauchy sequence in \(X^{s, b}([0, T])\). In particular, denoting the limit by
defined in (1.24) is a Cauchy sequence in \(X^{s, b}([0, T])\). In particular, denoting the limit by  , we have
, we have 
for any \(\varepsilon > 0\), almost surely.
Given Banach spaces \(B_1\) and \(B_2\), we use \({\mathcal {L}}(B_1; B_2)\) to denote the space of bounded linear operators from \(B_1\) to \(B_2\). We also set
endowed with the norm given by
for some small \(\theta >0\).
Lemma 3.5
Let \(\alpha > 0\) and \(T_0>0\). Then, given sufficiently small \(\delta _1, \delta _2 > 0\), the sequence of the random operators  defined in (1.21) is a Cauchy sequence in the class \( {\mathcal {L}}^{\frac{1}{2} + \delta _1, \frac{1}{2} +\delta _1, \frac{1}{2} +\delta _2}_{T_0}\), almost surely. In particular, denoting the limit by
defined in (1.21) is a Cauchy sequence in the class \( {\mathcal {L}}^{\frac{1}{2} + \delta _1, \frac{1}{2} +\delta _1, \frac{1}{2} +\delta _2}_{T_0}\), almost surely. In particular, denoting the limit by  , we have
, we have

almost surely.
The following trilinear estimate is an immediate consequence of Lemma 2.7.
Lemma 3.6
Let \(\alpha > 0\). Let \(\delta _1, \delta _2, \varepsilon > 0\) be sufficiently small such that \(2\delta _1 + \varepsilon \le \alpha \). Then, we have

for any \(0 < T \le 1\).
3.2 Proof of Theorem 1.1
In this section, we prove the following proposition. Theorem 1.1 then follows from this proposition and Lemmas 3.1 - 3.5.
Proposition 3.7
Let \(\alpha > 0\), \(s > \frac{1}{2}\), and \(T_0 >0\). Then, there exists small \(\varepsilon = \varepsilon (\alpha , s)\), \(\delta _1 = \delta _1(\alpha , s) \), \(\delta _2 = \delta _2(\alpha , s) >0\) such that if
-
 is a distribution-valued function belonging to \(C([0, T_0]; W^{\alpha -\frac{1}{2} - \varepsilon , \infty }({\mathbb {T}}^3))\),
is a distribution-valued function belonging to \(C([0, T_0]; W^{\alpha -\frac{1}{2} - \varepsilon , \infty }({\mathbb {T}}^3))\), -
 is a distribution-valued function belonging to \(C([0, T_0]; W^{\alpha - \varepsilon , \infty }({\mathbb {T}}^3))\),
is a distribution-valued function belonging to \(C([0, T_0]; W^{\alpha - \varepsilon , \infty }({\mathbb {T}}^3))\), -
 is a distribution-valued function belonging to \(C([0, T_0]; W^{\alpha -\frac{1}{2} - \varepsilon , \infty }({\mathbb {T}}^3))\),
is a distribution-valued function belonging to \(C([0, T_0]; W^{\alpha -\frac{1}{2} - \varepsilon , \infty }({\mathbb {T}}^3))\), -
 is a function belonging to \(X^{\alpha + \frac{1}{2} -\varepsilon , \frac{1}{2} +\delta _2}([0, T_0])\),
is a function belonging to \(X^{\alpha + \frac{1}{2} -\varepsilon , \frac{1}{2} +\delta _2}([0, T_0])\), -
 is a function belonging to \(X^{\alpha + \frac{1}{2} -\varepsilon , \frac{1}{2} +\delta _2}([0, T_0])\),
is a function belonging to \(X^{\alpha + \frac{1}{2} -\varepsilon , \frac{1}{2} +\delta _2}([0, T_0])\), -
the operator
 belongs to the class \( {\mathcal {L}}^{\frac{1}{2} + \delta _1, \frac{1}{2} +\delta _1, \frac{1}{2} +\delta _2}_{T_0}\) defined in (3.1),
belongs to the class \( {\mathcal {L}}^{\frac{1}{2} + \delta _1, \frac{1}{2} +\delta _1, \frac{1}{2} +\delta _2}_{T_0}\) defined in (3.1),
then the Eq. (1.25) is locally well-posed in \({\mathcal {H}}^{s}({\mathbb {T}}^3)\). More precisely, given any \((u_0, u_1)\in {\mathcal {H}}^{s}({\mathbb {T}}^3)\), there exist \(0 < T \le T_0\) and a unique solution v to the cubic SNLW (1.25) on [0, T] in the class
Furthermore, the solution v depends continuously on the enhanced data set

in the class
Proof
Given \(\alpha > 0\) and \(s > \frac{1}{2}\), fix small \(\varepsilon > 0\) such that \(\varepsilon < \min (\alpha , s - \frac{1}{2} )\). Given an enhanced data set \(\Xi \) as in (3.3), we set

and

where \({\mathcal {L}}^{\frac{1}{2} + \delta _1, \frac{1}{2} + \delta _1, \frac{1}{2} + \delta _2}_{T_0}\) is as in (3.2). In the following, we assume that
for some \(K \ge 1\).
Given the enhanced data set \(\Xi \) in (3.3), define a map \(\Gamma _\Xi \) by

Fix \(0 < T \le T_0\). From Lemmas 2.5 and 2.4 with (3.4), we have

and

for some \(\theta > 0\). Similarly, we have

From Lemma 2.5 and Lemma 2.2 with (3.4), we have

provided that \(\delta _1 + \varepsilon \le \alpha \). From (3.2) and (3.4), we have

Hence, by applying Lemmas 2.3 and 2.5, then Lemma 2.6, (3.5), Lemma 3.6, (3.6), (3.8), (3.9), (3.7), and Lemma 3.4 with (3.4), we have
An analogous computation yields a difference estimate on \(\Gamma _\Xi ( v_1) - \Gamma _\Xi ( v_2)\). Therefore, Proposition 3.7 follows from a standard contraction argument. \(\square \)
4 Regularities of the stochastic terms
In this section, we present the proof of Lemmas 3.1 - 3.5, which are basic tools in applying Proposition 3.7 to finally prove Theorem 1.1. In view of the local well-posedness result in [51], we assume that \(0 < \alpha \le \frac{1}{4}\) in the following. Without loss of generality, we assume that \(T \le 1\). The main tools in this section are the counting estimates from [12, Section 4] and the random matrix estimate (see Lemma C.3 below) from [18], which capture the multilinear dispersive effect of the wave equation. For readers’ convenience, we collect the relevant counting estimates in Appendix A and the relevant definitions and estimates for random matrices and tensors in Appendix C. We show in details how to reduce the relevant stochastic estimates to some basic counting and (random) matrix/tensor estimates studied in [12, Section 4] and [18].
In the remaining part of this section, we assume \(0< T < T_0 \le 1\).
4.1 Basic stochastic terms
We first present the proof of Lemma 3.1.
Proof
(i) Let \(t \ge 0\). From (1.16), we have

for any \(n \in {\mathbb {Z}}^3\) and \(N \ge 1\). Also, by the mean value theorem and an interpolation argument as in [26], we have

for any \(\theta \in [0, 1]\), \(n \in {\mathbb {Z}}^3\), and \(0 \le t_2 \le t_1 \le T\) with \(t_1-t_2 \le 1\), uniformly in \(N \in {\mathbb {N}}\). Hence, from Lemma 2.10, we conclude that  for any \(\varepsilon > 0\), almost surely. Moreover, a slight modification of the argument, using Lemma 2.10, yields that
for any \(\varepsilon > 0\), almost surely. Moreover, a slight modification of the argument, using Lemma 2.10, yields that  is almost surely a Cauchy sequence in \(C([0, T]; W^{\alpha -\frac{1}{2} - \varepsilon , \infty }({\mathbb {T}}^3))\), thus converging to some limit
is almost surely a Cauchy sequence in \(C([0, T]; W^{\alpha -\frac{1}{2} - \varepsilon , \infty }({\mathbb {T}}^3))\), thus converging to some limit  . Since the required modification is exactly the same as in [26], we omit the details here.
. Since the required modification is exactly the same as in [26], we omit the details here.
Remark 4.1
In the remaining part of this section, we establish uniform (in N) regularity bounds on the truncated stochastic terms (such as  ) but may omit the convergence part of the argument. Furthermore, as for
) but may omit the convergence part of the argument. Furthermore, as for  studied in Lemma 3.3, we only establish a uniform (in N) regularity bound on
studied in Lemma 3.3, we only establish a uniform (in N) regularity bound on  for each fixed \(0 < t \le T \le 1\). A slight modification as above yields continuity in time but we omit details.
for each fixed \(0 < t \le T \le 1\). A slight modification as above yields continuity in time but we omit details.
(ii) It is possible to prove this part by proceeding as in [26, 45] (i.e. without the use of the \(X^{s, b}\)-spaces). In the following, however, we follow Bringmann’s approach [12], adapted to the stochastic PDE setting. More precisely, we show that given any \(\delta _1> 0\) and sufficiently small \( \delta _2 > 0\), the sequence  is a Cauchy sequence in \(X^{\alpha - 1 - \delta _1, - \frac{1}{2} + \delta _2}([0, T])\), almost surely, and thus converges almost surely to
is a Cauchy sequence in \(X^{\alpha - 1 - \delta _1, - \frac{1}{2} + \delta _2}([0, T])\), almost surely, and thus converges almost surely to  in the same space, where
in the same space, where  is the almost sure limit of
is the almost sure limit of  in \(C([0,T];W^{3\alpha -\frac{3}{2} - ,\infty }({\mathbb {T}}^3))\) discussed in Sect. 1.
in \(C([0,T];W^{3\alpha -\frac{3}{2} - ,\infty }({\mathbb {T}}^3))\) discussed in Sect. 1.
Our first goal is to prove the following bound; given any \(\delta _1> 0\) and sufficiently small \( \delta _2 > 0\), there exists \(\theta > 0\) such that

for any \(p \ge 1\) and \(0 < T \le 1\), uniformly in \(N \in {\mathbb {N}}\).
Let us first compute the space-time Fourier transform of  (with a time cutoff function). From (1.14) with (1.12), we can write the spatial Fourier transform
(with a time cutoff function). From (1.14) with (1.12), we can write the spatial Fourier transform  as the following multiple Wiener–Ito integral (as in [41]):
as the following multiple Wiener–Ito integral (as in [41]):

We emphasize that the renormalization in (1.14) is embedded in the definition of the multiple Wiener–Ito integral.
We now compute the space-time Fourier transform of  , where \({\mathbf {1}}_{[0, T]}\) denotes the sharp cutoff function on the time interval [0, T]. From (4.3) and the stochastic Fubini theorem ([15, Theorem 4.33]; see also Lemma B.2), we have
, where \({\mathbf {1}}_{[0, T]}\) denotes the sharp cutoff function on the time interval [0, T]. From (4.3) and the stochastic Fubini theorem ([15, Theorem 4.33]; see also Lemma B.2), we have

where \(F_{n_1, n_2, n_3} (t_1, t_2, t_3, \tau ) \) is defined by
Note that \(F_{n_1, n_2, n_3} (t_1, t_2, t_3, \tau ) \) is symmetric in \(t_1, t_2, t_3\).
Given dyadic \(N_j \ge 1\), \(j = 1, 2, 3\), let us denote by \(A^N_{N_1, N_2, N_3}\) the contribution to  from \(|n_j|\sim N_j\), \(j = 1, 2, 3\), in (4.4). We first compute the \(X^{s-1, b }\)-norm of \(A^N_{N_1, N_2, N_3}\) with \(b = -\frac{1}{2} - \delta \) for \(\delta > 0\). We then interpolate it with the trivial \(X^{0, 0}\)-bound. Recall the trivial bound:
from \(|n_j|\sim N_j\), \(j = 1, 2, 3\), in (4.4). We first compute the \(X^{s-1, b }\)-norm of \(A^N_{N_1, N_2, N_3}\) with \(b = -\frac{1}{2} - \delta \) for \(\delta > 0\). We then interpolate it with the trivial \(X^{0, 0}\)-bound. Recall the trivial bound:
for any \(s, b \in {\mathbb {R}}\). Then, defining \(\kappa ({\bar{n}}) = \kappa _{\varepsilon _0, \varepsilon _1, \varepsilon _2, \varepsilon _3}(n_1, n_2, n_3)\) by
with \(\varepsilon _j \in \{-1, 1\}\) for \(j = 0,1,2,3\), it follows from (4.6), (4.4), Fubini’s theorem, Ito’s isometry, and expanding the sine functions in (4.5) in terms of the complex exponentials that
for any \(\delta > 0\), uniformly in dyadic \(N_j \ge 1\), \(j = 1, 2, 3\). By noting
we can reduce the right-hand side of (4.8) to the setting of the Hartree nonlinearity studied in [12]. In particular, from (4.8) with (4.9) and the cubic sum estimate (Lemma A.1), we obtain
where \(N_{\max } = \max (N_1, N_2, N_3)\). This provides an estimate for \(s < \alpha \) and \(b = - \frac{1}{2} - \delta < -\frac{1}{2}\).
On the other hand, using (4.4), we have
for some \(\theta > 0\). Hence, it follows from interpolating (4.10) and (4.11) and then applying the Wiener chaos estimate (Lemma 2.9) that given \(s < \alpha \), there exist small \(\delta _2 > 0\) and \(\varepsilon > 0\) such that
for any \(p \ge 1\), uniformly in dyadic \(N_j \ge 1\), \(j = 1, 2, 3\). By summing over dyadic blocks \(N_j\ge 1\), \(j = 1, 2, 3\), we obtain the bound (4.2) (with \(b = -\frac{1}{2} + \delta _2 > -\frac{1}{2}\)).
As for the convergence of  to
to  in \(X^{\alpha - 1 - \delta _1, - \frac{1}{2} + \delta _2}([0, T])\), we can simply repeat the computation above to estimate the difference
in \(X^{\alpha - 1 - \delta _1, - \frac{1}{2} + \delta _2}([0, T])\), we can simply repeat the computation above to estimate the difference  for \(M \ge N \ge 1\). Fix \(s < \alpha \). Then, in (4.8), we replace the restriction \(|n_j| \le N \) in the summation of \(n_j\), \(j = 1, 2, 3\), by \(N \le \max (|n_1|, |n_2|, |n_3|) \le M\), which allows us to gain a small negative power of N. As a result, in place of (4.10), we obtain
for \(M \ge N \ge 1\). Fix \(s < \alpha \). Then, in (4.8), we replace the restriction \(|n_j| \le N \) in the summation of \(n_j\), \(j = 1, 2, 3\), by \(N \le \max (|n_1|, |n_2|, |n_3|) \le M\), which allows us to gain a small negative power of N. As a result, in place of (4.10), we obtain
for any small \(\varepsilon > 0\) and \(M \ge N \ge 1\). Then, the interpolation argument with (4.11) as above yields that given \(s < \alpha \), there exist small \(\delta _2>0\) and \(\varepsilon > 0\) such that

for any \(p \ge 1\) and \(M \ge N \ge 1\). Then, by applying Chebyshev’s inequality and the Borel–Cantelli lemma, we conclude the almost sure convergence of  . See [51].
. See [51].
Finally, fix \(s< \alpha \). Given \(N \in {\mathbb {N}}\), let  . Then, we have
. Then, we have

for \(t \in [0, T]\), Note that from (4.4), we have \( \widehat{H}_N(n, t) \in {\mathcal {H}}_3\) and, furthermore, by the independence of \(\{B_n\}_{n \in {\mathbb {Z}}^3}\) (modulo \(B_{-n} = \overline{B}_n\)), we have
for any \(t_1, t_2 \in {\mathbb {R}}\). Then, by (4.13), Sobolev’s inequality (with finite \(r\gg 1\) such that \(r\delta _0 > 3\) for some small \( \delta _0 > 0\)), Minkowski’s integral inequality, the Wiener chaos estimate (Lemma 2.9) with (4.14), Hausdorff–Young’s inequality (in time), we have, for any \(p \ge \max (q, r) \gg 1\),

Now, by the triangle inequality: \(\langle \tau \rangle ^{\delta _0}\lesssim \langle |\tau | - \langle n \rangle \rangle ^{\delta _0} \langle n \rangle ^{\delta _0}\), Hölder’s inequality (in \(\tau \)), followed by the nonhomogeneous linear estimate (Lemma 2.5) and (4.12) (with \(p = 2\), \(M = \infty \), and s replaced by \(s + 2\delta _0 < \alpha \)), we obtain

by choosing \(\delta _0 > 0\) sufficiently small. Then, the regularity and convergence claim for  follows from applying Chebyshev’s inequality and the Borel–Cantelli lemma as before. \(\square \)
follows from applying Chebyshev’s inequality and the Borel–Cantelli lemma as before. \(\square \)
Remark 4.2
Given a function \(f \in L^2(({\mathbb {Z}}^3\times {\mathbb {R}}_+)^k)\), define the multiple stochastic integral \(I_k[f]\) by
See Appendix B for the basic definitions and properties of multiple stochastic integrals. In terms of multiple stochastic integrals, we can express (4.3) as

where \(f_{n, t}\) is defined by
for \((n_1,t_1, n_2, t_2,n_3,t_3) \in ({\mathbb {Z}}^3 \times {\mathbb {R}}) ^3\). Then, by Fubini’s theorem for multiple stochastic integrals (Lemma B.2), we have

where \({\mathcal {F}}_t\) denotes the Fourier transform in time. With this notation, it follows from Lemma B.1 that we can write the second moment of the \(X^{s, b}\)-norm of \(A^N_{N_1, N_2, N_3}\), appearing in (4.8) and (4.11), in a concise manner:
where \(f_{n, t}^{{\bar{N}}}\) is given by
In the following, for conciseness of the presentation, we express various stochastic objects as multiple stochastic integrals on \(({\mathbb {Z}}^3\times {\mathbb {R}}_+)^k\) and carry out analysis. For this purpose, we set
and use the following short-hand notation:
Note, however, that one may also carry out equivalent analysis at the level of multiple Wiener–Ito integrals as in the proof of Lemma 3.1 presented above.
Next, we briefly discuss the proof of Lemma 3.3.
Proof of Lemma 3.3
By the paraproduct decomposition (2.3), we have

In view of Lemma 2.1 with (2.19), the paraproducts  and
and  belong to \(C([0,T];W^{\alpha - \frac{1}{2} - \varepsilon ,\infty }({\mathbb {T}}^3))\) for any \(\varepsilon >0\), almost surely. Hence, it remains to study the resonant product
belong to \(C([0,T];W^{\alpha - \frac{1}{2} - \varepsilon ,\infty }({\mathbb {T}}^3))\) for any \(\varepsilon >0\), almost surely. Hence, it remains to study the resonant product  . We only study the regularity of the resonant product for a fixed time since the continuity in time and the convergence follow from a systematic modification. In the following, we show
. We only study the regularity of the resonant product for a fixed time since the continuity in time and the convergence follow from a systematic modification. In the following, we show

for any \(n \in {\mathbb {Z}}^3\) and \(N \ge 1\). Note the bound (4.17) together with Lemma 2.10 shows that the resonant product  is smoother and has (spatial) regularity \( 2\alpha - \frac{1}{2} - = (\alpha - ) + \big (\alpha - \frac{1}{2}-\big )\).
is smoother and has (spatial) regularity \( 2\alpha - \frac{1}{2} - = (\alpha - ) + \big (\alpha - \frac{1}{2}-\big )\).
As in [41], by decomposing  into components in the homogeneous Wiener chaoses \({\mathcal {H}}_k\), \(k = 2, 4\), we have
into components in the homogeneous Wiener chaoses \({\mathcal {H}}_k\), \(k = 2, 4\), we have

where  and
and  . See, for example, [43, Proposition 1.1.2] and Lemma B.4 on the product formula for multiple Wiener–Ito integrals (and it also follows from Ito’s lemma as explained in [41]). From the orthogonality of \({\mathcal {H}}_4\) and \({\mathcal {H}}_2\), we have
. See, for example, [43, Proposition 1.1.2] and Lemma B.4 on the product formula for multiple Wiener–Ito integrals (and it also follows from Ito’s lemma as explained in [41]). From the orthogonality of \({\mathcal {H}}_4\) and \({\mathcal {H}}_2\), we have

Hence, it suffices to prove (4.17) for  , \(j = 2, 4\).
, \(j = 2, 4\).
From a slight modificationFootnote 17 of (4.8) with Lemma A.2, we have

for any \(n \in {\mathbb {Z}}^3\) and \(N \ge 1\). Then, from Jensen’s inequality (see (B.2)),Footnote 18 (4.1), (4.18), and Lemma 2.8, we have

for any \(n \in {\mathbb {Z}}^3\) and \(N \ge 1\), where \(|n_1|\sim |n- n_1|\) signifies the resonant product  . This yields (4.17) for
. This yields (4.17) for  .
.
From Ito’s lemma (see also the product formula, Lemma B.4), (1.12), and (4.3) with (4.15), we have

where \(g_{n, t, t'}\) is defined by
Note that \(g_{n, t, t'}(z_2, z_3)\) is symmetric (in \(z_2\) and \(z_3\)). From Fubini’s theorem (Lemma B.2), we have

We now apply Lemma B.1 to compute the second moment of(4.21). Then, with \(\kappa ({\bar{n}})\) as in (4.7), it follows from expanding the sine functions in (4.20) in terms of the complex exponentials and switching the order of integration in \(t'\) and \(t_1\) that

Under the condition \(|n_1| \sim |n_{123}|\) and \(n = n_2 + n_3\), we have \(|n_1|\gtrsim |n|\). Then, by applying the basic resonant estimate (Lemma A.3) and Lemma 2.8, we obtain

This computation with Lemma 2.10 shows that  is even smoother and has (spatial) regularity \(4\alpha -\).
is even smoother and has (spatial) regularity \(4\alpha -\).
Therefore, putting (4.19) and (4.22) together, we obtain the desired bound (4.17). \(\square \)
4.2 Quintic stochastic term
In this subsection, we present the proof of Lemma 3.4 (i) on the quintic stochastic process  defined in (1.22). In view of Lemma 2.5, we prove the following bound; given any \(\varepsilon >0\) and sufficiently small \(\delta _2 >0\), there exists \(\theta >0\) such that
defined in (1.22). In view of Lemma 2.5, we prove the following bound; given any \(\varepsilon >0\) and sufficiently small \(\delta _2 >0\), there exists \(\theta >0\) such that

for any \(p \ge 1\) and \(0 < T \le 1\), uniformly in \(N \in {\mathbb {N}}\).
We start by computing the space-time Fourier transform of  with a time cutoff. As shown in (1.22), the quintic stochastic objects
with a time cutoff. As shown in (1.22), the quintic stochastic objects  is a convolution of
is a convolution of  in (1.15) and
in (1.15) and  in (1.14):
in (1.14):

Using Lemma B.2, we can write  and
and  as multiple stochastic integrals:
as multiple stochastic integrals:

where \(f_{n, t, t'}\) and \(g_{n, t}\) are defined by
By the product formula (Lemma B.4) to (4.24), we can decompose  into the components in the homogeneous Wiener chaoses \({\mathcal {H}}_k\), \(k = 1, 3, 5\):
into the components in the homogeneous Wiener chaoses \({\mathcal {H}}_k\), \(k = 1, 3, 5\):

where  ,
,  , and
, and  . By taking the Fourier transforms in time, the relation (4.27) still holds. Then, by using the orthogonality of \({\mathcal {H}}_5\), \({\mathcal {H}}_3\), and \({\mathcal {H}}_1\), we have
. By taking the Fourier transforms in time, the relation (4.27) still holds. Then, by using the orthogonality of \({\mathcal {H}}_5\), \({\mathcal {H}}_3\), and \({\mathcal {H}}_1\), we have

Hence, it suffices to prove (4.23) for each  , \(j = 1, 3, 5\).
, \(j = 1, 3, 5\).
Case (i): Non-resonant term
 . From (4.25) and (4.26), we have
. From (4.25) and (4.26), we have

where \(f^{(5)}_{n, t}\) is defined by
Let \({{\,\mathrm{\mathtt {Sym}}\,}}(f^{(5)}_{n, t})\) be the symmetrization of \(f^{(5)}_{n, t}\) defined in (B.1). Then, from Lemma B.1 (ii), we have

Then, by taking the temporal Fourier transform and applying Fubini’s theorem (Lemma B.2), we have

Then, by (4.6), Fubini’s theorem, and Lemma B.1 (iii) with (4.15) and (4.16), we have

where \({\bar{z}} = (z_1, \dots , z_5)\).
By expanding the sine functions in (4.28) in terms of the complex exponentials, we have
where \(F_1(z_1, \dots , z_5)\) is independent of t and \( t'\) with \(|F_1|\le 1\). Here, \({\mathcal {E}}\), \(\widehat{\varepsilon }\), \(\kappa _1({\bar{n}})\), and \(\kappa _2({\bar{n}})\) are defined by
By integrating in \(t'\), we have
where \(t_{123}^* = \max (t_1, t_2, t_3)\). Then, from (4.30) and (4.32), we have
where \(\kappa _3({\bar{n}})\) and \(\kappa _4({\bar{n}})\) are defined by
Given dyadic \(N_j \ge 1\), \(j = 1,2,3,4,5\), we denote by \(B^N_{N_1,\cdots ,N_5}\) the contribution to  from \(|n_j| \sim N_j\) in (4.33). Let \({\mathcal {E}}_0 = {\mathcal {E}}\cup \{\varepsilon _0 \in \{-1, 1\}\}\) and \(N_{\max } = \max (N_1,\dots ,N_5)\). Then, from (4.29), Jensen’s inequality (B.2), and (4.33) with (1.23), we have
from \(|n_j| \sim N_j\) in (4.33). Let \({\mathcal {E}}_0 = {\mathcal {E}}\cup \{\varepsilon _0 \in \{-1, 1\}\}\) and \(N_{\max } = \max (N_1,\dots ,N_5)\). Then, from (4.29), Jensen’s inequality (B.2), and (4.33) with (1.23), we have
for some \(\theta > 0\), provided that \(\delta > 0\). In the last step, we used the following bound:
for \(\delta > 0\). Then, by applying Lemma A.4 to (4.35), we obtain
for some \(\delta _0>0\), provided that \(\varepsilon , \delta > 0\). Using (4.29) and (4.33), a crude bound shows
for some (possibly large) \(K > 0\). By interpolating (4.36) and (4.37), applying the Winner chaos estimate (Lemma 2.9), and then summing over dyadic \(N_j\), \(j = 1, \dots ,5\), we obtain

for some \(\theta >0\), uniformly in \(N \in {\mathbb {N}}\). Proceeding as in the end of the proof of Lemma 3.1 (ii) on  , a slight modification of the argument above yields convergence of
, a slight modification of the argument above yields convergence of  to
to  . Since the required modification is straightforward, we omit details. A similar comment applies to
. Since the required modification is straightforward, we omit details. A similar comment applies to  and
and  studied below.
studied below.
Case (ii): Single-resonance term
 . In view of the product formula (Lemma B.4)Footnote 19 and Definition B.3 together with (4.25) and (4.26), we have
. In view of the product formula (Lemma B.4)Footnote 19 and Definition B.3 together with (4.25) and (4.26), we have

where \(f^{(3)}_{n, t}\) is defined by
By the Wiener chaos estimate (Lemma 2.9) and Hölder’s inequality, we have

for small \(\delta _2> 0\). Hence, (4.23) follows once we prove

for \(\varepsilon >0\), uniformly in \(N \in {\mathbb {N}}\).
With the symmetrization \({{\,\mathrm{\mathtt {Sym}}\,}}(f^{(3)}_{n, t})\) defined in (B.1), it follows from Lemma B.1 and Jensen’s inequality (B.2) that

where \({\mathfrak {I}}^{(3)} (z_1, z_2, t_4) \) is defined by
By switching the order of the integrals in (4.41) (with \(a = \max (t_1,t_2)\)):
and integrating in \(t'\) first, we have
where \(\kappa _2({\bar{n}})\) is as in (4.31). Hence, from (4.40), (4.42), and Lemma A.3, we obtain

By applying Lemma 2.8 iteratively, we then obtain

provided that \(\delta _1 > 0\). This yields (4.39).
Case (iii): Double-resonance term
 . As in Case (ii), from the product formula (Lemma B.4) and Definition B.3 together with (4.25) and (4.26), we have
. As in Case (ii), from the product formula (Lemma B.4) and Definition B.3 together with (4.25) and (4.26), we have

where \(f^{(1)}_{n, t}\) is defined by
Arguing as in (4.38), it suffices to show

for \(\varepsilon >0\), uniformly in \(N \in {\mathbb {N}}\).
With the symmetrization \({{\,\mathrm{\mathtt {Sym}}\,}}(f^{(1)}_{n, t})\) defined in (B.1), it follows from Lemma B.1 and Jensen’s inequality (B.2) that

where \({\mathfrak {I}}^{(1)} (z_1) \) is defined by
By switching the order of the integrals in (4.45) and integrating in \(t'\) first, we have
where \(\kappa _2({\bar{n}})\) is as in (4.31). Hence, from (4.44) and (4.46), we obtain

Now, apply the dyadic decompositions \(|n_j|\sim N_j\), \(j = 1, 2, 3\). By noting that \(\langle n_{12} \rangle ^\alpha \lesssim N_1^\alpha N_2^\alpha \) and that \(|\kappa _2({\bar{n}}) - m |\le 1\) implies \(|m| \lesssim N_{\max } = \max (N_1, N_2, N_3)\), it follows from Lemma A.5 that

provided that \(\varepsilon > 0\), where \(\gamma =\gamma (\varepsilon , \alpha ) > 0\) is sufficiently small. This yields (4.43).
This concludes the proof of Lemma 3.4 (i).
4.3 Septic stochastic term
In this subsection, we present the proof of Lemma 3.4 (ii) on the septic stochastic term  defined in (1.24). Proceeding as in (4.38), it suffices to show
defined in (1.24). Proceeding as in (4.38), it suffices to show

for \(\varepsilon > 0\), uniformly in \(N \in {\mathbb {N}}\). As in the previous subsections, we decompose  into the components in the homogeneous Wiener chaoses \({\mathcal {H}}_k\), \(k = 1, 3, 5, 7\):
into the components in the homogeneous Wiener chaoses \({\mathcal {H}}_k\), \(k = 1, 3, 5, 7\):

where  . From the orthogonality of \({\mathcal {H}}_k\), we have
. From the orthogonality of \({\mathcal {H}}_k\), we have

Hence, it suffices to prove (4.47) for ,  \(j = 0,1,2,3\).
\(j = 0,1,2,3\).
Case (i): Non-resonant septic term We first study the non-resonant term  . From (1.12) and (4.25) with (4.26) and (4.15), we have
. From (1.12) and (4.25) with (4.26) and (4.15), we have

where \(f^{(7)}_{n, t}\) is defined by
By defining the amplitude \(\Phi \) by
we have
Let \(\kappa _2({\bar{n}})\) be as in (4.31). Then, from (4.51), we have
where \(K (n_1,n_2,n_3)\) is defined by
Note that from Lemma A.1, we have
for any \(\gamma > 0\). In view of (4.52) and (4.31), \(K (n_1,n_2,n_3)\) depends on \(\varepsilon _{123}, \varepsilon _1, \varepsilon _2, \varepsilon _3 \in \{-1, 1\}\). In the following, however, we drop the dependence on \(\varepsilon _{123}, \varepsilon _1, \varepsilon _2, \varepsilon _3 \in \{-1, 1\}\) since (4.53) uniformly in \(\varepsilon _{123}, \varepsilon _1, \varepsilon _2, \varepsilon _3 \in \{-1, 1\}\). The same comment applies to (4.54) below.
With the symmetrization \({{\,\mathrm{\mathtt {Sym}}\,}}(f^{(7)}_{n, t})\) defined in (B.1), it follows from Lemma B.1, Jensen’s inequality (B.2), and Lemma 2.8 (to sum over \(n_7\)) that

for some \(\theta > 0\), provided that \(\delta _1 > 0\). By applying the dyadic decomposition \(|n_j| \sim N_j\), \(j = 1, \dots , 7\), and then applying (4.53), we then obtain

as long as \(\gamma < 2\alpha \). This proves (4.47).
Case (ii): General septic terms As we saw in the previous subsections, all other terms in (4.48) come from the contractions of the product of  . In order to fully describe these terms, we recall the notion of a pairing from [12, Definition 4.30] to describe the structure of the contractions.
. In order to fully describe these terms, we recall the notion of a pairing from [12, Definition 4.30] to describe the structure of the contractions.
Definition 4.3
(pairing) Let \(J\ge 1\). We call a relation \({\mathcal {P}} \subset \{1,\dots ,J\}^2\) a pairing if
-
(i)
\({\mathcal {P}}\) is reflexive, i.e. \((j,j) \notin {\mathcal {P}}\) for all \(1 \le j \le J\),
-
(ii)
\({\mathcal {P}}\) is symmetric, i.e. \((i,j) \in {\mathcal {P}}\) if and only if \((j,i) \in {\mathcal {P}}\),
-
(iii)
\({\mathcal {P}}\) is univalent, i.e. for each \(1 \le i \le J\), \((i,j) \in {\mathcal {P}}\) for at most one \(1 \le j \le J\).
If \((i,j) \in {\mathcal {P}}\), the tuple (i, j) is called a pair. If \(1 \le j \le J\) is contained in a pair, we say that j is paired. With a slight abuse of notation, we also write \(j \in {\mathcal {P}}\) if j is paired. If j is not paired, we also say that j is unpaired and write \(j \notin {\mathcal {P}}\). Furthermore, given a partition \({\mathcal {A}} = \{A_\ell \}_{\ell = 1}^L\) of \(\{1, \cdots , J\}\), we say that \({\mathcal {P}}\) respects \({\mathcal {A}}\) if \(i,j\in A_\ell \) for some \(1 \le \ell \le L\) implies that \((i,j)\notin {\mathcal {P}}\). Namely, \({\mathcal {P}}\) does not pair elements of the same set \(A_\ell \in {\mathcal {A}}\). We say that \((n_1, \dots , n_J) \in ({\mathbb {Z}}^3)^J\) is admissible if \((i,j) \in {\mathcal {P}}\) implies that \(n_i + n_j = 0\).
In order to represent  , \(k = 1, 3, 5\), as multiple stochastic integrals as in (4.49), we start with (4.50) and perform a contraction over the variables \(z_j = (n_j, t_j)\), namely, we consider a (non-trivial)Footnote 20 pairing on \(\{1, \dots , 7\}\). Then, by integrating in \(t'\) and \(t''\) first in (4.50) after a contraction, a computation analogous to that in Case (i) yields
, \(k = 1, 3, 5\), as multiple stochastic integrals as in (4.49), we start with (4.50) and perform a contraction over the variables \(z_j = (n_j, t_j)\), namely, we consider a (non-trivial)Footnote 20 pairing on \(\{1, \dots , 7\}\). Then, by integrating in \(t'\) and \(t''\) first in (4.50) after a contraction, a computation analogous to that in Case (i) yields

where K is as in (4.52) and the non-resonant frequency \(n_{\text {nr}}\) is defined by
Here, \(\Pi _k\) denotes the collection of pairings \({\mathcal {P}}\) on \(\{1, \dots , 7\}\) such that (i) \({\mathcal {P}}\) respects the partition \({\mathcal {A}}= \big \{\{1,2,3\}, \{4,5,6\}, \{7\}\big \}\) and (ii) \(|{\mathcal {P}}| = 7-k\) (when we view \({\mathcal {P}}\) as a subset of \(\{1, \dots , 7\}\)). Note that the estimate on  discussed in Case (i) is a special case of (4.54) with \({\mathcal {P}} = \varnothing \). By applying Lemma A.6 (with (1.23)), we then obtain
discussed in Case (i) is a special case of (4.54) with \({\mathcal {P}} = \varnothing \). By applying Lemma A.6 (with (1.23)), we then obtain

provided that \(\varepsilon >0 \). This concludes the proof of Lemma 3.4 (ii).
4.4 Random operator
In this subsection, we present the proof of Lemma 3.5 on the random operator  defined in (1.21).
defined in (1.21).
In view of (3.1) and (3.2) in the definition of \( {\mathcal {L}}^{s_1, s_2, b}_{T_0}\), (1.21), and the nonhomogeneous linear estimate (Lemma 2.5), it suffices to show the following bound:

for some small \(\delta _1, \delta _2 >0\) and any \(p \ge 1\), uniformly in \(N \in {\mathbb {N}}\). From (2.9), we see that (4.56) follows once we prove

Furthermore, by inserting a sharp time-cutoff function on [0, 1], we may drop the supremum in T and reduce the bound (4.57) to proving

As in the proof of Lemma 3.1 (ii), we first prove

namely with \(b = - \frac{1}{2} - \delta < - \frac{1}{2}\) on the \(X^{s, b}\)-norm of  for \(\delta >0\). In fact, we prove a frequency-localized version of (4.59) (see (4.72) below) and interpolate it with a trivial \(X^{0, 0}\) estimate (see (4.73) below), as in the proof of Lemma 3.1 (ii) and Lemma 3.4 (i), to establish (4.58) with \(b = - \frac{1}{2} + 2\delta _2 > - \frac{1}{2}\)
for \(\delta >0\). In fact, we prove a frequency-localized version of (4.59) (see (4.72) below) and interpolate it with a trivial \(X^{0, 0}\) estimate (see (4.73) below), as in the proof of Lemma 3.1 (ii) and Lemma 3.4 (i), to establish (4.58) with \(b = - \frac{1}{2} + 2\delta _2 > - \frac{1}{2}\)
We start by computing the space-time Fourier transform of  . From (4.25) and (4.26), we have
. From (4.25) and (4.26), we have

where \(g_{n - n_3, t}(z_1, z_2)\) is as in (4.26). Now, write \(v = v_1 + v_{-1}\), where
Then, by noting \(|\widehat{v}(n, \tau )|^2 = |\widehat{v}_{1}(n, \tau )|^2+ |\widehat{v}_{-1}(n, \tau )|^2\), we have
With this in mind, we write

where \(\varepsilon _0, \varepsilon _3 \in \{-1, 1\}\) and the kernel \(H = H^{\varepsilon _0, \varepsilon _3}\) is given by
By Fubini’s theorem (Lemma B.2), we can write H as
where \(h_{n, n_3, \tau , \tau _3}\) is given by
Then, by (4.6), (4.61), Cauchy–Schwarz’s inequality, and (4.60), we have

as long as \(\delta , \delta _2 > 0\), where, in the last step, we used Minkowski’s integral inequality followed by Hölder’s inequality (in \(\tau \) and \(\tau _3\)). Here, we viewed \(H(n,n_3,\tau ,\tau _3)\) (for fixed \(\tau , \tau _3 \in {\mathbb {R}}\)) as an infinite dimensional matrix operator mapping from \(\ell ^2_{n_3}\) into \(\ell ^2_n\). Hence, the estimate (4.59) is reduced to proving
As mentioned above, we instead establish a frequency-localized version of (4.64):
for some small \(\delta _0 > 0\), uniformly in dyadic \(N_1, N_2, N_3\ge 1\), where \(N_{\max } = \max (N_1, N_2, N_3)\) and \(H_{N_1, N_2, N_3}\) is defined by (4.62) and (4.63) with extra frequency localizations \({\mathbf {1}}_{|n_j|\sim N_j}\), \(j = 1, 2, 3\). Namely, we have
where \(h^{N_1, N_2, N_3}_{n, n_3, \tau , \tau _3}\) is given by
with \(\kappa ({\bar{n}})\) as in (4.7).
For \(m \in {\mathbb {Z}}\), define the tensor \({\mathfrak {h}}^m\) by
Then, from (4.66), (4.67), and (4.68), we have
where \({\mathfrak {H}}^m_{n_3, \tau , \tau _3}\) is given by
Performing t-integration, we have
Then from Lemma C.3, (4.70), and Lemma C.2 (with (1.23)), there exists \(\delta _3 > 0\) such that
for any \(\varepsilon >0\), provided that \(\delta _1 < \alpha \), which is needed to apply Lemma C.2. Hence, by noting that the condition \(|\kappa ({\bar{n}}) - m|\le 1\) implies \(|m| \lesssim N_{\max }\) and summing over \(m \in {\mathbb {Z}}\), the bound (4.65) follows from (4.69) and (4.71) (by taking \(\varepsilon >0\) sufficiently small), which in turn implies

for some \(\delta _0 > 0\), where \(v_{N_3} = {\mathcal {F}}_x^{-1} ({\mathbf {1}}_{|n|\sim N_3} \widehat{v}(n))\) and

Namely, the frequencies \(n_1\), \(n_2\), and \(n_3\) are localized to the dyadic blocks \(\{|n_j|\sim N_j\}\), \(j = 1, 2, 3\).
On the other hand, a crude bound shows

for some (possibly large) \(K > 0\). By interpolating (4.72) and (4.73) and then summing over dyadic \(N_j\), \(j = 1, \dots ,3\), we obtain (4.58) for some small \( \delta _2 > 0\).
Lastly, as for the convergence of  to
to  , we can simply repeat the computation above to estimate the difference
, we can simply repeat the computation above to estimate the difference  for \(M \ge N \ge 1\). In considering the difference of the tensors \({\mathfrak {h}}^m\) in (4.68), we then obtain a new restriction \( \max (|n_1|, |n_2|) \gtrsim N\), which allows us to gain a small negative power of N. As a result, we obtain
for \(M \ge N \ge 1\). In considering the difference of the tensors \({\mathfrak {h}}^m\) in (4.68), we then obtain a new restriction \( \max (|n_1|, |n_2|) \gtrsim N\), which allows us to gain a small negative power of N. As a result, we obtain

for some small \(\varepsilon , \delta _0' > 0\), Then, interpolating this with (4.73) and summing over dyadic blocks, we then obtain

for any \(p \ge 1\) and \(M \ge N \ge 1\). Then, by applying Chebyshev’s inequality, summing over \(N \in {\mathbb {N}}\), and applying the Borel–Cantelli lemma, we conclude the almost sure convergence of  . This concludes the proof of Lemma 3.5.
. This concludes the proof of Lemma 3.5.
Data availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Notes
In this discussion, we only discuss spatial regularities. Moreover, we do not worry about the regularity of the initial data \((u_0, u_1)\).
Here, non-triviality means that the limiting process u is not zero or a linear solution. As we see below, the limiting process u admits a decomposition
 , where the residual term v satisfies the nonlinear equation (1.25). See Remark 1.4 (ii) on a triviality result for the unrenormalized equation. See also [30, 47, 51, 54] for related triviality results.
, where the residual term v satisfies the nonlinear equation (1.25). See Remark 1.4 (ii) on a triviality result for the unrenormalized equation. See also [30, 47, 51, 54] for related triviality results.In [12], Bringmann studied the corresponding deterministic Hartree NLW with random initial data.
We point out that the scope of the papers [12, 48] goes much further than what is described here. The main goal of [48] is to study the focusing problem, in particular the (non-)construction of the focusing Gibbs measure associated to the focusing Hartree SNLW. They identified the critical value \(\beta = 2\) and proved sharp global well-posedness of the focusing problem (with a small coefficient in front of the nonlinearity when \(\beta = 2\)). On the other hand, the main goal in [12] is the construction of global-in-time dynamics in the defocusing case, where there was a significant difficulty in adapting Bourgain’s invariant measure argument [8, 9]. This is due to (i) the singularity of the associated Gibbs measure with respect to the base Gaussian free field for \(0 < \beta \le \frac{1}{2}\) [11, 48] and (ii) the paracontrolled structure imposed in the local theory, which must be propagated in the construction of global-in-time solutions. See the introductions of [12, 48] for further discussion.
Or a general \(\gamma \)-radonifying operator \(\phi \) as in [21], where the authors proved local well-posedness of the one-dimensional stochastic cubic nonlinear Schrödinger equation with an almost space-time white noise.
Namely, the Langevin equation with the momentum \(v = \partial _tu\).
By convention, we endow \({\mathbb {T}}^3\) with the normalized Lebesgue measure \((2\pi )^{-3} dx\).
Hereafter, we use \(a-\) (and \(a+\)) to denote \(a- \varepsilon \) (and \(a+ \varepsilon \), respectively) for arbitrarily small \(\varepsilon > 0\). If this notation appears in an estimate, then an implicit constant is allowed to depend on \(\varepsilon > 0\) (and it usually diverges as \(\varepsilon \rightarrow 0\)).
In our spatially homogeneous setting, the variance \(\sigma _N(t)\) is independent of \(x \in {\mathbb {T}}^3\).
Namely, if we only take into account the (uniformly bounded in N) regularity \(3\alpha - \frac{3}{2} -\) of
 and one degree of smoothing from the Duhamel integral operator \({\mathcal {I}}\) without taking into account the product structure and the oscillatory nature of the linear wave propagator.
and one degree of smoothing from the Duhamel integral operator \({\mathcal {I}}\) without taking into account the product structure and the oscillatory nature of the linear wave propagator.By “regularity”, we mean the spatial regularity s of
 as an element in \(C([0,T];W^{s,\infty }({\mathbb {T}}^3))\), uniformly bounded in \(N \in {\mathbb {N}}\).
as an element in \(C([0,T];W^{s,\infty }({\mathbb {T}}^3))\), uniformly bounded in \(N \in {\mathbb {N}}\).As for the unknown v, we measure its regularity in (the local-in-time version of) the \(X^{s, \frac{1}{2}+}\)-norm.
We also mention a recent preprint [61], where the random matrix approach is also used to prove probabilistic local well-posedness of the Zakharov–Yukawa system on the two-dimensional torus \({\mathbb {T}}^2\).
For simplicity, we write the definition of the Ornstein-Uhlenbeck operator L when \(B = {\mathbb {R}}^d\).
We impose \(h \ge - t\) such that \(t + h \ge 0\).
Namely, with \(s = 0\) and dropping the summation over n in (4.8).
Note that both \(f_{n, t, t'}\) and \(g_{n, t}\) in (4.26) are symmetric in their arguments.
Namely, \({\mathcal {P}} = \varnothing \).
By identifying a function \(f \in \ell ^2_{\pmb {n}}(({\mathbb {Z}}^3)^k;L^2_{t, \pmb {t}}([0, T]^{k+1}))\) with a sequence \(\{f_{\pmb {n}}\}_{\pmb {n} \in ({\mathbb {Z}}^3)^k}\subset L^2_{t, \pmb {t}}([0, T]^{k+1})\), we can approximate each \(f_{\pmb {n}}\) by a smooth function \(\varphi _{\pmb {n}}\) such that \(\Vert f_{\pmb {n}} - \varphi _{\pmb {n}}\Vert _{L^2_{t, \pmb {t}}([0, T]^{k+1})} < \varepsilon _{\pmb {n}}\) such that \(\varepsilon _{\pmb {n}}\) is symmetric in \(\pmb {n}\) and \(\sum _{\pmb {n} \in ({\mathbb {Z}}^3)^k} \varepsilon _{\pmb {n}} = \varepsilon \). Then, the function \(\varphi \cong \{\varphi _{\pmb {n}}\}_{\pmb {n}\in ({\mathbb {Z}}^3)^k}\) approximates f within distance \(\varepsilon \) in \(\ell ^2_{\pmb {n}}(({\mathbb {Z}}^3)^k;L^2_{t, \pmb {t}}([0, T]^{k+1}))\). Since f is symmetric, we can choose \(\varphi \) to be symmetric.
References
Bahouri, H., Chemin, J.-Y., Danchin, R.: Fourier analysis and nonlinear partial differential equations. In: Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 343, pp. xvi+523. Springer, Heidelberg (2011)
Bényi, Á., Oh, T., Pocovnicu, O.: Wiener randomization on unbounded domains and an application to almost sure well-posedness of NLS. In: Excursions in Harmonic Analysis, vol. 4, pp. 3–25, Appl. Numer. Harmon. Anal. Birkhäuser/Springer, Cham (2015)
Bényi, Á., Oh, T., Pocovnicu, O.: On the probabilistic Cauchy theory of the cubic nonlinear Schrödinger equation on \({{\mathbb{R}}}^3\), \(d\ge 3\). Trans. Am. Math. Soc. Ser. B 2, 1–50 (2015)
Bényi, Á., Oh, T., Pocovnicu, O.: Higher order expansions for the probabilistic local Cauchy theory of the cubic nonlinear Schrödinger equation on \({{\mathbb{R}}}^3\). Trans. Am. Math. Soc. B 6, 114–160 (2019)
Bogachev, V.: Gaussian measures. In: Mathematical Surveys and Monographs, vol. 62, pp. xii+433. American Mathematical Society, Providence (1998)
Bony, J.-M.: Calcul symbolique et propagation des singularités pour les équations aux dérivées partielles non linéaires. Ann. Sci. École Norm. Sup. 14(2), 209–246 (1981)
Bourgain, J.: Fourier transform restriction phenomena for certain lattice subsets and applications to nonlinear evolution equations, I: Schrödinger equations. Geom. Funct. Anal. 3, 107–156 (1993)
Bourgain, J.: Periodic nonlinear Schrödinger equation and invariant measures. Commun. Math. Phys. 166(1), 1–26 (1994)
Bourgain, J.: Invariant measures for the 2D-defocusing nonlinear Schrödinger equation. Commun. Math. Phys. 176(2), 421–445 (1996)
Bourgain, J.: Invariant measures for the Gross–Piatevskii equation. J. Math. Pures Appl. 76(8), 649–702 (1997)
Bringmann, B.: Invariant Gibbs measures for the three-dimensional wave equation with a Hartree nonlinearity I: measures. Stoch. Partial Differ. Equ. Anal. Comput. (2021). https://doi.org/10.1007/s40072-021-00193-y
Bringmann, B.: Invariant Gibbs measures for the three-dimensional wave equation with a Hartree nonlinearity II: dynamics, to appear in J. Eur. Math. Soc
Burq, N., Tzvetkov, N.: Probabilistic well-posedness for the cubic wave equation. J. Eur. Math. Soc. (JEMS) 16(1), 1–30 (2014)
Catellier, R., Chouk, K.: Paracontrolled distributions and the 3-dimensional stochastic quantization equation. Ann. Probab. 46(5), 2621–2679 (2018)
Da Prato, G., Zabczyk, J.: Stochastic equations in infinite dimensions. In: Encyclopedia of Mathematics and its Applications, 2nd edn, vol. 152, pp. xviii+493. Cambridge University Press, Cambridge (2014)
de Bouard, A., Debussche, A.: The stochastic nonlinear Schrödinger equation in \(H^1\). Stoch. Anal. Appl. 21(1), 97–126 (2003)
Deng, Y., Nahmod, A., Yue, H.: Invariant Gibbs measures and global strong solutions for nonlinear Schrödinger equations in dimension two. arXiv:1910.08492 [math.AP]
Deng, Y., Nahmod, A., Yue, H.: Random tensors, propagation of randomness, and nonlinear dispersive equations. Invent. Math. (2021). https://doi.org/10.1007/s00222-021-01084-8
Deya, A.: A nonlinear wave equation with fractional perturbation. Ann. Probab. 47(3), 1775–1810 (2019)
Deya, A.: On a non-linear 2D fractional wave equation. Ann. Inst. Henri Poincaré Probab. Stat. 56(1), 477–501 (2020)
Forlano, J., Oh, T., Wang, Y.: Stochastic cubic nonlinear Schrödinger equation with almost space-time white noise. J. Aust. Math. Soc. 109(1), 44–67 (2020)
Ginibre, J., Tsutsumi, Y., Velo, G.: On the Cauchy problem for the Zakharov system. J. Funct. Anal. 151(2), 384–436 (1997)
Ginibre, J., Velo, G.: Generalized Strichartz inequalities for the wave equation. J. Funct. Anal. 133, 50–68 (1995)
Gubinelli, M., Imkeller, P., Perkowski, N.: Paracontrolled distributions and singular PDEs. Forum Math. Pi 3, e6, 75 (2015)
Gubinelli, M., Koch, H., Oh, T.: Renormalization of the two-dimensional stochastic nonlinear wave equations. Trans. Am. Math. Soc. 370(10), 7335–7359 (2018)
Gubinelli, M., Koch, H., Oh, T.: Paracontrolled approach to the three-dimensional stochastic nonlinear wave equation with quadratic nonlinearity, to appear in J. Eur. Math. Soc
Gubinelli, M., Koch, H., Oh, T., Tolomeo, L.: Global dynamics for the two-dimensional stochastic nonlinear wave equations. Int. Math. Res. Not. (2021). https://doi.org/10.1093/imrn/rnab
Hadac, M., Herr, S., Koch, H.: Well-posedness and scattering for the KP-II equation in a critical space. Ann. Inst. H. Poincaré Anal. Non Linéaire 26 (2009), no. 3, 917–941. Erratum to “Well-posedness and scattering for the KP-II equation in a critical space”, Ann. Inst. H. Poincaré Anal. Non Linéaire 27, no. 3, 971–972 (2010)
Hairer, M.: A theory of regularity structures. Invent. Math. 198(2), 269–504 (2014)
Hairer, M., Ryser, M.D., Weber, H.: Triviality of the 2D stochastic Allen–Cahn equation. Electron. J. Probab. 17(39), 14 (2012)
Herr, S., Tataru, D., Tzvetkov, N.: Global well-posedness of the energy-critical nonlinear Schrödinger equation with small initial data in \(H^1({{\mathbb{T}}}^3)\). Duke Math. J. 159(2), 329–349 (2011)
Keel, M., Tao, T.: Endpoint Strichartz estimates. Am. J. Math. 120(5), 955–980 (1998)
Killip, R., Stovall, B., Visan, M.: Blowup behaviour for the nonlinear Klein–Gordon equation. Math. Ann. 358(1–2), 289–350 (2014)
Klainerman, S., Machedon, M.: Space-time estimates for null forms and the local existence theorem. Commun. Pure Appl. Math. 46, 1221–1268 (1993)
Klainerman, S., Selberg, S.: Bilinear estimates and applications to nonlinear wave equations. Commun. Contemp. Math. 4(2), 223–295 (2002)
Klainerman, S., Tataru, D.: On the optimal local regularity for Yang–Mills equations in \({{\mathbb{R}}}^{4+1}\). J. Am. Math. Soc. 12(1), 93–116 (1999)
Koch, H., Tataru, D.: A priori bounds for the 1D cubic NLS in negative Sobolev spaces. Int. Math. Res. Not. no. 16, Art. ID rnm053, 36 (2007)
Lindblad, H., Sogge, C.: On existence and scattering with minimal regularity for semilinear wave equations. J. Funct. Anal. 130, 357–426 (1995)
Mourrat, J.-C., Weber, H.: Global well-posedness of the dynamic \(\Phi ^4\) model in the plane. Ann. Probab. 45(4), 2398–2476 (2017)
Mourrat, J.-C., Weber, H.: The dynamic \(\Phi ^4_3\) model comes down from infinity. Commun. Math. Phys. 356(3), 673–753 (2017)
Mourrat, J.-C., Weber, H., Xu, W.: Construction of \(\Phi ^4_3\) diagrams for pedestrians. In: From Particle Systems to Partial Differential Equations, Springer Proceedings of Mathematics and Statistics, vol. 209, pp. 1–46, Springer, Cham (2017)
Nelson, E.: A quartic interaction in two dimensions. In: 1966 Mathematical Theory of Elementary Particles (Proc. Conf., Dedham, Mass.), pp. 69–73. M.I.T. Press, Cambridge (1965)
Nualart, D.: The Malliavin calculus and related topics. In: Probability and Its Applications (New York), 2nd edn, pp. xiv+382. Springer, Berlin (2006)
Oh, T., Okamoto, M.: On the stochastic nonlinear Schrödinger equations at critical regularities. Stoch. Partial Differ. Equ. Anal. Comput. 8(4), 869–894 (2020)
Oh, T., Okamoto, M.: Comparing the stochastic nonlinear wave and heat equations: a case study. Electron. J. Probab. 26, paper no. 9, 44 (2021)
Oh, T., Okamoto, M., Pocovnicu, O.: On the probabilistic well-posedness of the nonlinear Schrödinger equations with non-algebraic nonlinearities. Discrete Contin. Dyn. Syst. A 39(6), 3479–3520 (2019)
Oh, T., Okamoto, M., Robert, T.: A remark on triviality for the two-dimensional stochastic nonlinear wave equation. Stoch. Process. Appl. 130(9), 5838–5864 (2020)
Oh, T., Okamoto, M., Tolomeo, L.: Focusing \(\Phi ^4_3\)-model with a Hartree-type nonlinearity (2020). arXiv:2009.03251 [math.PR]
Oh, T., Okamoto, M., Tolomeo, L.: Stochastic quantization of the \(\Phi ^3_3\)-model. arXiv:2108.06777 [math.PR]
Oh, T., Okamoto, M., Tzvetkov, N.: Uniqueness and non-uniqueness of the Gaussian free field evolution under the two-dimensional Wick ordered cubic wave equation, preprint
Oh, T., Pocovnicu, O., Tzvetkov, N.: Probabilistic local well-posedness of the cubic nonlinear wave equation in negative Sobolev spaces, to appear in Ann. Inst. Fourier (Grenoble)
Oh, T., Pocovnicu, O., Wang, Y.: On the stochastic nonlinear Schrödinger equations with non-smooth additive noise. Kyoto J. Math. 60(4), 1227–1243 (2020)
Oh, T., Robert, T., Tzvetkov, N.: Stochastic nonlinear wave dynamics on compact surfaces. arXiv:1904.05277 [math.AP]
Oh, T., Robert, T., Sosoe, P., Wang, Y.: On the two-dimensional hyperbolic stochastic sine-Gordon equation. Stoch. Partial Differ. Equ. Anal. Comput. 9(1), 1–32 (2021)
Oh, T., Robert, T., Sosoe, P., Wang, Y.: Invariant Gibbs dynamics for the dynamical sine-Gordon model. Proc. R. Soc. Edinb. Sect. A 151(5), 1450–1466 (2021)
Oh, T., Robert, T., Wang, Y.: On the parabolic and hyperbolic Liouville equations. Commun. Math. Phys. 387(3), 1281–1351 (2021)
Oh, T., Thomann, L.: Invariant Gibbs measure for the 2-\(d\) defocusing nonlinear wave equations. Ann. Fac. Sci. Toulouse Math. 29(1), 1–26 (2020)
Pocovnicu, O.: Probabilistic global well-posedness of the energy-critical defocusing cubic nonlinear wave equations on \({{\mathbb{R}}}^4\). J. Eur. Math. Soc. (JEMS) 19, 2321–2375 (2017)
Richards, G.: Invariance of the Gibbs measure for the periodic quartic gKdV. Ann. Inst. H. Poincaré Anal. Non Linéaire 33(3), 699–766 (2016)
Ryang, S., Saito, T., Shigemoto, K.: Canonical stochastic quantization. Progr. Theor. Phys. 73(5), 1295–1298 (1985)
Seong, K.: Invariant Gibbs dynamics for the two-dimensional Zakharov–Yukawa system. arXiv:2111.11195 [math.AP]
Shigekawa, I.: Stochastic analysis. In: Translated from the 1998 Japanese Original by the Author. Translations of Mathematical Monographs. Iwanami Series in Modern Mathematics, vol. 224, pp. xii+182. American Mathematical Society, Providence (2004)
Simon, B.: The \(P(\varphi )_2\) Euclidean (quantum) field theory. In: Princeton Series in Physics, pp. xx+392. Princeton University Press, Princeton (1974)
Tao, T.: Nonlinear dispersive equations. In: Local and Global Analysis, CBMS Regional Conference Series in Mathematics. Published for the Conference Board of the Mathematical Sciences, Washington, DC, vol. 106, pp. xvi+373. American Mathematical Society, Providence (2006)
Thomann, L., Tzvetkov, N.: Gibbs measure for the periodic derivative nonlinear Schrödinger equation. Nonlinearity 23(11), 2771–2791 (2010)
Tolomeo, L.: Global well-posedness of the two-dimensional stochastic nonlinear wave equation on an unbounded domain. Ann. Probab. 49(3), 1402–1426 (2021)
Acknowledgements
T.O. would like to thank István Gyöngy for his kind continual support since T.O.’s arrival in Edinburgh in 2013 and also for joyful chat over the daily tea break. Y.W. would like to thank István Gyöngy for his kindness and teaching during his stay at Edinburgh in 2016–2017. T.O. and Y.Z. were supported by the European Research Council (grant no. 864138 “SingStochDispDyn"). Y.W. was supported by supported by the EPSRC New Investigator Award (Grant No. EP/V003178/1). Lastly, the authors wish to thank the anonymous referee for the helpful comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is dedicated to István Gyöngy on the occasion of his 70th birthday.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Counting estimates
In this section, we state the counting estimates used in Sect. 4 to study the regularities of the stochastic terms. These lemmas are taken from Bringmann [12]. Note that some statements are given in a slightly simplified form. The same comment applies to Lemma C.2.
Lemma A.1
(Proposition 4.20 in [12]) Let \(0 < s \le \frac{1}{2}\) and \(0 \le \beta \le \frac{1}{2}\). Given \(\varepsilon _j \in \{-1, 1 \}\) for \(j = 0,1,2,3\), let \(\kappa ({\bar{n}}) = \kappa _{\varepsilon _0, \varepsilon _1, \varepsilon _2, \varepsilon _3}(n_1, n_2, n_3)\) be as in (4.7). Then, we have
uniformly in dyadic \(N_1,N_2,N_3 \ge 1\) and \(\varepsilon _j \in \{-1, 1 \}\) for \(j = 0,1,2,3\), where \(N_{\max } = \max (N_1,N_2,N_3)\).
Lemma A.2
(Lemma 4.22 (i) in [12]) Given \(\varepsilon _j \in \{-1, 1\}\) for \(j = 0,1,2,3\), let \(\kappa ({\bar{n}}) = \kappa _{\varepsilon _0, \varepsilon _1, \varepsilon _2, \varepsilon _3}(n_1, n_2, n_3)\) be as in (4.7). Then, we have
uniformly in dyadic \(N_1,N_2,N_3 \ge 1\) and \(\varepsilon _j \in \{-1, 1 \}\) for \(j = 0,1,2,3\).
Next, we recall the basic resonant estimate.
Lemma A.3
(Lemma 4.25 in [12]) Given \(\varepsilon _j \in \{- 1, 1\}\) for \(j = 0,1,2,3\), let \(\kappa ({\bar{n}}) = \kappa _{\varepsilon _0, \varepsilon _1, \varepsilon _2, \varepsilon _3}(n_1, n_2, n_3)\) be as in (4.7). Then, we have
uniformly in dyadic \(N_1 \ge 1\) and \(\varepsilon _j \in \{-1, 1 \}\) for \(j = 0,1,2,3\).
The next two lemmas (and Lemma A.3 above) are used for estimating the quintic stochastic term.
Lemma A.4
Let \(s \le \frac{1}{2} - \eta \) and \(\beta > 0\) for some \(\eta > 0\). Given \(\varepsilon _{123}, \varepsilon _j \in \{- 1, 1\}\) for \(j = 0, \dots , 5\), let \(\kappa _2({\bar{n}})\), \(\kappa _3({\bar{n}})\), and \(\kappa _4({\bar{n}})\) be as in (4.31) and (4.34). Then, we have
for any \(\varepsilon > 0\), uniformly in dyadic \(N_1,\dots ,N_5 \ge 1\) and \(\varepsilon _{123}, \varepsilon _j \in \{- 1, 1\}\) for \(j = 0, \dots , 5\), where \(N_{\max } = \max (N_1,\dots ,N_5)\).
Lemma A.4 is essentially Lemma 4.27 in [12], where the condition \( |\kappa _4({\bar{n}}) -m'|\le 1\) in (A.1) is replaced by \( |\kappa _4({\bar{n}}) + \varepsilon _{123}\langle n_{123} \rangle -m'|\le 1\). We point out that this modification does not make any difference in the proof. In our notation, the first step of the proof of Lemma 4.27 in [12] is to sum over \(n_5\), using [12, Lemma 4.17], for which the conditions \( |\kappa _4({\bar{n}}) -m'|\le 1\) in (A.1) and \( |\kappa _4({\bar{n}}) + \varepsilon _{123}\langle n_{123} \rangle -m'|\le 1\) do not make any difference since the extra term \( \varepsilon _{123}\langle n_{123} \rangle \) is fixed in summing over \(n_5\).
Lemma A.5
(Lemma 4.29 in [12]) Let \(\beta > 0\). Given \(\varepsilon _{123}, \varepsilon _j \in \{- 1, 1\}\) for \(j = 1, 2, 3\), let \(\kappa _2({\bar{n}})\) be as in (4.31). Then, we have
for any \(\varepsilon >0\), uniformly in dyadic \(N_1,N_2,N_3 \ge 1\) and \(\varepsilon _{123}, \varepsilon _j \in \{- 1, 1\}\) for \(j = 1,2, 3\).
Lastly, we state the septic counting estimate. See Definition 4.3 in Sect. 4.3 for the definition of a paring.
Lemma A.6
(Lemma 4.31 in [12])
Let \(\frac{1}{2}< s < 1\) and \(\beta > 0\). Given \(\varepsilon _{123}, \varepsilon _j \in \{- 1, 1\}\) for \(j = 1, 2, 3\), let \(\kappa _2({\bar{n}})\) be as in (4.31) and set
Let \({\mathcal {P}}\) be a pairing on \(\{1, \cdots , 7\}\) which respects the partition \(\big \{\{1,2,3\}, \{4, 5, 6\}, \{7\}\big \}\). Then, we have
for any \(\varepsilon > 0\), uniformly in dyadic \(N_{1234567}, N_{1237}, N_{456}, N_7 \ge 1\) and \(\varepsilon _{123}, \varepsilon _j \in \{- 1, 1\}\) for \(j = 1,2, 3\), where \(N_{\max } = \max (N_1, \cdots , N_7)\) and \(n_{nr }\) is as in (4.55).
Appendix B: Multiple stochastic integrals
In this section, we go over the basic definitions and properties of multiple stochastic integrals. See [43] and also [12, Section 4] for further discussion.
Let \(\lambda \) be the measure on \(Z: = {\mathbb {Z}}^3 \times {\mathbb {R}}_+\) defined by
where dn is the counting measure on \({\mathbb {Z}}^3\). Given \( k \in {\mathbb {N}}\), we set \(\lambda _k = \bigotimes _{j =1}^k \lambda \) and \(L^2(Z^k) = L^2( ({\mathbb {Z}}^3 \times {\mathbb {R}}_+)^k, \lambda _k )\). Given a function \(f \in L^2(Z^k)\), we can adapt the discussion in [43, Section 1.1] (in particular, [43, Example 1.1.2]) to the complex-valued setting and define the multiple stochastic integral \(I_k[f]\) by
Given a function \(f \in L^2(Z^k)\), we define its symmetrization \({{\,\mathrm{\mathtt {Sym}}\,}}(f)\) by
where \(z_j = (n_j, t_j)\) as in (4.15) and \(S_k\) denotes the symmetric group on \(\{1, \dots , k\}\). Note that by Jensen’s equality, we have
for any \(p \ge 1\). We say that f is symmetric if \({{\,\mathrm{\mathtt {Sym}}\,}}(f) = f\). We now recall some basic properties of multiple stochastic integrals.
Lemma B.1
Let \(k, \ell \in {\mathbb {N}}\). The following statements hold for any \(f \in L^2(Z^k)\) and \(g \in L^2(Z^\ell )\):
-
(i)
\(I_k : L^2(Z^k) \rightarrow {\mathcal {H}}_k \subset L^2(\Omega )\) is a linear operator, where \({\mathcal {H}}_k\) denotes the kth Wiener chaos.
-
(ii)
\(I_k[ \mathtt {Sym}(f)] = I_k[ f] \).
-
(iii)
Ito isometry:

-
(iv)
Furthermore, suppose that f is symmetric. Then, we have
$$\begin{aligned} I_k[f] = k! \sum _{n_1, \cdots , n_k \in {\mathbb {Z}}^3} \int _{0}^\infty \int _{0}^{t_1} \int _{0}^{t_{k-1}} f(n_1,t_1, \dots , n_k,t_k) dB_{n_k}(t_k) \cdots dB_{n_1}(t_1), \end{aligned}$$where the iterated integral on the right-hand side is understood as an iterated Ito integral.
We state a version of Fubini’s theorem for multiple stochastic integrals that is convenient for our purpose. See, for example, [15, Theorem 4.33] for a version of the stochastic Fubini theorem.
Lemma B.2
Let \(k \ge 1\). Given finite \(T> 0\), let \(f \in L^2 ( ({\mathbb {Z}}^3 \times [0, T])^k \times [0, T], d \lambda _k \otimes dt \big )\). (In particular, we assume that the temporal support (for the variables \(t_1, \dots , t_k, t\)) of f is contained in \([0, T]^{k+1}\) for any \((n_1, \dots , n_k)\).) Then, we have
in \(L^2(\Omega )\).
Proof
From Lemma B.1 (ii), we may assume that \(f(z_1, \dots , z_k, t)\) is symmetric in \(z_j = (n_j, t_j)\), \(j = 1, \dots , k\). Let \(\pmb {n} = (n_1, \dots , n_k)\) and \(\pmb {t} = (t_1, \dots , t_k)\). From Minkowski’s integral inequality, Lemma B.1 (iii), and Cauchy–Schwarz’s inequality, we have
On the other hand, by Lemma B.1 (iii) and Cauchy–Schwarz’s inequality, we have
Hence, it follows from (B.4), (B.5) and the densityFootnote 21 of \(\ell ^2_{\pmb {n}}(({\mathbb {Z}}^3)^k;C^\infty _{t, \pmb {t}}([0, T]^{k+1}))\) in \(\ell ^2_{\pmb {n}}(({\mathbb {Z}}^3)^k; L_{t, \pmb {t}}^2([0, T]^{k+1}))\) that we may assume that f is symmetric and belongs to \(\ell ^2_{\pmb {n}}(({\mathbb {Z}}^3)^k;C^\infty _{t, \pmb {t}}([0, T]^{k+1}))\). Furthermore, we may assume that f has a compact support in \(\pmb {n}\). Namely, there exists \(K > 0\) such that if \(\max (|n_1|, \dots , |n_k|) > K\), then \(f(n_1, t_1, \dots , n_k, t_k, t) = 0\) for any \(t_1, \dots , t_k, t \in [0, T]\). Then, together with Lemma B.1 (iv), we have
since the summation is over a finite set of indices \(\pmb {n} = (n_1, \dots , n_k)\) and f is symmetric. Hence, it remains to justifying the t-integration with the stochastic integrals for each fixed \(\pmb {n} = (n_1, \dots , n_k)\). For this reason, we suppress the dependence of f on \(\pmb {n} = (n_1, \dots , n_k)\) in the following.
When \(k = 1\), we can exploit the smoothness of f and have
where, at the second equality, we used the standard Fubini’s theorem in view of the almost sure boundedness of \(B_{n_1}\) on [0, T]. This proves (B.3) when \(k = 1\).
For the general case, let us first consider the innermost integral in (B.6). For notational simplicity, let us suppress all the variables of f except for \(t_k\) and t. Let \(\Delta _m = \{ 0 \le \tau _0< \tau _1< \cdots < \tau _m \le T\}\) be a partition of [0, T] and define a step function \(f_m(\cdot , t)\) by setting \(f_m(\tau , t) = f(\tau _{j-1}, t)\) for \(\tau _{j-1} < \tau \le \tau _j\). Then, by defining \(J_m\) by
it follows from the definition of the Wiener integral that
as \(m \rightarrow \infty \) (such that \(|\Delta _m|\rightarrow 0\)). By integrating (B.7) in t, we have
By the definition of the Wiener integral once again, we have
while from Minkowski’s integral inequality, (B.8), and the bounded convergence theorem (recall that f is smooth), we have
as \(m \rightarrow \infty \). Hence, from (B.9), (B.10), and (B.11), we conclude that
Next, we consider
Given the partition \(\Delta _m\) of [0, T] as above, we define an adaptive step function \(F_m(\cdot , t)\) by setting \(F_m(\tau , t;\omega ) = F(\tau _{j-1}, t;\omega )\) for \(\tau _{j-1} < \tau \le \tau _j\). Then, we can simply repeat the previous computation (but with Ito integrals instead of Wiener integrals) and obtain
in \(L^2(\Omega )\). Combining (B.13) and (B.14) with (B.12), we then obtain
in \(L^2(\Omega )\). By iterating this process, we conclude
in \(L^2(\Omega )\). Together with (B.6), this proves (B.3). \(\square \)
We conclude this section by stating the product formula (Lemma B.4). Before doing so, we first recall the contraction of two functions.
Definition B.3
Let \(k, \ell \in {\mathbb {N}}\). Given an integer \(0 \le r \le \min (k,l)\), we define the contraction \( f \otimes _r g \) of r indices of \(f\in L^2(Z^k)\) and \(g\in L^2(Z^\ell )\) by
where \(\zeta _j = (m_j, s_j)\) and \(\widetilde{\zeta }_j = (-m_j, s_j)\).
Note that even if f and g are symmetric, their contraction \(f\otimes _r g\) is not symmetric in general. We now state the product formula. See [43, Proposition 1.1.3].
Lemma B.4
(product formula) Let \(k, \ell \in {\mathbb {N}}\). Let \(f \in L^2(Z^k)\) and \(g \in L^2(Z^\ell )\) be symmetric functions. Then, we have
Appendix C: Random tensors
In this section, we provide the basic definition and some lemmas on (random) tensors from [12, 18]. See [18, Sections 2 and 4] and [12, Section 4] for further discussion.
Definition C.1
Let A be a finite index set. We denote by \(n_A\) the tuple \( (n_j : j \in A)\). A tensor \(h = h_{n_A}\) is a function: \(({\mathbb {Z}}^3)^{A} \rightarrow {\mathbb {C}} \) with the input variables \(n_A\). Note that the tensor h may also depend on \(\omega \in \Omega \). The support of a tensor h is the set of \(n_A\) such that \(h_{n_A} \ne 0\).
Given a finite index set A, let (B, C) be a partition of A. We define the norms \(\Vert \cdot \Vert _{n_A}\) and \(\Vert \cdot \Vert _{n_{B} \rightarrow n_{C}}\) by
and
where we used the short-hand notation \(\sum _{n_Z}\) for \(\sum _{n_Z \in ({\mathbb {Z}}^3)^Z}\) for a finite index set Z. Note that, by duality, we have \(\Vert h \Vert _{n_{B} \rightarrow n_{C}} = \Vert h \Vert _{n_{C} \rightarrow n_{B}} = \Vert \overline{h} \Vert _{n_{B} \rightarrow n_{C}}\) for any tensor \(h = h_{n_A}\). If \(B = \varnothing \) or \(C = \varnothing \), then we have \( \Vert h \Vert _{n_{B} \rightarrow n_{C}} = \Vert h \Vert _{n_A}\).
For example, when \(A = \{1, 2\}\), the norm \(\Vert h \Vert _{n_{1} \rightarrow n_{2}}\) denotes the usual operator norm \(\Vert h \Vert _{\ell ^2_{n_{1}} \rightarrow \ell ^2_{n_{2}}}\) for an infinite dimensional matrix operator \(\{h_{n_1 n_2}\}_{n_1, n_2 \in {\mathbb {Z}}^3}\). By bounding the matrix operator norm by the Hilbert–Schmidt norm (= the Frobenius norm), we have
Let (B, C) be a partition of A. Then, by duality, we can write (C.1) as
from which we obtain
Next, we recall a key deterministic tensor bound in the study of the random cubic NLW from [12].
Lemma C.2
(Lemma 4.33 in [12])
Let \(s < \frac{1}{2}+ \beta \) for some \(\beta > 0\). Given \(\varepsilon _j \in \{-1, 1\}\) for \(j = 0,1,2,3\), let \(\kappa ({\bar{n}})\) be as in (4.7). For \(m \in {\mathbb {Z}}\), define the tensor \(h^m\) by
Then, there exists \(\delta _0 > 0\) such that
uniformly in \(N \ge 1\), \(m\in {\mathbb {Z}}\), dyadic \(N_1,N_2,N_3 \ge 1\), and \(\varepsilon _j \in \{-1, 1 \}\) for \(j = 0,1,2,3\).
We conclude this section with the following random matrix estimate. This lemma is essentially Propositions 2.8 and 4.14 in [18]; see also Proposition 4.50 in [12]. In our stochastic PDE setting, however, we need a slightly different formulation (in particular, adapted to multiple stochastic integrals with general integrands) and thus for readers’ convenience, we present its proof.
Let A be a finite index set. As in (4.15) and (4.16), we set \(z_A = (k_A,t_A)\) for \((k_A, t_A) \in ({\mathbb {Z}}^3)^A\times {\mathbb {R}}^A\) and write \(f_{z_A} = f(z_A) = f(n_A, t_A)\).
Lemma C.3
Let A be a finite index set with \(k = |A| \ge 1\). Let \(h = h_{bcn_A}\) be a tensor such that \(n_j \in {\mathbb {Z}}^3\) for each \(j \in A\) and \((b,c) \in ({\mathbb {Z}}^3)^d\) for some integer \(d \ge 2\). Given \(N \ge 1\), assume that
Given a (deterministic) tensor \(h_{bcn_A} \in \ell ^2_{bcn_A}\), define the tensor \(H = H_{bc}\) by
for \(f \in \ell ^{\infty }_{n_A}(({\mathbb {Z}}^3)^A; L^2_{t_A}({\mathbb {R}}_+^A ))\), where \(I_k\) denotes the multiple stochastic integral defined in Appendix B. Then, for any \(\theta > 0\), we have
where the maximum is taken over all partitions (B, C) of A.
Remark C.4
-
(i)
The assumption that \(h_{bcn_A} \in \ell ^2_{bcn_A}\) and \(f \in \ell ^{\infty }_{n_A}(({\mathbb {Z}}^3)^A; L^2_{t_A}({\mathbb {R}}_+^A ))\) ensures that the multiple stochastic integral \(I_k \big [ h_{bcn_A} f_{z_A}\big ]\) in (C.5) is well defined. Note that if for instance we have a stronger condition \(f \in \ell ^2 \big ( ({\mathbb {Z}}^3)^A; L^{2}({\mathbb {R}}_+^A) \big ) \), then the conclusion (C.6) trivially holds without any loss in N. We also note that even if the tensor h is random, Lemma C.3 holds with the same proof as long as h is independent of the Brownian motions \(\{B_{n_A}\}\) defining multiple stochastic integrals.
-
(ii)
By translation invariance, we may replace the condition (C.4) in Lemma C.3 by
$$\begin{aligned} {{\,\mathrm{supp}\,}}h \subset \big \{ |b - b_*|, |c - c_*|, |n_j - n_{j, *}| \lesssim N \text { for each }j \in A \big \} \end{aligned}$$for some \((b_*, c_* ) \in ({\mathbb {Z}}^3)^d\) and \(n_{j, *} \in {\mathbb {Z}}^3\), \(j \in A\).
Proof of Lemma C.3
We follow the proof of Proposition 4.14 in [18] and use a higher order version of Bourgain’s \(TT^*\)-argument [9]. Let \(T : \ell ^2_c \rightarrow \ell ^2_b\) be the linear operator whose kernel is \(H_{bc}\). Namely, T is defined by
For \(j \in {\mathbb {N}}\), we define the operator \(T_j\) by \(T_j = (T T^*)^m\) if \(j = 2m\), and \(T_j = (TT^*)^m T\) if \(j = 2m +1\). We claim that \(T_j\) has a kernel which is given by a linear combination of terms \({\mathcal {T}}_j\) of the form
for some finite index set D and \(\ell = |D| \le k j\), where \(y_{bb'}(z_D)\) (or \(y_{bc}(z_D)\)) satisfies the following bound:
where the maximum is taken over all partitions (B, C) of A. Here, the implicit constant depends on k, \(\ell \), and j. While it grows with j (and \(\ell \)), this does not cause an issue since for a given small \(\theta > 0\) in (C.6), we fix \(j = j(\theta ) \gg 1\).
Let \(j = 1\). In this case, comparing (C.8) with (C.7) and (C.5) and using Lemma B.1 (ii), we have \(y_{bc}(z_D) = {{\,\mathrm{\mathtt {Sym}}\,}}(h_{bc n_A} f(z_A))\) with \(D = A\) and thus the bound (C.9) follows from Hölder’s inequality. Note that, in this case, it follows from Lemma B.1 (iii) that
where the right-hand side is the second moment of the Hilbert–Schmidt norm of the operator T. By taking higher powers \(T_j\), we control the operator norm of T.
Now, assume that the claim with (C.8) and (C.9) hold true for \(j - 1\). We assume that j is odd. The proof for even j is analogous. Noting that \(T_j = T_{j-1}T\), it follows from the inductive hypothesis (C.8) with (C.5) and Lemma B.1 (ii) that the kernel for \(T_j\) is given by a linear combination of terms \({\mathcal {T}}_j\) of the form
Then, from the product formula (Lemma B.4), we have
Hence, it suffices to show that \( \sum _{b'} ( {{\,\mathrm{\mathtt {Sym}}\,}}(y_{bb'}) \otimes _r {{\,\mathrm{\mathtt {Sym}}\,}}(h_{b'c} f) ) \) satisfies (C.9) for each \(0 \le r \le \min (k,\ell )\). For notational simplicity, we drop \({{\,\mathrm{\mathtt {Sym}}\,}}\) in \({{\,\mathrm{\mathtt {Sym}}\,}}(y_{bb'})\) and \({{\,\mathrm{\mathtt {Sym}}\,}}(h_{b'c} f) \) in the following. Note that this does not cause any issue since, in taking the \(L^2(\Omega )\)-norm, we can remove \({{\,\mathrm{\mathtt {Sym}}\,}}\) by Jensen’s inequality (B.2) as in Sect. 4.
Fix \(0 \le r \le \min (k, \ell )\). From Definition B.3 on the contraction, we have
where \(\widetilde{z}_C = (- n_C, t_C)\) for given \(z_C = (n_C, t_C)\). Here, \(B_1\), \(B_2\), and C are pairwise disjoint sets such that \(|B_1| = \ell - r\), \(|B_2| = k - r\), \( |C| = r \), \(B = B_1 \cup B_2\), and (by suitable relabeling of indices)
Then, from (C.10), Cauchy–Schwarz’s inequality (in \(t_C\)), Minkowski’s integral inequality (with \(L^2_{t_B} = L^2_{t_{B_1}}L^2_{t_{B_2}}\), (C.1), and the identification in (C.11), we have
Moreover, from (C.1), we have
where the maximum is taken over all partitions \((A_1,A_2)\) of A. Hence, from (C.12), (C.13), and the inductive hypothesis (C.9) (with \(j -1\) in place of j), we obtain (C.9) for j. Therefore, by induction, the claim holds for any \(j \in {\mathbb {N}}\).
We are now ready to prove (C.6). Consider the product \(T_{2m} = (TT^*)^m \) for \(m \ge 1\). Let us denote by \({\mathcal {R}}_{2m}\) the kernel of \(T_{2m}\), which consists of terms \({\mathcal {T}}_j\), satisfying (C.8) and (C.9). Namely, we have
for some \(J \ge 1\), \(0 \le \ell _j \le m\), and \(y_{bb'}^{(j)}\), satisfying (C.9). Note that we have \({\mathcal {R}}_{2m} \in {\mathcal {H}}_{\le 2mk}\). Then, by the standard \(TT^*\) argument, (C.2), Minkowski’s integral inequality, (C.14), the Wiener chaos estimate (Lemma 2.9), Lemma B.1 (iii), and (C.9), we obtain
for any \(p \ge 4m\). Moreover, from (C.4) and (C.3), we have
Therefore, by combining (C.15) and (C.16) and taking m sufficiently large, we obtain the desired bound (C.6). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Oh, T., Wang, Y. & Zine, Y. Three-dimensional stochastic cubic nonlinear wave equation with almost space-time white noise. Stoch PDE: Anal Comp 10, 898–963 (2022). https://doi.org/10.1007/s40072-022-00237-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40072-022-00237-x



 but that such independence will be lost for a general Hilbert–Schmidt operator
but that such independence will be lost for a general Hilbert–Schmidt operator  maps functions of regularity
maps functions of regularity  converges to some limit, denoted by
converges to some limit, denoted by  , as
, as  via the random matrix approach [
via the random matrix approach [ has regularity
has regularity  converges to some limit, denoted by
converges to some limit, denoted by  , as
, as  thanks to the smoothing on the noise and the use of space-time estimates, which allows us to place v in the subcritical regularity
thanks to the smoothing on the noise and the use of space-time estimates, which allows us to place v in the subcritical regularity  , where
, where  , the remainder term
, the remainder term  satisfies
satisfies 
 . As a result, the product
. As a result, the product 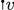 in (
in ( and v is negative. As in (
and v is negative. As in (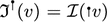 , using the random matrix estimates. However, there is an issue in handling the “high
, using the random matrix estimates. However, there is an issue in handling the “high  , which avoids the undesirable high
, which avoids the undesirable high 


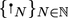 defined in (
defined in ( (formally given by (
(formally given by (
 defined in (
defined in ( , we have
, we have 
 . Lemma
. Lemma 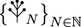 defined in (
defined in ( , we have
, we have 
 defined in (
defined in ( , we have
, we have 
 is a distribution-valued function belonging to
is a distribution-valued function belonging to  is a distribution-valued function belonging to
is a distribution-valued function belonging to  is a distribution-valued function belonging to
is a distribution-valued function belonging to  is a function belonging to
is a function belonging to  is a function belonging to
is a function belonging to  belongs to the class
belongs to the class  , where the residual term v satisfies the nonlinear equation (
, where the residual term v satisfies the nonlinear equation ( and one degree of smoothing from the Duhamel integral operator
and one degree of smoothing from the Duhamel integral operator  as an element in
as an element in  in Section 4 of [
in Section 4 of [