Strong convergence rates for explicit space-time discrete numerical approximations of stochastic Allen-Cahn equations

Abstract

Strong convergence rates for fuly discrete numerical approximations of space-time white noise driven SPDEs with superlinearly growing nonlinearities, such as the stochastic Allen–Cahn equation with space-time white noise, are shown. The obtained strong rates of convergence are essentially sharp.

1 Introduction

In this article we are interested in strong convergence rates for fully discrete numerical approximations of space-time white noise driven SPDEs with superlinearly growing nonlinearities, such as stochastic Allen–Cahn equations of the form

$$\begin{aligned} \tfrac{\partial }{\partial t}X_t(x) = \tfrac{\partial ^2}{\partial x^2} X_t(x) + m_0^2 X_t(x) - \lambda ^2 \left( X_t(x) \right) ^3 + \tfrac{\partial }{\partial t}W_t(x) \end{aligned}$$

(1)

for $x \in (0,1)$, $t \in [0, T]$, $\lambda , m_0\ge 0$, where $T \in (0, \infty )$ is a real number and $(W_t)_{t \in [0,T]}$ is an $Id _{L^2( (0,1); {\mathbb {R}})}$-cylindrical Wiener process. Note that $(W_t)_{t \in [0,T]}$ is the space derivative of a Brownian sheet and $\tfrac{\partial }{\partial t}W_t(x)$, $x \in (0,1)$, $t \in [0,T]$, is usually referred to as space-time white noise.

SPDEs of the type (1) occur in several applications, including, for example, the quantization of the Euclidean $\phi ^4_1$ quantum field theory [13, Section 0.7 and Section 13.7], fluctuations in reaction diffusion equations [13, Section 0.7] and in neurophysiology in terms of the Nagumo equation [13, Section 0.8]. In these applications, the case of fixed coefficients $\lambda , m_0\ge 0$ is relevant, while in the analysis of binary phase separation, particular emphasis lies on the sharp interface regime $\lambda = m_0 \nearrow \infty$ (cf., e.g., [14, 41], and the references therein). The focus of the present work lies on the case of fixed parameters $\lambda , m_0\ge 0$, addressing the difficulties arising from the irregularity of the noise in (1).

The literature contains a number of numerical approximation results for SPDEs with superlinearly growing nonlinearities (cf., e.g., [4, 6, 8, 9, 15,16,17, 21, 24, 25, 27, 29]). The articles [15,16,17, 21] establish the strong convergence of numerical approximations for such SPDEs, without estimates on the speed of strong convergence. Such estimates have been developed in the contributions [4, 25, 27, 29], in the following sense: The article [4] establishes strong convergence rates for semi-discrete temporal numerical approximations of space-time white noise driven SPDEs with superlinearly growing nonlinearities such as stochastic Allen–Cahn equations. The papers [25, 27, 29] prove strong convergence rates for fully discrete (temporal and spatial discrete) numerical approximations for SPDEs with superlinearly growing nonlinearities in the case of the more regular trace class noise.

This leaves open the problem of essentially sharp strong convergence rates for fully discrete numerical approximation schemes for space-time white noise driven SPDE with a superlinearly growing nonlinearity, such as the stochastic Allen–Cahn equation (1). This open problem is solved in the present work, by providing essentially sharp estimates on strong rates of convergence.

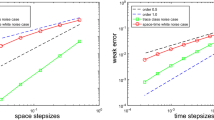
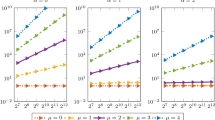
A key difficulty in the case of fully discrete numerical approximations for space-time white noise driven SPDEs with superlinearly growing nonlinearities is to derive appropriate uniform a priori moment bounds for the numerical approximation processes. In this article we overcome this difficulty (cf. (9)–(10) below for our approach to this challenge) and establish essentially sharp strong convergence rates for fully discrete numerical approximations of space-time white noise driven SPDEs with superlinearly growing nonlinearities such as stochastic Allen–Cahn equations with space-time white noise; see Theorem 5.5 in Sect. 5 below for the main convergence rate result in this work. To illustrate Theorem 5.5, we now present in Theorem 1.1 below the specialization of Theorem 5.5 to the case of stochastic Allen–Cahn equations.

Theorem 1.1

Let $T \in (0,\infty )$, $( H, \langle \cdot , \cdot \rangle _H, \left\| \cdot \right\| \!_H ) = ( L^2( (0,1); {\mathbb {R}}), \langle \cdot , \cdot \rangle _{ L^2( (0,1); {\mathbb {R}}) }, \left\| \cdot \right\| \!_{ L^2( (0,1) ; {\mathbb {R}}) } )$, $a_0, a_1, a_2 \in {\mathbb {R}}$, $a_3 \in (-\infty ,0]$, $(e_n)_{ n \in {\mathbb {N}}} \subseteq H$, $( P_n )_{ n \in {\mathbb {N}}} \subseteq L( H )$, $F :L^{6}( (0,1) ; {\mathbb {R}}) \rightarrow H$ satisfy for all $n \in {\mathbb {N}}$, $v \in L^{6}( (0,1) ; {\mathbb {R}})$ that $e_n(\cdot ) = \sqrt{2} \sin ( n\pi (\cdot ) )$, $F(v) = \sum _{ k=0 }^3 a_k v^k$, $P_n(v) = \sum _{ k=1 }^n \langle e_k, v \rangle _H \, e_k$, and $a_2 \mathbb {1}_{\{0\}}(a_3) = 0$, let $A :D(A)$ $\subseteq H \rightarrow H$ be the Laplacian with Dirichlet boundary conditions on H, let $( \Omega , {\mathcal {F}}, {\mathbb {P}})$ be a probability space, let $( W_t )_{ t \in [0,T] }$ be an $Id _H$-cylindrical Wiener process, let $\xi \in D( (-A)^{\nicefrac {1}{2}} )$, $\gamma \in (\nicefrac {1}{6}, \nicefrac {1}{4})$, $\chi \in (0, \nicefrac {\gamma }{3} - \nicefrac {1}{18} ]$, and let ${\mathfrak {O}}_{}^{M,N} :[0,T] \times \Omega \rightarrow P_N(H)$, $M,N \in {\mathbb {N}}$, and ${\mathfrak {X}}_{}^{M,N} :[0,T] \times \Omega \rightarrow P_N( H )$, $M,N \in {\mathbb {N}}$, be stochastic processes which satisfy that for all $M,N \in {\mathbb {N}}$, $m \in \{ 0, 1, 2, \ldots , M-1 \}$, $t \in (\nicefrac {mT}{M}, \nicefrac {(m+1)T}{M} ]$ it holds ${\mathbb {P}}$-a.s. that

$$\begin{aligned} {\mathfrak {O}}_{0}^{M,N} = {\mathfrak {X}}_{0}^{M,N} = P_N \, \xi , \qquad {\mathfrak {O}}_{t}^{M,N} = e^{(t-\nicefrac {mT}{M})A} \left[ {\mathfrak {O}}_{\nicefrac {mT}{M}}^{M,N} + \int _{\nicefrac {mT}{M}}^t P_{ N } \, dW_s \right] , \end{aligned}$$

(2)

and

$$\begin{aligned} {\mathfrak {X}}_{t}^{M,N}&= e^{(t-\nicefrac {mT}{M})A} \, {\mathfrak {X}}_{\nicefrac {mT}{M}}^{M,N} + {\mathfrak {O}}_{t}^{M,N} - e^{(t-\nicefrac {mT}{M})A} \, {\mathfrak {O}}_{\nicefrac {mT}{M}}^{M,N} \\&\quad + P_N A^{-1} ( e^{(t-\nicefrac {mT}{M})A} - Id _H ) \, \mathbb {1}_{ \{ \Vert (-A)^{\gamma } {\mathfrak {X}}_{\nicefrac {mT}{M}}^{M,N} \Vert _{ H } + \Vert (-A)^{\gamma } {\mathfrak {O}}_{\nicefrac {mT}{M}}^{M,N} \Vert _{ H } {\le } (M/T)^{\chi } \} } \, F( {\mathfrak {X}}_{\nicefrac {mT}{M}}^{M,N} ) . \end{aligned}$$

(3)

Then

• (i) we have that there exists an up to indistinguishability unique stochastic process $X :[0,T] \times \Omega \rightarrow L^{6}( (0,1); {\mathbb {R}})$ with continuous sample paths which satisfies for all $t \in [0,T]$, $p \in (0,\infty )$ that $\sup _{ s \in [0,T] } {\mathbb {E}}\big [ \Vert X_s \Vert _{ L^{6}( (0,1); {\mathbb {R}}) }^p \big ] < \infty$ and

  $$\begin{aligned} {\mathbb {P}}\!\left( X_t = e^{tA} \xi + \int _0^t e^{(t-s)A} F(X_s) \, ds + \int _0^t e^{(t-s)A} \, dW_s \right) = 1, \end{aligned}$$

  (4)

• (ii) we have for all $p \in (0,\infty )$ that $\sup _{ r \in (-\infty , \gamma ] } \sup _{ M, N \in {\mathbb {N}}} \sup _{ t \in [0,T] } {\mathbb {E}}\big [ \Vert (-A)^r {\mathfrak {X}}_{t}^{M,N} \Vert _{ H }^p \big ] < \infty$, and

• (iii) we have for all $p, \varepsilon \in (0,\infty )$ that there exists a real number $C \in {\mathbb {R}}$ such that for all $M,N \in {\mathbb {N}}$ it holds that

  $$\begin{aligned} \sup _{ t \in [0,T] } \left( {\mathbb {E}}\big [ \Vert X_t - {\mathfrak {X}}_{t}^{M,N} \Vert _{ H }^p \big ] \right) ^{\!\nicefrac {1}{p}} \le C ( M^{(\varepsilon -\nicefrac {1}{4})} + N^{(\varepsilon -\nicefrac {1}{2})} ) . \end{aligned}$$

  (5)

Theorem 1.1 follows from Corollary 6.10 which, in turn, follows from our main result, Theorem 5.5 below. Theorem 5.5 also proves strong convergence rates for fully discrete numerical approximations of a more general class of SPDEs than Theorem 1.1 above.

Next we would like to point out that the numerical approximation scheme (3) has been proposed in Hutzenthaler et al. [21] and has there been referred to as a nonlinearity-truncated approximation scheme (cf. [21, (3) in Section 1] and, e.g., [17,18,19,20, 24, 25, 35, 36, 38, 40] for further research articles on explicit approximation schemes for stochastic differential equations with superlinearly growing nonlinearities). Moreover, note that Theorem 1.1, in particular, implies that the fully discrete numerical approximations in (3) converge for every $\varepsilon \in (0, \nicefrac {1}{4})$ strongly to the solution of the stochastic Allen–Cahn equation (4) with the spatial rate of convergence $\nicefrac {1}{2} - \varepsilon$ and the temporal rate of convergence $\nicefrac {1}{4} - \varepsilon$. We can choose $M = N^2$ to balance the temporal and spatial error terms on the right hand side of (5) in Theorem 1.1. More specifically, observe that (5) implies that for all $p, \epsilon \in (0,\infty )$ there exists a real number $C \in {\mathbb {R}}$ such that for all $N \in {\mathbb {N}}$ it holds that

$$\begin{aligned} \sup _{ t \in [0,T] } \left( {\mathbb {E}}\big [ \Vert X_t - {\mathfrak {X}}_t^{N^2\!, N} \Vert _{ H }^p \big ] \right) ^{\!\nicefrac {1}{p}} \le C N^{(\varepsilon -\nicefrac {1}{2})} . \end{aligned}$$

(6)

We observe that for all $M, N \in {\mathbb {N}}$ we have that MN realizations of standard normal random variables are used to calculate one realization of ${\mathfrak {X}}_{T}^{M,N}$. This shows that for all $N \in {\mathbb {N}}$ we have that $N^3$ realizations of standard normal random variables are used to calculate one realization of ${\mathfrak {X}}_T^{N^2\!, N}$. Combining (6) with the computational effort $N^3$ illustrates that for all $\varepsilon \in (0, \nicefrac {1}{6})$ we have that the approximation scheme in (2)–(3) converges with the overall rate $\nicefrac {1}{6} - \varepsilon$ with respect to the number of used independent standard normal random variables.

We also would like to point out that the strong convergence rates established in Theorem 1.1 can, in general, not essentially be improved. More formally, [3, Corollary 2.7] proves in the case where $\sum _{i=0}^3 |a_i| = 0$ and $\xi = 0$ in the framework of Theorem 1.1 that there exist real numbers $c, C \in (0,\infty )$ such that for all $M, N \in {\mathbb {N}}$ we have that

$$\begin{aligned}&c \, M^{-\nicefrac {1}{4}} \le \lim _{ n \rightarrow \infty } \sup _{ t \in [0,T] } \left( {\mathbb {E}}\big [ \Vert X_t - {\mathfrak {X}}_t^{M,n} \Vert _{ H }^p \big ] \right) ^{\!\nicefrac {1}{p}} \le C M^{-\nicefrac {1}{4}} \end{aligned}$$

(7)

and

$$\begin{aligned}&c \, N^{-\nicefrac {1}{2}} \le \lim _{ m \rightarrow \infty } \sup _{ t \in [0,T] } \left( {\mathbb {E}}\big [ \Vert X_t - {\mathfrak {X}}_t^{m,N} \Vert _{ H }^p \big ] \right) ^{\!\nicefrac {1}{p}} \le C N^{-\nicefrac {1}{2}} . \end{aligned}$$

(8)

Inequalities (7) and (8) thus show that the spatial rate $\nicefrac {1}{2} - \varepsilon$ and the temporal rate $\nicefrac {1}{4} - \varepsilon$ established in Theorem 1.1 can essentially not be improved. Further related lower bounds for strong approximation errors in the linear case $\sum _{i=0}^3 |a_i| = 0$ can, e.g., be found in Müller-Gronbach et al. [32, Theorem 1], Müller-Gronbach and Ritter [31, Theorem 1], Müller-Gronbach et al. [33, Theorem 4.2], Conus et al. [10, Lemma 6.2], and Jentzen and Kurniawan [23, Corollary 9.4].

Finally, we would like to add some comments on the proof of Theorem 1.1 above and Theorem 5.5 below, respectively. The main difficulty to prove Theorem 1.1 is to obtain uniform a priori moment bounds for the space-time discrete numerical approximations (3) (see Sects. 2 and 5.4 below). Once the uniform a priori moment bounds have been established, we exploit the fact that the nonlinearity of the stochastic Allen–Cahn equation satisfies a global monotonicity property (see (180)–(182) in the proof of Lemma 6.9 in this article below and, e.g., [4, Lemma 6.7]) to prevent that the local discretization errors accumulate too quickly. It thus remains to sketch our procedure to establish uniform a priori moment bounds for the numerical approximations. We first subtract the noise process from (3) as it is often done in the literature. The key idea that we use to derive uniform a priori bounds for the subtracted equation is then to employ a suitable path-dependent Lyapunov-type function which on the one hand incorporates the dissipative dynamics of the stochastic Allen–Cahn equation (4) and which on the other hand respects the spatial spectral Galerkin approximations used for the spatial discretization of (4). More formally, a key contribution of this work is to reveal that there exists a suitable ${\mathcal {B}}( {\mathcal {C}}([0,T], L^{\infty }( (0,1); {\mathbb {R}}) ) ) / {\mathcal {B}}( [0,\infty ) )$-measurable mapping $\phi :{\mathcal {C}}([0,T], L^{\infty }( (0,1); {\mathbb {R}}) ) \rightarrow [0,\infty )$ such that for every $N \in {\mathbb {N}}$ we have that the mapping

$$\begin{aligned}&P_N(H) \times {\mathcal {C}}( [0,T], L^{\infty }( (0,1); {\mathbb {R}}) ) \ni (v,w) \mapsto \Vert (-A)^{\nicefrac {1}{2}} v \Vert _H^2 + \phi (w) \Vert v \Vert _H^2 \in {\mathbb {R}}\end{aligned}$$

(9)

is an appropriate path dependent Lyapunov-type function for the system of the N-dimensional spatial spectral Galerkin approximation of the subtracted equation associated to the stochastic Allen–Cahn equation (4) (variable $v \in P_N(H)$) and the N-dimensional spatial spectral Galerkin approximation of the Ornstein–Uhlenbeck process (variable $w \in {\mathcal {C}}([0,T], L^{\infty }( (0,1); {\mathbb {R}}) )$). It is crucial that the Lyapunov-type function (9) does not only depend on $w_T$ but on the whole path $w_t$, $t \in [0,T]$, of w. Observe that for every realization of the Ornstein–Uhlenbeck process $\int _0^t e^{(t-s)A} \, dW_s$, $t \in [0,T]$, we have that the systems of the N-dimensional spatial spectral Galerkin approximation of the subtracted equation associated to the stochastic Allen–Cahn equation (4) and the N-dimensional spatial spectral Galerkin approximation of the Ornstein–Uhlenbeck process is nothing else but a time dependent PDE (with the time variable entering only through the path $w \in {\mathcal {C}}([0,T], L^{\infty }( (0,1); {\mathbb {R}}) )$ of the Ornstein–Uhlenbeck process. In that sense it is natural that the Lyapunov-type function which we propose and verify in this article (see (9) above) depends on the whole path $w_t$, $t \in [0,T]$. Details can be found in the proof of Lemma 6.1 below. Applying the fundamental theorem of calculus to (9) results, roughly speaking, in the coercivity type condition that there exist real numbers $\epsilon \in [0,1)$, $c \in (0,\infty )$ and ${\mathcal {B}}( {\mathcal {C}}([0,T], L^{\infty }( (0,1); {\mathbb {R}}) ) ) / {\mathcal {B}}( [0,\infty ) )$-measurable mappings $\phi , \Phi :{\mathcal {C}}([0,T], L^{\infty }( (0,1); {\mathbb {R}}) ) \rightarrow [0,\infty )$ such that for every $N \in {\mathbb {N}}$, $v \in P_N(H)$, $w \in {\mathcal {C}}( [0,T], L^{\infty }( (0,1); {\mathbb {R}}) )$ we have that

$$\begin{aligned}&\sup _{ t \in [0,T] } \left( \langle (-A)^{\nicefrac {1}{2}} v, (-A)^{\nicefrac {1}{2}} P_N F(v+w_t) \rangle _{ H } + \phi (w) \langle v, F(v+w_t) \rangle _H \right) \\&\quad \le \epsilon \Vert A v \Vert _{ H }^2 + (c + \phi (w)) \Vert (-A)^{\nicefrac {1}{2}} v \Vert _{ H }^2 + c \phi (w) \Vert v \Vert _H^2 + \Phi (w) . \end{aligned}$$

(10)

Essentially, the coercivity type condition (10) appears as one of our assumptions of Theorem 5.5 below (see (84) in Sect. 5.1 below for details). The functions $\phi , \Phi :{\mathcal {C}}([0,T], L^{\infty }( (0,1); {\mathbb {R}}) ) \rightarrow [0,\infty )$ in the coercivity type condition (10) in the case of (4) above can be chosen to satisfy that for all $\epsilon \in (0,1)$, $c \in [\frac{32}{\epsilon }\max \{\frac{|a_2|^2}{|a_3|+\mathbb {1}_{\{0\}}^{{\mathbb {R}}}(a_3)},|a_3|\},\infty )$, $w \in C([0,T], H_1)$ it holds that there exists a real number $C \in [0, \infty )$ such that

$$\begin{aligned} \phi (w)= & {} C \left[ \textstyle \sup _{ t \in [0,T] } \Vert w_t \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + 1 \right] \qquad \text {and} \qquad \nonumber \\ \Phi (w)= & {} c \left[ \textstyle \sup _{ t \in [0,T] } \Vert w_t \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^8 + 1 \right] \end{aligned}$$

(11)

(see Lemma 6.1 in Sect. 6 and (188)–(189) in the proof of Lemma 6.9 in Sect. 6 below). Our proposal for this specific Lyapunov-type function is partially inspired by the arguments in Section 4 in Bianchi et al. [5] (cf. [5, Theroem 4.1 and Lemma 4.4]).

As mentioned above, in our previous article [4] we establish strong convergence rates for semi-discrete temporal numerical approximations of space-time white noise driven SPDEs with superlinearly growing nonlinearities such as stochastic Allen–Cahn equations. It is, however, unclear how and whether the arguments in [4] can be extended to analyze fully discrete numerical approximation schemes as considered in this article. In [4] the desired regularity is achieved by means of employing an appropriate polynomial Lyapunov-type function. Such polynomial Lyapunov-type functions allow to establish a priori moment bounds for the substracted equation associated to the stochastic Allen–Cahn equation (4) and the Ornstein–Uhlenbeck process, but such polynomial Lyapunov-type functions do not provide a priori moment bounds for its finite dimensional spatial spectral Galerkin approximation. Roughly speaking, the techniques in [4] cannot be applied in this situation as polynomials do not commute with spatial spectral Galerkin projection operators. In this work we overcome this issue by bringing appropriate path dependent Lyapunov-type functions according to (9)–(11) above into play.

After the preprint version of this work has appeared, a series of research articles related to this work have appeared. We refer to Bréhier and Goudenège [8, 9], Bréhier et al. [7], Liu and Qiao [28], Wang [39], Qi and Wang [34], and Cui and Hong [11] for details.

The remainder of this article is structured as follows. Section 2 establishes suitable a priori bounds for the numerical approximations. In Sect. 3 the error analysis for the considered nonlinearity-truncated approximation schemes is carried out in the pathwise sense and in Sect. 4 we perform the error analysis for these numerical schemes in the strong $L^p$-sense. In Sect. 5 we combine the results from Sect. 4 with appropriate uniform a priori moment bounds for the numerical approximation processes (see Sect. 2) to establish Theorem 5.5 which is the main result of this article. In Sect. 6 we finally verify that the assumptions of Theorem 5.5 are satisfied in the case of stochastic Allen–Cahn equations.

1.1 Notation

Throughout this article the following notation is used. For every measurable space $(A, {\mathcal {A}})$ and every measurable space $(B, {\mathcal {B}})$ we denote by ${\mathcal {M}}( {\mathcal {A}}, {\mathcal {B}} )$ the set of all ${\mathcal {A}} / {\mathcal {B}}$-measurable functions. For every set A we denote by $\#_A \in \{ 0, 1, 2, \ldots \} \cup \{ \infty \}$ the number of elements of A, we denote by ${\mathcal {P}}(A)$ the power set of A, and we denote by ${\mathcal {P}}_0(A)$ the set given by ${\mathcal {P}}_0(A) = \{ B \in {\mathcal {P}}(A) :\#_B < \infty \}$. For every set A and every set ${\mathcal {A}}$ with ${\mathcal {A}} \subseteq {\mathcal {P}}(A)$ we denote by $\sigma _A( {\mathcal {A}} )$ the smallest sigma-algebra on A which contains ${\mathcal {A}}$. For every topological space $(X, \tau )$ we denote by ${\mathcal {B}}(X)$ the set given by ${\mathcal {B}}(X) = \sigma _X( \tau )$. For every natural number $d \in {\mathbb {N}}$ and every set $A \in {\mathcal {B}}({\mathbb {R}}^d)$ we denote by $\lambda _A :{\mathcal {B}}(A) \rightarrow [0, \infty ]$ the Lebesgue-Borel measure on A. We denote by $\lfloor \cdot \rfloor _{h} :{\mathbb {R}}\rightarrow {\mathbb {R}}$, $h \in (0,\infty )$, the functions which satisfy for all $h \in (0,\infty )$, $t \in {\mathbb {R}}$ that $\lfloor t \rfloor _{h} = \max \!\left( \{ 0, h, -h, 2h, -2h, \ldots \} \cap (-\infty , t] \right)$. For every measure space $(\Omega , {\mathcal {F}}, \nu )$, every measurable space $(S, {\mathcal {S}})$, every set R, and every function $f :\Omega \rightarrow R$ we denote by $[f]_{\nu ,{\mathcal {S}}}$ the set given by $[f]_{\nu ,{\mathcal {S}}} = \{ g \in {\mathcal {M}}({\mathcal {F}},{\mathcal {S}}) :( \exists \, A \in {\mathcal {F}}:\nu (A) = 0 \text { and } \{ \omega \in \Omega :f(\omega ) \ne g(\omega ) \} \subseteq A ) \}$. For every set $\Omega$ and every set A we denote by $\mathbb {1}_A^{\Omega } :\Omega \rightarrow {\mathbb {R}}$ the function which satisfies for all $x \in \Omega$ that

$$\begin{aligned}&\mathbb {1}_A^{\Omega }(x) = {\left\{ \begin{array}{ll} 1 &{} :x \in A \\ 0 &{} :x \notin A . \end{array}\right. } \end{aligned}$$

(12)

2 A priori bounds for the numerical approximation

In this section we establish in (19) below pathwise a priori bounds for the difference of the processes ${\mathfrak {X}}_{} :[0,T] \rightarrow P(H)$ and ${\mathfrak {O}}_{} \in {\mathcal {C}}( [0,T], P(H) )$ in Lemma 2.2 below. In the proof of Lemma 5.4 in Sect. 5.4 below we will employ the pathwise a priori bounds in (19) to establish a priori moment bounds for the stochastic processes ${\mathfrak {X}}_{}^{M,I} :[0,T] \times \Omega \rightarrow H_{ \gamma }$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$, in (86) in Sect. 5.1 below.

Loosely speaking, the process ${\mathfrak {O}}_{} \in {\mathcal {C}}( [0,T], P(H) )$ in Lemma 2.2 below corresponds to one sample path of ${\mathfrak {O}}_{}^{M,N} :[0,T] \times \Omega \rightarrow P_N(H)$, $M,N \in {\mathbb {N}}$, in (2) and the process ${\mathfrak {X}}_{} :[0,T] \rightarrow P(H)$ corresponds to one sample path of ${\mathfrak {X}}_{}^{M,N} :[0,T] \times \Omega \rightarrow P_N( H )$, $M,N \in {\mathbb {N}}$, in (3) above. Roughly speaking, in the example of the stochastic Allen–Cahn equation in Theorem 1.1 above and Sect. 6.4 below the functions $\phi :{\mathcal {C}}([0,T], P(H)) \rightarrow [0,\infty )$ and $\Phi :{\mathcal {C}}([0,T], P(H)) \rightarrow [0,\infty )$ on the right hand side of (19) in Lemma 2.2 below correspond to polynomial powers of appropriate norms (see (188)–(189) in the proof of Lemma 6.9 in Sect. 6 below for details). This and the fact that the processes in (2) are Gaussian allow us to uniformly bound the right hand side of (19) in Lemma 2.2 below (see the proof of Lemma 6.9 in Sect. 6 below for details).

Observe that in Lemma 2.1 below we assume that $(H_r, \langle \cdot , \cdot \rangle _{H_r}, \left\| \cdot \right\| \!_{H_r} )$, $r \in {\mathbb {R}}$, is a family of interpolation spaces associated to $-A$ (cf., e.g., [37, Section 3.7]). This ensures that for all $r \in (0,\infty )$ it holds that $H_r = D((-A)^r) = \{ v \in H :\sum _{ h \in {\mathbb {H}}} | (-\mu _h)^r \langle h, v \rangle _H |^2 < \infty \}$. In particular, we have that $H_0 = H$, $H_1 = D(A)$, $H_2 = D(A^2)$, $\ldots$. Moreover, observe that in (16) we assume that for all $u, v \in P(H)$ we have that $\Vert F(u) - F(v) \Vert _H^2 \le C \max \{ 1, \Vert u \Vert _{ H_{\gamma } }^{\varphi } \} \Vert u-v \Vert _{ H_{\rho } }^2 + C \Vert u-v \Vert _{ H_{\rho } }^{(2+\varphi )}$. Note that this is equivalent to the condition that for all $u, v \in P(H)$ we have that $\Vert F(u) - F(v) \Vert _H^2 \le C \max \{ 1, \min \{ \Vert u \Vert _{ H_{\gamma } }^{\varphi }, \Vert v \Vert _{ H_{\gamma } }^{\varphi }\} \} \Vert u-v \Vert _{ H_{\rho } }^2 + C \Vert u-v \Vert _{ H_{\rho } }^{(2+\varphi )}$. The following well known lemma is used frequently throughout this article.

Lemma 2.1

Let $( H, \langle \cdot , \cdot \rangle _H, \left\| \cdot \right\| _H )$ be a separable ${\mathbb {R}}$-Hilbert space, let ${\mathbb {H}}\subseteq H$ be a non-empty orthonormal basis of H, let $x \in [0, 1]$, $s \in [0, \infty )$, $\mu :{\mathbb {H}}\rightarrow {\mathbb {R}}$ satisfy $\sup _{ h \in {\mathbb {H}}} \mu _h < 0$, let $A :D(A) \subseteq H \rightarrow H$ be the linear operator which satisfies $D(A) = \{ v \in H :\sum _{ h \in {\mathbb {H}}} | \mu _h \langle h, v \rangle _H |^2 < \infty \}$ and $\forall \, v \in D(A) :Av = \sum _{ h \in {\mathbb {H}}} \mu _h \langle h,v \rangle _H h$, and let $(H_r, \langle \cdot , \cdot \rangle _{H_r}, \left\| \cdot \right\| \!_{H_r} )$, $r \in {\mathbb {R}}$, be a family of interpolation spaces associated to $-A$ (cf., e.g., [37, Section 3.7]). Then we have that

$$\begin{aligned} \Vert (-sA)^{-x} (e^{sA} - Id _H) \Vert _{ L(H) } \le 1 \end{aligned}$$

(13)

and

$$\begin{aligned} \Vert (-sA)^{x} e^{sA} \Vert _{ L(H) } \le 1 . \end{aligned}$$

(14)

Lemma 2.2

Consider the notation in Sect. 1.1, let $( H, \langle \cdot , \cdot \rangle _H, \left\| \cdot \right\| _H )$ be a separable ${\mathbb {R}}$-Hilbert space, let ${\mathbb {H}}\subseteq H$ be a non-empty orthonormal basis of H, let $T, \varphi , c \in (0,\infty )$, $C \in [0,\infty )$, $\epsilon , \kappa , \rho \in [0,1)$, $\gamma \in (\rho ,1)$, $\chi \in (0,\nicefrac {(\gamma -\rho )}{(1+\nicefrac {\varphi }{2})}] \cap (0,\nicefrac {(1-\rho )}{(1+\varphi )}]$, $M \in {\mathbb {N}}$, $\mu :{\mathbb {H}}\rightarrow {\mathbb {R}}$ satisfy $\sup _{ h \in {\mathbb {H}}} \mu _h < 0$, let $A :D(A) \subseteq H \rightarrow H$ be the linear operator which satisfies $D(A) = \{ v \in H :\sum _{ h \in {\mathbb {H}}} | \mu _h \langle h, v \rangle _H |^2 < \infty \}$ and $\forall \, v \in D(A) :Av = \sum _{ h \in {\mathbb {H}}} \mu _h \langle h,v \rangle _H h$, let $(H_r, \langle \cdot , \cdot \rangle _{H_r}, \left\| \cdot \right\| \!_{H_r} )$, $r \in {\mathbb {R}}$, be a family of interpolation spaces associated to $-A$ (cf., e.g., [37, Section 3.7]), let $I \in {\mathcal {P}}_0({\mathbb {H}})$, $P \in L(H)$ satisfy for all $v \in H$ that $P(v) = \sum _{ h \in I } \langle h,v \rangle _H h$, and let ${\mathfrak {X}}_{} :[0,T] \rightarrow P(H)$, ${\mathfrak {O}}_{} \in {\mathcal {C}}( [0,T], P(H) )$, $F \in {\mathcal {C}}( P(H),H )$, $\phi , \Phi :{\mathcal {C}}([0,T], P(H)) \rightarrow [0,\infty )$ satisfy for all $u,v \in P(H)$, $w \in {\mathcal {C}}([0,T], P(H))$, $t \in [0,T]$ that

$$\begin{aligned} \Vert F(u) \Vert _H^2\le & {} C \max \{ 1, \Vert u \Vert _{H_{\gamma }}^{(2+\varphi )} \}, \end{aligned}$$

(15)

$$\begin{aligned} \Vert F(u) - F(v) \Vert _H^2\le & {} C \max \{ 1, \Vert u \Vert _{ H_{\gamma } }^{\varphi } \} \Vert u-v \Vert _{ H_{\rho } }^2 + C \Vert u-v \Vert _{ H_{\rho } }^{(2+\varphi )}, \end{aligned}$$

(16)

(17)

$$\begin{aligned} \text {and} \qquad {\mathfrak {X}}_{t} = \int _0^t P e^{(t-s)A} \mathbb {1}_{ [ 0, (\nicefrac {M}{T})^{\chi } ] }^{{\mathbb {R}}} ( \Vert {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } \Vert _{ H_{\gamma } } + \Vert {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } \Vert _{ H_{\gamma } } ) \, F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \, ds + {\mathfrak {O}}_{t}.\nonumber \\ \end{aligned}$$

(18)

Then

• (i) we have that the function $[0,T] \ni t \mapsto {\mathfrak {X}}_{t} - {\mathfrak {O}}_{t} \in P(H)$ is continuous and

• (ii) we have that

  $$\begin{aligned}&\sup _{ t \in [0,T] } \big ( \Vert {\mathfrak {X}}_{t} - {\mathfrak {O}}_{t} \Vert _{H_{\nicefrac {1}{2}}}^2 + \phi ({\mathfrak {O}}_{}) \Vert {\mathfrak {X}}_{t} - {\mathfrak {O}}_{t} \Vert _{H}^2 \big ) \\&\quad \le \frac{ e^{2cT} }{ c } \left( \Phi ({\mathfrak {O}}_{}) + \frac{ \max \{1, \phi ({\mathfrak {O}}_{})\} C(c+1) }{2(1-\epsilon )(1-\kappa )c} \left[ \tfrac{\max \{1,T\} (1+\sqrt{C})}{(1-\rho )} \right] ^{\!(2+\varphi )} \right) . \end{aligned}$$

  (19)

Proof of Lemma 2.2

Throughout this proof assume w.l.o.g. that $I \ne \emptyset$ and let $\bar{{\mathfrak {X}}}_{} :[0,T] \rightarrow P(H)$ and $Z :[0,T] \rightarrow \{0,1\}$ be the functions which satisfy for all $s \in [0,T]$ that

$$\begin{aligned} \bar{{\mathfrak {X}}}_{s} = {\mathfrak {X}}_{s} - {\mathfrak {O}}_{s} \qquad \text {and} \qquad Z_s = \mathbb {1}_{ [ 0, (\nicefrac {M}{T})^{\chi } ] }^{{\mathbb {R}}} ( \Vert {\mathfrak {X}}_{s} \Vert _{ H_{\gamma } } + \Vert {\mathfrak {O}}_{s} \Vert _{ H_{\gamma } } ). \end{aligned}$$

(20)

Observe that, e.g., Lemma 2.4 in [26] (with $V = P(H)$, $\left\| \cdot \right\| \!_V = P(H) \ni v \mapsto \left\| v \right\| \!_H^2 \in [0,\infty )$, $T = T$, $\eta = 0$, $A = P(H) \ni v \mapsto Av \in P(H)$, ${\mathbb {V}} = P(H) \ni v \mapsto \Vert v \Vert _{H_{\nicefrac {1}{2}}}^2 + \phi ({\mathfrak {O}}_{}) \Vert v \Vert _H^2 \in {\mathbb {R}}$, $Z = [0,T] \times \Omega \ni (t, \omega ) \mapsto Z_t(\omega ) \in {\mathbb {R}}$, $Y = {\mathfrak {X}}_{}$, $O = {\mathfrak {O}}_{}$, ${\mathbb {O}} = {\mathfrak {O}}_{}$, $F = P(H) \ni v \mapsto PF(v) \in P(H)$, $\phi = V \ni v \mapsto 2c \in {\mathbb {R}}$, $f = V \ni v \mapsto 0 \in {\mathbb {R}}$, $h = \nicefrac {T}{M}$ in the notation of Lemma 2.4 in [26]) implies that item (i) holds and that for all $t \in [0,T]$ it holds that

$$\begin{aligned}&e^{-2ct} \left[ \Vert \bar{{\mathfrak {X}}}_{t} \Vert _{H_{\nicefrac {1}{2}}}^2 + \phi ({\mathfrak {O}}_{}) \Vert \bar{{\mathfrak {X}}}_{t} \Vert _H^2 \right] \\&\quad = 2 \int _0^t e^{-2cs} \, \Big [ \langle \bar{{\mathfrak {X}}}_{s}, A \bar{{\mathfrak {X}}}_{s} + Z_{ \lfloor s \rfloor _{T\!/\!M} } P F( \bar{{\mathfrak {X}}}_{s} + {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \rangle _{H_{\nicefrac {1}{2}}} \\&\qquad + \phi ({\mathfrak {O}}_{}) \langle \bar{{\mathfrak {X}}}_{s}, A \bar{{\mathfrak {X}}}_{s} + Z_{ \lfloor s \rfloor _{T\!/\!M} } P F( \bar{{\mathfrak {X}}}_{s} + {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \rangle _H \Big ] \, ds \\&\qquad + 2 \int _0^t e^{-2cs} \, Z_{ \lfloor s \rfloor _{T\!/\!M} } \Big [ \langle \bar{{\mathfrak {X}}}_{s}, P [ F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) - F( \bar{{\mathfrak {X}}}_{s} + {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } ) ] \rangle _{H_{\nicefrac {1}{2}}} \\&\qquad + \phi ({\mathfrak {O}}_{}) \langle \bar{{\mathfrak {X}}}_{s}, P [ F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) - F( \bar{{\mathfrak {X}}}_{s} + {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } ) ] \rangle _H \Big ] \, ds \\&\qquad - 2c \int _0^t e^{-2cs} \left[ \Vert \bar{{\mathfrak {X}}}_{s} \Vert _{H_{\nicefrac {1}{2}}}^2 + \phi ({\mathfrak {O}}_{}) \Vert \bar{{\mathfrak {X}}}_{s} \Vert _H^2 \right] ds . \end{aligned}$$

(21)

The fact that $P \in L(H)$ is symmetric and the fact that $\forall \, s \in [0,T] :\bar{{\mathfrak {X}}}_{s} \in P(H)$ imply for all $t \in [0,T]$ that

$$\begin{aligned}&e^{-2ct} \left[ \Vert \bar{{\mathfrak {X}}}_{t} \Vert _{H_{\nicefrac {1}{2}}}^2 + \phi ({\mathfrak {O}}_{}) \Vert \bar{{\mathfrak {X}}}_{t} \Vert _H^2 \right] \\&\quad = -2 \int _0^t e^{-2cs} \left[ \langle (-A) \bar{{\mathfrak {X}}}_{s}, (-A) \bar{{\mathfrak {X}}}_{s} \rangle _H + \phi ({\mathfrak {O}}_{}) \langle (-A)^{\nicefrac {1}{2}} \bar{{\mathfrak {X}}}_{s}, (-A)^{\nicefrac {1}{2}} \bar{{\mathfrak {X}}}_{s} \rangle _H \right] ds \\&\qquad + 2 \int _0^t e^{-2cs} \, Z_{ \lfloor s \rfloor _{T\!/\!M} } \left[ \langle \bar{{\mathfrak {X}}}_{s}, P F( \bar{{\mathfrak {X}}}_{s} + {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \rangle _{H_{\nicefrac {1}{2}}} \right. \\&\left. \qquad + \phi ({\mathfrak {O}}_{}) \langle \bar{{\mathfrak {X}}}_{s}, F( \bar{{\mathfrak {X}}}_{s} + {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \rangle _H \right] ds \\&\qquad + 2 \int _0^t e^{-2cs} \, Z_{ \lfloor s \rfloor _{T\!/\!M} } \Big [ \langle (-A) \bar{{\mathfrak {X}}}_{s}, P [ F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) - F( \bar{{\mathfrak {X}}}_{s} + {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } ) ] \rangle _H \\ {}&\qquad + \phi ({\mathfrak {O}}_{}) \langle \bar{{\mathfrak {X}}}_{s}, F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) - F( \bar{{\mathfrak {X}}}_{s} + {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \rangle _H \Big ] \, ds \\ {}&\qquad - 2c \int _0^t e^{-2cs} \left[ \Vert \bar{{\mathfrak {X}}}_{s} \Vert _{H_{\nicefrac {1}{2}}}^2 + \phi ({\mathfrak {O}}_{}) \Vert \bar{{\mathfrak {X}}}_{s} \Vert _H^2 \right] ds . \end{aligned}$$

(22)

This, the Cauchy–Schwarz inequality, and fact that $\forall \, x,y \in {\mathbb {R}}:xy \le \nicefrac {x^2}{2} + \nicefrac {y^2}{2}$ prove that for all $t \in [0,T]$ we have that

$$\begin{aligned}&e^{-2ct} \left[ \Vert \bar{{\mathfrak {X}}}_{t} \Vert _{H_{\nicefrac {1}{2}}}^2 + \phi ({\mathfrak {O}}_{}) \Vert \bar{{\mathfrak {X}}}_{t} \Vert _H^2 \right] \nonumber \\ {}&\quad \le -2 \int _0^t e^{-2cs} \left[ \Vert \bar{{\mathfrak {X}}}_{s} \Vert _{H_1}^2 + ( c + \phi ({\mathfrak {O}}_{}) ) \Vert \bar{{\mathfrak {X}}}_{s} \Vert _{H_{\nicefrac {1}{2}}}^2 + c \, \phi ({\mathfrak {O}}_{}) \Vert \bar{{\mathfrak {X}}}_{s} \Vert _H^2 \right] ds \nonumber \\ {}&\qquad + 2 \int _0^t e^{-2cs} \, Z_{ \lfloor s \rfloor _{T\!/\!M} } \left[ \langle \bar{{\mathfrak {X}}}_{s}, P F( \bar{{\mathfrak {X}}}_{s} + {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \rangle _{H_{\nicefrac {1}{2}}} \right. \nonumber \\&\left. \qquad + \phi ({\mathfrak {O}}_{}) \langle \bar{{\mathfrak {X}}}_{s}, F( \bar{{\mathfrak {X}}}_{s} + {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \rangle _H \right] ds \nonumber \\ {}&\qquad + \int _0^t e^{-2cs} \, Z_{ \lfloor s \rfloor _{T\!/\!M} } \bigg [ 2 (1-\epsilon ) \, \Vert \bar{{\mathfrak {X}}}_{s} \Vert _{H_1}^2 + \tfrac{1}{2(1-\epsilon )} \, \Vert P \Vert _{ L(H) }^2 \, \Vert F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } )\nonumber \\&\qquad - F( \bar{{\mathfrak {X}}}_{s} + {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \Vert _H^2 \nonumber \\ {}&\qquad + 2c(1-\kappa ) \, \phi ({\mathfrak {O}}_{}) \Vert \bar{{\mathfrak {X}}}_{s} \Vert _H^2 + \tfrac{\phi ({\mathfrak {O}}_{})}{2c(1-\kappa )} \, \Vert F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) - F( \bar{{\mathfrak {X}}}_{s} + {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \Vert _H^2 \bigg ] \, ds . \end{aligned}$$

(23)

The fact $\Vert P \Vert _{ L(H) } \le 1$ therefore shows for all $t \in [0,T]$ that

$$\begin{aligned}&\Vert \bar{{\mathfrak {X}}}_{t} \Vert _{H_{\nicefrac {1}{2}}}^2 + \phi ({\mathfrak {O}}_{}) \Vert \bar{{\mathfrak {X}}}_{t} \Vert _H^2 \\ {}&\quad \le -2 \int _0^t e^{2c(t-s)} \left[ \epsilon Z_{ \lfloor s \rfloor _{T\!/\!M} } \Vert \bar{{\mathfrak {X}}}_{s} \Vert _{H_1}^2 {+} ( c + \phi ({\mathfrak {O}}_{}) ) \Vert \bar{{\mathfrak {X}}}_{s} \Vert _{H_{\nicefrac {1}{2}}}^2 {+} \kappa c \, \phi ({\mathfrak {O}}_{}) \Vert \bar{{\mathfrak {X}}}_{s} \Vert _H^2 \right] ds \\ {}&\qquad + 2 \int _0^t e^{2c(t-s)} \, Z_{ \lfloor s \rfloor _{T\!/\!M} } \left[ \langle \bar{{\mathfrak {X}}}_{s}, P F( \bar{{\mathfrak {X}}}_{s} + {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \rangle _{H_{\nicefrac {1}{2}}} \right. \\&\left. \qquad + \phi ({\mathfrak {O}}_{}) \langle \bar{{\mathfrak {X}}}_{s}, F( \bar{{\mathfrak {X}}}_{s} + {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \rangle _H \right] ds \\ {}&\qquad + \left[ \frac{1}{2(1-\epsilon )} + \frac{\phi ({\mathfrak {O}}_{})}{2c(1-\kappa )} \right] \int _0^t e^{2c(t-s)} \, Z_{ \lfloor s \rfloor _{T\!/\!M} } \Vert F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \\&\qquad - F( \bar{{\mathfrak {X}}}_{s} + {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \Vert _H^2 \, ds . \end{aligned}$$

(24)

Moreover, note that the triangle inequality implies that for all $s \in [0,T]$ we have that

$$\begin{aligned}&Z_{ \lfloor s \rfloor _{T\!/\!M} } \Vert \bar{{\mathfrak {X}}}_{s} - \bar{{\mathfrak {X}}}_{ \lfloor s \rfloor _{T\!/\!M} } \Vert _{ H_{\rho } } \\&\quad = Z_{ \lfloor s \rfloor _{T\!/\!M} } \Vert ({\mathfrak {X}}_{s} - {\mathfrak {O}}_{s}) - ({\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } - {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }) \Vert _{ H_{\rho } } \\ {}&\quad \le Z_{ \lfloor s \rfloor _{T\!/\!M} } \Vert (e^{(s- \lfloor s \rfloor _{T\!/\!M} )A} - Id _H) ({\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } - {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }) \Vert _{ H_{\rho } } \\ {}&\qquad + Z_{ \lfloor s \rfloor _{T\!/\!M} } \Vert ({\mathfrak {X}}_{s} - {\mathfrak {O}}_{s}) - e^{(s- \lfloor s \rfloor _{T\!/\!M} )A}({\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } - {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }) \Vert _{ H_{\rho } } \\ {}&\quad \le Z_{ \lfloor s \rfloor _{T\!/\!M} } \Vert (-A)^{-(\gamma -\rho )}(e^{(s- \lfloor s \rfloor _{T\!/\!M} )A} - Id _H) \Vert _{L(H)} \Vert {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } - {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } \Vert _{ H_{\gamma } } \\ {}&\qquad + Z_{ \lfloor s \rfloor _{T\!/\!M} } \int _{ \lfloor s \rfloor _{T\!/\!M} }^s \Vert P e^{(s-u)A} Z_{ \lfloor u \rfloor _{T\!/\!M} } F( {\mathfrak {X}}_{ \lfloor u \rfloor _{T\!/\!M} } ) \Vert _{ H_{\rho } } \, du . \end{aligned}$$

(25)

Lemma 2.1, the triangle inequality, the fact that $\Vert P \Vert _{ L(H) } \le 1$, and (15) hence ensure for all $s \in [0,T]$ that

(26)

Combining this and the fact that $\forall x {\in } (0, \infty ) :\max \{ x^{(\gamma -\rho -\chi )}, \max \{ x^{(1-\rho )}, x^{(1+\nicefrac {\varphi }{2})\chi } \} \} \le \max \{ x, x^{(\gamma -\rho -\chi )}, x^{(1+\nicefrac {\varphi }{2})\chi } \}$ shows that for all $s \in [0,T]$ we have that

$$\begin{aligned}&Z_{ \lfloor s \rfloor _{T\!/\!M} } \Vert \bar{{\mathfrak {X}}}_{s} - \bar{{\mathfrak {X}}}_{ \lfloor s \rfloor _{T\!/\!M} } \Vert _{ H_{\rho } } \\ {}&\quad \le |\nicefrac {T}{M}|^{(\gamma -\rho -\chi )} + \sqrt{C} \max \!\left\{ 1, |\nicefrac {M}{T}|^{(1+\nicefrac {\varphi }{2})\chi } \right\} \frac{ (s- \lfloor s \rfloor _{T\!/\!M} )^{(1-\rho )} }{ (1-\rho ) } \\ {}&\quad \le \frac{1}{(1-\rho )} \left[ |\nicefrac {T}{M}|^{(\gamma -\rho -\chi )} + \sqrt{C} \max \!\left\{ |\nicefrac {T}{M}|^{(1-\rho )}, |\nicefrac {T}{M}|^{(1-\rho -(1+\nicefrac {\varphi }{2})\chi )} \right\} \right] \\ {}&\quad \le \frac{(1+\sqrt{C})}{(1-\rho )} \max \!\left\{ \nicefrac {T}{M}, |\nicefrac {T}{M}|^{(\gamma -\rho -\chi )}, |\nicefrac {T}{M}|^{(1-\rho -(1+\nicefrac {\varphi }{2})\chi )} \right\} . \end{aligned}$$

(27)

Next observe that (16) ensures for all $s \in [0,T]$ that

$$\begin{aligned}&Z_{ \lfloor s \rfloor _{T\!/\!M} } \Vert F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) - F( \bar{{\mathfrak {X}}}_{s} + {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \Vert _H^2 \\ {}&\quad \le C Z_{ \lfloor s \rfloor _{T\!/\!M} } \! \Big [ \max \{ 1, \Vert {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } \Vert _{ H_{\gamma } }^{\varphi } \} \Vert \bar{{\mathfrak {X}}}_{ \lfloor s \rfloor _{T\!/\!M} } - \bar{{\mathfrak {X}}}_{s} \Vert _{ H_{\rho } }^2 + \Vert \bar{{\mathfrak {X}}}_{ \lfloor s \rfloor _{T\!/\!M} } - \bar{{\mathfrak {X}}}_{s} \Vert _{ H_{\rho } }^{(2+\varphi )} \Big ] \\ {}&\quad \le C Z_{ \lfloor s \rfloor _{T\!/\!M} } \Vert \bar{{\mathfrak {X}}}_{ \lfloor s \rfloor _{T\!/\!M} } - \bar{{\mathfrak {X}}}_{s} \Vert _{ H_{\rho } }^2 \Big [ \max \{ 1, |\nicefrac {M}{T}|^{\varphi \chi } \} + Z_{ \lfloor s \rfloor _{T\!/\!M} } \Vert \bar{{\mathfrak {X}}}_{ \lfloor s \rfloor _{T\!/\!M} } - \bar{{\mathfrak {X}}}_{s} \Vert _{ H_{\rho } }^{\varphi } \Big ] \\ {}&\quad \le 2 C Z_{ \lfloor s \rfloor _{T\!/\!M} } \Vert \bar{{\mathfrak {X}}}_{ \lfloor s \rfloor _{T\!/\!M} } - \bar{{\mathfrak {X}}}_{s} \Vert _{ H_{\rho } }^2 \Big [ \max \!\big \{ 1, |\nicefrac {M}{T}|^{\varphi \chi }, Z_{ \lfloor s \rfloor _{T\!/\!M} } \Vert \bar{{\mathfrak {X}}}_{ \lfloor s \rfloor _{T\!/\!M} } - \bar{{\mathfrak {X}}}_{s} \Vert _{ H_{\rho } }^{\varphi } \big \} \Big ] \\ {}&\quad = 2 C Z_{ \lfloor s \rfloor _{T\!/\!M} } \Vert \bar{{\mathfrak {X}}}_{ \lfloor s \rfloor _{T\!/\!M} } - \bar{{\mathfrak {X}}}_{s} \Vert _{ H_{\rho } }^2 \Big [ \max \!\big \{ 1, |\nicefrac {M}{T}|^{\chi }, Z_{ \lfloor s \rfloor _{T\!/\!M} } \Vert \bar{{\mathfrak {X}}}_{ \lfloor s \rfloor _{T\!/\!M} } - \bar{{\mathfrak {X}}}_{s} \Vert _{ H_{\rho } } \big \} \Big ]^{\varphi } . \end{aligned}$$

(28)

This together with (27) proves for all $s \in [0,T]$ that

$$\begin{aligned}&Z_{ \lfloor s \rfloor _{T\!/\!M} } \Vert F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) - F( \bar{{\mathfrak {X}}}_{s} + {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \Vert _H^2 \\ {}&\quad \le \frac{2 C (1+\sqrt{C})^{(2+\varphi )}}{(1-\rho )^{(2+\varphi )}} \left| \max \!\left\{ \nicefrac {T}{M}, |\nicefrac {T}{M}|^{(\gamma -\rho -\chi )}, |\nicefrac {T}{M}|^{(1-\rho -(1+\nicefrac {\varphi }{2})\chi )} \right\} \right| ^2 \\ {}&\qquad \cdot \left| \max \!\left\{ 1, |\nicefrac {M}{T}|^{\chi }, \nicefrac {T}{M}, |\nicefrac {T}{M}|^{(\gamma -\rho -\chi )}, |\nicefrac {T}{M}|^{(1-\rho -(1+\nicefrac {\varphi }{2})\chi )} \right\} \right| ^{\varphi } \\ {}&\quad = \frac{2 C (1+\sqrt{C})^{(2+\varphi )}}{(1-\rho )^{(2+\varphi )}} \left| \max \!\left\{ \nicefrac {T}{M}, |\nicefrac {T}{M}|^{(\gamma -\rho -\chi )}, |\nicefrac {T}{M}|^{(1-\rho -(1+\nicefrac {\varphi }{2})\chi )} \right\} \right| ^2 \\ {}&\qquad \cdot \left| \max \!\left\{ \nicefrac {T}{M}, |\nicefrac {M}{T}|^{\chi }, |\nicefrac {T}{M}|^{(\gamma -\rho -\chi )}, |\nicefrac {T}{M}|^{(1-\rho -(1+\nicefrac {\varphi }{2})\chi )} \right\} \right| ^{\varphi } . \end{aligned}$$

(29)

In addition, note that the assumption that $\chi \in (0,\nicefrac {(\gamma -\rho )}{(1+\nicefrac {\varphi }{2})}] \cap (0,\nicefrac {(1-\rho )}{(1+\varphi )}]$ ensures that

$$\begin{aligned}&\gamma -\rho -\chi \in (0,1), \qquad 1-\rho -(1+\nicefrac {\varphi }{2})\chi \in (0,1) , \end{aligned}$$

(30)

and

$$\begin{aligned}&\min \{ \gamma -\rho -(1+\nicefrac {\varphi }{2})\chi , 1-\rho -(1+\varphi )\chi \} \in [0,1) . \end{aligned}$$

(31)

This implies that for all $h \in (0,1]$ we have that

$$\begin{aligned}&\left| \max \!\left\{ h, h^{(\gamma -\rho -\chi )}, h^{(1-\rho -(1+\nicefrac {\varphi }{2})\chi )} \right\} \right| ^2 \left| \max \!\left\{ h, h^{-\chi }, h^{(\gamma -\rho -\chi )}, h^{(1-\rho -(1+\nicefrac {\varphi }{2})\chi )} \right\} \right| ^{\varphi } \\&\quad = h^{2\min \{\gamma -\rho -\chi ,1-\rho -(1+\nicefrac {\varphi }{2})\chi \}} h^{-\varphi \chi } = h^{2\min \{\gamma -\rho -(1+\nicefrac {\varphi }{2})\chi ,1-\rho -(1+\varphi )\chi \}} \le 1 . \end{aligned}$$

(32)

Moreover, observe that (30) shows for all $h \in (1,\infty )$ that

$$\begin{aligned}&\left| \max \!\left\{ h, h^{(\gamma -\rho -\chi )}, h^{(1-\rho -(1+\nicefrac {\varphi }{2})\chi )} \right\} \right| ^2 \left| \max \!\left\{ h, h^{-\chi }, h^{(\gamma -\rho -\chi )}, h^{(1-\rho -(1+\nicefrac {\varphi }{2})\chi )} \right\} \right| ^{\varphi } \\&\quad = h^{(2+\varphi )} . \end{aligned}$$

(33)

Combining (29) with (32) and (33) yields that for all $s \in [0,T]$ we have that

$$\begin{aligned}&Z_{ \lfloor s \rfloor _{T\!/\!M} } \Vert F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) - F( \bar{{\mathfrak {X}}}_{s} + {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \Vert _H^2 \le 2 C \left[ \frac{\max \{1,T\} (1+\sqrt{C})}{(1-\rho )} \right] ^{\!(2+\varphi )} . \end{aligned}$$

(34)

Furthermore, note that (17) and the assumption that ${\mathfrak {O}}_{} \in {\mathcal {C}}( [0,T], P(H) )$ hence guarantee for all $s \in [0,T]$ that

$$\begin{aligned}&\langle \bar{{\mathfrak {X}}}_{s}, P F(\bar{{\mathfrak {X}}}_{s}+{\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }) \rangle _{ H_{\nicefrac {1}{2}} } + \phi ({\mathfrak {O}}_{}) \langle \bar{{\mathfrak {X}}}_{s}, F(\bar{{\mathfrak {X}}}_{s}+{\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }) \rangle _H \nonumber \\&\quad \le \epsilon \Vert \bar{{\mathfrak {X}}}_{s} \Vert _{H_1}^2 + (c + \phi ({\mathfrak {O}}_{})) \Vert \bar{{\mathfrak {X}}}_{s} \Vert _{ H_{\nicefrac {1}{2}} }^2 + \kappa c \phi ({\mathfrak {O}}_{}) \Vert \bar{{\mathfrak {X}}}_{s} \Vert _H^2 + \Phi ({\mathfrak {O}}_{}) . \end{aligned}$$

(35)

Combining this with (24) and (34) demonstrates that for all $t \in [0,T]$ we have that

$$\begin{aligned}&\Vert \bar{{\mathfrak {X}}}_{t} \Vert _{H_{\nicefrac {1}{2}}}^2 + \phi ({\mathfrak {O}}_{}) \Vert \bar{{\mathfrak {X}}}_{t} \Vert _H^2 \\&\quad \le - 2 \int _0^t e^{2c(t-s)} \left[ \epsilon Z_{ \lfloor s \rfloor _{T\!/\!M} } \Vert \bar{{\mathfrak {X}}}_{s} \Vert _{H_1}^2 + ( c + \phi ({\mathfrak {O}}_{}) ) \Vert \bar{{\mathfrak {X}}}_{s} \Vert _{ H_{\nicefrac {1}{2}} }^2 + \kappa c \phi ({\mathfrak {O}}_{}) \Vert \bar{{\mathfrak {X}}}_{s} \Vert _H^2 \right] ds \\ {}&\qquad + 2 \int _0^t e^{2c(t-s)} \, Z_{ \lfloor s \rfloor _{T\!/\!M} } \left[ \epsilon \Vert \bar{{\mathfrak {X}}}_{s} \Vert _{H_1}^2 + (c + \phi ({\mathfrak {O}}_{})) \Vert \bar{{\mathfrak {X}}}_{s} \Vert _{ H_{\nicefrac {1}{2}} }^2 \right. \\&\left. \qquad + \kappa c \phi ({\mathfrak {O}}_{}) \Vert \bar{{\mathfrak {X}}}_{s} \Vert _H^2 + \Phi ({\mathfrak {O}}_{}) \right] ds \\ {}&\qquad + 2 C \left[ \frac{1}{2(1-\epsilon )} + \frac{\phi ({\mathfrak {O}}_{})}{2c(1-\kappa )} \right] \! \left[ \frac{\max \{1,T\} (1+\sqrt{C})}{(1-\rho )} \right] ^{\!(2+\varphi )} \left[ \int _0^t e^{2c(t-s)} \, ds \right] . \end{aligned}$$

(36)

This shows that for all $t \in [0,T]$ we have that

$$\begin{aligned}&\Vert \bar{{\mathfrak {X}}}_{t} \Vert _{H_{\nicefrac {1}{2}}}^2 + \phi ({\mathfrak {O}}_{}) \Vert \bar{{\mathfrak {X}}}_{t} \Vert _H^2 \\&\quad \le \frac{ \Phi ({\mathfrak {O}}_{}) \left[ e^{2ct} - 1 \right] }{ c } + \frac{ C \left[ e^{2ct} - 1 \right] }{ c } \left[ \frac{1}{2(1-\epsilon )} \right. \\&\left. \qquad + \frac{\phi ({\mathfrak {O}}_{})}{2c(1-\kappa )} \right] \! \left[ \frac{\max \{1,T\} (1+\sqrt{C})}{(1-\rho )} \right] ^{\!(2+\varphi )} . \end{aligned}$$

(37)

Hence, we obtain that

$$\begin{aligned}&\sup _{ t \in [0,T] } \Big [ \Vert \bar{{\mathfrak {X}}}_{t} \Vert _{H_{\nicefrac {1}{2}}}^2 + \phi ({\mathfrak {O}}_{}) \Vert \bar{{\mathfrak {X}}}_{t} \Vert _H^2 \Big ] \\&\quad \le \frac{ \left( e^{2cT} - 1 \right) }{ c } \left( \Phi ({\mathfrak {O}}_{}) + \frac{ C }{ 2 } \left[ \frac{1}{(1-\epsilon )} + \frac{\phi ({\mathfrak {O}}_{})}{c(1-\kappa )} \right] \! \left[ \tfrac{\max \{1,T\} (1+\sqrt{C})}{(1-\rho )} \right] ^{\!(2+\varphi )} \right) \\ {}&\quad \le \frac{ \left( e^{2cT} - 1 \right) }{ c } \left( \Phi ({\mathfrak {O}}_{}) + \frac{ C \max \{ 1, \phi ({\mathfrak {O}}_{}) \} }{ 2(1-\epsilon ) (1-\kappa ) } \left[ 1 + \frac{1}{c} \right] \! \left[ \tfrac{\max \{1,T\} (1+\sqrt{C})}{(1-\rho )} \right] ^{\!(2+\varphi )} \right) \\ {}&\quad = \frac{ \left( e^{2cT} - 1 \right) }{ c } \left( \Phi ({\mathfrak {O}}_{}) + \frac{ \max \{ 1, \phi ({\mathfrak {O}}_{}) \} C ( 1 + c ) }{ 2(1-\epsilon ) (1-\kappa ) c } \left[ \tfrac{\max \{1,T\} (1+\sqrt{C})}{(1-\rho )} \right] ^{\!(2+\varphi )} \right) . \end{aligned}$$

(38)

The proof of Lemma 2.2 is thus completed. $\square$

3 Pathwise error estimates

3.1 Setting

Consider the notation in Sect. 1.1, let $( H, \langle \cdot , \cdot \rangle _H, \left\| \cdot \right\| _H )$ be a separable ${\mathbb {R}}$-Hilbert space, let ${\mathbb {H}}\subseteq H$ be a non-empty orthonormal basis of H, let $T, c, \varphi \in (0,\infty )$, $C \in [0,\infty )$, $M \in {\mathbb {N}}$, $\mu :{\mathbb {H}}\rightarrow {\mathbb {R}}$ satisfy $\sup _{ h \in {\mathbb {H}}} \mu _h < 0$, let $A :D(A) \subseteq H \rightarrow H$ be the linear operator which satisfies $D(A) = \{ v \in H :\sum _{ h \in {\mathbb {H}}} | \mu _h \langle h, v \rangle _H |^2 < \infty \}$ and $\forall \, v \in D(A) :Av = \sum _{ h \in {\mathbb {H}}} \mu _h \langle h,v \rangle _H h$, let $( V, \left\| \cdot \right\| _V )$ be an ${\mathbb {R}}$-Banach space with $D(A) \subseteq V \subseteq H$ continuously and densely, and let $O, {\mathfrak {O}}_{}, {\mathbf {X}}_{}, {\mathfrak {X}}_{} :[0,T] \rightarrow V$ and ${\mathcal {V}}:V \times V \rightarrow [0,\infty )$ be functions, and let $X \in {\mathcal {C}}( [0,T], V )$, $F \in {\mathcal {C}}( V,H )$, $I \in {\mathcal {P}}_0({\mathbb {H}})$, $P \in L(H)$ satisfy¹ for all $v,w \in D(A)$, $t \in [0,T]$ that

$$\begin{aligned}&P(v) = \textstyle \sum _{ h \in I } \langle h,v \rangle _H h , \qquad \langle v-w, Av + F(v) - Aw - F(w) \rangle _H \le c \Vert v-w \Vert _H^2 , \end{aligned}$$

(39)

$$\begin{aligned}&\Vert F(v) - F(w) \Vert _H^2 \le C \Vert v-w \Vert _V^2 ( 1 + \Vert v \Vert _V^{\varphi } + \Vert w \Vert _V^{\varphi } ) , \end{aligned}$$

(40)

$$\begin{aligned}&X_t = \int _0^t e^{(t-s)A} F( X_s ) \, ds + O_t , \qquad {\mathbf {X}}_{t} = \int _0^t P e^{(t-s)A} F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \, ds + P O_t , \end{aligned}$$

(41)

$$\begin{aligned}&\text {and} \qquad {\mathfrak {X}}_{t} = \int _0^t P e^{(t-s)A} \mathbb {1}_{ [ 0, \nicefrac {M}{T} ] }^{{\mathbb {R}}} ( {\mathcal {V}}({\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} },{\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }) ) \, F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \, ds + {\mathfrak {O}}_{t} . \end{aligned}$$

(42)

3.2 On the separability of a certain Banach space

The next elementary lemma, Lemma 3.1, ensures that the ${\mathbb {R}}$-Banach space $(V, \left\| \cdot \right\| \!_V)$ in Sect. 3.1 is separable. Lemma 3.1 is well-known in the literature. A proof of Lemma 3.1 can, e.g., be found in the extended arXiv version of this article [2, Section 3.2].

Lemma 3.1

Let $( V, \left\| \cdot \right\| _V )$ be a separable ${\mathbb {R}}$-Banach space and let $( W, \left\| \cdot \right\| _W )$ be an ${\mathbb {R}}$-Banach space with $V \subseteq W$ continuously and densely. Then $( W, \left\| \cdot \right\| _W )$ is a separable ${\mathbb {R}}$-Banach space.

3.3 Analysis of the error between the Galerkin projection of the exact solution and the Galerkin projection of the semilinear integrated version of the numerical approximation

In our error analysis in Lemma 3.3 below we employ the following elementary result, Lemma 3.2 below, on mild solutions of certain semilinear evolution equations. A proof of Lemma 3.2 can, e.g., be found in the extended arXiv version of this article [2, Section 3.3].

Lemma 3.2

Consider the notation in Sect. 1.1, let $(V, \left\| \cdot \right\| \!_V)$ be a separable ${\mathbb {R}}$-Banach space, and let $A \in L(V)$, $T \in (0,\infty )$, $Y :[0,T] \rightarrow V$, $Z \in {\mathcal {C}}( [0,T], V )$ satisfy for all $t \in [0,T]$ that $Y_t = \int _0^t e^{(t-s)A} Z_s \, ds$. Then

• (i) we have that Y is continuously differentiable,

• (ii) we have for all $t \in [0,T]$ that $Y_t = \int _0^t (A Y_s + Z_s) \, ds$, and

• (iii) we have for all $t \in [0,T]$ that $\frac{d}{dt} Y_t = A Y_t + Z_t$.

Lemma 3.3

Assume the setting in Sect. 3.1 and let $\kappa \in (2,\infty )$, $t \in [0,T]$. Then

$$\begin{aligned} \Vert P X_t - {\mathbf {X}}_{t} \Vert _H^2&\le \frac{C e^{\kappa cT} }{ \left( \kappa - 2 \right) c } \int _0^t \left[ \Vert X_s - P X_s \Vert _V + \Vert {\mathbf {X}}_{s} - {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } \Vert _V \right] ^2 \\&\quad \cdot \left( 1 + \Vert X_s \Vert _V^{\varphi } + \Vert P X_s \Vert _V^{\varphi } + \Vert {\mathbf {X}}_{s} \Vert _V^{\varphi } + \Vert {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } \Vert _V^{\varphi } \right) ds . \end{aligned}$$

(43)

Proof of Lemma 3.3

Throughout this proof assume w.l.o.g. that $t \in (0,T]$ (otherwise the proof is clear). Observe that Lemma 3.2 (with $V = P(H)$, $A = ( P(H) \ni v \mapsto Av \in P(H) )$, $T = T$, $Y = ( [0,T] \ni s \mapsto P(X_s - O_s) \in P(H) )$, $Z = ( [0,T] \ni s \mapsto P F( X_s ) \in P(H) )$ in the notation of Lemma 3.2) shows that the function $[0,T] \ni s \mapsto P(X_s - O_s) \in P(H)$ is continuously differentiable and that for all $s \in [0,T]$ we have that

$$\begin{aligned} P(X_s - O_s) = \int _0^s A P (X_u-O_u) + P F( X_u ) \, du . \end{aligned}$$

(44)

Next note that Lemma 2.1 in Hutzenthaler et al. [21] (with $V = H$, $A = A$, $T = T$, $h = \nicefrac {T}{M}$, $Y = ( [0,T] \ni s \mapsto {\mathbf {X}}_{s} - P O_s \in H )$, $Z = ( [0,T] \ni s \mapsto P F({\mathfrak {X}}_{s}) \in H )$ in the notation of Lemma 2.1 in Hutzenthaler et al. [21]) implies that for all $s \in [0,T]$ we have that ${\mathbf {X}}_{s} - P O_s \in D(A)$, that the function $[0,T] \ni s \mapsto {\mathbf {X}}_{s} - P O_s \in D(A)$ is continuous, that the function $[0,T]\setminus \{0, \frac{T}{M}, \frac{2T}{M}, \ldots \} \ni s \mapsto {\mathbf {X}}_{s} - P O_s \in H$ is continuously differentiable, and that for all $s \in [0,T]$ we have that

$$\begin{aligned} {\mathbf {X}}_{s} - P O_s = \int _0^s A ({\mathbf {X}}_{u}- P O_u) + P F( {\mathfrak {X}}_{ \lfloor u \rfloor _{T\!/\!M} } ) \, du . \end{aligned}$$

(45)

This, (44), the fundamental theorem of calculus, and the fact that

$$\begin{aligned} \forall \, s \in [0,T] :A P X_s, A {\mathbf {X}}_{s} \in P(H) \end{aligned}$$

(46)

prove that

$$\begin{aligned}&e^{-\kappa c t} \left\| P X_t - {\mathbf {X}}_{t} \right\| _H^2 = e^{-\kappa c t} \left\| P (X_t - O_t) - ({\mathbf {X}}_{t} - P O_t) \right\| _H^2 \nonumber \\&\quad = 2 \int _0^t e^{-\kappa c s} \, \big< P X_s - {\mathbf {X}}_{s}, A P (X_s-O_s) + P F( X_s ) \nonumber \\&\qquad - A ({\mathbf {X}}_{s} - P O_s) - P F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \big>_H \, ds \nonumber \\&\qquad - \kappa c \int _0^t e^{-\kappa c s} \left\| P X_s - {\mathbf {X}}_{s} \right\| _H^2 ds \nonumber \\&\quad = 2 \int _0^t e^{-\kappa c s} \, \big< P X_s - {\mathbf {X}}_{s}, A P X_s + P F( X_s ) - A {\mathbf {X}}_{s} - P F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \big>_H \, ds \nonumber \\&\qquad - \kappa c \int _0^t e^{-\kappa c s} \left\| P X_s - {\mathbf {X}}_{s} \right\| _H^2 ds \nonumber \\&\quad = 2 \int _0^t e^{-\kappa c s} \, \big < P X_s - {\mathbf {X}}_{s}, P \big [ A P X_s + F( X_s ) - A {\mathbf {X}}_{s} - F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \big ] \big >_H \, ds \nonumber \\&\qquad - \kappa c \int _0^t e^{-\kappa c s} \left\| P X_s - {\mathbf {X}}_{s} \right\| _H^2 ds . \end{aligned}$$

(47)

The fact that $P \in L(H)$ is symmetric together with the fact that

$$\begin{aligned} \forall \, s \in [0,T] :P X_s, {\mathbf {X}}_{s} \in P(H) \end{aligned}$$

(48)

therefore ensures that

$$\begin{aligned}&e^{-\kappa c t} \left\| P X_t - {\mathbf {X}}_{t} \right\| _H^2 \\ {}&\quad = 2 \int _0^t e^{-\kappa c s} \, \big< P X_s - {\mathbf {X}}_{s}, A P X_s + F( X_s ) - A {\mathbf {X}}_{s} - F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \big>_H \, ds \\ {}&\qquad - \kappa c \int _0^t e^{-\kappa c s} \left\| P X_s - {\mathbf {X}}_{s} \right\| _H^2 ds \\ {}&\quad = 2 \int _0^t e^{-\kappa c s} \, \big< P X_s - {\mathbf {X}}_{s}, A P X_s + F( P X_s ) - A {\mathbf {X}}_{s} - F( {\mathbf {X}}_{s} ) \big>_H \, ds \\ {}&\qquad + 2 \int _0^t e^{-\kappa c s} \, \big < P X_s - {\mathbf {X}}_{s}, F( X_s ) - F( P X_s) + F( {\mathbf {X}}_{s} ) - F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \big >_H \, ds \\ {}&\qquad - \kappa c \int _0^t e^{-\kappa c s} \left\| P X_s - {\mathbf {X}}_{s} \right\| _H^2 ds . \end{aligned}$$

(49)

The Cauchy–Schwarz inequality, (39), and the fact that $\forall \, x,y \in {\mathbb {R}}:xy \le \nicefrac {x^2}{2} + \nicefrac {y^2}{2}$ hence demonstrate that

$$\begin{aligned}&e^{-\kappa c t} \left\| P X_t - {\mathbf {X}}_{t} \right\| _H^2 \nonumber \\&\quad \le 2 c \int _0^t e^{-\kappa c s} \left\| P X_s - {\mathbf {X}}_{s} \right\| _H^2 ds - \kappa c \int _0^t e^{-\kappa c s} \left\| P X_s - {\mathbf {X}}_{s} \right\| _H^2 ds \nonumber \\&\qquad + 2 \int _0^t e^{-\kappa c s} \, \Vert P X_s - {\mathbf {X}}_{s} \Vert _H \, \Vert F( X_s ) - F( P X_s) + F( {\mathbf {X}}_{s} ) - F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \Vert _H \, ds \nonumber \\&\quad = \left( 2-\kappa \right) c \int _0^t e^{-\kappa c s} \left\| P X_s {-} {\mathbf {X}}_{s} \right\| _H^2 ds {+} 2 \int _0^t e^{-\kappa c s} \left[ \sqrt{ \left( \kappa {-} 2 \right) c } \left\| P X_s {-} {\mathbf {X}}_{s} \right\| _H \right] \nonumber \\&\qquad \cdot \left[ \tfrac{1}{ \sqrt{ \left( \kappa - 2 \right) c } } \, \Vert F( X_s ) - F( P X_s) + F( {\mathbf {X}}_{s} ) - F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \Vert _H \right] ds \nonumber \\&\quad \le \left( 2-\kappa \right) c \int _0^t e^{-\kappa c s} \left\| P X_s - {\mathbf {X}}_{s} \right\| _H^2 ds + \int _0^t e^{-\kappa c s} \, \bigg [ \left( \kappa - 2 \right) c \left\| P X_s - {\mathbf {X}}_{s} \right\| _H^2 \nonumber \\&\qquad + \tfrac{1}{ \left( \kappa - 2 \right) c } \, \Vert F( X_s ) - F( P X_s) + F( {\mathbf {X}}_{s} ) - F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \Vert _H^2 \bigg ] \, ds . \end{aligned}$$

(50)

The triangle inequality, (40), the assumption that $D(A) \subseteq V$ densly, and the assumption that $F \in C(V,H)$ therefore yield that

$$\begin{aligned}&e^{-\kappa c t} \left\| P X_t - {\mathbf {X}}_{t} \right\| _H^2 \\ {}&\quad \le \frac{1}{ \left( \kappa - 2 \right) c } \int _0^t e^{-\kappa c s} \left[ \big \Vert F( X_s ) - F( P X_s) \big \Vert _H + \big \Vert F( {\mathbf {X}}_{s} ) - F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \big \Vert _H \right] ^2 ds \\ {}&\quad \le \frac{C}{ \left( \kappa - 2 \right) c } \int _0^t e^{-\kappa c s} \, \bigg [ \Vert X_s - P X_s \Vert _V \, \sqrt{ 1 + \Vert X_s \Vert _V^{\varphi } + \Vert P X_s \Vert _V^{\varphi } } \\ {}&\qquad + \Vert {\mathbf {X}}_{s} - {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } \Vert _V \, \sqrt{ 1 + \Vert {\mathbf {X}}_{s} \Vert _V^{\varphi } + \Vert {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } \Vert _V^{\varphi } } \, \bigg ]^2 \, ds . \end{aligned}$$

(51)

This completes the proof of Lemma 3.3. $\square$

3.4 Analysis of the error between the numerical approximation and the Galerkin projection of the semilinear integrated version of the numerical approximation

For the formulation of the next lemma we recall that Setting 3.1 ensures that ${\mathcal {V}}:V \times V \rightarrow [0, \infty )$ is a function from $V \times V$ to $[0, \infty )$.

Lemma 3.4

Assume the setting in Sect. 3.1 and let $\alpha \in (0,\infty )$, $\rho \in [0,1)$, $t \in [0,T]$ satisfy $\sup _{ s \in (0,T] } s^{\rho } \Vert e^{sA} \Vert _{ L(H, V) }$ $< \infty$. Then

$$\begin{aligned}&\Vert {\mathbf {X}}_{t} - {\mathfrak {X}}_{t} \Vert _V \le \frac{ T^{\alpha } }{ M^{\alpha } } \left[ \sup _{ s \in (0,T) } s^{\rho } \, \big \Vert e^{sA} \big \Vert _{ L(H,V) } \right] \\&\int _0^t \left( t-s \right) ^{-\rho } \big | {\mathcal {V}}({\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} },{\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }) \big |^{\alpha } \, \Vert F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \Vert _H \, ds + \Vert P O_t - {\mathfrak {O}}_{t} \Vert _V . \end{aligned}$$

(52)

Proof of Lemma 3.4

Throughout this proof we assume w.l.o.g. that $t \in (0,T]$ (otherwise the proof is clear). Observe that

$$\begin{aligned}&\Vert {\mathbf {X}}_{t} - {\mathfrak {X}}_{t} \Vert _V \nonumber \\&\quad \le \int _0^t \big \Vert P e^{(t-s)A} \big [ 1 - \mathbb {1}_{ [ 0, \nicefrac {M}{T} ] }^{{\mathbb {R}}} ( {\mathcal {V}}({\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} },{\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }) ) \big ] F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \big \Vert _V \, ds \nonumber \\&\qquad ( + \Vert P O_t - {\mathfrak {O}}_{t} \Vert _V\nonumber \\&\quad \le \left[ \sup _{ s \in (0,T) } s^{\rho } \, \big \Vert e^{sA} \big \Vert _{ L(H,V) } \right] \int _0^t \left( t-s \right) ^{-\rho } \big \Vert \mathbb {1}_{ ( \nicefrac {M}{T}, \infty ) }^{{\mathbb {R}}} ( {\mathcal {V}}({\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} },{\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }) ) \, \nonumber \\&\qquad P F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \big \Vert _H \, ds + \Vert P O_t - {\mathfrak {O}}_{t} \Vert _V \nonumber \\&\quad \le \left[ \sup _{ s \in (0,T) } s^{\rho } \, \big \Vert e^{sA} \big \Vert _{ L(H,V) } \right] \int _0^t \left( t-s \right) ^{-\rho } \mathbb {1}_{ ( \nicefrac {M}{T}, \infty ) }^{{\mathbb {R}}} ( {\mathcal {V}}({\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} },{\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }) ) \nonumber \\&\quad \qquad \left[ \tfrac{ T }{ M } {\mathcal {V}}({\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} },{\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }) \right] ^{\alpha } \!\cdot \! \Vert P \Vert _{ L(H) } \, \Vert F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \Vert _H \, ds \!+\! \Vert P O_t \!-\! {\mathfrak {O}}_{t} \Vert _V .\quad \quad \end{aligned}$$

(53)

This and the fact that $\Vert P \Vert _{ L(H) } \le 1$ complete the proof of Lemma 3.4. $\square$

3.5 Temporal regularity for the Galerkin projection of the semilinear integrated version of the numerical approximation

Lemma 3.5

Assume the setting in Sect. 3.1 and let $\rho \in [0,1)$, $\varrho \in [0, 1-\rho )$, $t_1 \in [0,T)$, $t_2 \in (t_1, T]$ satisfy $\sup _{ s \in (0,T] } s^{\rho } \Vert e^{sA} \Vert _{ L(H, V) } < \infty$. Then

$$\begin{aligned}&\Vert {\mathbf {X}}_{t_1} - {\mathbf {X}}_{t_2} \Vert _V \le \left[ \sup _{ s \in (0,T) } s^{\rho } \, \big \Vert e^{sA} \big \Vert _{ L(H,V) } \right] \Bigg [ \int _{t_1}^{t_2} \left( t_2 - s \right) ^{-\rho } \Vert F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \Vert _H \, ds \nonumber \\ {}&\qquad + 2^{(\rho +\varrho )} \left( t_2 - t_1 \right) ^{\varrho } \int _0^{t_1} \left( t_1-s \right) ^{-(\rho +\varrho )} \Vert F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \Vert _H \, ds \Bigg ] + \Vert P ( O_{t_2} - O_{t_1} ) \Vert _V . \end{aligned}$$

(54)

Proof of Lemma 3.5

Observe that

$$\begin{aligned}&\Vert {\mathbf {X}}_{t_2} - {\mathbf {X}}_{t_1} \Vert _V \\ {}&\quad \le \int _{t_1}^{t_2} \big \Vert P e^{(t_2-s)A} F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \big \Vert _V \, ds + \int _0^{t_1} \big \Vert P \big ( e^{(t_2-s)A} - e^{(t_1-s)A} \big ) F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \big \Vert _V \, ds\\&\qquad + \big \Vert P ( O_{t_2} - O_{t_1} ) \big \Vert _V \\ {}&\quad \le \left[ \sup _{ s \in (0,T) } s^{\rho } \, \big \Vert e^{sA} \big \Vert _{ L(H,V) } \right] \int _{t_1}^{t_2} \left( t_2 - s \right) ^{-\rho } \big \Vert P F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \big \Vert _H \, ds + \big \Vert P ( O_{t_2} - O_{t_1} ) \big \Vert _V \\ {}&\qquad + \left[ \sup _{ s \in (0,T) } s^{\rho } \, \big \Vert e^{sA} \big \Vert _{ L(H,V) } \right] \int _0^{t_1} \left[ \frac{2}{t_1-s} \right] ^{\rho } \big \Vert P e^{\frac{1}{2}(t_1-s)A} \left( e^{(t_2-t_1)A} \right. \\&\quad \qquad \left. - Id _H \right) F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \big \Vert _H \, ds . \end{aligned}$$

(55)

This, Lemma 2.1, and the fact that $\Vert P \Vert _{ L(H) } \le 1$ prove that

$$\begin{aligned}&\Vert {\mathbf {X}}_{t_2} - {\mathbf {X}}_{t_1} \Vert _V \\ {}&\quad \le \left[ \sup _{ s \in (0,T) } s^{\rho } \, \big \Vert e^{sA} \big \Vert _{ L(H,V) } \right] \int _{t_1}^{t_2} \left( t_2 - s \right) ^{-\rho } \big \Vert P \big \Vert _{ L(H) } \big \Vert F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \big \Vert _H \, ds \\&\qquad + \big \Vert P ( O_{t_2} - O_{t_1} ) \big \Vert _V \\ {}&\qquad + 2^{\rho } \left[ \sup _{ s \in (0,T) } s^{\rho } \, \big \Vert e^{sA} \big \Vert _{ L(H,V) } \right] \int _0^{t_1} \left( t_1-s \right) ^{-\rho } \big \Vert (-A)^{\varrho } \, e^{\frac{1}{2}(t_1-s)A} \big \Vert _{ L(H) } \\ {}&\qquad \cdot \big \Vert (-A)^{-\varrho } \left( e^{(t_2-t_1)A} - Id _H \right) \! \big \Vert _{ L(H) } \big \Vert P \big \Vert _{ L(H) } \big \Vert F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \big \Vert _H \, ds \\ {}&\quad \le \left[ \sup _{ s \in (0,T) } s^{\rho } \, \big \Vert e^{sA} \big \Vert _{ L(H,V) } \right] \int _{t_1}^{t_2} \left( t_2 - s \right) ^{-\rho } \big \Vert F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \big \Vert _H \, ds + \big \Vert P ( O_{t_2} - O_{t_1} ) \big \Vert _V \\ {}&\qquad + 2^{(\rho +\varrho )} \left( t_2 - t_1 \right) ^{\varrho } \left[ \sup _{ s \in (0,T) } s^{\rho } \, \big \Vert e^{sA} \big \Vert _{ L(H,V) } \right] \int _0^{t_1} \left( t_1-s \right) ^{-(\rho +\varrho )} \big \Vert F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} } ) \big \Vert _H \, ds . \end{aligned}$$

(56)

The proof of Lemma 3.5 is thus completed. $\square$

4 Strong error estimates

4.1 Setting

Consider the notation in Sect. 1.1, let $( H, \langle \cdot , \cdot \rangle _H, \left\| \cdot \right\| _H )$ be a separable ${\mathbb {R}}$-Hilbert space, let ${\mathbb {H}}\subseteq H$ be a non-empty orthonormal basis of H, let $T, c, C, \varphi \in (0,\infty )$, ${\mathcal {D}}\subseteq {\mathcal {P}}_0({\mathbb {H}})$, $\mu :{\mathbb {H}}\rightarrow {\mathbb {R}}$ satisfy $\sup _{ h \in {\mathbb {H}}} \mu _h < 0$, let $A :D(A) \subseteq H \rightarrow H$ be the linear operator which satisfies $D(A) = \{ v \in H :\sum _{ h \in {\mathbb {H}}} | \mu _h \langle h, v \rangle _H |^2 < \infty \}$ and $\forall \, v \in D(A) :Av = \sum _{ h \in {\mathbb {H}}} \mu _h \langle h,v \rangle _H h$, let $( V, \left\| \cdot \right\| _V )$ be an ${\mathbb {R}}$-Banach space with $D(A) \subseteq V \subseteq H$ continuously and densely, let $F \in {\mathcal {C}}( V,H )$, $( P_I )_{ I \in {\mathcal {P}}({\mathbb {H}}) } \subseteq L(H)$ satisfy for all $v,w \in D(A)$, $I \in {\mathcal {P}}({\mathbb {H}})$ that

$$\begin{aligned}&\langle v-w, Av + F(v) - Aw - F(w) \rangle _H \le c \Vert v-w \Vert _H^2, \end{aligned}$$

(57)

$$\begin{aligned}&\Vert F(v) - F(w) \Vert _H^2 \le C \Vert v-w \Vert _V^2 ( 1 + \Vert v \Vert _V^{\varphi } + \Vert w \Vert _V^{\varphi } ), \end{aligned}$$

(58)

and $P_I(v) = \sum _{ h \in I } \langle h,v \rangle _H h$, let $( \Omega , {\mathcal {F}}, {\mathbb {P}})$ be a probability space, let $X :[0,T] \times \Omega \rightarrow V$ be a stochastic process with continuous sample paths, let ${\mathbf {X}}_{}^{M,I} :[0,T] \times \Omega \rightarrow V$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$, and ${\mathfrak {X}}_{}^{M,I} :[0,T] \times \Omega \rightarrow V$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$, be stochastic processes, let $O :[0,T] \times \Omega \rightarrow V$ and ${\mathfrak {O}}_{}^{M,I} :[0,T] \times \Omega \rightarrow V$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$, be stochastic processes, let ${\mathcal {V}}\in {\mathcal {M}}\big ( {\mathcal {B}}( V \times V ), {\mathcal {B}}( [0,\infty ) ) \big )$, and assume for all $t \in [0,T]$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ that

$$\begin{aligned}&X_t = \int _0^t e^{(t-s)A} F( X_s ) \, ds + O_t , \quad {\mathbf {X}}_{t}^{M,I} = \int _0^t P_I e^{(t-s)A} F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} ) \, ds + P_I O_t , \nonumber \\\end{aligned}$$

(59)

$$\begin{aligned}&\quad \text {and} \quad {\mathfrak {X}}_{t}^{M,I} = \int _0^t P_I e^{(t-s)A} \mathbb {1}_{ \{ {\mathcal {V}}({\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I},{\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I}) \le M/T \} }^{\Omega } \, F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} ) \, ds + {\mathfrak {O}}_{t}^{M,I} .\nonumber \\ \end{aligned}$$

(60)

4.2 Analysis of the error between the Galerkin projection of the exact solution and the Galerkin projection of the semilinear integrated version of the numerical approximation

Lemma 4.1

Assume the setting in Sect. 4.1 and let $\kappa \in (2,\infty )$, $t \in [0,T]$, $p \in [2,\infty )$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ satisfy $\sup _{ s \in (0,T) } {\mathbb {E}}\big [ \Vert X_s \Vert _V^{p\varphi } + \Vert P_I X_s \Vert _V^{p\varphi } + \Vert {\mathbf {X}}_{s}^{M,I} \Vert _V^{p\varphi } + \Vert {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _V^{p\varphi } \big ] < \infty$. Then

$$\begin{aligned}&\Vert P_I X_t - {\mathbf {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p({\mathbb {P}}; H) } \le \frac{\sqrt{ C T e^{\kappa c T} } }{ \sqrt{ \left( \kappa - 2 \right) c } } \left[ \sup _{ s \in (0,T) } \left( \Vert P_{ {\mathbb {H}}\setminus I } X_s \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) } \right. \right. \nonumber \\&\left. \left. \qquad + \Vert {\mathbf {X}}_{s}^{M,I} - {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) } \right) \right] \nonumber \\&\quad \cdot \left[ 1 + \sup _{ s \in (0,T) } \left( \Vert X_s \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}} + \Vert P_I X_s \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}} \right. \right. \nonumber \\&\left. \left. \qquad + \Vert {\mathbf {X}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}} + \Vert {\mathfrak {X}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}} \right) \right] . \end{aligned}$$

(61)

Proof of Lemma 4.1

Note that Lemma 3.3 and Hölder’s inequality ensure that

$$\begin{aligned}&\Vert P_I X_t - {\mathbf {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p({\mathbb {P}}; H) }^2 \nonumber \\&\quad = \big \Vert \Vert P_I X_t - {\mathbf {X}}_{t}^{M,I} \Vert _H^2 \big \Vert _{ {\mathcal {L}}^{\nicefrac {p}{2}}({\mathbb {P}}; {\mathbb {R}}) } \nonumber \\ {}&\quad \le \frac{C e^{\kappa cT} }{ \left( \kappa - 2 \right) c } \int _0^t \bigg \Vert \! \left[ \Vert X_s - P_I X_s \Vert _V + \Vert {\mathbf {X}}_{s}^{M,I} - {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _V \right] ^2 \nonumber \\ {}&\qquad \cdot \left( 1 + \Vert X_s \Vert _V^{\varphi } + \Vert P_I X_s \Vert _V^{\varphi } + \Vert {\mathbf {X}}_{s}^{M,I} \Vert _V^{\varphi } + \Vert {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _V^{\varphi } \right) \! \bigg \Vert _{ {\mathcal {L}}^{\nicefrac {p}{2}}({\mathbb {P}};{\mathbb {R}}) } \, ds \nonumber \\ {}&\quad \le \frac{ C e^{\kappa cT} }{ \left( \kappa - 2 \right) c } \int _0^t \big \Vert \Vert X_s - P_I X_s \Vert _V + \Vert {\mathbf {X}}_{s}^{M,I} - {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _V \big \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};{\mathbb {R}}) }^2 \nonumber \\ {}&\qquad \cdot \big \Vert 1 + \Vert X_s \Vert _V^{\varphi } + \Vert P_I X_s \Vert _V^{\varphi } + \Vert {\mathbf {X}}_{s}^{M,I} \Vert _V^{\varphi } + \Vert {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _V^{\varphi } \big \Vert _{ {\mathcal {L}}^p({\mathbb {P}};{\mathbb {R}}) } \, ds . \end{aligned}$$

(62)

This shows that

$$\begin{aligned}&\Vert P_I X_t - {\mathbf {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p({\mathbb {P}}; H) }^2 \\ {}&\quad \le \frac{C e^{\kappa cT} }{ \left( \kappa - 2 \right) c } \int _0^t \left[ \Vert X_s - P_I X_s \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) } + \Vert {\mathbf {X}}_{s}^{M,I} - {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) } \right] ^2 \\ {}&\qquad \cdot \left[ 1 + \Vert X_s \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\varphi } + \Vert P_I X_s \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\varphi } + \Vert {\mathbf {X}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\varphi } + \Vert {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\varphi } \right] ds \\ {}&\quad \le \frac{ C T e^{\kappa cT} }{ \left( \kappa - 2 \right) c } \left[ \sup _{ s \in (0,T) } \left( \Vert P_{ {\mathbb {H}}\setminus I } X_s \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) } + \Vert {\mathbf {X}}_{s}^{M,I} - {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) } \right) \right] ^{\!2} \\ {}&\qquad \cdot \left[ 1 + \sup _{ s \in (0,T) } \left( \Vert X_s \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\varphi } \Vert P_I X_s \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\varphi } + \Vert {\mathbf {X}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\varphi } + \Vert {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\varphi } \right) \right] . \end{aligned}$$

(63)

Combining this with the fact that $\forall \, n \in {\mathbb {N}}$,$x_1, \ldots , x_n \in [0,\infty ) :\sqrt{ x_1 + \ldots + x_n } \le \sqrt{x_1} + \ldots + \sqrt{x_n}$ completes the proof of Lemma 4.1. $\square$

4.3 Analysis of the error between the numerical approximation and the Galerkin projection of the semilinear integrated version of the numerical approximation

Lemma 4.2

Assume the setting in Sect. 4.1 and let $\alpha \in (0,\infty )$, $\rho \in [0,1)$, $t \in [0,T]$, $p \in [1,\infty )$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ satisfy $\sup _{ s \in (0,T] } s^{\rho } \Vert e^{sA} \Vert _{ L(H,V) } + \sup _{ s \in [0,T) } {\mathbb {E}}\big [ | {\mathcal {V}}({\mathfrak {X}}_{s}^{M,I},{\mathfrak {O}}_{s}^{M,I}) |^{2p\alpha } + \Vert F( {\mathfrak {X}}_{s}^{M,I} ) \Vert _H^{2p} \big ] < \infty$. Then

$$\begin{aligned}&\Vert {\mathbf {X}}_{t}^{M,I} - {\mathfrak {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p({\mathbb {P}}; V) } \\ {}&\quad \le \frac{ T^{(1+\alpha -\rho )} }{ \left( 1-\rho \right) M^{\alpha } } \left[ \sup _{ s \in (0,T) } s^{\rho } \, \Vert e^{sA} \Vert _{ L(H,V) } \right] \\&\qquad \! \left[ \sup _{ s \in [0,T) } \left( \Vert {\mathcal {V}}({\mathfrak {X}}_{s}^{M,I},{\mathfrak {O}}_{s}^{M,I}) \Vert _{ {\mathcal {L}}^{2p\alpha }( {\mathbb {P}}; {\mathbb {R}}) }^{\alpha } \Vert F( {\mathfrak {X}}_{s}^{M,I} ) \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; H) } \right) \right] \\ {}&\qquad + \Vert P_I O_t - {\mathfrak {O}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p({\mathbb {P}}; V) } . \end{aligned}$$

(64)

Proof of Lemma 4.2

Note that Lemma 3.4 and Hölder’s inequality imply that

$$\begin{aligned}&\Vert {\mathbf {X}}_{t}^{M,I} - {\mathfrak {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p({\mathbb {P}}; V) } \\ {}&\quad \le \frac{ T^{\alpha } }{ M^{\alpha } } \left[ \sup _{ s \in (0,T) } s^{\rho } \, \Vert e^{sA} \Vert _{ L(H,V) } \right] \\&\quad \qquad \left[ \int _0^t \left( t-s \right) ^{-\rho } \big \Vert | {\mathcal {V}}({\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I},{\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I}) |^{\alpha } \, \Vert F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} ) \Vert _H \big \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; {\mathbb {R}}) } \, ds \right] \\ {}&\qquad + \Vert P_I O_t - {\mathfrak {O}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p({\mathbb {P}}; V) } \\ {}&\quad = \frac{ T^{\alpha } }{ M^{\alpha } } \left[ \sup _{ s \in (0,T) } s^{\rho } \, \Vert e^{sA} \Vert _{ L(H,V) } \right] \\&\quad \qquad \left[ \int _0^t \left( t-s \right) ^{-\rho } \left( {\mathbb {E}}\left[ | {\mathcal {V}}({\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I},{\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I}) |^{p \alpha } \Vert F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} ) \Vert _H^p \right] \right) ^{\nicefrac {1}{p}} ds \right] \\ {}&\qquad + \Vert P_I O_t - {\mathfrak {O}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p({\mathbb {P}}; V) } \\ {}&\quad \le \frac{ T^{\alpha } }{ M^{\alpha } } \left[ \sup _{ s \in (0,T) } s^{\rho } \, \Vert e^{sA} \Vert _{ L(H,V) } \right] \\ {}&\qquad \cdot \left[ \int _0^t \left( t-s \right) ^{-\rho } \left( {\mathbb {E}}\left[ | {\mathcal {V}}({\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I},{\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I}) |^{2 p \alpha } \right] \right) ^{\frac{\alpha }{2p\alpha }} \left( {\mathbb {E}}\left[ \Vert F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} ) \Vert _H^{2p} \right] \right) ^{\frac{1}{2p}} ds \right] \\ {}&\qquad + \Vert P_I O_t - {\mathfrak {O}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p({\mathbb {P}}; V) } . \end{aligned}$$

(65)

This and the fact that $\int _0^t (t-s)^{-\rho } \, ds = \frac{ t^{(1-\rho )} }{ (1-\rho ) }$ complete the proof of Lemma 4.2. $\square$

4.4 Temporal regularity for the Galerkin projection of the semilinear integrated version of the numerical approximation

Lemma 4.3

Assume the setting in Sect. 4.1 and let $\rho \in [0,1)$, $\varrho \in [0, 1-\rho )$, $t_1 \in [0,T)$, $t_2 \in (t_1, T]$, $p \in [1,\infty )$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ satisfy $\sup _{ s \in (0,T] } s^{\rho } \Vert e^{sA} \Vert _{ L(H,V) } < \infty$. Then

$$\begin{aligned}&\Vert {\mathbf {X}}_{t_1}^{M,I} - {\mathbf {X}}_{t_2}^{M,I} \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; V ) } \le \Vert P_I ( O_{t_1} - O_{t_2} ) \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; V ) } \nonumber \\&\quad + \frac{ 3 \, T^{ (1 - \rho - \varrho ) } \left( t_2 - t_1 \right) ^{\varrho } }{ \left( 1 - \rho - \varrho \right) } \left[ \sup _{ s \in (0,T) } s^{\rho } \, \Vert e^{sA} \Vert _{ L(H,V) } \right] \left[ \sup _{ s \in [0,T) } \Vert F( {\mathfrak {X}}_{s}^{M,I} ) \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; H ) } \right] .\nonumber \\ \end{aligned}$$

(66)

Proof of Lemma 4.3

Observe that Lemma 3.5 proves that

$$\begin{aligned}&\Vert {\mathbf {X}}_{t_1}^{M,I} - {\mathbf {X}}_{t_2}^{M,I} \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; V ) } \nonumber \\&\quad \le \left[ \sup _{ s \in (0,T) } s^{\rho } \, \Vert e^{sA} \Vert _{ L(H,V) } \right] \left[ \sup _{ s \in [0,T) } \Vert F( {\mathfrak {X}}_{s}^{M,I} ) \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; H ) } \right] \Bigg [ \int _{t_1}^{t_2} \left( t_2 - s \right) ^{-\rho } ds \nonumber \\&\qquad + 2^{(\rho +\varrho )} \left( t_2 - t_1 \right) ^{\varrho } \int _0^{t_1} \left( t_1-s \right) ^{-(\rho +\varrho )} ds \Bigg ] + \Vert P_I ( O_{t_2} - O_{t_1} ) \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; V ) } \nonumber \\&\quad = \left[ \sup _{ s \in (0,T) } s^{\rho } \, \Vert e^{sA} \Vert _{ L(H,V) } \right] \left[ \sup _{ s \in [0,T) } \Vert F( {\mathfrak {X}}_{s}^{M,I} ) \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; H ) } \right] \nonumber \\&\qquad \cdot \Bigg [ \frac{ \left( t_2 - t_1 \right) ^{(1-\rho )} }{ \left( 1 - \rho \right) } + \frac{ 2^{(\rho +\varrho )} \left( t_2 - t_1 \right) ^{\varrho } | t_1 |^{ (1-\rho -\varrho ) } }{ \left( 1 - \rho - \varrho \right) } \Bigg ] + \Vert P_I ( O_{t_2} - O_{t_1} ) \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; V ) }.\nonumber \\ \end{aligned}$$

(67)

This completes the proof of Lemma 4.3. $\square$

4.5 Analysis of the error between the exact solution and the numerical approximation

Proposition 4.4

Assume the setting in Sect. 4.1 and let $\alpha \in (0,\infty )$, $\rho \in [0,1)$, $\varrho \in [0,1-\rho )$, $\kappa \in (2,\infty )$, $p \in [\max \{2,\nicefrac {1}{\varphi }\}, \infty )$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$. Then

$$\begin{aligned}&\sup _{ t \in [0,T] } \Vert X_t - {\mathfrak {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; H ) } \nonumber \\&\quad \le \frac{ 4^{(2+\varphi )} \max \{ 1, T^{(\nicefrac {3}{2} + \alpha - \rho + \nicefrac {\varphi }{2} - \nicefrac {\rho \varphi }{2} )} \} \max \{ 1, C^{(1+\nicefrac {\varphi }{4})} \} \sqrt{ e^{\kappa c T } } }{ \min \{ 1, \sqrt{ c \left( \kappa - 2 \right) } \} \left( 1 - \rho - \varrho \right) ^{(1+\nicefrac {\varphi }{2})} } \nonumber \\&\quad \qquad \Bigg [ \sup _{ t \in [0,T] } \Vert P_{ {\mathbb {H}}\setminus I } X_t \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) } + M^{-\min \{\alpha ,\varrho \} } \nonumber \\ {}&\qquad + \sup _{ t \in (0,T) } \Vert P_I ( O_{t} - O_{ \lfloor t \rfloor _{T\!/\!M} } ) \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; V ) } + \sup _{ t \in [0,T] } \Vert P_I O_t - {\mathfrak {O}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}}; V) } \Bigg ] \nonumber \\&\quad \qquad \cdot \max \!\left\{ 1, \sup _{ v \in V \setminus \{0\} } \frac{ \Vert v \Vert _H }{ \Vert v \Vert _V } \right\} \nonumber \\ {}&\quad \cdot \Bigg [ 1 + \sup _{ s \in (0,T) } \Vert X_s \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}} + \sup _{ s \in (0,T) } \Vert P_I X_s \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}} + \sup _{ s \in [0,T) } \Vert {\mathfrak {X}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}}\nonumber \\&\qquad + \sup _{ s \in (0,T) } \Vert P_I O_s \Vert _{ {\mathcal {L}}^{p\varphi }( {\mathbb {P}}; V ) }^{\nicefrac {\varphi }{2}} \Bigg ] \nonumber \\ {}&\qquad \cdot \left[ 1 + \sup _{ s \in [0,T) } \Vert {\mathcal {V}}({\mathfrak {X}}_{s}^{M,I},{\mathfrak {O}}_{s}^{M,I}) \Vert _{ {\mathcal {L}}^{4p\alpha }( {\mathbb {P}}; {\mathbb {R}}) }^{\alpha } \right] \max \!\left\{ 1, \sup _{ s \in (0,T) } \left[ s^{\rho } \, \Vert e^{sA} \Vert _{ L(H,V) } \right] ^{(1+\nicefrac {\varphi }{2})} \right\} \nonumber \\ {}&\qquad \cdot \left[ \max \!\left\{ 1, \sup _{ s \in [0,T) } \Vert {\mathfrak {X}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p(1+\nicefrac {\varphi }{2})\max \{4,\varphi \}}( {\mathbb {P}}; V ) }^{[(1+\nicefrac {\varphi }{2})^2]} \right\} + \Vert F(0) \Vert _H^{ (1+\nicefrac {\varphi }{2}) } \right] . \end{aligned}$$

(68)

Proof of Proposition 4.4

Throughout this proof assume w.l.o.g. that

$$\begin{aligned}&\sup _{ s \in (0,T) } \left( s^{\rho } \Vert e^{sA} \Vert _{ L(H,V) } + {\mathbb {E}}\big [ \Vert P_I O_s \Vert _V^{p\varphi } + \Vert P_I X_s \Vert _V^{p\varphi } + \Vert X_s \Vert _V^{p\varphi } \big ] \right) \nonumber \\&\qquad + \sup _{ s \in [0,T) } {\mathbb {E}}\left[ | {\mathcal {V}}({\mathfrak {X}}_{s}^{M,I},{\mathfrak {O}}_{s}^{M,I}) |^{4p\alpha } + \Vert {\mathfrak {X}}_{s}^{M,I} \Vert _V^{ p(1+\nicefrac {\varphi }{2})\max \{4,\varphi \} } \right] < \infty . \end{aligned}$$

(69)

Note that the fact that

$$\begin{aligned} \forall \, v,w \in V :\Vert F(v) - F(w) \Vert _H^2 \le C \Vert v-w \Vert _V^2 ( 1 + \Vert v \Vert _V^{\varphi } + \Vert w \Vert _V^{\varphi } ) \end{aligned}$$

(70)

and the fact that $\forall \, x,y \in [0, \infty ) :\sqrt{ x + y} \le \sqrt{x} + \sqrt{y}$ imply for all $s \in [0,T]$ that

$$\begin{aligned} \Vert F( {\mathfrak {X}}_{s}^{M,I} ) \Vert _H&\le \Vert F( {\mathfrak {X}}_{s}^{M,I} ) - F(0) \Vert _H + \Vert F(0) \Vert _H \\&\le \sqrt{ C \, \Vert {\mathfrak {X}}_{s}^{M,I} \Vert _V^2 \big ( 1 + \Vert {\mathfrak {X}}_{s}^{M,I} \Vert _V^{\varphi } \big ) } + \Vert F(0) \Vert _H \\ {}&\le \sqrt{ C } \, \Vert {\mathfrak {X}}_{s}^{M,I} \Vert _V \big ( 1 + \Vert {\mathfrak {X}}_{s}^{M,I} \Vert _V^{\nicefrac {\varphi }{2}} \big ) + \Vert F(0) \Vert _H \\&= \sqrt{C} \left( \Vert {\mathfrak {X}}_{s}^{M,I} \Vert _V + \Vert {\mathfrak {X}}_{s}^{M,I} \Vert _V^{(1+\nicefrac {\varphi }{2})} \right) + \Vert F(0) \Vert _H . \end{aligned}$$

(71)

Hence, we obtain for all $q \in [1,\infty )$ that

$$\begin{aligned} \sup _{ s \in [0,T) } \Vert F( {\mathfrak {X}}_{s}^{M,I} ) \Vert _{ {\mathcal {L}}^q( {\mathbb {P}}; H ) } \le 2 \, \sqrt{C} \max \!\left\{ 1, \sup _{ s \in [0,T) } \Vert {\mathfrak {X}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{q(1+\nicefrac {\varphi }{2})}( {\mathbb {P}}; V ) }^{(1+\nicefrac {\varphi }{2})} \right\} + \Vert F(0) \Vert _H . \end{aligned}$$

(72)

We establish (68) by an application of (61) in Lemma 4.1 above (cf. (76)) and, thereafter, by estimating the right hand side of (61) (cf. (79)). To estimate the right hand side of (63) in Lemma 4.1 above we now establish upper bounds for the quantity $\sup _{ s \in (0,T) } \Vert {\mathbf {X}}_{s}^{M,I} - {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}}; V) }$ (cf. (73) below) and the quantity $\sup _{ s \in (0,T) } \Vert {\mathbf {X}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p\varphi }( {\mathbb {P}}; V ) }$ (cf. (73) below). More formally, observe that the triangle inequality, Lemma 4.2, Lemma 4.3, and Hölder’s inequality imply that

$$\begin{aligned}&\sup _{ s \in (0,T) } \Vert {\mathbf {X}}_{s}^{M,I} - {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}}; V) } \nonumber \\&\quad \le \sup _{ s \in (0,T) } \Vert {\mathbf {X}}_{s}^{M,I} - {\mathbf {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}}; V) } + \sup _{ s \in [0,T) } \Vert {\mathbf {X}}_{s}^{M,I} - {\mathfrak {X}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}}; V) } \nonumber \\&\quad \le \frac{ 3 \, T^{ (1 - \rho ) } }{ \left( 1 - \rho - \varrho \right) M^{\varrho } } \left[ \sup _{ s \in (0,T) } s^{\rho } \, \Vert e^{sA} \Vert _{ L(H,V) } \right] \left[ \sup _{ s \in [0,T) } \Vert F( {\mathfrak {X}}_{s}^{M,I} ) \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; H ) } \right] \nonumber \\&\qquad + \frac{ T^{(1+\alpha -\rho )} }{ \left( 1-\rho \right) M^{\alpha } } \left[ \sup _{ s \in (0,T) } s^{\rho } \, \Vert e^{sA} \Vert _{ L(H,V) } \right] \nonumber \\&\qquad \cdot \left[ \sup _{ s \in [0,T) } \Vert {\mathcal {V}}({\mathfrak {X}}_{s}^{M,I},{\mathfrak {O}}_{s}^{M,I}) \Vert _{ {\mathcal {L}}^{4p\alpha }( {\mathbb {P}}; {\mathbb {R}}) }^{\alpha } \right] \! \left[ \sup _{ s \in [0,T) } \Vert F( {\mathfrak {X}}_{s}^{M,I} ) \Vert _{ {\mathcal {L}}^{4p}( {\mathbb {P}}; H) } \right] \nonumber \\&\qquad + \sup _{ s \in (0,T) } \Vert P_I ( O_{s} - O_{ \lfloor s \rfloor _{T\!/\!M} } ) \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; V ) } + \sup _{ s \in [0,T) } \Vert P_I O_s - {\mathfrak {O}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}}; V) } \nonumber \\&\quad \le \frac{ 3 \max \{ 1, T^{(1+\alpha -\rho )} \} }{ \left( 1-\rho - \varrho \right) M^{\min \{\alpha ,\varrho \}} } \left[ \sup _{ s \in (0,T) } s^{\rho } \, \Vert e^{sA} \Vert _{ L(H,V) } \right] \! \nonumber \\&\qquad \cdot \left[ 1 + \sup _{ s \in [0,T) } \Vert {\mathcal {V}}({\mathfrak {X}}_{s}^{M,I},{\mathfrak {O}}_{s}^{M,I}) \Vert _{ {\mathcal {L}}^{4p\alpha }( {\mathbb {P}}; {\mathbb {R}}) }^{\alpha } \right] \nonumber \\&\quad \cdot \left[ \sup _{ s \in [0,T) } \Vert F( {\mathfrak {X}}_{s}^{M,I} ) \Vert _{ {\mathcal {L}}^{4p}( {\mathbb {P}}; H) } \right] + \sup _{ s \in (0,T) } \Vert P_I ( O_{s} - O_{ \lfloor s \rfloor _{T\!/\!M} } ) \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; V ) } \nonumber \\&\qquad + \sup _{ s \in [0,T) } \Vert P_I O_s - {\mathfrak {O}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}}; V) }. \end{aligned}$$

(73)

Moreover, note that (72) and the fact that $\Vert P_I \Vert _{ L(H) } \le 1$ yields that

$$\begin{aligned}&\sup _{ s \in (0,T) } \Vert {\mathbf {X}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p\varphi }( {\mathbb {P}}; V ) } \\ {}&\quad \le \sup _{ s \in (0,T) } \left\| \int _0^s P_I e^{(s-u)A} F( {\mathfrak {X}}_{ \lfloor u \rfloor _{T\!/\!M} }^{M,I} ) \, du \right\| _{ {\mathcal {L}}^{p\varphi }( {\mathbb {P}}; V ) } + \sup _{ s \in (0,T) } \Vert P_I O_s \Vert _{ {\mathcal {L}}^{p\varphi }( {\mathbb {P}}; V ) } \\ {}&\quad \le \sup _{ s \in (0,T) } \int _0^s \Vert e^{(s-u)A} \Vert _{ L(H,V) } \Vert P_I \Vert _{ L(H) } \Vert F( {\mathfrak {X}}_{ \lfloor u \rfloor _{T\!/\!M} }^{M,I} ) \Vert _{ {\mathcal {L}}^{p\varphi }( {\mathbb {P}}; H ) } \, du \\&\qquad + \sup _{ s \in (0,T) } \Vert P_I O_s \Vert _{ {\mathcal {L}}^{p\varphi }( {\mathbb {P}}; V ) } \\ {}&\quad \le \left[ \sup _{ s \in (0,T) } s^{\rho } \, \Vert e^{sA} \Vert _{ L(H,V) } \right] \left[ \sup _{ s \in [0,T) } \Vert F( {\mathfrak {X}}_{s}^{M,I} ) \Vert _{ {\mathcal {L}}^{p\varphi }( {\mathbb {P}}; H ) } \right] \left[ \sup _{ s \in (0,T) } \int _0^s \left( s-u \right) ^{-\rho } du \right] \\ {}&\qquad + \sup _{ s \in (0,T) } \Vert P_I O_s \Vert _{ {\mathcal {L}}^{p\varphi }( {\mathbb {P}}; V ) } \\ {}&\quad \le \frac{ T^{(1-\rho )} }{ \left( 1-\rho \right) } \left[ \sup _{ s \in (0,T) } s^{\rho } \, \Vert e^{sA} \Vert _{ L(H,V) } \right] \left[ \sup _{ s \in [0,T) } \Vert F( {\mathfrak {X}}_{s}^{M,I} ) \Vert _{ {\mathcal {L}}^{p\varphi }( {\mathbb {P}}; H ) } \right] \\&\quad \quad + \sup _{ s \in (0,T) } \Vert P_I O_s \Vert _{ {\mathcal {L}}^{p\varphi }( {\mathbb {P}}; V ) } < \infty . \end{aligned}$$

(74)

Combining this, (73), and the fact that

$$\begin{aligned} \forall \, x,y \in [0,\infty ) :(x+y)^{\nicefrac {\varphi }{2}} \le 2^{\max \{0,\nicefrac {\varphi }{2}-1\}} ( x^{\nicefrac {\varphi }{2}} + y^{\nicefrac {\varphi }{2}} ) \end{aligned}$$

(75)

with Lemma 4.1 proves that

$$\begin{aligned}&\sup _{ t \in [0,T] } \Vert P_I X_t - {\mathbf {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p({\mathbb {P}}; H) }\nonumber \\&\quad \le \frac{ 2^{\max \{0,\nicefrac {\varphi }{2}-1\}} \sqrt{ C T e^{\kappa c T} } }{ \sqrt{ \left( \kappa - 2 \right) c } } \Bigg ( \sup _{ s \in (0,T) } \Vert P_{ {\mathbb {H}}\setminus I } X_s \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) } \nonumber \\&\qquad + \sup _{ s \in (0,T) } \Vert P_I ( O_{s} - O_{ \lfloor s \rfloor _{T\!/\!M} } ) \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; V ) }\nonumber \\&\qquad + \sup _{ s \in [0,T) } \Vert P_I O_s - {\mathfrak {O}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}}; V) } + \frac{ 3 \max \{ 1, T^{(1+\alpha -\rho )} \} }{ \left( 1-\rho - \varrho \right) M^{\min \{\alpha ,\varrho \}} } \left[ \sup _{ s \in (0,T) } s^{\rho } \, \Vert e^{sA} \Vert _{ L(H,V) } \right] \nonumber \\&\qquad \cdot \left[ 1 + \sup _{ s \in [0,T) } \Vert {\mathcal {V}}({\mathfrak {X}}_{s}^{M,I},{\mathfrak {O}}_{s}^{M,I}) \Vert _{ {\mathcal {L}}^{4p\alpha }( {\mathbb {P}}; {\mathbb {R}}) }^{\alpha } \right] \! \left[ \sup _{ s \in [0,T) } \Vert F( {\mathfrak {X}}_{s}^{M,I} ) \Vert _{ {\mathcal {L}}^{4p}( {\mathbb {P}}; H) } \right] \Bigg )\nonumber \\&\qquad \cdot \Bigg ( 1 + \sup _{ s \in (0,T) } \Vert X_s \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}} + \sup _{ s \in (0,T) } \Vert P_I X_s \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}} + \sup _{ s \in [0,T) } \Vert {\mathfrak {X}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}}\nonumber \\&\qquad + \frac{ T^{(1-\rho )\nicefrac {\varphi }{2}} }{ \left( 1-\rho \right) ^{\nicefrac {\varphi }{2}} } \left[ \sup _{ s \in (0,T) } s^{\rho } \, \Vert e^{sA} \Vert _{ L(H,V) } \right] ^{\nicefrac {\varphi }{2}} \left[ \sup _{ s \in [0,T) } \Vert F( {\mathfrak {X}}_{s}^{M,I} ) \Vert _{ {\mathcal {L}}^{p\varphi }( {\mathbb {P}}; H ) } \right] ^{\nicefrac {\varphi }{2}}\nonumber \\&\qquad + \sup _{ s \in (0,T) } \Vert P_I O_s \Vert _{ {\mathcal {L}}^{p\varphi }( {\mathbb {P}}; V ) }^{\nicefrac {\varphi }{2}} \Bigg ) . \end{aligned}$$

(76)

Hence, we obtain that

$$\begin{aligned}&\sup _{ t \in [0,T] } \Vert P_I X_t - {\mathbf {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p({\mathbb {P}}; H) } \\ {}&\quad \le \frac{ 3 \cdot 2^{\max \{0,\nicefrac {\varphi }{2}-1\}} \max \{ 1, T^{(\nicefrac {3}{2} + \alpha - \rho + \nicefrac {\varphi }{2} - \nicefrac {\rho \varphi }{2} )} \} \sqrt{ C e^{\kappa c T} } }{ \left( 1 - \rho - \varrho \right) ^{(1+\nicefrac {\varphi }{2})} \sqrt{ \left( \kappa - 2 \right) c } } \Bigg [ \sup _{ s \in (0,T) } \Vert P_{ {\mathbb {H}}\setminus I } X_s \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) } \\ {}&\qquad + \sup _{ s \in (0,T) } \Vert P_I ( O_{s} - O_{ \lfloor s \rfloor _{T\!/\!M} } ) \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; V ) } \\&\qquad + \sup _{ s \in [0,T) } \Vert P_I O_s - {\mathfrak {O}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}}; V) } + M^{-\min \{\alpha ,\varrho \}} \Bigg ] \\ {}&\qquad \cdot \Bigg [ 2 + \sup _{ s \in (0,T) } \Vert X_s \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}} + \sup _{ s \in (0,T) } \Vert P_I X_s \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}} + \sup _{ s \in [0,T) } \Vert {\mathfrak {X}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}} \\ {}&\qquad + \sup _{ s \in (0,T) } \Vert P_I O_s \Vert _{ {\mathcal {L}}^{p\varphi }( {\mathbb {P}}; V ) }^{\nicefrac {\varphi }{2}} \Bigg ] \left[ 1 + \sup _{ s \in [0,T) } \Vert {\mathcal {V}}({\mathfrak {X}}_{s}^{M,I},{\mathfrak {O}}_{s}^{M,I}) \Vert _{ {\mathcal {L}}^{4p\alpha }( {\mathbb {P}}; {\mathbb {R}}) }^{\alpha } \right] \\ {}&\qquad \cdot \max \!\left\{ 1, \sup _{ s \in (0,T) } \left[ s^{\rho } \, \Vert e^{sA} \Vert _{ L(H,V) } \right] ^{(1+\nicefrac {\varphi }{2})} \right\} \max \!\left\{ 1, \sup _{ s \in [0,T) } \Vert F( {\mathfrak {X}}_{s}^{M,I} ) \Vert _{ {\mathcal {L}}^{p\max \{4,\varphi \}}( {\mathbb {P}}; H) }^{(1+\nicefrac {\varphi }{2})} \right\} . \end{aligned}$$

(77)

In the next step observe that the triangle inequality implies that

$$\begin{aligned}&\sup _{ t \in [0,T] } \Vert X_t - {\mathfrak {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; H ) } \nonumber \\&\quad \le \sup _{ t \in [0,T] } \left[ \Vert X_t - P_I X_t \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; H ) } + \Vert P_I X_t - {\mathbf {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; H ) } \right. \nonumber \\&\left. \qquad + \Vert {\mathbf {X}}_{t}^{M,I} - {\mathfrak {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; H ) } \right] \nonumber \\&\quad \le \sup _{ t \in [0,T] } \Vert P_I X_t - {\mathbf {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; H ) } \nonumber \\&\qquad + \left[ \sup _{ v \in V \setminus \{0\} } \frac{ \Vert v \Vert _H }{ \Vert v \Vert _V } \right] \sup _{ t \in [0,T] } \left[ \Vert P_{ {\mathbb {H}}\setminus I } X_t \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; V ) } + \Vert {\mathbf {X}}_{t}^{M,I} - {\mathfrak {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; V ) } \right] \nonumber \\&\quad \le \left[ \sup _{ t \in [0,T] } \Vert P_I X_t - {\mathbf {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; H ) } + \sup _{ t \in [0,T] } \left[ \Vert P_{ {\mathbb {H}}\setminus I } X_t \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; V ) } \right. \right. \nonumber \\&\left. \left. \qquad + \Vert {\mathbf {X}}_{t}^{M,I} - {\mathfrak {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; V ) } \right] \right] \cdot \max \!\left\{ 1, \sup _{ v \in V \setminus \{0\} } \frac{ \Vert v \Vert _H }{ \Vert v \Vert _V } \right\} . \end{aligned}$$

(78)

This, (77), and Lemma 4.2 prove that

$$\begin{aligned}&\sup _{ t \in [0,T] } \Vert X_t - {\mathfrak {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; H ) } \nonumber \\&\quad \le \frac{ \left[ 3 \cdot 2^{\max \{1,\nicefrac {\varphi }{2}\}} + 1 \right] \max \{ 1, T^{(\nicefrac {3}{2} + \alpha - \rho + \nicefrac {\varphi }{2} - \nicefrac {\rho \varphi }{2} )} \} \max \{ 1, \sqrt{ C e^{\kappa c T } } \} }{ \min \{ 1, \sqrt{ \left( \kappa - 2 \right) c } \} \left( 1 - \rho - \varrho \right) ^{(1+\nicefrac {\varphi }{2})} } \nonumber \\&\qquad \Bigg [ \sup _{ t \in [0,T] } \Vert P_{ {\mathbb {H}}\setminus I } X_t \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) } \nonumber \\&\qquad + M^{-\min \{\alpha ,\varrho \}} + \sup _{ t \in (0,T) } \Vert P_I ( O_{t} - O_{ \lfloor t \rfloor _{T\!/\!M} } ) \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; V ) } \nonumber \\&\qquad + \sup _{ t \in [0,T] } \Vert P_I O_t - {\mathfrak {O}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}}; V) } \Bigg ] \nonumber \\&\qquad \cdot \Bigg [ 1 + \sup _{ s \in (0,T) } \Vert X_s \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}} + \sup _{ s \in (0,T) } \Vert P_I X_s \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}} \nonumber \\&\qquad + \sup _{ s \in [0,T) } \Vert {\mathfrak {X}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}} + \sup _{ s \in (0,T) } \Vert P_I O_s \Vert _{ {\mathcal {L}}^{p\varphi }( {\mathbb {P}}; V ) }^{\nicefrac {\varphi }{2}} \Bigg ] \nonumber \\&\qquad \cdot \left[ 1 + \sup _{ s \in [0,T) } \Vert {\mathcal {V}}({\mathfrak {X}}_{s}^{M,I},{\mathfrak {O}}_{s}^{M,I}) \Vert _{ {\mathcal {L}}^{4p\alpha }( {\mathbb {P}}; {\mathbb {R}}) }^{\alpha } \right] \max \!\left\{ 1, \sup _{ s \in (0,T) } \left[ s^{\rho } \, \Vert e^{sA} \Vert _{ L(H,V) } \right] ^{(1+\nicefrac {\varphi }{2})} \right\} \nonumber \\&\qquad \cdot \max \!\left\{ 1, \sup _{ s \in [0,T) } \Vert F( {\mathfrak {X}}_{s}^{M,I} ) \Vert _{ {\mathcal {L}}^{p\max \{4,\varphi \}}( {\mathbb {P}}; H ) }^{(1+\nicefrac {\varphi }{2})} \right\} \max \!\left\{ 1, \sup _{ v \in V \setminus \{0\} } \frac{ \Vert v \Vert _H }{ \Vert v \Vert _V } \right\} . \end{aligned}$$

(79)

Next note that (69), (72), and the fact that

$$\begin{aligned} \forall \, x,y \in [0,\infty ) :(x+y)^{\nicefrac {(1+\varphi }{2})} \le 2^{\nicefrac {\varphi }{2}} ( x^{\nicefrac {(1+\varphi }{2})} + y^{\nicefrac {(1+\varphi }{2})} ) \end{aligned}$$

(80)

ensure that

$$\begin{aligned}&\max \!\left\{ 1, \sup _{ s \in [0,T) } \Vert F( {\mathfrak {X}}_{s}^{M,I} ) \Vert _{ {\mathcal {L}}^{p\max \{4,\varphi \}}( {\mathbb {P}}; H ) }^{(1+\nicefrac {\varphi }{2})} \right\} \\ {}&\quad \le \left[ 2 \max \{ 1, \sqrt{C} \} \max \!\left\{ 1, \sup _{ s \in [0,T) } \Vert {\mathfrak {X}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p(1+\nicefrac {\varphi }{2})\max \{4,\varphi \}}( {\mathbb {P}}; V ) }^{(1+\nicefrac {\varphi }{2})} \right\} + \Vert F(0) \Vert _H \right] ^{ (1+\nicefrac {\varphi }{2}) } \\ {}&\quad \le 2^{(1+\varphi )} \max \{ 1, C^{(\nicefrac {1}{2}+\nicefrac {\varphi }{4})} \} \left[ \max \!\left\{ 1, \sup _{ s \in [0,T) } \Vert {\mathfrak {X}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p(1+\nicefrac {\varphi }{2})\max \{4,\varphi \}}( {\mathbb {P}}; V ) }^{[(1+\nicefrac {\varphi }{2})^2]} \right\} \right. \\&\left. \qquad + \Vert F(0) \Vert _H^{ (1+\nicefrac {\varphi }{2}) } \right] < \infty . \end{aligned}$$

(81)

Combining this with (79) and the fact that

$$\begin{aligned} \left[ 3 \cdot 2^{\max \{ 1, \nicefrac {\varphi }{2} \}} + 1 \right] \cdot 2^{(1+\varphi )}&\le 3 \cdot 2^{\max \{ 1, \nicefrac {\varphi }{2} \}} \left[ 1 + \nicefrac {1}{6} \right] \cdot 2^{(1+\varphi )} \\&= 7 \cdot 2^{ \max \{ 1+\varphi , \nicefrac {3\varphi }{2} \} } \le 4^{ (2+\varphi ) } \end{aligned}$$

(82)

completes the proof of Proposition 4.4. $\square$

5 Main result

5.1 Setting

Consider the notation in Sect. 1.1, let $( H , \langle \cdot , \cdot \rangle _H, \left\| \cdot \right\| _H )$ be a separable ${\mathbb {R}}$-Hilbert space, let ${\mathbb {H}}\subseteq H$ be a non-empty orthonormal basis of H, let $T, c ,\varphi \in (0, \infty )$, $\epsilon \in [0,1)$, $\rho \in [0,\nicefrac {1}{2})$, $\gamma \in (\rho , \nicefrac {1}{2}]$, $\chi \in (0, \nicefrac {(\gamma -\rho )}{(1+\nicefrac {\varphi }{2})}] \cap (0, \nicefrac {(1-\rho )}{(1+\varphi )}]$, ${\mathcal {D}}\subseteq {\mathcal {P}}_0({\mathbb {H}}) \setminus \{ \emptyset \}$, $\mu :{\mathbb {H}}\rightarrow {\mathbb {R}}$ satisfy $\sup _{ h \in {\mathbb {H}}} \mu _h < 0$, let $A :D(A) \subseteq H \rightarrow H$ be the linear operator which satisfies that $D(A) = \{ v \in H :\sum _{ h \in {\mathbb {H}}} | \mu _h \langle h, v\rangle _H |^2 < \infty \}$ and $\forall \, v \in D(A) :Av = \sum _{ h \in {\mathbb {H}}} \mu _h \langle h,v \rangle _H \, h$, let $( H_r, \langle \cdot , \cdot \rangle _{ H_r }, \left\| \cdot \right\| \!_{ H_r } )$, $r \in {\mathbb {R}}$, be a family of interpolation spaces associated to $-A$ (cf., e.g., [37, Section 3.7]), let $( V, \left\| \cdot \right\| \!_V )$ be an ${\mathbb {R}}$-Banach space with $H_{ \rho } \subseteq V \subseteq H$ continuously and densely, let $\phi , \Phi :{\mathcal {C}}([0,T], H_{1}) \rightarrow [0,\infty )$ be ${\mathcal {B}}({\mathcal {C}}([0,T], H_{1})) / {\mathcal {B}}( [0,\infty ) )$-measurable functions, let $F \in {\mathcal {C}}( V, H )$, $( P_I )_{ I \in {\mathcal {P}}_0({\mathbb {H}}) } \subseteq L(H)$ satisfy for all $I \in {\mathcal {P}}_0({\mathbb {H}})$, $u \in H$, $v,w \in P_I(H)$, $x \in {\mathcal {C}}([0,T], H_1)$ that

$$\begin{aligned} P_I(u) = \textstyle \sum _{ h \in I } \langle h,u \rangle _H \, h, \quad \langle v-w, Av + F(v) - Aw - F(w) \rangle _H \le c \Vert v-w \Vert _H^2,\nonumber \\ \end{aligned}$$

(83)

$$\begin{aligned}&\sup _{ t \in [0,T] } \big ( \langle v, P_I F(v+x_t) \rangle _{ H_{ \nicefrac {1}{2} } } + \phi (x) \langle v, F(v+x_t) \rangle _H \big ) \\&\quad \le \epsilon \Vert v \Vert _{ H_1 }^2 + (c + \phi (x)) \Vert v \Vert _{ H_{ \nicefrac {1}{2} } }^2 + c \phi (x) \Vert v \Vert _H^2 + \Phi (x), \end{aligned}$$

(84)

$$\begin{aligned}&\quad \text {and} \qquad \Vert F(v) - F(w) \Vert _H^2 \le c \Vert v-w \Vert _{ V }^2 ( 1 + \Vert v \Vert _{ V }^{\varphi } + \Vert w \Vert _{ V }^{\varphi } ), \end{aligned}$$

(85)

let $( \Omega , {\mathcal {F}}, {\mathbb {P}})$ be a probability space, let $X,O :[0,T] \times \Omega \rightarrow V$ and ${\mathfrak {O}}_{}^{M,I} :[0,T] \times \Omega \rightarrow H_1$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$, be stochastic processes with continuous sample paths, let ${\mathfrak {X}}_{}^{M,I} :[0,T] \times \Omega \rightarrow H_{ \gamma }$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$, be stochastic processes, and assume for all $t \in [0,T]$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ that ${\mathfrak {O}}_{}^{M,I}([0,T] \times \Omega ) \subseteq P_I(H)$ and

$$\begin{aligned}&{\mathbb {P}}\!\left( X_t = \int _0^t e^{(t-s)A} F( X_s ) \, ds + O_t \right) \nonumber \\&\quad = {\mathbb {P}}\!\left( {\mathfrak {X}}_{t}^{M,I} = \int _0^t P_I \, e^{(t-s)A} \, \mathbb {1}_{ \{ \Vert {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _{ H_{\gamma } } + \Vert {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _{ H_{\gamma } } \le (M/T)^{\chi } \} }^{\Omega } \, F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} ) \, ds\right. \nonumber \\&\left. \qquad + {\mathfrak {O}}_{t}^{M,I} \right) = 1 . \end{aligned}$$

(86)

5.2 Comments on the setting

The next two results, Lemmas 5.1 and 5.2 below, disclose a few elementary consequences of the framework in Sect. 5.1. Proofs of Lemmas 5.1 and 5.2 can, e.g., be found in the extended arXiv version of this article [2, Section 5.2].

Lemma 5.1

Assume the setting in Sect. 5.1 and let $r \in [0,\infty )$. Then $\overline{{\text {span}}({\mathbb {H}})}^{H_r} = H_r$.

Lemma 5.2

Assume the setting in Sect. 5.1. Then

• (i) we have that ${\text {span}}({\mathbb {H}}) = \cup _{ I \in {\mathcal {P}}_0({\mathbb {H}}) } P_I(H)$,

• (ii) we have for all $r \in [0,\infty )$ that $\overline{\cup _{ I \in {\mathcal {P}}_0({\mathbb {H}}) } P_I(H)}^{H_r} = H_r$,

• (iii) we have for all $v,w \in H_1$ that $\langle v-w, Av + F(v) - Aw - F(w) \rangle _H \le c \Vert v-w \Vert _H^2$, and

• (iv) we have for all $v,w \in V$ that $\Vert F(v) - F(w) \Vert _H^2 \le c \Vert v-w \Vert _{ V }^2 ( 1 + \Vert v \Vert _{ V }^{\varphi } + \Vert w \Vert _{ V }^{\varphi } )$.

5.3 On the measurability of a certain function

In our proof of Theorem 5.5 (the main result of this article) we employ the following well-known result, Lemma 5.3 below. Lemma 5.3 is, e.g., proved as Lemma 5.3 in the extended arXiv version of this article [2, Section 5.3].

Lemma 5.3

Consider the notation in Sect. 1.1, let $(V, \left\| \cdot \right\| _V )$ be a separable ${\mathbb {R}}$-Banach space, let $(W, \left\| \cdot \right\| _W )$ be an ${\mathbb {R}}$-Banach space with $V \subseteq W$ continuously and densely, let $(S, {\mathcal {S}})$ be a measurable space, let $s \in S$, let $\psi :V \rightarrow {\mathcal {S}}$ be a ${\mathcal {B}}(V) / {\mathcal {S}}$-measurable function, and let $\Psi :W \rightarrow S$ be the function which satisfies for all $v \in W$ that

$$\begin{aligned}&\Psi (v) = {\left\{ \begin{array}{ll} \psi (v) &{} :v \in V \\ s &{} :v \in W \setminus V . \end{array}\right. } \end{aligned}$$

(87)

Then we have that $\Psi :W \rightarrow {\mathcal {S}}$ is a ${\mathcal {B}}(W) / {\mathcal {S}}$-measurable function.

5.4 A priori moment bounds for the numerical approximation

Lemma 5.4

Assume the setting in Sect. 5.1, let $p \in [1, \infty )$, $\sigma \in [0,\gamma ]$, and assume that

$$\begin{aligned} \sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ t \in [0,T] } {\mathbb {E}}\big [ \Vert {\mathfrak {O}}_{t}^{M,I} \Vert _{ H_{\sigma } }^{2p} + | \Phi ( {\mathfrak {O}}_{}^{M,I} ) |^p + | \phi ( {\mathfrak {O}}_{}^{M,I} ) |^p \big ] < \infty . \end{aligned}$$

(88)

Then

$$\begin{aligned} \sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ t \in [0,T] } {\mathbb {E}}\big [ \Vert {\mathfrak {X}}_{t}^{M,I} \Vert _{H_{ \sigma }}^{2p} \big ] < \infty . \end{aligned}$$

(89)

Proof of Lemma 5.4

Throughout this proof let $\chi _I :C([0,T], P_I(H) ) \rightarrow C([0,T], H_1)$, $I \in {\mathcal {D}}$, be the functions which satisfy for all $I \in {\mathcal {D}}$, $w \in C([0,T], P_I(H) )$, $t \in [0,T]$ that

$$\begin{aligned} \left( \chi _I(w) \right) \! (t) = w(t), \end{aligned}$$

(90)

let $\kappa \in (0,1)$ be a real number, let $\tilde{{\mathfrak {X}}}_{}^{M,I} :[0,T] \times \Omega \rightarrow P_I(H)$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$, be the functions which satisfy for all $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$, $t \in [0,T]$ that

$$\begin{aligned}&\tilde{{\mathfrak {X}}}_{t}^{M,I} = \int _0^t P_I \, e^{(t-s)A} \, \mathbb {1}_{ \{ \Vert \tilde{{\mathfrak {X}}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _{ H_{\gamma } } + \Vert {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _{ H_{\gamma } } \le (M/T)^{\chi } \} }^{\Omega } \, F( \tilde{{\mathfrak {X}}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} ) \, ds + {\mathfrak {O}}_{t}^{M,I} , \end{aligned}$$

(91)

and let $C,K \in [0, \infty ]$ be given by

$$\begin{aligned} K&= \sqrt{c} \max \!\left\{ 1, \sup _{ v \in (V \cap H_{\rho }) \setminus \{0\} } \frac{ \Vert v \Vert _V^{(1+\nicefrac {\varphi }{2})} }{ \Vert v \Vert _{H_{\rho }}^{(1+\nicefrac {\varphi }{2})} } \right\} \end{aligned}$$

(92)

and

$$\begin{aligned} C= & {} \max \!\left\{ 3 K^2 ( 1+ 2^{\max \{0,\varphi -1\}} ) \left[ 1 + \sup _{ v \in H_{\gamma }\setminus \{0\} } \frac{ \Vert v \Vert _{H_{\rho }}^{\varphi } }{ \Vert v \Vert _{H_{\gamma }}^{\varphi } } \right] ,\right. \nonumber \\&\left. ( 8 K^2 + 2 \Vert F(0) \Vert _H^2 ) \max \!\left\{ 1, \sup _{ v \in H_{\gamma }\setminus \{0\} } \frac{ \Vert v \Vert _{H_{\rho }}^{(2+\varphi )} }{ \Vert v \Vert _{H_{\gamma }}^{(2+\varphi )} } \right\} \right\} . \end{aligned}$$

(93)

Moreover, observe that in (91) we assume that the processes $\tilde{{\mathfrak {X}}}_{}^{M,I} :[0,T] \times \Omega \rightarrow P_I(H)$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$, satisfy (91) for every trajectory while in (86) we assume that the processes ${\mathfrak {X}}_{}^{M,I} :[0,T] \times \Omega \rightarrow H_{ \gamma }$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$, satisfy this relation with probability 1. Note that the fact that $H_{\gamma } \subseteq H_{\rho } \subseteq V$ continuously ensures² that $C,K \in [0,\infty )$. In the next step observe that item (iv) in Lemma 5.2 and the fact that $\forall \, x,y,z \in [0,\infty ) :\sqrt{x+y+z} \le \sqrt{x} + \sqrt{y} + \sqrt{z}$ imply for all $v,w \in H_{\gamma }$ that

$$\begin{aligned}&\Vert F(v) - F(w) \Vert _H \le \sqrt{ c \Vert v-w \Vert _V^2 \left( 1 + \left\| v \right\| _V^{\varphi } + \left\| w \right\| _V^{\varphi } \right) } \\&\quad \le \sqrt{c} \left[ \sup _{ u \in H_{\rho } \setminus \{0\} } \frac{ \Vert u \Vert _V }{ \Vert u \Vert _{H_{\rho }} } \right] \Vert v-w \Vert _{ H_{\rho } } \! \left( 1 + \left[ \sup _{ u \in H_{\rho } \setminus \{0\} } \frac{ \Vert u \Vert _V^{\varphi } }{ \Vert u \Vert _{H_{\rho }}^{\varphi } } \right] \Big [ \Vert v \Vert _{ H_{\rho } }^{\varphi } + \Vert w \Vert _{ H_{\rho } }^{\varphi } \Big ] \right) ^{\!\!\nicefrac {1}{2}} \\&\quad \le K \Vert v-w \Vert _{ H_{\rho } } \left( 1 + \Vert v \Vert _{ H_{\rho } }^{\nicefrac {\varphi }{2}} + \Vert w \Vert _{ H_{\rho } }^{\nicefrac {\varphi }{2}} \right) . \end{aligned}$$

(94)

Combining this with Lemma 2.4 in Hutzenthaler et al. [21] (with $(V, \left\| \cdot \right\| \!_{V}) = (H_{\gamma }, \left\| \cdot \right\| \!_{H_{\gamma }})$, $({\mathcal {V}}, \left\| \cdot \right\| \!_{{\mathcal {V}}}) = (H_{\rho }, \left\| \cdot \right\| \!_{H_{\rho }})$, $(W, \left\| \cdot \right\| \!_{W}) = (H, \left\| \cdot \right\| \!_{H})$, $({\mathcal {W}}, \left\| \cdot \right\| \!_{{\mathcal {W}}}) = (H, \left\| \cdot \right\| \!_{H})$, $\epsilon = K$, $\theta = C$, $\varepsilon = \nicefrac {\varphi }{2}$, $\vartheta = \varphi$, $F = H_{\gamma } \ni v \mapsto F(v) \in H$ in the notation of Lemma 2.4 in Hutzenthaler et al. [21]) implies that for all $u,v \in H_{\gamma }$ we have that

$$\begin{aligned}&\Vert F(u) \Vert _H^2 \le C \max \{ 1, \Vert u \Vert _{H_{\gamma }}^{(2+\varphi )} \} \end{aligned}$$

(95)

and

$$\begin{aligned}&\Vert F(u) - F(v) \Vert _H^2 \le C \max \{ 1, \Vert u \Vert _{ H_{\gamma } }^{\varphi } \} \Vert u-v \Vert _{ H_{\rho } }^2 + C \Vert u-v \Vert _{ H_{\rho } }^{(2+\varphi )} . \end{aligned}$$

(96)

Moreover, observe that (84) and (90) ensure³ that for all $I \in {\mathcal {D}}$, $v \in P_I(H)$, $w \in {\mathcal {C}}([0,T], P_I(H))$, $t \in [0,T]$ we have that

$$\begin{aligned}&\langle v, P_I F(v+w_t) \rangle _{ H_{ \nicefrac {1}{2} } } + \phi (\chi _I(w)) \langle v, F(v+w_t) \rangle _H \\ {}&\le \epsilon \Vert v \Vert _{ H_1 }^2 + (\tfrac{c}{\kappa } + \phi (\chi _I(w)) \Vert v \Vert _{ H_{ \nicefrac {1}{2} } }^2 + c \phi (\chi _I(w)) \Vert v \Vert _H^2 + \Phi (\chi _I(w)) . \end{aligned}$$

(97)

This together with (91), (95), and (96) allows us to apply Lemma 2.2 (with $H = H$, ${\mathbb {H}}= {\mathbb {H}}$, $T = T$, $\varphi = \varphi$, $c = \nicefrac {c}{\kappa }$, $C = C$, $\epsilon = \epsilon$, $\kappa = \kappa$, $\rho = \rho$, $\gamma = \gamma$, $\chi = \chi$, $M = M$, $\mu = \mu$, $A = A$, $I = I$, $P = P_I$, ${\mathfrak {X}}_{} = [0,T] \ni t \mapsto \tilde{{\mathfrak {X}}}_{t}^{M,I}(\omega ) \in P_I(H)$, ${\mathfrak {O}}_{} = [0,T] \ni t \mapsto {\mathfrak {O}}_{t}^{M,I}(\omega ) \in P_I(H)$, $F = P_I(H) \ni v \mapsto F(v) \in H$, $\phi = {\mathcal {C}}([0,T], P_I(H)) \ni v \mapsto \phi ( [0,T] \ni t \mapsto v(t) \in H_1) \in [0,\infty )$, $\Phi = {\mathcal {C}}([0,T], P_I(H)) \ni v \mapsto \Phi ( [0,T] \ni t \mapsto v(t) \in H_1) \in [0,\infty )$ for $I \in {\mathcal {D}}$, $M \in {\mathbb {N}}$, $\omega \in \Omega$ in the notation of Lemma 2.2) to obtain that for every $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$, $\omega \in \Omega$ we have that the function $[0,T] \ni t \mapsto \tilde{{\mathfrak {X}}}_{t}^{M,I}(\omega ) - {\mathfrak {O}}_{t}^{M,I}(\omega ) \in P_I(H)$ is continuous and that

$$\begin{aligned}&\sup _{ t \in [0,T] } \big ( \Vert \tilde{{\mathfrak {X}}}_{t}^{M,I}(\omega ) - {\mathfrak {O}}_{t}^{M,I}(\omega ) \Vert _{ H_{\nicefrac {1}{2}} }^2 + \phi ({\mathfrak {O}}_{}^{M,I}(\omega )) \Vert \tilde{{\mathfrak {X}}}_{t}^{M,I}(\omega ) - {\mathfrak {O}}_{t}^{M,I}(\omega ) \Vert _{ H }^2 \big ) \\&\quad \le \frac{ \kappa }{ c } \exp \!\left( \frac{2cT}{\kappa }\right) \left( \Phi ({\mathfrak {O}}_{}^{M,I}(\omega )) + \frac{\max \{1, \phi ({\mathfrak {O}}_{}^{M,I}(\omega ))\} C(c+\kappa )}{2(1-\epsilon )(1-\kappa )c} \right. \\&\left. \qquad \cdot \left[ \tfrac{\max \{1,T\} (1+\sqrt{C})}{(1-\rho )} \right] ^{\!(2+\varphi )} \right) . \end{aligned}$$

(98)

This, in particular, implies for all $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ that

$$\begin{aligned} \left( \Omega \ni \omega \mapsto \sup \nolimits _{ t \in [0,T] } \Vert \tilde{{\mathfrak {X}}}_{t}^{M,I}(\omega ) - {\mathfrak {O}}_{t}^{M,I}(\omega ) \Vert _{ H_{\nicefrac {1}{2}} } \in {\mathbb {R}}\right) \in {\mathcal {M}}( {\mathcal {F}}, {\mathcal {B}}({\mathbb {R}}) ) . \end{aligned}$$

(99)

The assumption that $p \ge 1$, the fact that $\forall \, x,y \in [0,\infty ) :\sqrt{ x + y } \le \sqrt{x} + \sqrt{y}$, and (98) hence ensure for all $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ that

(100)

In addition, observe that the fact that for every $r \in {\mathbb {R}}$, $I \in {\mathcal {D}}$ we have that $P_I(H) \subseteq H_{r}$ continuously and, e.g., Andersson et al. [1, Lemma 2.2] (with $V_0 = H_{r}$, $\left\| \cdot \right\| \!_{V_0} = \left\| \cdot \right\| \!_{H_{r}}$, $V_1 = P_I(H)$, $\left\| \cdot \right\| \!_{V_1} = P_I(H) \ni v \mapsto \Vert v\Vert _H \in [0,\infty )$ for $I \in {\mathcal {D}}$, $r \in {\mathbb {R}}$ in the notation of Andersson et al. [1, Lemma 2.2]) prove that for all $I \in {\mathcal {D}}$ we have that

$$\begin{aligned} {\mathcal {B}}( P_I(H) ) = \big \{ S \in {\mathcal {P}}(P_I(H)) :\big ( \exists \, B \in {\mathcal {B}}( H_{r} ) :S = B \cap P_I(H) \big ) \big \} \subseteq {\mathcal {B}}( H_{r} ) . \end{aligned}$$

(101)

The hypothesis that ${\mathfrak {O}}_{}^{M,I} :[0,T] \times \Omega \rightarrow H_1$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$, are stochastic processes therefore demonstrates that for every $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ we have that $\tilde{{\mathfrak {X}}}_{:}^{M,I}[0,T] \times \Omega \rightarrow P_I(H)$ is a stochastic process. Combining this with (101) shows that for all $B \in {\mathcal {B}}( H_{\gamma } )$, $t \in [0,T]$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ we have that

$$\begin{aligned}&\left( \Omega \ni \omega \mapsto \tilde{{\mathfrak {X}}}_{t}^{M,I}(\omega ) \in H_{\gamma } \right) ^{-1} \!\!(B) = \left( \Omega \ni \omega \mapsto \tilde{{\mathfrak {X}}}_{t}^{M,I}(\omega ) \in H_{\gamma } \right) ^{-1} \!\!\big ( B \cap P_I(H) \big ) \\ {}&\quad = \left( \Omega \ni \omega \mapsto \tilde{{\mathfrak {X}}}_{t}^{M,I}(\omega ) \in P_I(H) \right) ^{-1} \!\!\big ( B \cap P_I(H) \big ) = \left( \tilde{{\mathfrak {X}}}_{t}^{M,I} \right) ^{-1} \!\!\big ( \underbrace{B \cap P_I(H)}_{ \in {\mathcal {B}}( P_I(H) ) } \big ) \in {\mathcal {F}}. \end{aligned}$$

(102)

Hence, we obtain for all $t \in [0,T]$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ that

$$\begin{aligned} \big \{ \omega \in \Omega :{\mathfrak {X}}_{t}^{M,I}(\omega ) = \tilde{{\mathfrak {X}}}_{t}^{M,I}(\omega ) \big \} \in {\mathcal {F}}. \end{aligned}$$

(103)

The assumption that for every $t \in [0,T]$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ we have that

$$\begin{aligned} {\mathbb {P}}\!\left( {\mathfrak {X}}_{t}^{M,I} = \int _0^t P_I \, e^{(t-s)A} \, \mathbb {1}_{ \{ \Vert {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _{ H_{\gamma } } + \Vert {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _{ H_{\gamma } } \le (M/T)^{\chi } \} }^{\Omega } \, F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} ) \, ds + {\mathfrak {O}}_{t}^{M,I} \right) = 1 \end{aligned}$$

(104)

therefore implies that for all $t \in [0,T]$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ we have that ${\mathbb {P}}\big ( {\mathfrak {X}}_{t}^{M,I} = \tilde{{\mathfrak {X}}}_{t}^{M,I} \big ) = 1$. This and the triangle inequality assure that

$$\begin{aligned}&\sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ t \in [0,T] } \Vert {\mathfrak {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; H_{ \sigma } ) } = \sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ t \in [0,T] } \Vert \tilde{{\mathfrak {X}}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; H_{ \sigma } ) } \\ {}&\quad \le \sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ t \in [0,T] } \left[ \Vert \tilde{{\mathfrak {X}}}_{t}^{M,I} - {\mathfrak {O}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; H_{ \sigma } ) } + \Vert {\mathfrak {O}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; H_{ \sigma } ) } \right] \\ {}&\quad \le \left[ \sup _{ v \in H_{\nicefrac {1}{2}} \setminus \{ 0 \} } \frac{ \Vert v \Vert _{ H_{ \sigma } } }{ \Vert v \Vert _{ H_{\nicefrac {1}{2}} } } \right] \left[ \sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \big \Vert \sup \nolimits _{ t \in [0,T] } \Vert \tilde{{\mathfrak {X}}}_{t}^{M,I} - {\mathfrak {O}}_{t}^{M,I} \Vert _{ H_{ \nicefrac {1}{2} } } \big \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; {\mathbb {R}}) } \right] \\ {}&\qquad + \sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ t \in [0,T] } \Vert {\mathfrak {O}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; H_{\sigma } ) } . \end{aligned}$$

(105)

The assumption that

$$\begin{aligned} \sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ t \in [0,T] } {\mathbb {E}}\big [ \Vert {\mathfrak {O}}_{t}^{M,I} \Vert _{ H_{\sigma } }^{2p} + | \Phi ( {\mathfrak {O}}_{}^{M,I} ) |^p + | \phi ( {\mathfrak {O}}_{}^{M,I} ) |^p \big ] < \infty , \end{aligned}$$

(106)

the fact that $H_{\nicefrac {1}{2}} \subseteq H_{ \sigma }$ continuously, and (100) hence prove that

$$\begin{aligned}&\sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ t \in [0,T] } \Vert {\mathfrak {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; H_{ \sigma } ) } \\ {}&\quad \le \left[ \sup _{ v \in H_{\nicefrac {1}{2}} \setminus \{ 0 \} } \frac{ \Vert v \Vert _{ H_{ \sigma } } }{ \Vert v \Vert _{ H_{\nicefrac {1}{2}} } } \right] \Bigg [ \frac{ \sqrt{\kappa } }{ \sqrt{c} } \exp \!\left( \frac{cT}{\kappa }\right) \sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \Vert \Phi ( {\mathfrak {O}}_{}^{M,I} ) \Vert _{ {\mathcal {L}}^{p}({\mathbb {P}}; {\mathbb {R}}) }^{\nicefrac {1}{2}} \\ {}&\qquad + \left( \sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \Vert \phi ({\mathfrak {O}}_{}^{M,I}) \Vert _{ {\mathcal {L}}^{p}({\mathbb {P}}; {\mathbb {R}}) }^{\nicefrac {1}{2}} + 1 \right) \frac{ \sqrt{C(c+\kappa )} \exp \!\left( \frac{cT}{\kappa }\right) }{c\sqrt{2(1-\epsilon )(\nicefrac {1}{\kappa }-1)}} \\&\qquad \cdot \left[ \tfrac{\max \{1,T\} (1+\sqrt{C})}{(1-\rho )} \right] ^{\!(1+\nicefrac {\varphi }{2})} \Bigg ] \\ {}&\qquad + \sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ t \in [0,T] } \Vert {\mathfrak {O}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; H_{\sigma } ) } < \infty . \end{aligned}$$

(107)

This completes the proof of Lemma 5.4. $\square$

5.5 Main result

Theorem 5.5

Assume the setting in Sect. 5.1, let $\vartheta \in (0,\infty )$, $p \in [ \max \{ 2, \nicefrac {1}{\varphi } \}, \infty )$, $\varrho \in [0,1-\rho )$, and assume that

$$\begin{aligned}&\sup _{ t \in [0,T] } \sup _{ I \in {\mathcal {D}}} {\mathbb {E}}\big [ \Vert X_t \Vert _{ V }^{p(1+\nicefrac {\varphi }{2})\max \{2,\varphi \}} + \Vert P_I O_t \Vert _{ V }^{p\varphi } \big ] \\ {}&\qquad + \sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ t \in [0,T] } {\mathbb {E}}\!\left[ \big | \Vert {\mathfrak {O}}_{t}^{M,I} \Vert _{ H_{\gamma } }^2 \right. \\&\left. \qquad + \Phi ( {\mathfrak {O}}_{}^{M,I} ) + \phi ( {\mathfrak {O}}_{}^{M,I} ) \big |^{p\max \{2\vartheta , 2+\varphi , (1+\nicefrac {\varphi }{2})\nicefrac {\varphi }{2} \}} \right] < \infty . \end{aligned}$$

(108)

Then we have

• (i) that $\sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ t \in [0,T] } {\mathbb {E}}\big [ \Vert {\mathfrak {X}}_{t}^{M,I} \Vert _{ H_{\gamma } }^{p\max \{4\vartheta , 4+2\varphi , \varphi (1+\nicefrac {\varphi }{2}) \}} \big ] < \infty$ and

• (ii) that there exists a real number $C \in (0,\infty )$ such that for all $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ it holds that

  $$\begin{aligned}&\sup _{ t \in [0,T] } \left( {\mathbb {E}}\big [ \Vert X_t - {\mathfrak {X}}_{t}^{M,I} \Vert _{ H }^p \big ] \right) ^{\!\nicefrac {1}{p}} \le C \bigg [ M^{-\min \{\vartheta \chi ,\varrho \}} + \Vert (-A)^{-\varrho } ( Id _H - P_I ) \Vert _{ L(H) } \\&\qquad + \sup _{ t \in [0,T] } \left( {\mathbb {E}}\big [ \Vert ( Id _H - P_I ) O_t \Vert _{ V }^{2p} + \Vert P_I O_{t} - {\mathfrak {O}}_{t}^{M,I} \Vert _{ V }^{2p} \right. \\&\left. \qquad + \Vert P_I( O_{t} - O_{ \lfloor t \rfloor _{T\!/\!M} } ) \Vert _{ V }^{2p} \big ] \right) ^{\!\nicefrac {1}{2p}} \bigg ] . \end{aligned}$$

  (109)

Proof of Theorem 5.5

Throughout this proof let $\kappa \in (2,\infty )$ be a real number, let $({\mathfrak {P}}_I )_{ I \in {\mathcal {P}}({\mathbb {H}}) } \subseteq L(H)$ be the linear operators which satisfy⁴ for all $I \in {\mathcal {P}}({\mathbb {H}})$, $v \in H$ that

$$\begin{aligned} {\mathfrak {P}}_I(v) = \sum _{ h \in I } \langle h, v \rangle _H h , \end{aligned}$$

(110)

let ${\mathcal {V}}:V \times V \rightarrow [0,\infty )$ be the function which satisfies for all $v,w \in V$ that

$$\begin{aligned}&{\mathcal {V}}(v,w) = {\left\{ \begin{array}{ll} ( \Vert v \Vert _{ H_{\gamma } } + \Vert w \Vert _{ H_{\gamma } } )^{\nicefrac {1}{\chi }} &{} :(v,w) \in H_{\gamma } \times H_{\gamma } \\ 0 &{} :(v,w) \in (V \times V) \setminus (H_{\gamma } \times H_{\gamma }) \end{array}\right. } \end{aligned}$$

(111)

(cf. (58)–(59) in Setting 4.1), let $\tilde{{\mathfrak {X}}}_{}^{M,I} :[0,T] \times \Omega \rightarrow H_{\gamma }$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$, be the functions which satisfy for all $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$, $t \in [0,T]$ that

$$\begin{aligned}&\tilde{{\mathfrak {X}}}_{t}^{M,I} = \int _0^t P_I \, e^{(t-s)A} \, \mathbb {1}_{ \{ \Vert \tilde{{\mathfrak {X}}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _{ H_{\gamma } } + \Vert {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _{ H_{\gamma } } \le (M/T)^{\chi } \} }^{\Omega } \, F( \tilde{{\mathfrak {X}}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} ) \, ds + {\mathfrak {O}}_{t}^{M,I}, \end{aligned}$$

(112)

let ${\tilde{\Omega }} \subseteq \Omega$ be the set given by

$$\begin{aligned} {\tilde{\Omega }}&= \left\{ \forall \, t \in [0,T] :X_t = \int \nolimits _0^t e^{(t-s)A} F(X_s) \, ds + O_t \right\} \\ {}&= \left\{ \forall \, t \in [0,T] \cap {\mathbb {Q}} :X_t = \int \nolimits _0^t e^{(t-s)A} F(X_s) \, ds + O_t \right\} , \end{aligned}$$

(113)

and let ${\tilde{X}} :[0,T] \times \Omega \rightarrow V$ and ${\tilde{O}} :[0,T] \times \Omega \rightarrow V$ be the functions which satisfy for all $t \in [0,T]$ that ${\tilde{X}}_t = X_t \mathbb {1}_{{\tilde{\Omega }}}^{\Omega }$ and

$$\begin{aligned} {\tilde{O}}_t = O_t \mathbb {1}_{{\tilde{\Omega }}}^{\Omega } - \left[ \int _0^t e^{(t-s)A} F(0) \, ds \right] \mathbb {1}_{\Omega \backslash {\tilde{\Omega }}}^{\Omega } = O_t \mathbb {1}_{{\tilde{\Omega }}}^{\Omega } + A^{-1} ( Id _H - e^{tA} ) F(0) \mathbb {1}_{\Omega \backslash {\tilde{\Omega }}}^{\Omega } . \end{aligned}$$

(114)

Next note that the fact that $H_1 \subseteq H_{\gamma }$ continuously and, e.g., Andersson et al. [1, Lemma 2.2] (with $V_0 = H_{\gamma }$, $\left\| \cdot \right\| \!_{ V_0 } = \left\| \cdot \right\| \!_{ H_{\gamma } }$, $V_1 = H_1$, $\left\| \cdot \right\| \!_{ V_1 } = \left\| \cdot \right\| \!_{ H_{1} }$ in the notation of Andersson et al. [1, Lemma 2.2]) ensure that

$$\begin{aligned}&{\mathcal {B}}(H_1) = \left\{ S \in {\mathcal {P}}(H_1) :\big ( \exists \, B \in {\mathcal {B}}( H_{\gamma } ) :S = B \cap H_1 \big ) \right\} \subseteq {\mathcal {B}}( H_{\gamma } ) . \end{aligned}$$

(115)

The hypothesis that ${\mathfrak {O}}_{}^{M,I} :[0,T] \times \Omega \rightarrow H_1$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$, are stochastic processes therefore demonstrates that for every $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ we have that $\tilde{{\mathfrak {X}}}_{}^{M,I} :[0,T] \times \Omega \rightarrow H_{\gamma }$ is a stochastic process. Hence, we obtain for all $t \in [0,T]$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ that

$$\begin{aligned} \big \{ \omega \in \Omega :{\mathfrak {X}}_{t}^{M,I}(\omega ) = \tilde{{\mathfrak {X}}}_{t}^{M,I}(\omega ) \big \} \in {\mathcal {F}}. \end{aligned}$$

(116)

The assumption that for every $t \in [0,T]$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ we have that

$$\begin{aligned} {\mathbb {P}}\!\left( {\mathfrak {X}}_{t}^{M,I} = \int _0^t P_I \, e^{(t-s)A} \, \mathbb {1}_{ \{ \Vert {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _{ H_{\gamma } } + \Vert {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} \Vert _{ H_{\gamma } } \le (M/T)^{\chi } \} }^{\Omega } \, F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I} ) \, ds + {\mathfrak {O}}_{t}^{M,I} \right) = 1 \end{aligned}$$

(117)

therefore implies that for all $t \in [0,T]$, $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ we have that

$$\begin{aligned} {\mathbb {P}}\big ( {\mathfrak {X}}_{t}^{M,I} = \tilde{{\mathfrak {X}}}_{t}^{M,I} \big ) = 1 . \end{aligned}$$

(118)

Combining this and (108) with Lemma 5.4 demonstrates that

$$\begin{aligned}&\sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ t \in [0,T] } \Vert \tilde{{\mathfrak {X}}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^{p\max \{4\vartheta , 4+2\varphi , \varphi (1+\nicefrac {\varphi }{2}) \}}( {\mathbb {P}}; H_{\gamma } ) } \\ {}&\quad = \sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ t \in [0,T] } \Vert {\mathfrak {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^{p\max \{4\vartheta , 4+2\varphi , \varphi (1+\nicefrac {\varphi }{2}) \}}( {\mathbb {P}}; H_{\gamma } ) } < \infty . \end{aligned}$$

(119)

This establishes item (i). Moreover, note that the assumption that $\forall \, t \in [0,T] :{\mathbb {P}}( X_t = \int _0^t e^{(t-s)A} F( X_s ) \, ds$ $+ O_t ) = 1$ yields that ${\mathbb {P}}( {\tilde{\Omega }} ) = 1$. Hence, we obtain for all $t \in [0,T]$ that ${\mathbb {P}}( {\tilde{X}}_t = X_t ) \ge {\mathbb {P}}( {\tilde{\Omega }} ) = 1$. Combining this with (108) ensures that

$$\begin{aligned} \sup _{ t \in [0,T] } \Vert {\tilde{X}}_t \Vert _{ {\mathcal {L}}^{p(1+\nicefrac {\varphi }{2})\max \{2,\varphi \}}( {\mathbb {P}}; V ) } = \sup _{ t \in [0,T] } \Vert X_t \Vert _{ {\mathcal {L}}^{p(1+\nicefrac {\varphi }{2})\max \{2,\varphi \}}( {\mathbb {P}}; V ) } < \infty . \end{aligned}$$

(120)

Furthermore, observe that Lemma 2.1, the triangle inequality, and item (iv) in Lemma 5.2 show for all $t \in (0,T]$ that

$$\begin{aligned}&\int _0^t \Vert (-A)^{(\rho +\varrho )} e^{(t-s)A} F( {\tilde{X}}_s ) \Vert _{ {\mathcal {L}}^{p\max \{2,\varphi \}}( {\mathbb {P}}; H ) } \, ds \\ {}&\quad \le \int _0^t \Vert (-A)^{(\rho +\varrho )} e^{(t-s)A} \Vert _{ L(H) } \, \Vert F( {\tilde{X}}_s ) \Vert _{ {\mathcal {L}}^{p\max \{2,\varphi \}}( {\mathbb {P}}; H ) } \, ds \\ {}&\quad \le \int _0^t \left( t-s\right) ^{-(\rho +\varrho )} \left[ \Vert F( {\tilde{X}}_s ) - F(0) \Vert _{ {\mathcal {L}}^{p\max \{2,\varphi \}}( {\mathbb {P}}; H ) } + \Vert F(0) \Vert _H \right] ds \\ {}&\quad \le \int _0^t \left( t-s\right) ^{-(\rho +\varrho )} \left[ \Big \Vert \sqrt{c} \, \Vert {\tilde{X}}_s \Vert _V \big ( 1 + \Vert {\tilde{X}}_s \Vert _V^{\nicefrac {\varphi }{2}} \big ) \Big \Vert _{ {\mathcal {L}}^{p\max \{2,\varphi \}}( {\mathbb {P}}; {\mathbb {R}}) } + \Vert F(0) \Vert _H \right] ds \\ {}&\quad \le \int _0^t \left( t-s\right) ^{-(\rho +\varrho )} \left[ \sqrt{c} \, \Big ( \Vert {\tilde{X}}_s \Vert _{ {\mathcal {L}}^{p\max \{2,\varphi \}}( {\mathbb {P}}; V ) } + \Vert {\tilde{X}}_s \Vert _{ {\mathcal {L}}^{p(1+\nicefrac {\varphi }{2})\max \{2,\varphi \}}( {\mathbb {P}}; V ) }^{\nicefrac {(1+\varphi }{2})} \Big ) \right. \\&\left. \qquad + \Vert F(0) \Vert _H \right] ds . \end{aligned}$$

(121)

Inequality (120) hence implies for all $t \in (0,T]$ that

$$\begin{aligned}&\int _0^t \Vert (-A)^{(\rho +\varrho )} e^{(t-s)A} F( {\tilde{X}}_s ) \Vert _{ {\mathcal {L}}^{p\max \{2,\varphi \}}( {\mathbb {P}}; H ) } \, ds \\&\quad \le \int _0^t \left( t-s\right) ^{-(\rho +\varrho )} \left[ 2 \sqrt{c} \max \!\left\{ 1, \Vert {\tilde{X}}_s \Vert _{ {\mathcal {L}}^{p(1+\nicefrac {\varphi }{2})\max \{2,\varphi \}}( {\mathbb {P}}; V ) }^{(1+\nicefrac {\varphi }{2})} \right\} + \Vert F(0) \Vert _H \right] ds \\&\quad \le \left[ 2 \sqrt{c} \max \!\left\{ 1, \sup _{ s \in (0,t) } \Vert {\tilde{X}}_s \Vert _{ {\mathcal {L}}^{p(1+\nicefrac {\varphi }{2})\max \{2,\varphi \}}( {\mathbb {P}}; V ) }^{(1+\nicefrac {\varphi }{2})} \right\} + \Vert F(0) \Vert _H \right] \left[ \int _0^t \left( t-s\right) ^{-(\rho +\varrho )} ds \right] \\&\quad \le \left[ 2 \sqrt{c} \max \!\left\{ 1, \sup _{ s \in (0,T) } \Vert {\tilde{X}}_s \Vert _{ {\mathcal {L}}^{p(1+\nicefrac {\varphi }{2})\max \{2,\varphi \}}( {\mathbb {P}}; V ) }^{(1+\nicefrac {\varphi }{2})} \right\} + \Vert F(0) \Vert _H \right] \frac{ T^{(1-\rho -\varrho )} }{ (1-\rho -\varrho ) } < \infty . \end{aligned}$$

(122)

This and the fact that

$$\begin{aligned} \forall \, t \in [0,T] :{\tilde{X}}_t = \int _0^t e^{(t-s)A} F( {\tilde{X}}_s ) \, ds + {\tilde{O}}_t \end{aligned}$$

(123)

prove that

$$\begin{aligned}&\sup _{ t \in [0,T] } \Vert {\tilde{X}}_t - {\tilde{O}}_t \Vert _{ {\mathcal {L}}^{p\max \{2,\varphi \}}( {\mathbb {P}}; H_{(\rho +\varrho )} ) } \\&\quad \le \sup _{ t \in [0,T] } \left( \int _0^t \Vert e^{(t-s)A} F( {\tilde{X}}_s ) \Vert _{ {\mathcal {L}}^{p\max \{2,\varphi \}}( {\mathbb {P}}; H_{(\rho +\varrho )} ) } \, ds \right) < \infty . \end{aligned}$$

(124)

In addition, observe that the triangle inequality assures for all $I \in {\mathcal {D}}$ that

$$\begin{aligned}&\sup _{ t \in [0,T] } \Vert {\mathfrak {P}}_{ {\mathbb {H}}\setminus I } {\tilde{X}}_t \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) } \le \sup _{ t \in [0,T] } \left[ \Vert {\mathfrak {P}}_{ {\mathbb {H}}\setminus I } ({\tilde{X}}_t - {\tilde{O}}_t) \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) } + \Vert {\mathfrak {P}}_{ {\mathbb {H}}\setminus I } {\tilde{O}}_t \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) } \right] \nonumber \\&\quad \le \left[ \sup _{ v \in H_{\rho } \setminus \{0\} } \frac{ \Vert v \Vert _V }{ \Vert v \Vert _{ H_{\rho } } } \right] \left[ \sup _{ t \in [0,T] } \Vert {\mathfrak {P}}_{ {\mathbb {H}}\setminus I } ({\tilde{X}}_t - {\tilde{O}}_t) \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};H_{\rho }) } \right] + \sup _{ t \in [0,T] } \Vert {\mathfrak {P}}_{ {\mathbb {H}}\setminus I } {\tilde{O}}_t \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) } \nonumber \\&\quad = \left[ \sup _{ v \in H_{\rho } \setminus \{0\} } \frac{ \Vert v \Vert _V }{ \Vert v \Vert _{ H_{\rho } } } \right] \left[ \sup _{ t \in [0,T] } \Vert (-A)^{-\varrho } \, {\mathfrak {P}}_{ {\mathbb {H}}\setminus I } (-A)^{(\rho + \varrho )} ({\tilde{X}}_t - {\tilde{O}}_t) \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};H) } \right] \nonumber \\&\qquad + \sup _{ t \in [0,T] } \Vert {\mathfrak {P}}_{ {\mathbb {H}}\setminus I } {\tilde{O}}_t \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) } . \end{aligned}$$

(125)

The fact that $\forall \, I \in {\mathcal {P}}({\mathbb {H}}) :\Vert {\mathfrak {P}}_{ {\mathbb {H}}\setminus I } \Vert _{ L(H) } \le 1$ hence guarantees for all $I \in {\mathcal {D}}$ that

$$\begin{aligned}&\sup _{ t \in [0,T] } \Vert {\mathfrak {P}}_{ {\mathbb {H}}\setminus I } {\tilde{X}}_t \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) } \\ {}&\quad \le \left[ \sup _{ v \in H_{\rho } \setminus \{0\} } \frac{ \Vert v \Vert _V }{ \Vert v \Vert _{ H_{\rho } } } \right] \left[ \sup _{ t \in [0,T] } \Vert {\mathfrak {P}}_{ {\mathbb {H}}\setminus I } ({\tilde{X}}_t - {\tilde{O}}_t) \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};H_{(\rho +\varrho )}) } \, \right] \Vert (-A)^{-\varrho } \, {\mathfrak {P}}_{ {\mathbb {H}}\setminus I } \Vert _{ L(H) } \\ {}&\qquad + \sup _{ t \in [0,T] } \Vert {\mathfrak {P}}_{ {\mathbb {H}}\setminus I } {\tilde{O}}_t \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) } \\ {}&\quad \le \left[ \sup _{ v \in H_{\rho } \setminus \{0\} } \frac{ \Vert v \Vert _V }{ \Vert v \Vert _{ H_{\rho } } } \right] \left[ \sup _{ t \in [0,T] } \Vert {\tilde{X}}_t - {\tilde{O}}_t \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};H_{(\rho +\varrho )}) } \, \right] \Vert (-A)^{-\varrho } \, {\mathfrak {P}}_{ {\mathbb {H}}\setminus I } \Vert _{ L(H) } \\ {}&\qquad + \sup _{ t \in [0,T] } \Vert {\mathfrak {P}}_{ {\mathbb {H}}\setminus I } {\tilde{O}}_t \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) }. \end{aligned}$$

(126)

Furthermore, observe that the triangle inequality, the fact that $\forall \, I \in {\mathcal {P}}_0({\mathbb {H}}) :\Vert P_I \Vert _{ L(H) } \le 1$, the fact that $H_{(\rho +\varrho )} \subseteq V$ continuously, the fact that

$$\begin{aligned} \forall \, t \in [0,T] :{\mathbb {P}}( O_t = {\tilde{O}}_t ) \ge {\mathbb {P}}( {\tilde{\Omega }} ) = 1 , \end{aligned}$$

(127)

the assumption that

$$\begin{aligned} \sup _{ t \in [0,T] } \sup _{ I \in {\mathcal {D}}} {\mathbb {E}}\big [ \Vert P_I O_t \Vert _V^{p\varphi } \big ] < \infty , \end{aligned}$$

(128)

and (124) imply that

$$\begin{aligned}&\sup _{ t \in [0,T] } \sup _{ I \in {\mathcal {D}}} \Vert P_I {\tilde{X}}_t \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}}; V) } \\&\quad \le \sup _{ t \in [0,T] } \sup _{ I \in {\mathcal {D}}} \Vert P_I {\tilde{X}}_t - P_I {\tilde{O}}_t \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}}; V) } + \sup _{ t \in [0,T] } \sup _{ I \in {\mathcal {D}}} \Vert P_I {\tilde{O}}_t \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}}; V) } < \infty . \end{aligned}$$

(129)

In the next step we note that the hypothesis that $H_{\rho } \subseteq V$ continuously and Lemma 2.1 ensure that

$$\begin{aligned} \sup _{ t \in (0,T) } t^{\rho } \Vert e^{tA} \Vert _{ L(H,V) } \le \left[ \sup _{ v \in H_{\rho }\backslash \{0\} } \frac{ \Vert v \Vert _V }{ \Vert v \Vert _{ H_{\rho } } } \right] \left[ \sup _{ t \in (0,T) } \sup _{ v \in H\backslash \{0\} } \frac{ \Vert (-tA)^{\rho } e^{tA} v \Vert _H }{ \Vert v \Vert _H } \right] < \infty . \end{aligned}$$

(130)

Moreover, observe that, e.g., Lemma 5.3 (with $V = H_{\gamma } \times H_{\gamma }$, $W = V \times V$, $S = [0,\infty )$, ${\mathcal {S}} = {\mathcal {B}}( [0,\infty ) )$, $s = 0$, $\psi = H_{\gamma } \times H_{\gamma } \ni (v,w) \mapsto ( \Vert v \Vert _{ H_{\gamma } } + \Vert w \Vert _{ H_{\gamma } } )^{ \nicefrac {1}{\chi } } \in [0,\infty )$, $\Psi = {\mathcal {V}}$ in the notation of Lemma 5.3) establishes that

$$\begin{aligned}&{\mathcal {V}}\in {\mathcal {M}}\big ( {\mathcal {B}}( V \times V ) , {\mathcal {B}}( [0,\infty ) ) \big ). \end{aligned}$$

(131)

Combining the fact that $\forall \, t \in [0,T] :{\tilde{X}}_t = \int _0^t e^{(t-s)A} F( {\tilde{X}}_s ) \, ds + {\tilde{O}}_t$, (112), (130), item (iii) in Lemma 5.2, item (iv) in Lemma 5.2, and, e.g., Andersson et al. [1, Lemma 2.2] with Proposition 4.4 (with $H = H$, ${\mathbb {H}}= {\mathbb {H}}$, $T = T$, $c = c$, $\varphi = \varphi$, $C = c$, ${\mathcal {D}}= {\mathcal {D}}$, $\mu = \mu$, $A = A$, $V = V$, ${\mathcal {V}}= {\mathcal {V}}$, $F = F$, $(P_J)_{ J \in {\mathcal {P}}({\mathbb {H}}) } \subseteq L(H) = ({\mathfrak {P}}_J)_{ J \in {\mathcal {P}}({\mathbb {H}}) } \subseteq L(H)$, $(\Omega , {\mathcal {F}}, {\mathbb {P}}) = ( \Omega , {\mathcal {F}}, {\mathbb {P}})$, $X_t(\omega ) = {\tilde{X}}_t(\omega )$, $O_t(\omega ) = {\tilde{O}}_t(\omega )$, ${\mathbf {X}}_{t}^{M,I}(\omega ) = \int _0^t P_I e^{(t-s)A} F( \tilde{{\mathfrak {X}}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,I}(\omega ) ) \, ds + P_I ( {\tilde{O}}_t(\omega ) )$, ${\mathfrak {X}}_{t}^{M,I}(\omega ) = \tilde{{\mathfrak {X}}}_{t}^{M,I}(\omega )$, ${\mathfrak {O}}_{t}^{M,I}(\omega ) = {\mathfrak {O}}_{t}^{M,I}(\omega )$, $\alpha = \vartheta \chi$, $\rho = \rho$, $\varrho = \varrho$, $\kappa = \kappa$, $p = p$, $M = M$, $I = I$ for $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$, $t \in [0,T]$, $\omega \in \Omega$ in the notation of Proposition 4.4), the fact that $\forall \, t \in [0,T] :{\mathbb {P}}( X_t = {\tilde{X}}_t ) \ge {\mathbb {P}}( {\tilde{\Omega }} ) = 1$, the fact that $\forall \, t \in [0,T] :{\mathbb {P}}( O_t = {\tilde{O}}_t ) \ge {\mathbb {P}}( {\tilde{\Omega }} ) = 1$, and (111) hence proves that for all $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ we have that

$$\begin{aligned}&\sup _{ t \in [0,T] } \Vert X_t - \tilde{{\mathfrak {X}}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; H ) } = \sup _{ t \in [0,T] } \Vert {\tilde{X}}_t - \tilde{{\mathfrak {X}}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; H ) } \nonumber \\&\quad \le \frac{ 4^{(2+\varphi )} \max \{1, T^{(\nicefrac {3}{2}+\vartheta \chi -\rho + \nicefrac {\varphi }{2} - \nicefrac {\rho \varphi }{2}) } \} \max \{ 1, c^{(1+\nicefrac {\varphi }{4})} \} \sqrt{ e^{\kappa c T } } }{ \min \{ 1, \sqrt{ c \left( \kappa - 2 \right) } \} \left( 1 - \rho - \varrho \right) ^{(1+\nicefrac {\varphi }{2})} } \nonumber \\&\qquad \cdot \Bigg [ \sup _{ t \in [0,T] } \Vert {\mathfrak {P}}_{ {\mathbb {H}}\setminus I } {\tilde{X}}_t \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) } + M^{-\min \{\vartheta \chi ,\varrho \} } \nonumber \\&\qquad \qquad + \sup _{ t \in (0,T) } \Vert P_I ( O_{t} - O_{ \lfloor t \rfloor _{T\!/\!M} } ) \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; V ) } + \sup _{ t \in [0,T] } \Vert P_I O_t - {\mathfrak {O}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}}; V) } \Bigg ] \nonumber \\&\quad \qquad \cdot \max \!\left\{ 1, \sup _{ v \in V \setminus \{0\} } \frac{ \Vert v \Vert _H }{ \Vert v \Vert _V } \right\} \nonumber \\&\quad \cdot \Bigg [ 1 + \sup _{ s \in (0,T) } \Vert {\tilde{X}}_s \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}} + \sup _{ s \in (0,T) } \Vert P_I {\tilde{X}}_s \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}} + \sup _{ s \in [0,T) } \Vert \tilde{{\mathfrak {X}}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}} \nonumber \\&\quad \qquad + \sup _{ s \in (0,T) } \Vert P_I O_s \Vert _{ {\mathcal {L}}^{p\varphi }( {\mathbb {P}}; V ) }^{\nicefrac {\varphi }{2}} \Bigg ] \nonumber \\&\quad \cdot \left[ 1 + \sup _{ s \in [0,T) } \left\{ \Vert \tilde{{\mathfrak {X}}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{4p\vartheta }({\mathbb {P}}; H_{\gamma }) } + \Vert {\mathfrak {O}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{4p\vartheta }({\mathbb {P}}; H_{\gamma }) } \right\} ^{\vartheta } \right] \nonumber \\&\quad \qquad \cdot \max \!\left\{ 1, \sup _{ s \in (0,T) } \left[ s^{\rho } \Vert e^{sA} \Vert _{ L(H,V) } \right] ^{(1+\nicefrac {\varphi }{2})} \right\} \nonumber \\&\qquad \cdot \left[ \max \!\left\{ 1, \sup _{ s \in [0,T) } \Vert \tilde{{\mathfrak {X}}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p(1+\nicefrac {\varphi }{2})\max \{4,\varphi \}}( {\mathbb {P}}; V ) }^{[(1+\nicefrac {\varphi }{2})^2]} \right\} + \Vert F(0) \Vert _H^{ (1+\nicefrac {\varphi }{2}) } \right] . \end{aligned}$$

(132)

The fact that

$$\begin{aligned} \forall \, M \in {\mathbb {N}}, I \in {\mathcal {D}}, t \in [0,T] :{\mathbb {P}}( {\mathfrak {X}}_{t}^{M,I} = \tilde{{\mathfrak {X}}}_{t}^{M,I} ) = 1 , \end{aligned}$$

(133)

the fact that

$$\begin{aligned} \forall \, t \in [0,T] :{\mathbb {P}}( O_t = {\tilde{O}}_t ) \ge {\mathbb {P}}( {\tilde{\Omega }} ) = 1 , \end{aligned}$$

(134)

the fact that $\forall \, I \in {\mathcal {D}}:\Vert P_I \Vert _{ L(H) } \le 1$, (126), and (130) therefore assure that for all $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ we have that

$$\begin{aligned}&\sup _{ t \in [0,T] } \Vert X_t - {\mathfrak {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; H ) } = \sup _{ t \in [0,T] } \Vert X_t - \tilde{{\mathfrak {X}}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; H ) } \nonumber \\&\quad \le \frac{ 4^{(2+\varphi )} \max \{1, T^{(\nicefrac {3}{2}+\vartheta \chi -\rho + \nicefrac {\varphi }{2} - \nicefrac {\rho \varphi }{2}) } \} \max \{ 1, c^{(1+\nicefrac {\varphi }{4})} \} \sqrt{ e^{\kappa c T } } }{ \min \{ 1, \sqrt{ c \left( \kappa - 2 \right) } \} \left( 1 - \rho - \varrho \right) ^{(1+\nicefrac {\varphi }{2})} } \nonumber \\&\quad \qquad \cdot \Bigg [ \sup _{ t \in [0,T] } \Vert {\mathfrak {P}}_{ {\mathbb {H}}\setminus I } O_t \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};V) } \nonumber \\&\qquad + \sup _{ t \in [0,T] } \Vert {\tilde{X}}_t - {\tilde{O}}_t \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}};H_{(\rho +\varrho )}) } \, \Vert (-A)^{-\varrho } \, {\mathfrak {P}}_{ {\mathbb {H}}\setminus I } \Vert _{ L(H) } + M^{-\min \{\vartheta \chi ,\varrho \} } \nonumber \\&\qquad + \sup _{ t \in (0,T) } \Vert P_I ( O_{t} - O_{ \lfloor t \rfloor _{T\!/\!M} } ) \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; V ) } + \sup _{ t \in [0,T] } \Vert P_I O_t - {\mathfrak {O}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}}; V) } \Bigg ] \nonumber \\&\quad \qquad \cdot \max \!\left\{ 1, \sup _{ v \in V \setminus \{0\} } \frac{ \Vert v \Vert _H }{ \Vert v \Vert _V } \right\} \nonumber \\&\qquad \cdot \Bigg [ 1 + \sup _{ s \in (0,T) } \Vert {\tilde{X}}_s \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}} + \sup _{ s \in (0,T) } \Vert P_I {\tilde{X}}_s \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};V) }^{\nicefrac {\varphi }{2}} + \sup _{ s \in [0,T) } \Vert \tilde{{\mathfrak {X}}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}};H_{\gamma }) }^{\nicefrac {\varphi }{2}} \nonumber \\&\quad \qquad + \sup _{ s \in (0,T) } \Vert P_I O_s \Vert _{ {\mathcal {L}}^{p\varphi }( {\mathbb {P}}; V ) }^{\nicefrac {\varphi }{2}} \Bigg ] \nonumber \\&\qquad \cdot \left[ 1 + \sup _{ s \in [0,T) } \left\{ \Vert \tilde{{\mathfrak {X}}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{4p\vartheta }({\mathbb {P}}; H_{\gamma }) } + \Vert {\mathfrak {O}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{4p\vartheta }({\mathbb {P}}; H_{\gamma }) } \right\} ^{\vartheta } \right] \nonumber \\&\quad \qquad \cdot \max \!\left\{ 1, \sup _{ v \in H_{\gamma } \setminus \{0\} } \frac{ \Vert v \Vert _V^{ [(1+\nicefrac {\varphi }{2})^2 + \nicefrac {\varphi }{2} ] } }{ \Vert v \Vert _{ H_{\gamma } }^{ [(1+\nicefrac {\varphi }{2})^2 + \nicefrac {\varphi }{2}] } } \right\} \nonumber \\&\qquad \cdot \left[ \max \!\left\{ 1, \sup _{ s \in [0,T) } \Vert \tilde{{\mathfrak {X}}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p(1+\nicefrac {\varphi }{2})\max \{4,\varphi \}}( {\mathbb {P}}; H_{\gamma } ) }^{[(1+\nicefrac {\varphi }{2})^2]} \right\} + \Vert F(0) \Vert _H^{ (1+\nicefrac {\varphi }{2}) } \right] \nonumber \\&\qquad \cdot \max \!\left\{ 1, \sup _{ v \in H_{\rho } \setminus \{0\} } \frac{ \Vert v \Vert _V^{ (2+\nicefrac {\varphi }{2}) } }{ \Vert v \Vert _{ H_{\rho } }^{ (2+\nicefrac {\varphi }{2}) } } \right\} . \end{aligned}$$

(135)

The fact that $H_{\gamma } \subseteq H_{\rho } \subseteq V \subseteq H$ continuously, (119), (120), (124), (129), and the fact that

$$\begin{aligned} \sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ t \in [0,T] } \big [ \Vert {\mathfrak {O}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^{4p\vartheta }({\mathbb {P}}; H_{\gamma }) } + \Vert P_I O_t \Vert _{ {\mathcal {L}}^{p\varphi }( {\mathbb {P}}; V ) } \big ] < \infty \end{aligned}$$

(136)

therefore establish item (ii). The proof of Theorem 5.5 is thus completed. $\square$

Corollary 5.6

Assume the setting in Sect. 5.1, let $\theta \in [0,\infty )$, $\vartheta \in (0,\infty )$, $p \in [ \max \{ 2, \nicefrac {1}{\varphi } \}, \infty )$, $\varrho \in [0,1-\rho )$, and assume that

$$\begin{aligned}&\sup _{ t \in [0,T] } {\mathbb {E}}\big [ \Vert X_t \Vert _V^{p(1+\nicefrac {\varphi }{2})\max \{2,\varphi \}} \big ] \\&\qquad + \sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ t \in [0,T] } \left( M^{\theta } \! \left\{ \left( {\mathbb {E}}\big [ \Vert P_I( O_{t} - O_{ \lfloor t \rfloor _{T\!/\!M} } ) \Vert _V^{2p} \big ] \right) ^{\!\frac{1}{2p}}\right. \right. \\&\left. \left. \quad \qquad + \left( {\mathbb {E}}\big [ \Vert P_I O_{t} - {\mathfrak {O}}_{t}^{M,I} \Vert _V^{p\max \{2,\varphi \}} \big ] \right) ^{\!\frac{1}{p\max \{2,\varphi \}}} \right\} \right) \\ {}&\qquad + \sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ t \in [0,T] } {\mathbb {E}}\!\left[ \big | \Vert {\mathfrak {O}}_{t}^{M,I} \Vert _{ H_{\gamma } }^2 + \Phi ( {\mathfrak {O}}_{}^{M,I} ) + \phi ( {\mathfrak {O}}_{}^{M,I} ) \big |^{p\max \{2\vartheta , 2+\varphi , (1+\nicefrac {\varphi }{2})\nicefrac {\varphi }{2} \} } \right] \\&\quad < \infty . \end{aligned}$$

(137)

Then we have

• (i) that $\sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ t \in [0,T] } {\mathbb {E}}\big [ \Vert {\mathfrak {X}}_{t}^{M,I} \Vert _{H_{\gamma }}^{p\max \{4\vartheta , 4+2\varphi , \varphi (1+\nicefrac {\varphi }{2}) \}} \big ] < \infty$ and

• (ii) that there exists a real number $C \in (0,\infty )$ such that for all $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ it holds that

  $$\begin{aligned}&\sup _{ t \in [0,T] } \left( {\mathbb {E}}\big [ \Vert X_t - {\mathfrak {X}}_{t}^{M,I} \Vert _H^p \big ] \right) ^{\!\nicefrac {1}{p}} \\ {}&\le C \left[ M^{-\min \{\vartheta \chi ,\varrho ,\theta \}} + \Vert (-A)^{-\varrho } (Id _H - P_I) \Vert _{ L(H) } \right. \\&\left. \qquad + \sup _{ t \in [0,T] } \Vert (Id _H - P_I) O_t \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; V ) } \right] . \end{aligned}$$

  (138)

Proof of Corollary 5.6

Note that the triangle inequality, (137), and the fact that $H_{\gamma } \subseteq V$ continuously yield that

$$\begin{aligned}&\sup _{ I \in {\mathcal {D}}} \sup _{ s \in (0,T) } \Vert P_I O_s \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}}; V) } \\&\quad \le \sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ s \in (0,T) } \left[ \Vert P_I O_s - {\mathfrak {O}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}}; V) } + \Vert {\mathfrak {O}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}}; V) } \right] \\&\quad \le \sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ s \in (0,T) } \Vert P_I O_s - {\mathfrak {O}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}}; V) } \\&\qquad + \left[ \sup _{ v \in H_{\gamma } \setminus \{0\} } \frac{ \Vert v \Vert _V }{ \Vert v \Vert _{H_{\gamma }} } \right] \left[ \sup _{ M \in {\mathbb {N}}} \sup _{ I \in {\mathcal {D}}} \sup _{ s \in (0,T) } \Vert {\mathfrak {O}}_{s}^{M,I} \Vert _{ {\mathcal {L}}^{p\varphi }({\mathbb {P}}; H_{\gamma }) } \right] < \infty . \end{aligned}$$

(139)

This together with (137) allows us to apply Theorem 5.5 to obtain that item (i) holds and that there exists a real number $K \in (0,\infty )$ such that for all $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ we have that

$$\begin{aligned}&\sup _{ t \in [0,T] } \Vert X_t - {\mathfrak {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; H) } \le K \bigg ( M^{-\min \{\vartheta \chi ,\varrho \}} + \Vert (-A)^{-\varrho } (Id _H - P_I) \Vert _{ L(H) } \\ {}&\qquad + \sup _{ t \in [0,T] } \left[ \Vert (Id _H - P_I) O_t \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; V ) } + \Vert P_I O_{t} - {\mathfrak {O}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; V ) } \right. \\&\left. \qquad + \Vert P_I( O_{t} - O_{ \lfloor t \rfloor _{T\!/\!M} } ) \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; V ) } \right] \bigg ) . \end{aligned}$$

(140)

Hence, we obtain that for all $M \in {\mathbb {N}}$, $I \in {\mathcal {D}}$ we have that

$$\begin{aligned}&\sup _{ t \in [0,T] } \Vert X_t - {\mathfrak {X}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; H) } \\ {}&\quad \le K \Bigg ( \Vert (-A)^{-\varrho } (Id _H - P_I) \Vert _{ L(H) } + \sup _{ t \in [0,T] } \Vert (Id _H - P_I) O_t \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; V ) } + M^{-\min \{\vartheta \chi ,\varrho , \theta \}} \\ {}&\qquad \cdot \left\{ 1 + \sup _{ t \in [0,T] } \left( M^{\theta } \left[ \Vert P_I O_{t} - {\mathfrak {O}}_{t}^{M,I} \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; V ) } + \Vert P_I( O_{t} - O_{ \lfloor t \rfloor _{T\!/\!M} } ) \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; V ) } \right] \right) \right\} \Bigg ) \\ {}&\quad \le K \left[ 1 + \sup _{ N \in {\mathbb {N}}} \sup _{ J \in {\mathcal {D}}} \sup _{ t \in [0,T] } \left( N^{\theta } \left[ \Vert P_J( O_{t} - O_{ \lfloor t \rfloor _{T/N} } ) \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; V ) } \right. \right. \right. \\&\left. \left. \left. \quad + \Vert P_J O_{t} - {\mathcal {O}}^{N,J}_t \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; V ) } \right] \right) \right] \\ {}&\qquad \cdot \left[ M^{-\min \{\vartheta \chi ,\varrho ,\theta \}} + \Vert (-A)^{-\varrho } (Id _H - P_I) \Vert _{ L(H) } + \sup _{ t \in (0,T) } \Vert (Id _H - P_I) O_t \Vert _{ {\mathcal {L}}^{2p}( {\mathbb {P}}; V ) } \right] . \end{aligned}$$

(141)

Combining this with (137) establishes item (ii). The proof of Corollary 5.6 is thus completed. $\square$

6 Stochastic Allen–Cahn equations

6.1 Setting

Consider the notation in Sect. 1.1, let $T, \nu \in (0,\infty )$, $a_0, a_1, a_2 \in {\mathbb {R}}$, $a_3 \in (-\infty ,0]$, $( H, \langle \cdot , \cdot \rangle _H, \left\| \cdot \right\| \!_H )$ $= ( L^2(\lambda _{(0,1)}; {\mathbb {R}}),$ $\langle \cdot , \cdot \rangle _{ L^2(\lambda _{(0,1)}; {\mathbb {R}}) }, \left\| \cdot \right\| \!_{ L^2(\lambda _{(0,1)}; {\mathbb {R}}) } )$, $(e_n)_{ n \in {\mathbb {N}}} \subseteq H$, $F :L^{6}(\lambda _{(0,1)}; {\mathbb {R}}) \rightarrow H$, $(P_n)_{ n \in {\mathbb {N}}} \subseteq L(H)$ satisfy for all $n \in {\mathbb {N}}$, $v \in L^{6}(\lambda _{(0,1)}; {\mathbb {R}})$ that $a_2 \, \mathbb {1}_{\{0\}}^{{\mathbb {R}}}(a_3) = 0$, $e_n = [ (\sqrt{2}\sin (n \pi x))_{ x \in (0,1) } ]_{ \lambda _{(0,1)}, {\mathcal {B}}({\mathbb {R}}) }$, $F(v) = \sum _{ k=0 }^{3} a_k v^k$, $P_n(v) = \sum _{ k=1 }^n \langle e_k, v \rangle _H \, e_k$, let $A :D(A) \subseteq H \rightarrow H$ be the Laplacian with Dirichlet boundary conditions on H times the real number $\nu$, let $( H_r, \langle \cdot , \cdot \rangle _{H_r}, \left\| \cdot \right\| \!_{H_r} )$, $r \in {\mathbb {R}}$, be a family of interpolation spaces associated to $-A$ (cf., e.g., [37, Section 3.7]), let $( \Omega , {\mathcal {F}}, {\mathbb {P}})$ be a probability space, let $(W_t)_{ t \in [0,T] }$ be an $Id _H$-cylindrical Wiener process, and let $({\underline{\cdot }}) :\big \{ [v]_{\lambda _{(0,1)},{\mathcal {B}}({\mathbb {R}})} \in H :( v \in {\mathcal {C}}( (0,1), {\mathbb {R}}) \text { is a uniformly continuous function} ) \big \} \rightarrow {\mathcal {C}}( (0,1), {\mathbb {R}})$ be the function which satisfies for all uniformly continuous functions $v :(0,1) \rightarrow {\mathbb {R}}$ that $\underline{[v]_{\lambda _{(0,1)}, {\mathcal {B}}({\mathbb {R}})}} = v$.

6.2 Properties of the nonlinearities of stochastic Allen–Cahn equations

Lemma 6.1

Assume the setting in Sect. 6.1 and let $\epsilon \in (0,1)$, $c \in [\frac{32}{\epsilon }\max \{\frac{|a_2|^2}{|a_3|+\mathbb {1}_{\{0\}}^{{\mathbb {R}}}(a_3)},|a_3|\},\infty )$. Then there exists a real number $C \in (0,\infty )$ such that for all $N \in {\mathbb {N}}$, $v \in P_N(H)$, $w \in {\mathcal {C}}([0,T],H_1)$, $t \in [0,T]$ we have that

$$\begin{aligned}&\langle v, P_N F(v + w_t) \rangle _{H_{\nicefrac {1}{2}}} + c \big [ \textstyle \sup _{ s \in [0,T] } \Vert w_s \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + 1 \big ] \langle v, F(v + w_t) \rangle _H \\ {}&\quad \le \epsilon \Vert v \Vert _{ H_1 }^2 + \Big ( | a_1 | + \tfrac{ |a_2|^2 }{ 3|a_3| + \mathbb {1}_{\{0\}}^{{\mathbb {R}}}(a_3) } \Big ) \Vert v \Vert _{ H_{\nicefrac {1}{2}} }^2 \\ {}&\qquad + c \big [ \textstyle \sup _{ s \in [0,T] } \Vert w_s \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + 1 \big ] \Big ( | a_0 | + \tfrac{3 |a_1|}{2} \Big ) \Vert v \Vert _H^2 \\ {}&\qquad + C \big [ \textstyle \sup _{ s \in [0,T] } \Vert w_s \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^{8} + 1 \big ] . \end{aligned}$$

(142)

Proof of Lemma 6.1

Throughout this proof let $\eta :{\mathbb {N}}_0 \times {\mathbb {N}}_0 \rightarrow (0,\infty )$ be a function which satisfies that

$$\begin{aligned}&\mathbb {1}_{(-\infty ,0)}^{{\mathbb {R}}}(a_3) \left( a_3 + \frac{1}{2} \sum _{ k = 0 }^3 \sum _{ j = 0 }^{ \min \{k,2\} } \left( {\begin{array}{c}k\\ j\end{array}}\right) (j+1) \, | a_k | \, | \eta (k,j) |^{\frac{4}{(j+1)}} \right) \le 0 . \end{aligned}$$

(143)

Observe that the fact that for every $N \in {\mathbb {N}}$ we have that $P_N$ is symmetric implies that for all $N \in {\mathbb {N}}$, $v \in P_N(H)$, $w \in {\mathcal {C}}([0,T], H_1)$, $t \in [0,T]$ we have that

$$\begin{aligned}&\langle v, \textstyle \sum _{ k = 0 }^3 a_k P_N [v + w_t]^k \rangle _{H_{\nicefrac {1}{2}}} \nonumber \\&\quad = \sum _{ k = 0 }^3 a_k \langle (-A)^{\nicefrac {1}{2}} v, (-A)^{\nicefrac {1}{2}} P_N [v + w_t]^k \rangle _H = \sum _{ k = 0 }^3 a_k \langle (-A) v, P_N [v + w_t]^k \rangle _H \nonumber \\&\quad = - \sum _{ k = 0 }^3 a_k \langle A P_N v, [v + w_t]^k \rangle _H = - \sum _{ k = 0 }^3 a_k \langle A v, [v + w_t]^k \rangle _H . \end{aligned}$$

(144)

This shows that for all $N \in {\mathbb {N}}$, $v \in P_N(H)$, $w \in {\mathcal {C}}([0,T], H_1)$, $t \in [0,T]$ we have that

$$\begin{aligned}&\langle v, \textstyle \sum _{ k = 0 }^3 a_k P_N [v + w_t]^k \rangle _{H_{\nicefrac {1}{2}}} \\ {}&\quad = -\nu \sum _{ k = 0 }^3 a_k \langle v'', [v + w_t]^k \rangle _H = -\nu \sum _{ k = 0 }^3 \sum _{ j = 0 }^k \left( {\begin{array}{c}k\\ j\end{array}}\right) a_k \langle v'', v^j (w_t)^{(k-j)} \rangle _H \\ {}&\quad = -\nu \sum _{ k=1 }^3 \left( {\begin{array}{c}k\\ k\end{array}}\right) a_k \langle v'', v^k \rangle _H - \nu \sum _{ k = 0 }^3 \sum _{ j = 0 }^{\max \{0, k-1\}} \left( {\begin{array}{c}k\\ j\end{array}}\right) a_k \langle v'', v^j (w_t)^{(k-j)} \rangle _H . \end{aligned}$$

(145)

Moreover, note that integration by parts and the fact that

$$\begin{aligned} \forall \, x,y \in {\mathbb {R}}, r \in (0,\infty ) :x \sqrt{2r} \cdot \tfrac{y}{\sqrt{2r}} \le r x^2 + \tfrac{y^2}{4r} \end{aligned}$$

(146)

prove that for all $N \in {\mathbb {N}}$, $v \in P_N(H)$ we have that

$$\begin{aligned}&-\nu \sum _{ k=1 }^3 a_k \langle v'', v^k \rangle _H = \nu \sum _{ k=1 }^3 k a_k \langle v', v^{(k-1)} v' \rangle _H \\ {}&\quad \le 3\nu a_3 \int _0^1 [ {\underline{v}}'(x) ]^2 \, [ {\underline{v}}(x) ]^2 \, dx + 2\nu |a_2| \int _0^1 [ {\underline{v}}'(x) ]^2 \, | {\underline{v}}(x) | \, dx + \nu |a_1| \, \Vert v' \Vert _H^2 \\ {}&\quad \le 3\nu a_3 \int _0^1 [ {\underline{v}}'(x) ]^2 \, [ {\underline{v}}(x) ]^2 \, dx + \nu \int _0^1 [ {\underline{v}}'(x) ]^2 \left( 3 |a_3| [ {\underline{v}}(x) ]^2 + \frac{ 4 |a_2|^2 }{ 4\big ( 3 |a_3| + \mathbb {1}_{\{0\}}^{{\mathbb {R}}}(a_3) \big ) } \right) dx \\ {}&\qquad + \nu |a_1| \Vert v' \Vert _H^2 \\ {}&\quad = \nu \left( |a_1| + \frac{ |a_2|^2 }{ 3 |a_3| + \mathbb {1}_{\{0\}}^{{\mathbb {R}}}(a_3) } \right) \Vert v' \Vert _H^2 = \left( |a_1| + \frac{ |a_2|^2 }{ 3 |a_3| + \mathbb {1}_{\{0\}}^{{\mathbb {R}}}(a_3) } \right) \Vert v \Vert _{ H_{\nicefrac {1}{2}} }^2 . \end{aligned}$$

(147)

Furthermore, observe that the fact that

$$\begin{aligned} \forall \, x,y \in {\mathbb {R}}:xy \le \epsilon x^2 + \tfrac{y^2}{4\epsilon } \end{aligned}$$

(148)

shows that for all $N \in {\mathbb {N}}$, $v \in P_N(H)$, $w \in {\mathcal {C}}([0,T], H_1)$, $t \in [0,T]$ we have that

$$\begin{aligned}&-\nu \sum _{ k = 0 }^3 \sum _{ j = 0 }^{\max \{0, k-1\}} \left( {\begin{array}{c}k\\ j\end{array}}\right) a_k \langle v'', v^j (w_t)^{(k-j)} \rangle _H \nonumber \\&\quad \le \nu \sum _{ k = 0 }^3 \sum _{ j = 0 }^{\max \{0, k-1\}} \left( {\begin{array}{c}k\\ j\end{array}}\right) | a_k | \int _0^1 | {\underline{v}}''(x) | \, | {\underline{v}}(x) |^j \, | \underline{w_t}(x) |^{ (k-j) } \, dx \nonumber \\&\quad = \int _0^1 \nu \, | {\underline{v}}''(x) | \left[ \sum _{ k = 0 }^3 \sum _{ j = 0 }^{\max \{0, k-1\}} \left( {\begin{array}{c}k\\ j\end{array}}\right) | a_k | \, | {\underline{v}}(x) |^j \, | \underline{w_t}(x) |^{ (k-j) } \right] dx \nonumber \\&\quad \le \epsilon \nu ^2 \Vert v'' \Vert _H^2 + \frac{1}{4\epsilon } \int _0^1 \left[ \sum _{ k = 0 }^3 \sum _{ j = 0 }^{\max \{0, k-1\}} \left( {\begin{array}{c}k\\ j\end{array}}\right) | a_k | \, | {\underline{v}}(x) |^j \, | \underline{w_t}(x) |^{ (k-j) } \right] ^{\!2} dx .\nonumber \\ \end{aligned}$$

(149)

The fact that

$$\begin{aligned} \forall \, x_1, x_2, \ldots , x_7 \in {\mathbb {R}}:[x_1 + x_2 + \ldots + x_7]^2 \le 7([x_1]^2 + [x_2]^2 + \ldots + [x_7]^2)\nonumber \\ \end{aligned}$$

(150)

hence assures that for all $N \in {\mathbb {N}}$, $v \in P_N(H)$, $w \in {\mathcal {C}}([0,T], H_1)$, $t \in [0,T]$ we have that

$$\begin{aligned}&-\nu \sum _{ k = 0 }^3 \sum _{ j = 0 }^{\max \{0, k-1\}} \left( {\begin{array}{c}k\\ j\end{array}}\right) a_k \langle v'', v^j (w_t)^{(k-j)} \rangle _H \\ {}&\quad \le \epsilon \nu ^2 \Vert v'' \Vert _{H}^2 + \frac{7}{4\epsilon } \sum _{ k = 0 }^3 \sum _{ j = 0 }^{\max \{0, k-1\}} \left[ \textstyle \left( {\begin{array}{c}k\\ j\end{array}}\right) |a_k| \right] ^2 \int _0^1 | {\underline{v}}(x) |^{2j} \, | \underline{w_t}(x) |^{ 2(k-j) } \, dx \\ {}&\quad = \epsilon \Vert v \Vert _{H_1}^2 + \frac{7}{4\epsilon } \sum _{ k = 0 }^3 |a_k|^2 \int _0^1 | \underline{w_t}(x) |^{ 2k } \, dx \\ {}&\qquad + \frac{7}{4\epsilon } \sum _{ k = 2 }^3 \sum _{ j = 1 }^{k-1} \left[ \textstyle \left( {\begin{array}{c}k\\ j\end{array}}\right) |a_k| \right] ^2 \int _0^1 | {\underline{v}}(x) |^{2j} \, | \underline{w_t}(x) |^{ 2(k-j) } \, dx . \end{aligned}$$

(151)

This and the fact that

$$\begin{aligned} \forall \, x, y \in {\mathbb {R}}:xy \le \tfrac{x^2}{2} + \tfrac{y^2}{2} \end{aligned}$$

(152)

imply that for all $N \in {\mathbb {N}}$, $v \in P_N(H)$, $w \in {\mathcal {C}}([0,T], H_1)$, $t \in [0,T]$ we have that

$$\begin{aligned}&-\nu \sum _{ k = 0 }^3 \sum _{ j = 0 }^{\max \{0, k-1\}} \left( {\begin{array}{c}k\\ j\end{array}}\right) a_k \langle v'', v^j (w_t)^{(k-j)} \rangle _H \nonumber \\&\quad \le \epsilon \Vert v \Vert _{H_1}^2 + \frac{7}{\epsilon } \left[ \max _{ k \in \{0,1,2,3\} } | a_k |^2 \right] \int _0^1 \max \{ | \underline{w_t}(x) |^{ 6 },1 \} \, dx \nonumber \\&\qquad + \frac{7}{4\epsilon } \left[ \max _{ k \in \{2,3\},j \in \{1,2\} } \textstyle \left( {\begin{array}{c}k\\ j\end{array}}\right) | a_k | \right] ^{\!2} \int _0^1 \Big [ | {\underline{v}}(x) |^{2} \, | \underline{w_t}(x) |^{ 2 } + | {\underline{v}}(x) |^{2} \, | \underline{w_t}(x) |^{ 4 } \nonumber \\&\qquad + | {\underline{v}}(x) |^{4} \, | \underline{w_t}(x) |^{ 2 } \Big ] \, dx \nonumber \\&\quad \le \epsilon \Vert v \Vert _{H_1}^2 + \frac{7}{\epsilon } \left[ \max _{ k \in \{0,1,2,3\} } | a_k |^2 \right] \left( \Vert w_t \Vert _{ L^6( \lambda _{(0,1)} ; {\mathbb {R}}) }^6 + 1 \right) \nonumber \\&\qquad + \frac{7}{4\epsilon } \left[ \max _{ k \in \{2,3\},j \in \{1,2\} } \textstyle \left( {\begin{array}{c}k\\ j\end{array}}\right) | a_k | \right] ^{\!2} \int _0^1 \Big [ | {\underline{v}}(x) |^{4} \, + | \underline{w_t}(x) |^{ 4 } + | {\underline{v}}(x) |^{4} | \underline{w_t}(x) |^{ 4 } \Big ] \, dx .\nonumber \\ \end{aligned}$$

(153)

Hölder’s inequality therefore ensures that for all $N \in {\mathbb {N}}$, $v \in P_N(H)$, $w \in {\mathcal {C}}([0,T], H_1)$, $t \in [0,T]$ we have that

(154)

In the next step we combine (145) with (147) and (154) to obtain that for all $N \in {\mathbb {N}}$, $v \in P_N(H)$, $w \in {\mathcal {C}}([0,T], H_1)$, $t \in [0,T]$ we have that

$$\begin{aligned}&\langle v, \textstyle \sum _{ k = 0 }^3 a_k P_N [v + w_t]^k \rangle _{H_{\nicefrac {1}{2}}} \\ {}&\quad \le \epsilon \Vert v \Vert _{H_1}^2 + \left( |a_1| + \frac{ |a_2|^2 }{ 3 |a_3| + \mathbb {1}_{\{0\}}^{{\mathbb {R}}}(a_3) } \right) \Vert v \Vert _{ H_{\nicefrac {1}{2}} }^2 \\&\qquad + \left[ \max _{ k \in \{0,1,2,3\} } \tfrac{ 5 | a_k | }{ \sqrt{\epsilon } } \right] ^{\!2} \left[ \Vert w_t \Vert _{ L^6( \lambda _{(0,1)} ; {\mathbb {R}}) }^6 + 1 \right] \\ {}&\qquad + \frac{c |a_3|}{2} \left[ \Vert w_t \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + 1 \right] \Vert v \Vert _{ L^4( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 . \end{aligned}$$

(155)

In addition, note that for all $N \in {\mathbb {N}}$, $v \in P_N(H)$, $w \in {\mathcal {C}}([0,T], H_1)$, $t \in [0,T]$ we have that

$$\begin{aligned}&\langle v, \textstyle \sum _{ k = 0 }^3 a_k [v + w_t]^k \rangle _H \nonumber \\&\quad = \sum _{ k = 0 }^3 a_k \langle v, [v + w_t]^k \rangle _H = \sum _{ k = 0 }^3 \sum _{ j = 0 }^k \left( {\begin{array}{c}k\\ j\end{array}}\right) a_k \langle v, v^j (w_t)^{(k-j)} \rangle _H \nonumber \\&\quad = a_3 \Vert v \Vert _{ L^4( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + \sum _{ k = 0 }^3 \sum _{ j = 0 }^{ \min \{k,2\} } \left( {\begin{array}{c}k\\ j\end{array}}\right) a_k \langle v, v^j (w_t)^{(k-j)} \rangle _H \nonumber \\&\quad \le a_3 \Vert v \Vert _{ L^4( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + \sum _{ k = 0 }^3 \sum _{ j = 0 }^{ \min \{k,2\} } \left( {\begin{array}{c}k\\ j\end{array}}\right) | a_k | \int _0^1 | {\underline{v}}(x) |^{(j+1)} \, | \underline{w_t}(x) |^{(k-j)} \, dx .\nonumber \\ \end{aligned}$$

(156)

Young’s inequality hence demonstrates that for all $N \in {\mathbb {N}}$, $v \in P_N(H)$, $w \in {\mathcal {C}}([0,T], H_1)$, $t \in [0,T]$, $r \in [0,\infty )$ we have that

$$\begin{aligned}&r \langle v, \textstyle \sum _{ k = 0 }^3 a_k [v + w_t]^k \rangle _H \\ {}&\quad \le r a_3 \Vert v \Vert _{ L^4( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + r \sum _{ k = 0 }^3 \sum _{ j = 0 }^{ \min \{k,2\} } \left( {\begin{array}{c}k\\ j\end{array}}\right) | a_k | \int _0^1 | \eta (k,j) | \, | {\underline{v}}(x) |^{(j+1)} \, \frac{ | \underline{w_t}(x) |^{(k-j)} }{ | \eta (k,j) | } \, dx \\ {}&\quad \le r a_3 \Vert v \Vert _{ L^4( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 \\ {}&\qquad + r \sum _{ k = 0 }^3 \sum _{ j = 0 }^{ \min \{k,2\} } \left( {\begin{array}{c}k\\ j\end{array}}\right) | a_k | \int _0^1 \left[ \tfrac{ (j+1) }{ 4 } | \eta (k,j) |^{\frac{4}{(j+1)}} | {\underline{v}}(x) |^{4} + \frac{ (3-j) | \underline{w_t}(x) |^{\frac{ 4(k-j) }{ (3-j) } } }{ 4 | \eta (k,j) |^{\frac{4}{(3-j)} } } \right] dx . \end{aligned}$$

(157)

Therefore, we obtain that for all $N \in {\mathbb {N}}$, $v \in P_N(H)$, $w \in {\mathcal {C}}([0,T], H_1)$, $t \in [0,T]$, $r \in [0,\infty )$ we have that

$$\begin{aligned}&\mathbb {1}_{ (-\infty ,0) }^{ {\mathbb {R}}}(a_3) \, r \langle v, \textstyle \sum _{ k = 0 }^3 a_k [v + w_t]^k \rangle _H \\ {}&\quad \le r \Vert v \Vert _{ L^4( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 \mathbb {1}_{ (-\infty ,0) }^{ {\mathbb {R}}}(a_3) \! \left[ a_3 + \frac{1}{4} \sum _{ k = 0 }^3 \sum _{ j = 0 }^{ \min \{k,2\} } \left( {\begin{array}{c}k\\ j\end{array}}\right) (j+1) \, | a_k | \, | \eta (k,j) |^{\frac{4}{(j+1)}} \right] \\ {}&\qquad + r \sum _{ k = 0 }^3 \sum _{ j = 0 }^{ \min \{k,2\} } \left( {\begin{array}{c}k\\ j\end{array}}\right) \frac{ (3-j) | a_k | }{ 4 | \eta (k,j) |^{\frac{4}{(3-j)} } } \int _0^1 \max \{ 1, | \underline{w_t}(x) |^4 \} \, dx \\ {}&\quad \le \frac{ r a_3 }{ 2 } \Vert v \Vert _{ L^4( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + r \sum _{ k = 0 }^3 \sum _{ j = 0 }^{ \min \{k,2\} } \left( {\begin{array}{c}k\\ j\end{array}}\right) \frac{ (3-j) | a_k | }{ 4 | \eta (k,j) |^{\frac{4}{(3-j)} } } \left[ \Vert w_t \Vert _{ L^4( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + 1 \right] . \end{aligned}$$

(158)

Moreover, note that the fact that

$$\begin{aligned} \forall \, x, y \in [0,\infty ) :xy \le \tfrac{x^2}{2} + \tfrac{y^2}{2} \end{aligned}$$

(159)

ensures that for all $N \in {\mathbb {N}}$, $v \in P_N(H)$, $w \in {\mathcal {C}}([0,T], H_1)$, $t \in [0,T]$, $r \in [0,\infty )$ we have that

$$\begin{aligned}&r \langle v, \textstyle \sum _{ k = 0 }^1 a_k [v + w_t]^k \rangle _H \\&\quad \le r \int _0^1 | a_0 | \, | {\underline{v}}(x) | + | a_1 | \, | {\underline{v}}(x) |^2 + | a_1 | \, | {\underline{v}}(x) | \, | \underline{w_t}(x) | \, dx \\&\quad \le r \int _0^1 | a_0 | \left( 1 + | {\underline{v}}(x) |^2 \right) + | a_1 | \, | {\underline{v}}(x) |^2 + \frac{| a_1 |}{2} \left( | {\underline{v}}(x) |^2 + | \underline{w_t}(x) |^2 \right) dx \\ {}&\quad = r \left( | a_0 | + \tfrac{3 | a_1 |}{2} \right) \Vert v \Vert _H^2 + r \left( | a_0 | + \tfrac{| a_1 |}{2} \Vert w_t \Vert _H^2 \right) \\ {}&\quad \le r \left( | a_0 | + \tfrac{3 | a_1 |}{2} \right) \Vert v \Vert _H^2 + r \left( | a_0 | + \tfrac{| a_1 |}{2} \right) \left[ \Vert w_t \Vert _{ L^4( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + 1 \right] . \end{aligned}$$

(160)

Hence, we obtain that for all $N \in {\mathbb {N}}$, $v \in P_N(H)$, $w \in {\mathcal {C}}([0,T], H_1)$, $t \in [0,T]$, $r \in [ \Vert w_t \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + 1, \infty )$ we have that

$$\begin{aligned}&\langle v, {\textstyle \sum _{ k = 0 }^3} a_k P_N [v + w_t]^k \rangle _{H_{\nicefrac {1}{2}}} + c r \langle v, \textstyle \sum _{ k = 0 }^3 a_k [v + w_t]^k \rangle _H \\&\quad = \langle v, {\textstyle \sum _{ k = 0 }^3} a_k P_N [v + w_t]^k \rangle _{H_{\nicefrac {1}{2}}} + c r \langle v, \textstyle \sum _{ k = 0 }^3 a_k [v + w_t]^k \rangle _H \mathbb {1}_{ (-\infty ,0) }^{ {\mathbb {R}}}(a_3) \\ {}&\qquad + c r \langle v, \textstyle \sum _{ k = 0 }^3 a_k [v + w_t]^k \rangle _H \mathbb {1}_{ \{0\} }^{ {\mathbb {R}}}(a_3) \\ {}&\quad = \langle v, {\textstyle \sum _{ k = 0 }^3} a_k P_N [v + w_t]^k \rangle _{H_{\nicefrac {1}{2}}} + c r \langle v, \textstyle \sum _{ k = 0 }^3 a_k [v + w_t]^k \rangle _H \mathbb {1}_{ (-\infty ,0) }^{ {\mathbb {R}}}(a_3) \\ {}&\qquad + c r \langle v, \textstyle \sum _{ k = 0 }^1 a_k [v + w_t]^k \rangle _H \mathbb {1}_{ \{0\} }^{ {\mathbb {R}}}(a_3) \\ {}&\quad \le \langle v, {\textstyle \sum _{ k = 0 }^3} a_k P_N [v + w_t]^k \rangle _{H_{\nicefrac {1}{2}}} + c r \langle v, \textstyle \sum _{ k = 0 }^3 a_k [v + w_t]^k \rangle _H \mathbb {1}_{ (-\infty ,0) }^{ {\mathbb {R}}}(a_3) \\ {}&\qquad + cr \left( | a_0 | + \tfrac{3 | a_1 |}{2} \right) \Vert v \Vert _H^2 + cr \left( | a_0 | + \tfrac{| a_1 |}{2} \right) \left[ \Vert w_t \Vert _{ L^4( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + 1 \right] . \end{aligned}$$

(161)

Combining this with (155) and (158) assures that for all $N \in {\mathbb {N}}$, $v \in P_N(H)$, $w \in {\mathcal {C}}([0,T], H_1)$, $t \in [0,T]$, $r \in [ \Vert w_t \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + 1, \infty )$ we have that

$$\begin{aligned}&\langle v, {\textstyle \sum _{ k = 0 }^3} a_k P_N [v + w_t]^k \rangle _{H_{\nicefrac {1}{2}}} + c r \langle v, \textstyle \sum _{ k = 0 }^3 a_k [v + w_t]^k \rangle _H \\ {}&\quad \le \epsilon \Vert v \Vert _{H_1}^2 + \left( |a_1| + \frac{ |a_2|^2 }{ 3 |a_3| + \mathbb {1}_{\{0\}}^{{\mathbb {R}}}(a_3) } \right) \Vert v \Vert _{ H_{\nicefrac {1}{2}} }^2 + c r \left( | a_0 | + \tfrac{3 | a_1 |}{2} \right) \Vert v \Vert _H^2 \\ {}&\qquad + \frac{cr}{2} \Vert v \Vert _{ L^4( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 \left( a_3 + |a_3| \right) + \left[ \max _{ k \in \{0,1,2,3\} } \tfrac{ 5 | a_k | }{ \sqrt{\epsilon } } \right] ^{\!2} \left[ \Vert w_t \Vert _{ L^6( \lambda _{(0,1)} ; {\mathbb {R}}) }^6 + 1 \right] \\ {}&\qquad + c r \left[ | a_0 | + \frac{| a_1 |}{2} + \sum _{ k = 0 }^3 \sum _{ j = 0 }^{ \min \{k,2\} } \left( {\begin{array}{c}k\\ j\end{array}}\right) \frac{ (3-j) | a_k | }{ 4 | \eta (k,j) |^{\frac{4}{(3-j)} } } \right] \left[ \Vert w_t \Vert _{ L^4( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + 1 \right] . \end{aligned}$$

(162)

Hölder’s inequality and the fact that

$$\begin{aligned} a_3 + |a_3| = a_3 - a_3 = 0 \end{aligned}$$

(163)

therefore prove that for all $N \in {\mathbb {N}}$, $v \in P_N(H)$, $w \in {\mathcal {C}}([0,T], H_1)$, $t \in [0,T]$, $r \in [ \Vert w_t \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + 1, \infty )$ we have that

$$\begin{aligned}&\langle v, {\textstyle \sum _{ k = 0 }^3} a_k P_N [v + w_t]^k \rangle _{H_{\nicefrac {1}{2}}} + c r \langle v, \textstyle \sum _{ k = 0 }^3 a_k [v + w_t]^k \rangle _H \\ {}&\quad \le \epsilon \Vert v \Vert _{H_1}^2 + \left( |a_1| + \frac{ |a_2|^2 }{ 3 |a_3| + \mathbb {1}_{\{0\}}^{{\mathbb {R}}}(a_3) } \right) \Vert v \Vert _{ H_{\nicefrac {1}{2}} }^2 + c r \left( | a_0 | + \tfrac{3 | a_1 |}{2} \right) \Vert v \Vert _H^2 \\ {}&\qquad + \left[ \max _{ k \in \{0,1,2,3\} } \tfrac{ 5 | a_k | }{ \sqrt{\epsilon } } \right] ^{\!2} \left[ \Vert w_t \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^6 + 1 \right] \\&\qquad + c r^2 \! \left[ | a_0 | + \frac{| a_1 |}{2} + \sum _{ k = 0 }^3 \sum _{ j = 0 }^{ \min \{k,2\} } \! \left( {\begin{array}{c}k\\ j\end{array}}\right) \frac{ (3-j) | a_k | }{ 4 | \eta (k,j) |^{\frac{4}{(3-j)} } } \right] . \end{aligned}$$

(164)

The fact that

$$\begin{aligned} \forall \, x, y \in (0,\infty ) :(x+y)^2 \le 2(x^2+y^2) \end{aligned}$$

(165)

hence implies that for all $N \in {\mathbb {N}}$, $v \in P_N(H)$, $w \in {\mathcal {C}}([0,T], H_1)$, $t \in [0,T]$ we have that

$$\begin{aligned}&\langle v, {\textstyle \sum _{ k = 0 }^3} a_k P_N [v + w_t]^k \rangle _{H_{\nicefrac {1}{2}}} + c \left[ \sup _{ s \in [0,T] } \Vert w_s \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + 1 \right] \langle v, \textstyle \sum _{ k = 0 }^3 a_k [v + w_t]^k \rangle _H \\ {}&\quad \le \epsilon \Vert v \Vert _{H_1}^2 + \left( |a_1| + \frac{ |a_2|^2 }{ 3 |a_3| + \mathbb {1}_{\{0\}}^{{\mathbb {R}}}(a_3) } \right) \Vert v \Vert _{ H_{\nicefrac {1}{2}} }^2 \\ {}&\qquad + c \left[ \sup _{ s \in [0,T] } \Vert w_s \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + 1 \right] \left( | a_0 | + \tfrac{3 | a_1 |}{2} \right) \Vert v \Vert _H^2 \\&\qquad + \left[ \max _{ k \in \{0,1,2,3\} } \tfrac{ 5 | a_k | }{ \sqrt{\epsilon } } \right] ^{\!2} \left[ \Vert w_t \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^8 + 2 \right] \\&\qquad + c \left[ 2 | a_0 | + | a_1 | + \sum _{ k = 0 }^3 \sum _{ j = 0 }^{ \min \{k,2\} } \left( {\begin{array}{c}k\\ j\end{array}}\right) \frac{ (3-j) | a_k | }{ 2 | \eta (k,j) |^{\frac{4}{(3-j)} } } \right] \left[ \sup _{ s \in [0,T] } \Vert w_s \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^8 + 1 \right] . \end{aligned}$$

(166)

Hence, we obtain that for all $N \in {\mathbb {N}}$, $v \in P_N(H)$, $w \in {\mathcal {C}}([0,T], H_1)$, $t \in [0,T]$ we have that

$$\begin{aligned}&\langle v, {\textstyle \sum _{ k = 0 }^3} a_k P_N [v + w_t]^k \rangle _{H_{\nicefrac {1}{2}}} + c \left[ \sup _{ s \in [0,T] } \Vert w_s \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + 1 \right] \langle v, \textstyle \sum _{ k = 0 }^3 a_k [v + w_t]^k \rangle _H \nonumber \\&\quad \le \epsilon \Vert v \Vert _{H_1}^2 + \left( | a_1 | + \frac{ |a_2|^2 }{ 3 |a_3| + \mathbb {1}_{\{0\}}^{{\mathbb {R}}}(a_3) } \right) \Vert v \Vert _{ H_{\nicefrac {1}{2}} }^2 \nonumber \\&\qquad + c \left[ \sup _{ s \in [0,T] } \Vert w_s \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + 1 \right] \left( | a_0 | + \frac{3 |a_1|}{2} \right) \Vert v \Vert _H^2 \nonumber \\&\qquad + \left[ \left[ \max _{ k \in \{0,1,2,3\} } \tfrac{ 8 | a_k | }{ \sqrt{\epsilon } } \right] ^{\!2} + 2c | a_0 | + c| a_1 | + c \sum _{ k = 0 }^3 \! \sum _{ j = 0 }^{ \min \{k,2\} } \left( {\begin{array}{c}k\\ j\end{array}}\right) \frac{ (3-j) | a_k | }{ 2 | \eta (k,j) |^{\frac{4}{(3-j)} } } \right] \nonumber \\&\qquad \cdot \left[ \sup _{ s \in [0,T] } \Vert w_s \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^8 + 1 \right] . \end{aligned}$$

(167)

The proof of Lemma 6.1 is thus completed. $\square$

Lemma 6.2

Assume the setting in Sect. 6.1 and let $q \in [6, \infty )$, $v, w \in L^q( \lambda _{ (0,1) }; {\mathbb {R}})$. Then

$$\begin{aligned} \Vert F(v) - F(w) \Vert _{ H }^2&\le 36 \left[ \max _{j\in \{1,2,3\}} \left| a_j \right| \right] ^2 \Vert v-w \Vert _{ L^q( \lambda _{ (0,1) }; {\mathbb {R}}) }^2 \left( 1 + \Vert v \Vert _{ L^q( \lambda _{ (0,1) }; {\mathbb {R}}) }^{4} \right. \\&\left. \quad + \Vert w \Vert _{ L^q( \lambda _{ (0,1) }; {\mathbb {R}}) }^{4} \right) . \end{aligned}$$

(168)

Proof of Lemma 6.2

Observe that the fundamental theorem of calculus and Jensen’s inequality ensure for all $k \in {\mathbb {N}}$, $x,y \in {\mathbb {R}}$ that

$$\begin{aligned} | x^k - y^k |&= \left| \int _0^1 k \left( y + r\left( x-y \right) \right) ^{(k-1)} \left( x-y \right) dr \right| \\&\le k \left| x-y \right| \int _0^1 \left| rx + \left( 1-r\right) y \right| ^{(k-1)} dr \\ {}&\le k \left| x-y \right| \int _0^1 \left( r \, | x |^{(k-1)} + \left( 1-r\right) | y |^{(k-1)} \right) dr . \end{aligned}$$

(169)

Combining this and Hölder’s inequality implies that

$$\begin{aligned}&\left\| F(v) - F(w) \right\| _H \nonumber \\&\quad = \left\| \textstyle \sum _{ k=0 }^3 a_k \left( v^k - w^k \right) \right\| _H \le \sum _{ k=1 }^{ 3 } \left| a_k \right| \Vert v^k - w^k \Vert _H \nonumber \\&\quad \le \sum _{ k=1 }^3 k \left| a_k \right| \int _0^1 \left\| | v-w | \left( r \, | v |^{(k-1)} + \left( 1-r\right) | w |^{(k-1)} \right) \right\| _H dr \nonumber \\&\quad \le \sum _{ k=1 }^3 k \left| a_k \right| \int _0^1 \Vert v-w \Vert _{ L^q( \lambda _{ (0,1) }; {\mathbb {R}}) } \left\| r \, | v |^{(k-1)} + \left( 1-r\right) | w |^{(k-1)} \right\| _{ L^{\nicefrac {2q}{(q-2)}}(\lambda _{ (0,1) }; {\mathbb {R}}) } dr \nonumber \\&\quad \le \Vert v-w \Vert _{ L^q( \lambda _{ (0,1) }; {\mathbb {R}}) } \Bigg [ \left| a_1 \right| \nonumber \\&\qquad + \sum _{ k=2 }^3 k \left| a_k \right| \int _0^1 \left( r \, \Vert v \Vert _{ L^{\nicefrac {2q(k-1)}{(q-2)}}(\lambda _{ (0,1) }; {\mathbb {R}}) }^{(k-1)} + \left( 1-r\right) \Vert w \Vert _{ L^{\nicefrac {2q(k-1)}{(q-2)}}(\lambda _{ (0,1) }; {\mathbb {R}}) }^{(k-1)} \right) dr \Bigg ] .\nonumber \\ \end{aligned}$$

(170)

Again Hölder’s inequality therefore demonstrates that

$$\begin{aligned}&\Vert F(v) - F(w) \Vert _H \\ {}&\quad \le \Vert v-w \Vert _{ L^q( \lambda _{ (0,1) }; {\mathbb {R}}) } \Bigg [ \left| a_1 \right| + \frac{1}{2} \sum _{ k=2 }^3 k \left| a_k \right| \left( \Vert v \Vert _{ L^{\nicefrac {2q(k-1)}{(q-2)}}(\lambda _{ (0,1) }; {\mathbb {R}}) }^{(k-1)} \right. \\&\left. \qquad + \Vert w \Vert _{ L^{\nicefrac {2q(k-1)}{(q-2)}}(\lambda _{ (0,1) }; {\mathbb {R}}) }^{(k-1)} \right) \Bigg ] \\ {}&\quad \le \Vert v-w \Vert _{ L^q( \lambda _{ (0,1) }; {\mathbb {R}}) } \Bigg [ \left| a_1 \right| + \frac{1}{2} \sum _{ k=2 }^3 k \left| a_k \right| \left( \Vert v \Vert _{ L^q( \lambda _{ (0,1) }; {\mathbb {R}}) }^{(k-1)} + \Vert w \Vert _{ L^q( \lambda _{ (0,1) }; {\mathbb {R}}) }^{(k-1)} \right) \Bigg ] \\ {}&\quad \le \frac{1}{2} \Vert v-w \Vert _{ L^q( \lambda _{ (0,1) }; {\mathbb {R}}) } \left[ \max _{ j \in \{1,2,3\} } \left| a_j \right| \right] \sum _{ k=1 }^3 k \left( \Vert v \Vert _{ L^q( \lambda _{ (0,1) }; {\mathbb {R}}) }^{(k-1)} + \Vert w \Vert _{ L^q( \lambda _{ (0,1) }; {\mathbb {R}}) }^{(k-1)} \right) \\ {}&\quad \le 3 \Vert v-w \Vert _{ L^q( \lambda _{ (0,1) }; {\mathbb {R}}) } \left[ \max _{ j \in \{1,2,3\} } \left| a_j \right| \right] \left( \max \!\left\{ 1, \Vert v \Vert _{ L^q( \lambda _{ (0,1) }; {\mathbb {R}}) }^{2} \right\} \right. \\&\left. \qquad + \max \!\left\{ 1, \Vert w \Vert _{ L^q( \lambda _{ (0,1) }; {\mathbb {R}}) }^{2} \right\} \right) \\ {}&\quad \le 6 \Vert v-w \Vert _{ L^q( \lambda _{ (0,1) }; {\mathbb {R}}) } \left[ \max _{ j \in \{1,2,3\} } \left| a_j \right| \right] \max \!\left\{ 1, \Vert v \Vert _{ L^q( \lambda _{ (0,1) }; {\mathbb {R}}) }^{2}, \Vert w \Vert _{ L^q( \lambda _{ (0,1) }; {\mathbb {R}}) }^{2} \right\} . \end{aligned}$$

(171)

This completes the proof of Lemma 6.2. $\square$

6.3 Properties of stochastic convolutions

In this subsection we present a few elementary regularity and approximation results for stochastic convolutions; see Lemmas 6.3–6.7 and Corollary 6.8 below. Similar regularity and approximation results for stochastic convolutions can, e.g., be found in Hutzenthaler et al. [21, Lemma 5.6, Corollary 5.8, and Lemma 5.9]. Proofs of Lemmas 6.3–6.7 and Corollary 6.8 can, e.g., be found in the extended arXiv version of this article [2, Section 6.3].

Lemma 6.3

Assume the setting in Sect. 6.1, let $\gamma \in [0, \nicefrac {1}{4})$, $\beta \in (\nicefrac {1}{4},\nicefrac {1}{2}-\gamma )$, $B \in HS( H, H_{-\beta } )$, and let $\varphi :[0,T] \rightarrow [0,T]$ be a ${\mathcal {B}}([0,T]) / {\mathcal {B}}([0,T])$-measurable function which satisfies for all $t \in [0,T]$ that $\varphi (t) \le t$. Then there exists an up to indistinguishability unique stochastic process $O :[0,T] \times \Omega \rightarrow H_{\gamma }$ with continuous sample paths which satisfies for all $t \in [0,T]$ that

$$\begin{aligned}{}[ O_t ]_{ {\mathbb {P}}, {\mathcal {B}}(H) } = \int _0^t e^{(t-\varphi (s))A} B \, dW_s . \end{aligned}$$

(172)

Lemma 6.4

Assume the setting in Sect. 6.1 and let $p,q \in [2,\infty )$, $\theta \in [\frac{1}{4}-\frac{1}{2q},\frac{1}{4})$, $\xi \in {\mathcal {L}}^p( {\mathbb {P}}; H_{2\theta } )$. Then there exists a stochastic process $O :[0,T] \times \Omega \rightarrow L^q(\lambda _{(0,1)};{\mathbb {R}})$ with continuous sample paths which satisfies

• (i) that for all $t \in [0,T]$ we have that $[ O_t - e^{tA} \xi ]_{ {\mathbb {P}}, {\mathcal {B}}(H) } = \int _0^t e^{(t-s)A} \, dW_s$ and

• (ii) that

  $$\begin{aligned}&\sup _{ N \in {\mathbb {N}}} \sup _{ 0 \le s< t \le T } \left( \frac{ \Vert P_{N} (O_t - O_{s} ) \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; L^{q}( \lambda _{(0,1)} ; {\mathbb {R}}) ) } }{ (t-s)^{\theta } } \right) \\&\qquad + \sup _{ N \in {\mathbb {N}}} \sup _{ t \in [0,T] } \big ( N^{2\theta } \, \Vert O_t - P_{N} O_t \Vert _{ {\mathcal {L}}^p( {\mathbb {P}}; L^{q}( \lambda _{(0,1)} ; {\mathbb {R}}) ) } \big ) < \infty . \end{aligned}$$

  (173)

Lemma 6.5

Assume the setting in Sect. 6.1 and let $p \in [2,\infty )$, $\theta \in [0,\nicefrac {1}{4})$, $\xi \in {\mathcal {L}}^p( {\mathbb {P}}; H_{\theta } )$. Then there exist stochastic processes ${\mathfrak {O}}_{}^{M,N} :[0,T] \times \Omega \rightarrow P_N(H)$, $M, N \in {\mathbb {N}}$, with continuous sample paths which satisfy

• (i) that for all $t \in [0,T]$, $M, N \in {\mathbb {N}}$ we have that $[ {\mathfrak {O}}_{t}^{M,N} - P_{N} e^{tA} \xi ]_{ {\mathbb {P}}, {\mathcal {B}}(H) } = \int _0^t P_{N} e^{(t- \lfloor s \rfloor _{T\!/\!M} )A} \, dW_s$ and

• (ii) that $\sup _{ \gamma \in [0,\theta ] } \sup _{ M,N \in {\mathbb {N}}} \sup _{ t \in [0,T] } {\mathbb {E}}\big [ \Vert {\mathfrak {O}}_{t}^{M,N} \Vert _{ H_{\gamma } }^p \big ] < \infty$.

Lemma 6.6

Assume the setting in Sect. 6.1, let $p \in [1,\infty )$, $\xi \in \cup _{ r \in (\nicefrac {1}{4}, \infty ) } {\mathcal {L}}^p( {\mathbb {P}}; H_r )$, and let ${\mathfrak {O}}_{}^{M,N} :[0,T] \times \Omega \rightarrow P_N(H)$, $M,N \in {\mathbb {N}}$, be stochastic processes with continuous sample paths which satisfy for all $M, N \in {\mathbb {N}}$, $t \in [0,T]$ that

$$\begin{aligned} {[}{\mathfrak {O}}_{t}^{M,N} - P_N e^{tA} \xi ]_{ {\mathbb {P}}, {\mathcal {B}}(H) } = \int _0^t P_N e^{(t- \lfloor s \rfloor _{T\!/\!M} )A} \, dW_s . \end{aligned}$$

(174)

Then

$$\begin{aligned} \sup _{ M,N \in {\mathbb {N}}} {\mathbb {E}}\big [ \textstyle \sup _{ t \in [0,T] } \Vert {\mathfrak {O}}_{t}^{M,N} \Vert _{ L^{\infty }( \lambda _{ (0,1) } ; {\mathbb {R}}) }^p \big ] < \infty . \end{aligned}$$

(175)

Lemma 6.7

Assume the setting in Sect. 6.1, let $p,q \in [2,\infty )$, $\xi \in {\mathcal {L}}^p( {\mathbb {P}}; L^q( \lambda _{ (0,1) }; {\mathbb {R}}) )$, $\theta \in [0,\nicefrac {1}{4})$, and let $O :[0,T] \times \Omega \rightarrow L^q( \lambda _{ (0,1) }; {\mathbb {R}})$ and ${\mathfrak {O}}_{}^{M,N} :[0,T] \times \Omega \rightarrow P_N(H)$, $M, N \in {\mathbb {N}}$, be stochastic processes which satisfy for all $t \in [0,T]$, $M,N \in {\mathbb {N}}$ that $[ O_t - e^{tA} \xi ]_{ {\mathbb {P}}, {\mathcal {B}}(H) } = \int _0^t e^{(t-s)A} \, dW_s$ and $[ {\mathfrak {O}}_{t}^{M,N} - P_{N} e^{tA} \xi ]_{ {\mathbb {P}}, {\mathcal {B}}(H) } = \int _0^t P_{N} e^{(t- \lfloor s \rfloor _{T\!/\!M} )A} \, dW_s$. Then we have that

$$\begin{aligned} \sup _{ M,N \in {\mathbb {N}}} \sup _{ t \in [0,T] } \left[ M^{\theta } \left( {\mathbb {E}}\Big [ \Vert P_N O_t - {\mathfrak {O}}_{t}^{M,N} \Vert _{ L^q( \lambda _{ (0,1) } ; {\mathbb {R}}) }^p \Big ] \right) ^{\!\nicefrac {1}{p}} \right] < \infty . \end{aligned}$$

(176)

Corollary 6.8

Assume the setting in Sect. 6.1 and let $p,q \in [2,\infty )$, $\theta \in [\nicefrac {1}{4}-\nicefrac {1}{2q},\nicefrac {1}{4})$, $\xi \in \cup _{ r \in (\nicefrac {1}{4},\infty ) \cap [2\theta ,\infty ) } {\mathcal {L}}^p( {\mathbb {P}}; H_r )$. Then there exist stochastic processes $O :[0,T] \times \Omega \rightarrow L^{q}( \lambda _{(0,1)} ; {\mathbb {R}})$ and ${\mathfrak {O}}_{}^{M,N} :[0,T] \times \Omega \rightarrow P_N(H)$, $M, N \in {\mathbb {N}}$, with continuous sample paths which satisfy

• (i) that for all $t \in [0,T]$ we have that $[ O_t - e^{tA} \xi ]_{ {\mathbb {P}}, {\mathcal {B}}(H) } = \int _0^t e^{(t-s)A} \, dW_s$,

• (ii) that for all $M, N \in {\mathbb {N}}$, $t \in [0,T]$ we have that $[ {\mathfrak {O}}_{t}^{M,N} - P_{N} e^{tA} \xi ]_{ {\mathbb {P}}, {\mathcal {B}}(H) } = \int _0^t P_{N} e^{(t- \lfloor s \rfloor _{T\!/\!M} )A} \, dW_s$, and

• (iii) that for all $\gamma \in [0,2\theta ] \cap [0,\nicefrac {1}{4})$ we have that

  $$\begin{aligned}&\sup _{ M,N \in {\mathbb {N}}} \sup _{ t \in [0,T] } \left[ M^{\theta } \! \left( {\mathbb {E}}\big [ \Vert P_{N} (O_t - O_{ \lfloor t \rfloor _{T\!/\!M} } ) \Vert _{ L^{q}( \lambda _{(0,1)} ; {\mathbb {R}}) }^p \right. \right. \\&\left. \left. \qquad + \Vert P_{N} O_t - {\mathfrak {O}}_{t}^{M,N} \Vert _{ L^{q}( \lambda _{(0,1)} ; {\mathbb {R}}) }^p \big ] \right) ^{\!\nicefrac {1}{p}} \right] \\ {}&\qquad + \sup _{ M,N \in {\mathbb {N}}} \sup _{ t \in [0,T] } {\mathbb {E}}\big [ \Vert {\mathfrak {O}}_{t}^{M,N} \Vert _{ H_{\gamma } }^p \big ] + \sup _{ N \in {\mathbb {N}}} \sup _{ t \in [0,T] } N^{2\theta } \! \left( {\mathbb {E}}\big [ \Vert O_t - P_{N} O_t \Vert _{ L^{q}( \lambda _{(0,1)} ; {\mathbb {R}}) }^p \big ] \right) ^{\!\nicefrac {1}{p}} \\ {}&\qquad + \sup _{ M,N \in {\mathbb {N}}} {\mathbb {E}}\big [ {\textstyle \sup _{ t \in [0,T] } } \Vert {\mathfrak {O}}_{t}^{M,N} \Vert _{ L^{\infty }( \lambda _{ (0,1) } ; {\mathbb {R}}) }^p \big ] < \infty . \end{aligned}$$

  (177)

6.4 Strong convergence rates for numerical approximations of stochastic Allen–Cahn equations

Lemma 6.9

Assume the setting in Sect. 6.1, let $p \in [2,\infty )$, $\vartheta \in (0,\infty )$, $\theta \in [\nicefrac {1}{6}, \nicefrac {1}{4} )$, $\gamma \in (\nicefrac {1}{6}, \nicefrac {1}{4})$, $\chi \in (0, \nicefrac {\gamma }{3}-\nicefrac {1}{18} ]$, $\xi \in \cup _{ r \in (\nicefrac {1}{4},\infty ) \cap [2\theta ,\infty ) } {\mathcal {L}}^{16p\max \{3,\vartheta \}}({\mathbb {P}}; H_r )$, let $X :[0,T] \times \Omega \rightarrow L^{6}( \lambda _{(0,1)}; {\mathbb {R}})$ be a stochastic process with continuous sample paths which satisfies for all $t \in [0,T]$ that $[ X_t - e^{tA}\xi - \int _0^t e^{(t-s)A} F(X_s) \, ds ]_{ {\mathbb {P}}, {\mathcal {B}}(H) } = \int _0^t e^{(t-s)A} \, dW_s$ and $\sup _{ s \in [0,T] } {\mathbb {E}}\big [ \Vert X_s \Vert _{ L^{6}( \lambda _{(0,1)}; {\mathbb {R}}) }^{12p} \big ] < \infty$, and let ${\mathfrak {X}}_{}^{M,N} :[0,T] \times \Omega \rightarrow H_{\gamma }$, $M,N \in {\mathbb {N}}$, and ${\mathfrak {O}}_{}^{M,N} :[0,T] \times \Omega \rightarrow P_N(H)$, $M,N \in {\mathbb {N}}$, be stochastic processes which satisfy for all $M,N \in {\mathbb {N}}$, $t \in [0,T]$ that $[ {\mathfrak {O}}_{t}^{M,N} - P_N e^{tA} \xi ]_{ {\mathbb {P}}, {\mathcal {B}}(H) } = \int _0^t P_{ N } e^{ (t- \lfloor s \rfloor _{T\!/\!M} ) A } \, dW_s$ and

$$\begin{aligned} {\mathbb {P}}\Big ( {\mathfrak {X}}_{t}^{M,N} = \textstyle \int _0^t P_N \, e^{(t-s)A} \, \mathbb {1}_{ \{ \Vert {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,N} \Vert _{ H_{\gamma } } + \Vert {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,N} \Vert _{ H_{\gamma } } \le (M/T)^{\chi } \} }^{\Omega } \, F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,N} ) \, ds + {\mathfrak {O}}_{t}^{M,N} \Big ) = 1 . \end{aligned}$$

(178)

Then we have

• (i) that $\sup _{ M,N \in {\mathbb {N}}} \sup _{ t \in [0,T] } {\mathbb {E}}\big [ \Vert {\mathfrak {X}}_{t}^{M,N} \Vert _{ H_{\gamma } }^{4p\max \{3,\vartheta \}} \big ] < \infty$ and

• (ii) that there exists a real number $C \in {\mathbb {R}}$ such that for all $M,N \in {\mathbb {N}}$ we have that

  $$\begin{aligned} \sup _{ t \in [0,T] } \left( {\mathbb {E}}\big [ \Vert X_t - {\mathfrak {X}}_{t}^{M,N} \Vert _{ H }^p \big ] \right) ^{\!\nicefrac {1}{p}} \le C ( M^{-\min \{\vartheta \chi ,\theta \}} + N^{-2\theta } ) . \end{aligned}$$

  (179)

Proof of Lemma 6.9

Throughout this proof let $(V, \left\| \cdot \right\| \!_V) = ( L^{6}(\lambda _{(0,1)}; {\mathbb {R}}), \left\| \cdot \right\| \!_{ L^{6}(\lambda _{(0,1)}; {\mathbb {R}}) } )$ and let $\epsilon \in (0,1)$, be real numbers. Note that, e.g., [4, Lemma 6.7] proves that for all $v, w \in L^{18}(\lambda _{ (0,1) }; {\mathbb {R}})$ with $v-w \in H_1$ we have that

$$\begin{aligned}&\langle v-w, A(v-w) + F(v) - F(w) \rangle _H \\&\quad \le 2 \max \{ 1, \nicefrac {1}{(|a_3| + \mathbb {1}_{\{0\}}^{{\mathbb {R}}}(a_3))} \} \max \!\left\{ 1, \max _{ k \in \{ 1,2\} } \big [ k | a_k | \big ]^{2} \right\} \Vert v-w \Vert _H^2 . \end{aligned}$$

(180)

The fact that $H_1 \subseteq L^{18}(\lambda _{ (0,1) }; {\mathbb {R}})$ therefore implies that for all $v,w \in H_1$ we have that

(181)

Combining this, Lemma 6.1 (with $\epsilon =\epsilon$, $c=C$ in the notation of Lemma 6.1) and Lemma 6.2 ensures that there exit a real number $c \in (0,\infty )$ such that

• (a) we have for all $N \in {\mathbb {N}}$, $v,w \in P_N(H)$ that

  $$\begin{aligned}&\langle v-w, Av + F(v) - Aw - F(w) \rangle _H \le c \Vert v-w \Vert _H^2 , \end{aligned}$$

  (182)

• (b) we have for all $N \in {\mathbb {N}}$, $v \in P_N(H)$, $w \in {\mathcal {C}}( [0,T], H_1 )$, $t \in [0,T]$ that

  $$\begin{aligned}&\langle v, P_N F(v + w_t) \rangle _{H_{\nicefrac {1}{2}}} + C \left[ \sup _{ s \in [0,T] } \Vert w_s \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + 1 \right] \langle v, F(v + w_t) \rangle _H \\&\quad \le \epsilon \Vert v \Vert _{ H_1 }^2 + c \Vert v \Vert _{ H_{\nicefrac {1}{2}} }^2 + c \, C \left[ \sup _{ s \in [0,T] } \Vert w_s \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + 1 \right] \Vert v \Vert _{ H }^2 \\&\qquad + c \! \left[ \sup _{ s \in [0,T] } \Vert w_s \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^{8} + 1 \right] , \end{aligned}$$

  (183)

  and

• (c) we have for all $N \in {\mathbb {N}}$, $v,w \in P_N(H)$ that

  $$\begin{aligned} \Vert F(v) - F(w) \Vert _H^2 \le c \Vert v - w \Vert _V^2 \, \big ( 1 + \Vert v \Vert _V^{4} + \Vert w \Vert _V^{4} \big ) . \end{aligned}$$

  (184)

Moreover, note that Corollary 6.8 (with $p=16p\max \{3,\vartheta \}$, $q=6$, $\theta =\theta$, $\xi =\xi$ in the notation of Corollary 6.8) and the fact that $2\theta > \gamma$ imply that there exist stochastic processes $O :[0,T] \times \Omega \rightarrow V$ and $\tilde{{\mathfrak {O}}}_{}^{M,N} :[0,T] \times \Omega \rightarrow P_N(H)$, $M,N \in {\mathbb {N}}$, with continuous sample paths which satisfy that

$$\begin{aligned}&\sup _{ M,N \in {\mathbb {N}}} \sup _{ t \in [0,T] } \Big ( M^{\theta } \big \Vert \Vert P_{N} (O_t - O_{ \lfloor t \rfloor _{T\!/\!M} } ) \Vert _{ V } + \Vert P_{N} O_t - \tilde{{\mathfrak {O}}}_{t}^{M,N} \Vert _{ V } \big \Vert _{ {\mathcal {L}}^{16p\max \{3, \vartheta \}}( {\mathbb {P}}; {\mathbb {R}}) } \Big ) \\&\qquad + \sup _{ M,N \in {\mathbb {N}}} \sup _{ t \in [0,T] } \big \Vert \Vert \tilde{{\mathfrak {O}}}_{t}^{M,N} \Vert _{ H_{\gamma } } + N^{2\theta } \Vert O_t - P_{N} O_t \Vert _{ V } \big \Vert _{ {\mathcal {L}}^{16p\max \{3, \vartheta \}}( {\mathbb {P}}; {\mathbb {R}}) } \\ {}&\qquad + \sup _{ M,N \in {\mathbb {N}}} \big \Vert {\textstyle \sup _{ t \in [0,T] } } \Vert \tilde{{\mathfrak {O}}}_{t}^{M,N} \Vert _{ L^{\infty }( \lambda _{ (0,1) } ; {\mathbb {R}}) } \big \Vert _{ {\mathcal {L}}^{16p\max \{3, \vartheta \}}({\mathbb {P}}; {\mathbb {R}}) } < \infty , \end{aligned}$$

(185)

that for all $t \in [0,T]$ we have that

$$\begin{aligned} {[} O_t - e^{tA} \xi ]_{ {\mathbb {P}}, {\mathcal {B}}(H) }&= \textstyle \int _0^t e^{(t-s)A} \, dW_s, \end{aligned}$$

(186)

and that for all $t \in [0,T]$, $M,N \in {\mathbb {N}}$ we have that

$$\begin{aligned} {[} \tilde{{\mathfrak {O}}}_{t}^{M,N} - P_N \, e^{tA} \xi ]_{ {\mathbb {P}}, {\mathcal {B}}(H) }&= \textstyle \int _0^t P_N \, e^{(t- \lfloor s \rfloor _{T\!/\!M} )A} \, dW_s . \end{aligned}$$

(187)

Observe that (186) and the fact that $\forall \, t \in [0,T]$, $\forall \, M,N \in {\mathbb {N}}:{\mathbb {P}}( {\mathfrak {O}}_{t}^{M,N} = \tilde{{\mathfrak {O}}}_{t}^{M,N} ) = 1$ guarantee for all $t \in [0,T]$, $M,N \in {\mathbb {N}}$ that

$$\begin{aligned}&{\mathbb {P}}\Big ( X_t = \textstyle \int _0^t e^{(t-s)A} F(X_s) \, ds + O_t \Big ) \\ {}&\quad = {\mathbb {P}}\Big ( {\mathfrak {X}}_{t}^{M,N} = \textstyle \int _0^t P_N \, e^{(t-s)A} \, \mathbb {1}_{ \{ \Vert {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,N} \Vert _{ H_{\gamma } } + \Vert \tilde{{\mathfrak {O}}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,N} \Vert _{ H_{\gamma } } \le (M/T)^{\chi } \} }^{\Omega } \, \\&\qquad F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,N} ) \, ds + \tilde{{\mathfrak {O}}}_{t}^{M,N} \Big ) = 1 . \end{aligned}$$

(188)

Combining (182)–(184) and (185)–(188) allows us to apply Corollary 5.6 (with $H = H$, ${\mathbb {H}}= \{ e_k :k \in {\mathbb {N}}\}$, $T = T$, $c = c$, $\varphi = 4$, $\epsilon = \epsilon$, $\rho = \nicefrac {1}{6}$, $\gamma = \gamma$, $\chi = \chi$, ${\mathcal {D}}= \{ \{ e_1 \}, \{ e_1, e_2 \}, \{ e_1, e_2, e_3 \}, \ldots \}$, $\mu (e_N) = -\nu \pi ^2 N^2$, $A = A$, $H_r = H_r$, $V = V$, $F = F$, $\phi = C([0,T], H_1) \ni w \mapsto C [ \sup _{ t \in [0,T] }$ $\Vert w_t \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^4 + 1 ] \in [0,\infty )$, $\Phi = C([0,T], H_1) \ni w \mapsto c [ \sup _{ t \in [0,T] } \Vert w_t \Vert _{ L^{\infty }( \lambda _{(0,1)} ; {\mathbb {R}}) }^8 + 1 ] \in [0,\infty )$, $P_{\{ e_1, e_2, \ldots , e_N \}}(v) = \sum _{ k=1 }^N \langle e_k,v \rangle _H \, e_k$, $(\Omega , {\mathcal {F}}, {\mathbb {P}}) = (\Omega , {\mathcal {F}}, {\mathbb {P}})$, $X = X$, $O = O$, ${\mathfrak {O}}^{M,\{ e_1, e_2, \ldots , e_N \}} = [0,T] \times \Omega \ni (\omega ,t) \mapsto \tilde{{\mathfrak {O}}}_{t}^{M,N}(\omega ) \in H_1$, ${\mathfrak {X}}^{M,\{ e_1, e_2, \ldots , e_N \}} = {\mathfrak {X}}_{}^{M,N}$, $\theta = \theta$, $\vartheta = \vartheta$, $p = p$, $\varrho = \theta$ for $N \in {\mathbb {N}}$, $r \in {\mathbb {R}}$, $v \in H$ in the notation of Corollary 5.6) to obtain that item (i) holds and that there exists a real number $K \in (0,\infty )$ such that for all $M, N \in {\mathbb {N}}$ we have that

$$\begin{aligned}&\sup _{ t \in [0,T] } \Vert X_t - {\mathfrak {X}}_{t}^{M,N} \Vert _{ {\mathcal {L}}^p({\mathbb {P}}; H) } \\&\quad \le K \left[ M^{ -\min \{ \vartheta \chi , \theta \} } + \Vert (-A)^{-\theta } (Id _H - P_N) \Vert _{ L(H) } + \sup _{ t \in [0,T] } \Vert O_t - P_N O_t \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}}; V) } \right] . \end{aligned}$$

(189)

The fact that

$$\begin{aligned} \forall \, N \in {\mathbb {N}}:\Vert (-A)^{-\theta } (Id _H - P_N) \Vert _{ L(H) } = (\nu \pi ^2 (N+1)^2)^{-\theta } \end{aligned}$$

(190)

hence yields that for all $M, N \in {\mathbb {N}}$ we have that

$$\begin{aligned}&\sup _{ t \in [0,T] } \Vert X_t - {\mathfrak {X}}_{t}^{M,N} \Vert _{ {\mathcal {L}}^p({\mathbb {P}}; H) } \\&\quad \le K \left[ M^{ -\min \{ \vartheta \chi , \theta \} } + N^{-2\theta } \left( \frac{ N^{2\theta } }{ \nu ^{\theta } \pi ^{2\theta } (N+1)^{2\theta } } \right. \right. \\&\left. \left. \qquad + \sup _{ t \in [0,T] } \left[ N^{2\theta } \Vert O_t - P_N O_t \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}}; V) } \right] \right) \right] \\&\quad \le K \left[ M^{ -\min \{ \vartheta \chi , \theta \} } + N^{-2\theta } \left( \frac{ 1 }{ \nu ^{\theta } \pi ^{2\theta } } + \sup _{ t \in [0,T] } \left[ N^{2\theta } \Vert O_t - P_N O_t \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}}; V) } \right] \right) \right] \\&\quad \le K \max \!\left\{ 1, \frac{1}{\nu ^{\theta }} + \sup _{ t \in [0,T] } \left[ N^{2\theta } \Vert O_t - P_N O_t \Vert _{ {\mathcal {L}}^{2p}({\mathbb {P}}; V) } \right] \right\} \left[ M^{ -\min \{ \vartheta \chi , \theta \} } + N^{-2\theta } \right] . \end{aligned}$$

(191)

Combining this with (185) completes the proof of Lemma 6.9. $\square$

Corollary 6.10

Assume the setting in Sect. 6.1, let $\xi \in \cap _{ p\in [1,\infty ) } {\mathcal {L}}^{p}({\mathbb {P}}; H_{\nicefrac {1}{2}})$, $\gamma \in (\nicefrac {1}{6}, \nicefrac {1}{4} )$, $\chi \in (0, \nicefrac {\gamma }{3} - \nicefrac {1}{18} ]$, and let ${\mathfrak {X}}_{}^{M,N} :[0,T] \times \Omega \rightarrow P_N(H)$, $M,N \in {\mathbb {N}}$, and ${\mathfrak {O}}_{}^{M,N} :[0,T] \times \Omega \rightarrow P_N(H)$, $M,N \in {\mathbb {N}}$, be stochastic processes which satisfy for all $M,N \in {\mathbb {N}}$, $t \in [0,T]$ that $[ {\mathfrak {O}}_{t}^{M,N} - P_N e^{tA} \xi ]_{ {\mathbb {P}}, {\mathcal {B}}(H) } = \int _0^t P_{ N } e^{ (t- \lfloor s \rfloor _{T\!/\!M} ) A } \, dW_s$ and

$$\begin{aligned} {\mathbb {P}}\Big ( {\mathfrak {X}}_{t}^{M,N}&\displaystyle = \int _0^t P_N \, e^{(t-s)A} \, \mathbb {1}_{ \{ \Vert {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,N} \Vert _{ H_{\gamma } } + \Vert {\mathfrak {O}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,N} \Vert _{ H_{\gamma } } \le (M/T)^{\chi } \} }^{\Omega } \, F( {\mathfrak {X}}_{ \lfloor s \rfloor _{T\!/\!M} }^{M,N} ) \, ds + {\mathfrak {O}}_{t}^{M,N} \Big ) = 1 . \end{aligned}$$

(192)

Then

• (i) we have that there exists an up to indistinguishability unique stochastic process $X :[0,T] \times \Omega \rightarrow L^{6}( \lambda _{(0,1)}; {\mathbb {R}})$ with continuous sample paths which satisfies for all $t \in [0,T]$, $p \in (0,\infty )$ that $\sup _{ s \in [0,T] } {\mathbb {E}}\big [ \Vert X_s \Vert _{ L^{6}( \lambda _{(0,1)}; {\mathbb {R}}) }^p \big ] < \infty$ and

  $$\begin{aligned}&\displaystyle \big [ X_t - e^{tA} \xi -\int _0^t e^{(t-s)A} F(X_s) \, ds \big ]_{ {\mathbb {P}}, {\mathcal {B}}(H) } = \textstyle \int _0^t e^{(t-s)A} \, dW_s , \end{aligned}$$

  (193)

• (ii) we have for all $p \in (0,\infty )$ that $\sup _{ r \in (-\infty ,\gamma ] } \sup _{ M, N \in {\mathbb {N}}} \sup _{ t \in [0,T] } {\mathbb {E}}\big [ \Vert {\mathfrak {X}}_{t}^{M,N} \Vert _{ H_{r} }^p \big ] < \infty$, and

• (iii) we have for all $p \in (0,\infty )$, $r \in [0,\nicefrac {1}{4})$ that there exists a real number $C \in {\mathbb {R}}$ such that for all $M,N \in {\mathbb {N}}$ it holds that

  $$\begin{aligned} \sup _{ t \in [0,T] } \left( {\mathbb {E}}\big [ \Vert X_t - {\mathfrak {X}}_{t}^{M,N} \Vert _{ H }^p \big ] \right) ^{\!\nicefrac {1}{p}} \le C ( M^{-r} + N^{-2r} ) . \end{aligned}$$

  (194)

Proof of Corollary 6.10

Note that under the assumptions of Corollary 6.10 it is well known (cf., e.g., [30, Theorem 3.4.1 (ii) in Section 3.4, Lemma 2.4.2 in Section 2, and Definition 2.7 in Section 2], [22, Lemma 28 in Section 3.2], Lemma 6.2, the hypothesis that $\xi \in \cap _{ p\in [1,\infty ) } {\mathcal {L}}^{p}({\mathbb {P}}; H_{\nicefrac {1}{2}})$, and [12, (A.46) in Section A.5.2]) that there exist stochastic processes ${\tilde{X}}_q :[0,T] \times \Omega \rightarrow L^{q}( \lambda _{ (0,1) }; {\mathbb {R}})$, $q \in \{6, 7, 8,\ldots \}$, with continuous sample paths which satisfy for all $t \in [0,T]$, $q \in \{6, 7, 8,\ldots \}$ that $\sup _{ s \in [0,T] } {\mathbb {E}}\big [ \Vert {\tilde{X}}_{q,s} \Vert _{ L^{q}( \lambda _{ (0,1) }; {\mathbb {R}}) }^q \big ] < \infty$ and

$$\begin{aligned} \big [ {\tilde{X}}_{q,t} - e^{tA} \xi - \int _0^t e^{(t-s)A} F({\tilde{X}}_{q,s}) \, ds \big ]_{ {\mathbb {P}}, {\mathcal {B}}(H) } = \int _0^t e^{(t-s)A} \, dW_s . \end{aligned}$$

(195)

Combining this with (192), the assumption that $\xi \in \cap _{ p\in [1,\infty ) } {\mathcal {L}}^{p}({\mathbb {P}}; H_{\nicefrac {1}{2}})$, and, e.g., Lemma 2.2 in Andersson et al. [1] allows us to apply Lemma 6.9 (with $p = p$, $\vartheta = \vartheta$, $\theta = r$, $\xi = \xi$, $\gamma = \gamma$, $\chi = \chi$, $X = [0,T] \times \Omega \ni (t,\omega ) \mapsto {\tilde{X}}_{p,t}(\omega ) \in L^{6}( \lambda _{ (0,1) }; {\mathbb {R}})$, ${\mathfrak {X}}_{}^{M,N} = [0,T] \times \Omega \ni (t,\omega ) \mapsto {\mathfrak {X}}_{t}^{M,N}(\omega ) \in H_{\gamma }$, ${\mathfrak {O}}_{}^{M,N} = {\mathfrak {O}}_{}^{M,N}$ for $p \in \{6, 7, 8, \ldots \}$, $\vartheta \in [\nicefrac {r}{\chi }, \infty )$, $r \in [\nicefrac {1}{6}, \nicefrac {1}{4})$, $M,N \in {\mathbb {N}}$ in the notation of Lemma 6.9) to obtain that there exists a function $C :[2,\infty ) \times [\nicefrac {1}{6},\nicefrac {1}{4}) \rightarrow {\mathbb {R}}$ such that for all $p \in \{6, 7, 8, \ldots \}$, $r \in [\nicefrac {1}{6},\nicefrac {1}{4})$, $M,N \in {\mathbb {N}}$ we have that

$$\begin{aligned} \textstyle \sup _{ t \in [0,T] } \Vert {\tilde{X}}_{p,t} - {\mathfrak {X}}_{t}^{M,N} \Vert _{ {\mathcal {L}}^p({\mathbb {P}};H) } \le C_{p,r} ( M^{-r} + N^{-2r} ) . \end{aligned}$$

(196)

Next observe that the triangle inequality ensures that for all $p_1, p_2 \in \{6, 7, 8, \ldots \}$ with $p_1 \le p_2$ we have that

$$\begin{aligned}&\textstyle \sup _{ t \in [0,T] } \Vert {\tilde{X}}_{p_1,t} - {\tilde{X}}_{p_2,t} \Vert _{ {\mathcal {L}}^{p_1}({\mathbb {P}};H) } \\&\quad \le \textstyle \limsup _{ M \rightarrow \infty } \textstyle \limsup _{ N \rightarrow \infty } \textstyle \sup _{ t \in [0,T] } \left[ \Vert {\tilde{X}}_{p_1,t} - {\mathfrak {X}}_{t}^{M,N} \Vert _{ {\mathcal {L}}^{p_1}({\mathbb {P}};H) } \right. \\&\left. \quad + \Vert {\tilde{X}}_{p_2,t} - {\mathfrak {X}}_{t}^{M,N} \Vert _{ {\mathcal {L}}^{p_1}({\mathbb {P}};H) } \right] . \end{aligned}$$

(197)

Hölder’s inequality and (196) hence prove that for all $p_1, p_2 \in \{6,7,8, \ldots \}$, $r \in (\nicefrac {1}{6},\nicefrac {1}{4})$ with $p_1 \le p_2$ we have that

$$\begin{aligned}&\textstyle \sup _{ t \in [0,T] } \Vert {\tilde{X}}_{p_1,t} - {\tilde{X}}_{p_2,t} \Vert _{ {\mathcal {L}}^{p_1}({\mathbb {P}};H) } \\&\quad \le C_{p_1,r} \textstyle \limsup _{ M \rightarrow \infty } \textstyle \limsup _{ N \rightarrow \infty } \left[ M^{-r} + N^{-2r} \right] \\&\qquad + C_{p_2,r} \textstyle \limsup _{ M \rightarrow \infty } \textstyle \limsup _{ N \rightarrow \infty } \left[ M^{-r} + N^{-2r} \right] = 0 . \end{aligned}$$

(198)

This implies that for all $q_1, q_2 \in \{ 6,7,8, \ldots \}$, $t \in [0,T]$ we have that ${\mathbb {P}}( {\tilde{X}}_{q_1,t} = {\tilde{X}}_{q_2,t} ) = 1$. In the next step let ${\tilde{\Omega }} \subseteq \Omega$ be the set given by ${\tilde{\Omega }} = \{ \omega \in \Omega :( \, \forall \, q_1, q_2 \in \{ 6,7,8, \ldots \}, t \in [0,T] :{\tilde{X}}_{q_1,t}(\omega ) = {\tilde{X}}_{q_2,t}(\omega ) ) \}$ and let $X :[0,T] \times \Omega \rightarrow L^{6}( \lambda _{ (0,1) }; {\mathbb {R}})$ be the function which satisfies for all $t \in [0,T]$, $\omega \in \Omega$ that $X_t(\omega ) = {\tilde{X}}_{6,t}(\omega ) \mathbb {1}_{{\tilde{\Omega }}}(\omega )$. Note that the fact that every $q \in \{ 6,7,8, \ldots \}$ we have that ${\tilde{X}}_q :[0,T] \times \Omega \rightarrow L^{q}( \lambda _{ (0,1) }; {\mathbb {R}})$ has continuous sample paths shows that

$$\begin{aligned} {\tilde{\Omega }}&= \big \{ \omega \in \Omega :\big ( \, \forall \, q_1, q_2 \in \{ 6,7,8, \ldots \} , t \in [0,T] \cap {\mathbb {Q}} :{\tilde{X}}_{q_1,t}(\omega ) = {\tilde{X}}_{q_2,t}(\omega ) \big ) \big \} \\&= \cap _{ q_1, q_2 \in \{ 6,7,8, \ldots \} } \cap _{ t \in [0,T] \cap {\mathbb {Q}} } \big \{ {\tilde{X}}_{q_1,t}(\omega ) = {\tilde{X}}_{q_2,t}(\omega ) \big \} . \end{aligned}$$

(199)

Combining this with the fact that ${\mathbb {P}}( {\tilde{X}}_{q_1,t} = {\tilde{X}}_{q_2,t} ) = 1$ ensures that ${\tilde{\Omega }} \in {\mathcal {F}}$ and ${\mathbb {P}}( {\tilde{\Omega }} ) = 1$. Next observe that the fact that ${\tilde{X}} :[0,T] \times \Omega \rightarrow L^{6}( \lambda _{ (0,1) }; {\mathbb {R}})$ has continuous sample paths demonstrates that X has continuous sample paths. Moreover, note that the fact that for all $t \in [0,T]$, $\omega \in \Omega$ we have that $X_t(\omega ) = {\tilde{X}}_{6,t}(\omega ) \mathbb {1}_{{\tilde{\Omega }}}(\omega )$ ensures that for all $q \in \{ 6, 7, 8, \ldots \}$ we have that ${\mathbb {P}}( \forall \, t \in [0,T] :{\tilde{X}}_{q,t} = X_t ) = 1$. Combining this with (195) demonstrates that for all $t \in [0,T]$, $p \in (0,\infty )$ we have that $\sup _{ s \in [0,T] } {\mathbb {E}}[ \Vert X_s \Vert _{ L^{6}( \lambda _{(0,1)}; {\mathbb {R}}) }^p ] < \infty$ and

$$\begin{aligned} \big [ X_t - e^{tA} \xi - \textstyle \int _0^t e^{(t-s)A} F(X_s) \, ds \big ]_{ {\mathbb {P}}, {\mathcal {B}}(H) } = \textstyle \int _0^t e^{(t-s)A} \, dW_s . \end{aligned}$$

(200)

This, the fact that $X :[0,T] \times \Omega \rightarrow L^{6}( \lambda _{ (0,1) }; {\mathbb {R}})$ has continuous sample paths, and again Lemma 6.9 (with $p = p$, $\vartheta = \vartheta$, $\theta = \theta$, $\xi = \xi$, $\gamma = \gamma$, $\chi = \chi$, $X = X$, ${\mathfrak {X}}_{}^{M,N} = [0,T] \times \Omega \ni (t,\omega ) \mapsto {\mathfrak {X}}_{t}^{M,N}(\omega ) \in H_{\gamma }$, ${\mathfrak {O}}_{}^{M,N} = {\mathfrak {O}}_{}^{M,N}$ for $p \in [2, \infty )$, $\vartheta \in [\nicefrac {\theta }{\chi }, \infty )$, $\theta \in [\nicefrac {1}{6}, \nicefrac {1}{4})$, $M,N \in {\mathbb {N}}$ in the notation of Lemma 6.9) ensures that for every stochastic processes ${\mathbf {X}} :[0,T] \times \Omega \rightarrow L^6(\lambda _{ (0,1) }; {\mathbb {R}})$ with continuous sample paths with $\forall \, t \in [0,T], p \in (0,\infty ) :\sup _{ s \in [0,T] } {\mathbb {E}}\big [ \Vert {\mathbf {X}}_s \Vert _{ L^{6}( \lambda _{(0,1)}; {\mathbb {R}}) }^p \big ]$ $< \infty$ and

$$\begin{aligned} \big [ {\mathbf {X}}_t - e^{tA} \xi - \textstyle \int _0^t e^{(t-s)A} F({\mathbf {X}}_s) \, ds \big ]_{ {\mathbb {P}}, {\mathcal {B}}(H) } = \textstyle \int _0^t e^{(t-s)A} \, dW_s \end{aligned}$$

(201)

we have that for all $p \in (0,\infty )$ it holds that $\sup _{ r \in (-\infty ,\gamma ] } \sup _{ M, N \in {\mathbb {N}}} \sup _{ t \in [0,T] } {\mathbb {E}}\big [ \Vert {\mathfrak {X}}_{t}^{M,N} \Vert _{ H_{r} }^p \big ] < \infty$ and we have that for all $p \in (0,\infty )$, $r \in [0,\nicefrac {1}{4})$ there exists a real number $C \in {\mathbb {R}}$ such that for all $M,N \in {\mathbb {N}}$ it holds that

$$\begin{aligned} \sup _{ t \in [0,T] } \left( {\mathbb {E}}\big [ \Vert {\mathbf {X}}_t - {\mathfrak {X}}_{t}^{M,N} \Vert _{ H }^p \big ] \right) ^{\!\nicefrac {1}{p}} \le C ( M^{-r} + N^{-2r} ) . \end{aligned}$$

(202)

Combining this with (200) yields that ${\mathbb {P}}( \forall \, t \in [0,T] :X_t = {\mathbf {X}}_t ) = 1$. This together with (202) establishes item (i), item (ii), and item (iii). The proof of Corollary 6.10 is thus completed. $\square$