Cubature methods for stochastic (partial) differential equations in weighted spaces

Abstract

The cubature on Wiener space method, a high-order weak approximation scheme, is established for SPDEs in the case of unbounded characteristics and unbounded test functions. We first describe a recently introduced flexible functional analytic framework, so called weighted spaces, where Feller-like properties hold. A refined analysis of vector fields on weighted spaces then yields optimal convergence rates of cubature methods for stochastic partial differential equations of Da Prato–Zabczyk type. The ubiquitous stability for the local approximation operator within the functional analytic setting is proved for SPDEs, however, in the infinite dimensional case we need a newly introduced technical assumption on weak symmetry of the cubature formula. Computational results for a cubature discretization of a spatially extended stochastic FitzHugh–Nagumo model, an SPDE model from mathematical biology, are shown, illustrating the applicability of our theory.

1 Introduction

Cubature on Wiener space, a realization of the abstract KLV high order method after Kusuoka [21] and Lyons and Victoir [24], is a weak approximation scheme for stochastic differential equations. Significant advantages in comparison to other weak approximation schemes such as Taylor methods, see Kloeden and Platen [20], are that it respects the geometry of the problem, and that at least theoretically, it is possible to reach arbitrarily high rates of convergence without requiring the calculation of higher derivatives, see Lyons and Victoir [24, Theorem 2.4, Prop. 2.5]. The concrete construction of such cubature paths of high order is still quite difficult, see Gyurkó and Lyons [15] for cubature formulas (on the Lie algebra level) up to degree 11 for a single driving Brownian motion. Cubature schemes provide a time-discretization approximating the unknown expected value of a functional of the solution process of the SPDE by an expectation of an iteratively constructed function on a high-dimensional discrete product space. Often a direct evaluation of the functional on the discrete probability space is too expensive, therefore, several methods to speed-up the evaluation of cubature schemes such as recombination, see Litterer and Lyons [23] and Schmeiser et al. [31], or tree-based branching, see Crisan and Lyons [5], have emerged. Alternatively, the functionals can be evaluated using Monte Carlo or Quasi Monte Carlo algorithms on the discrete product probability space.

The combination with Quasi Monte Carlo integration algorithms makes high-order weak approximation schemes a particularly interesting alternative to standard multi-level Monte Carlo schemes. Indeed, multi-level Monte Carlo schemes lead to complexity estimates of order ${\mathcal {O}}(\epsilon ^{-2})$, i.e., a number of operations of order $\epsilon ^{-2}$ is necessary to reach accuracy $\epsilon$, see Giles [13] and Giles and Szpruch [14]. In contrast, QMC evaluations of weak, high-order approximation schemes of order $k$ lead to complexity estimates of order (almost) ${\mathcal {O}}(\epsilon ^{-1-1/k})$, as long as the QMC integration yields optimal convergence (this in turn also depends on the dimension of integration space, which is moderate for high order methods). We therefore believe that it is worth analysing the functional analytic framework of cubature schemes in depth, i.e., we aim to construct a pool of Banach spaces of test functions and Banach spaces of characteristics flexible enough to embed relevant problems from practice.

In this work, we shall relax the regularity assumptions of the cubature method, similarly as was done in Dörsek [9] and Dörsek and Teichmann [11, 12] for the splitting approach of Ninomiya and Victoir [26]. Consider a stochastic differential equation on ${\mathbb {R}}^n$ in its Stratonovich form,

$$\begin{aligned} \mathrm{d}X^{x}_t = \sum _{j=0}^{d}V_{j}(X^{x}_t)\circ \mathrm{d}B^{j}_{t} \, . \end{aligned}$$

(1.1)

In this article ${(B^j_t)}_{t \ge 0}$, for $j=1,\ldots ,d$, always denotes the j-th component of a d-dimensional Brownian motion, running time is encoded for convenience by the zeroth component $B^0_t = t$, for $t \ge 0$, and usually $V_j : {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n$, for $j=0,\ldots ,d$ denote vector fields. A deterministic initial value is supposed, i.e. $X^x_0 = x$, for $x \in {\mathbb {R}}^n$. All initial work was based on the fundamental assumption that the vector fields $V_j:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ are bounded and $\hbox {C}^{\infty }$-bounded. This is also a typical assumption in other approximation methods for stochastic differential equations, e.g., in Talay and Tubaro [32]. Some success in relaxing these assumptions, which are rarely satisfied in practical problems, was achieved for approximations of the splitting type in Alfonsi [1] and Tanaka and Kohatsu-Higa [33]. While the first one focuses on the CIR process and the second one on Lévy driving noise, it was recognised in both works that polynomially bounded test functions are the correct context for problems with Lipschitz continuous vector fields.

Another approach was taken in Dörsek and Teichmann [11]. There, splitting schemes were analyzed on general weighted spaces, allowing in particular the approximation of Da Prato–Zabczyk stochastic partial differential equations where the drift part, the infinitesimal generator of a strongly continuous semigroup on the infinite dimensional state space, is not even continuous.

All these approaches profited from the special structure of splitting schemes, as there the stability or power boundedness of the discrete approximation operator can be shown by investigating every part separately. Instead, we follow a similar idea as was applied to the stochastic Navier–Stokes equations in Dörsek [10]. We extend the results of Bayer and Teichmann [2], where strong conditions are imposed on the vector fields, to more general coefficients and test functions. This allows us to obtain methods of order higher than 2 without having to resort to extrapolation, see Blanes and Casas [3] and Oshima et al. [27]. The weighted spaces developed originally in Röckner and Sobol [29] and used for the numerical analysis of weak approximation methods in Dörsek and Teichmann [11] are a suitable tool for our needs, and we provide a refined analysis of the vector fields defined on these spaces. This allows us to do a Taylor expansion of the cubature approximations to compute the local approximation order.

We use two different approaches for proving stability. In the finite dimensional case with sufficiently smooth vector fields, the Gronwall inequality yields the claim in a straightforward manner under a reasonable assumption of compatibility between the vector fields and the weight function. In the infinite dimensional case, we apply the method of the moving frame from Teichmann [35]. This leads to time dependent vector fields that are nonsmooth in the time component. As this makes a Taylor expansion impossible, we introduce a weak symmetry condition on cubature paths, a technical assumption usually satisfied by cubature schemes. This allows us to obtain stability not only for Da Prato–Zabczyk equations with pseudocontractive generator, but also for stochastic differential equations on infinite dimensional state spaces where the vector fields depend roughly, i.e., continuously, but not differentiably, on time.

As a numerical example, we consider a cubature discretization of degree $m=5$ corresponding to weak convergence order 2 of a stochastic FitzHugh–Nagumo model, extending the stochastic model from Tang et al. [34] spatially using methods from Tuckwell [36]. We formulate the necessary functional analytic setting, and show results of the numerical simulation of two quantities of interest that correspond to purely noise induced state changes. Our computations establish the effectivity of the proposed algorithm. It is worth pointing out that the cubature discretization of stochastic FitzHugh–Nagumo is locally deterministic, i.e., we can perform local random walk like studies within this model setting that approximate the original model of high order 2. This might be very useful in applications. To the best of our knowledge such high order random walk approximations of FitzHugh–Nagumo have been unknown.

There are many successful discretisation schemes for stochastic partial differential equations that can be applied to the stochastic FitzHugh–Nagumo model and similar equations. Jentzen and Kloeden [17] give an overview of strong and pathwise schemes. Weak approximation schemes are more difficult. Recently, it was proved in Debussche [8] that an implicit Euler scheme converges with weak rate almost 1/2 for equations driven by space–time white noise, doubling the corresponding strong rate of convergence; see also the references in Debussche [8] for more background on weak approximation schemes for stochastic partial differential equations with space–time white noise. In contrast, we restrict ourselves to finite-dimensional driving noise, but obtain the same optimal high order weak convergence as for finite-dimensional state spaces. Additionally we obtain by the cubature method itself deterministic construction recipes of typical trajectories of the model.

The paper is organised as follows. Sections 2 and 3 contain an exposition of the theory of ${\mathcal {B}}^{\psi }$ spaces, originally introduced in Röckner and Sobol [29], and explain how directional derivatives can be analysed in this setting, extending results from Dörsek and Teichmann [11, 12]. In Sect. 4, we prove stability of cubature schemes in ${\mathcal {B}}^{\psi }$ spaces under various assumptions on the vector fields, using a technical assumption of weak symmetry of the underlying cubature paths in the infinite-dimensional case. Section 5 is devoted to the convergence proofs of cubature schemes. Finally, in Sect. 6, we present numerical results for a spatially extended stochastic FitzHugh–Nagumo model.

2 ${\mathcal {B}}^{\psi }$ spaces

We recall the following definition of spaces of functions with controlled growth, see also Röckner and Sobol [29] for their use in the construction of the solution of martingale problems in infinite dimension, and Dörsek [9, 10] and Dörsek and Teichmann [11, 12] for their application to the analysis of splitting schemes for stochastic partial differential equations.

Definition 2.1

Let $(X,||\cdot ||_{X})$ be the dual space of a separable Banach space, and $\varphi :X\rightarrow (0,\infty )$ be bounded from below by some $\delta >0$. For a Banach space $(Y,||\cdot ||_{Y})$, we set

$$\begin{aligned} \hbox {B}^{\varphi }(X;Y) := \left\{ f:X\rightarrow Y:\sup _{x\in X}\varphi (x)^{-1}||f(x)||_{Y}<\infty \right\} , \end{aligned}$$

(2.1)

endowed with the $\varphi$-norm

$$\begin{aligned} ||f||_{\varphi } := \sup _{x\in X}\varphi (x)^{-1}||f(x)||_{Y}. \end{aligned}$$

(2.2)

Let $k\ge 0$. If $\varphi =(\varphi _j)_{j=0,\ldots ,k}, \varphi _j:X\rightarrow (0,\infty )$ bounded from below by some $\delta >0, j=0,\ldots ,k$, we set

$$\begin{aligned}&\hbox {B}^{\varphi }_k(X;Y) := \left\{ f\in \hbox {C}^{k}(X;Y):\sup _{x\in X}\varphi _j(x)^{-1}||D^{j} f(x)||_{L_j(X;Y)}<\infty \right. \nonumber \\&\qquad \qquad \qquad \qquad \left. \text {for } j=0,\ldots ,k \right\} . \end{aligned}$$

(2.3)

$\hbox {B}^{\varphi }_{k}(X;Y)$ is endowed with the norm

$$\begin{aligned} ||f||_{\varphi ,k} := ||f||_{\varphi _0} + \sum _{j=1}^{k}|f|_{\varphi _j,j}, \end{aligned}$$

(2.4)

where the seminorms $|\cdot |_{\varphi _j,j}$ are given by

$$\begin{aligned} |f|_{\varphi _j,j} := \sup _{x\in X}\varphi _j(x)^{-1}||D^j f(x)||_{L_j(X;Y)}. \end{aligned}$$

(2.5)

Here, $L_j(X;Y)$ denotes the space of bounded multilinear forms $a:X^j\rightarrow Y$, and is endowed with the norm

$$\begin{aligned} ||a||_{L_j(X;Y)} := \sup _{||h_i||\le 1, i=1,\ldots ,j}||a(h_1,\ldots ,h_j)||_{Y}. \end{aligned}$$

(2.6)

For simplicity, we set $L_0(X;Y):=Y$; we remark that $L_1(X;Y)$ is the space of bounded linear operators $X\rightarrow Y$, and in this case, the above norm is the usual operator norm. If $Y={\mathbb {R}}$, we define $\hbox {B}^{\varphi }(X):=\hbox {B}^{\varphi }(X;{\mathbb {R}})$ and $\hbox {B}^{\varphi }_k(X):=\hbox {B}^{\varphi }_k(X;{\mathbb {R}})$.

Definition 2.2

Let $(X,||\cdot ||_{X})$ be the dual space of a separable Banach space. A function $\varphi$ is called admissible weight function if and only if $\varphi :X\rightarrow (0,\infty )$ is such that $K_R:=\left\{ x\in X:\varphi (x)\le R \right\}$ is weak-$*$ compact for all $R>0$ and bounded from below by some $\delta > 0$.

It is called D-admissible weight function if and only if it is an admissible weight function and for every $x\in X$, there exists some $R>0$ such that $B_\varepsilon (x)\subset K_R$ for some $\varepsilon >0$, where $B_\varepsilon (x):=\left\{ y\in X:||y-x||_X\le \varepsilon \right\}$ is the closed $\varepsilon$-ball around $x$.

It is called C-admissible weight function if and only if $\varphi$ is bounded from below by some $\delta > 0$, weak-$*$ lower semicontinuous, and if for every $x\in X$, there exists some $\varepsilon >0$ such that $\varphi$ is bounded on $B_{\varepsilon }(x)$.

Remark 2.3

We do not require C-admissible weight functions to be admissible. However, $\varphi$ is D-admissible if and only if it is admissible and C-admissible.

Theorem 2.4

Let $k\in {\mathbb {N}}$, and assume that $\varphi =(\varphi _j)_{j=0,\ldots ,k}$ is a vector of C-admissible weight functions. Then, $\hbox {B}^{\varphi }_k(X;Y)$ is a Banach space.

Proof

Let $(f_n)_{n\in {\mathbb {N}}}$ be a Cauchy sequence in this space. It is clear that $f_n$ admits a pointwise limit f. Moreover, it follows that for every $x\in X$ and every closed $\varepsilon$-ball $B_{\varepsilon }(x), f_n|_{B_{\varepsilon }(x)}$ are Cauchy sequences in $\hbox {C}^k(B_{\varepsilon }(x);Y)$. But this entails that $f|_{B_{\varepsilon }(x)}\in \hbox {C}^k(B_{\varepsilon }(x);Y)$. As differentiability is a local property, we see that $f\in \hbox {C}^k(X;Y)$. The necessary estimates for f and its derivatives are now easy to see. $\square$

Definition 2.5

Let $(X,||\cdot ||_{X})$ be the dual space of a separable Banach space, its predual being $W, X=W^{*}$, and $(Y,||\cdot ||_{Y})$ a Banach space. The space of bounded smooth cylindrical functions is defined by

$$\begin{aligned}&{\mathcal {A}}(X,Y) := \bigl \{ f:X\rightarrow Y :f=g(\langle \cdot ,w_1\rangle ,\ldots ,\langle \cdot ,w_{n}\rangle ) \nonumber \\&\qquad \qquad \qquad \quad \text {for some}\;g\in \hbox {C}_b^\infty ({\mathbb {R}}^n;Y), \nonumber \\&\qquad \qquad \qquad \quad w_i\in W, i=1,\ldots ,n, n\in {\mathbb {N}} \bigr \}. \end{aligned}$$

(2.7)

Here, $\langle \cdot ,\cdot \rangle$ denotes the dual pairing of $X$ and $W$ and $\hbox {C}_b^{\infty }({\mathbb {R}}^n;Y)$ the space of infinitely often differentiable functions from $Y$ to ${\mathbb {R}}$ that are bounded with all their derivatives bounded. For $Y={\mathbb {R}}$, we set ${\mathcal {A}}(X):={\mathcal {A}}(X,{\mathbb {R}})$.

Definition 2.6

Let $(X,||\cdot ||_{X})$ be the dual space of a separable Banach space and $(Y,||\cdot ||_{Y})$ be a Banach space. Let $\psi$ be an admissible weight function on $X$.

The space ${\mathcal {B}}^{\psi }(X;Y)$ is the closure of ${\mathcal {A}}(X,Y)$ in $\hbox {B}^{\psi }(X;Y)$. For $Y={\mathbb {R}}$, we set ${\mathcal {B}}^{\psi }(X):={\mathcal {B}}^{\psi }(X;{\mathbb {R}})$.

Remark 2.7

[11, Theorem 4.2] shows that our definition of ${\mathcal {B}}^{\psi }(X)$ here agrees with our earlier definition from Dörsek and Teichmann [11, Definition 2.2]. Due to Dörsek and Teichmann [11, Theorem 2.7], the functions in ${\mathcal {B}}^{\psi }(X)$ are characterized by the property that both $f|_{K_R}\in \hbox {C}( (K_R)_{w*} )$ and

$$\begin{aligned} \lim _{R\rightarrow \infty }\sup _{x\in X\setminus K_R}\psi (x)^{-1}|f(x)|= 0. \end{aligned}$$

(2.8)

Definition 2.8

Let $(X,||\cdot ||_{X})$ be the dual space of a separable Banach space and $(Y,||\cdot ||_{Y})$ be a Banach space. Let $\psi =(\psi _j)_{j=0,\ldots ,k}$ with $\psi _j$ D-admissible weight functions for $j=0,\ldots ,k$. The space ${\mathcal {B}}^{\psi }_{k}(X;Y)$ is the closure of ${\mathcal {A}}(X,Z)$ in $\hbox {B}^{\psi }_k(X;Y)$. For $Y={\mathbb {R}}$, we set ${\mathcal {B}}^{\psi }_k(X):={\mathcal {B}}^{\psi }_k(X;{\mathbb {R}})$. In particular, by Theorem 2.4, it follows that ${\mathcal {B}}^{\psi }_k(X)$ is a separable Banach space.

One essential property of ${\mathcal {B}}^\psi (X)$ spaces is that the dual space of this separable Banach space is a well understood space of Radon measures, such as in the case of $C_0(X)$ for locally compact spaces X. The following result follows from the theory of Röckner and Sobol [29] (see also Dörsek and Teichmann [11] and [12]).

Proposition 2.9

(Riesz representation for ${\mathcal {B}}^\psi (X)$) Let $\ell :{\mathcal {B}}^\psi (X)\rightarrow {\mathbb {R}}$ be a continuous linear functional. Then, there exists a finite signed Radon measure $\mu$ on X such that

$$\begin{aligned} \ell (f)=\mathop \int \limits _{X}f(x)\mu (\mathrm{d}x)\qquad \text {for all}\;f\in {\mathcal {B}}^\psi (X). \end{aligned}$$

(2.9)

Furthermore,

$$\begin{aligned} \mathop \int \limits _{X}\psi (x)|\mu |(\mathrm{d}x) = ||\ell ||_{L({\mathcal {B}}^\psi (X),{\mathbb {R}})}, \end{aligned}$$

(2.10)

where $|\mu |$ denotes the total variation measure of $\mu$.

As every such measure defines a continuous linear functional on ${\mathcal {B}}^\psi (X)$, this completely characterizes the dual space of ${\mathcal {B}}^\psi (X)$. This allows for the introduction of the generalized Feller property, such that we can speak about strongly continuous semigroups on spaces of functions with growth controlled by $\psi$, in particular functions which are in general unbounded.

Let $(P_t)_{t\ge 0}$ be a family of bounded linear operators $P_t:{\mathcal {B}}^{\psi }(X)\rightarrow {\mathcal {B}}^{\psi }(X)$ with the following properties:

(F1) :

$P_0=I$, the identity on ${\mathcal {B}}^{\psi }(X)$,

(F2) :

$P_{t+s}=P_tP_s$ for all $t, s\ge 0$,

(F3) :

for all $f\in {\mathcal {B}}^{\psi }(X)$ and $x\in X, \lim _{t\rightarrow 0+}P_t f(x)=f(x)$,

(F4) :

there exist a constant $C\in {\mathbb {R}}$ and $\varepsilon >0$ such that for all $t\in [0,\varepsilon ], ||P_t||_{L({\mathcal {B}}^{\psi }(X))}\le C$,

(F5) :

$P_t$ is positive for all  $t\ge 0$, that is, for $f\in {\mathcal {B}}^{\psi }(X), f\ge 0$, we have $P_t f\ge 0$.

Alluding to Kallenberg [19, Chapter 17], such a family of operators will be called a generalized Feller semigroup. This is justified by the following result, which is a direct consequence of Lebesgue’s dominated convergence theorem with respect to the measure existing due to Riesz representation. Its proof is given in Dörsek and Teichmann [11, Theorem 3.2] and [12, Corollary 4].

Proposition 2.10

Let $(P_t)_{t\ge 0}$ satisfy F1 to F4. Then, $(P_t)_{t\ge 0}$ is strongly continuous on ${\mathcal {B}}^{\psi }(X)$, that is,

$$\begin{aligned} \lim _{t\rightarrow 0+}||P_t f-f||_{\psi }=0 \qquad \text {for all}\; f\in {\mathcal {B}}^{\psi }(X). \end{aligned}$$

(2.11)

3 Vector fields and directional derivatives

When we ask for convergence rates we have to specify large enough sets of test functions within the basic ${\mathcal {B}}^\psi (X)$-spaces. For this purpose we need to analyze directional derivatives and their functional analytic behavior. This can be done within the setting of ${\mathcal {B}}_k^\psi (X;Y)$ spaces.

Let $(X,||\cdot ||_{X})$ be the dual space of a separable Banach space. Given $(Z,||\cdot ||_{Z})$ the dual space of another separable Banach space that is embedded in $X$, we derive conditions on $V:Z\rightarrow X$ such that the directional derivative $g\in {\mathcal {B}}^{\hat{\psi }}_{k-1}(Z)$, where

$$\begin{aligned} g(z) := Df(z)(V(z)) \quad \text {for}\;z\in Z \end{aligned}$$

(3.1)

and $f\in {\mathcal {B}}^{\psi }_{k}(X)$. Here, $\psi =(\psi _j)_{j=0,\ldots ,k}$ and $\hat{\psi }=(\hat{\psi }_j)_{j=0,\ldots ,k-1}$ are vectors of D-admissible weight functions on X and Z, respectively.

We shall assume that $V\in \hbox {B}^\varphi _{k-1}(Z;X)$ for some vector $\varphi =(\varphi _j)_{j=0,\ldots ,k-1}$ of C-admissible weight functions on Z. Then, V is $k-1$ times continuously Fréchet differentiable. As $f\in \hbox {C}^{k}(X)$, the Leibniz rule yields

$$\begin{aligned} D^j g(z)(h_1,\ldots ,h_j) \!=\! \sum _{i=0}^{j}\frac{1}{i!(j-i)!}\sum _{\sigma \in {\mathcal {S}}_j}g_{j,i}(z,h_{\sigma _1},\ldots ,h_{\sigma _j}), \quad j\!=\!0,\!\ldots \!,k\!-\!1.\nonumber \\ \end{aligned}$$

(3.2)

Here, ${\mathcal {S}}_j$ denotes the symmetric group with j elements, and

$$\begin{aligned} g_{j,i}(z,h_1,\ldots ,h_j) := D^{i+1}f(z)(h_{1},\ldots ,h_{i}, D^{j-i} V(z)(h_{i+1},\ldots ,h_{j})).\qquad \end{aligned}$$

(3.3)

In particular, if we assume that for some constant $C>0$,

$$\begin{aligned} \hat{\psi }_j(z) \ge C^{-1}\sum _{i=0}^{j}\left( {\begin{array}{c}j\\ i\end{array}}\right) \psi _{i+1}(z)\varphi _{j-i}(z) \quad \text {for}\, j=0,\ldots ,k-1, \end{aligned}$$

(3.4)

it follows that $g\in \hbox {B}^{\hat{\psi }}_{k-1}(Z)$.

It is not so straightforward to prove that g can also be approximated by functions in ${\mathcal {A}}(X)$, which would imply $g\in {\mathcal {B}}^{\hat{\psi }}_{k-1}(Z)$. In Dörsek [9], a general theory for multiplication operators on ${\mathcal {B}}^\psi$ spaces is derived. Here, we take a different route, focusing on the problem at hand. The following definition is essential.

Definition 3.1

Given a Banach space $(X,||\cdot ||_X)$ and the dual space $(Z,||\cdot ||_Z)$ of a separable Banach space. Let $V\in \hbox {B}^{\varphi }_k(Z;X)$ with $\varphi$ a given vector of C-admissible weight functions on Z. We say that $V\in {\mathcal {C}}^{\varphi }_k(Z;X)$ if and only if for every $y\in X^*$, there exists a constant $C_{V,y}>0$ such that for each $R>0$, there exists a sequence $(v_n)_{n\in {\mathbb {N}}}\subset {\mathcal {A}}(Z)$ (depending on $R > 0$ and $y \in X^*$) with $\sup _{n\in {\mathbb {N}}}||v_n||_{\varphi ,k}\le C_{V,y}$ such that, with $v:=y\circ V$,

$$\begin{aligned} \lim _{n\rightarrow \infty }||v - v_n ||_{\hbox {C}^k(B_R(0))}=0. \end{aligned}$$

(3.5)

Here, $B_R(0)$ is the closed ball of radius R in Z, and

$$\begin{aligned} ||g||_{\hbox {C}^k(B_R(0))} := \sum _{j=0}^{k}\sup _{z\in B_R(0)}||D^j g(z)||_{L_j(Z)} \, . \end{aligned}$$

(3.6)

Remark 3.2

It is clear that vector fields such as those from Dörsek and Teichmann [12], Sect. 3.1.2] satisfy the above assumption. More generally, if Z is a Hilbert space and is compactly embedded into a larger Hilbert space Y such that $y\circ V$ can be extended to a smooth mapping $Y\rightarrow {\mathbb {R}}$ lying in $\hbox {C}_b^k(Y;{\mathbb {R}})$ for all $y\in X^{*}$, then the above assumption is satisfied, i.e., $V\in {\mathcal {C}}^{\varphi }_k(Z;X)$ for every vector $\varphi$ of C-admissible weight functions on Z. Indeed, the extension of $y \circ V$ and its derivatives are continuous on Y, whence uniformly continuous on the compact set $B_R(0)$. Let us fix a sequence of increasing finite-dimensional, orthogonal projections $\pi _n \rightarrow \mathrm{id }_Y$ converging strongly to the identity: composing the extension of $y \circ V$ with $\pi _n$ yields a pointwise converging, equicontinous sequence of cylindrical function on $B_R(0)$, which is—up to a smoothing argument—the desired assertion.

Comparable arguments are also used in Dörsek and Teichmann [12, Theorem 5] and Dörsek [9, Theorem 2.39]. In particular, this implies that Nemytskii operators are included in our setup if Z is a Sobolev space of sufficiently smooth functions, see also Dörsek [9, Example 2.48].

This definition should also be compared to the form of the multiplicative noise suggested in Debussche [8, Remark 2.3]. It is similar in spirit to the definition of ${\mathcal {C}}^{\varphi }_k(H;H)$, as there, A is assumed to be a negative self-adjoint operator with a compact inverse. Hence, if we consider a single component of the noise, $x\mapsto \tilde{\sigma }( (-A)^{-1/4}x )$, with $\tilde{\sigma }:H\rightarrow H$ a $\hbox {C}^3$-function with derivatives bounded up to order 3, it satisfies our assumptions given above and hence lies in ${\mathcal {C}}^{\varphi }_3(H)$ with $\varphi _0(x):=(1+||x||_H^2)^{1/2}$ and $\varphi _j(x):=1, j\ge 1$.

Theorem 3.3

Fix $k\ge 1$. Let $\psi =(\psi _i)_{i=0,\ldots ,k}$ be a vector of D-admissible weight functions on X, and $\hat{\psi }=(\hat{\psi }_j)_{j=0,\ldots ,k-1}$ a vector of D-admissible and $\varphi =(\varphi _j)_{j=0,\ldots ,k-1}$ a vector of C-admissible weight functions on Z. Suppose (3.4).

Then, the Lie derivative ${\mathcal {L}}:{\mathcal {C}}^{\varphi }_{k-1}(Z;X)\times {\mathcal {B}}^{\psi }_{k}(X)\rightarrow {\mathcal {B}}^{\hat{\psi }}_{k-1}(Z)$ defined through

$$\begin{aligned} {\mathcal {L}}(V,f)(z) := {\mathcal {L}}_V f(z) :=Df(z)(V(z)) \end{aligned}$$

(3.7)

is a bilinear, bounded operator.

Remark 3.4

Clearly, $V\in {\mathcal {C}}^{\varphi }_k(Z;X)$ is necessary if ${\mathcal {L}}_V f\in {\mathcal {B}}^{\hat{\psi }}_k(Z)$ is supposed to hold for $f\in {\mathcal {B}}^{\psi }_{k+1}(X)$ for a sufficiently large class of weight functions $\psi$. Indeed, choose $\psi _0(x):=\rho (||x||_X)$ with some increasing, left continuous and superlinear function $\rho$, and $\psi _j$ arbitrary D-admissible weight functions on X. Then, $f:=y\in {\mathcal {B}}^{\psi }_{k+1}(X)$ for all $y\in X^{*}$. Hence, ${\mathcal {L}}_V f(z)=y(V(z))$, and $y\circ V\in {\mathcal {B}}^{\hat{\psi }}_k(Z)$ implies $V\in {\mathcal {C}}^{\varphi }_k(Z;X)$.

Proof

The claimed boundedness of ${\mathcal {L}}$ was remarked above, and follows straight away from (3.4).

Hence, we only need to prove that ${\mathcal {L}}_V f\in {\mathcal {B}}^{\hat{\psi }}_{k-1}(Z)$ for given $V\in {\mathcal {C}}^{\varphi }_{k-1}(Z;X)$ and $f=g(\langle \cdot ,w_1\rangle ,\ldots ,\langle \cdot ,w_n\rangle )\in {\mathcal {A}}(X)$; the result then follows from a density argument. Fix $\varepsilon >0$. We shall construct $g_{\varepsilon }\in {\mathcal {A}}(Z)$ such that $||{\mathcal {L}}_V f - g_{\varepsilon } ||_{\hat{\psi },k}<C\varepsilon$ with some constant $C>0$ independent of $\varepsilon$.

Choose a dual set of vectors $(\zeta _i)_{i=1,\ldots ,n}\subset Z$ of $(w_i)_{i=1,\ldots ,n}$, i.e., $\langle \zeta _i,w_j\rangle = \delta _{ij}$. Let $Z_n:={{\mathrm{span}}}\left\{ \zeta _i:i=1,\ldots ,n \right\}$, and define $\pi :X\rightarrow Z_n$ by $\pi x:=\sum _{i=1}^{n}\langle x,w_i\rangle \zeta _i$. Then, $f\circ \pi =f$, and

$$\begin{aligned} {\mathcal {L}}_V f(z) = \sum _{i=1}^{n}Df(z)(\zeta _i)\langle V(z), w_i\rangle . \end{aligned}$$

(3.8)

Clearly, $w_i\in X^{*}$, and thus by Definition 3.1, there exists $C_V{:=}\max _{i=1,\ldots ,n}C_{V,w_i}{>}0$ such that for each $R>0$, we can find $v^i_{R,\varepsilon }\in {\mathcal {A}}(Z)$ with $||v^i_{R,\varepsilon }||_{\varphi ,k-1}\le C_V$ and

$$\begin{aligned} ||w_i\circ V - v^i_{R,\varepsilon }||_{\hbox {C}^{k-1}(B_R(0))} < \varepsilon , \end{aligned}$$

(3.9)

where $B_R(0)$ denotes the closed ball in Z. Setting $g_{\varepsilon }:=\sum _{i=1}^{n}Df(\cdot )(\zeta _i)v^i_{R,\varepsilon }\in {\mathcal {A}}(Z)$, it follows that with a constant $C_f>0$ independent of $R>0$,

$$\begin{aligned} ||{\mathcal {L}}_V f - g_{\varepsilon } ||_{\hbox {C}^{k-1}(B_R(0))} < C_f\varepsilon . \end{aligned}$$

(3.10)

Choose $R_{\varepsilon }>0$ large enough such that $\psi _j(z)>\varepsilon ^{-1}$ for $||z||_{Z}>R_{\varepsilon }$. This is possible as the embedding $Z\rightarrow X$ is continuous. Hence, as f and all its derivatives are bounded,

$$\begin{aligned} \hat{\psi }_j(z)^{-1}||D^j {\mathcal {L}}_V f(z)||_{L_j(Z)}<C_f\varepsilon \quad \text {for}\; ||z||_Z>R_{\varepsilon }, \quad j=0,\ldots ,k-1,\qquad \end{aligned}$$

(3.11)

where $C_f$ is independent of $\varepsilon$. Furthermore,

$$\begin{aligned} \hat{\psi }_j(z)^{-1}||D^j g_{\varepsilon }(z)||_{L_j(Z)} \le C_{f,V}\varepsilon \quad \text {for}\; ||z||_Z>R_{\varepsilon }, \quad j=0,\ldots ,k-1,\qquad \end{aligned}$$

(3.12)

where $C_{f,V}>0$ depends on f and V, but not on $\varepsilon$ or $R_{\varepsilon }$. Plugging the results together proves the claim. $\square$

Let us consider two special cases.

Corollary 3.5

Let $(H,||\cdot ||_{H})$ be a Hilbert space, $(Z,||\cdot ||_{Z})$ a continuously embedded Hilbert space. Define the D-admissible weight functions $\psi _j(x):=\cosh (||x||_H)$ on H and $\hat{\psi }_j(x):=\cosh (||x||_Z)$ on Z and the C-admissible weight functions $\varphi _j(x):=1$ on $Z, j\ge 0$. Then, for every $k\ge 0$, the mapping

$$\begin{aligned} {\mathcal {L}}:{\mathcal {C}}^{\varphi }_{k-1}(Z;X) \times {\mathcal {B}}^{\psi }_k(X) \rightarrow {\mathcal {B}}^{\hat{\psi }}_{k-1}(Z), \quad (V,f)\mapsto {\mathcal {L}}_V f, \end{aligned}$$

(3.13)

given by ${\mathcal {L}}_V f(x):=Df(x)V(x)$, is bounded and bilinear.

Remark 3.6

If $Z=H$, this has the simple interpretation that bounded vector fields map $\cosh$-weighted spaces into themselves.

Proof

This is straightforward from Theorem 3.3, as the $\hat{\psi }_j$ defined there is only a multiple of $\hat{\psi }_j$ in this case. $\square$

The following special case is very useful in the analysis of stochastic partial differential equations of Da Prato–Zabczyk type.

Corollary 3.7

Let $(H,||\cdot ||_{H})$ be a Hilbert space, $(Z,||\cdot ||_{Z})$ a continuously embedded Hilbert space. Fix $n\in {\mathbb {N}}$. Define the D-admissible weight functions $\psi _j(x):=(1+||x||_H^2)^{(n-j)/2}$ on $H$ and $\hat{\psi }_j(x):=(1+||x||_Z^{2})^{(n-j)/2}$ on $Z, j=0,\ldots ,n-1$, and the C-admissible weight functions $\varphi _0(x):=(1+||x||_{Z}^2)^{1/2}$ and $\varphi _j(x):=1$ on $Z, j\in {\mathbb {N}}$. Then, for $k\le n-1$, the mapping

$$\begin{aligned} {\mathcal {L}}:{\mathcal {C}}^{\varphi }_{k-1}(Z;X) \times {\mathcal {B}}^{\psi }_k(X) \rightarrow {\mathcal {B}}^{\hat{\psi }}_{k-1}(Z), \quad (V,f)\mapsto {\mathcal {L}}_V f, \end{aligned}$$

(3.14)

given by ${\mathcal {L}}_V f(x):=Df(x)V(x)$, is bounded and bilinear.

Remark 3.8

This means that linearly bounded vector fields $Z\rightarrow X$ with bounded derivatives (hence also Lipschitz continuous) map polynomially bounded functions to polynomially bounded functions, with the same weights. In particular, if the linear operator $A:{{\mathrm{dom}}}A\subset H\rightarrow H$ is densely defined and closed, then $V_A\in {\mathcal {C}}^{\varphi }_k({{\mathrm{dom}}}A;H)$ for all $k\ge 0$, where $\varphi$ is defined as in Corollary 3.7, ${{\mathrm{dom}}}A$ is endowed with the operator norm, and $V_A(x):=Ax$ for $x\in {{\mathrm{dom}}}A$.

Proof

Calculating

$$\begin{aligned}&(1+||x||_{Z}^2)^{(n-1)/2} (1+||x||_{Z}^2)^{1/2} +\sum _{i=0}^{j}\left( {\begin{array}{c}j\\ i\end{array}}\right) (1+||x||_{Z}^2)^{(n-i-1)/2} \nonumber \\&\quad \le C\hat{\psi }_j(x), \end{aligned}$$

(3.15)

the claim again follows from an application of Theorem 3.3. $\square$

4 Stability of cubature schemes

We shall now prove stability of cubature on Wiener space in the setting of weighted spaces. Consider from now on the following setup. Let on [0,1] be given Lipschitz-continuous paths $(\omega ^{(1)}_i)_{i=1,\ldots ,N}, \omega ^{(1)}_i(s)=(\omega ^{(1),j}_i(s))_{j=0,\ldots ,d}, \omega ^{(1),0}_i(s)=s$ starting at 0, and weights $(\lambda _i)_{i=1,\ldots ,N}$ of a cubature on Wiener space of degree $m\ge 1$ for a $d$-dimensional Brownian motion, i.e., for all multi-indices $(j_1,\ldots ,j_k)$ with $k+\#\left\{ i:j_i=0 \right\} \le m$ and a $d$-dimensional Brownian motion $(B^j_t)_{j=1,\ldots ,d, t\ge 0}$,

$$\begin{aligned}&{\mathbb {E}}\left[ \int \cdots \mathop \int \limits _{0\le s_1\le \dots \le s_k\le 1}\circ \mathrm{d}B^{j_1}_{s_1}\dots \circ \mathrm{d}B^{j_k}_{s_k} \right] \\&\quad = \sum _{i=1}^{N} \lambda _i \int \cdots \mathop \int \limits _{0\le s_1\le \dots \le s_k\le 1}\mathrm{d}\omega _i^{(1),j_1}(s_1)\dots \circ \mathrm{d}\omega _i^{(1),j_k}(s_k). \nonumber \end{aligned}$$

(4.1)

Here, we have set $B^0_t:=t$ and $\circ \mathrm{d}B^0_t:=\mathrm{d}t$ for ease of notation. For a general time interval $[0,\Delta t]$, we set

$$\begin{aligned} \omega ^{(\Delta t),0}_i(s):=s \quad \text {and} \quad \omega ^{(\Delta t),j}_i(s):=\sqrt{\Delta t}\omega ^{(1),j}_i(s/\Delta t), \quad j=1,\ldots ,d,\qquad \end{aligned}$$

(4.2)

so that $(\omega ^{(\Delta t)}_i)_{i=1,\ldots ,N}$ and $(\lambda _i)_{i=1,\ldots ,N}$ define a cubature formula on Wiener space of degree m on $[0,\Delta t]$. The approximation of the Markov semigroup $(P_t)_{t\ge 0}$, given by $P_t f(x):={\mathbb {E}}[f(X^x_t)]$ for a function $f:H\rightarrow {\mathbb {R}}$, where $(X^x_t)_{t\ge 0}$ solves the Stratonovich stochastic differential equation

$$\begin{aligned} \mathrm{d}X^{x}_{t} = \sum _{j=0}^{d}V_j(X^x_t)\circ \mathrm{d}B^{j}_{t}, \quad X^{x}_0 = x, \end{aligned}$$

(4.3)

on some state space H, then reads

$$\begin{aligned} P_t f(x) \approx Q_{(t/n)}^n f(x), \end{aligned}$$

(4.4)

where the one step approximation operator is defined by

$$\begin{aligned} Q_{(\Delta t)}f(x) := \sum _{i=1}^{N}\lambda _i f\left( X^{x}_{\Delta t}\left( \omega _i^{(\Delta t)}\right) \right) , \end{aligned}$$

(4.5)

with $X^{x}_{t}(\omega _i^{(\Delta t)})$ the solution of the problem

$$\begin{aligned} \mathrm{d}X^{x}_{s}(\omega ^{(\Delta t)}_i) = \sum _{j=0}^{d}V_j\left( X^x_s\left( \omega ^{(\Delta t)}_i\right) \right) \mathrm{d}\omega ^{(\Delta t),j}_i(s), \quad X^{x}_0\left( \omega ^{(\Delta t)}_i\right) = x. \end{aligned}$$

(4.6)

Under certain smoothness assumptions on the vector fields $V_j, j=0,\ldots ,d$, and the test function f, we expect that

$$\begin{aligned} |P_t f(x) - Q_{(t/n)}^n f(x) |\le Cn^{-(m-1)/2}, \end{aligned}$$

(4.7)

where the constant $C>0$ can depend on $f, V_j, j=0,\ldots ,d$, and $x\in H$. For the case H finite-dimensional and f and $V_j$ bounded and $\hbox {C}^{\infty }$-bounded, $j=0,\ldots ,d$, it is known that C depends on the supremum norms of f and its derivatives, but not on $x\in H$, see Lyons and Victoir [24]. For more background on the method, see Bayer and Teichmann [2], Crisan and Ghazali [4] and Lyons and Victoir [24]. An alternative approach can be found in Kusuoka [21, 22]. Its implementation as a splitting method is given in Ninomiya and Victoir [26], see also Alfonsi [1], Ninomiya and Ninomiya [25], and Tanaka and Kohatsu-Higa [33].

Our strategy is as follows. First, we consider the finite dimensional case. Here, the analysis is straightforward. Afterwards, we turn to the infinite dimensional setting. Here, our aim is to prove stability for Da Prato–Zabczyk equations with pseudodissipative generator. We prove first the auxiliary result in Theorem 4.4, which might be of independent interest. The method of the moving frame then yields first Theorem 4.7, and the Szőkefalvi–Nagy theorem allows us to conclude in Corollary 4.8.

4.1 Finite dimensional state space

Given a Stratonovich SDE on ${\mathbb {R}}^n$,

$$\begin{aligned} \mathrm{d}X^{x}_{t} = \sum _{j=0}^{d}V_j(X^x_t)\circ \mathrm{d}B^{j}_{t}, \quad X^{x}_0 = x, \end{aligned}$$

(4.8)

we let the local discretisation of $P_t f(x):={\mathbb {E}}[f(X^x_t)]$ be defined by

$$\begin{aligned} Q_{(\Delta t)}f(x) := \sum _{i=1}^{N}\lambda _i f\left( X^{x}_{\Delta t}\left( \omega _i^{(\Delta t)}\right) \right) , \end{aligned}$$

(4.9)

where $X^{x}_{t}(\omega _i^{(\Delta t)})$ is the solution of the problem

$$\begin{aligned} \mathrm{d}X^{x}_{s}(\omega ^{(\Delta t)}_i) = \sum _{j=0}^{d}V_j\left( X^x_s\left( \omega ^{(\Delta t)}_i\right) \right) \mathrm{d}\omega ^{(\Delta t),j}_i(s), \quad X^{x}_0(\omega ^{(\Delta t)}_i) = x. \end{aligned}$$

(4.10)

Theorem 4.1

Let $\psi$ be an admissible weight function on ${\mathbb {R}}^{n}$, and assume that

$$\begin{aligned} |V_i V_j\psi (x) |+ |V_i\psi (x) |\le C\psi (x) \quad \text {for}\; i=0,\ldots ,d\; \text {and}\; j=1,\ldots ,d,\qquad \end{aligned}$$

(4.11)

where we require that all the necessary derivatives are well-defined.

Then, there exists a constant $\tilde{C}>0$ independent of $0 < \Delta t \le T$ such that

$$\begin{aligned} Q_{(\Delta t)}\psi (x) \le \exp (\tilde{C}\Delta t)\psi (x). \end{aligned}$$

(4.12)

Proof

We define the intermediate operator

$$\begin{aligned} Q_{(\Delta t,s)}f(x) := \sum _{i=1}^{N}\lambda _i f\left( X^{x}_{s}\left( \omega _i^{(\Delta t)}\right) \right) \quad \text {for}\; s\in [0,t] \end{aligned}$$

(4.13)

and note that $Q_{(\Delta t)}=Q_{(\Delta t,\Delta t)}$. The definition of the iteration step yields

$$\begin{aligned} \psi (X^{x}_{s}(\omega ^{(\Delta t)}_{i}))&= \psi (x) + \sum _{j=0}^{d}\mathop \int \limits _{0}^{s}V_j\psi \left( X^{x}_{r}\left( \omega ^{(\Delta t)}_i\right) \right) \mathrm{d}\omega ^{(\Delta t),j}_{i}(r) \nonumber \\&= \psi (x) + \mathop \int \limits _{0}^{s}V_0\psi \left( X^{x}_{r}\left( \omega ^{(\Delta t)}_{i}\right) \right) \mathrm{d}r + \sum _{j=1}^{d}V_j\psi (x)\omega ^{(\Delta t),j}_i(s) \nonumber \\&+ \sum _{j=1}^{d}\sum _{k=0}^{d}\mathop \int \limits _{0}^{s}\mathop \int \limits _{0}^{r}V_k V_j\psi \left( X^{x}_{q}\left( \omega ^{(\Delta t)}_i\right) \right) \mathrm{d}\omega ^{(\Delta t),k}_i(q)\mathrm{d}\omega ^{(\Delta t),j}_i(r). \nonumber \\ \end{aligned}$$

(4.14)

By (4.11),

$$\begin{aligned} \mathop \int \limits _{0}^{s}V_0\psi \left( X^{x}_{r}\left( \omega ^{(\Delta t)}_{i}\right) \right) \mathrm{d}r \le C\mathop \int \limits _{0}^{s}\psi \left( X^{x}_{r}\left( \omega ^{(\Delta t)}_{i}\right) \right) \mathrm{d}r. \end{aligned}$$

(4.15)

Furthermore, as $|\omega ^{(\Delta t),j}_{i}(s)|\le \hat{C}(\Delta t)^{1/2}$ and $|\frac{\partial }{\partial s}\omega ^{(\Delta t),j}_{i}(s)|\le \hat{C}(\Delta t)^{-1/2}$ with some constant $\hat{C}>0$ independent of $0 < \Delta t \le T$ (notice the case $j=0$), Fubini’s theorem yields

$$\begin{aligned}&\mathop \int \limits _{0}^{s}\mathop \int \limits _{0}^{r} V_{k}V_{j}\psi \left( X^{x}_{q}\left( \omega ^{(\Delta t)}_{i}\right) \right) \mathrm{d}\omega ^{(\Delta t),k}_i(q)\mathrm{d}\omega ^{(\Delta t),j}_{i}(r) \nonumber \\&\quad \le C\mathop \int \limits _{0}^{s}|\omega ^{(\Delta t),j}_i(s)-\omega ^{(\Delta t),j}_i(q) |\psi \left( X^{x}_{q}\left( \omega ^{(\Delta t)}_i\right) \right) \left|\frac{\partial }{\partial q}\omega ^{(\Delta t),k}_i(q)\right|\mathrm{d}q \nonumber \\&\quad \le 2\hat{C}^2C\mathop \int \limits _{0}^{s}\psi \left( X^{x}_{q}\left( \omega ^{(\Delta t)}_i\right) \right) \mathrm{d}q. \end{aligned}$$

(4.16)

Thus, we see that for some $C'>0$,

$$\begin{aligned}&Q_{(\Delta t,s)}\psi (x) = \sum _{i=1}^{N}\lambda _i \psi \left( X^{x}_{s}\left( \omega ^{(\Delta t)}_{i}\right) \right) \\&\quad \le \psi (x) + \sum _{j=1}^{d}V_j\psi (x)\sum _{i=1}^{N}\lambda _i\omega ^{(\Delta t),j}_i(s) + C'\mathop \int \limits _{0}^{s}Q_{(\Delta t,r)}\psi (x)\mathrm{d}r. \nonumber \end{aligned}$$

(4.17)

Defining $\alpha _{\Delta t,s}(x):=\sum _{j=1}^{d}V_j\psi (x)\sum _{i=1}^{N}\lambda _i\omega ^{(\Delta t),j}_i(s)$, the Gronwall inequality yields

$$\begin{aligned} Q_{(\Delta t,s)}\psi (x) \le \psi (x) + \alpha _{\Delta t,s}(x) + \mathop \int \limits _{0}^{s}\left( \psi (x)+\alpha _{\Delta t,r}(x) \right) C'\exp (C'(s-r))\mathrm{d}r.\nonumber \\ \end{aligned}$$

(4.18)

Note that $\alpha _{\Delta t,\Delta t}(x)=0$ by the equality $\sum _{i=1}^{N}\lambda _i\omega ^{(\Delta t),j}_i(\Delta t)=0$. Furthermore,

$$\begin{aligned} \alpha _{\Delta t,r}(x) \le C\sqrt{\Delta t}\psi (x) \le \frac{C}{2}(1+\Delta t)\psi (x) \le \frac{C}{2}\exp (\Delta t)\psi (x). \end{aligned}$$

(4.19)

This proves

$$\begin{aligned} Q_{(\Delta t)}\psi (x)&= Q_{(\Delta t,\Delta t)}\psi (x) \le \psi (x)\left( 1+\left( 1+\frac{C}{2}\exp (\Delta t)\right) ( \exp (C'\Delta t)-1 ) \right) \nonumber \\&\le \exp (\tilde{C}\Delta t)\psi (x), \end{aligned}$$

(4.20)

where $\tilde{C}:=\max (C/2(1+C')+1,C'+1)$, which is the required estimate. $\square$

4.2 Time-dependent stochastic ordinary differential equations on Hilbert space

Let $H$ be a Hilbert space, and consider the nonautonomous stochastic ordinary differential equation

$$\begin{aligned} \mathrm{d}X^x_t = \sum _{j=0}^{d}V_j(t,X^x_t)\circ \mathrm{d}B^j_t, \quad X^x_0 = x, \end{aligned}$$

(4.21)

on $H$. We define cubature approximations of (4.21) by

$$\begin{aligned} \mathrm{d}X^{t,x}_s\left( \omega ^{(\Delta t)}_i\right) = \sum _{j=0}^{d}V_j\left( t+s,X^{t,x}_s\left( \omega ^{(\Delta t)}_i\right) \right) \mathrm{d}\omega ^{(\Delta t),j}_i(s), \quad X^{t,x}_0 = x, \end{aligned}$$

(4.22)

and the approximation operator by

$$\begin{aligned} Q^{t}_{(\Delta t)}f(x) := \sum _{i=1}^{N}\lambda _i f\left( X^{t,x}_{\Delta t}\left( \omega ^{(\Delta t)}_i\right) \right) . \end{aligned}$$

(4.23)

Definition 4.2

A cubature formula $(\omega ^{(\Delta t)}_i, \lambda _i )_{i=1,\ldots ,N}$ is called symmetric if for every $i\in \{1,\ldots ,N\}$, there exists some $i'\in \left\{ 1,\ldots ,N \right\}$ such that $\lambda _i=\lambda _{i'}$ and

$$\begin{aligned} \omega ^{(\Delta t),j}_i(s)=-\omega ^{(\Delta t),j}_{i'}(s) \quad \text {for all}\;s\in [0,\Delta t]\; \text {and}\; j=1,\ldots ,d. \end{aligned}$$

(4.24)

It is called weakly symmetric if for $j=1,\ldots ,d$,

$$\begin{aligned} \sum _{i=1}^{N}\lambda _i\omega ^{(\Delta t),j}_i(s) = 0 \quad \text {for}\quad s\in [0,\Delta t]. \end{aligned}$$

(4.25)

Remark 4.3

In words symmetry means that with every cubature path $\omega$ also its space-component-wise negative, i.e., $(s,- \omega ^1(s),\ldots ,-\omega ^d(s))$, for $s \in [0,\Delta t]$ is among the cubature paths. Notice that time is not reversed. Clearly, all symmetric cubature formulas are also weakly symmetric. Note that many known cubature formulas are actually symmetric. Moreover, a non-symmetric cubature formula can be made symmetric by adding the space-component-wise negatives of the paths with the same weights to it and dividing all weights by two. This will at most double the number of paths. Thus, if we use a cubature formula with a small number of paths in high dimensions, we can also find a symmetric cubature formula with this property. Also notice that we only need weak symmetry of cubature formulas for our considerations, but we introduced symmetry for convenience.

Theorem 4.4

Suppose that the cubature formula used in the definition of $Q^t_{(\Delta t)}$ is weakly symmetric. Let $\psi$ be an admissible weight function on $H$ and suppose

$$\begin{aligned}&||D\psi (x)||\le C_1(1+||x||^2)^{-1/2}\psi (x) \quad \text {and} \end{aligned}$$

(4.26)

$$\begin{aligned}&||D^2\psi (x)||\le C_1(1+||x||^2)^{-1}\psi (x) \end{aligned}$$

(4.27)

with some constant $C_1>0$, Furthermore, assume that for some constant $C_2>0$,

$$\begin{aligned} ||V_j(t,x)||\le C_2( 1+||x||^2 )^{1/2} \quad \text {for}\; j=0,\ldots ,d, x\in X \text {and}\; t\in [0,T],\qquad \end{aligned}$$

(4.28)

and that $x\mapsto V_j(t,x)$ is continuously differentiable with derivative bounded uniformly in $t\in [0,T]$ for $j=1,\ldots ,d$.

Then, there exists a constant $\tilde{C}>0$ such that for all $t\in [0,T]$ and $\Delta t\in [0,T-t]$,

$$\begin{aligned} Q^t_{(\Delta t)}\psi (x) \le \exp (\tilde{C}t)\psi (x) \quad \text {for all}\; x\in H. \end{aligned}$$

(4.29)

Remark 4.5

The above result is remarkable as we do not assume that the vector fields $V_j$ are differentiable with respect to $t$. This is also the reason why we cannot directly use the ideas in Theorem 4.1 to conclude.

Proof

Define the intermediate approximation for $s\in [0,\Delta t]$ by

$$\begin{aligned} Q^{t}_{(\Delta t,s)}f(x) := \sum _{i=1}^{N}\lambda _i f\left( X^{t,x}_{s}\left( \omega ^{(\Delta t)}_i\right) \right) . \end{aligned}$$

(4.30)

As in the proof of Theorem 4.1, we note that $Q^{t}_{(\Delta t,\Delta t)}=Q^{t}_{(\Delta t)}$. For $0\le s\le \Delta t$,

$$\begin{aligned}&\psi \left( X^{t,x}_{s}\left( \omega ^{(\Delta t)}_i\right) \right) = \nonumber \\&\quad \psi (x) \!+\! \sum _{j=0}^{d}\mathop \int \limits _{0}^{s}D\psi \left( X^{t,x}_{r}\left( \omega ^{(\Delta t)}_i\right) \right) V_j\left( t\!+\!r,X^{t,x}_{r}\left( \omega ^{(\Delta t)}_i\right) \right) \mathrm{d}\omega ^{(\Delta t),j}_i(r).\qquad \qquad \end{aligned}$$

(4.31)

Consider $g_j(r,x):=D\psi (x)V_j(t+r,x)$. Then,

$$\begin{aligned}&g_j(\rho ,\, X^{t,x}_{r}(\omega ^{(\Delta t)}_i)) = g_j(\rho ,x) \nonumber \\&\quad + \sum _{k=0}^{d}\mathop \int \limits _{0}^{r}D_x g_j\left( \rho ,X^{t,x}_{q}\left( \omega ^{(\Delta t)}_{i}\right) \right) V_k\left( t+q,X^{t,x}_{q}\left( \omega ^{(\Delta t)}_i\right) \right) \mathrm{d}\omega ^{(\Delta t),k}_i(q).\qquad \qquad \end{aligned}$$

(4.32)

From (4.26) to (4.28), we obtain that for $0\le s\le \Delta t\le T$,

$$\begin{aligned} |g_0(r,x)|&= |D\psi (x)V_0(t+r,x) |\le ||D\psi (x)||\cdot ||V_0(t+r,x)||\nonumber \\&\le C_1 C_2\psi (x). \end{aligned}$$

(4.33)

We argue in a similar manner for $D_x g_j(r,x)V_{k}(t+q,x), j=1,\ldots ,d, k=0,\ldots ,d$, to obtain that for $0\le q\le r\le \Delta t$,

$$\begin{aligned}&|D_x g_j(r,x)V_k(t+q,x) |= |D^2\psi (x)( V_j(t+r,x), V_k(t+q,x) ) \nonumber \\&\quad + D\psi (x)D_xV_j(t+r,x)V_k(t+q,x) |\nonumber \\&\quad \le C_1(C_2^2+C_2)\psi (x). \end{aligned}$$

(4.34)

An application of Fubini’s theorem just as in the proof of Theorem 4.1 gives

$$\begin{aligned}&\psi \left( X^{t,x}_s\left( \omega ^{(\Delta t)}_i\right) \right) \nonumber \\&\quad = \psi (x) + \mathop \int \limits _{0}^{s}g_0\left( r,X^{t,x}_{r}\left( \omega ^{(\Delta t)}_i\right) \right) \mathrm{d}r + \sum _{j=1}^{d}\mathop \int \limits _{0}^{s}g_j(r,x)\mathrm{d}\omega ^{(\Delta t),j}_i(r) \nonumber \\&\qquad +\sum _{j=1}^{d}\sum _{k=0}^{d}\mathop \int \limits _{0}^{s}\mathop \int \limits _{0}^{r}D_x g_j\left( r,X^{t,x}_{q}\left( \omega ^{(\Delta t)}_i\right) \right) V_k\left( t+q,X^{t,x}_{q}\left( \omega ^{(\Delta t)}_{i}\right) \right) \mathrm{d}\omega ^{(\Delta t),k}_i(q)\mathrm{d}\omega ^{(\Delta t),j}_i(r) \nonumber \\&\qquad \le \psi (x) + C'\mathop \int \limits _{0}^{s}\psi \left( X^{x}_{r}\left( \omega ^{(\Delta t)}_i\right) \right) \mathrm{d}r + \sum _{j=1}^{d}\mathop \int \limits _{0}^{s}g_{j}(r,x)\mathrm{d}\omega ^{(\Delta t),j}_i(r) \end{aligned}$$

(4.35)

with a constant $\tilde{C}>0$ depending on $C_1$ and $C_2$, where we apply that $\Delta t\le T$. As from the weak symmetry of the cubature paths,

$$\begin{aligned}&\sum _{i=1}^{N}\lambda _i\sum _{j=1}^{d}\mathop \int \limits _{0}^{s}g_j(r,x)\mathrm{d}\omega ^{(\Delta t),j}_i(r) = \sum _{j=1}^{d}\mathop \int \limits _{0}^{s}g_j(r,x)\mathrm{d}\left( \sum _{i=1}^{N}\lambda _i\omega ^{(\Delta t),j}_i(r) \right) \nonumber \\&\quad = 0, \end{aligned}$$

(4.36)

we obtain

$$\begin{aligned} Q_{(\Delta t,s)}\psi (x) \le \psi (x) + \tilde{C}\mathop \int \limits _{0}^{s}Q_{(\Delta t,r)}\psi (x)\mathrm{d}r. \end{aligned}$$

(4.37)

An application of Gronwall’s lemma yields $Q_{(\Delta t)}\psi (x) \le \exp (\tilde{C}\Delta t)\psi (x)$, which proves the result. $\square$

Remark 4.6

It is clear that the given assumptions on the vector fields and the weight function are not the only ones possible. Instead, we could also require the vector fields to be bounded uniformly in $t\in [0,T]$, and allow the weight function to satisfy $||D\psi (x)||+ ||D^2\psi (x)||\le C\psi (x)$. While the situation above corresponds to polynomially growing weight functions and linearly bounded vector fields, this variant corresponds to exponentially growing weight functions and bounded vector fields, see also Corollaries 3.5 and 3.7.

Such an approach might be more appropriate when dealing with exponentials of stochastic processes such as Lévy processes, which are ubiquitous in applications in mathematical finance, as they ensure nonnegativity in a simple manner and allow us to work on the natural scale of the problem.

4.3 Da Prato–Zabczyk equations

Suppose now that

$$\begin{aligned} \mathrm{d}X^x_t = AX^x_t\mathrm{d}t + \sum _{j=0}^{d}V_j(X^x_t)\circ \mathrm{d}B^j_t, \quad X^x_0 = x, \end{aligned}$$

(4.38)

is a stochastic partial differential equation of Da Prato–Zabczyk type on some Hilbert space $H$, see Da Prato and Zabczyk [6, 7] for a comprehensive exposition of the theory of such equations. Here, solutions are understood in the mild sense,

$$\begin{aligned} X^x_t = \exp (tA)x + \sum _{j=0}^{d}\mathop \int \limits _{0}^{t}\exp ( (t-s)A )V_j(X^x_t)\circ \mathrm{d}B^j_s, \end{aligned}$$

(4.39)

and we also define the cubature discretisations in the mild sense,

$$\begin{aligned} X^x_t\left( \omega ^{(\Delta t)}_i\right) \!=\! \exp (tA)x \!+\! \sum _{j=0}^{d}\mathop \int \limits _{0}^{t}\exp ( (t\!-\!s)A )V_j\left( X^x_t\left( \omega ^{(\Delta t)}_i\right) \right) \mathrm{d}\omega ^{(\Delta t),j}_i(s).\qquad \end{aligned}$$

(4.40)

Again, the approximation of the Markov semigroup $P_t f(x):={\mathbb {E}}[f(X^x_t)]$ is given by

$$\begin{aligned} Q_{(\Delta t)}f(x) := \sum _{i=1}^{N}\lambda _i f\left( X^{x}_{\Delta t}\left( \omega ^{(\Delta t)}_i\right) \right) . \end{aligned}$$

(4.41)

Here we do only treat Da Prato–Zabczyk equations driven by finitely many Brownian motions, since there are no generically infinite dimensional cubature approaches known for Da Prato–Zabczyk equations driven by infinitely many Brownian motions. Certainly approximation arguments would always work but are not considered in this article.

Theorem 4.7

Suppose that $A$ is the generator of a group $S_t=\exp (tA), t\in {\mathbb {R}}$, with growth estimate $||S_t||\le M\exp ( \lambda |t|)$ for $t\in {\mathbb {R}}$ and for some numbers $M \ge 1$ and $\lambda \in {\mathbb {R}}$ (which always exist!), and that the cubature formula used in the definition of $Q_{(\Delta t)}$ is weakly symmetric. Let $\psi$ be an admissible weight function on $H$. Suppose that for some $C>0$ depending on $A, \psi$, and $V_j, j=1,\ldots ,d, \psi (S_tx)\le \exp (Ct)\psi (x)$ for all $x\in H$ and $t>0$,

$$\begin{aligned}&||D\psi (x)||\le C(1+||x||^2)^{-1/2}\psi (x), \end{aligned}$$

(4.42a)

$$\begin{aligned}&||D^2\psi (x)||\le C(1+||x||^2)^{-1}\psi (x), \quad \text {and} \end{aligned}$$

(4.42b)

$$\begin{aligned}&||V_j(x)||\le C( 1+||x||^2 )^{1/2} \quad \text {for}\; j=0,\ldots ,d, \end{aligned}$$

(4.42c)

and that $V_j$ is continuously differentiable with derivative bounded by $C$ for $j=1,\ldots ,d$.

Then, for any $T>0$, there exists a constant $\tilde{C}>0$ depending on $C$ and $T$ such that for every $\Delta t\in [0,T]$, the operator $Q_{(\Delta t)}$ satisfies

$$\begin{aligned} Q_{(\Delta t)}\psi (x) \le \exp (\tilde{C}\Delta t)\psi (x) \quad \text {for all}\; x\in H. \end{aligned}$$

(4.43)

Proof

We apply the method of the moving frame from [35]. This yields that $X^x_t=S_t Y^x_t$, where $(Y^x_t)_{t\ge 0}$ satisfies the Hilbert space stochastic ordinary differential equation

$$\begin{aligned} \mathrm{d}Y^x_t = \sum _{j=0}^{d}\tilde{V}_j(t,Y^x_t)\circ \mathrm{d}B^j_t, \quad Y^x_0 = x, \end{aligned}$$

(4.44)

with $\tilde{V}_j(t,y)=S_{-t}V_j(S_ty)$. Thus, rewriting the cubature discretisations of $(X^{x}_{t})_{t\ge 0}$ using $(Y^{x}_{t})_{t\ge 0}$,

$$\begin{aligned} \mathrm{d}Y^{x}_s\left( \omega ^{(\Delta t)}_i\right) = \sum _{j=0}^{d}\tilde{V}_j\left( s,Y^{x}_s\left( \omega ^{(\Delta t)}_i\right) \right) \mathrm{d}\omega ^{(\Delta t),j}_i(s), \end{aligned}$$

(4.45)

we see that, if we define

$$\begin{aligned} \tilde{Q}_{(\Delta t)}f(y) := \sum _{i=1}^{N}\lambda _i f\left( Y^{y}_{\Delta t}\left( \omega ^{(\Delta t)}_i\right) \right) \end{aligned}$$

(4.46)

for $f:H\rightarrow {\mathbb {R}}$, then $Q_{(\Delta t)}h(x)=\tilde{Q}_{(\Delta t)}g(x)$, where $g(y):=h(S_{\Delta t}y)$. In particular,

$$\begin{aligned} Q_{(\Delta t)}\psi (x) = \tilde{Q}_{(\Delta t)}(\psi \circ S_{\Delta t})(x) \le \exp (C\Delta t)\tilde{Q}_{(\Delta t)}\psi (x), \end{aligned}$$

(4.47)

where we apply the assumptions on $\psi$ and the positivity of $\tilde{Q}_{(\Delta t)}$.

But now, we are in the situation of Theorem 4.4: The estimates for $\psi$ are clear by assumption, and for $\tilde{V}_j(s,y)$, we note that, as $s\in [0,T]$,

$$\begin{aligned}&||\tilde{V}_j(s,y) ||= ||S_{-s}V_j(S_s y)||\le CM^2\exp (2 \lambda T)(1+||y||^{2})^{1/2}\end{aligned}$$

(4.48)

$$\begin{aligned}&\quad \text {and } ||D_y\tilde{V}_j(s,y)||= ||S_{-s}D_y V_j(S_s y)S_s||\le C M^2\exp (2 \lambda T) \quad \text {for}\; j=1,\ldots ,d.\nonumber \\ \end{aligned}$$

(4.49)

An appeal to Theorem 4.4 yields

$$\begin{aligned} \tilde{Q}_{(\Delta t)}\psi (x) \le \exp (\tilde{C}\Delta t)\psi (x) \end{aligned}$$

(4.50)

with some constant $\tilde{C}>0$, and the result follows. $\square$

The Szőkefalvi–Nagy theorem now allows us to obtain a corresponding result for pseudocontractive semigroups.

Corollary 4.8

Suppose that $A$ is the generator of a semigroup of pseudocontractions $S_t=\exp (tA), t\ge 0$. Let $\psi (x)=\rho (||x||^2)$ with some increasing and left continuous function $\rho :[0,\infty )\rightarrow (0,\infty )$ (see also Dörsek and Teichmann [11, Example 4.1]) which satisfies $\rho (Cu)\le C\rho (u)$ for all $u\ge 0$ and $C>0$, and which is twice differentiable and satisfies

$$\begin{aligned} \rho '(u)\le C(1+u)^{-1}\rho (u) \quad \text {and}\quad \rho ''(u)\le C(1+u)^{-2}\rho (u). \end{aligned}$$

(4.51)

Furthermore, assume that $||V_j(x)||\le C( 1+||x||^2 )^{1/2}$ for $j=0,\ldots ,d$, and that $V_j$ is continuously differentiable with bounded derivative for $j=1,\ldots ,d$, and that the cubature formula used in the definition of $Q_{(\Delta t)}$ is weakly symmetric.

Then, for any $T>0$, there exists a constant $\tilde{C}>0$ such that for every $\Delta t\in [0,T]$, the operator $Q_{(\Delta t)}$ satisfies

$$\begin{aligned} Q_{(\Delta t)}\psi (x) \le \exp (\tilde{C}\Delta t)\psi (x) \quad \text {for all}\; x\in H. \end{aligned}$$

(4.52)

Proof

Assume without loss of generality that $(S_t)_{t\ge 0}$ is a semigroup of contractions. By the Szőkefalvi–Nagy theorem [28, p. 452, Théorème IV], we see that we can find a Hilbert space $({\mathcal {H}},||\cdot ||_{{\mathcal {H}}})$ containing H as a closed subspace and a strongly continuous group $({\mathcal {S}}_t)_{t\in {\mathbb {R}}}$ of unitary mappings such that $S_t=\pi {\mathcal {S}}_t$, where $\pi :{\mathcal {H}}\rightarrow H$ is the orthogonal projection.

Define $\psi _{{\mathcal {H}}}(y):=\rho (||y||_{{\mathcal {H}}}^2)$ and $V^{{\mathcal {H}}}_j(y):=V_j(\pi y)$, then it is easy to see that the assumptions of Theorem 4.7 are satisfied. The results of Teichmann [35] prove that the solution of

$$\begin{aligned} X^{{\mathcal {H}},y}_t = {\mathcal {S}}_t y + \sum _{j=0}^{d}\mathop \int \limits _{0}^{t}{\mathcal {S}}_{t-s}V^{{\mathcal {H}}}_j\left( X^{{\mathcal {H}},y}_s\right) \circ \mathrm{d}B^{j}_s \end{aligned}$$

(4.53)

satisfies $X^x_t=\pi X^{{\mathcal {H}},x}_t$, and similarly for the cubature approximations. Setting

$$\begin{aligned} Q^{{\mathcal {H}}}_{(\Delta t)}f(y) := \sum _{i=1}^{N}\lambda _i f\left( X^{{\mathcal {H}},y}_{\Delta t}\left( \omega ^{(\Delta t)}_i\right) \right) , \end{aligned}$$

(4.54)

Theorem 4.7 yields that $Q^{{\mathcal {H}}}_{(\Delta t)}\psi _{{\mathcal {H}}}(y)\le \exp (\tilde{C}\Delta t)\psi _{{\mathcal {H}}}(y)$ with some constant $\tilde{C}>0$, and from $\psi _{{\mathcal {H}}}(x)=\psi (x)$ for $x\in H$ we obtain that for $x\in H$,

$$\begin{aligned}&Q_{(\Delta t)}\psi (x) = \sum _{i=1}^{N}\lambda _i\rho \left( ||\pi X^{{\mathcal {H}},x}_{\Delta t}\left( \omega ^{(\Delta t)}_i\right) ||^2\right) \le \sum _{i=1}^{N}\lambda _i\rho \left( ||X^{{\mathcal {H}},x}_{\Delta t}\left( \omega ^{(\Delta t)}_i\right) ||_{{\mathcal {H}}}^2\right) \nonumber \\&\quad = Q^{{\mathcal {H}}}_{(\Delta t)}\psi _{{\mathcal {H}}}(x) \le \exp (\tilde{C}\Delta t)\psi _{{\mathcal {H}}}(x) = \exp (\tilde{C}\Delta t)\psi (x). \end{aligned}$$

(4.55)

The result is thus proved. $\square$

5 Convergence estimates of cubature schemes

We are now ready to prove rates of convergence for cubature on Wiener space on weighted spaces. We shall only prove these results in the infinite-dimensional setting; corresponding results in finite dimensions are obtained in a similar manner.

Let H be a Hilbert space and A the infinitesimal generator of a strongly continuous semigroup of pseudocontractions on H. Fix $\ell _0\in {\mathbb {N}}$. For $\ell =0,\ldots ,\ell _0$, let $H_{\ell }$ be subspaces of $H$ endowed with Hilbert norms $||\cdot ||_{H_{\ell }}, H_0=H$, such that for $\ell =0,\ldots ,\ell _0-1, H_{\ell +1}\subset H_{\ell }$ and $A:H_{\ell +1}\rightarrow H_{\ell }$ is a bounded linear operator. On $H_{\ell }$, we define D-admissible weight functions

$$\begin{aligned} \psi _{\ell }^{s}(x) := \left( 1+||x||_{H_{\ell }}^2 \right) ^{s/2}, \quad s\ge 1, \quad \ell =0,\ldots ,\ell _0, \quad \psi ^{s}:=\psi _{0}^{s}, \end{aligned}$$

(5.1)

and the functions

$$\begin{aligned} \varphi _{\ell ,0}(x) := \left( 1+||x||_{H_{\ell }}^2 \right) ^{1/2}, \quad \varphi _{\ell ,j}(x) := 1, \quad j\ge 1. \end{aligned}$$

(5.2)

Define the vectors of weight functions $\psi _{\ell }^{(n)}:=(\psi _{\ell }^{n-j})_{j=0,\ldots ,k}, k<n$, and $\varphi _{\ell }:=(\varphi _{\ell ,j})_{j=0,\ldots ,k}$.

Assumption 5.1

The vector fields satisfy

$$\begin{aligned} V_j\in {\mathcal {C}}^{\varphi _{\ell }}_k( H_{\ell }, H_\ell ) \quad \text {for} j=0,\ldots ,d\,\, \text {and}\,\, \ell =0,\ldots ,\ell _0. \end{aligned}$$

(5.3)

Remark 3.8 shows that $A\in {\mathcal {C}}^{\varphi _{\ell +1}}_k(H_{\ell +1},H_{\ell })$ for $\ell =0,\ldots ,\ell _0-1$. For $x\in H_{\ell }, \ell =0,\ldots ,\ell _0$, we can then consider the Da Prato–Zabczyk equation

$$\begin{aligned} \mathrm{d}X^x_t = AX^x_t\mathrm{d}t + \sum _{j=0}^{d}V_j(X^x_t)\circ \mathrm{d}B^j_t, \quad X^x_0 = x, \end{aligned}$$

(5.4)

on $H_{\ell }$. As the assumptions on the vector fields $V_j$ essentially mean that they are Lipschitz continuous with bounded derivatives, all these equations have unique solutions, agreeing if we vary $\ell$ for sufficiently smooth initial conditions.

Assumption 5.2

The Markov semigroup $(P_t)_{t\ge 0}, P_t f(x):={\mathbb {E}}[f(X^x_t)]$, is strongly continuous on ${\mathcal {B}}^{\psi _{\ell }^{n}}( H_{\ell } )$ for all $n\in {\mathbb {N}}$ and $\ell =0,\ldots ,\ell _0$. For some $k_0\in {\mathbb {N}}, P_t$ is a bounded map from ${\mathcal {B}}^{\psi _{\ell }^{(n)}}_k( H_{\ell } )$ into itself for $k=0,\ldots ,k_0$ and $n\in {\mathbb {N}}, n>k$, with norm bounded uniformly in $t\in [0,T]$ for every $T>0$.

See also Dörsek and Teichmann [11], Sect. 4, Lemma 7.19] for sufficient conditions for these assumptions.

5.1 Taylor expansion of stochastic partial differential equations

Theorem 5.3

Let $\ell =1,\ldots ,\ell _0$. Consider the strongly continuous semigroup $(P_t)_{t\ge 0}$ on the space ${\mathcal {B}}^{\psi _{\ell }^{n}}( H_{\ell } )$ with $n\ge 4$. Denote its generator by $({\mathcal {G}},{{\mathrm{dom}}}{\mathcal {G}})$.

Then, ${\mathcal {B}}^{\psi _{\ell -1}^{(n)}}_2( H_{\ell -1} )\subset {{\mathrm{dom}}}{\mathcal {G}}$, and

$$\begin{aligned}&{\mathcal {G}}f(x) = Df(x)(Ax) + {\mathcal {L}}_{V_0}f(x) + \frac{1}{2}\sum _{j=1}^{d}{\mathcal {L}}_{V_j}^2 f(x) \\&\quad \text {for}\; f\in {\mathcal {B}}^{\psi _{\ell -1}^{(n)}}_2( H_{\ell -1})\; \text {and}\; x\in H_{\ell }. \nonumber \end{aligned}$$

(5.5)

Proof

By the Itô formula, see, e.g., Da Prato and Zabczyk [7, Theorem 7.2.1], it follows that for $f\in A( H_{\ell -1} )$, we have $f\in {{\mathrm{dom}}}{\mathcal {G}}$ and f satisfies (5.5). Corollary 3.7 shows that the right hand side of (5.5) is a continuous linear operator ${\mathcal {B}}^{\psi _{\ell -1}^{(n)}}_{2}( H_{\ell -1} )\rightarrow {\mathcal {B}}^{\psi _{\ell }^{n}}( H_{\ell } )$. The closedness of ${\mathcal {G}}$ proves the claim. $\square$

The next result follows directly from Corollary 3.7, together with the explicit representation in (5.5).

Corollary 5.4

Let $k\ge 0$. Under the assumptions of Theorem 5.3, the infinitesimal generator ${\mathcal {G}}$ satisfies the mapping property

$$\begin{aligned} {\mathcal {G}}:{\mathcal {B}}^{\psi _{\ell -1}^{(n)}}_{k+2}( H_{\ell -1} ) \rightarrow {\mathcal {B}}^{\psi _{\ell }^{(n)}}_{k}( H_{\ell } ), \quad \ell =1,\ldots ,\ell _0. \end{aligned}$$

(5.6)

Induction now yields:

Corollary 5.5

Let $j=\ell ,\ldots ,\ell _0$. Under the assumptions of Theorem 5.3, the powers of the infinitesimal generator ${\mathcal {G}}$ satisfy

$$\begin{aligned} {\mathcal {G}}^j:{\mathcal {B}}^{\psi _{\ell -j}^{(n)}}_{k+2j}( H_{\ell -j} ) \rightarrow {\mathcal {B}}^{\psi _{\ell }^{(n)}}_{k}( H_{\ell } ). \end{aligned}$$

(5.7)

They are given explicitly by taking the powers of (5.5).

This allows us to obtain a Taylor expansion of $P_t f$ for smooth enough f, which we will compare to the Taylor expansion of cubature approximations.

Corollary 5.6

Let $f\in {\mathcal {B}}^{\psi _{\ell -(k+1)}^{(n)}}_{2(k+1)}( H_{\ell -(k+1)} ), k+1\le \ell \le \ell _0, n\ge 2(k+2)$.

Then,

$$\begin{aligned} P_t f = \sum _{j=0}^{k}\frac{t^j}{j!}{\mathcal {G}}^j f + t^{k+1}R_{t,k}f, \end{aligned}$$

(5.8)

where the linear operator $R_{t,k}:{\mathcal {B}}^{\psi _{\ell -(k+1)}^{(n)}}_{2(k+1)}( H_{\ell -(k+1)} )\rightarrow {\mathcal {B}}^{\psi _{\ell }^{n}}( H_{\ell } )$ satisfies

$$\begin{aligned} ||R_{t,k}f||_{\psi _{\ell }^{n}} \le C_T ||f||_{\psi _{\ell -(k+1)}^{(n)},2(k+1)} \quad \text {for}\; t\in [0,T] \end{aligned}$$

(5.9)

for a constant $C_T>0$ independent of f.

5.2 Taylor expansion of cubature approximations

For a multiindex $\alpha =(i_1,\ldots ,i_k)$, we define $\deg (\alpha ):=k+\#\left\{ j=1,\ldots ,k:i_j=0 \right\}$. The empty multiindex is denoted by $\emptyset$, corresponds to $k=0$, and satisfies $\deg (\emptyset )=0$. We set

$$\begin{aligned} {\mathcal {A}}_m:=\left\{ \alpha :\deg (\alpha )\le m \right\} \quad \text {and}\quad {\mathcal {A}}_m^{*}:={\mathcal {A}}_m\setminus \left\{ \emptyset ,(0) \right\} . \end{aligned}$$

(5.10)

Theorem 5.7

Assume that the cubature formula is of degree $m=2k+1$. For $f\in {\mathcal {B}}^{\psi _{\ell -(k+1)}^{(n)}}_{2(k+1)}( H_{\ell -(k+1)} ), k+1\le \ell \le \ell _0, n\ge 2(k+2)$,

$$\begin{aligned} Q_{(\Delta t)}f = \sum _{j=0}^{k}\frac{(\Delta t)^j}{j!}{\mathcal {G}}^{j} f + (\Delta t)^{k+1}\hat{R}_{\Delta t,k}f, \end{aligned}$$

(5.11)

where the linear operator $\hat{R}_{\Delta t,k}:{\mathcal {B}}^{\psi _{\ell -(k+1)}^{(n)}}_{2(k+1)}( H_{\ell -(k+1)} )\rightarrow {\mathcal {B}}^{\psi _{\ell }^{n}}( H_{\ell } )$ satisfies

$$\begin{aligned} ||\hat{R}_{\Delta t,k}f||_{\psi _{\ell }^{n}} \le C_T ||f||_{\psi _{\ell -(k+1)}^{(n)},2(k+1)} \quad \text {for}\; \Delta t\in [0,T] \end{aligned}$$

(5.12)

for a constant $C_T>0$ independent of f.

Proof

Under the assumptions on the vector fields, we can easily see that for every $f\in A(H_{\ell -(k+1)})$, we have the Taylor expansion

$$\begin{aligned}&f\left( X^x_{\Delta t} \left( \omega ^{(\Delta t)}_i\right) \right) \nonumber \\&\quad = \sum _{(i_1,\ldots ,i_k)\in {\mathcal {A}}_m}V_{i_1}\dots V_{i_k}f(x) I^{(i_1,\ldots ,i_k)}_{\Delta t}\left( \omega ^{(\Delta t)}_i\right) + \hat{R}^{i}_{\Delta t,k}f(x), \end{aligned}$$

(5.13)

where we define the iterated integrals by

$$\begin{aligned}&I^{(i_1,\ldots ,i_k)}_{\Delta t} \left( \omega _i^{(\Delta t)},g\right) \\&\quad := \mathop \int \limits _{0<t_1<\dots <t_k<\Delta t}g\left( X^x_{t_1}\left( \omega ^{(\Delta t)}_i\right) \right) \mathrm{d}\omega ^{(t),i_1}_{i}(t_1)\dots \mathrm{d}\omega ^{(t),i_k}_{i}(t_k), \nonumber \end{aligned}$$

(5.14)

$I^{(i_1,\ldots ,i_k)}_{\Delta t}(\omega ^{(\Delta t)}_{i}):=I^{(i_1,\ldots ,i_k)}_{\Delta t}(\omega ^{(\Delta t)}_{i},1\!)$, the remainder term $\hat{R}^{i}_{\Delta t,k}f$ satisfies

$$\begin{aligned} \hat{R}^{i}_{\Delta t,k}f(x) = \sum _{\begin{array}{c} (i_1,\ldots ,i_k)\in {\mathcal {A}}_m\\ (i_0,i_1,\ldots ,i_k)\notin {\mathcal {A}}_{m} \end{array}} I^{(i_0,\ldots ,i_k)}_{\Delta t}(\omega ^{(\Delta t)}_i,f_{(i_0,\ldots ,i_k)}), \end{aligned}$$

(5.15)

and we set $\beta _0(x):=Ax+V_0(x), \beta _j(x):=V_j(x), j=1,\ldots ,d$, and $f_{(i_0,\ldots ,i_k)}:=\beta _{i_0}\dots \beta _{i_k}f, (i_0,\ldots ,i_k)\in \left\{ 0,\ldots ,d \right\} ^{k+1}$. Summing up, it is easy to see by the scaling of the cubature paths that we can find a remainder term $(\Delta t)^{k+1}$ as in the claim of the theorem with the correct estimates. To see that the initial terms have the form given, we use the degree $2k+1$ of the cubature and the explicit formula of ${\mathcal {G}}$ from Theorem 5.3. A density argument proves the result. $\square$

5.3 The rate of convergence

We can now present our main result.

Theorem 5.8

For $f\in {\mathcal {B}}^{\psi _{\ell -(k+1)}^{(n)}}_{2(k+1)}( H_{\ell -(k+1)} ), k+1\le \ell \le \ell _0, n>2(k+1), 2(k+1)\le k_0$,

$$\begin{aligned} ||P_T f - Q_{(T/n)}^n f||_{\psi _{\ell }^{n}} \le C_T n^{-k}||f||_{\psi _{\ell -(k+1)}^{(n)},2(k+1)} \end{aligned}$$

(5.16)

with a constant $C_T$ independent of f.

Proof

The local estimate follows from a combination of Corollary 5.6 and Theorem 5.7. In the core of the argument lies the very definition of cubature formulas, where the expectations of iterated Brownian integrals is mimicked, see formula (4.1). The stability of $Q_{(T/n)}$ from Corollary 4.8 and the assumed invariance of ${\mathcal {B}}^{\psi _{\ell -(k+1)}^{(n)}}_{2(k+1)}( H_{\ell -(k+1)} )$ with respect to $P_t$ prove the claim by means of the telescoping sum

$$\begin{aligned} (P_T f - Q_{(T/n)}^n) f = \sum _{i=1}^{n-1} {\left( Q_{(\frac{T}{n})}\right) }^{(n-i)} \left( P_{(\frac{T}{n})} - Q_{\frac{t}{n}}\right) P_{\frac{iT}{n}} f \, \end{aligned}$$

(5.17)

for $f \in {\mathcal {B}}^{\psi _{\ell -(k+1)}^{(n)}}_{2(k+1)}( H_{\ell -(k+1)} )$. $\square$

Example 5.9

Let $H_\ell ={\mathbb {R}}^N, \ell \ge 0$, be finite-dimensional, and assume $n\ge 5$; in the finite-dimensional setting, we do not need to consider subspaces of the state space. Then, $f_{m,i}\in {\mathcal {B}}^{\psi ^{(n)}}_{k}(H)$ for all $k\ge 0$, where $f_{m,i}(y)=y_i^m, i=1,\ldots ,n, y=(y_1,\ldots ,y_N)$, and $m=1,\ldots ,4$. This implies that not only the expected value and the variance, but also the skewness and kurtosis are accurately computed by our scheme. Similarly, mixed moments are determined to high accuracy, and if n is even larger, this also holds true for higher degree moments. Such a property is very useful in risk management, where high precision in higher moments means an accurate evaluation of risk. Similar observations were made in [1] and [33].

Example 5.10

The Heath–Jarrow–Morton framework is included in our setup. As explained in [12], it is more natural to use $\cosh$-weighted spaces instead of polynomially weighted spaces in this case. The more general definition of vector fields in Definition 3.1 allows us to enlarge the class of admissible equations considerably compared to [12].

6 Numerical example

The FitzHugh–Nagumo model is a popular model for the behaviour of neurons and allows the analysis of noise-induced phase changes. We consider the SODE model with multiplicative and additive noise from [34], spatially extended similarly as in [36]. The stochastic partial differential equation we analyse reads

$$\begin{aligned}&\varepsilon \mathrm{d}u(t,x) = \frac{\partial ^2}{\partial x^2}u(t,x)\mathrm{d}t + ( u(t,x)(u(t,x)-1)(a-u(t,x)) - bv(t,x) )\mathrm{d}t \nonumber \\&\qquad \qquad \qquad \quad + 2\alpha u(t,x)(u(t,x)-1)\circ \mathrm{d}W^{d-1}_t, \end{aligned}$$

(6.1a)

$$\begin{aligned}&\mathrm{d}v(t,x) = ( z(u(t,x)-c) - v(t,x) )\mathrm{d}t \nonumber \\&\qquad \qquad \qquad + 2\beta u(t,x)\circ \mathrm{d}W^d_t + 2\gamma \sum _{j=1}^{d-2}\varphi _{j}(x)\circ \mathrm{d}W^j_t, \end{aligned}$$

(6.1b)

complemented by Neumann boundary conditions, $\frac{\partial }{\partial x}u(t,0)=\frac{\partial }{\partial x}u(t,1)=0, t>0$, and initial values, $u(0,x)=u_0(x), v(0,x)=v_0(x), x\in (0,1)$. This implies that there is no signal, i.e., no deterministic inhomogeneous Neumann boundary condition or forcing, so the only reason for phase changes, i.e., deflecting the system out of equilibrium, comes from the multiplicative noise terms $2\alpha u(t,x)(u(t,x)-1)\circ \mathrm{d}W^{d-1}_t$ and $2\beta u(t,x)\circ \mathrm{d}W^d_t$ or the additive noise term $2\gamma \sum _{j=1}^{d-2}\varphi _j(x)\circ \mathrm{d}W^j_t$. Here, u denotes the fast, v the slow variable, $(W^1_t,\ldots ,W^d_t)_{t\ge 0}$ is d-dimensional Brownian motion, $\varepsilon >0, a\in (0,1), b, c, z, \alpha , \beta , \gamma >0$, and $\varphi _j:[0,1]\rightarrow {\mathbb {R}}$ are some smooth functions.

While the Nemytskii nonlinearities in the equation for u are non-Lipschitz, they can be cut off in a smooth manner to Lipschitz continuous functions outside a large enough interval including [0,1]. This approach seems to be reasonable, as we are interested in the behaviour of the system only for functions u with values in this interval where the stable equilibria of the corresponding deterministic system lie. Furthermore, in our numerical examples, we never observed values for u outside $[-5\cdot 10^{-3},1+5\cdot 10^{-3}]$. It then follows that (6.1) has solutions lying in all Sobolev spaces $\hbox {H}^\ell (0,1), \ell \in {\mathbb {N}}$, provided the initial values for u and v and the functions $\varphi _j, j=1,\ldots ,d-2$, are regular enough. Hence, (6.1) falls into the setting of our numerical schemes: Using the notation from Sect. 5, we set

$$\begin{aligned} H_{\ell }:&= \Biggl \{ (u,v):u, v\in \hbox {H}^{1+2\ell }(0,1)\; \text {with}\; \frac{\partial ^{1+2i}}{\partial x^{1+2i}}u(0)\nonumber \\&= \frac{\partial ^{1+2i}}{\partial x^{1+2i}}u(1)=0\; \text {for}\; i=1,\ldots ,\ell \Biggr \}, \end{aligned}$$

(6.2)

$A(u,v):=(\frac{\partial ^2}{\partial x^2}u,0)$, together with Neumann boundary conditions, and

$$\begin{aligned}&V_0(u,v):=( u(u-1)(a-u) - bv, z(u-c)-v ), \end{aligned}$$

(6.3)

$$\begin{aligned}&V_j(u,v):=(0,2\gamma \varphi _j), j=1,\ldots ,d-2, \end{aligned}$$

(6.4)

$$\begin{aligned}&V_{d-1}(u,v):=(2\alpha u(u-1),0), \quad \text {and}\end{aligned}$$

(6.5)

$$\begin{aligned}&V_d(u,v):=(0,2\beta u). \end{aligned}$$

(6.6)

After cutting off $V_0$ and $V_{d-1}$ as suggested above, all these vector fields satisfy Definition 3.1 by applying Runst and Sickel [30, p. 381, Theorem 2; p. 32, Theorem 1]. It follows that we have optimal weak rates of convergence for sufficiently smooth test functions. If rates of convergence are to be analysed without cutting off the vector fields, an approach similarly as in Dörsek [10] using a quickly growing weight function might be applicable. We stress that this problem, not even with cut off vector fields, can be analysed using the theory from Dörsek [10] or Dörsek and Teichmann [12], as Nemytskii operators are not contained in either setting. Similarly, the results of Bayer and Teichmann [2], Sect. 4] are not applicable because the vector fields $V_{d-1}$ and $V_d$ do not have any smoothing properties.

In order to gauge phase transitions, we want to determine the probability that the system ends up in one stable equilibrium, given that it started in the other. Fixing the parameters to be $\varepsilon =0.01, a=c=0.47, b=0.1$, and $z=1.0$, as in Tang et al. [34], the two stable equilibria are given approximately by $(u^\infty _{1},v^\infty _{1})=(.112702,-.357298)$ and $(u^\infty _{2},v^\infty _{2})=(.887298,.417298)$. We choose the initial value $u_0(x):=u^{\infty }_1, v_0(x):=v^{\infty }_1, x\in (0,1)$. The two functions whose expected values we approximate are $f_i(u,v):=\exp (-||u-u^\infty _i||_{\hbox {L}^2(0,1)}^2/\delta ), i=1,2$, with $\delta =0.05$, which serve as proxy for the probability that u ends up in the state $u^{\infty }_i, i=1,2$. These functions are smooth and bounded on $\hbox {H}^\ell (0,1)$ for $\ell \ge 0$, and by the compact embedding $\hbox {H}^{\ell +1}(0,1)\rightarrow \hbox {H}^{\ell }(0,1), \ell \ge 0$, and Dörsek and Teichmann [12, Theorem 5], they are included in ${\mathcal {B}}^{\psi }_{k}(H^\ell )$ for $\ell \ge 0$, where the weight functions are chosen as in Sect. 5. We set $\alpha =0.008, \beta =0.0001, \gamma =0.003, d=6$, and $\varphi _j(x)=\cos ( (j-1)\pi x)$, i.e., we force the low modes, and want to determine

$$\begin{aligned} {\mathbb {E}}[f_i(u(T,\cdot ))], \quad i=1,2, \end{aligned}$$

(6.7)

for $T=10$.

For the space discretisation, we employ a cosine expansion, writing

$$\begin{aligned} u(t,x)=\sum _{i=0}^{M-1}u_i(t)\cos (i\pi x) \quad \text {and}\quad v(t,x)=\sum _{i=0}^{M-1}v_i(t)\cos (i\pi x) \, , \end{aligned}$$

(6.8)

which is efficient due to forcing of low modes. In the time variable, we first perform a Strang-type splitting. The split equations read

$$\begin{aligned} \varepsilon \mathrm{d}u^{0}(t,x)&= \left( \frac{\partial ^2}{\partial x^2}u^{0}(t,x) + u^{0}(t,x)(u^{0}(t,x)-1)(a-u^{0}(t,x)) - bv^{0}(t,x)\right) \mathrm{d}t, \nonumber \\ \mathrm{d}v^{0}(t,x)&= (z(u^{0}(t,x)-c)-v^{0}(t,x))\mathrm{d}t, \quad \text {and} \end{aligned}$$

(6.9)

$$\begin{aligned} \varepsilon \mathrm{d}u^1(t,x)&= 2\alpha u^1(t,x)(u^1(t,x)-1)\circ \mathrm{d}W^{d-1}_t, \nonumber \\ \mathrm{d}v^1(t,x)&= 2\beta u^1(t,x)\circ \mathrm{d}W^d_t + 2\gamma \sum _{j=1}^{d-2}\varphi _j(x)\circ \mathrm{d}W^j_t. \end{aligned}$$

(6.10)

The equations for $(u^1,v^1)$ are solved by a degree 5 cubature scheme on path level, cf. Lyons and Victoir [24] (see Gyurkó and Lyons [15] for an alternative degree 5 scheme on flow level), which is evaluated via Quasi Monte Carlo integration. The equations for $(u^0,v^0)$ are split further into

$$\begin{aligned} \varepsilon \mathrm{d}u^{01}(t,x)&= \frac{\partial ^2}{\partial x^2}u^{01}(t,x) \mathrm{d}t, \nonumber \\ \mathrm{d}v^{01}(t,x)&= 0, \quad \text {and} \end{aligned}$$

(6.11)

$$\begin{aligned} \varepsilon \mathrm{d}u^{02}(t,x)&= ( u^{02}(t,x)(u^{02}(t,x)-1)(a-u^{02}(t,x)) - bv^{02}(t,x) )\mathrm{d}t, \nonumber \\ \mathrm{d}v^{02}(t,x)&= (z(u^{02}(t,x)-c)-v^{02}(t,x))\mathrm{d}t. \end{aligned}$$

(6.12)

Due to the particular choice of the spatial discretisation, (6.11) can be solved analytically. As we want to use large timesteps, we choose a geometric integrator for the approximation of (6.12), the extended Störmer–Verlet scheme from Hairer et al. [16], Sect. 1.8]. The resulting non-linear equations are solved by the Newton algorithm. This is efficient, as (6.12) corresponds to entirely separated ODEs at the discretisation points, whence the non-linear equations to be solved are one-dimensional.

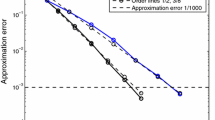
Finally, the split problems are concatenated using the symmetrically weighted sequential splitting, see Oshima et al. [27]. Hence, we expect to observe second order weak convergence. This is illustrated in Fig. 1, where we show the somehow more expressive relative errors with respect to the reference value (in contrast to Theorem 5.8, where errors of norms relative to the norm of the initial value are estimated)

$$\begin{aligned} \frac{ |{\mathbb {E}}_{\hbox {app}}[f_i(u(T,\cdot ))] - {\mathbb {E}}_{\hbox {ref}}[f_i(u(T,\cdot ))] |}{ {\mathbb {E}}_{\hbox {ref}}[f_i(u(T,\cdot ))] }, \quad i=1,2. \end{aligned}$$

(6.13)

The computations were performed using 16 cores of a ProLiant DL385 G7 with 24 AMD Opteron 6174 cores and 128 GB RAM in total. The reference values ${\mathbb {E}}_{\hbox {ref}}[f_i(u(T,\cdot ))]$ were obtained using $M=128$ terms in the cosine expansions, $N=256$ timesteps, and $K=2^{20}$ Quasi Monte Carlo points, applying the Sobol’ sequences of Joe and Kuo [18]. They were found to be ${\mathbb {E}}_{\hbox {ref}}[f_1(u(T,\cdot ))]\approx 0.471830$ and ${\mathbb {E}}_{\hbox {ref}}[f_2(u(T,\cdot ))]\approx 0.397405$. In the computation of the approximate values ${\mathbb {E}}_{\hbox {app}}[f_i(u(T,\cdot ))]$, we fixed $M=32$ and $K=2^{16}$, and used the number N of timesteps indicated in Fig. 1. The numerical results show second order convergence, perturbed probably because we compare not to an exact reference value, but to an approximate one. In particular, we obtain a relative error of less that $2\cdot 10^{-3}$ with only 64 timesteps. This calculation takes 10 s, which establishes the effectivity of the proposed algorithm.

Fig. 1

Errors in weak approximation of the stochastic FitzHugh–Nagumo equation

7 Conclusions

We considered the weak approximation of marginal distributions of stochastic (partial) differential equations. We extended the functional analytic framework of Röckner and Sobol [29], used for the numerical analysis of stochastic evolution equations in Dörsek [10] and Dörsek and Teichmann [11, 12], to more general characteristics through a flexible formulation of directional derivatives in weighted spaces. This setting was then used to prove optimal rates of convergence of cubature schemes for more general equations. Results of numerical computations for an example from mathematical biology, a spatially extended stochastic FitzHugh–Nagumo model, were shown to demonstrate that our theoretical findings can be applied to practically relevant problems.