Abstract
In the present paper, a behavioral model is proposed for study of the individual contributions to shear capacity in shear-critical reinforced concrete members. On the basis of the relationship between shear and bending moment (V = dM/dx) in beams subjected to combined shear and moment loads, the shear resistant mechanism is explicitly decoupled into the base components—beam action and arch action. Then the overall behavior of a beam is explained in terms of the combination of these two base components. The gross compatibility condition between the deformations associated with the two actions is formulated utilizing the truss idealization together with some approximations. From this compatibility condition, the ratio of the shear contribution by the tied arch action is determined. The performance of the model is examined by a comparison with the experimental data in literatures. The results show that the proposed model can explain beam shear behavior in consistent way with clear physical significance.
Similar content being viewed by others
1 Introduction
Up to now, the beam shear problem remains one of the more controversial aspects of structural reinforced concrete analysis and design, and it has been generally agreed that the truss model theory provides a more promising way to treat the problem. That is not only because it provides a clear concept of how a reinforced concrete beam resists shear after cracking, but also because the effect of various loading conditions can be included in a logical way (ASCE-ACI Committee 445 1998; ASCE-ACI Committee 426 1973; Hsu 1993).
The classical shear analysis of Ritter and Mörsch explains the shear behavior in the cracked state by a truss analogy, using a truss with parallel chords with 45° inclined concrete struts and no stresses across the cracks. In this model the bending moment is carried by the top chord (concrete compression zone) and the bottom chord (main longitudinal reinforcement), and the applied shear force is fully carried by the web by means of inclined compressive stresses in the concrete and tension in the stirrups. This simplified version of truss model has long provided the basis for the formulation of general shear design codes, such as in ACI-318 (1999) and Eurocode-2 (Commission of the European Communities 1991). During last four decades, the concept of the truss model theory has been greatly extended, and now several approaches have been developed (Marti 1985; Nielsen 1984; Vecchio and Collins 1986; Schlaich et al. 1987; Ramirez and Breen 1991). An excellent review of the current theories as well as available experimental evidences are given by ASCE-ACI Committee (ASCE-ACI Committee 445; ASCE-ACI Committee 426).
One approach (ACI Committee 318) has been to add a concrete contribution term to the web shear reinforcement contribution, assuming a parallel chord truss with the strut angle of 45°. Another approach (CEB/FIP 1990; Commission of the European Communities 1991) has been the use of a parallel chord truss with a variable angle of inclination of the diagonal struts. This approach is referred to as the standard truss model with no explicit concrete contribution, and is explained by the existence of aggregate interlocking and the dowel action, which make a lower inclination of the concrete struts and a higher effectiveness of the stirrups. A combination of the variable-angle truss with parallel chords and a concrete contribution has also been proposed. This approach has been referred to as the modified truss model (American Association of State Highway and Transportation Officials 2002; Ramirez and Breen 1991).
These resent approaches, however, does not directly account for the individual components of the concrete contribution in shear resistant mechanism, such as the shear carried by the concrete compression zone, the dowel action, and the aggregate interlocking action, which are distinguishable from one another (Taylor 1974). The constituent resistant components of various truss approaches are summarized and compared at Table 1. It can be seen that the shear force by the concrete compression zone is not directly accounted.
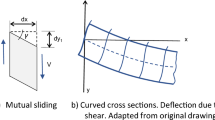
In the early investigations (Lorentsen 1965; Leonhardt 1965; Kani 1964), complex models combined with arch and truss, as typically shown in Fig. 1, were recognized from the observation of crack patterns and the evidences measured in different beams. In this model the compression chord of the truss is curved, so that the behavior of a beam is represented partly by tied arch and partly by beam. Thus, a substantial load is carried essentially by the tied arch action. Leonhardt (1965) observed that a remarkable shear is resisted by an inclined top chord (the concrete compression zone). In the normal T beams he tested, the web element carried less than half of the total shear force even under ultimate loading stages, and the distribution ratio was largely dependent upon the ratio between web stiffness and chord stiffness. In spite of better representation of the behavior of beams, however, this model has been used largely as a conceptual tool to describe beam behavior rather than a precise analytical model. This is mainly because the geometry of the arch rib (inclined top chord) cannot be precisely defined due to the nature of a statically indeterminate system (ASCE-ACI Committee 426).
Therefore, the present work is intended to numerically formulate the truss model with an inclined compression chord shown in Fig. 1 by decoupling the beam behavior into the tied arch and the beam. The theoretical base concept for the present approach is based on the relationship between shear and bending moment in a cracked reinforced concrete beam, i.e., V = dM/dx. Utilizing some idealizations together with the recent elaborations by Collins and Mitchell (1991) and Hsu (1993), a gross compatibility condition is established and formulated between the deformation associated with the tied arch and the deformation with the web. Thereby, the beam shear resistant mechanism is decoupled into the base components. The performance of the present approach is briefly examined by a comparison with the existing experimental data and a sensitivity study. It is also shown that the theoretical results can explain in a rigorous and consistent way the experimentally observed behavior of beam failing in shear.
2 Derivation of Base Concept
Consider a simply supported reinforced concrete beam directly loaded as shown in Fig. 2a, in which shear force V and moment M act simultaneously throughout the shear span. After flexural cracking the moment on a cross section is resisted by the internal force couple C and T with the lever arm of z, that is M = Tz = Cz. When this relationship of the flexural resistance is combined with the well-known relationship between shear and the rate of change of bending moment along a beam V = dM/dx, the shear force can be expressed as a sum of two terms (Park and Paulay 1975; Kim and Jeong 2011a, b, c):
As known from various proceeding studies, the first term arises from the transmission of a steel force into the concrete by means of bond stresses, and it is said to be the shear resistant component by beam action (Kani 1964; Park and Paulay 1975). Consider a segment cut out from the beam between two adjacent vertical cross sections distance dx apart in Fig. 2a, the difference of tension dT causes shear force on the bottom face of the web element mnop as shown in Fig. 2b. As the same manner, the difference of compressive resultant dC acts on the upper face. These shear forces on the top and bottom of the web element produce a couple moment zdT (=zdC), which must be balanced by the moment of shear forces acting on the vertical faces mn and op. Thus, the vertical shear force is expressed by the first term of Eq. (1).
The second term in Eq. (1) directly implies the vertical component of the inclined compression resultant force C, and it is referred to the shear component by arch action (Kani 1964); Park and Paulay 1975). That is because the compression resultant is equal to the tension resultant T and the slope of the resultant is mathematically expressed dz/dx as shown in Fig. 2c. This means that the beam behaves as a tied-arch, and a part of the applied shear is carried by the inclined top chord.
From such mechanical interpretation on Eq. (1), it is seen that the applied shear is essentially resisted by a combination of the two base components that are distinctively different actions—beam action and arch action. Thus, the extent to which each action contributes to shear resistance in a beam will depend on the compatibility of deformations associated with these actions. If such beam shear behavior could be decoupled into the base components, the shear resistant mechanism would be much clearly described. Accordingly, for the purpose of the present study, it is to employ a factor-α defined by follows (Kim and Jeong 2011a, 2011b, 2011c):
By this definition, the value of α varies between 0 and 1 and depends on the compatibility condition of the deformations associated with the beam and arch action.
2.1 Smeared Truss Idealization with Inclined Chord
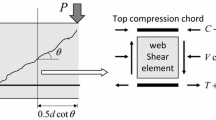
As in a usual smeared truss modeling (Hsu 1993), the stress field in the beam segment shaded in Fig. 2a can be idealized to have three discrete elements with each having a different function to resist the applied loads as shown in Fig. 3a. The area within the compression stress block is assumed to concentrate at the location of the resultant C and form the top chord. The longitudinal tensile steel bars and the surrounding concrete are also assumed to be concentrated at the geometric centroid and constitute the bottom chord. The middle element separated from the tension and compression chords can be treated as a web shear element subjected to pure shear.
In order to include the shear resistant mechanism due to the arch action, an inclined top chord is installed in the present model, instead of a paralleled chord, With its inclination, the top chord has a function to resist not only against the compression resultant C caused by the applied moment M but also against the part of the applied shear αV, and in turns the rest of the shear (1 − α)V must be allocated to the web shear element. Consecutively extending such idealization to whole span of a beam may lead to an idealized form of a tied arch having a membrane shear element inside as shown in Fig. 4a, in which the lever arm z varies from z0 at the maximum moment section to 0 at the support section. The force transmitted between the elements is dC/dx (=dT/dx). This force acts as a form of shear flow on the web shear element, while it acts as a form of distributed axial force on the chords.
In a simple strut-and-tie model, the tensile force of the tie (bottom chord) is constant throughout the span (dT/dx = 0), so that beam action cannot be developed in the web shear element. Accordingly, the shear and moment must be fully resisted by the inclined top (strut) and bottom chords, as shown in Fig. 3c. From the view of the present model, it is said that a simple strut-and-tie model is the extreme case of the present model when α is 1.0. On the other hand, a parallel chord truss model (dz/dx = 0 as seen in Fig. 3b) cannot rely on the arch action to sustain shear, thus it is the other extreme case of the present model with α of 0. It may be realized therefore that the internal force flow of usual beams can be closely described by a proper assignment of the value of α, as conceptually illustrated in Fig. 3d.
2.2 Gross Compatibility Condition
The idealization above make it possible to evaluate the state of the cross sectional deformation of a reinforced concrete beam. Consider the deformation of the element mnop in a beam under a concentrated load as shown in Fig. 4a. The final deformation of the element can be decomposed into the two base components—the deformation associated with the arch action and the deformation associated with the beam action. As stated before, the bending moment causes the internal couple C and T at the chords, resulting in the axial shortening of the top chord and the axial elongation of the bottom chord. Thus these axial deformations eventually produce a bending curvature on the element as shown in Fig. 4b.
The element further undergoes a shear deformation because it is subjected to a pure shear dT/dx, which is equal to (1 − α)V/z, as shown in Fig. 4c. Linear distortion can be assumed with the average shear strain of γ w . It is seen from the figure that the shear strain is equal to the amount that the upper edge displaces horizontally with respect to the lower side divided by the depth of the element. Consequently, this shear deformation of the web shear element should be compatible with the relative displacements of the top and bottom chord with respect to the bending planes m′–n′, which are designated by u m and u n respectively in Fig. 4c, because the element is connected to the chords. The relative displacements of the chords can be visualized easily if the bending deformation and the couple C and T acting on the chords are omitted and the all elements are stretched as shown in Fig. 4e.
By the symmetry, the relative displacement of the top chord at the loading section must be zero. And the displacement of the top chord u m at the section m–n, a–x apart from the loading section, is equal to the elongation of the top chord due to the distributed axial force dC/dx over the length of a–x. Therefore, the u m can be obtained by successive integrations over the length. As the same manner, together with zero displacement at the support section due to the support restraint, the relative displacement of the bottom chord u n is also obtained. Thus,
where (EA) tc and (EA) bc are the axial stiffness of the top chord and the bottom chord respectively. These relative displacements of the chords should be compatible with the shear deformation of the web shear element as sketched in Fig. 4e. Thus, the following relationship should be satisfied:
From the view of the gross compatibility relationship above, it can be seen that the ratio of contribution by each action to total shear resistance in a beam is dependent on the relative stiffness ratio between the chords and the web (Kim and Jeong 2011a, 2011b, 2011c).
2.3 Simplified Arch Shape Function
The presence of non-zero values of dz/dx in the present approach is eventually leading to variable lever arm length z over the span of a beam. Combining the definition of αV = Cdz/dx with the relationship of C = Vx/z in a prismatic simple beam subjected to a direct point loading, the factor-α can be expressed in terms of z and x as follow:
For the establishment of the present approach, the value of α is assumed to remain constant over the shear span in a given prismatic beam. Then, with the boundary condition of z = z o at x = a, the general solution of Eq. (5) can be obtained in term of the lever arm z over the shear span as the following form:
where z o is the lever arm calculated from the conventional beam theory. Figure 5 shows the geometrical expressions of Eq. (6) as α varies from 0 to 1.0. As seen in the figure, Eq. (6) represents a simple arch shape, and its curvature is mainly dependent on the value of α. For example, when α = 0, Eq. (6) becomes z x = z o with dz/dx = 0 over the entire span, corresponding to the traditional beam theory with no arch action. While, when α = 1.0, Eq. (6) stands for a straight line from the support to the loading point, representing the situation in which the load is carried by a simple strut-and-tie action.
It is noted that for the beams subjected to other type of loadings rather than direct point loadings, the corresponding arch shape function can be obtained by the same manner above, and it will be the following general form (Kim and Jeong 2011a, b, c):
where M max is the maximum moment at a zero shear section. Utilizing this general expression, the arch shape can be easily formulated for a beam subjected to various types of loadings, such as uniform loaded beams or eccentrically loaded columns, on condition that an appropriate α is known. Now it becomes clear that the crux of the present approach is the assignment of a value to the factor-α, and the value can be determined from the gross compatibility condition of Eq. (4).
3 Formulation
3.1 Web Shear Element
As stated before, the web shear element can be treated as a membrane element subjected to pure shear force (1 − α)V. After diagonal cracking, the concrete is separated by diagonal cracks into a series of concrete struts as shown in Fig. 6a. The shear force produces a set of bi-axial stress field constituted with the compressive principal stress f 2 and the tensile principal stress f 1 with inclination angle of θ as shown in Fig. 6. The reinforcing bars are assumed to be a link member transmitting axial force only. The behavior of such a membrane element is well explained by either Collins’ MCFT (Vecchio and Collins 1986) or Hsu’s STM (Hsu 1993).
The equilibrium conditions, which relate the concrete stresses and the stirrup stress to the applied shear stress, can be expressed in terms of average stresses. These relationships are derived from the Mohr’s circle shown in Fig. 6. These are
where v is an average shear stress defined by V/b w z, f2 is positive in compression, and f1 is positive in tension. From the vertical force equilibrium the transverse concrete stress f t of Eq. (9) must be balanced by the stirrup stress:
In the same manner, the longitudinal concrete stress f x of Eq. (10) is balanced by the chords and the horizontal web steels, if any. When the horizontal web steels are not provided, it is transferred to the top and bottom chord. The equilibrium of the resultants on the right face is shown by the force polygon in Fig. 6b, and the longitudinal compressive resultant N b produced by the f x is
The acting point of this resultant will be z/2 from the center of the bottom chord. The average stress and average strain of the concrete in each principal direction (axis 1–2 in Fig. 6a) is assumed to obey the material laws developed by Vecchio and Collins (Vecchio and Collins 1986), as summarized in Figs. 7a and 7b. Thus, after diagonal cracking with taking f cr = 0.33 \( \sqrt {f_{c}^{'} } \) (MPa), for principal tensile direction;
For principal compressive direction with taking ɛ co = 0.002;
In beams having vertical stirrups, the transverse average strain ɛ t can be approximately evaluated using CEB/FIP MC-90 (1990) the equation for tension stiffening effect, which is shown in Fig. 7c. Replacing f s by f v of Eq. (11), then ɛ sm corresponds to ɛ t . Thus the following relationship is obtained:
From the compatibility condition satisfying Mohr’s strain circle shown in Fig. 7d, the average shear strain γ w of the web shear element is expressed in terms of ɛ1, ɛ2, and ɛ t as follows:
Substituting Eqs. (13), (14) and (15) for ɛ1, ɛ2 and ɛ t respectively in Eq. (16), the shear strain γ w of the web element is eventually expressed in terms of f1, f2 and θ.
3.2 Redistribution of Resultants in a Section
As previously stated, the vertical component of the axial force in the inclined top chord is the shear carried by the arch action, and it is designated by αV. This shear force will be combined with flexural compression resultant C, eventually leading to form an inclined thrust line (arch). For the extension of the present approach to a simple strut-and tie model, it may be technically required that the shear force αV is accompanied by the longitudinal resultant N a , and whose acting point is temporarily denoted by z a as shown in Fig. 8. That is,
It has been known that significant longitudinal forces are caused by each base action. By such induction of the longitudinal forces at a cross section, the internal couple C o and T o calculated from the conventional beam theory due to the bending moment is redistributed to meet the equilibrium condition over the section. Figure 9 shows the forces N a and N b acting on the points z a and 0.5z from the reinforcement level in addition to the internal force couple C o − ΔC and T o + ΔT. To satisfy the equilibrium condition in longitudinal direction, the change in the compression resultant ΔC and that in steel tension ΔT are seen to be
The redistributed compression resultant C o − ΔC and the longitudinal force due to the arch action N a should be combined to form a final compression resultant C in a section. Hence, as shown in Fig. 9, the final acting point z will be
The lever arm length z above is established on the basis of the force equilibrium conditions at a section. Whereas the z defined by Eq. (7) is mathematically derived on the basis of the assumption of constant α throughout the shear span. These values of z must be identical to each other. By equating these two equations with substituting Eqs. (12), (17) and (18) and the approximation of z a ≅ z, the inclined angle θ is expressed in terms of α and f1:
where R x = M x /Mmax, that is the sectional moment ratio with respect to the maximum moment of a beam.
From the moment equilibrium at a section with z a ≅ z, the final compression force C in the top chord and the tension force T in the bottom chord should be
Figure 10 shows the final configuration of the resultants acting at a section. From the figure, it can be realized that the equilibriums in both the shear and the moment are simultaneously satisfied at the section. Also, the slope of the thrust in the top chord is V a /C, which is equivalent to dz/dx in Fig. 2c. As the section approaches toward the support, the slope dz/dx becomes steeper because C becomes smaller owing to the smaller sectional moment. This is the primary reason for which a tied-arch action is formed in cracked reinforced concrete beams.
3.3 Relative Displacements of Top and Bottom Chord
As described before, the relative displacements of the top and bottom chords u m and u n can be evaluated by Eq. (3). Utilizing Eqs. (2) and (7) together with Fig. 4, dC/dx and dT/dx at each section are simply expressed in terms of α and V x :
For the evaluation of the axial stiffness of the top and bottom chord, some approximations are required because the actual stress distributions are relatively complex. It may be reasonable estimation that the effective depth of the compression chord is equal to the depth of the rectangular compression stress block and remains constant along the span as sketched in Fig. 11. With this approximation and the substitution of Eq. (22), Eq. (3a) becomes
where E c is the concrete elastic modulus, and A tc is the effective area of the top chord estimated based on the effective depth defined above. The axial deformation of the tension chord due to dT/dx, which corresponds to the relative displacement u n , is approximately evaluated using CEB/FIP MC-90 the tension stiffening effect expression (Fig. 7c). In applying this formula to a beam, the height of the effective tensile tie is normally assumed to be about 2.5(h − d) as shown in Fig. 11 (CEB-FIP 1990). Hence, Eq. (3b) can be rewritten as follow:
where \( \rho_{eff} = \frac{{A_{s} }}{b \cdot 2.5(h - d)} \) and x is distance from the support.
3.4 Solution Algorithm
All of the relationships required to determine the value of α have been discussed above. For a specific section in a beam with vertical stirrups at a given load, a suitable iterative procedure is as follows:
-
Step-1: Assume a value of α
-
Step-2: Choose a value of ɛ1, then calculate f1 from Eq. (13)
Then, check that γ w from Eq. (16a) = γ w from Eq. (16b) or not.
If γ w from Eq. (16a) ≠ γ w from Eq. (16b), return to Step-2.
If γ w from Eq. (16a) ≅ γ w from Eq. (16b), go to Step-7.
-
Step-7: Calculate u m from Eq. (23a), and u n from Eq. (23b)
-
Step-8: Check that γ w = (u m + u n )/z or not.
If γ w ≠ (u m + u n )/z, return to Step-1 and repeat
If γ w ≅ (u m + u n )/z, take the last assumed α value.
With the help of a spread sheet calculator, the procedure above is easily performed. As a tip for fast iteration, it is recommended to use the inverse value of the shear span-to-depth ratio of the beam considered as an initial value of α in Step-1.
4 Verification
As part of a large investigation of the shear behavior in reinforced concrete beams at Stuttgart University in early 1960s, Leonhardt (1965) investigated the effectiveness of stirrups on the shear strength of beams. The four beams he tested had the identical web reinforcement and longitudinal reinforcement with the same geometry, and only the web width varied in these beams. Accordingly, ρ and ρ v were changed as listed in Table 2. This work is the most comprehensive investigation reported on typical shear-critical reinforced concrete beams under combined action of bending and shear, and it is used here as the basis of the examination for the principle described above.
At several loading stages after cracking, the values of α are calculated at the mid-shear span of each beam utilizing the procedure described in previous section, and the results are summarized in Fig. 12. From the figure, it can be observed that the values gradually increase and converge to a certain ultimate value as the load increases from the cracking load through the failure load. The results clearly imply that after formation of diagonal cracks, the resistant mechanisms have gradually changed from the beam action to the arch action with increasing load intensity. With increase of applied load in each beam, the internal force flow experiences three different stages; uncracked stage, transient stage and stabilized stage as illustrated in Fig. 12. Since the ultimate limit state of members is the most concern, the value of α at the ultimate load stage of each beam is denoted by α u .
The α u of the four beams is also listed in Table 2. And it is seen that as the web width decreases, the higher value of α u is resulted in with varying between 0.29 for ET1 and 0.46 for ET4. This means that 29–46 % of the applied shear force is carried by the arch action. It may be worthwhile to note that Leonhardt stated in his paper (1965) that 15–25 % of total shear was carried by the inclined compression chord in those beams.
Parametric studies are now carried out to investigate the variation of the value of α u with respect to the important factors involved. A close examination of the present approach may reveal that the value of α u is mainly affected by the geometry of the beam, the amount of web reinforcement and the amount of longitudinal reinforcement. The four curves in Fig. 13 show the variation of the α u for the beams tested by Kani (1964) and Kim et al. (1998) with respect to the span-to-depth ratio a/d. Because each curve represents a different amount of reinforcement in the beam, the influence of each parameter can be visualized.
Figure 13 indicates that the a/d ratio is the most dominant parameter that affects magnitude of α, and the value decreases with increasing a/d ratio. The rate of decrease is larger for high ratio of web reinforcement. Figure 13 also shows that the longitudinal steel ratio ρ has also a pronounced influence on the variation of α, and the higher ρ causes the greater α. Such trend is well agreed with the discussion that is based on the relative stiffness ratio between the chords and the web element.
4.1 Section Analysis
When a proper α is obtained for a specific beam at a certain load stage, the geometry of the new truss model proposed can be determined. Here, ET1, ET3 are selected as an example for how assembles the truss at the ultimate load stage. The geometry of the top chord (arch) is determined from the arch shape function of Eq. (6) together with α of 0.36–0.42 as illustrated in Fig. 14. Also, the angles of the diagonal struts at every section are calculated by Eq. (20) with α = 0.39 (mean) and f1 calculated at the corresponding section. The results are also displayed over the shear span in Fig. 14, and compared with the actually recorded cracks in the beam. This comparison demonstrates that the predicted angle along the span shows a good agreement with the crack angles in the actual beam.
In determining the geometry of the present approach above, average stresses and average strains have been considered. However, the local stresses that occur at a crack are different from the calculated average values. At a crack the concrete tensile stress goes to zero, whilst the steel tension becomes larger. Also, the shear behavior of a beam is mainly governed by the forces transmitted across the crack.
Figure 15 shows the forces acting at an inclined cracked section of a beam provided with vertical stirrups. Here, the inclined crack angles are assumed to coincide with the direction of principal compressive stresses. It is seen that at the section the shear force is resisted by the combined actions of the stirrups, the compression zone and the aggregate interlocking. Recognizing that the shear resisted by the compression zone corresponds to that by arch action αV, the shear sustained by the uncracked compression zone is depending on the value of the corresponding α in beams. Assuming that the portion of the shear resisted by the dowel action of the longitudinal steel is negligible, the internal shear force is composed of three base components (Kim and Jeong 2011a, b, c).
The sum of the first two terms is normally referred to the concrete contribution V c , and the last term is referred to the steel contribution. In view of the present approach, the first term is the component resisted by the arch action, and the sum of the last two terms, which is equal to (1 − α)V, is the component resisted by the web element by means of the beam action.
After the formation of inclined cracks, no tension force perpendicular to the crack can be transmitted across it. However, as long as the crack is narrow, it can still transmit forces in its own plane through the interlocking of the rough surface. So, sizable interlocking shear force V ci (MPa) has been measured. This shear component will be analytically predicted using the expression developed by Bhide and Collins (1989).
where d a is the maximum aggregate size, and w is the crack width. The crack width is taken as the product of the principal tensile strain ɛ1 and the average spacing of the cracks. The detailed information on Eq. (25) should be referred by Nielsen (1984).
In actual beams, however, a portion of shear is resisted by dowel action and/or frame action in addition to the aggregate interlocking Leonhardt (1965). If these beneficial contributions are accounted as an equivalent term of V ci , the magnitude of V ci in beams may differ from that evaluated based on the interlocking action alone. Therefore, an alternative simple expression may be required. From the view of Eq. (24), the ultimate shear strengths of sufficiently slender beams with no web reinforcement are purely rely on V ci alone because both αV and V s cannot be developed in such beams. Hence, it seems reasonable that the lowest shear strength from ACI-318 shear expression (ACI Committee 318 1999) is taken as the simple practical expression for V ci :
This expression is an alternative for a practical evaluation of V ci (MPa) and is appropriate for the ultimate limit state rather than the service stages.
4.2 Steel Stresses
After the development of shear cracks in a beam provided with vertical stirrups, the concrete struts in the web shear element are subjected mainly to compression, the vertical stirrups act as vertical tension tie, and the longitudinal reinforcement acts as horizontal tension tie, thus forming a truss action to resist shear. The shear carried by this truss action, which is the so-called stirrup contribution V s , is equal to (1 − α)V − V ci from Eq. (24). This shear force must be balanced by the forces acting at the stirrups crossing the crack A v f v (z/s) cot θ. From this equilibrium, the stirrup stress f v is expressed as
Figure 16 shows the comparison between the stirrup stresses calculated from Eq. (27) and those measured at the mid-shear span of the four beams tested at Stuttgart. In calculating each stirrup stress using Eq. (27), two methods are employed. One is the theoretical calculation in which the theoretical values of α (Fig. 12) and V ci of Eq. (25) corresponding to every load intensity are used, and the other is a simple practical calculation in which the fixed value of α u and V ci from Eq. (26) are used without considering the load intensity. As seen from Fig. 16, there are excellent agreements between the calculated and the measured.
As shown in Fig. 15, the truss action in the web also produces the longitudinal compression force V s tanθ. From the sectional moment equilibrium, the longitudinal steel tension T at a cracked section is expressed by
It may be interesting to note that Eq. (28) with α = 0 (z x = z o ) and V ci = 0 coincides with the steel tension in the variable-angle truss model, whereas that with α = 1 and V ci = 0 corresponds to the steel tension in a simple strut-and-tie model. To examine Eq. (28), one of the specimen tested by Kim et al. (1998) is selected because its whole load-tension histories at three sections in the shear span are available as illustrated in Fig. 17. In calculating T x by Eq. (28) for all loading stages, the simple practical method with α u = 0.51 and the fixed V ci from Eq. (26) is used, and the results are compared with the measured values in Figs. 17a and 17b. As seen in the figures, good agreements are observed between the calculated and the measured with increase of load, and also the distribution of the tension predicted over the span near the ultimate load stage is also well agreed with the measured.
The accuracy of the theoretically calculated tension of the vertical tie (stirrup) and the horizontal tie (longitudinal steel) may strongly confirm the rationale of the present approach although the solution procedure is too complicated to be used. The fact that the simple practical calculation method is accurate enough may also confirm the practical applicability of the present approach. Moreover, it can be seen from Fig. 16 that the shear prior to diagonal cracking is maintained during the stirrup stresses rise to yield level. This confirms the fact that both the arch and the beam action are the essential mechanisms in resisting the applied load in stabilized stage up to failure.
4.3 Ultimate Shear Strength V u
The shear strength at the ultimate when the stirrups start to yield V u,y is derived from Eq. (27) by substituting the yield strength of the stirrups f vy for f v .
where V u,f is the shear force when flexural failure occurs. Figure 18 shows the comparison of the strengths predicted from Eq. (29) with the measured results of the four beams tested at Stuttgart. It is seen that the three beams failed by stirrup yielding, the other (ET1) failed by flexure in which the shear strength exceeded the flexural strength. Within this comparison it can be said that Eq. (29) yields a very close predictions for the shear strengths of beams failed by stirrup yielding. The failures associated with the arch action will be the crushing/splitting of concrete arch, the yielding of steel tie, and the anchorage failure in the joint between arch and tie. All of these failure modes and the web concrete crushing failure are not dealt with in the present paper.
5 Conclusions
On the basis of the relationship between shear and the rate of change in bending moment (V = dM/dx = zdT/dx + Tdz/dx) in reinforced concrete beams subjected to shear and bending, a behavioral model has been proposed in the present paper. In the model the rate of the change in the lever arm (dz/dx) is accounted for, so that the shear resistant mechanism has been decoupled into two base components—the arch action and the beam action. The ratio (denoted by factor-α) of contribution to shear resistance by the tied arch action in a beam is numerically derived from the gross compatibility of deformations associated with the base actions. Then, the actual behavior of shear-critical beams is formulated by means of interpolating between the sectional approach and the tied arch approach using the value of the factor-α. The adequacy of the new approach has been briefly examined by some test results in literatures, and the results show an excellent agreement between the predicted and the measured. From the present study, it can be concluded that the factor-α is appeared to be the most crucial parameter for understanding the behavior of shear-critical reinforced concrete members.
References
ACI Committee 318. (1999). Building code requirement for reinforced concrete and commentary (318R-99) (p. 391). Detroit, MI: ACI.
American Association of State Highway and Transportation Officials (2002), AASHTO LRFD Bridge Design Specifications, 2002 Interim Revisions, pp. 305–315.
ASCE-ACI Committee 426. (1973). The shear strength of reinforced concrete members. Journal of Structural Division, ASCE,99(6), 1091–1187.
ASCE-ACI Committee 445. (1998). Recent approaches to shear design of structural concrete. Journal of Structural Engineering,124(5), 1375–1417.
Bhide, S. B., & Collins, M. P. (1989). Influence of axial tension on the shear capacity of reinforced concrete member. ACI Structural Journal,86(5), 570–581.
Collins, M. P., & Mitchell, D. (1991). Prestressed concrete structures (pp. 210–220). Eaglewood Cliffs, NJ: Prentice-Hall.
Comite Euro International Du Beton (CEB/FIP)(1990), CEB-FIP Model Code for Concrete Structures, Bulletin d’Information No. 124/125, p. 437.
Commission of the European Communities (1991), Eurocode No. 2: Design of Concrete Structures, Part 1: General rules and Rules for Buildings, ENV 1992-1-1, p. 253.
Hsu, T. T. C. (1993). Unified theory of reinforced concrete (pp. 250–350). Boca Raton, FL: CRC.
Kani, G. N. J. (1964). The riddle of shear failure and its solution. ACI Journal,61(4), 441–467.
Kim, W., & Jeong, J.-P. (2011a). Non-Bernoulli-compatibility truss model for RC member subjected to combined action of flexure and shear, part I-its derivation of theoretical concept. KSCE Journal of Civil Engineering,15(1), 101–108.
Kim, W., & Jeong, J.-P. (2011b). Non-Bernoulli-Compatibility truss model for RC member subjected to combined action of flexure and shear, part II-its practical solution. KSCE Journal of Civil Engineering,15(1), 109–117.
Kim, W., & Jeong, J.-P. (2011c). Decoupling of arch action in shear-critical reinforced concrete beam. ACI Structural Journal,108(4), 395–404.
Kim, D.-J., Kim, W., & White, R. N. (1998). Prediction of reinforcement tension produced by arch action in RC beams. ASCE, Journal of Structural Engineering,124(6), 611–622.
Leonhardt, F. (1965). Reducing the shear reinforcement in reinforced concrete beams and slabs. Magazine of Concrete Research,17(53), 187–198.
Lorentsen, M. (1965). Theory for the combined action of bending moment and shear in reinforced concrete and prestressed concrete beams. ACI Journal,62(4), 420–430.
Marti, P. (1985). Basic tools of reinforced concrete beam design. ACI Journal,82(1), 46–56.
Nielsen, M. P. (1984). Limit analysis and Concrete Plasticity. Eaglewood Cliffs, NJ: Prentice-Hall. 420.
Park, R., & Paulay, T. (1975). Reinforced concrete structures (pp. 133–138). New York, NY: Wiley.
Ramirez, J. A., & Breen, J. A. (1991). Evaluation of a modified truss model approach for beams in shear. ACI Structural Journal,88(5), 562–571.
Schlaich, J., Schafer, I., & Jennewein, M. (1987). Towards a consistent design of structural concrete. PCI Journal,32(3), 74–150.
Taylor, H. P. J. (1974). The fundamental behavior of reinforced concrete beams in bending and shear (pp. 43–77). Detroit, MI: ACI SP-42.
Vecchio, F. J., & Collins, M. P. (1986). The modified compression field theory for reinforced concrete elements subjected to shear. ACI Journal,83(2), 219–231.
Acknowledgments
This work was supported by LINC (Leaders in Industry-university Cooperation) in Honam University and NRF (National Research Foundation of Korea). The authors wish to gratefully acknowledge this financial support.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This article is published under license to BioMed Central Ltd. Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Jeong, JP., Kim, W. Shear Resistant Mechanism into Base Components: Beam Action and Arch Action in Shear-Critical RC Members. Int J Concr Struct Mater 8, 1–14 (2014). https://doi.org/10.1007/s40069-013-0064-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40069-013-0064-x