1 Introduction

Different forms of non-linear PDEs like advection–diffusion, reaction–diffusion or many more have been modelled and analyzed corresponding to some real-life phenomenon or scientific processes so far [2, 4, 16, 24, 34, 44]. Non-linear reaction diffusion equations having fourth order derivative terms, frame problems in the vast category of fields under science and engineering. These equations occur in both the form of ordinary differential equation (ODE) and partial differential equation (PDE). The wide applications of these problems have made it the topic of research worldwide since long ago. In [62] a non-linear PDE modelling the under-ground water flow problem, which is a serious problem for the living-beings has been considered. In [59] a non-linear PDE modelling the propagation of optic pulses in optic fibers has been solved analytically. Applications of various non-linear partial differential equations and non availability of the compact form of solution in most of the cases, demands an efficient technique for analysing the phenomenon. Earlier, non-linear PDEs have been treated numerically as well as analytically [1, 38] to study the solution behaviour of these problems. Various forms of non-linear reaction–diffusion equations having vast field of applications has been studied so far [14, 35, 42, 66]. Extended Fisher Kolmogorov (EFK) equation is an example of such type of reaction diffusion equation involving linear diffusion term and non-linear logistic term f(u). Consider the general form of non-linear reaction diffusion fourth order parabolic partial differential equation.

$$\begin{aligned} u_t+\varepsilon u_{\zeta \zeta \zeta \zeta }-u_{\zeta \zeta }+f(u)=0\quad (\zeta , t) \in (a, b) \times (0, T], \end{aligned}$$
(1)

with \(\varepsilon > 0\) and f(u) as a non-linear polynomial function of u.

Initially, \(u(\zeta ,0)\)= \(u_0 (\zeta )\) \(\zeta \in (a, b).\)

The boundary conditions are defined as:

$$\begin{aligned} u(a, t)=g_1 (t)&\quad u(b, t)=g_2 (t) \nonumber \\ u_{\zeta \zeta } (a,t)=g_3(t)&\quad u_{\zeta \zeta } (b,t)=g_4(t). \end{aligned}$$
(2)

where, \(g_1(t), g_2(t), g_3(t)\) and \(g_4(t)\) are continuous functions of t and \(f(u) = u-u^m, \ m > 1.\) For \(f(u)=u-u^3,\) the Eq. (1) is introduced as Extended Fisher–Kolmogorov (EFK) equation with perturbation parameter \(0 \le \varepsilon \le 1.\) For \(\varepsilon = 0,\) Eq. (1) is standard Fisher–Kolmogorov equation given by Fisher and Kolmogorov which models complex biological processes in gene theory [6, 28]. The requirement \(\varepsilon > 0\) is chosen for stability of Eq. (1) at short wavelength [23]. Various physical phenomenon like pattern formation due to propagating fronts [23, 64], spatial temporal chaos in bi-stable systems [19], chemical waves [27], transition of phase and propagation of fronts near a Lipschitz point [33, 67], instabilities in liquid crystals [18, 67], propagating waves in reaction–diffusion systems [29, 55] have been framed by Eq. (1) which approaches the amplitude near certain degenerate points [57]. Also, in [56], the transition from periodic patterns by Ginzburg–Landau equation to the multi-bump solutions predicted by EFK equation has been discussed. Periodicity, chaotic, stationary behavior, uniqueness of the solution and existence of kinks, travelling wave solutions etc. have also been considered [22, 47, 49,50,51, 57, 63].

In literature, non-linear parabolic PDEs have been analyzed by different numerical techniques [9, 53]. Various elliptic non-linear second order PDEs having compact form of solution have been treated with generalized finite difference method given in [30]. Due to the complex nature, compact form of solution exists only for some non-linear higher order PDEs. Complexity of the equation enhances the requirement of numerical techniques. EFK equation has been analyzed by variational method for investigating the nature of saddle-focus equilibria connections [36]. Topological shooting method has been applied for the existence of kinks and analyzing their properties [48]. Numerically, it has been implemented with the differential quadrature method [13, 54], orthogonal cubic spline collocation method [21], quintic B- spline collocation method [46], mixed finite element method [65], quintic trigonometric differential quadrature method [7], finite element method [20], Galerkin approximation technique [31], compact difference method [37] etc. Quasi-Exact solution has been obtained in [39]. Local radial basis function, finite difference method [25] has also been implemented for numerical solution of EFK equation.

In present study collocation method with Hermite splines has been discussed. Collocation technique is basically a three-step process

  1. 1.

    Suitable choice of the finite degree polynomial lying in finite dimensional space for the discretization process.

  2. 2.

    Suitable choice of collocation points for space discretization.

  3. 3.

    Making that polynomial solution to satisfy the equation at the collocation points.

In the present study, a hybrid Crank–Nicolson quintic Hermite spline method accomplished by the reduction of the order of the aforementioned differential equation has been considered. The considered mesh is uniform in both space and time directions. This technique improves the efficiency of collocation technique in approximation by interpolating the function and its derivatives up-to second order at nodal points. Quintic Hermite splines are simple, smooth, easy to implement and can be implemented to the variety of boundary value problems having high order and high degree of non-linearity. Travelling wave behaviour has been analysed with different values of various parameters and the non-linear function f(u). Quintic Hermite splines (QHS) provide super convergence up to fourth order in spatial direction and Crank–Nicolson scheme is second order convergent. Earlier, the technique has been applied to second order, singularly perturbed non-linear partial differential equations [8, 11, 12]. The computational work for the approximation of fully discrete system is comparatively easy to program.

The paper is fabricated by the introduction of EFK equation in Sect. 1. Second order splitting method has been explained briefly under Sect. 2. Hybrid quintic Hermite spline collocation method has been elaborated in Sect. 3 whereas in Sect. 4 stability analysis has been discussed. The existence of error bounds and convergence analysis has been discussed in Sect. 5. The application of QHS with Crank Nicolson scheme has been discussed in Sect. 6 and the conclusions of the entire study is given in Sect. 7.

2 Second order splitting of EFK equation

Fourth order non-linear equations involve concerned differential equation and four constraints. To apply any numerical technique, these constraints play an important role to discretize the equation. Quintic Hermite splines by construction involve the discretized form of the differential equation at collocation points and two constraints at the boundary of the interpolating polynomial. Therefore, to apply quintic Hermite splines on fourth order differential equation, it must be split into second order differential equation by introducing second order continuously differentiable function to reduce the number of constraints to two for each interpolating polynomial.

Theorem 2.1

[5] Any Hermite interpolation problem of any order \(n \in N\) is applicable on two point boundary value problems.

Consider the non-linear EFK type Eq. (1). For the implementation of proposed technique, a twice continuously differentiable function \(v(\zeta , t)\) has been introduced such that:

$$\begin{aligned} v(\zeta , t)=- u_{\zeta \zeta }(\zeta , t). \end{aligned}$$

On substitution [26], the induced coupled system of differential equations is obtained as under:

$$\begin{aligned} v+u_{\zeta \zeta }&=0, \end{aligned}$$
(3)
$$\begin{aligned} u_t -\varepsilon v_{\zeta \zeta }+ v +f(u)&=0, \end{aligned}$$
(4)

with \(f(u)=u-u^m,\) subject to the following initial and boundary conditions:

$$\begin{aligned} u(\zeta , 0)&=u_0(\zeta ), \end{aligned}$$
(5)
$$\begin{aligned} u(a, t)&=g_1(t)\quad u(b, t)=g_2(t), \end{aligned}$$
(6)
$$\begin{aligned} v(a,t)&=0\quad v(b, t)=0. \end{aligned}$$
(7)

Hence, a fourth order equation has been reduced to a system of equations with one equation is linear and another is semi-linear. This splitting of non-linear EFK equation gives a semi-linear parabolic equation in two function u and v.

3 Hybrid quintic hermite spline collocation method

The hybrid technique consists of discretization using time and space semi-discretizing techniques. This two-step process has been implemented to the second order coupled system of singularly perturbed PDEs:

3.1 Time discretization

For discretization in time direction, the Crank–Nicolson scheme has been followed as a special case of weighted finite difference scheme [60]. This Crank–Nicolson scheme is based on the concept of nearest neighbourhood points to analyse the behaviour without any jump in time direction [15]. For implementation of the technique to the reduced coupled system for EFK equation, let \( v^{n+1}\) and \(u^{n+1}\) be the approximating polynomial function at time step \(t_{n+1}.\) Also, let \(\Delta t = T/M,\ \ M > 0\) then \( t_n = n \Delta t\) for \(n= 0, 1, 2,\ldots , M.\) The semi-discretized form of the coupled system follows as:

$$\begin{aligned} v^{n+\frac{1}{2}}&=-u_{\zeta \zeta }^{n+\frac{1}{2} }, \end{aligned}$$
(8)
$$\begin{aligned} \frac{u^{n+1}-u^n}{\Delta t}&= \varepsilon v_{\zeta \zeta }^{n+\frac{1}{2}}- v^{n+\frac{1}{2}} - (u^m -u )^{n+\frac{1}{2} } , \end{aligned}$$
(9)

with corresponding boundary conditions are given by Eqs. (6) and (7), respectively. For any function F,

$$\begin{aligned} F^{n+\frac{1}{2}} = \frac{F^{n+1}+ F^n}{2}. \end{aligned}$$
(10)

3.2 Space discretization

Let \( \Pi : a = \zeta _0< \zeta _1< \zeta _2< \cdots <\zeta _n = b ,\) \(\zeta _i^\prime s \in I\) be the partition of the domain \(I = [a, b]\) and let \(h_i = \zeta _{i+1} - \zeta _i\) and \( I_i\) denotes \([\zeta _i , \zeta _{i+1}].\) Corresponding to each subinterval \( I_i,\) six collocation points have been taken including two boundary or node points. Collocation points are the roots of shifted Legendre polynomial of order six which are not equidistant to the average and the details of these collocation points is given elsewhere [10].

In space direction, the quintic Hermite interpolating polynomials \(P_i(\eta ), \bar{P_i}(\eta )\) and \(\bar{\bar{P_i}}(\eta )\) are introduced to approximate the trial function within each partition \(I_i\) of the domain. The approximate function is considered as:

$$\begin{aligned} u(\zeta )=u(\zeta _i)\sum _{i=1}^{2}P_i(\zeta )+u^\prime (\zeta _i)\sum _{i=1}^{2} \bar{P_i}(\zeta ) +u^{\prime \prime }(\zeta _i)\sum _{i=1}^{2}\bar{\bar{P_i}}(\zeta ), \end{aligned}$$
(11)

where \(P_i(\zeta )\) interpolates the function \(u(\zeta )\) at the nodal points of the sub-interval \( I_i\) and \(\bar{P_i}(\zeta ),\) \(\bar{\bar{P_i}}(\zeta )\) interpolates slope and curvature at the nodal points, respectively.

(12)

To apply orthogonal collocation, within each subinterval \(I_i\) a new variable \(\omega \) is introduced such that \(\omega = \frac{(\zeta -\zeta _i)}{h_i}\) , where \(\omega \) varies from 0 to 1 as \(\zeta \) varies from \(\zeta _i\) to \(\zeta _{i+1}.\) This transformation reduces the polynomial structure Eq. (12) to the tabular form presented in Table 1. The quintic Hermite polynomials are presented on the interval \([\zeta _i, \zeta _{i+1}]\) in Table 1 and the values of Hermite splines and its derivatives are presented in Table 2 at \(\omega = 0\) and 1. The approximating function at each time level \(t_{n+1}\) within each sub-interval is taken as

$$\begin{aligned} u^{n+1}(\omega )=\sum _{i=1}^{6}c_i^{n+1}H_i(\omega );\quad v^{n+1}(\omega )=\sum _{i=1}^{6}d_i^{n+1}H_i(\omega ). \end{aligned}$$
(13)

The next step is the choice of collocation points. It plays an important role in Hermite collocation. Zeros of orthogonal polynomials are taken as the collocation points such as Jacobi polynomials. Legendre and Chebyshev polynomials are special cases of Jacobi polynomials. In the present study, zeros of shifted Legendre polynomials have been taken as collocation points.

Table 1 Presentation of quintic Hermite splines
Full size table
Table 2 Value of quintic Hermite splines and corresponding first and second order derivative at boundary points
Full size table

After semi-discretization of the aforementioned equation for \(f(u)=u-u^m,\) coupled system of equations on using Eq. (10) in (9) and (8) is defined as:

$$\begin{aligned} \left\{ \frac{ v^{n+1}+v^n}{2}\right\}{} & {} =-\left\{ \frac{ u_{\zeta \zeta }^{n+1}+u_{\zeta \zeta }^n}{2}\right\} , \end{aligned}$$
(14)
$$\begin{aligned} u^{n+1}-u^n{} & {} =\varepsilon \Delta t\left\{ \frac{ v_{\zeta \zeta }^{n+1}+v_{\zeta \zeta }^n}{2}\right\} -\Delta t\left\{ \frac{ v^{n+1}+v^n}{2}\right\} \nonumber \\{} & {} \quad -\frac{\Delta t}{2} \left\{ f^{n+1}(u)+f^n(u)\right\} . \end{aligned}$$
(15)

The quasi linearisation of \(f(u)=u^m-u\) has been taken with Taylor series approximation given in [41, 58] as:

$$\begin{aligned} u^m(t+\Delta t)&=u^m(t) +\Delta t (u^m)_t +O(\Delta t)^2\nonumber \\&=u^m(t) +\Delta t m u^{m-1}u_t +{\mathcal {O}}(\Delta t)^2. \end{aligned}$$
(16)

Again using finite difference approximation i.e.

$$\begin{aligned} u(t+\Delta t) = u(t)+\Delta t u_t+{\mathcal {O}}(\Delta t)^2. \end{aligned}$$
(17)

This implies,

$$\begin{aligned}&\Delta t u_t + O(\Delta t)^2= u(t+\Delta t)-u(t)\nonumber \\&\quad \implies u^m(t+\Delta t)=u^m(t)+ mu^{m-1}(u(t+\Delta t)-u(t))+{\mathcal {O}}(\Delta t)^2. \end{aligned}$$
(18)

At \(t=t_n\)

$$\begin{aligned} u^m(t_{n+1})=u^m(t_n)+ mu^{m-1}(t_n) u(t_{n+1}) - mu^{m}(t_n)+{\mathcal {O}}(\Delta t)^2. \end{aligned}$$
(19)

Using Eq. (19) omitting the second order truncation term, one gets the following coupled system of equations:

$$\begin{aligned} v^{n+1}+ u_{\zeta \zeta }^{n+1}{} & {} =-\big ( v^n+u_{\zeta \zeta }^n\big ), \end{aligned}$$
(20)
$$\begin{aligned} u^{n+1}-u^n{} & {} =\varepsilon \Delta t\Big (\frac{ v_{\zeta \zeta }^{n+1}+v_{\zeta \zeta }^n}{2}\Big )-\Delta t\Big (\frac{ v^{n+1}+v^n}{2}\Big ) +\Delta t\Big ( \frac{u^{n+1}+u^n}{2}\Big ) \nonumber \\{} & {} \quad -\Delta t\Big ( \frac{ m u^{n+1} (u^{m-1})^n - (m-2)(u^m)^n}{2} \Big ), \end{aligned}$$
(21)

and rearranging the terms, the following coupled system of equations is obtained:

$$\begin{aligned}&\frac{(v^{n+1}+u_{\zeta \zeta }^{n+1} )}{2}= -\frac{(v^n+ u_{\zeta \zeta }^n )}{2}, \end{aligned}$$
(22)
$$\begin{aligned}&u^{n+1}+\frac{\Delta t}{2}\left[ -\varepsilon v_{\zeta \zeta }^{n+1}+ v^{n+1}-u^{n+1} + mu^{n+1}(u^{m-1})^n \right] \nonumber \\&\quad =u^n+\frac{\Delta t}{2}[\varepsilon v_{\zeta \zeta }^n - v^n + u^n + (m-2)(u^m)^n ]. \end{aligned}$$
(23)

For space discretization, consider the different approximations \(u^{n+1}\) and \(v^{n+1}\) for u and v,  respectively as:

\(u^{n+1}=\sum _{i=1}^6 c_i^{n+1} H_i (\omega )\) and \( v^{n+1}=\sum _{i=1}^6 d_i^{n+1} H_i (\omega ),\) \(0 \le \omega \le 1.\)

The approximate solution lies in each subinterval \(I_i,\) of \(\Pi ,\) where \(H_i (\omega )\) are quintic Hermite splines defined over the interval [0, 1]. The system of collocation equations obtained after discretization are explained hereunder:

$$\begin{aligned} \sum _{i=1}^6 \left\{ c_{4(r-1)+i}^{n+1} \kappa _{ji}+ d_{4(r-1)+i}^{n+1} \eta _{ji}\right\}&=\sum _{i=1}^6 \left\{ c_{4(r-1)+i}^n \nu _{ji}+ d_{4(r-1)+i}^n \alpha _{ji}\right\} , \end{aligned}$$
(24)
$$\begin{aligned} \sum _{i=1}^6 \left\{ c_{4(r-1)+i}^{n+1} \rho _{ji} + d_{4(r-1)+i}^{n+1} \gamma _{ji} \right\}&=\sum _{i=1}^6 \left\{ c_{4(r-1)+i}^n \chi _{ji}+ d_{4(r-1)+i}^n \lambda _{ji}\right\} \nonumber \\&\quad +\frac{(m-2)\Delta t}{2}\left[ \sum _{i=1}^6 c_{4(r-1)+i}^n H_i (\omega _j )\right] ^m, \end{aligned}$$
(25)

where, \(r = 1, 2, 3,\ldots , N. \ j = 1, 2, 3, 4.\) \(c_i\) and \(d_i\) are unknown coefficients and the constant parameters are defined as:

$$\begin{aligned} \rho _{ji}&=H_i(\omega _j)-\frac{\Delta t}{2}H_i(\omega _j)+\frac{m\Delta t}{2} H_i(\omega _j)\left\{ \sum _{i=1}^{6}c_{4(r-1)+i}^n H_i(\omega _j)\right\} ^{m-1,}\nonumber \\ \lambda _{ji}&=\frac{\varepsilon \Delta t}{2h^2}H_i^{\prime \prime }(\omega _j)-\frac{\Delta t}{2}H_i(\omega _j), \nonumber \\ \gamma _{ji}&=\frac{-\varepsilon \Delta t}{2h^2}H_i^{\prime \prime }(\omega _j)+\frac{\Delta t}{2} H_i(\omega _j);\quad \nu _{ji}=\frac{-1}{2h^2}H_i^{\prime \prime }(\omega _j), \nonumber \\ \chi _{ji}&=H_i(\omega _j)+\frac{\Delta t}{2}H_i(\omega _j);\quad \eta _{ji}=\frac{1}{2} H_i(\omega _j), \nonumber \\ \kappa _{ji}&=\frac{1}{2h^2}H_i^{\prime \prime }(\omega _j);\quad \alpha _{ji}=-\frac{1}{2}H_i(\omega _j). \end{aligned}$$
(26)

Total number of variables are \(8N+4\) and the collocation equations are 8N. The extra four variables are computed from the boundary conditions. Again, in compact form, the system of EFK equation can be written as:

$$\begin{aligned} {[}{} {\textbf {L}}]y^{n+1} = [{\textbf {J}}]y^n +{\textbf {f}}^n , \end{aligned}$$
(27)

this implies

$$\begin{aligned} {\textbf {y}}^{n+1} = [{\textbf {L}}^{-1}{} {\textbf {J}}]{\textbf {y}}^n + {[}{} {\textbf {L}}^{-1}{} {\textbf {f}}^n ], \end{aligned}$$
(28)

where L and J are \(8N \times 8N\) diagonal dominated matrices with each block \({\textbf {L}}_r \) and \( {\textbf {J}}_r\) for \(r = 2,\ldots , N-1\) of order \(8\times 12.\) Due to boundary constraints \({\textbf {L}}_1,\ \ {\textbf {L}}_N \ \text {and}\ {\textbf {J}}_1,\ {\textbf {J}}_N\) are of order \(8 \times 10.\) \(y^{n+1} \ is \ 8N\times 1\) column matrix. \({\textbf {f}}^n\) contains the non-linear term \(\Delta t[\sum _{i=1}^6 c_{4(r-1)+i}^n H_i (\omega _j )]^m/2\) and the non-homogenous boundary data. The fully discretized algebraic system of Eq. (27) is solved using the MATLAB software.

$$\begin{aligned} {\textbf {y}}^n= & {} \left[ \begin{array}{c} {\textbf {d}}^n(i)\\ {\textbf {c}}^n(i) \end{array} \right] _{8N\times 1},\quad {\textbf {d}}^n=\left[ \begin{array}{c} d_1^n \\ d_2^n\\ \vdots \\ d_{4N}^n\\ \end{array} \right] _{4N \times 1},\quad {\textbf {c}}^n=\left[ \begin{array}{c} c_1^n \\ c_2^n\\ \vdots \\ c_{4N}^n\\ \end{array} \right] _{4N \times 1},\\ {\textbf {L}}= & {} \left[ \begin{array}{ccccccc} L_1&{} &{} &{} &{} &{} &{} \\ &{} L_2&{} &{} &{} &{} &{} \\ &{} &{}\ddots &{} &{} &{} &{}\\ &{} &{} &{} L_r &{} &{} &{} \\ &{} &{} &{} &{}\ddots &{} &{} \\ &{} &{} &{} &{} &{}L_{N-1} &{} \\ &{} &{} &{} &{} &{} &{} L_N \\ \end{array} \right] _{8N\times 8N},\quad {\textbf {J}}=\left[ \begin{array}{ccccccc} J_1&{} &{} &{} &{} &{} &{} \\ &{} J_2&{} &{} &{} &{} &{} \\ &{} &{}\ddots &{} &{} &{} &{}\\ &{} &{} &{} J_r &{} &{} &{} \\ &{} &{} &{} &{}\ddots &{} &{} \\ &{} &{} &{} &{} &{}J_{N-1} &{} \\ &{} &{} &{} &{} &{} &{} J_N \\ \end{array} \right] _{8N\times 8N}. \end{aligned}$$

Computationally, each block \({\textbf {L}}_r \) and \({\textbf {J}}_r \) also contains sub-blocks of order \(2 \times 2\) having the structure as

$$\begin{aligned} {\textbf {L}}_r=\left[ \left[ \begin{array}{cc} \eta _{ij} &{} \kappa _{ij} \\ \gamma _{ij} &{} \rho _{ij}\\ \end{array} \right] _{ij} \right] ,\quad {\textbf {J}}_r=\left[ \left[ \begin{array}{cc} \alpha _{ij} &{} \mu _{ij} \\ \lambda _{ij} &{} \chi _{ij}\\ \end{array} \right] _{ij} \right] , \end{aligned}$$

where \(i=1,2,3,4\) and \(j=1,2,\ldots ,6\) except for the case of \(r=1\ \text {and}\ N\) then \(j=1,2,3,4,5\) due to known boundary data.

$$\begin{aligned} {\textbf {f}}^n=\left[ \begin{array}{c} 0\\ (m-2)\frac{\Delta t}{2}\left\{ \sum _{i=1}^{6}a_i^nH_i(\omega _j)\right\} ^m \\ \vdots \\ 0\\ (m-2)\frac{\Delta t}{2}\left\{ \sum _{i=1}^{6}a_{4(r-1)+i}^nH_i(\omega _j)\right\} ^m\\ \vdots \\ 0\\ (m-2)\frac{\Delta t}{2}\left\{ \sum _{i=1}^{6}a_{4(N-1)+i}^n H_i(\omega _j)\right\} ^m\\ \end{array} \right] _{8N \times 1}. \end{aligned}$$

4 Stability analysis

For any numerical technique involving iterations for analysing transient partial differential equations, stability is one of the most important concept to be considered for ensuring the control over the errors. Otherwise, the accumulation of errors at one stage may overwhelm the solution.

The stability of the proposed numerical algorithm of hybrid nature is completely stored in the component matrices of \([{\textbf {L}}^{-1}{} {\textbf {J}}]\) which improves the initial solution at each iteration.

The component matrices \({\textbf {L}}\) and \({\textbf {J}}\) both depends on the perturbation parameters, grid sizes towards both space and time directions and the Hermite splines adopted for approximation.

Let \(\lambda \) be the eigen value of the matrix \([{\textbf {L}}^{-1}{} {\textbf {J}}].\) It is observed computationally that the magnitude of eigen values of matrix \([{\textbf {L}}^{-1}{} {\textbf {J}}]\) are bounded by unity. The behaviour of eigenvalues is shown in Figs. 1 and 2 for \(N=128\) and \(N=50\) corresponding to \(\varepsilon =0.0001\) and \(\varepsilon =0.1,\) respectively (Fig. 3).

Fig. 1
figure 1

Behaviour of eigen values at \(N=128\) and \(N=50\) with \(\varepsilon =0.0001\)

Full size image
Fig. 2
figure 2

Behaviour of eigen values at \(N=128\) and \(N=50\) with \(\varepsilon =0.1\)

Full size image
Fig. 3
figure 3

Behavior of wave solution \(u(\zeta , t)\) and absolute error with \(N=50\) and \(\Delta t=0.01\) for Example 6.1

Full size image

It is observed that the imaginary part of eigen values is zero and the real part of eigen values is less than unity, i.e., \(\mid \lambda \mid \le 1\) which signifies the stability of the proposed iterative technique by Lax–Richtmyer definition for stability.

NOTE: u has been considered as locally constant \(\eta \) (say) for the quasi linearization of the non-linear term. The implemented technique comprises both the operators \({\mathcal {F}}\) and \({\mathcal {T}}\) operate on both u and v i.e. \({\mathcal {F}}_{u,v}\) and \({\mathcal {T}}_{u,v}\) simultaneously and thus approximating two set of values at each iteration at the chosen collocation points for the two approximate solutions \(\widetilde{u}\) and \(\widetilde{v}.\) Thus, the iterative scheme at each time step, approximate a function consisting of two component functions u and v i.e. \({\textbf {U}} = \left\{ u, v\right\} \) using the different Hermite interpolating polynomial function i.e. \({\textbf {H}}=\left\{ \bar{H}_1, \bar{H}_2\right\} .\) Since, u is bounded, hence operators can be linearised by considering \(\eta \) as the maximum bound of \((u^{m-1})^n,\) where \((u^{m-1})^n= u(t_n)^{m-1}\)

For Crank–Nicolson scheme, the operators are represented as:

\({\mathcal {F}}_{u,v}(\omega _i)=P_1(u^j(\omega _i),v^j(\omega _i))\) and \( {\mathcal {T}}_{u,v}(\omega _i)=P_2(u^j(\omega _i),v^j(\omega _i)) \),

where,

$$\begin{aligned}&{\mathcal {F}} ({\textbf {U}}(\omega _i))={\mathcal {F}}_{u,v}(\omega _i) =v^{j+1}(\omega _i)+u_{\zeta \zeta }^{j+1}(\omega _i), \\&{\mathcal {T}}({\textbf {U}}(\omega _i))={\mathcal {T}}_{u,v}(\omega _i) =u^{j+1}(\omega _i)-\frac{\Delta t}{2}\big (\varepsilon v_{\zeta \zeta }^{j+1}(\omega _i)-v^{j+1}(\omega _i)+(1-m\eta ) u^{j+1}(\omega _i)\big ),\\&P_1\left( u^j(\omega _i),v^j(\omega _i)\right) =-v^j(\omega _i) - u_{\zeta \zeta }^j(\omega _i), \\&P_2(u^j(\omega _i),v^j(\omega _i))=u^{j}(\omega _i)+\frac{\Delta t}{2}\big (\varepsilon v_{\zeta \zeta }^{j}(\omega _i) - v^{j}(\omega _i)+(1+ (m-2)\eta ) u^{j}(\omega _i). \end{aligned}$$

The matrix notation for the parameters and collocation equations can be written as:

$$\begin{aligned} Ly^{j+1}= \left[ \begin{array}{c} {\mathcal {F}}_{u,v}\\ {\mathcal {T}}_{u,v} \end{array} \right] , \; Jy^j= \left[ \begin{array}{c} P_1^j \\ P_2^j \end{array} \right] ,\; y^j= \left[ \begin{array}{c} d_i^j\\ c_i^j \end{array} \right] , \end{aligned}$$

where \(y^j\) contains the coefficients of Hermite polynomials.

Let \(\widetilde{{\textbf {U}}}\ =\lbrace \widetilde{u} , \widetilde{v}\rbrace \) be the approximation of \({\textbf {U}}= \lbrace u, v \rbrace \) and \({\textbf {H}}=\left\{ \bar{H}_1, \bar{H}_2\right\} \) be the Hermite approximation to the function \({\textbf {U}}= \lbrace u, v \rbrace .\) These functions have two component functions and are defined on \(C^{6} [a, b].\)

5 Convergence analysis

Lemma 5.1

[17, 40] For Crank–Nicolson scheme,  local truncation error \(e_{n+1}\) estimate and global truncation error \(E_{n+1}\) estimate are of \({\mathcal {O}}(\Delta t)^3\) and \({\mathcal {O}}(\Delta t)^2,\) respectively,  i.e.

$$\begin{aligned} \mid \mid e_{n+1}\mid \mid _\infty \le C (\Delta t)^3\quad \text {and}\quad \mid \mid E_{n+1}\mid \mid _\infty \le C(\Delta t)^2 . \end{aligned}$$

Theorem 5.2

[40] Let \(U(\zeta ,t)\) be the function such that \(\pounds U=0\) and \(U\le C,\) C being an arbitrary constant then \(U_t\) is also bounded by some constant C.

Lemma 5.3

[61] Let \(u(\zeta , 0)\) be the positive continuous initial solution of non-linear reaction–diffusion equation with \( 0 \le u(\zeta , 0)\le 1\) then the bounds for solution \(u(\zeta , t)\) remains constant with time.

Through out the paper C denotes the generic constant.

Theorem 5.4

[43] If any Hermite interpolation problem based on at the most two distinct points has a unique solution in \(\Omega \) then any Hermite interpolation problem has a unique solution in \(\Omega .\) This implies any Hermite interpolation problem has a unique solution in the polynomial space \(P_n\) of degree n on I.

Theorem 5.5

[43] The univariate Hermite interpolating polynomials are regular for any set of nodes. Moreover,  Hermite interpolating polynomials are regular for any nodal set as well as for any choice of derivatives to be interpolated.

Theorem 5.6

[43] Let \(\bar{\mathcal {H}}\) be the space of all Hermite interpolating polynomials of order 5 defined on [0 1]. Then the Hermite splines of order 5 are bounded with upper bound unity. Moreover,  \(\sum _{i=1}^{6}\mid H_i(\zeta )\mid \le 6,\) for all \(0 \le \zeta \le 1.\)

Theorem 5.7

[32, 52] Suppose H \(\in H_{\Delta \zeta }^{2q}(\zeta )\) be the piecewise Hermite spline of degree \(2q-1\) over the subinterval \([\zeta _i, \zeta _{i+1}]\) approximating \({\textbf {U}}\) \(\in C^{2q}[\)a, b] then \(\mid \mid {\textbf {H}}^{(r)}-{\textbf {U}}^{(r)}\mid \mid _\infty \le O(h^{2q-r)}, r=1,2,\ldots , q-1.\)

Proof

Let us define a function

$$\begin{aligned} {\bar{H}}(\zeta )= & {} \sum _{j=1}^{2}u(\zeta _j)\varphi _{j1}(\zeta )+ \sum _{j=1}^{2}u^\prime (\zeta _j)\varphi _{j2}(\zeta )+\cdots + \sum _{j=1}^{2}u^{q-1}(\zeta _j)\varphi _{jq}(\zeta ), \end{aligned}$$
(29)
$$\begin{aligned} \bar{\bar{H}}(\zeta )= & {} \sum _{j=1}^{2}v(\zeta _j)\mho _{j1}(\zeta )+ \sum _{j=1}^{2}v^\prime (\zeta _j)\mho _{j2}(\zeta )+\cdots + \sum _{j=1}^{2}{v^{q-1}(\zeta _j)\mho _{jq}(\zeta )}, \end{aligned}$$
(30)

where both the sets \(\lbrace \varphi _{ji}(\zeta )\rbrace \) and \(\lbrace \psi _{ji\ }(\zeta )\rbrace \) are of total 2q polynomial members, each of degree \(2q-1\) satisfying

$$\begin{aligned} \varphi _{ji}^{(i-1)}(\zeta _k)=\delta _{jk}\quad \text {and}\quad \mho _{ji}^{(i-1)}(\zeta _k)=\delta _{jk} \end{aligned}$$
(31)

where \(\zeta _k\) is the node point \(i= 1, 2, 3, 4,\ldots , q\) and at node points \({\textbf {H}}(\zeta )\) satisfies

$$\begin{aligned} {\textbf {H}}^{(r)}(\zeta _i)= {\textbf {U}}^{(r)}(\zeta _i), \end{aligned}$$
(32)

for \(r = 0, 1, 2,\ldots , q-1\) and \({\textbf {H}}^{(r)}(\zeta _i)=\left\{ {\bar{H}}^{(r)}(\zeta _i),\bar{\bar{H}}^{(r)}(\zeta _i)\right\} \) and \({\textbf {U}}^{(r)}(\zeta _i) = \left\{ u^{(r)}(\zeta _i),v^{(r)}(\zeta _i)\right\} \) with

$$\begin{aligned} {\bar{H}}^r(\zeta _i)=u^r(\zeta _i)\quad \text {and}\quad \bar{\bar{H}}^r(\zeta _i)= v^r(\zeta _i), \end{aligned}$$

considering above Eq. (32) and Rolle’s theorem, \({\textbf {H}}^{(r)}(\zeta )\ - {\textbf {U}}^{(r)}(\zeta )\) has \(r+2\) zeros in \([\zeta _1, \zeta _2]\)

$$\begin{aligned} \zeta _1=z_{1\ }\le \ z_{2\ }\le \cdots \le z_{r+1\ }\le z_{r+2\ }=\zeta _2\quad \hbox {for }r = 0, 1,\ldots , q-1. \end{aligned}$$

Let us define a function \({{\textbf {D}}}(\zeta )=\left\{ D_1(\zeta ),D_2(\zeta )\right\} \) on domain having the collection \(z_i^{\prime }\) s glued with \(\vartheta \), as its zeroes such that

$$\begin{aligned} {{\textbf {D}}}(\zeta )= \left[ {\textbf {U}}^{(r)}(\zeta )-{\textbf {H}}^{(r)}(\zeta )\right] -\left[ {\textbf {U}}^{(r)}(\vartheta )-{\textbf {H}}^{(r)}(\vartheta )\right] \frac{{{\textbf {S}}}(\zeta )}{ {{\textbf {S}}}(\vartheta )}, \end{aligned}$$
(33)

for \(r = 0, 1, 2,\ldots , q-1,\) where \({{\textbf {S}}}(\zeta )\) is defined as a polynomial function of degree \(2q-r\) having \(z_i^{\prime } s\) as single zeroes except \(z_1\) and \(z_2 \) of equal multiplicity and \(\vartheta \) is any arbitrary point of domain \([\zeta _1, \zeta _2]\) differ from \(z_i^{\prime } s\).

For any r,  \({{\textbf {D}}}\)(\(\zeta \)) has \(r+3\) zeros, the degree of polynomial \({{\textbf {S}}}\)(\(\zeta \)) decreases as r increases.

Combine Eq. (31), Eq. (32) and Rolle’s theorem, it is ready that \((q-r-1)\)th order derivative of \({{\textbf {D}}}\)(\(\zeta \)) has a total of \(q+2\) zeroes.

This assures the existence of a real \(\xi \in [a, b]\) (say) such that

$$\begin{aligned}{} & {} {{{\textbf {D}}}}^{(2q-r)}(\xi )=0, \end{aligned}$$
(34)
$$\begin{aligned}{} & {} {\textbf {U}}^{(2q)}(\xi )-\frac{ {\textbf {U}}^{(r)}(\vartheta )- {\textbf {H}}^{(r)}(\vartheta )}{ {{\textbf {S}}}(\vartheta )}(2q-r)! = 0, \end{aligned}$$
(35)
$$\begin{aligned}{} & {} \Rightarrow {\textbf {U}}^{(r)}(\vartheta )-{\textbf {H}}^{(r)}(\vartheta )=\frac{{\textbf {U}}^{(2q)}(\xi )}{(2q-r)!}{{\textbf {S}}}(\vartheta ), \end{aligned}$$
(36)

since maximum of \(\mid (\zeta -\zeta _1)(\zeta -\zeta _2)\mid \ is\ (\zeta _2-\zeta _1)^2/2^2\) and \(\vartheta \) is arbitrary point in \([\zeta _1, \zeta _2],\) one gets

$$\begin{aligned} \mid \mid \ {\textbf {U}}^{(r)}(\zeta )- {\textbf {H}}^{(r)}(\zeta )\mid \mid _\infty \ \le \ \alpha _rh^{2q-r}, \end{aligned}$$
(37)

for \(h= \zeta _{i+1}-\zeta _i\) and \(\alpha _r=\frac{||u^{(2q)}(\xi )||}{2^{2q-[r]}(2m-r)!}\)\(r=0, 1, 2,\ldots ,q-1\) and [r] = r + 1 for r odd, otherwise [r] = r. \(\square \)

For \(q = 2\) Theorem 5.7 gives error bounds for cubic Hermite splines and for \(q = 3\) Theorem 5.7 gives error bounds for quintic Hermite splines.

Theorem 5.8

Let \(\bar{{\textbf {U}}}(\zeta )\) be the approximate solution of the function \({\textbf {U}}(\zeta )\) defined on [a, b] such that \({\textbf {U}}(\zeta ) \in C^6[a, b]\) and \({\textbf {H}}(\zeta )\) be the quintic Hermite splines interpolate of \({\textbf {U}}(\zeta ).\) Then the error estimate \(\mid \mid {\textbf {U}}-\bar{{\textbf {U}}}\mid \mid \) is defined by : 

$$\begin{aligned} \mid \mid {\textbf {U}}(\zeta )-\bar{{\textbf {U}}}(\zeta )\mid \mid _\infty \le C\Bigg (\alpha _0h^{6} +max\left\{ h^{4}(\alpha _{2}+\alpha _{0}h^{2}), h^4 \left( \frac{\varepsilon \Delta t \alpha _2}{2} + \frac{\Delta t \alpha _0}{2}h^2 + (1+\frac{\Delta t (1-\eta m)}{2})\alpha _0 h^2\right) \right\} \Bigg ). \end{aligned}$$

Proof

Let \( \bar{U}_1(\zeta )\) and \(\bar{U}_2(\zeta )\) be the appropriate approximating functions defined by Theorem 5.4, with \(\bar{{\textbf {U}}}= \left\{ \bar{U}_1, \bar{U}_2\right\} ,\) corresponding to the uniform grid in space direction with nodal gap h. Let \({\textbf {H}}(\zeta )=\{\bar{H}(\zeta ), \bar{\bar{H}}(\zeta )\}\) be the quintic Hermite spline approximating \({\textbf {U}}(\zeta )=\{u(\zeta ), v(\zeta )\}.\) \(\bar{H}(\zeta )\) be the quintic Hermite spline of \(u(\zeta )\) and \(\bar{\bar{H}}(\zeta )\) be the quintic Hermite spline of \(v(\zeta ).\) Now,

$$\begin{aligned} \mid \mid {\mathcal {F}} {\textbf {U}}(\zeta _i)-{\mathcal {F}} {\textbf {H}}(\zeta _i)\mid \mid _\infty&=\mid \mid v(\zeta _i)-\bar{\bar{H}}(\zeta _i)+ u^{\prime \prime }(\zeta _i)-\bar{H}^{\prime \prime }(\zeta _i)\mid \mid _\infty , \end{aligned}$$
(38)
$$\begin{aligned} \mid \mid {\mathcal {T}} {\textbf {U}}(\zeta _i)-{\mathcal {T}} {\textbf {H}}(\zeta _i)\mid \mid _\infty&=\mid \mid \left( u(\zeta _i)-\bar{H}(\zeta _i)\right) -\frac{\varepsilon \Delta t}{2}\left( v^{\prime \prime }(\zeta _i)-\bar{\bar{H}}^{\prime \prime }(\zeta _i)\right) \nonumber \\&\quad +\frac{\Delta t}{2} \left( v(\zeta _i)-\bar{\bar{H}}(\zeta _i)\right) -\frac{\Delta t (1-\eta m)}{2}\left( u(\zeta _i)-\bar{H}(\zeta _i)\right) \mid \mid _\infty . \end{aligned}$$
(39)

Using Theorem 5.7, one gets

$$\begin{aligned} \mid \mid {\mathcal {F}} {\textbf {U}}(\zeta _i) -{\mathcal {F}} {\textbf {H}}(\zeta _i)\mid \mid _\infty&\le Ch^{6}+Ch^{4}\nonumber \\&\le Ch^{4}(1+h^2) , \end{aligned}$$
(40)

and

$$\begin{aligned} \mid \mid {\mathcal {T}} {\textbf {U}}(\zeta _i)-{\mathcal {T}} {\textbf {H}}(\zeta _i)\mid \mid _\infty&\le C \left( h^6+\frac{\varepsilon \Delta t}{2} h^{4}+\frac{\Delta t}{2} h^{6}+\frac{\Delta t (1-\eta m)}{2}h^6\right) \nonumber \\&\le Ch^4 \left( \frac{\varepsilon \Delta t}{2} + \frac{\Delta t}{2}h^2 + (1+\frac{\Delta t (1-\eta m)}{2})h^2\right) . \end{aligned}$$
(41)

Now, consider:

$$\begin{aligned} \mid \mid {\mathcal {F}} {\textbf {H}}(\zeta _i) -{\mathcal {F}} \bar{{\textbf {U}}}(\zeta _i)\mid \mid _\infty =\,\, \mid \mid P_{1}(\zeta _i) - {\mathcal {F}} \bar{{\textbf {U}}}(\zeta _i)\mid \mid _\infty \ , \\ \mid \mid {\mathcal {T}} {\textbf {H}}(\zeta _i) -{\mathcal {T}} \bar{{\textbf {U}}}(\zeta _i)\mid \mid _\infty =\,\, \mid \mid P_{2}(\zeta _i) -{\mathcal {T}} \bar{U}(\zeta _i)\mid \mid _\infty , \end{aligned}$$

where \( {\mathcal {F}} {\textbf {H}}(\zeta _i) = P_{1}(\zeta _i)\) and \({\mathcal {T}} {\textbf {H}}(\zeta _i) = P_{2}(\zeta _i)\) are the fully discretized explicit form of differential problem mentioned in Sect. 4.

$$\begin{aligned} \mid \mid {\mathcal {F}} {\textbf {H}}(\zeta _i)-{\mathcal {F}} \bar{{\textbf {U}}}(\zeta _i)\mid \mid _\infty&\le \,\, \mid \mid {\mathcal {F}} {\textbf {U}}(\zeta _i)-{\mathcal {F}} \bar{{\textbf {U}}}(\zeta _i)\mid \mid _\infty \nonumber \\&\le \,\,Ch^{4}(1+h^2) ,\nonumber \\ \mid \mid {\mathcal {T}} {\textbf {H}}(\zeta _i)-{\mathcal {T}} \bar{{\textbf {U}}}(\zeta _i)\mid \mid _\infty&\le \,\, \mid \mid {\mathcal {T}} {\textbf {U}}(\zeta _i)-{\mathcal {T}} \bar{{\textbf {U}}}(\zeta _i)\mid \mid _\infty \nonumber \\&\le \,\, Ch^4 \left( \frac{\varepsilon \Delta t}{2} + \frac{\Delta t}{2}h^2 + (1+\frac{\Delta t (1-\eta m)}{2})h^2\right) . \end{aligned}$$
(42)

Equation (42) has been obtained using the above equation and again, using

$$\begin{aligned} {\mathcal {F}} \bar{{\textbf {U}}}(\zeta _i) = \hat{P}_{1}(\zeta _i)\quad \text {and}\quad {\mathcal {T}} \bar{{\textbf {U}}}(\zeta _i) = \hat{P}_{2}(\zeta _i), \end{aligned}$$

its compact matrix representation

$$\begin{aligned} {\textbf {L}}\hat{y}^{n+1}={\textbf {J}}\hat{y}^n +{\textbf {f}}^n . \end{aligned}$$
(43)

This implies, using Eqs. (43) and (27), one gets

$$\begin{aligned}{} & {} {\textbf {L}}[y^{n+1}-\hat{y}^{n+1}]={\textbf {J}}[y^n-\hat{y}^n],\nonumber \\{} & {} \quad \Rightarrow \quad [y^{n+1}-\hat{y}^{n+1}]={\textbf {L}}^{-1}{} {\textbf {J}}[y^n-\hat{y}^n ]. \end{aligned}$$
(44)

Again, L is non-singular and boundedness of Hermite splines by unity implies that

$$\begin{aligned} \mid \mid {\textbf {L}}^{-1}\mid \mid _\infty \le C , \end{aligned}$$
(45)

where C is some arbitrary constant. Now,

$$\begin{aligned} \mid \mid {\textbf {J}}(y^n-\hat{y}^n)\mid \mid _\infty&\le max\left\{ \mid P_{1}(\zeta _i)- \hat{P}_{1}(\zeta _i)\mid ,\mid P_{2}(\zeta _i)-\hat{P}_{2}(\zeta _i)\mid \right\} \nonumber \\&\le max\left\{ \mid {\mathcal {F}} {\textbf {H}}(\zeta _i)-{\mathcal {F}} \bar{{\textbf {U}}}(\zeta _i)\mid ,\mid {\mathcal {T}} H(\zeta _i)-{\mathcal {T}} \bar{U}(\zeta _i)\mid \right\} \nonumber \\&\le C\ max\left\{ h^{4}(1+h^{2}),\ \ h^4 \left( \frac{\varepsilon \Delta t}{2} + \frac{\Delta t}{2}h^2 + (1+\frac{\Delta t (1-\eta m)}{2})h^2\right) \right\} . \end{aligned}$$
(46)

From Eqs. (44), (45) and (46) one derives

$$\begin{aligned} \mid \mid y^{n+1}-\hat{y}^{n+1}\mid \mid _\infty \le C\ max\left\{ h^{4}(1+h^{2}),\ \ h^4 \left( \frac{\varepsilon \Delta t}{2} + \frac{\Delta t}{2}h^2 + (1+\frac{\Delta t (1-\eta m)}{2})h^2\right) \right\} . \end{aligned}$$
(47)

Moving towards the error bounds of

$$\begin{aligned} \mid \mid \bar{\bar{H}}(\zeta )- \bar{v}(\zeta )\mid \mid _\infty \&=\left\| \sum _{i=1}^{6}(d_i(t)-{\hat{d}}_i(t))H_i(\zeta )\right\| _\infty \nonumber \\&\le \sum _{i=1}^{6}{\mid H_i(\eta )\mid \mid \mid d_i(t)-\hat{d}_i(t))\mid \mid }_\infty \nonumber \\&\le Ch^{4}(\alpha _{2}+\alpha _{0}h^{2}). \end{aligned}$$
(48)

Equation (48) is obtained using Eq. (47) and boundedness of \(H_i(\zeta )\) by 1. Similarly,

$$\begin{aligned} \mid \mid \bar{H}(\zeta )- \bar{u}(\zeta )\mid \mid _\infty= & {} \left\| \sum _{i=1}^{6}(c_i(t)-{\hat{c}}_i(t))H_i(\zeta )\right\| _\infty \ \nonumber \\\le & {} \sum _{i=1}^{6}{\mid H_i(\eta )\mid \mid \mid c_i(t)-\hat{c}_i(t))\mid \mid }_\infty \nonumber \\\le & {} Ch^4 \left( \frac{\varepsilon \Delta t \alpha _2}{2} + \frac{\Delta t \alpha _0}{2}h^2 + \left( 1+\frac{\Delta t (1-\eta m)}{2}\right) \alpha _0 h^2\right) . \end{aligned}$$
(49)

Combining the above results in Eqs. (48) and (49), one gets

$$\begin{aligned} \mid \mid {\textbf {H}}(\zeta )-\bar{{\textbf {U}}}(\zeta )\mid \mid _\infty\le & {} C\ max\Bigg \{h^{4}(\alpha _{2}+\alpha _{0}h^{2}),\nonumber \\{} & {} \quad h^4 \left( \frac{\varepsilon \Delta t \alpha _2}{2} + \frac{\Delta t \alpha _0}{2}h^2 + \left( 1+\frac{\Delta t (1-\eta m)}{2}\right) \alpha _0 h^2\right) \Bigg \}. \end{aligned}$$
(50)

now,

$$\begin{aligned} \mid \mid {\textbf {U}}(\zeta )-\bar{{\textbf {U}}}(\zeta )\mid \mid _\infty \le \mid \mid {\textbf {U}}(\zeta )-{\textbf {H}}(\zeta )\mid \mid _\infty + \mid \mid {\textbf {H}}(\zeta )-\bar{{\textbf {U}}}(\zeta )\mid \mid _\infty , \end{aligned}$$

using Theorem 5.7 and Eq. (50)

$$\begin{aligned}{} & {} \mid \mid {\textbf {U}}(\zeta )-\bar{{\textbf {U}}}(\zeta )\mid \mid _\infty \le C\alpha _0h^{6}+C\ max\left\{ h^{4}(\alpha _{2}+\alpha _{0}h^{2}), h^4 \left( \frac{\varepsilon \Delta t \alpha _2}{2} + \frac{\Delta t \alpha _0}{2}h^2 +\left( 1+\frac{\Delta t (1-\eta m)}{2}\right) \alpha _0 h^2\right) \right\} \nonumber \\{} & {} \quad \le C\Bigg (\alpha _0h^{6}+\ max\left\{ h^{4}(\alpha _{2}+\alpha _{0}h^{2}), h^4 \left( \frac{\varepsilon \Delta t \alpha _2}{2} + \frac{\Delta t \alpha _0}{2}h^2 + \left( 1+\frac{\Delta t (1-\eta m)}{2}\right) \alpha _0 h^2\right) \right\} \Bigg ).\nonumber \\ \end{aligned}$$
(51)

\(\square \)

Theorem 5.9

Let \(\bar{{\textbf {U}}}(\zeta , t)\) be the approximate solution of the function \({\textbf {U}}(\zeta , t)\) defined on \([a, b]\times (0, T]\) such that \({\textbf {U}}(\zeta , t) \in C^6[a, b]\) and \({\textbf {H}}(\zeta )\) be the quintic Hermite splines interpolate of \({\textbf {U}}(\zeta , t)\) with Crank Nicolson scheme in time direction. Then the error estimate \(\mid \mid {\textbf {U}}-\bar{{\textbf {U}}}\mid \mid _\infty \) is defined by : 

$$\begin{aligned} \mid \mid {\textbf {U}}-\bar{{\textbf {U}}}\mid \mid _\infty \le C\Bigg ((\Delta t)^2+\alpha _0h^{6}+ max\left\{ h^{4}(\alpha _{2}+\alpha _{0}h^{2}), h^4 \left( \frac{\varepsilon \Delta t \alpha _2}{2} + \frac{\Delta t \alpha _0}{2}h^2 + (1+\frac{\Delta t (1-\eta m)}{2})\alpha _0 h^2\right) \right\} \Bigg ). \end{aligned}$$

Proof

Directly from Theorem 5.8 and Lemma 5.1. \(\square \)

5.1 Parameter uniform rate of convergence

For the problems,where exact solution not known, nodal error is estimated by using the following formula:

$$\begin{aligned} e_\varepsilon ^{N,M} (i,m)= \mid U^{N,M} (i,m)-U^{2N,M} (i,m)\mid . \end{aligned}$$

Maximum nodal error has been calculated by

$$\begin{aligned} E_{\varepsilon ,N,M}=max_{i} {e_\varepsilon ^{N,M} (i,m) }. \end{aligned}$$

Maximum \(\varepsilon \)—uniform nodal error has been calculated by

$$\begin{aligned} E_{N,M}=max_\varepsilon E_{\varepsilon ,N,M} , \end{aligned}$$

And the parameter \(\varepsilon \)—uniform rate of convergence has been evaluated by using double mesh principle [45]

$$\begin{aligned} R_N = \frac{log(E_{N,M}) - log(E_{2N,M})}{log(2)} . \end{aligned}$$

6 Results and discussion

In this part of manuscript, various fourth order EFK type equation with different non-linear function f(u) has been investigated by the proposed technique. Solution behaviour has been analysed with respect to the different parameters of the technique and the perturbation parameter. The numerical results are presented in the form of graphs and tables. \(L_2\)- norm, \(L_\infty \)-norm and Global relative error (GRE) has been computed as-

$$\begin{aligned} \mid \mid u \mid \mid _2&=\sqrt{ h^2\sum _{j=1}^N u^2(\zeta _{j}, t)}, \nonumber \\ \mid \mid u \mid \mid _\infty&= max_i u(\zeta _i,t), \nonumber \\ GRE&=\frac{\sum _{j=1}^N \mid u(\zeta _{j},t)-\tilde{u}(\zeta _{j},t) \mid }{\sum _{i=1}^N \mid u(\zeta _i, t)\mid }, \end{aligned}$$
(52)

where \(u(\zeta ,t)\) denotes the approximate solution and \(\tilde{u}(\zeta , t)\) denotes the analytic solution. For computation of \(L_2\)-norm and \(L_\infty \)-norm for error, function \( u(\zeta ,t)\) has been replaced by the error.

Fig. 4
figure 4

Behavior of wave solution \(u(\zeta , t)\) and \(v(\zeta ,t)\) with \(\varepsilon =10^{-1}\) for Example 6.1

Full size image
Fig. 5
figure 5

Behavior of wave solution \(u(\zeta , t),\) \(v(\zeta ,t)\) with \(\varepsilon =10^{-4}\) for Example 6.1

Full size image

Example 6.1

Consider the EFK equation with initial and the boundary conditions defined as:

$$\begin{aligned}{} & {} u(\zeta ,0) = -sin(\pi \zeta )\quad x \in [-4, 4], \\{} & {} u (-4, t) = 0 ,\quad u (4, t) = 0, \\{} & {} u_{\zeta \zeta } (-4,t)=0,\quad u_{\zeta \zeta } (4,t)=0. \end{aligned}$$
Table 3 Parameter uniform convergence rate at \(T=0.2\) for Example 6.1
Full size table
Table 4 Comparison of \(L_2,\) \(L_\infty \) and GRE norm due to \(\Delta t=0.01\) and \(\Delta t=0.001\) for Example 6.1 with \(N=64\)
Full size table
Table 5 Comparison of \(L_2\)-norm \(L_\infty \)-norm and GRE with respect to partitions in space and time directions for Example 6.1 at \(T=2\)
Full size table
Table 6 Comparison of \(L_\infty \)-norm with the results with EFG method for Example 6.1
Full size table
Table 7 Comparison of absolute error at different values of \(\zeta \) for Example 6.1 with \(\Delta t=0.01\) and \(N=64\)
Full size table
Fig. 6
figure 6

Stable behavior of solution \(u(\zeta , t),\) \(v(\zeta , t)\) for Gaussian initial function for Example 6.2(a)

Full size image
Fig. 7
figure 7

Behavior of solution \(u(\zeta , t),\) \(v(\zeta , t)\) for Example 6.2(b)

Full size image

The problem has been analyzed for two cases, first when the equation is homogenous and second when it has a non-homogenous part

\(f(\zeta ,t)=\exp (-t)sin(\pi \zeta )(\exp (-2t)sin^2(\pi \zeta )+\pi ^2+\pi ^4-2).\) For non-homogenous case i.e. \(f(\zeta ,t)\ne 0\) perturbation parameter \(\varepsilon =1\) has been considered.

In first case, \(\Delta t = 0.01\) and N = 100. which is quite less than as considered in [7] with \(\varepsilon \) is taken to be 0.0001 and 0.1. Numerical profile of \(u(\zeta , t)\) and \(v(\zeta , t)\) has been shown graphically in Figs. 3 and 4 for \(\varepsilon \) = 0.1 and 0.0001 respectively. Stable solution profile of EFK is shown for both \(\varepsilon \) = 0.0001 and \(\varepsilon \) = 0.1. The solution \(u(\zeta , t)\) moves to zero at 40th time step with \(\Delta t\) = 0.01. The effect of perturbation parameter has been studied and shown in Table 3.

In second case, the analytic form of solution is \(u(\zeta ,t)=\exp (-t)sin(\pi \zeta )\) and the initial function has been taken as \(u(\zeta ,0)=sin(\pi \zeta ).\) The solution behaviour and the error profile has been depicted in the Fig. 5. The non-homogenous part delays the stable state value in comparison to the homogenous case. \(L_2\)-norm, \(L_\infty \)-norm and GRE at different time level with respect to \(\Delta t\) = 0.01 and \(\Delta t\) = 0.001 has been reported in Table 4. The effect of \(\Delta t\) and h on \(L_2\)-norm, \(L_\infty \)-norm and GRE has been studied in Table 5. At different time level, step size and \(\Delta t,\) a comparison of \(L_\infty \)-norm has been given in Table 6 with the results available in [3]. Again the behaviour of absolute error at some node points corresponding to different time levels has been reported in Table 7.

Example 6.2

Consider EFK equation with Gaussian initial condition

  1. (a)

    u(\(\zeta \), 0) = \(10^{-3}\exp (-\zeta ^2)\)\(\zeta \in \) [− a, a] with boundary conditions

    \(u(-a, t) = 1\ \ \ \ \ u (a, t) = 1 ,\ \ \)

    \(u_{\zeta \zeta } (-a, t)=0\ \ \ \ \ \ u_{\zeta \zeta }(a, t)=0 .\)

  2. (b)

    \(u(\zeta , 0) = -10^{-3}\exp (-\zeta ^2) \)\(\zeta \in \) [− a, a] and boundary conditions

    \(u (-a, t) = -1 \ \ \ \ \ \ \ u (a, t) = -1,\)

    \(u_{\zeta \zeta } (-a,t)=0\ \ \ \ \ \ u_{\zeta \zeta }(a, t)=0.\)

For case (a), computations for \(\Delta t = 0.01,\) \(N= 50,\) and \(\varepsilon = 0.0001\) has been considered. Corresponding to different time steps, up-to \(T=5,\) for the domain \([-4, 4]\) and up to \(T=8\) for the spatial domain \([-10, 10],\) the numerical profiles are shown in Fig. 6. With the passage of time, the solution decays to the stable state boundary value 1. With the change in domain from \([-4, 4]\) to \([-10, 10],\) the behaviour of \(u(\zeta ,t)\) delays in the stable state value 1 with increments in the path length for the solution waves at different time. When the initial function is \(u(\zeta , 0) = \exp (-\zeta ^2)\) the solution moves to the stable state faster.

Table 8 Effects on the norms due to domain for Example 6.2(a) with \(\Delta t=0.01\) and \(N=50\) and \(\varepsilon =0.0001\)
Full size table
Table 9 Effects on the norms due to domain for Example 6.2(b) with \(\Delta t=0.01\) and \(N=64\) and \(\varepsilon =0.01\)
Full size table
Fig. 8
figure 8

Behavior of solution profile \(u(\zeta , t)\) for Example 6.3 for \(\varepsilon =1\) corresponding to different domain

Full size image

Case(b) In this case, \(\Delta \)t = 0.01, \(N= 50\) and \(\varepsilon \) = 0.0001 has been taken. Corresponding to different values of time, up-to \(T=5\) for the domain \([-4, 4]\) and up to \(T=8\) for the domain \([-10, 10],\) the behavior of computed values at the node points has been shown in Fig. 7. In this case also, the solution moves towards the stable state boundary value \(-1\) as the time progresses. For both the cases Examples 6.2(a) and 6.2(b) with change in domain, \(L_2\)-norm gets effected as compared to \(L_\infty \)-norm signifying the delay in stable state as shown in Tables 8 and 9.

Table 10 Variations in \(L_2\)-norm and \(L_\infty \)-norm due to domain for Example 6.3 with \(\Delta t\)=0.01 and \(N=64\) and \(\varepsilon =0.01\)
Full size table
Fig. 9
figure 9

Behavior of solution profile \(u(\zeta , t)\) for Example 6.4(a) for different \(\varepsilon \)

Full size image
Fig. 10
figure 10

Behavior of solution \(u(\zeta , t)\) and \(v(\zeta , t)\) for \(\varepsilon \) = 0.1 and 0.01 for Example 6.4(b)

Full size image

Example 6.3

Consider the Eq. (1) for non-linear function f(u) as Fisher’s reaction–diffusion type function:

$$\begin{aligned} u_t+\varepsilon u_{\zeta \zeta \zeta \zeta } - u_{\zeta \zeta }+ u^2 - u =0\quad (\zeta , t) \in [-4, 4] \times (0, T] , \end{aligned}$$
(53)

with initial and boundary conditions \(u(\zeta ,0)=(1+exp(\frac{\zeta }{\sqrt{6}}))^{-2} ,\)

$$\begin{aligned} \begin{array}{ll} u(0,t)=\left( 1+exp\left( \frac{(-5t)}{\sqrt{6}}\right) \right) ^{-2} , &{}\quad u(1, t)=\left( 1+exp\left( \frac{(1-5t)}{\sqrt{6}}\right) \right) ^{-2} ,\\ u_{\zeta \zeta } (0, t)=0, &{}\quad u_{\zeta \zeta } (1, t) = 0 . \end{array} \end{aligned}$$
Table 11 Presentation of \(L_2\)-norm and \(L_\infty \)-norm with \(\Delta t=0.01\) and \(N=50\) for Example 6.4
Full size table
Table 12 Parameter uniform convergence rate at \(T=0.04\) for Example 6.4
Full size table
Fig. 11
figure 11

Absolute error profile of Example 6.5

Full size image

With \(\Delta \)t = 0.01 up to \(t=5\) and \(N= 50.\) It has been observed that for different values of perturbation parameter the solution wave profile remained same. Corresponding to the different bounded domains with \(\varepsilon \) = 1 the computed solution has been reported in Fig. 8. It is observed that for the domain \([-4,4],\) the solution approaches the stable state and attains stable value 1. For the domain \([-10, 10]\) an uplifting wave at right boundary has been observed within same time range. While for the domain \([-30, 30],\) the solution behaviour is wavy like a fluid falling down an inclined plane. The effect of domain on the wave behaviour at any time can also be observed from \(L_2\)-norm and \(L_\infty \)-norm along the row in Table 10.

Example 6.4

Consider the EFK equation

$$\begin{aligned} u_t+\varepsilon u_{\zeta \zeta \zeta \zeta } - u_{\zeta \zeta }+ u^3 - u =0\quad (\zeta , t) \in [0, 1] \times (0, T] , \end{aligned}$$
(54)

with initial and boundary conditions are defined as:

(a) u(\(\zeta ,\) 0) = \(\zeta ^2 (1-\zeta )^2 ,\) (b) u(\(\zeta ,\) 0) = \(\zeta ^3 (1-\zeta )^3 ,\)

\( u(0,t)=0 \ \ \ \ \ \ \ \ \ \ u(1, t)=0 ,\)

\(u_{\zeta \zeta } (0, t)=0\ \ \ \ \ \ \ \ u_{\zeta \zeta } (1, t) = 0 .\)

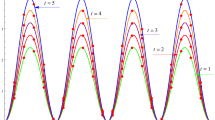
With \(\Delta \)t = 0.01, \(N= 50\) and \(\varepsilon \) = 0.01, 0.1 and 1. For initial condition (a) the behaviour of solution profile corresponding to different time steps and different values of \(\varepsilon \) has been shown in Fig. 9. For initial condition (b) with \(\varepsilon =0.1\) and with \(\varepsilon =0.01\) the behavior of solution profile \(u(\zeta , t)\) and \(v(\zeta , t)\) corresponding to different time steps has been shown in Fig. 10a, b, c and d, respectively.

For \(\varepsilon \) = 0.01 the solution profile moves to stable state value uniformly, but with a slight increment in the value of perturbation parameter the solution approaches to its stable state with alternating waves having different amplitudes, one with a slight oscillation. Further, when \(\varepsilon \) = 1, the stable state value has been attained but again the waves’ behaviour is alternating, one oscillatory wave with above the stable state and another oscillatory wave below the stable state value. It is observed from the Table 11 that the perturbation parameter effects the nature of waves as compared to the technique parameters for both space and time discretization. Parameter uniform rate of convergence of order one for Example 6.4(b) has been reported in Table 12 with \(\Delta t = 10^{-3}.\)

Example 6.5

Consider the fourth order differential equation

$$\begin{aligned} u_t +\gamma u_{\zeta \zeta \zeta \zeta }-u_{\zeta \zeta }=\alpha u^5 + \beta u^3 + \kappa u^2\quad (\zeta , t) \in [a, b]\times [0, T] , \end{aligned}$$
(55)

For \(\alpha =24,\) \(\beta = -2\) and \(\kappa = -2\) and \(\gamma =1\) the exact form of solution of Eq. (55) is

$$\begin{aligned} u(\zeta , t) = \frac{1}{\zeta +2t}\quad (\zeta , t) \in [a, b] \times [0,T]. \end{aligned}$$
(56)

The absolute error has been shown in Fig. 11. There is no major improvement in the error as time step decreases from \(\Delta t=0.01\) to \(\Delta t=0.001\) with \(N=50\) as in Table 13. The effect of time on the \(L_2\) norm and \(L_\infty \) norm can be observed along the column of Table 13. Again, the effect of perturbation parameters on \(L_2\)-norm, \(L_\infty \)-norm and GRE has been studied in Table 14. It is observed that the increment in the non-linearity of polynomial f(u) does not effect the approximation efficiency and accuracy. Parameter uniform rate of convergence of order two has been reported in Table 15 with \(\Delta t = 10^{-2}.\)

Table 13 \(L_2\)-norm and \(L_\infty \)-norm for error at \(\Delta t= 0.01\) and \(\Delta t= 0.001\) for Example 6.5
Full size table
Table 14 Comparison of \(L_2\)-norm \(L_\infty \)-norm and GRE with respect to space and time partitions for Example 6.5 at \(T=0.5\)
Full size table
Table 15 Parameter uniform convergence rate at \(T=0.2\) for Example 6.5
Full size table
Fig. 12
figure 12

Solution profile of Example 6.6 for different values of \(\gamma \) and \(\alpha \)

Full size image
Table 16 \(L_2\)-norm and \(L_\infty \)-norm with \(\Delta t=0.01\) and \(N=32,\) \(\alpha =1\) for Example 6.6
Full size table
Table 17 Computed \(L_2\)-norm and \(L_\infty \)-norm with \(\Delta t=0.01\) and \(N=50\) and \(\alpha =-1\) for Example 6.6
Full size table

Example 6.6

Consider the fourth order differential equation having bistable cubic non-linearity

$$\begin{aligned} u_t +\varepsilon u_{\zeta \zeta \zeta \zeta }-u_{\zeta \zeta }= u(u-\alpha )(1-u)\quad (\zeta , t) \in [a, b]\times [0, T], \end{aligned}$$
(57)

with the initial and boundary conditions

$$\begin{aligned} u(\zeta , 0)&= \frac{1}{2}+\frac{1}{2}tanh\left( \frac{\sqrt{2}\zeta }{4}\right) , \\ u(a,t)&= \frac{1}{2}+\frac{1}{2}tanh\left( \frac{\sqrt{2}a+(1-2\alpha )t}{4}\right) , \\ u(b,t)&= \frac{1}{2}+\frac{1}{2}tanh\left( \frac{\sqrt{2}b+(1-2\alpha )t}{4}\right) . \end{aligned}$$

For \(\varepsilon =1\) and \(\alpha =1\) and \(-1,\) the travelling wave configuration has been observed. For \(\varepsilon =1\) the travelling wave have a constant phase but as \(\gamma \) decreases i.e. for \(\varepsilon =0\) the wave configuration has some phase turning point as can be observed from the Fig. 12 which shows the boundary layer effect due to perturbation parameter \(\varepsilon .\) It has also been observed that for positive \(\alpha \) the solution profile has decreasing nature while for negative \(\alpha \) the wave profile is increasing with time, can be observed along the column in Tables 16 and 17. The effect of perturbation parameter can be observed from any row of the Tables 16 and 17 for both the cases \(\alpha =1\) and \(\alpha =-1.\)

7 Conclusions and discussion

The proposed technique has been implemented to various forms of fourth order semi-linear dissipative, reaction–diffusion equations which are analysed with fairly known initial functions. Travelling wave behaviour propagating in reaction–diffusion dissipative media has been studied using the proposed hybrid technique. For problems having exact form of solution the error in the form of \(L_2\) norm and \(L_\infty \) norm has been reported in tables. These equations have mono-stable and bi-stable non-linearity.

Error analysis shows that the hybrid technique is significantly effective for higher order problems with higher degree of non-linearity.

The equations exhibited wave behaviour and the effect of perturbation parameter has been studied. In Example 3 non-linear fourth order problem with Fisher equation type non-linearity has been considered. Effect of the bounded domain on the wave behaviour has also been observed. In Example 6 fourth order equation with bi-stable cubic non-linearity has been considered. The effect of perturbation parameter \(\varepsilon \) and the parameter \(\alpha \) has been studied. Both the equations model the problems in population dynamics. These mono-stable and bi-stable non-linear problems have travelling wave configurations. Parameter Uniform convergence rate has been studied for analysing the effect of perturbation parameter \(\varepsilon \) and the rate of convergence in certain cases found to be greater than 1.