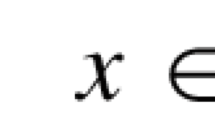A note on the inhomogeneous fractional nonlinear Schrödinger equation

Abstract

This paper investigates some well-posedness issues of the fractional inhomogeneous Schrödinger equation

$$\begin{aligned} i\dot{u}-(-\Delta )^\gamma u=\pm |x|^\rho |u|^{p-1}u, \end{aligned}$$

where $0<\gamma <1$ and $\rho <0$. Here, one considers the inter-critical regime $0<s_c:=\frac{N}{2}-\frac{2\gamma +\rho }{p-1}<\gamma$, where $s_c$ is the energy critical exponent, which is the only one real number satisfying $\Vert \kappa ^\frac{2\gamma +\rho }{p-1}u_0(\kappa \cdot )\Vert _{\dot{H}^{s_c}}=\Vert u_0\Vert _{\dot{H}^{s_c}}$. In order to avoid a loss of regularity in Strichartz estimates, one assumes that the datum is spherically symmetric. First, using a sharp Gagliardo–Nirenberg-type estimate, one develops a local theory in the space $\dot{H}^\gamma \cap \dot{H}^{s_c}$. Then, one investigates the $L^{\frac{N(p-1)}{\rho +2\gamma }}$ concentration of finite-time blow-up solutions bounded in $\dot{H}^{s_c}$. Finally, one proves the existence of non-global solutions with negative energy. Since one considers the homogeneous Sobolev space $\dot{H}^{s_c}$, the main difficulty here is to avoid the mass conservation law.

1 Introduction

This work deals with the initial value problem for an inhomogeneous nonlinear Schrödinger equation

$$\begin{aligned} \left\{ \begin{matrix} i\dot{u}-(-\Delta )^\gamma u+\epsilon |x|^\rho |u|^{p-1}u=0;\\ u_{|t=0}= u_0. \end{matrix} \right. \end{aligned}$$

(1.1)

The nonlinear equations of Schrödinger type have a deep influence in physical modeling. The fractional Schrödinger equation was derived in Refs. [8, 9] by extending the Feynman path integral from the Brownian-like to the Lévy-like quantum mechanical paths. It is a fundamental equation of fractional quantum mechanics. If $\rho = 0$, the homogeneous fractional Schrödinger equation (1.1) arises in plasma physics, fluid mechanics and nonlinear optics [1]. If $\rho \ne 0$, it can model the laser beam propagation in some inhomogeneous medium [2, 6, 11, 19].

Here and hereafter, $N\ge 2$ and u is a complex valued function of the variable $(t,x)\in {\mathbb {R}}_+\times {\mathbb {R}}^N$. The defocusing or focusing regime is given by $\epsilon \in \{\pm 1\}$. The fractional Laplacian exponent is $\gamma \in (0,1)$. The inhomogeneous unbounded term is $|\cdot |^\rho$, $\rho <0$. The equation (1.1) satisfies the scaling invariance

$$\begin{aligned} u_\kappa :=\kappa ^\frac{2\gamma +\rho }{p-1}u(\kappa ^{2\gamma } \cdot ,\kappa \cdot ),\quad \kappa >0. \end{aligned}$$

The following homogeneous Sobolev norm gives the critical Sobolev index:

$$\begin{aligned} \Vert u_\kappa \Vert _{\dot{H}^s}=\kappa ^{s-\frac{N}{2}+\frac{2\gamma +\rho }{p-1}}\Vert u(\kappa ^{2\gamma }\cdot )\Vert _{\dot{H}^s}:=\kappa ^{s-s_c}\Vert u(\kappa ^{2\gamma }\cdot )\Vert _{\dot{H}^s}. \end{aligned}$$

The mass-critical case $s_c=0$ corresponds to $p=p_*=:1+\frac{2(2\gamma +\rho )}{N}$, which is related to the mass conservation law

$$\begin{aligned} M[u(t)]:=\int \limits _{{\mathbb {R}}^N}|u(t,x)|^2\,\text {d}x=M[u_0]. \end{aligned}$$

The energy-critical case $s_c=\gamma$ which corresponds to $p=p^*=:1+\frac{2(2\gamma +\rho )}{N-2\gamma }$ is related to the energy conservation law

$$\begin{aligned} E[u(t)]:=\int \limits _{{\mathbb {R}}^N}\left( \frac{1}{2}|(-\Delta )^\frac{\gamma }{2}u(t,x)|^2- \frac{\epsilon }{1+p}|x|^\rho |u(t,x)|^{1+p}\right) \text {d}x=E[u_0]. \end{aligned}$$

It is standard that if $\epsilon <0$, the energy is non-negative and the problem (1.1) is said to be defocusing. In such a case, an energy sub-critical solution is claimed to be a global one. Otherwise, it is focusing and the Sobolev norm $\Vert \cdot \Vert _{\dot{H}^\gamma }$ of a local solution is no longer estimated with use of the conserved laws. In such a case, a local solution may concentrate in finite time.

To the authors knowledge, the inhomogeneous nonlinear fractional Schrödinger equation was considered in few papers. Indeed, for $\rho <0$, the first author [15] developed a local theory in the energy space $H^\gamma$. Indeed, using a sharp Gagliardo–Nirenberg estimate, the existence of energy local solutions was established. Moreover, taking account of the Potential-well theory, the local solution extends to a global one, via the existence of ground states. In the complementary case $\rho <0$, the local theory was considered in Ref. [13]. In fact, using an inhomogeneous Gagliardo–Nirenberg-type inequality, the ground-state threshold of global existence versus finite tine blow-up was obtained. Moreover, the existence of non-global solutions was proved, for negative energy and spherically symmetric data, following the method of Ref. [3]. Some blow-up dynamics of mass-critical focusing inhomogeneous fractional nonlinear Schrödinger equation, with a mass larger than the ground-state one, were investigated in Ref. [14].

The purpose of this manuscript is to develop a local theory of the fractional Schrödinger problem (1.1) in the space $\dot{H}^\gamma \cap \dot{H}^{s_c}$. The main difference with the previous work [13] is the lack of a mass conservation, which gives some technical problems. The limiting case $s=1$ was considered in a recent note [4]. Finally, one needs to deal with the non-local free operator and the unbounded inhomogeneous term $|\cdot |^\rho$. Note that in the previous work [16], the first author studied similar questions for the non-fractional regime, namely $\gamma =1$ and a non-local source term. Here, one needs to deal with the non-local fractional Laplacian operator which gives serious complications. In particular, there is no classical variance identity and one uses a localized one in the spirit of Ref. [3].

The note is organized as follows. In Sect. 2, one gives the contribution and some standard estimates. Section 3 contains a Gagliardo–Nirenberg estimate. Section 4 deals with the local well-posedness. Sections 5 and 6 deal with the finite-time blow-up of solutions.

Here and hereafter, one denotes for simplicity the Lebesgue and Sobolev spaces and their standard norms by

$$\begin{aligned} L^p&:=L^p({\mathbb {R}}^N),\quad \Vert \cdot \Vert _p:=\Vert \cdot \Vert _{L^p}\quad \text{ and } \quad \Vert \cdot \Vert :=\Vert \cdot \Vert _2;\\ \dot{H}^{\gamma ,p}&:=(-\Delta )^{-\frac{\gamma }{2}}L^p,\quad \dot{H}^\gamma :=\dot{H}^{\gamma ,2}\quad \text{ and } \quad \Vert \cdot \Vert _{\dot{H}^\gamma }:=\Vert (-\Delta )^\frac{\gamma }{2} \cdot \Vert . \end{aligned}$$

If $T>0$ and Y is a Lebesgue or Sobolev space, one defines

$$\begin{aligned} C_T(Y)&:=C([0,T],Y),\quad L_T^p(Y):=L^p([0,T],Y);\\ \dot{H}^\gamma _{rd}&:=\{f\in \dot{H}^\gamma ,\quad f(\cdot )=f(|\cdot |)\}. \end{aligned}$$

Eventually, $[0,T^*)$ is the maximal existence interval of an eventual solution of (1.1).

2 Main results and background

This section contains the contribution of this work and some standard estimates needed in the sequel.

2.1 Notations

One denotes, here and hereafter, the real numbers

$$\begin{aligned} B&:=B(N,p,b,s):=\frac{Np-N-2b}{2s};\\ A&:=A(N,p,b,s):=1+p-B(p,b);\\ p_c&:=\frac{2N}{N-2s_c}=\frac{N(p-1)}{\rho +2\gamma }. \end{aligned}$$

In the spirit of [3], denote $\zeta _R:=R^2\zeta (\frac{\cdot }{R})$, where $\zeta \in C_0^\infty ({\mathbb {R}}^N)$ is spherically symmetric and

$$\begin{aligned} \zeta :r\longmapsto \left\{ \begin{array}{ll} \frac{1}{2}r^2,&{}\quad r\le 1;\\ 0,&{}\quad r\ge 10, \end{array} \right. \quad \text{ and }\quad \zeta ''\le 1. \end{aligned}$$

With a direct calculus

$$\begin{aligned} \zeta _R'(r)\le r,\quad \zeta _R''\le 1\quad \text{ and }\quad \Delta \zeta _R\le N. \end{aligned}$$

Moreover, $|\nabla ^j\zeta _R|\lesssim R^{2-j}$ for $0\le j\le 4$ and

$$\begin{aligned} supp(\nabla ^j\zeta _R)\subset \left\{ \begin{array}{ll} |x|\le 10R, &{}\quad j=1,2;\\ R\le |x|\le 10R, &{}\quad j=3,4. \end{array} \right. \end{aligned}$$

Denote the localized Virial

$$\begin{aligned} M_\zeta [u]:=2\Im \int \limits _{{\mathbb {R}}^N}{{\bar{u}}}\nabla \zeta \cdot \nabla u\,\text {d}x = 2\Im \int \limits _{{\mathbb {R}}^N}{{\bar{u}}}\partial _k\zeta \partial _k u\,\text {d}x. \end{aligned}$$

Let the differential operator acting on functions as follows:

$$\begin{aligned} \Gamma _\zeta u:=-i\Big [\nabla \zeta \cdot \nabla u+\nabla \cdot (u\nabla \zeta ) \Big ]. \end{aligned}$$

Thus, $\langle u,\Gamma _\zeta u\rangle =M_\zeta [u]$. Eventually, one denotes the sequence of functions

$$\begin{aligned} u_n&=\left( \frac{\sin (\pi s)}{\pi }\right) ^\frac{1}{2}{\mathcal {F}}^{-1} \left( \frac{{\mathcal {F}}{u}}{|\cdot |^2+n}\right) . \end{aligned}$$

2.2 Main results

Let us give the Theorems established in this note. First, one derives an inhomogeneous Gagliardo–Nirenberg estimate.

Theorem 2.1

Let $N\ge 2$, $\gamma \in (0,1)$, $-2\gamma<\rho <0$ and $p>1$. Then,

• 1. there exists a positive constant $C(N,p,\rho ,\gamma )$, such that for any $u\in \dot{H}^\gamma \cap L^{p_c}$,

  $$\begin{aligned} \int \limits _{{\mathbb {R}}^N}|u|^{1+p}|x|^\rho \,dx\le C(N,p,\rho ,\gamma )\Vert u\Vert _{p_c}^{p-1}\Vert (-\Delta )^\frac{\gamma }{2}u\Vert ^2. \end{aligned}$$

  (2.1)

• 2. Moreover, if $1+\frac{2\rho }{N}<p<p^*$, then

  • a. The minimization problem

    $$\begin{aligned} \frac{1}{C_{opt}}=\inf \left\{ \frac{\Vert u\Vert _{p_c}^{p-1}\Vert (-\Delta )^\frac{\gamma }{2}u\Vert ^2}{\int _{{\mathbb {R}}^N}|u|^{1+p}|x|^\rho \,dx},\quad 0\ne u\in \dot{H}^\gamma \cap L^{p_c}\right\} \end{aligned}$$

    is attained in some $\psi \in H^\gamma$ satisfying ${C_{opt}}=\int _{{\mathbb {R}}^N}|u|^{1+p}|x|^\rho \,dx$ and

    $$\begin{aligned} 2(-\Delta )^\gamma \psi -(p-1)|\psi |^{p_c-2}\psi +\frac{p+1}{C_{opt}}|x|^\rho |\psi |^{p-1}\psi =0; \end{aligned}$$

    (2.2)

  • b. Furthermore

    $$\begin{aligned} C_{opt}=\frac{1+p}{2}\Vert \phi \Vert _{p_c}^{-(p-1)}, \end{aligned}$$

    (2.3)

    where $\phi$ is a ground-state solution to

    $$\begin{aligned} (-\Delta )^\gamma \phi +|\phi |^{p_c-2}\phi -|x|^\rho |\phi |^{p-1}\phi =0,\quad 0\ne \phi \in \dot{H}^\gamma \cap L^{p_c}. \end{aligned}$$

    (2.4)

Remarks 2.2

• 1. The proof follows the method of Ref. [20];

• 2. A comparable estimate using the $L^2$ in the place of $L^{p_c}$ was proved in Ref. [13, Theorem 2.2];

• 3. Thanks to the Sobolev embedding $\dot{H}^{s_c}\hookrightarrow L^{p_c}$, the above estimate is adapted to the study of (1.1) in $\dot{H}^\gamma \cap \dot{H}^{s_c}$.

The Schrödinger problem (1.1) is locally well posed in $\dot{H}^\gamma _{rd}\cap \dot{H}^{s_c}$.

Theorem 2.3

Let $N\ge 2$, $\gamma \in \left( \frac{N}{2N-1},1\right)$, $-2\gamma<\rho <0$, $p_*< p< p^*$ and $u_0\in \dot{H}^\gamma _{rd}\cap \dot{H}^{s_c}$. Then, there is a unique local solution to (1.1),

$$\begin{aligned} u\in C_T(\dot{H}^\gamma _{rd}\cap \dot{H}^{s_c})\cap L^q_T(\dot{W}^{\gamma ,r}\cap \dot{W}^{s_c,r})\cap L^{q_1}_T(L^{r_1}), \end{aligned}$$

where $(q,r)\in \Gamma$ and $(q_1,r_1)\in \Gamma _{s_c}$. Moreover, the energy is conserved and u is global

• 1. In the defocusing case;

• 2. If $\Vert u\Vert _{L^\infty _{T^*}(\dot{H}^{s_c})}<\Vert \phi \Vert _{p_c}$, where $\phi$ is a ground state of (2.4).

Remarks 2.4

• 1. The sets $\Gamma$ and $\Gamma _{s_c}$ are defined in Remark 2.11;

• 2. The proof is based on a fixed point argument via Strichartz estimates and the fractional chain rules;

• 3. The main difficulty is to estimate the source term in some Sobolev norms;

• 4. The spherically symmetric assumption avoids a loss of regularity in Strichartz estimates [7].

Now, one investigates the finite-time blow-up of solutions in the repulsive regime.

Theorem 2.5

Take $\epsilon =1$. Let $N\ge 2$, $\gamma \in \left( \frac{N}{2N-1},1\right)$, $-2\gamma<\rho <0$, $p_*< p< p^*$ and $u_0\in \dot{H}^\gamma _{rd}\cap \dot{H}^{s_c}$. Let u be the maximal solution to (1.1) given by the above result. Assume that $T^*<\infty$ and $\Vert u\Vert _{L^\infty _{T^*}(\dot{H}^{s_c})}<\infty$. If

$$\begin{aligned} \lim _{t\rightarrow T^*}\lambda (t)\Vert (-\Delta )^\frac{\gamma }{2}u(t) \Vert ^\frac{1}{\gamma -s_c}=\infty \end{aligned}$$

then,

$$\begin{aligned} \liminf _{t\rightarrow T^*}\int \limits _{|x|\le \lambda (t)}|u(t,x)|^{p_c} \,dx\ge \Vert \phi \Vert _{p_c}^{p_c}, \end{aligned}$$

where $\phi$ is a ground state of (2.4).

Remarks 2.6

• 1. The above result studies the $L^{p_c}$ concentration of the non-global solutions, which blow-up for finite time in $\dot{H}^\gamma$;

• 2. Take for $0<t<T^*$, the scaled function $v_t(\tau ,x):=(\mu (t))^\frac{2\gamma +\rho }{p-1}u(t+(\mu (t))^{2\gamma }\tau ,\mu (t)x)$, defined for $0<\tau <\frac{1}{(\mu (t))^{2\gamma }}(T^*-t)$. Thus, $v_t$ satisfies (1.1) with datum $v_t(0,x)=(\mu (t))^\frac{2\gamma +\rho }{p-1}u(t,\mu (t)x)$. Therefore, $\Vert v_t(0)\Vert _{\dot{H}^\gamma }=(\mu (t))^{\gamma -s_c}\Vert u(t)\Vert _{\dot{H}^\gamma }$. Let us choose $\mu (t):=\Vert u(t)\Vert _{\dot{H}^\gamma }^\frac{1}{s_c-\gamma }$ so that $\Vert v_t(0)\Vert _{\dot{H}^\gamma }=1$. The local existence theory gives the existence of $0<\tau _1<\frac{1}{(\mu (t))^{2\gamma }}(T^*-t)$ such that $v_t$ is defined on $[0,\tau _1]$. This gives the blow-up rate

  $$\begin{aligned} \Vert u(t)\Vert _{\dot{H}^\gamma }\ge \frac{C}{(T^*-t)^\frac{\gamma -s_c}{2\gamma }}; \end{aligned}$$

• 3. the concentration happens at the origin because of the radial assumption.

Finally, one gives a finite-time blow-up solutions result in $L^\infty _{T^*}(\dot{H}^{s_c})$ for negative energy.

Theorem 2.7

Take $\epsilon =1$. Let $N\ge 2$, $\gamma \in \left( \frac{N}{2N-1},1\right)$, $-2\gamma<\rho <0$, $p_*< p<\min {\{1+4\gamma , p^*\}}$ and a solution of (1.1) denoted by $u\in C_T(\dot{H}^\gamma _{rd}\cap \dot{H}^{s_c})$ such that $u\in L^\infty _{T^*}(\dot{H}^{s_c})$. Then,

• 1. For any $R>0$ and any $\beta >0$, holds in [0, T),

  $$\begin{aligned} \frac{d}{dt}M_{\zeta _R}[u]\le & {} 4BE(u_0)+4(\gamma -B)\Vert u\Vert _{\dot{H}^\gamma }^2+\beta \Vert u\Vert _{\dot{H}^\gamma (|x|>R)}^2+C_\beta R^{-2(\gamma -s_c)}. \end{aligned}$$

• 2. If $E(u_0)<0$, then $T^*<\infty$.

Remarks 2.8

• 1. The above result gives some sufficient conditions to have the existence of blowing-up solutions in $\dot{H}^\gamma$, which are bounded in $\dot{H}^{s_c}$;

• 2. The extra assumption $p<1+4\gamma$ is due to the lack of a variance identity for the Schrödinger equation with fractional Laplacian;

• 3. The above result gives a meaning to Theorem 2.5.

2.3 Tools

Here, one lists some standard estimates needed along this manuscript.

Definition 2.9

One call admissible pair $(q,r)\in [2,\infty ]^2$ if

$$\begin{aligned} q\in \left[ \frac{4N+2}{2N-1},\infty \right] ,\quad \frac{2}{q}+\frac{2N-1}{r}\le N-\frac{1}{2}, \end{aligned}$$

or

$$\begin{aligned} q\in \left[ 2,\frac{4N+2}{2N-1}\right] ,\quad \frac{2}{q}+\frac{2N-1}{r}< N-\frac{1}{2}. \end{aligned}$$

Recall the so-called Strichartz estimate [7].

Proposition 2.10

Let $N \ge 2$, $s\in {\mathbb {R}}$, $\frac{N}{2N-1}<\gamma <1$ and $u_0\in H^s_{rd}$. Then,

$$\begin{aligned} \Vert u\Vert _{L^q_t(L^r)\cap L^\infty _t(\dot{H}^s)}\lesssim \Vert u_0\Vert _{\dot{H}^s}+\Vert i\dot{u}-(-\Delta )^\gamma u\Vert _{L^{{{\tilde{q}}}'}_t(L^{{{\tilde{r}}}'})}, \end{aligned}$$

if (q, r) and $({{\tilde{q}}},{{\tilde{r}}})$ are s-admissible pairs such that $({{\tilde{q}}},{{\tilde{r}}}, N)\ne (2,\infty , 2)$ or $(q, r, N)\ne (2,\infty , 2)$ and satisfy the condition

$$\begin{aligned} \frac{2\gamma }{q}+s=N\Big (\frac{1}{2}-\frac{1}{r}\Big ),\quad \frac{2\gamma }{{{\tilde{q}}}}-s=N\Big (\frac{1}{2}-\frac{1}{{{\tilde{r}}}}\Big ). \end{aligned}$$

Remark 2.11

For simplicity, one denotes the sets $\Gamma _s:=\{(q,r),\, s$-admissible$\}$, $\Gamma :=\Gamma _0$ and the norms

$$\begin{aligned} \Vert \cdot \Vert _{S(\dot{H}^s)}:=\sup _{(q,r)\in \Gamma _s}\Vert \cdot \Vert _{L^q(L^r)},\quad \Vert \cdot \Vert _{S'(\dot{H}^{-s})}:=\inf _{(q,r)\in \Gamma _{-s}}\Vert \cdot \Vert _{L^{q'}(L^{r'})}. \end{aligned}$$

The next fractional chain rule [5] will be useful.

Lemma 2.12

Let $N\ge 1$, $0<\gamma \le 1$, $\frac{1}{p}=\frac{1}{p_i}+\frac{1}{q_i}$, $i=1,2$ and $F\in C^1({\mathbb {C}})$. Then,

$$\begin{aligned} \Vert (-\Delta )^\frac{\gamma }{2}F(u)\Vert _{p}\lesssim \Vert (-\Delta )^\frac{\gamma }{2}u\Vert _{q_1}\Vert F'(u)\Vert _{p_1}, \end{aligned}$$

(2.5)

and

$$\begin{aligned} \Vert (-\Delta )^\frac{\gamma }{2}(uv)\Vert _{p}\lesssim \Vert (-\Delta )^\frac{\gamma }{2} u\Vert _{p_1}\Vert v\Vert _{q_1}+\Vert (-\Delta )^\frac{\gamma }{2} v\Vert _{p_2}\Vert u\Vert _{q_2}. \end{aligned}$$

(2.6)

Let us give a fractional Gagliardo–Nirenberg inequality [12].

Lemma 2.13

Let $1<p,p_2<\infty$, $0<\gamma <N$, $0<\theta<p<\infty$, and $1<p_1<\frac{N}{\gamma }$. Then, the fractional inequality

$$\begin{aligned} \Vert u\Vert _{p}\lesssim \Vert u\Vert _{p_2}^{1-\frac{\theta }{p}}\Vert (-\Delta )^{\frac{\gamma }{2}}u\Vert _{p_1}^{\frac{\theta }{p}}, \end{aligned}$$

holds whenever

$$\begin{aligned} 1=\frac{p-\theta }{p_2}+\theta \left( \frac{1}{p_1}-\frac{\gamma }{N}\right) . \end{aligned}$$

Let us recall a fractional Strauss type inequality [18].

Lemma 2.14

Let $N\ge 2$ and $\frac{1}{2}<\gamma <\frac{N}{2}$. Then,

$$\begin{aligned} \sup _{x\ne 0}|x|^{\frac{N}{2}-\gamma }|u(x)|\le C(N,\gamma )\Vert (-\Delta )^\frac{\gamma }{2}u\Vert , \end{aligned}$$

(2.7)

for any $u\in \dot{H}^\gamma _{rd}({\mathbb {R}}^N)$, where $\Gamma$ is the Gamma function and

$$\begin{aligned} C(N,\gamma )=\left( \frac{\Gamma (2\gamma -1)\Gamma (\frac{N}{2}-\gamma )\Gamma (\frac{N}{2})}{2^{2\gamma }\pi ^{\frac{N}{2}}\Gamma ^2(\gamma )\Gamma (\frac{N}{2}-1+\gamma )}\right) ^\frac{1}{2}. \end{aligned}$$

The next Sobolev injections [10, 17] will be useful.

Lemma 2.15

Let $N\ge 1$ and $1< p\le q <\infty$.

• 1. If $0< s < N$ and $\mu \ge 0$ such that

  $$\begin{aligned} \mu < \frac{N}{q}\quad \text{ and }\quad s =\frac{N}{p}-\frac{N}{q}+\mu . \end{aligned}$$

  Then, for any $u\in W^{s,p}$, one has

  $$\begin{aligned} \Vert |x|^{-\mu }u\Vert _q\le C(\mu , p, q, N, s) \Vert (-\Delta )^\frac{s}{2}u\Vert _p. \end{aligned}$$

• 2. If $0< 2s < N$, then

  • a. $H^s \hookrightarrow L^q$ for any $q\in [2,\frac{2N}{N-2s}]$;

  • b. $H^s_{rd} \hookrightarrow \hookrightarrow L^q$ is compact for $q\in (2,\frac{2N}{N-2s})$.

Finally, the next Sobolev injection is proved in the appendix.

Lemma 2.16

Let $N\ge 2$, $\gamma \in (0,1)$, $-2\gamma<\rho <0$ and $1+\frac{2\rho }{N}<p<p^*.$ Then, the following injection is compact:

$$\begin{aligned} \dot{H}^\gamma _{rd}\cap L^{p_c}\hookrightarrow \hookrightarrow L^{1+p}(|x|^\rho \,dx). \end{aligned}$$

(2.8)

3 Proof of Theorem 2.1

One proceeds in three steps.

3.1 Proof of the interpolation inequality (2.1)

Thanks to Lemma 2.15, one has

$$\begin{aligned} \int \limits _{{\mathbb {R}}^N}|u(x)|^{1+p}|x|^\rho \,dx\le & {} \Vert |x|^\frac{\rho }{2} u\Vert _{\frac{2p_c}{p_c-(p-1)}}^2\Vert u\Vert _{p_c}^{-1+p}\\\lesssim & {} \Vert (-\Delta )^\frac{\gamma }{2}u\Vert ^2\Vert u\Vert _{p_c}^{-1+p}. \end{aligned}$$

The proof is ended.

3.2 Proof of the equation (2.2)

One denotes by

$$\begin{aligned} \inf _{\dot{H}^\gamma \cap L^{s_c}}\frac{\Vert (-\Delta )^\frac{\gamma }{2}u \Vert ^2\Vert u\Vert _{p_c}^{-1+p}}{\int \limits _{{\mathbb {R}}^N}|u(x)|^{1+p}|x|^\rho \,dx}:=\frac{1}{C_{opt}}:=\beta . \end{aligned}$$

Taking account of (2.1), there is a sequence $(v_n)$ in $\dot{H}^\gamma \cap L^{s_c}$ satisfying

$$\begin{aligned} \beta =\lim _n\frac{\Vert (-\Delta )^\frac{\gamma }{2}u_n\Vert ^2\Vert u_n\Vert _{p_c}^{-1 +p}}{\int \limits _{{\mathbb {R}}^N}|x|^\rho |u_n(x)|^{1+p}\,dx}:=\lim _nI(v_n). \end{aligned}$$

Letting $u^{a,b}:=a u(b\cdot )$, one computes

$$\begin{aligned} a^2b^{2\gamma -N}\Vert (-\Delta )^\frac{\gamma }{2}u\Vert ^2&= \Vert (-\Delta )^\frac{\gamma }{2}u^{a,b}\Vert ^2;\\ ab^{-\frac{N}{p_c}}\Vert u\Vert _{p_c}&= \Vert u^{a,b}\Vert _{p_c};\\ a^{1+p}b^{-N-\rho }\int \limits _{{\mathbb {R}}^N}|u(x)|^{1+p}|x|^\rho \,\text {d}x&= \int \limits _{{\mathbb {R}}^N}|u^{a,b}(x)|^{1+p}|x|^\rho \,\text {d}x. \end{aligned}$$

Thus $I(u)=I(u^{a,b}).$ Let us pick

$$\begin{aligned} \mu _n:=\left( \frac{\Vert v_n\Vert _{p_c}}{\Vert (-\Delta )^\frac{\gamma }{2} v_n\Vert }\right) ^\frac{1}{\gamma -s_c}\quad \text{ and }\quad \lambda _n:=\frac{\Vert v_n\Vert ^{\frac{N-2\gamma }{2(\gamma -s_c)}}}{{\Vert (-\Delta )^\frac{\gamma }{2} v_n\Vert }^\frac{2\gamma +\rho }{(p-1)(\gamma -s_c)}}. \end{aligned}$$

Thus, $\psi _n:=v_n^{\lambda _n,\mu _n}$ satisfies

$$\begin{aligned} \Vert \psi _n\Vert _{p_c}=\Vert (-\Delta )^\frac{\gamma }{2}\psi _n\Vert =1\quad \text{ and }\quad \beta =\lim _nI(\psi _n). \end{aligned}$$

Therefore, $\psi _n\rightharpoonup \psi$ in $\dot{H}^\gamma \cap L^{p_c}$ and (2.8) implies that for a sub-sequence denoted also $(\psi _n)$, as $n\rightarrow \infty$,

$$\begin{aligned} I(\psi _n)=\frac{1}{\int _{{\mathbb {R}}^N}|\psi _n|^{1+p}|x|^\rho \,\text {d}x}\rightarrow \frac{1}{\int _{{\mathbb {R}}^N}|\psi |^{1+p}|x|^\rho \,\text {d}x}. \end{aligned}$$

The lower semi-continuity of the $\dot{H}^\gamma \cap L^{p_c}$ norm gives

$$\begin{aligned} \max \{\Vert \psi \Vert _{p_c},\Vert (-\Delta )^\frac{\gamma }{2}\psi \Vert \}\le 1. \end{aligned}$$

Then, $I(\psi )< \beta$ if $\Vert \psi \Vert \Vert (-\Delta )^\frac{\gamma }{2}\psi \Vert <1$. Thus,

$$\begin{aligned} \Vert \psi \Vert _{p_c}=1=\Vert (-\Delta )^\frac{\gamma }{2}\psi \Vert . \end{aligned}$$

Therefore,

$$\begin{aligned} \lim _n\Vert \psi _n-\psi \Vert _{\dot{H}^\gamma \cap L^{p_c}}=0,\quad \beta =I(\psi )=\frac{1}{\int _{{\mathbb {R}}^N}|\psi |^{1+p}|x|^\rho \,\text {d}x}. \end{aligned}$$

Let us write the Euler–Lagrange equation satisfied by the minimizer

$$\begin{aligned} \partial _\varepsilon I(\psi +\varepsilon \eta )_{|\varepsilon =0}=0,\quad \forall \eta \in C_0^\infty ({\mathbb {R}}^N). \end{aligned}$$

Hence, $\psi$ satisfies

$$\begin{aligned} 2(-\Delta )^\gamma \psi +(p-1)|\psi |^{p_c-2}\psi -\beta (1+p)|x|^\rho |\psi |^{p-1}\psi =0. \end{aligned}$$

This proof is complete.

3.3 Proof of the equation (2.3)

One keeps the notations in the previous subsection $\psi$ satisfies (2.2) and $C_{opt}=\frac{1}{\beta }=\int _{{\mathbb {R}}^N}|\psi (x)|^{1+p}|x|^\rho \,\text {d}x$. Let $\psi =\phi ^{a,b}:=a\phi (b\cdot )$. Then, the equation

$$\begin{aligned} 2(-\Delta )^\gamma \psi +(p-1)|\psi |^{p_c-2}\psi -\beta (1+p)|x|^\rho |\psi |^{p-1}\psi =0 \end{aligned}$$

gives

$$\begin{aligned} \frac{2}{p-1}a^{2-p_c}b^{2\gamma }(-\Delta )^\gamma \phi +|\phi |^{p_c-2}\phi -\frac{\beta (1+p)}{p-1}a^{p-p_c+1}b^{-\rho }|x|^\rho |\phi |^{p-1}\phi =0. \end{aligned}$$

Choosing

$$\begin{aligned} a&:=\left( \beta \frac{1+p}{2}\left( \frac{2}{p-1}\right) ^\frac{\rho +2\gamma }{2\gamma } \right) ^\frac{2N\gamma }{(\rho +2\gamma )[p_c(N-2\gamma )-2N]};\\ b&:=\left( \frac{p-1}{2}a^{p_c-2}\right) ^\frac{1}{2\gamma }\\&=\left( \frac{p-1}{2}\right) ^\frac{1}{2\gamma }\left( \beta \frac{1+p}{2}\left( \frac{2}{p-1} \right) ^\frac{\rho +2\gamma }{2\gamma }\right) ^\frac{N(p_c-2)}{(\rho +2\gamma )[p_c(N-2\gamma )-2N]}. \end{aligned}$$

It follows that

$$\begin{aligned} -(-\Delta )^\gamma \phi +|\phi |^{p_c-2}\phi -|x|^\rho |\phi |^{p-1}\phi =0. \end{aligned}$$

Finally, $\Vert \psi \Vert _{p_c}=1=ab^{-\frac{N}{p_c}}\Vert \phi \Vert$ gives $\beta =\frac{2}{1+p}\Vert \phi \Vert _{p_c}^{p-1}$ and finishes the proof.

4 Proof of Theorem 2.3

This section establishes the local well-posedness of the fractional inhomogeneous Schrödinger equation (1.1) in $\dot{H}^\gamma _{rd}\cap \dot{H}^{s_c}$.

4.1 Local existence

One starts with some nonlinear estimates.

Lemma 4.1

Let $N\ge 2$, $0<-\rho <2\gamma$ and $p_*<p<p^*$. Then, there exist $c,\theta ,\theta _1>0$ and $0<\theta _2<p-1$ such that

• 1. $\Vert (-\Delta )^\frac{\gamma }{2}(|x|^\rho |u|^{p-1}u)\Vert _{S'(I,L^2)}\le c(T^{\theta }+T^{\theta _1})\Vert (-\Delta )^\frac{\gamma }{2}u\Vert _{S(I,L^2)}^{p}$;

• 2. If $N=2$ and $p<1+\frac{\gamma -\sqrt{\gamma ^2-4(2+\rho ) \gamma -4\rho }}{2(1-\gamma )}$ or $N\ge 3$, one has

  $$\begin{aligned} \Vert (-\Delta )^{\frac{s_c}{2}}(|x|^\rho |u|^{p-1}u)\Vert _{S'(I,L^2)}\le c(T^{\theta }+T^{\theta _1})\Vert (-\Delta )^{\frac{s_c}{2}}u\Vert _{S(I,L^2)}^{p-1} \Vert (-\Delta )^{\frac{\gamma }{2}}u\Vert _{S(I,L^2)}; \end{aligned}$$

• 3. $\Vert |x|^\rho |u|^{p-1}u\Vert _{S'(I,\dot{H}^{-s_c})}\le c(T^{\theta }+T^{\theta _1}) \Vert (-\Delta )^{\frac{\gamma }{2}}u\Vert _{L^\infty (I,L^2)}^\theta \Vert u\Vert _{S(I,\dot{H}^{s_c})}^{p-\theta }$.

Proof

1. Let the admissible pair

$$\begin{aligned} (q,r):=\left( \frac{4\gamma (1+p)}{(N-2\gamma )(p-1)}, \frac{N(1+p)}{N+\gamma (p-1)}\right) \in \Gamma . \end{aligned}$$

One denotes here and hereafter the centered unit ball of ${\mathbb {R}}^N$ by B(1) and its complementary by $B^c(1)$. By Lemma 2.12 about the fractional chain rule, via Hölder estimate and Sobolev injections

$$\begin{aligned} \Vert (-\Delta )^\frac{\gamma }{2}(|x|^\rho |u|^{p-1}u)\Vert _{L^{r'}(B^c(1))}&\lesssim \Vert |x|^\rho \Vert _{L^a(B^c(1))}\Vert (-\Delta )^\frac{\gamma }{2}u\Vert _r \Vert u\Vert _{\frac{Nr}{N-r\gamma }}^{p-1}\\&\quad +\Vert |x|^{\rho -\gamma }\Vert _{L^c(B^c(1))}\Vert u \Vert ^p_{\frac{Nr}{N-r\gamma }}\nonumber \\&\lesssim \left( \Vert |x|^\rho \Vert _{L^a(B^c(1))}+\Vert |x|^{\rho -\gamma } \Vert _{L^c(B^c(1))}\right) \Vert (-\Delta )^\frac{\gamma }{2}u\Vert _r^{p}. \end{aligned}$$

Here,

$$\begin{aligned} \frac{1}{r'}=\frac{1}{a}+\frac{1}{r}+\frac{(p-1)(N-r\gamma )}{Nr} =\frac{1}{c}+\frac{p(N-r\gamma )}{Nr}. \end{aligned}$$

Thus,

$$\begin{aligned} 1&=\frac{1}{a}+\frac{2}{r}+\frac{(p-1)(N-r\gamma )}{Nr};\\ 1&=\frac{1}{c}+\frac{1}{r}+\frac{p(N-r\gamma )}{Nr}. \end{aligned}$$

This gives $\frac{N}{c}=\gamma +\frac{N}{a}$. Choosing a such that $\frac{N}{a}<-\rho$, then we have

$$\begin{aligned} \Vert (-\Delta )^\frac{\gamma }{2}(|x|^\rho |u|^{p-1}u)\Vert _{L_T^{q'}(L^{r'}(B^c(1)))} \lesssim T^{\theta }\Vert (-\Delta )^\frac{\gamma }{2}u\Vert _{L_T^q(L^r)}^{p}. \end{aligned}$$

Here, $\theta :=1-\frac{1+p}{q}>0$. Now, one estimates the term on the complementary of the unit ball. Let the admissible pair

$$\begin{aligned} (q_1,r_1):=\left( \frac{2(\rho +N)}{N-2\gamma },\frac{2N (\rho +N)}{N(N-2\gamma )+4\gamma ^2+\rho N}\right) \in \Gamma . \end{aligned}$$

By Lemma 2.12 about the fractional chain rule and Hölder estimates via Sobolev injections

$$\begin{aligned} \Vert (-\Delta )^\frac{\gamma }{2}(|x|^\rho |u|^{p-1}u)\Vert _{L^{r_1'}(B(1))}&\lesssim \Vert |x|^\rho \Vert _{L^{a_1}(B(1))}\Vert (-\Delta )^\frac{\gamma }{2}u \Vert _{r_1}\Vert u\Vert _{\frac{Nr_1}{N-r_1\gamma }}^{p-1}\\&\quad +\Vert |x|^{\rho -\gamma }\Vert _{L^{c_1}(B(1))}\Vert u \Vert ^p_{\frac{Nr_1}{N-r_1\gamma }}\\&\lesssim \Big (\Vert |x|^\rho \Vert _{L^{a_1}(B(1))}+\Vert |x|^{\rho -\gamma }\Vert _{L^{c_1}(B(1))}\Big )\Vert (-\Delta )^\frac{\gamma }{2}u\Vert _{r_1}^{p}. \end{aligned}$$

Here,

$$\begin{aligned} \frac{1}{r_1'}=\frac{1}{a_1}+\frac{1}{r_1}+\frac{(p-1)(N-r_1\gamma )}{Nr_1}=\frac{1}{c_1}+\frac{p(N-r_1\gamma )}{Nq_1}. \end{aligned}$$

The integrability condition $\Vert |x|^\rho \Vert _{L^{a_1}(B(1))}<\infty$ and $\Vert |x|^{\rho -\gamma }\Vert _{L^{c_1}(B^c(1))}<\infty$ read

$$\begin{aligned} N\left( 1-\frac{1+p}{r_1}\right) +\gamma (p-1)>-\rho . \end{aligned}$$

A direct computation via the fact that $p<p^*$ gives the above condition and so

$$\begin{aligned} \Vert (-\Delta )^\frac{\gamma }{2}(|x|^\rho |u|^{p-1}u)\Vert _{L_T^{q_1'}(L^{r_1'}(B(1)))} \lesssim T^{\theta _1}\Vert (-\Delta )^\frac{\gamma }{2}u\Vert _{L_T^{q_1}(L^r_1)}^{p}, \end{aligned}$$

where one takes $\theta _1:=1-\frac{1+p}{q_1}>0$. This first point is proved.

2. Using Sobolev injections, Strichartz and Hölder estimates, one has

$$\begin{aligned}&\Vert (-\Delta )^\frac{s_c}{2}(|x|^\rho |u|^{p-1}u)\Vert _{L^{\frac{2N}{2\gamma +N}}(B(1))}\nonumber \\&\quad \lesssim \Vert (-\Delta )^\frac{\gamma }{2}(|x|^\rho |u|^{p-1}u)\Vert _{L^{\frac{N(p-1)}{2\gamma (p-1)+2\gamma +\rho }}(B(1))}\nonumber \\&\quad \lesssim \Vert |x|^\rho \Vert _{L^a(B(1))}\Vert (-\Delta )^\frac{\gamma }{2}u\Vert _r\Vert u\Vert _{\frac{Nr}{N-rs_c}}^{p-1}\nonumber \\&\qquad +\Vert |x|^{\rho -\gamma }\Vert _{L^c(B(1))}\Vert u\Vert ^{p-1}_{\frac{Nr}{N-rs_c}}\Vert u\Vert _{\frac{Nr}{N-r\gamma }}\nonumber \\&\quad \lesssim \Big (\Vert |x|^\rho \Vert _{L^a(B(1))}+\Vert |x|^{\rho -\gamma }\Vert _{L^c(B(1))}\Big )\Vert (-\Delta )^\frac{\gamma }{2}u\Vert _r\Vert u\Vert _{\frac{Nr}{N-rs_c}}^{p-1}. \end{aligned}$$

Here,

$$\begin{aligned} -\rho>\frac{N}{a}&=2\gamma +\frac{2\gamma +\rho }{p-1}-\frac{Np}{r}+(p-1)s_c,\quad N>r\gamma . \end{aligned}$$

Denote by $x^+$ a real number near to x such that $x^+>x$ and $x^-$ a real number near to x such that $x^-<x$. Let us pick $(q,r)\in \Gamma$ such that

$$\begin{aligned} \left( \frac{Np(p-1)}{2\gamma +\rho +\frac{N}{2}(p-1)^2}\right) ^-:=r,\quad \left( \frac{4\gamma p(p-1)}{N(p-1)-2(2\gamma +\rho )}\right) ^+:=q. \end{aligned}$$

A direct calculus gives $2<r<\frac{2N}{N-2\gamma }$. Therefore, for $N\ge 4$, one has $\gamma r<\frac{2N}{N-2\gamma }\le N$. For $N\in \{2,3\}$, the condition $N>\gamma r$ is equivalent to

$$\begin{aligned} (N-2\gamma )x^2-2\gamma x+2(2\gamma +\rho )>0,\quad x:=p-1. \end{aligned}$$

(4.1)

$\bullet$ First case $N=2$. Then, the previous inequality reads

$$\begin{aligned} P(x):=(1-\gamma )x^2-\gamma x+2\gamma +\rho >0. \end{aligned}$$

The discriminant is

$$\begin{aligned} \Delta (P)&:=\gamma ^2-4(2\gamma +\rho )(1-\gamma )\\&=9\gamma ^2-4\gamma (2+\rho )-4\rho \\&:=Q(\gamma ). \end{aligned}$$

Moreover,

$$\begin{aligned} \Delta (Q)&:=4[(2+\rho )^2+9\rho ]\\&:=R(\rho ). \end{aligned}$$

Now, $\Delta (Q)<0$ for $\rho \in (-2\gamma ,\frac{-13+\sqrt{153}}{2})$ and $\Delta (Q)>0$ for $\rho \in (\frac{-13+\sqrt{153}}{2},0)$. Thus, $\Delta (P)>0$ for $\rho \in (-2\gamma ,\frac{-13+\sqrt{153}}{2})$ and, because $P(1)>0$, $\Delta (P)>0$ for $\rho \in (\frac{-13+\sqrt{153}}{2},0)$. Thus, $P(x)>0$ iif $p<1+\frac{\gamma -\sqrt{\gamma ^2-4(2+\rho )\gamma -4\rho }}{2(1-\gamma )}$.

$\bullet$ Second case $N=3$. Then, the inequality (4.1) reads

$$\begin{aligned} P(x):=(3-2\gamma )x^2-2\gamma x+2(2\gamma +\rho )>0. \end{aligned}$$

The discriminant is

$$\begin{aligned} \Delta (P)&:=\gamma ^2-2(2\gamma +\rho )(3-2\gamma )\\&= 9\gamma ^2-4(3-\rho )\gamma -6\rho \\&:= Q(\gamma ). \end{aligned}$$

Moreover,

$$\begin{aligned} \Delta (Q)&:=2[2(3-\rho )^2+27\rho ]\\&:=R(\rho ). \end{aligned}$$

Now, $\Delta (Q)<0$ for $\rho \in (-2\gamma ,-\frac{3}{2})$ and $\Delta (Q)>0$ for $\rho \in (-\frac{3}{2},0)$. Thus, $\Delta (P)>0$ for $\rho \in (-2\gamma ,-\frac{3}{2})$ and, since $Q(1)<0$ and $Q(-\frac{\rho }{2})>0$, $\Delta (P)>0$ for $[\gamma \in (-\frac{\rho }{2},\frac{2(3-\rho )-\sqrt{4(3-\rho )^2+54\rho }}{9})$ and $\rho \in (-\frac{3}{2},0)]$ and $\Delta (P)<0$ for $[\gamma \in (\frac{2(3-\rho )-\sqrt{4(3-\rho )^2+54\rho }}{9},1)$ and $\rho \in (-\frac{3}{2},0)]$. If $\Delta (P)<0$, we are done. Otherwise, the roots of P are positive and the smallest one $\frac{\gamma -\sqrt{Q(\gamma )}}{3-2\gamma }<1$. Thus, because $P(1)>0$, the two roots are less than one. We are done. Moreover, the admissibility condition reads $\frac{2}{q}+\frac{2N-1}{r}<N-\frac{1}{2}$ and is equivalent to $p>p_*$. In conclusion,

$$\begin{aligned} \Vert (-\Delta )^\frac{s_c}{2}(|x|^\rho |u|^{p-1}u)\Vert _{L^2(I,L^{\frac{2N}{2\gamma +N}}(B(1)))}&\lesssim \Vert \Vert (-\Delta )^\frac{\gamma }{2}u\Vert _r\Vert (-\Delta )^\frac{\gamma }{2}u\Vert _{r}^{p-1}\Vert _{L^2(I)}\\&\lesssim T^{\frac{1}{2}-\frac{p}{q}}\Vert (-\Delta )^\frac{\gamma }{2}u\Vert _{L^q(I,L^r)} \Vert (-\Delta )^\frac{\gamma }{2}u\Vert _{L^q(I,L^r)}^{p-1}. \end{aligned}$$

The condition $p<p^*$ gives $\frac{1}{2}-\frac{p}{q}>0$. The estimation of the term on the complementary of the unit ball follows similarly by taking

$$\begin{aligned} \left( \frac{Np(p-1)}{2\gamma +\rho +\frac{N}{2}(p-1)^2}\right) ^+:=r,\quad \left( \frac{4\gamma p(p-1)}{N(p-1)-2(2\gamma +\rho )}\right) ^-:=q. \end{aligned}$$

3. Letting $({{\tilde{q}}},r)\in \Gamma _{-s_c}$ and $(q,r)\in \Gamma _{s_c}$, Hölder and Sobolev estimates give

$$\begin{aligned} \Vert |u|^p|x|^\rho \Vert _{L^{{{\tilde{q}}}'}_T(L^{r'}(B(1))}\le & {} c\Vert |x|^\rho \Vert _{L^a(B(1))}\Vert u\Vert _{L_T^\infty \left( L^\frac{2N}{N-2\gamma }\right) }^\theta \Vert u\Vert _{L^q(L^r)}^{p-\theta }\\\le & {} cT^{\frac{1}{{{\tilde{q}}}'}-\frac{p-\theta }{q}}\Vert |x|^\rho \Vert _{L^a(B(1))}\Vert (-\Delta )^\frac{\gamma }{2}u\Vert _{L^\infty _T(L^2) }^\theta \Vert u\Vert _{L_T^q(L^r)}^{p-\theta }\\\le & {} cT^{\frac{1}{{{\tilde{q}}}'}-\frac{p-\theta }{q}}\Vert (-\Delta )^\frac{\gamma }{2}u\Vert _{L^\infty _T(L^2)}^\theta \Vert u\Vert _{L_T^q(L^r)}^{p-\theta }. \end{aligned}$$

Here, $\frac{1}{{{\tilde{q}}}'}-\frac{p-\theta }{q}>0$ and

$$\begin{aligned} \frac{N}{a}=N-\frac{\theta (N-2\gamma )}{2}-\frac{N(1+p-\theta )}{r}>-\rho . \end{aligned}$$

(4.2)

The first inequality is equivalent to $q>\frac{\gamma (1+p-\theta )}{\gamma -s_c}$. Let us take $0<\theta \ll 1$ and

$$\begin{aligned} q:=\left( \frac{\gamma (1+p-\theta )}{\gamma -s_c}\right) ^+, \quad r:=\left( \frac{2N(1+p-\theta )}{(N-2s_c)(1+p-\theta )-4(\gamma -s_c)}\right) ^-. \end{aligned}$$

A direct computation gives (4.2). The estimation of the term on the complementary of the unit ball follows similarly by taking

$$\begin{aligned} (q,r)=\left( \infty ,\frac{2N}{N-2s_c}\right) . \end{aligned}$$

This closes the proof. $\square$

Now, using Strichartz estimates, Duhamel formula and a fixed point method, one proves Theorem 2.3. One defines the function

$$\begin{aligned} f(u):=e^{i\cdot (-\Delta )^\frac{\gamma }{2}}u_0+\int \limits _0^\cdot e^{i(\cdot -s)(-\Delta )^\frac{\gamma }{2}}|x|^\rho |u|^{p-1}u\,ds. \end{aligned}$$

One denotes by $B_T(R)$ the centered ball with radius $R>0$ of the space

$$\begin{aligned} X_T:=\Big (\cap _{(q,r)\in \Gamma } L^q_T(\dot{W}^{\gamma ,r}\cap \dot{W}^{s_c,r})\Big )\cap \Big (\cap _{(q_1,r_1)\in \Gamma _{s_c}} L^{q_1}_T(L^{r_1})\Big ), \end{aligned}$$

endowed with the complete distance

$$\begin{aligned} d(u,v)&:=\sup _{(q,r)\in \Gamma }\Vert (-\Delta )^\frac{\gamma }{2}(u-v)\Vert _{L_T^q(L^r)} +\sup _{(q,r)\in \Gamma }\Vert (-\Delta )^\frac{s_c}{2}(u-v)\Vert _{L_T^q(L^r)}\\&\quad +\sup _{(q,r)\in \Gamma _{s_c}}\Vert u-v\Vert _{L_T^q(L^r)}. \end{aligned}$$

Thanks to the previous Lemma via Strichartz estimate, one has for $w:=u-v$,

$$\begin{aligned} d(f(u),f(v))&\lesssim \Vert (-\Delta )^\frac{\gamma }{2}[|x|^\rho (|u|^{p-1} +|v|^{p-1})w]\Vert _{S'((0,T),L^2)}\\&\quad +\Vert (-\Delta )^\frac{s_c}{2}[|x|^\rho (|u|^{p-1}+|v|^{p-1})w]\Vert _{S'((0,T),L^2)}\\&\quad +\Vert |x|^\rho (|u|^{p-1}+|v|^{p-1})w\Vert _{S'((0,T),\dot{H}^{s_c})}\\&\le c(T^{\theta }+T^{\theta _1})\Big [\Vert (-\Delta )^\frac{\gamma }{2}u \Vert _{S(I,L^2)}^{p-1}+\Vert (-\Delta )^{\frac{s_c}{2}}u\Vert _{S(I,L^2)}^{p-1}\\&\quad +\Vert (-\Delta )^{\frac{\gamma }{2}}u\Vert _{L^\infty (I,L^2)}^\theta \Vert u\Vert _{S(I,\dot{H}^{s_c})}^{p-1-\theta }\Big ]d(u,v)\\&\le c(T^{\theta }+T^{\theta _1})R^{p-1}d(u,v). \end{aligned}$$

Moreover, taking $v=0$ in the above lines and taking account of Strichartz estimates, one writes

$$\begin{aligned}&\sup _{(q,r)\in \Gamma }\Vert (-\Delta )^\frac{\gamma }{2}f(u)\Vert _{L_T^q(L^r)} +\sup _{(q,r)\in \Gamma }\Vert (-\Delta )^\frac{s_c}{2}f(u)\Vert _{L_T^q(L^r)} +\sup _{(q,r)\in \Gamma _{s_c}}\Vert f(u)\Vert _{L_T^q(L^r)}\\&\quad \le c\Vert u_0\Vert _{\dot{H}^\gamma \cap \dot{H}^{s_c}}+c(T^{\theta }+T^{\theta _1})R^{p}. \end{aligned}$$

Choose $R:=2c\Vert u_0\Vert _{\dot{H}^\gamma \cap \dot{H}^{s_c}}$ and $T>0$ such that $c(T^{\theta }+T^{\theta _1})<\frac{1}{2R^{p-1}}$.Thus, f is a contraction of $B_T(R)$. One concludes the proof by a fixed point Theorem.

4.2 Global existence

Here, one assumes that $\Vert u\Vert _{L^\infty _{T^*}(\dot{H}^{s_c})}<\Vert \phi \Vert _{p_c}$ and $T^*<\infty$. Then, by Theorem 2.1, one has

$$\begin{aligned} 2E(t)= & {} \Vert (-\Delta )^\frac{\gamma }{2}u\Vert ^2-\frac{2\epsilon }{p+1} \int \limits _{{\mathbb {R}}^N}|u|^{1+p}|x|^\rho \,\text {d}x\\\ge & {} \Vert (-\Delta )^\frac{\gamma }{2}u\Vert ^2-\frac{2C_{opt}}{p+1} \Vert u\Vert _{p_c}^{p-1}\Vert (-\Delta )^\frac{\gamma }{2}u\Vert ^2\\\ge & {} \left( 1-\left[ \frac{\Vert u\Vert _{p_c}}{\Vert \phi \Vert _{p_c}}\right] ^{p-1} \right) \Vert (-\Delta )^\frac{\gamma }{2}u\Vert ^2. \end{aligned}$$

Thus, $\sup _{0\le t<T^*}\Vert (-\Delta )^\frac{\gamma }{2}u(t)\Vert <\infty$. This contradiction closes the proof.

5 Proof of Theorem 2.5

Let the sequences

$$\begin{aligned} t_n\rightarrow T^*,\quad \beta _n:=\Vert (-\Delta )^\frac{\gamma }{2}u(t_n)\Vert ^{-\frac{1}{\gamma -s_c}},\quad v_n:=\beta _n^\frac{2\gamma +\rho }{p-1}u(t_n,\beta _n\cdot ), \end{aligned}$$

and compute

$$\begin{aligned} \Vert (-\Delta )^\frac{s_c}{2}v_n\Vert&=\Vert (-\Delta )^\frac{s_c}{2}u_n\Vert ;\\ \Vert (-\Delta )^\frac{\gamma }{2}v_n\Vert&=1;\\ E(v_n)&=\beta _n^{2(\gamma -s_c)}E(u_0). \end{aligned}$$

Thus,

$$\begin{aligned} \sup _n\Vert v_n\Vert _{\dot{H}^{s_c}\cap \dot{H}^\gamma }<\infty ,\quad E(v_n)\rightarrow 0. \end{aligned}$$

Denote by B(R) the centered ball of ${\mathbb {R}}^N$ with radius $R>0$ and $B(R)^c$ its complementary. Take $v_n\rightharpoonup v$ in $\dot{H}^{s_c}\cap \dot{H}^\gamma$. Since $\lambda (t_n)\gg \beta _n$, the weak limit lower semi-continuity gives for any $R>0$,

$$\begin{aligned} \int \limits _{B(R)}|v|^{p_c}\,\text {d}x\le & {} \liminf _n\int \limits _{B(R)}|v_n|^{p_c}\,\text {d}x\\= & {} \liminf _n\int \limits _{B(R\beta _n)}|u(t_n)|^{p_c}\,\text {d}x\\\le & {} \liminf _n\int \limits _{B(\lambda (t_n))}|u(t_n)|^{p_c}\,\text {d}x. \end{aligned}$$

Finally, (2.8) gives

$$\begin{aligned} 0=\liminf _nE(v_n)\ge \frac{1}{2}\left( 1-\left[ \frac{\Vert v\Vert _{p_c}}{\Vert \phi \Vert _{p_c}}\right] ^{p-1}\right) \Vert (-\Delta )^\frac{\gamma }{2}v\Vert ^2. \end{aligned}$$

Therefore,

$$\begin{aligned} \liminf _n\int \limits _{|x|<\lambda (t_n)}|u(t_n)|^{p_c}\,\text {d}x\ge \Vert \phi \Vert _{p_c}^{p_c}. \end{aligned}$$

The proof is achieved.

6 Proof of Theorem 2.7

This section is devoted to prove Theorem 2.7. Take for simplicity $\epsilon =1$ and denote the inhomogeneous nonlinear term

$$\begin{aligned} {\mathcal {I}}:={\mathcal {I}}_p:=-|x|^\rho |u|^{p-1}u. \end{aligned}$$

1. Localized variance identity.

Lemma 6.1

One has

$$\begin{aligned} \frac{d}{dt} M_\zeta [u(t)]&=\int \limits _0^\infty m^\gamma \int \limits _{{\mathbb {R}}^N}\Big (4\overline{\partial _ku_m} \partial ^2_{kl}\zeta \partial _lu_m-\Delta ^2\zeta |u_m|^2\Big )\,dx\,dm\\&\quad +\frac{4\rho }{1+p}\int \limits _{{\mathbb {R}}^N}x\cdot \nabla \zeta |u|^{1+p} |x|^{\rho -2}\,dx-\frac{2(p-1)}{1+p}\int \limits _{{\mathbb {R}}^N}\Delta \zeta |u|^{1+p}|x|^\rho \,dx. \end{aligned}$$

Proof

Compute using (1.1),

$$\begin{aligned} \frac{\text {d}}{\text {d}t} M_\zeta [u(t)] = \langle u(t),[(-\Delta )^s,i\Gamma _\zeta ]u(t)\rangle + \left\langle u(t),\left[ -\frac{{\mathcal {I}}}{u},i\Gamma _\zeta \right] u(t)\right\rangle . \end{aligned}$$

Here, the commutator reads $AB -BA:=[A,B]$. According to computation done in [3], one has

$$\begin{aligned} \langle u(t),[(-\Delta )^s,i\Gamma _\zeta ]u(t)\rangle =\int \limits _0^\infty m^\gamma \int \limits _{{\mathbb {R}}^N}\Big (4\overline{\partial _ku_m}\partial ^2_{kl} \zeta \partial _lu_m-\Delta ^2\zeta |u_m|^2\Big )\,\text {d}x\,\text {d}m. \end{aligned}$$

Let us write

$$\begin{aligned} (N_p)&:=\left\langle u,\left[ -\frac{{\mathcal {I}}_p}{u} ,i\Gamma _\zeta \right] u\right\rangle =\langle u,[-|u|^{p-1}|x|^\rho ,i\Gamma _\zeta ]u\rangle \\&=\langle u,[-|u|^{p-1}|x|^\rho ,div(\nabla \zeta \cdot )+\nabla \zeta \nabla \cdot ]u\rangle \\&=-\langle u,|x|^\rho |u|^{p-1}(div(\nabla \zeta u)+\nabla \zeta \nabla u)\rangle \\&\quad +\langle u,div(\nabla \zeta |x|^\rho |u|^{p-1}u)+\nabla \zeta \nabla (|x|^\rho |u|^{p-1}u)\rangle . \end{aligned}$$

Then,

$$\begin{aligned} (N_p)&=-\langle u,|x|^\rho |u|^{p-1}(\Delta \zeta u+2\nabla \zeta \nabla u )\rangle +\langle u,\Delta \zeta |x|^\rho |u|^{p-1}u+2\nabla \zeta \nabla (|x|^\rho |u|^{p-1}u)\rangle \\&=\langle u,\Delta \zeta |x|^\rho |u|^{p-1}u+2\nabla \zeta \nabla (|x|^\rho |u|^{p-1}u)-|x|^\rho |u|^{p-1}(\Delta \zeta u +2\nabla \zeta \nabla u)\rangle \\&=2\langle u,\nabla \zeta \nabla (|x|^\rho |u|^{p-1}u)-|x|^\rho |u|^{p-1}\nabla \zeta \nabla u\rangle \\&=2\left\langle u,\nabla \zeta \Big (\nabla (|x|^\rho )|u|^{p-1}u +|x|^\rho \nabla (|u|^{p-1})u\Big )\right\rangle . \end{aligned}$$

An integration by parts gives

$$\begin{aligned} (N_p)&=2\int \limits _{{\mathbb {R}}^N}\nabla \zeta \nabla (|x|^\rho )|u|^{1+p}\,\text {d}x +2\int \limits _{{\mathbb {R}}^N}|x|^\rho \nabla \zeta \nabla (|u|^{p-1})|u|^2\,\text {d}x\\&=2\int \limits _{{\mathbb {R}}^N}\nabla \zeta \nabla (|x|^\rho )|u|^{1+p}\,\text {d}x+\frac{2(p-1)}{1+p} \int \limits _{{\mathbb {R}}^N}\nabla \zeta \nabla (|u|^{1+p})|x|^\rho \,\text {d}x\\&=2\int \limits _{{\mathbb {R}}^N}\nabla \zeta \nabla (|x|^\rho )|u|^{1+p}\,\text {d}x-\frac{2(p-1)}{1+p} \int \limits _{{\mathbb {R}}^N}|u|^{1+p}\Big (\nabla (|x|^\rho )\nabla \zeta +|x|^\rho \Delta \zeta \Big )\,\text {d}x\\&=\frac{4}{1+p}\int \limits _{{\mathbb {R}}^N}\nabla \zeta \nabla (|x|^\rho )|u|^{1+p}\,\text {d}x -\frac{2(p-1)}{1+p}\int \limits _{{\mathbb {R}}^N}\Delta \zeta |x|^\rho |u|^{1+p}\,\text {d}x\\&=\frac{4\rho }{1+p}\int \limits _{{\mathbb {R}}^N}x.\nabla \zeta |u|^{1+p}|x|^{\rho -2}\,\text {d}x -\frac{2(p-1)}{1+p}\int \limits _{{\mathbb {R}}^N}\Delta \zeta |u|^{1+p}|x|^\rho \,\text {d}x. \end{aligned}$$

This finishes the proof. $\square$

Now, one establishes Theorem 2.7. Using the identities

$$\begin{aligned}&\int \limits _0^\infty m^\gamma \int \limits _{{\mathbb {R}}^N}|\nabla u_m|^2\,\text {d}x\,\text {d}m =\gamma \Vert (-\Delta )^\frac{\gamma }{2}u\Vert ^2;\\&\zeta _R=\frac{|\cdot |^2}{2},\quad \text{ for }\quad |x|<R, \end{aligned}$$

one has

$$\begin{aligned}&\frac{\text {d}}{\text {d}t} M_{\zeta _R} [u(t)]\\&\quad =\int \limits _0^\infty m^\gamma \int \limits _{{\mathbb {R}}^N}\Big (4\overline{\partial _ku_m} \partial ^2_{kl}\zeta _R\partial _lu_m-\Delta ^2\zeta _R|u_m|^2\Big )\,\text {d}x\,\text {d}m\\&\qquad +\frac{4\rho }{1+p}\int \limits _{{\mathbb {R}}^N}x\cdot \nabla \zeta _R|u|^{1+p} |x|^{\rho -2}\,dx-\frac{2(p-1)}{1+p}\int \limits _{{\mathbb {R}}^N}\Delta \zeta _R|u|^{1+p}|x|^\rho \,\text {d}x\\&\quad =4\gamma \Vert u\Vert _{\dot{H}^\gamma }^2-\frac{4\gamma B}{1+p} \int \limits _{{\mathbb {R}}^N}|u|^{1+p}|x|^\rho \,dx-4\gamma \Vert u\Vert _{\dot{H}^\gamma (|x|>R)}^2\\&\qquad -\int \limits _0^\infty m^\gamma \int \limits _{|x|>R}\Delta ^2\zeta _R |u_m|^2\,dx\,dm+4\int \limits _0^\infty m^\gamma \int \limits _{|x|>R} \overline{\partial _ku_m}\partial ^2_{kl}\zeta _R\partial _lu_m\,\text {d}x\,\text {d}m\\&\qquad -\frac{2(p-1)}{1+p}\int \limits _{|x|>R}(\Delta \zeta _R-N)|u|^{1+p} |x|^\rho \,dx+\frac{4\rho }{1+p}\int \limits _{|x|>R}(|x|^2-x\cdot \nabla \zeta _R) |u|^{1+p}|x|^{\rho -2}\,\text {d}x\\&\quad =4\gamma BE(u_0)-2\gamma (B-2)\Vert u\Vert _{\dot{H}^\gamma }^2 -4\gamma \Vert u\Vert _{\dot{H}^\gamma (|x|>R)}^2\\&\qquad -\int \limits _0^\infty m^\gamma \int \limits _{|x|>R}\Delta ^2\zeta _R|u_m |^2\,dx\,dm+4\int \limits _0^\infty m^\gamma \int \limits _{|x|>R}\overline{\partial _ku_m} \partial ^2_{kl}\zeta _R\partial _lu_m\,\text {d}x\\&\qquad -\frac{2(p-1)}{1+p}\int \limits _{|x|>R}(\Delta \zeta _R-N)|u|^{1+p} |x|^\rho \,dx+\frac{4\rho }{1+p}\int \limits _{|x|>R}(|x|^2-x.\nabla \zeta _R) |u|^{1+p}|x|^{\rho -2}\,\text {d}x. \end{aligned}$$

Thanks to the radial derivative formula

$$\begin{aligned} \partial _{jk}^2=\left( \delta _{jk}-\frac{x_jx_k}{r^2}\right) \frac{\partial _r}{r}+ \frac{x_jx_k}{r^2}\partial _r^2, \end{aligned}$$

one has

$$\begin{aligned} \int \limits _0^\infty m^\gamma \int \limits _{|x|>R}\overline{\partial _ku_m} \partial ^2_{kl}\zeta _R\partial _lu_m\,\text {d}x=\int \limits _0^\infty m^\gamma \int \limits _{|x|>R}\zeta _R''|\nabla u_m|^2\,\text {d}x\le \gamma \Vert u\Vert _{\dot{H}^\gamma }^2. \end{aligned}$$

Moreover, Lemma A.2 in Ref. [3] gives via Hölder estimate and Sobolev injection via the properties of $\zeta$,

$$\begin{aligned} \int \limits _0^\infty m^\gamma \int \limits _{|x|>R}\Delta ^2\zeta _R|u_m|^2\,\text {d}x\,\text {d}m&\lesssim \Vert \Delta ^2\zeta _R\Vert _\infty ^\gamma \Vert \Delta \zeta _R \Vert _\infty ^{1-\gamma }\Vert u\Vert _{L^2(|x|\le 10R)}^2\\&\lesssim R^{-2(\gamma -s_c)}\Vert u\Vert _{\dot{H}^{s_c}}^2. \end{aligned}$$

Then,

$$\begin{aligned}&\frac{\text {d}}{\text {d}t} M_{\zeta _R} [u(t)]\\&\quad =4\gamma BE(u_0)-2\gamma (B-2)\Vert u\Vert _{\dot{H}^\gamma }^2 -4\gamma \Vert u\Vert _{\dot{H}^\gamma (|x|>R)}^2\\&\qquad -\int \limits _0^\infty m^\gamma \int \limits _{|x|>R}\Delta ^2\zeta _R |u_m|^2\,\text {d}x\,\text {d}m+4\int \limits _0^\infty m^\gamma \int \limits _{|x|>R} \overline{\partial _ku_m}\partial ^2_{kl}\zeta _R\partial _lu_m\,\text {d}x\\&\qquad -\frac{2(p-1)}{1+p}\int \limits _{|x|>R}(\Delta \zeta _R-N)|u |^{1+p}|x|^\rho \,dx+\frac{4\rho }{1+p}\int \limits _{|x|>R}(|x|^2 -x\cdot \nabla \zeta _R)|u|^{1+p}|x|^{\rho -2}\,\text {d}x\\&\quad \le 4\gamma BE(u_0)-2\gamma (B-2)\Vert u\Vert _{\dot{H}^\gamma }^2 +R^{-2(\gamma -s_c)}\Vert u\Vert _{\dot{H}^{s_c}}^2+c\int \limits _{|x|>R}|u|^{1+p}|x|^\rho \,\text {d}x. \end{aligned}$$

In order to estimate the last term, one denotes the annulus $C_A:=C(A,2A)$ with respective small radius $A>0$ and large one 2A. Thus, thanks to Strauss inequality (2.7) and the properties of $\zeta _R$, one gets for $0<s<\frac{N}{2}$,

$$\begin{aligned} \int \limits _{C_A}|u|^{1+p}|x|^\rho \,\text {d}x\lesssim & {} \Vert |u|^{-1+p}|x|^\rho \Vert _{L^\infty (C_A)}\int \limits _{C_A}|u|^2\,\text {d}x\\\lesssim & {} \Vert |x|^{-(p-1)(\frac{N}{2}-s)+\rho }\Vert _{L^\infty (C_A)} \Vert u\Vert _{\dot{H}^s}^{p-1}\int \limits _{C_A}|u|^2\,\text {d}x. \end{aligned}$$

Using the interpolation inequality for $\frac{1}{2}<s<\gamma <\frac{N}{2}$ and the Sobolev estimate

$$\begin{aligned} \Vert (-\Delta )^\frac{eq1}{2}\cdot \Vert&\lesssim \Vert \cdot \Vert ^{1-\frac{s}{\gamma }}\Vert (-\Delta )^{\frac{\gamma }{2}}\cdot \Vert ^{\frac{s}{\gamma }},\end{aligned}$$

(6.1)

$$\begin{aligned} \Vert \cdot \Vert _{L^2(|x|\lesssim R)}&\lesssim R^{s_c}\Vert (-\Delta )^\frac{s_c}{2}\cdot \Vert _{L^2(|x|\lesssim R)}, \end{aligned}$$

(6.2)

one gets

$$\begin{aligned} \int \limits _{C_A}|u|^{1+p}|x|^\rho \,\text {d}x&\lesssim A^{-(p-1)(\frac{N}{2}-s)+\rho }\Vert u\Vert _{\dot{H}^\gamma }^{\frac{s(p-1)}{\gamma }}\left( \int \limits _{C_A}|u|^2\,\text {d}x\right) ^{1+\frac{p-1}{2}(1-\frac{s}{\gamma })}\\&\lesssim A^{-(p-1)(\frac{N}{2}-s)+\rho }\Vert u\Vert _{\dot{H}^\gamma }^{\frac{s(p-1)}{\gamma }}\Big (A^{s_c}\Vert (-\Delta )^\frac{s_c}{2}u\Vert _{L^2(|x|\lesssim R)} \Big )^{2+(p-1)(1-\frac{s}{\gamma })}\\&\lesssim A^{-(p-1)(\frac{N}{2}-s)+\rho +s_c(2+(p-1)(1-\frac{s}{\gamma }))} \Vert u\Vert _{\dot{H}^\gamma }^{\frac{s(p-1)}{\gamma }}\\&\lesssim A^{-2(\gamma -s_c)(1-\frac{s(p-1)}{2\gamma })}\Vert u\Vert _{\dot{H}^\gamma }^{\frac{s(p-1)}{\gamma }}. \end{aligned}$$

Since $p<1+4\gamma$, one takes $s=\left( \frac{1}{2}\right) ^+$, so that $\frac{s(p-1)}{\gamma }<2$. Therefore, by Young Lemma, for any $\beta >0$,

$$\begin{aligned} \int \limits _{C_A}|u|^{1+p}|x|^\rho \,\text {d}x\lesssim \beta \Vert u\Vert _{\dot{H}^\gamma }^2+C_\beta A^{-2(\gamma -s_c)}. \end{aligned}$$

Now, using a series expansion

$$\begin{aligned} \int \limits _{{\mathbb {R}}^N}|u|^{1+p}|x|^\rho \,\text {d}x&=\sum _{k=0}^\infty \int \limits _{C_{2^kR}}|u|^{1+p}|x|^\rho \,\text {d}x\\&\lesssim \beta \sum _{k=0}^\infty \Vert u\Vert _{\dot{H}^\gamma (C_{2^kR})}^2 +C_\beta \sum _{k=0}^\infty (2^kR)^{-2(\gamma -s_c)}\\&\lesssim \beta \Vert u\Vert _{\dot{H}^\gamma (|x|>R)}^2+C_\beta R^{-2(\gamma -s_c)}. \end{aligned}$$

Finally, since $u\in L^\infty _{T^*}(\dot{H}^{s_c})$, one gets

$$\begin{aligned} \frac{\text {d}}{\text {d}t} M_{\zeta _R} [u(t)]\le & {} 4\gamma BE(u_0)-2\gamma (B-2)\Vert u\Vert _{\dot{H}^\gamma }^2+\beta \Vert u\Vert _{\dot{H}^\gamma }^2+C_\beta R^{-2(\gamma -s_c)}. \end{aligned}$$

2. Finite time blow-up. Since $p>p_*$ and $E(u_0)<0$, taking $0<\beta \ll 1\ll R$, there is $c>0$ such that

$$\begin{aligned} \frac{\text {d}}{\text {d}t} M_{\zeta _R} [u(t)]< & {} -c\Vert u\Vert _{\dot{H}^\gamma }^2. \end{aligned}$$

Assume, with contradiction that $T^*=\infty$. Since $E(u_0)<0$, by Theorem 2.1, one gets $\inf _{[0,T^*)}\Vert u(t)\Vert _{\dot{H}^\gamma }>0$. Thus, by integrating in time, there is $t_0>0$ such that

$$\begin{aligned} M_{\zeta _R} [u(t)]&<0,\quad \forall \, t\ge t_0;\\ M_{\zeta _R} [u(t)]&<-c\int \limits _{t_0}^t\Vert u(\tau )\Vert _{\dot{H}^\gamma }\,\text {d}\tau ,\quad \forall \, t\ge t_0. \end{aligned}$$

Moreover, by Lemma 4.1 in Ref. [3], via the fact that $supp(\zeta _R)\subset \{|x|\le 10R\}$ and (6.1)–(6.2), there is $c:=c_{N,R}$ such that

$$\begin{aligned} M_{\zeta _R} [u]&\le c\left( \Vert (-\Delta )^\frac{1}{4} u\Vert _{L^2(|x|\lesssim R)}^2 +\Vert u\Vert _{L^2(|x|\lesssim R)}\Vert (-\Delta )^\frac{1}{4} u\Vert _{L^2(|x|\lesssim R)}\right) \\&\le c\left( \Vert u\Vert _{L^2(|x|\lesssim R)}^{2-\frac{1}{\gamma }} \Vert (-\Delta )^\frac{\gamma }{2} u\Vert _{L^2(|x|\lesssim R)}^\frac{1}{\gamma }+\Vert u\Vert _{L^2(|x|\lesssim R)}^{2-\frac{1}{2\gamma }}\Vert (-\Delta )^\frac{\gamma }{2} u\Vert _{L^2(|x|\lesssim R)}^\frac{1}{2\gamma }\right) \\&\le c\left( \Vert (-\Delta )^{\frac{s_c}{2}}u\Vert _{L^2(|x|\lesssim R)}^{2 -\frac{1}{\gamma }}\Vert (-\Delta )^\frac{\gamma }{2} u\Vert _{L^2(|x|\lesssim R)}^\frac{1}{\gamma }\right. \\&\left. \quad +\Vert (-\Delta )^{\frac{s_c}{2}}u\Vert _{L^2(|x|\lesssim R)}^{2- \frac{1}{2\gamma }}\Vert (-\Delta )^\frac{\gamma }{2} u\Vert _{L^2(|x|\lesssim R)}^\frac{1}{2\gamma }\right) \\&\le c\left( \Vert (-\Delta )^\frac{\gamma }{2} u\Vert _{L^2(|x|\lesssim R) }^\frac{1}{\gamma }+\Vert (-\Delta )^\frac{\gamma }{2} u\Vert _{L^2(|x|\lesssim R)}^\frac{1}{2\gamma }\right) \\&\le c\Vert (-\Delta )^\frac{\gamma }{2} u\Vert _{L^2(|x|\lesssim R)}^\frac{1}{\gamma }. \end{aligned}$$

In the last line, one uses

$$\begin{aligned} \inf _{0\le t<T^*}\Vert u(t)\Vert _{\dot{H}^\gamma }>0\quad \text{ and }\quad \sup _{0\le t<T^*}\Vert u(t)\Vert _{\dot{H}^{s_c}}<\infty . \end{aligned}$$

Then, for $\gamma >\frac{1}{2}$ and a finite $t_1 >0$,

$$\begin{aligned} M_{\zeta _R}[u(t)]\le -C_R|t - t_1 |^{1-2\gamma }\rightarrow -\infty ,\quad \text{ when } \quad t\rightarrow t_1. \end{aligned}$$

Finally, $T^* <\infty$.

7 Proof of Lemma 2.16

Take a functional sequence satisfying

$$\begin{aligned} \sup _n\Big (\Vert (-\Delta )^\frac{\gamma }{2}u_n\Vert +\Vert u_n\Vert _{p_c}\Big )<\infty \quad \text{ and }\quad u_n\rightharpoonup 0\quad \text{ in }\quad \dot{H}^\gamma \cap L^{p_c}. \end{aligned}$$

One will prove that

$$\begin{aligned} \int \limits _{{\mathbb {R}}^N}|x|^\rho |u_n|^{1+p}\,\text {d}x\rightarrow 0. \end{aligned}$$

Since $p_c<\frac{2N}{N-2\gamma }$, with an interpolation argument, one has

$$\begin{aligned} \sup _n\Vert u_n\Vert _q<\infty , \quad \forall q\in \left( p_c, \frac{2N}{N-2\gamma }\right) . \end{aligned}$$

Let $0<\varepsilon<<1$. Using Hölder estimate and Sobolev injection via $p<p^*$, one has

$$\begin{aligned} \int \limits _{|x|>R}|x|^\rho |u_n|^{1+p}\,\text {d}x\le & {} \Vert |x|^\rho \Vert _{L^{\frac{N+\varepsilon }{|\rho |}}(|x|>R)}\Vert u_n \Vert _{(\frac{N+\varepsilon }{|\rho |})'(1+p)}^{1+p}\\\le & {} CR^{-\varepsilon }\Vert u_n\Vert _{(\frac{N+\varepsilon }{|\rho |})'(1+p)}^{1+p}\\\le & {} CR^{-\varepsilon }. \end{aligned}$$

Here, one needs

$$\begin{aligned} \frac{N(p-1)}{\rho +2\gamma }=p_c<\left( \frac{N+\varepsilon }{|\rho |}\right) ' (1+p)=\frac{\varepsilon +N}{\varepsilon +N+\rho }(1+p)<\frac{2N}{N-2\gamma }. \end{aligned}$$

Indeed, the above condition read

$$\begin{aligned} \varepsilon ((N-\rho -2\gamma )p-(N+\rho +2\gamma ))&<N(N-2\gamma )(p^*-p);\\ \varepsilon \left( p-\frac{N+2\gamma }{N-2\gamma }\right)&<0<N(p-p^*). \end{aligned}$$

Take $R>(\frac{1}{\varepsilon })^\frac{1}{\varepsilon }$ and gets

$$\begin{aligned} \int \limits _{B(R)^c}|u_n|^{1+p}|x|^\rho \,dx\le c\varepsilon . \end{aligned}$$

(7.1)

Now, Poincare inequality and the compact Sobolev injections give for all $2<q<\frac{2N}{N-2\gamma }$,

$$\begin{aligned} \lim {n\rightarrow \infty }\Vert u_n\Vert _{L^q(B(R))}=0. \end{aligned}$$

Moreover, by Hölder estimate

$$\begin{aligned} \int \limits _{B(R)}|u_n|^{1+p}|x|^\rho \,\text {d}x\le & {} \Vert |x|^\rho \Vert _{L^a(B(R))}\Vert u_n\Vert _{a'(1+p)}^{1+p}. \end{aligned}$$

Here, one picks $a:=\frac{N}{|\rho |}-\varepsilon$. This gives $2<a'(1+p)<\frac{2N}{N-2\gamma }$ if $2(1+\frac{\rho }{N})<1+p<\frac{2(N+\rho )}{N-2\gamma }.$ Taking account of (7.1), the proof id achieved because $1+\frac{2\rho }{N}<p<p^*$.