A novel accelerated extragradient algorithm to solve pseudomonotone variational inequalities

Abstract

In this paper, we propose a new inertial iterative method to solve classical variational inequalities with pseudomonotone and Lipschitz continuous operators in the setting of a real Hilbert space. The proposed iterative scheme is basically analogous to the extragradient method used to solve the problems of variational inequalities in real Hilbert spaces. The strong convergence of the proposed algorithm is set up with the prior knowledge of Lipschitz’s constant of an operator. Finally, several computational experiments are listed to show the applicability and efficiency of the proposed algorithm.

1 Introduction

This article studies the iterative method that is used to estimate the solution of variational inequality problem (shortly, VIP) in the setting of a real Hilbert space. Let ${\mathcal {X}}$ be a real Hilbert space and ${\mathcal {D}}$ be a non-empty, closed, and convex subset of ${\mathcal {X}}.$ Let ${\mathcal {S}}: {\mathcal {X}} \rightarrow {\mathcal {X}}$ to be an operator. The problem (VIP) for ${\mathcal {S}}$ on ${\mathcal {D}}$ is given as follows [15, 22]:

$$\begin{aligned} \text {Find} \,\, u^{*} \in {\mathcal {D}} \,\, \text {such that} \,\, \big \langle {\mathcal {S}}(u^{*}), y - u^{*} \big \rangle \ge 0,\quad \forall \, y \, \in {\mathcal {D}}. \end{aligned}$$

(VIP)

Let us consider that $\Pi$ is the solution set of the problem (VIP). This idea of variational inequalities includes different disciplines such as partial differential equations, optimization, optimal control, mechanics, mathematical programming, and finance (see [6, 11,12,13,14, 18, 24]). This problem is an important topic in the physical sciences, and a considerable amount of discussion has been given to many authors who have dedicated themselves to studying not only the theory of existence and the stability of solutions but also the iterative method used to solve the problem.

Korpelevich [16] and Antipin [2] have established the following extragradient method. Their method consists of the following: Let $u_{0} \in {\mathcal {D}}$ and $0< \tau < \frac{1}{L}$ such that

$$\begin{aligned} \left\{ \begin{array}{l} y_{n} = P_{{\mathcal {D}}}{[u_{n} - \tau {\mathcal {S}}(u_{n})]}, \\ u_{n+1} = P_{{\mathcal {D}}}{[u_{n} - \tau {\mathcal {S}}(y_{n})]}. \\ \end{array} \right. \end{aligned}$$

(1)

On the other hand, many projection methods are used to figure out the numerical solution of variational inequalities. Many researchers have suggested various forms of projection techniques to solve the problem (VIP) (see for details [10, 16, 19, 25, 26, 28,29,30,31,32, 34, 36]). Almost all the methods for solving the problem (VIP) are based on the projection method, which is computed on the feasible set ${\mathcal {D}}.$ It is important to note that the above well-established method has two significant flaws, the first being the fixed constant step size, which involves the knowledge or approximation of the Lipschitz constant of the respective operator and is only weakly convergent in the Hilbert spaces. From the computational point of view, it might be problematic to use a fixed step size, and hence the convergence rate and appropriateness of the method could be affected.

The main contribution of this study is to develop an inertial-type method used to improve the convergence rate of the sequence. Previously, such approaches have been developed based on the oscillator equation with damping and conservative force restoration. This second-order dynamical structure is called a strong friction ball and was originally studied by Polyak in [20]. Primarily, the functionality of the inertial-type method is that it will use the two prior iterations to execute the next iteration.

Therefore, a natural question is raised:

“Is it possible to introduce new strongly convergent inertial extragradient-like method to solve the problem (VIP)”?

In this study, we give a positive answer to the above question, i.e., the gradient method indeed generates a strongly convergent iterative sequence by letting a fixed and variable step size rule. In this paper, we study a different method to obtain strong convergence and introduce a new iterative method for solving variational inequalities involving pseudomonotone and the Lipschitz operator in a real Hilbert space. Our method is inspired by one projection method [16] and the inertial technique in [20]. At each iteration, the method only needs to compute one projection onto the feasible set. Under some suitable conditions imposed on control parameters, the iterative sequences generated by our method converge strongly to some solution of the considered problem. We also provide numerical examples to illustrate the computational effectiveness of the new method over some existing methods.

The paper is organized in the following way. In Sect. 2, we review some concepts and preliminary results used in the paper. Section 3 deals with the description of the method and proves its convergence theorems. Finally, Sect. 4 presents some numerical results to illustrate the convergence and effectiveness of the proposed method.

2 Background

In this section of the manuscript, we have written a number of important identities and relevant lemmas and definitions.

For all $u, y \in {\mathcal {X}},$ we have

$$\begin{aligned} \Vert u + y\Vert ^{2} = \Vert u\Vert ^{2} + 2 \langle u, y \rangle + \Vert y\Vert ^{2}. \end{aligned}$$

A metric projection $P_{{\mathcal {D}}}(y_{1})$ of $y_{1} \in {\mathcal {X}}$ is defined by

$$\begin{aligned} P_{{\mathcal {D}}}(y_{1}) = \underset{}{\arg \min } \{ \Vert y_{1} - y_{2}\Vert : y_{2} \in {\mathcal {D}} \}. \end{aligned}$$

First, we list some of the important features of projection operator.

Lemma 2.1

[3] Suppose that $P_{{\mathcal {D}}} : {\mathcal {X}} \rightarrow {\mathcal {D}}$ is a metric projection. Then,  the following conditions were satisfied.

• (i) $y_{3} = P_{{\mathcal {D}}}(y_{1})$ if and only if

  $$\begin{aligned} \langle y_{1} - y_{3}, y_{2} - y_{3} \rangle \le 0, \quad \forall \, y_{2} \in {\mathcal {D}}. \end{aligned}$$
• (ii)
  $$\begin{aligned} \Vert y_{1} - P_{{\mathcal {D}}}(y_{2}) \Vert ^{2} + \Vert P_{{\mathcal {D}}}(y_{2}) - y_{2} \Vert ^{2} \le \Vert y_{1} - y_{2} \Vert ^{2}, \quad y_{1} \in {\mathcal {D}}, y_{2} \in {\mathcal {X}}. \end{aligned}$$
• (iii)
  $$\begin{aligned} \Vert y_{1} - P_{{\mathcal {D}}}(y_{1}) \Vert \le \Vert y_{1} - y_{2} \Vert ,\quad y_{2} \in {\mathcal {D}}, y_{1} \in {\mathcal {X}}. \end{aligned}$$

Lemma 2.2

[35] Assume that $\{p_{n}\} \subset [0, +\infty )$ is a sequence satisfies the following inequality:

$$\begin{aligned} p_{n+1} \le (1 - q_{n}) p_{n} + q_{n} r_{n},\quad \forall \, n \in {\mathbb {N}}. \end{aligned}$$

Furthermore,  $\{q_{n}\} \subset (0, 1)$ and $\{r_{n}\} \subset {\mathbb {R}}$ be two sequences such that

$$\begin{aligned} \lim _{n \rightarrow +\infty } q_{n} = 0,\quad \sum _{n=1}^{+\infty } q_{n} = +\infty \quad \text {and}\quad \limsup _{n \rightarrow +\infty } r_{n} \le 0. \end{aligned}$$

Then,  $\lim _{n \rightarrow +\infty } p_{n} = 0.$

Lemma 2.3

[17] Assume that $\{p_{n}\}$ is a sequence of real numbers such that there exists a subsequence $\{n_{i}\}$ of $\{n\}$ such that

$$\begin{aligned} p_{n_{i}} < p_{n_{i+1}} \quad \forall \ i \in {\mathbb {N}}. \end{aligned}$$

Then,  there is a non decreasing sequence $m_{k} \subset {\mathbb {N}}$ such that $m_{k} \rightarrow +\infty$ as $k \rightarrow +\infty ,$ and meet the following requirements for numbers $k \in {\mathbb {N}}{:}$

$$\begin{aligned} p_{m_{k}} \le p_{m_{k+1}} \quad \text {and} \quad p_{k} \le p_{m_{k+1}}. \end{aligned}$$

Indeed,  $m_{k} = \max \{ j \le k: p_{j} \le p_{j+1} \}.$

Next, we list some of the important identities that were used to prove the convergence analysis.

Lemma 2.4

[3] For any $y_{1}, y_{2} \in {\mathcal {X}}$ and $\ell \in {\mathbb {R}}.$ Then,  the following inequalities hold:

• (i)
  $$\begin{aligned} \Vert \ell y_{1} + (1 - \ell ) y_{2} \Vert ^{2} = \ell \Vert y_{1}\Vert ^{2} + (1 - \ell )\Vert y_{2} \Vert ^{2} - \ell (1 - \ell )\Vert y_{1} - y_{2}\Vert ^{2}. \end{aligned}$$
• (ii)
  $$\begin{aligned} \Vert y_{1} + y_{2} \Vert ^{2} \le \Vert y_{1}\Vert ^{2} + 2 \langle y_{2}, y_{1} + y_{2} \rangle . \end{aligned}$$

Lemma 2.5

[23] Assume that ${\mathcal {S}} : {\mathcal {D}} \rightarrow {\mathcal {X}}$ is a pseudomonotone and continuous operator. Then,  $u^{*}$ is a solution to the problem (VIP) if and only if $u^{*}$ is a solution to the following problem : 

$$\begin{aligned} \text {Find} \,\, u \in {\mathcal {D}} \,\, \text {such that} \,\, \langle {\mathcal {S}}(y), y - u \rangle \ge 0, \quad \forall \, y \in {\mathcal {D}}. \end{aligned}$$

3 Main results

To investigate the convergence analysis, it is considered that the following requirements are satisfied:

(${\mathcal {S}}1$) A solution set of problem (VIP) is denoted by $\Pi$ and it is non-empty;

(${\mathcal {S}}2$) An operator ${\mathcal {S}} : {\mathcal {X}} \rightarrow {\mathcal {X}}$ is said to be pseudomonotone if

$$\begin{aligned} \big \langle {\mathcal {S}}(y_{1}), y_{2} - y_{1} \big \rangle \ge 0 \Longrightarrow \big \langle {\mathcal {S}}(y_{2}), y_{1} - y_{2} \big \rangle \le 0,\quad \forall \, y_{1}, y_{2} \in {\mathcal {D}}; \end{aligned}$$

(${\mathcal {S}}3$) An operator ${\mathcal {S}} : {\mathcal {X}} \rightarrow {\mathcal {X}}$ is said to be Lipschitz continuous with constant $L >0$ if there exists $L >0$ such that

$$\begin{aligned} \Vert {\mathcal {S}}(y_{1}) - {\mathcal {S}}(y_{2}) \Vert \le L \Vert y_{1} - y_{2}\Vert , \quad \forall \, y_{1}, y_{2} \in {\mathcal {D}}; \end{aligned}$$

(${\mathcal {S}}4$) An operator ${\mathcal {S}} : {\mathcal {X}} \rightarrow {\mathcal {X}}$ is said to be sequentially weakly continuous if $\{{\mathcal {S}}(u_{n})\}$ converges weakly to ${\mathcal {S}}(u)$ for every sequence $\{u_{n}\}$ converges weakly to u.

The main algorithm is given the following form:

Lemma 3.1

Assume that ${\mathcal {S}} : {\mathcal {X}} \rightarrow {\mathcal {X}}$ satisfies the conditions (${\mathcal {S}}1$)–(${\mathcal {S}}4$). For a given $u^{*} \in \Pi \ne \emptyset ,$ we have

$$\begin{aligned} \Vert u_{n+1} - u^{*}\Vert ^{2} \le \Vert t_{n} - u^{*}\Vert ^{2} - (1 - \tau L)\Vert t_{n} - y_{n}\Vert ^{2} - (1 - \tau L) \Vert u_{n+1} - y_{n}\Vert ^{2}. \end{aligned}$$

Proof

First consider the following

$$\begin{aligned} \big \Vert u_{n+1} - u^{*} \big \Vert ^{2}&= \big \Vert P_{{\mathcal {D}}}[t_{n} - \tau {\mathcal {S}}(y_{n})] - u^{*} \big \Vert ^{2} \nonumber \\&= \big \Vert P_{{\mathcal {D}}} [t_{n} - \tau {\mathcal {S}}(y_{n})] + [t_{n} - \tau {\mathcal {S}}(y_{n})] - [t_{n} - \tau {\mathcal {S}}(y_{n})] - u^{*} \big \Vert ^{2} \nonumber \\&= \big \Vert [t_{n} - \tau {\mathcal {S}}(y_{n})] - u^{*} \big \Vert ^{2} + \big \Vert P_{{\mathcal {D}}} [t_{n} - \tau {\mathcal {S}}(y_{n})] - [t_{n} - \tau {\mathcal {S}}(y_{n})] \big \Vert ^{2} \nonumber \\&\quad + 2 \big \langle P_{{\mathcal {D}}} [t_{n} - \tau {\mathcal {S}}(y_{n})] - [t_{n} - \tau {\mathcal {S}}(y_{n})], [t_{n} - \tau {\mathcal {S}}(y_{n})] - u^{*} \big \rangle . \end{aligned}$$

(3)

It is given that $u^{*} \in \Pi \subset {\mathcal {D}}$ such that

$$\begin{aligned}&\big \Vert P_{{\mathcal {D}}} [t_{n} - \tau {\mathcal {S}}(y_{n})] - [t_{n} - \tau {\mathcal {S}}(y_{n})] \big \Vert ^{2} \nonumber \\&\qquad + \big \langle P_{{\mathcal {D}}} [t_{n} - \tau {\mathcal {S}}(y_{n})] - [t_{n} - \tau {\mathcal {S}}(y_{n})], [t_{n} - \tau {\mathcal {S}}(y_{n})] - u^{*} \big \rangle \nonumber \\&\quad = \big \langle [t_{n} - \tau {\mathcal {S}}(y_{n})] - P_{{\mathcal {D}}} [t_{n} - \tau {\mathcal {S}}(y_{n})], u^{*} - P_{{\mathcal {D}}} [t_{n} - \tau {\mathcal {S}}(y_{n})] \big \rangle \le 0, \end{aligned}$$

(4)

which implies that

$$\begin{aligned}&\big \langle P_{{\mathcal {D}}} [t_{n} - \tau {\mathcal {S}}(y_{n})] - [t_{n} - \tau {\mathcal {S}}(y_{n})], [t_{n} - \tau {\mathcal {S}}(y_{n})] - u^{*} \big \rangle \nonumber \\&\quad \le - \big \Vert P_{{\mathcal {D}}} [t_{n} - \tau {\mathcal {S}}(y_{n})] - [t_{n} - \tau {\mathcal {S}}(y_{n})] \big \Vert ^{2}. \end{aligned}$$

(5)

By the use of expressions (3) and (5), we obtain

$$\begin{aligned} \Vert u_{n+1} - u^{*} \Vert ^{2}&\le \big \Vert t_{n} - \tau {\mathcal {S}}(y_{n}) - u^{*} \big \Vert ^{2} - \big \Vert P_{{\mathcal {D}}} [t_{n} - \tau {\mathcal {S}}(y_{n})] - [t_{n} - \tau {\mathcal {S}}(y_{n})] \big \Vert ^{2} \nonumber \\&\le \Vert t_{n} - u^{*} \Vert ^{2} - \Vert t_{n} - u_{n+1} \Vert ^{2} + 2 \tau \big \langle {\mathcal {S}}(y_{n}), u^{*} - u_{n+1} \big \rangle . \end{aligned}$$

(6)

By given that $u^{*}$ is the solution of problem (VIP), we have

$$\begin{aligned} \langle {\mathcal {S}} (u^{*}), y - u^{*} \rangle \ge 0,\quad \text {for all}\ y \in {\mathcal {D}}. \end{aligned}$$

Due to the pseudomonotonicity of ${\mathcal {S}}$ on ${\mathcal {D}}$, we get

$$\begin{aligned} \langle {\mathcal {S}} (y), y - u^{*} \rangle \ge 0,\quad \text {for all}\ y \in {\mathcal {D}}. \end{aligned}$$

By substituting $y = y_{n} \in {\mathcal {D}},$ we get

$$\begin{aligned} \langle {\mathcal {S}} (y_{n}), y_{n} - u^{*} \rangle \ge 0. \end{aligned}$$

Thus, we have

$$\begin{aligned} \big \langle {\mathcal {S}}(y_{n}), u^{*} - u_{n+1} \big \rangle = \big \langle {\mathcal {S}}(y_{n}), u^{*} - y_{n} \big \rangle + \big \langle {\mathcal {S}}(y_{n}), y_{n} - u_{n+1} \big \rangle \le \big \langle {\mathcal {S}}(y_{n}), y_{n} - u_{n+1} \big \rangle . \end{aligned}$$

(7)

By the use of expressions (6) and (7), we obtain

$$\begin{aligned} \Vert u_{n+1} - u^{*} \Vert ^{2}&\le \Vert t_{n} - u^{*} \Vert ^{2} - \Vert t_{n} - u_{n+1} \Vert ^{2} + 2 \tau \big \langle {\mathcal {S}}(y_{n}), y_{n} - u_{n+1} \big \rangle \nonumber \\&\le \Vert t_{n} - u^{*} \Vert ^{2} - \Vert t_{n} - y_{n} + y_{n} - u_{n+1} \Vert ^{2} + 2 \tau \big \langle {\mathcal {S}}(y_{n}), y_{n} - u_{n+1} \big \rangle \nonumber \\&\le \Vert t_{n} - u^{*} \Vert ^{2} - \Vert t_{n} - y_{n} \Vert ^{2} - \Vert y_{n} - u_{n+1} \Vert ^{2} + 2 \big \langle t_{n} - \tau {\mathcal {S}}(y_{n}) - y_{n}, u_{n+1} - y_{n} \big \rangle . \end{aligned}$$

(8)

It is given that $u_{n+1} = P_{{\mathcal {D}}} [t_{n} - \tau {\mathcal {S}}(y_{n})]$, we have

$$\begin{aligned}&2 \big \langle t_{n} - \tau {\mathcal {S}}(y_{n}) - y_{n}, u_{n+1} - y_{n} \big \rangle \nonumber \\&\quad = 2 \big \langle t_{n} - \tau {\mathcal {S}}(t_{n}) - y_{n}, u_{n+1} - y_{n} \big \rangle + 2 \tau \big \langle {\mathcal {S}}(t_{n}) - {\mathcal {S}}(y_{n}), u_{n+1} - y_{n} \big \rangle \nonumber \\&\quad \le 2 \tau L \Vert t_{n} - y_{n}\Vert \Vert u_{n+1} - y_{n}\Vert \le \tau L \Vert t_{n} - y_{n}\Vert ^{2} + \tau L \Vert u_{n+1} - y_{n}\Vert ^{2}. \end{aligned}$$

(9)

Combining expressions (8) and (9), we obtain

$$\begin{aligned} \Vert u_{n+1} - u^{*}\Vert ^{2} \le \Vert t_{n} - u^{*}\Vert ^{2} - (1 - \tau L)\Vert t_{n} - y_{n}\Vert ^{2} - (1 - \tau L) \Vert u_{n+1} - y_{n}\Vert ^{2}. \end{aligned}$$

(10)

$\square$

Theorem 3.2

Let $\{u_{n}\}$ be a sequence generated by Algorithm 1 and satisfies the conditions (${\mathcal {S}}1$)-(${\mathcal {S}}4$). Moreover,  choose $\{\psi _{n}\} \subset (0, 1)$ meet the conditions,  i.e., 

$$\begin{aligned} \lim _{n \rightarrow +\infty } \psi _{n} = 0 \quad \text {and}\quad \sum _{n=1}^{+\infty } \psi _{n} = +\infty . \end{aligned}$$

Then,  $\{u_{n}\}$ strongly converges to $u^{*} \in \Pi .$ Moreover,  $P_{\Pi } (0) = u^{*}.$

Proof

It is given in expression (2) that

$$\begin{aligned} \lim _{n \rightarrow +\infty } \frac{\alpha _{n}}{\psi _{n}} \big \Vert u_{n} - u_{n-1} \big \Vert \le \lim _{n \rightarrow +\infty } \frac{\epsilon _{n}}{\psi _{n}} \big \Vert u_{n} - u_{n-1} \big \Vert = 0. \end{aligned}$$

(11)

By the use of definition of $\{t_{n}\}$ and inequality (11), we obtain

$$\begin{aligned} \big \Vert t_{n} - u^{*} \big \Vert&= \big \Vert u_{n} + \alpha _{n} (u_{n} - u_{n-1}) - \psi _{n} u_{n} - \alpha _{n} \psi _{n} (u_{n} - u_{n-1}) - u^{*} \big \Vert \nonumber \\&= \big \Vert (1 - \psi _{n}) (u_{n} - u^{*}) + (1 - \psi _{n}) \alpha _{n} (u_{n} - u_{n-1}) - \psi _{n} u^{*} \big \Vert \end{aligned}$$

(12)

$$\begin{aligned}&\le (1 - \psi _{n}) \big \Vert u_{n} - u^{*} \big \Vert + (1 - \psi _{n}) \alpha _{n} \big \Vert u_{n} - u_{n-1} \big \Vert + \psi _{n} \big \Vert u^{*} \big \Vert \nonumber \\&\le (1 - \psi _{n}) \Vert u_{n} - u^{*}\Vert + \psi _{n} M_{1}, \end{aligned}$$

(13)

where

$$\begin{aligned} (1 - \psi _{n}) \frac{\alpha _{n}}{\psi _{n}} \big \Vert u_{n} - u_{n-1} \big \Vert + \big \Vert u^{*} \big \Vert \le M_{1}. \end{aligned}$$

By the use of Lemma 3.1, we obtain

$$\begin{aligned} \Vert u_{n+1} - u^{*}\Vert ^{2} \le \Vert t_{n} - u^{*}\Vert ^{2},\quad \forall \, n \in {\mathbb {N}}. \end{aligned}$$

(14)

Combining (13) with (14), we obtain

$$\begin{aligned} \Vert u_{n+1} - u^{*}\Vert&\le (1 - \psi _{n}) \Vert u_{n} - u^{*}\Vert + \psi _{n} M_{1} \nonumber \\&\le \max \big \{ \Vert u_{n} - u^{*}\Vert , M_{1} \big \} \nonumber \\ \vdots \nonumber \\&\le \max \big \{ \Vert u_{0} - u^{*}\Vert , M_{1} \big \}. \end{aligned}$$

(15)

Thus, we conclude that the $\{u_{n}\}$ is bounded sequence. Indeed, by (13) we have

$$\begin{aligned} \big \Vert t_{n} - u^{*} \big \Vert ^{2}&\le (1 - \psi _{n})^{2} \Vert u_{n} - u^{*}\Vert ^{2} + \psi _{n}^{2} M_{1}^{2} + 2 M_{1} \psi _{n} (1 - \psi _{n}) \Vert u_{n} - u^{*}\Vert \nonumber \\&\le \Vert u_{n} - u^{*}\Vert ^{2} + \psi _{n} \big [ \psi _{n} M_{1}^{2} + 2 M_{1} (1 - \psi _{n}) \Vert u_{n} - u^{*}\Vert \big ] \nonumber \\&\le \Vert u_{n} - u^{*}\Vert ^{2} + \psi _{n} M_{2}, \end{aligned}$$

(16)

for some $M_{2} > 0.$ Combining the expressions (10) with (16), we have

$$\begin{aligned} \Vert u_{n+1} - u^{*}\Vert ^{2}&\le \Vert u_{n} - u^{*}\Vert ^{2} + \psi _{n} M_{2} \nonumber \\&\quad - (1 - \tau L) \Vert t_{n} - y_{n}\Vert ^{2} - (1 - \tau L) \Vert u_{n+1} - y_{n}\Vert ^{2}. \end{aligned}$$

(17)

Due to the Lipschitz-continuity and pseudomonotonicity of ${\mathcal {S}}$ implies that the solution set $\Pi$ is a closed and convex set. It is given that $u^{*} = P_{\Pi }(0)$ and using Lemma 2.1(ii), we have

$$\begin{aligned} \langle 0 - u^{*}, y - u^{*} \rangle \le 0,\quad \forall \, y \in \Pi . \end{aligned}$$

(18)

The remainder of the facts shall be split into the following two parts:

Case 1: Now consider that a fixed number $N_{1} \in {\mathbb {N}}$ such that

$$\begin{aligned} \Vert u_{n+1} - u^{*} \Vert \le \Vert u_{n} - u^{*} \Vert ,\quad \forall \, n \ge N_{1}. \end{aligned}$$

(19)

Thus, above implies that $\lim _{n \rightarrow +\infty } \Vert u_{n} - u^{*}\Vert$ exists and let $\lim _{n \rightarrow +\infty } \Vert u_{n} - u^{*}\Vert = l$, for some $l \ge 0.$ From the expression (17), we have

$$\begin{aligned}&(1 - \tau L) \Vert t_{n} - y_{n}\Vert ^{2} + (1 - \tau L) \Vert u_{n+1} - y_{n}\Vert ^{2} \nonumber \\&\quad \le \Vert u_{n} - u^{*}\Vert ^{2} + \psi _{n} M_{2} - \Vert u_{n+1} - u^{*} \Vert ^{2}. \end{aligned}$$

(20)

Due to existence of a limit of sequence $\Vert u_{n} - u^{*}\Vert$ and $\psi _{n} \rightarrow 0$, we infer that

$$\begin{aligned} \Vert t_{n} - y_{n}\Vert \rightarrow 0 \quad \text {and} \quad \Vert u_{n+1} - y_{n}\Vert \rightarrow 0 \quad \text {as} \ n \rightarrow +\infty . \end{aligned}$$

(21)

By the use of expression (21), we have

$$\begin{aligned} \lim _{n \rightarrow +\infty } \Vert t_{n} - u_{n+1}\Vert \le \lim _{n \rightarrow +\infty } \Vert t_{n} - y_{n}\Vert + \lim _{n \rightarrow +\infty } \Vert y_{n} - u_{n+1}\Vert = 0. \end{aligned}$$

(22)

Next, we will evaluate

$$\begin{aligned} \Vert t_{n} - u_{n}\Vert&= \Vert u_{n} + \alpha _{n} (u_{n} - u_{n-1}) - \psi _{n} \big [ u_{n} + \alpha _{n} (u_{n} - u_{n-1}) \big ] - u_{n} \Vert \nonumber \\&\le \alpha _{n} \Vert u_{n} - u_{n-1} \Vert + \psi _{n} \Vert u_{n}\Vert + \alpha _{n} \psi _{n} \Vert u_{n} - u_{n-1} \Vert \nonumber \\&= \psi _{n} \frac{\alpha _{n}}{\psi _{n}} \Vert u_{n} - u_{n-1} \Vert + \psi _{n} \Vert u_{n}\Vert + \psi _{n}^{2} \frac{\alpha _{n}}{\psi _{n}} \Vert u_{n} - u_{n-1} \Vert \longrightarrow 0. \end{aligned}$$

(23)

The above provides that

$$\begin{aligned} \lim _{n \rightarrow +\infty } \Vert u_{n} - u_{n+1}\Vert \le \lim _{n \rightarrow +\infty } \Vert u_{n} - t_{n}\Vert + \lim _{n \rightarrow +\infty } \Vert t_{n} - u_{n+1}\Vert = 0. \end{aligned}$$

(24)

The above explanation guarantees that the sequences $\{t_{n}\}$ and $\{y_{n}\}$ are also bounded. By the use of reflexivity of ${\mathcal {X}}$ and the boundedness of $\{u_{n}\}$ guarantees that there exits a subsequence $\{u_{n_{k}}\}$ in order that $\{u_{n_{k}}\} \rightharpoonup {\hat{u}} \in {\mathcal {X}}$ as $k \rightarrow +\infty .$ Next, we have to prove that ${\hat{u}} \in \Pi .$ This is provided that $y_{n_{k}} = P_{{\mathcal {D}}}[t_{n_{k}} - \tau {\mathcal {S}}(t_{n_{k}})]$ that is equivalent to

$$\begin{aligned} \langle t_{n_{k}} - \tau {\mathcal {S}}(t_{n_{k}}) - y_{n_{k}}, y - y_{n_{k}} \rangle \le 0,\quad \forall \, y \in {\mathcal {D}}. \end{aligned}$$

(25)

The above inequality implies that

$$\begin{aligned} \langle t_{n_{k}} - y_{n_{k}}, y - y_{n_{k}} \rangle \le \tau \langle {\mathcal {S}}(t_{n_{k}}), y - y_{n_{k}} \rangle , \quad \forall \, y \in {\mathcal {D}}. \end{aligned}$$

(26)

Thus, we shall obtain

$$\begin{aligned} \frac{1}{\tau } \langle t_{n_{k}} - y_{n_{k}}, y - y_{n_{k}} \rangle + \langle {\mathcal {S}}(t_{n_{k}}), y_{n_{k}} - t_{n_{k}} \rangle \le \langle {\mathcal {S}}(t_{n_{k}}), y - t_{n_{k}} \rangle , \quad \forall \, y \in {\mathcal {D}}. \end{aligned}$$

(27)

Due to boundedness of the sequence $\{t_{n_{k}}\}$ implies that $\{{\mathcal {S}}(t_{n_{k}})\}$ is also bounded. By the use of $\lim _{k \rightarrow \infty } \Vert t_{n_{k}} - y_{n_{k}} \Vert = 0$ and $k \rightarrow \infty$ in (27), we obtain

$$\begin{aligned} \liminf _{k \rightarrow \infty } \langle {\mathcal {S}}(t_{n_{k}}), y - t_{n_{k}} \rangle \ge 0,\quad \forall \, y \in {\mathcal {D}}. \end{aligned}$$

(28)

Moreover, we have

$$\begin{aligned}&\langle {\mathcal {S}}(y_{n_{k}}), y - y_{n_{k}} \rangle \nonumber \\&\quad = \langle {\mathcal {S}}(y_{n_{k}}) - {\mathcal {S}}(t_{n_{k}}), y - t_{n_{k}} \rangle + \langle {\mathcal {S}}(t_{n_{k}}), y - t_{n_{k}} \rangle + \langle {\mathcal {S}}(y_{n_{k}}), t_{n_{k}} - y_{n_{k}} \rangle . \end{aligned}$$

(29)

Since $\lim _{k \rightarrow \infty } \Vert t_{n_{k}} - y_{n_{k}} \Vert = 0$ and ${\mathcal {S}}$ is L-Lipschitz continuous on ${\mathcal {X}}$ implies that

$$\begin{aligned} \lim _{k \rightarrow \infty } \Vert {\mathcal {S}}(t_{n_{k}}) - {\mathcal {S}}(y_{n_{k}}) \Vert = 0. \end{aligned}$$

(30)

which together with (29) and (30), we obtain

$$\begin{aligned} \liminf _{k \rightarrow \infty } \langle {\mathcal {S}}(y_{n_{k}}), y - y_{n_{k}} \rangle \ge 0,\quad \forall \, y \in {\mathcal {D}}. \end{aligned}$$

(31)

Let consider a sequence of positive numbers $\{\epsilon _{k}\}$ that is decreasing and converge to zero. For each k, we denote $m_{k}$ by the smallest positive integer such that

$$\begin{aligned} \langle {\mathcal {S}}(t_{n_{i}}), y - t_{n_{i}} \rangle + \epsilon _{k} \ge 0,\quad \forall \, i \ge m_{k}. \end{aligned}$$

(32)

Due to $\{\epsilon _{k}\}$ is decreasing and $\{m_{k}\}$ is increasing.

Case I: If there is a $t_{n_{m_{k_{j}}}}$ subsequence of $t_{n_{m_{k}}}$ such that ${\mathcal {S}}(t_{n_{m_{k_{j}}}}) = 0$ ($\forall j$). Let $j \rightarrow \infty ,$ we obtain

$$\begin{aligned} \langle {\mathcal {S}}({\hat{u}}), y - {\hat{u}} \rangle = \lim _{j \rightarrow \infty } \langle {\mathcal {S}}(t_{n_{m_{k_{j}}}}), y - {\hat{u}} \rangle = 0. \end{aligned}$$

(33)

Hence ${\hat{u}} \in {\mathcal {D}}$, therefore we obtain ${\hat{u}} \in \Pi$.

Case II: If there exits $N_{0} \in {\mathbb {N}}$ such that for all $n_{m_{k}} \ge N_{0}$, ${\mathcal {S}}(t_{n_{m_{k}}}) \ne 0.$ Consider that

$$\begin{aligned} \Xi _{n_{m_{k}}} = \frac{{\mathcal {S}}(t_{n_{m_{k}}})}{\Vert {\mathcal {S}}(t_{n_{m_{k}}})\Vert ^{2}}, \quad \forall \, n_{m_{k}} \ge N_{0}. \end{aligned}$$

(34)

Due to the above definition, we obtain

$$\begin{aligned} \langle {\mathcal {S}}(t_{n_{m_{k}}}), \Xi _{n_{m_{k}}} \rangle = 1, \quad \forall \, n_{m_{k}} \ge N_{0}. \end{aligned}$$

(35)

Moreover, expressions (32) and (35), for all $n_{m_{k}} \ge N_{0},$ we have

$$\begin{aligned} \langle {\mathcal {S}}(t_{n_{m_{k}}}),\, y + \epsilon _{k} \Xi _{n_{m_{k}}} - t_{n_{m_{k}}} \rangle \ge 0. \end{aligned}$$

(36)

Due to the pseudomonotonicity of ${\mathcal {S}}$ for $n_{m_{k}} \ge N_{0},$

$$\begin{aligned} \langle {\mathcal {S}}(y + \epsilon _{k} \Xi _{n_{m_{k}}}),\, y + \epsilon _{k} \Xi _{n_{m_{k}}} - t_{n_{m_{k}}} \rangle \ge 0. \end{aligned}$$

(37)

For all $n_{m_{k}} \ge N_{0},$ we have

$$\begin{aligned} \langle {\mathcal {S}}(y), y - t_{n_{m_{k}}} \rangle \ge \langle {\mathcal {S}}(y) - {\mathcal {S}}(y + \epsilon _{k} \Xi _{n_{m_{k}}}),\, y + \epsilon _{k} \Xi _{n_{m_{k}}} - t_{n_{m_{k}}} \rangle - \epsilon _{k} \langle {\mathcal {S}}(y), \Xi _{n_{m_{k}}} \rangle . \end{aligned}$$

(38)

Due to $\{t_{n_{k}}\}$ weakly converges to ${\hat{u}} \in {\mathcal {D}}$ through ${\mathcal {S}}$ is sequentially weakly continuous on the set ${\mathcal {D}}$, we get $\{{\mathcal {S}}(t_{n_{k}})\}$ weakly converges to ${\mathcal {S}}({\hat{u}}).$ Suppose that ${\mathcal {S}}({\hat{u}}) \ne 0$, we have

$$\begin{aligned} \Vert {\mathcal {S}}({\hat{u}}) \Vert \le \liminf _{k \rightarrow \infty } \Vert {\mathcal {S}}(t_{n_{k}}) \Vert . \end{aligned}$$

(39)

Since $\{t_{n_{m_{k}}}\} \subset \{t_{n_{k}}\}$ and $\lim _{k \rightarrow \infty } \epsilon _{k} = 0,$ we have

$$\begin{aligned} 0 \le \lim _{k \rightarrow \infty } \Vert \epsilon _{k} \Xi _{n_{m_{k}}} \Vert = \lim _{k \rightarrow \infty } \frac{\epsilon _{k}}{\Vert {\mathcal {S}}(t_{n_{m_{k}}}) \Vert } \le \frac{0}{\Vert {\mathcal {S}}({\hat{u}})\Vert } = 0. \end{aligned}$$

(40)

Next, consider $k \rightarrow \infty$ in (38), we obtain

$$\begin{aligned} \langle {\mathcal {S}}(y), y - {\hat{u}} \rangle \ge 0,\quad \forall \, y \in {\mathcal {D}}. \end{aligned}$$

(41)

By the use of Minty Lemma 2.5, we infer ${\hat{u}} \in \Pi .$ Next, we have

$$\begin{aligned} \limsup _{n \rightarrow +\infty } \langle u^{*}, u^{*} - u_{n} \rangle = \lim _{k \rightarrow +\infty } \langle u^{*}, u^{*} - u_{n_k} \rangle = \langle u^{*}, u^{*} - {\hat{u}} \rangle \le 0. \end{aligned}$$

(42)

By the use of $\lim _{n \rightarrow +\infty } \big \Vert u_{n+1} - u_{n} \big \Vert = 0$. Therefore, (42) implies that

$$\begin{aligned}&\limsup _{n \rightarrow +\infty } \langle u^{*}, u^{*} - u_{n+1} \rangle \nonumber \\&\quad \le \limsup _{n \rightarrow +\infty } \langle u^{*}, u^{*} - u_{n} \rangle + \limsup _{n \rightarrow +\infty } \langle u^{*}, u_{n} - u_{n+1} \rangle \le 0. \end{aligned}$$

(43)

Consider the expression (12), we have

$$\begin{aligned}&\big \Vert t_{n} - u^{*} \big \Vert ^{2} \nonumber \\&\quad = \big \Vert u_{n} + \alpha _{n} (u_{n} - u_{n-1}) - \psi _{n} u_{n} - \alpha _{n} \psi _{n} (u_{n} - u_{n-1}) - u^{*} \big \Vert ^{2} \nonumber \\&\quad = \big \Vert (1 - \psi _{n}) (u_{n} - u^{*}) + (1 - \psi _{n}) \alpha _{n} (u_{n} - u_{n-1}) - \psi _{n} u^{*} \big \Vert ^{2} \nonumber \\&\quad \le \big \Vert (1 - \psi _{n}) (u_{n} - u^{*}) + (1 - \psi _{n}) \alpha _{n} (u_{n} - u_{n-1}) \big \Vert ^{2} + 2 \psi _{n} \langle - u^{*}, t_{n} - u^{*} \rangle \nonumber \\&\quad = (1 - \psi _{n})^{2} \big \Vert u_{n} - u^{*} \big \Vert ^{2} + (1 - \psi _{n})^{2} \alpha _{n}^{2} \big \Vert u_{n} - u_{n-1} \big \Vert ^{2} \nonumber \\&\qquad + 2 \alpha _{n} (1 - \psi _{n})^{2} \big \Vert u_{n} - u^{*} \big \Vert \big \Vert u_{n} - u_{n-1} \big \Vert + 2 \psi _{n} \langle - u^{*}, t_{n} - u_{n+1} \rangle + 2 \psi _{n} \langle - u^{*}, u_{n+1} - u^{*} \rangle \nonumber \\&\quad \le (1 - \psi _{n}) \big \Vert u_{n} - u^{*} \big \Vert ^{2} + \alpha _{n}^{2} \big \Vert u_{n} - u_{n-1} \big \Vert ^{2} + 2 \alpha _{n} (1 - \psi _{n}) \big \Vert u_{n} - u^{*} \big \Vert \big \Vert u_{n} - u_{n-1} \big \Vert \nonumber \\&\qquad + 2 \psi _{n} \big \Vert u^{*} \big \Vert \big \Vert t_{n} - u_{n+1} \big \Vert + 2 \psi _{n} \langle - u^{*}, u_{n+1} - u^{*} \rangle \nonumber \\&\quad = (1 - \psi _{n}) \big \Vert u_{n} - u^{*} \big \Vert ^{2} + \psi _{n} \Big [ \alpha _{n} \big \Vert u_{n} - u_{n-1} \big \Vert \frac{\alpha _{n}}{\psi _{n}} \big \Vert u_{n} - u_{n-1} \big \Vert \nonumber \\&\qquad + 2 (1 - \psi _{n}) \big \Vert u_{n} - u^{*} \big \Vert \frac{\alpha _{n}}{\psi _{n}} \big \Vert u_{n} - u_{n-1} \big \Vert + 2 \big \Vert u^{*} \big \Vert \big \Vert t_{n} - u_{n+1} \big \Vert + 2 \langle u^{*}, u^{*} - u_{n+1} \rangle \Big ]. \end{aligned}$$

(44)

From expressions (14) and (44), we obtain

$$\begin{aligned}&\big \Vert u_{n+1} - u^{*} \big \Vert ^{2} \nonumber \\&\quad \le (1 - \psi _{n}) \big \Vert u_{n} - u^{*} \big \Vert ^{2} + \psi _{n} \Big [ \alpha _{n} \big \Vert u_{n} - u_{n-1} \big \Vert \frac{\alpha _{n}}{\psi _{n}} \big \Vert u_{n} - u_{n-1} \big \Vert \nonumber \\&\qquad + 2 (1 - \psi _{n}) \big \Vert u_{n} - u^{*} \big \Vert \frac{\alpha _{n}}{\psi _{n}} \big \Vert u_{n} - u_{n-1} \big \Vert + 2 \big \Vert u^{*} \big \Vert \big \Vert t_{n} - u_{n+1} \big \Vert + 2 \langle u^{*}, u^{*} - u_{n+1} \rangle \Big ]. \end{aligned}$$

(45)

By the use of (22), (43), (45) and applying Lemma 2.2, conclude that $\lim _{n \rightarrow +\infty } \big \Vert u_{n} - u^{*} \big \Vert = 0$.

Case 2: Suppose there is one $\{n_{i}\}$ subsequence of $\{n\}$ such that

$$\begin{aligned} \Vert u_{n_i} - u^{*} \Vert \le \Vert u_{n_{i+1}} - u^{*} \Vert ,\quad \forall \, i \in {\mathbb {N}}. \end{aligned}$$

Using Lemma 2.3, there exists a sequence $\{m_{k}\} \subset {\mathbb {N}}$ as $\{m_{k}\} \rightarrow +\infty$ such that

$$\begin{aligned} \Vert u_{m_{k}} - u^{*} \Vert \le \Vert u_{m_{k+1}} - u^{*} \Vert \quad \text {and} \quad \Vert u_{k} - u^{*} \Vert \le \Vert u_{m_{k+1}} - u^{*} \Vert , \quad \text {for all}\ k \in {\mathbb {N}}. \end{aligned}$$

(46)

As in Case 1, the relation (20) gives that

$$\begin{aligned}&(1 - \tau L) \Vert t_{m_{k}} - y_{m_{k}}\Vert ^{2} + (1 - \tau L) \Vert u_{m_{k}+1} - y_{m_{k}}\Vert ^{2} \nonumber \\&\quad \le \Vert u_{m_{k}} - u^{*}\Vert ^{2} + \psi _{m_{k}} M_{2} - \Vert u_{m_{k}+1} - u^{*} \Vert ^{2}. \end{aligned}$$

(47)

Due to $\psi _{m_{k}} \rightarrow 0$, we deduce the following:

$$\begin{aligned} \lim _{k \rightarrow +\infty } \Vert t_{m_{k}} - y_{m_{k}}\Vert = \lim _{k \rightarrow +\infty } \Vert u_{m_{k}+1} - y_{m_{k}}\Vert = 0. \end{aligned}$$

(48)

It follows that

$$\begin{aligned} \lim _{k \rightarrow +\infty } \Vert u_{m_{k+1}} - t_{m_{k}}\Vert \le \lim _{k \rightarrow +\infty } \Vert u_{m_{k+1}} - y_{m_{k}}\Vert + \lim _{k \rightarrow +\infty } \Vert y_{m_{k}} - t_{m_{k}}\Vert = 0. \end{aligned}$$

(49)

Next, evaluate

$$\begin{aligned} \Vert t_{m_{k}} - u_{m_{k}}\Vert&= \Vert u_{m_{k}} + \alpha _{m_{k}} (u_{m_{k}} - u_{m_{k}-1}) - \psi _{m_{k}} \big [ u_{m_{k}} + \alpha _{m_{k}} (u_{m_{k}} - u_{m_{k}-1}) \big ] - u_{m_{k}} \Vert \nonumber \\&\le \alpha _{m_{k}} \Vert u_{m_{k}} - u_{m_{k}-1} \Vert + \psi _{m_{k}} \Vert u_{m_{k}}\Vert + \alpha _{m_{k}} \psi _{m_{k}} \Vert u_{m_{k}} - u_{m_{k}-1} \Vert \nonumber \\&= \psi _{m_{k}} \frac{\alpha _{m_{k}}}{\psi _{m_{k}}} \Vert u_{m_{k}} - u_{m_{k}-1} \Vert + \psi _{m_{k}} \Vert u_{m_{k}}\Vert + \psi _{m_{k}}^{2} \frac{\alpha _{m_{k}}}{\psi _{m_{k}}} \Vert u_{m_{k}} - u_{m_{k}-1} \Vert \longrightarrow 0. \end{aligned}$$

(50)

This follows that

$$\begin{aligned} \lim _{k \rightarrow +\infty } \Vert u_{m_{k}} - u_{m_{k}+1}\Vert \le \lim _{k \rightarrow +\infty } \Vert u_{m_{k}} - t_{m_{k}}\Vert + \lim _{k \rightarrow +\infty } \Vert t_{m_{k}} - u_{m_{k}+1}\Vert = 0. \end{aligned}$$

(51)

Using the same explanation as in the Case 1, such that

$$\begin{aligned} \limsup _{k \rightarrow +\infty } \langle u^{*}, u^{*} - u_{m_{k}+1} \rangle \le 0. \end{aligned}$$

(52)

Using the expressions (45) and (46), we get

$$\begin{aligned}&\big \Vert u_{m_{k}+1} - u^{*} \big \Vert ^{2} \nonumber \\&\quad \le (1 - \psi _{m_{k}}) \big \Vert u_{m_{k}} - u^{*} \big \Vert ^{2} + \psi _{m_{k}} \Big [ \alpha _{m_{k}} \big \Vert u_{m_{k}} - u_{m_{k}-1} \big \Vert \frac{\alpha _{m_{k}}}{\psi _{m_{k}}} \big \Vert u_{m_{k}} - u_{m_{k}-1} \big \Vert \nonumber \\&\qquad + 2 (1 - \psi _{m_{k}}) \big \Vert u_{m_{k}} - u^{*} \big \Vert \frac{\alpha _{m_{k}}}{\psi _{m_{k}}} \big \Vert u_{m_{k}} - u_{m_{k}-1} \big \Vert + 2 \big \Vert u^{*} \big \Vert \big \Vert t_{m_{k}} - u_{m_{k}+1} \big \Vert + 2 \langle u^{*}, u^{*} - u_{m_{k}+1} \rangle \Big ] \nonumber \\&\quad \le (1 - \psi _{m_{k}}) \big \Vert u_{m_{k+1}} - u^{*} \big \Vert ^{2} + \psi _{m_{k}} \Big [ \alpha _{m_{k}} \big \Vert u_{m_{k}} - u_{m_{k}-1} \big \Vert \frac{\alpha _{m_{k}}}{\psi _{m_{k}}} \big \Vert u_{m_{k}} - u_{m_{k}-1} \big \Vert \nonumber \\&\qquad + 2 (1 - \psi _{m_{k}}) \big \Vert u_{m_{k}} - u^{*} \big \Vert \frac{\alpha _{m_{k}}}{\psi _{m_{k}}} \big \Vert u_{m_{k}} - u_{m_{k}-1} \big \Vert + 2 \big \Vert u^{*} \big \Vert \big \Vert t_{m_{k}} - u_{m_{k}+1} \big \Vert + 2 \langle u^{*}, u^{*} - u_{m_{k}+1} \rangle \Big ]. \end{aligned}$$

(53)

Thus, above implies that

$$\begin{aligned}&\big \Vert u_{m_{k}+1} - u^{*} \big \Vert ^{2} \nonumber \\&\quad \le \Big [ \alpha _{m_{k}} \big \Vert u_{m_{k}} - u_{m_{k}-1} \big \Vert \frac{\alpha _{m_{k}}}{\psi _{m_{k}}} \big \Vert u_{m_{k}} - u_{m_{k}-1} \big \Vert \nonumber \\&\qquad + 2 (1 - \psi _{m_{k}}) \big \Vert u_{m_{k}} - u^{*} \big \Vert \frac{\alpha _{m_{k}}}{\psi _{m_{k}}} \big \Vert u_{m_{k}} - u_{m_{k}-1} \big \Vert + 2 \big \Vert u^{*} \big \Vert \big \Vert t_{m_{k}} - u_{m_{k}+1} \big \Vert + 2 \langle u^{*}, u^{*} - u_{m_{k}+1} \rangle \Big ]. \end{aligned}$$

(54)

Since $\psi _{m_{k}} \rightarrow 0,$ and $\big \Vert u_{m_{k}} - u^{*} \big \Vert$ is a bounded. Therefore, expressions (52) and (54) implies that

$$\begin{aligned} \Vert u_{m_{k}+1} - u^{*}\Vert ^{2} \rightarrow 0, \quad \text {as}\ k \rightarrow +\infty . \end{aligned}$$

(55)

This means that

$$\begin{aligned} \lim _{n \rightarrow +\infty } \Vert u_{k} - u^{*} \Vert ^{2} \le \lim _{n \rightarrow +\infty } \Vert u_{m_{k}+1} - u^{*}\Vert ^{2} \le 0. \end{aligned}$$

(56)

As a consequence $u_{n} \rightarrow u^{*}.$ This is going to conclude the proof of the theorem. $\square$

The second projection in Algorithm 1 is substituted with half-space to minimize computing cost, as inspired by Algorithm 4.1 in the paper [4]. The second main algorithm is written as follows:

Fig. 1

Numerical illustration of Algorithm 1 with Algorithm 1 in [16] and Algorithm 3.1 in [1] and Algorithm 3.1 in [27] while $m=5$

Fig. 2

Numerical illustration of Algorithm 1 with Algorithm 1 in [16] and Algorithm 3.1 in [1] and Algorithm 3.1 in [27] while $m=10$

Fig. 3

Numerical illustration of Algorithm 1 with Algorithm 1 in [16] and Algorithm 3.1 in [1] and Algorithm 3.1 in [27] while $m=20$

Fig. 4

Numerical illustration of Algorithm 1 with Algorithm 1 in [16] and Algorithm 3.1 in [1] and Algorithm 3.1 in [27] while $m=30$

4 Numerical illustrations

This section discusses two numerical tests to explain the efficacy of the proposed algorithms. All these numerical studies give a detailed understanding of how better control parameters can be chosen. Each of them shows the advantages of the proposed methods relative to the existing ones in the literature.

Example 4.1

First consider the HpHard problem which is taken from [7]. This example has been considered by many people for experimental test (see, [5, 8, 21]). A operator ${\mathcal {S}} : {\mathbb {R}}^{m} \rightarrow {\mathbb {R}}^{m}$ is defined by

$$ {\mathcal {S}}(u) = Mu + q $$

with $q \in {\mathbb {R}}^{m}$ and

$$\begin{aligned} M = N N^{T} + B + D. \end{aligned}$$

In above definition, we take $N = \hbox {rand}(m)$ to be a random matrix and $B = 0.5 K - 0.5 K^{\mathrm{T}}$ to be a skew-symmetric matrix with $K = \hbox {rand}(m)$ and $D = \hbox {diag}(\hbox {rand}(m,1))$ is a diagonal matrix. The set ${\mathcal {D}}$ is taken as follows:

$$\begin{aligned} {\mathcal {D}} = \{ u \in {\mathbb {R}}^{m} : Q u \le b \}, \end{aligned}$$

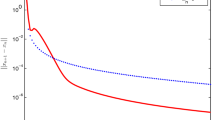
where $Q = \hbox {rand}(100,m)$ and $b = \hbox {rand}(100,1)$. It is obvious that ${\mathcal {S}}$ is monotone and that Lipschitz is continuous by $L = \Vert M\Vert .$ The starting point for this experiment are $u_{0} = u_{1}= (1, 1, \ldots , 1).$ The numerical consequences of these methods are seen in Figs. 1, 2, 3 and 4 and Tables 1 and 8. The control requirement shall be taken as follows:

(1) Algorithm 1 in [16] (shortly, Algorithm A): $\tau = \frac{0.7}{L}, D_{n} = \Vert u_{n} - y_{n}\Vert \le 10^{-4};$

(2) Algorithm 3.1 in [1] (shortly, Algorithm B): $\alpha = 0.60, \tau = \frac{0.7}{L}, \epsilon _{n} = \frac{1}{(n + 1)^{2}}, \psi _{n} = \frac{1}{(n+2)}, \theta _{n} = \frac{5}{10}(1 - \psi _{n}), D_{n} = \Vert t_{n} - y_{n}\Vert \le 10^{-4};$

(3) Algorithm 3.1 in [27] (shortly, Algorithm C): $\alpha = 0.60, \tau = \frac{0.7}{L}, \psi _{n} = \frac{1}{(n+2)}, \epsilon _{n} = \frac{1}{(n + 1)^{2}}, f(u) = \frac{u}{3}, D_{n} = \Vert t_{n} - y_{n}\Vert \le 10^{-4};$

(4) Algorithm 1 (shortly, Algorithm D): $\tau = \frac{0.7}{L}, \alpha = 0.60, \epsilon _{n} = \frac{1}{(n + 1)^{2}}, \psi _{n} = \frac{1}{(n + 2)}, D_{n} = \Vert t_{n} - y_{n}\Vert \le 10^{-4}$ (Table 2).

Example 4.2

Consider the non-linear complementarity problem of Kojima–Shindo where the operator ${\mathcal {S}} : {\mathbb {R}}^{4} \rightarrow {\mathbb {R}}^{4}$ is described by

$$\begin{aligned} {\mathcal {S}} (u) = \begin{pmatrix} u_1 + u_2 + u_3 + u_4 - 4 u_2 u_3 u_4 \\ u_1 + u_2 + u_3 + u_4 - 4 u_1 u_3 u_4 \\ u_1 + u_2 + u_3 + u_4 - 4 u_1 u_2 u_4 \\ u_1 + u_2 + u_3 + u_4 - 4 u_1 u_2 u_3 \\ \end{pmatrix}. \end{aligned}$$

Moreover, the feasible set ${\mathcal {D}}$ is defined by

$$\begin{aligned} {\mathcal {D}} = \{u \in {\mathbb {R}}^{4} : 1 \le u_{i} \le 5, \,\, i = 1,2,3,4\}. \end{aligned}$$

It is clear to see that ${\mathcal {S}}$ is not monotone on the set ${\mathcal {D}}.$ By the use of Monte-Carlo technique [9], it can be shown that ${\mathcal {S}}$ is pseudo-monotone on ${\mathcal {D}}.$ There exits a unique solution $u^*=(5,5,5,5)^{T}$ for given problem. The starting point for this experiment are $u_{0} = u_{1}= (1, 1, \ldots , 1)$ and $D_{n} = \Vert t_{n} - y_{n}\Vert \le 10^{-3}.$ The numerical consequences of these methods are seen in Tables 3, 4, 5 and 6. The control requirement shall be taken as follows: (1) Algorithm 1 in [16] (shortly, Algorithm A): $\tau = \frac{0.7}{L}, D_{n} = \Vert u_{n} - y_{n}\Vert \le 10^{-4};$

(2) Algorithm 3.1 in [1] (shortly, Algorithm B): $\alpha = 0.60, \tau = \frac{0.7}{L}, \epsilon _{n} = \frac{1}{(n + 1)^{2}}, \psi _{n} = \frac{1}{(n+2)}, \theta _{n} = \frac{5}{10}(1 - \psi _{n}), D_{n} = \Vert t_{n} - y_{n}\Vert \le 10^{-4};$

(3) Algorithm 3.1 in [27] (shortly, Algorithm C): $\alpha = 0.60, \tau = \frac{0.7}{L}, \psi _{n} = \frac{1}{(n+2)}, \epsilon _{n} = \frac{1}{(n + 1)^{2}}, f(u) = \frac{u}{3}, D_{n} = \Vert t_{n} - y_{n}\Vert \le 10^{-4};$

(4) Algorithm 1 (shortly, Algorithm D): $\tau = \frac{0.7}{L}, \alpha = 0.60, \epsilon _{n} = \frac{1}{(n + 1)^{2}}, \psi _{n} = \frac{1}{(n + 2)}, D_{n} = \Vert t_{n} - y_{n}\Vert \le 10^{-4}.$

Table 1 Numerical values for Figs. 1, 2, 3 and 4

Table 2 Numerical values for Figs. 1, 2, 3 and 4

Table 3 Example 4.2: Numerical study of Algorithm 1 in [16] and $u_{0}= u_{1} =(1,2,5,4)^{\mathrm{T}}$

Table 4 Example 4.2: Numerical study of Algorithm 1 in [16] and $u_{0}= u_{1} =(-3,-4,1,-5)^{\mathrm{T}}$

Table 5 Example 4.2: Numerical study of Algorithm 1 and $u_{0}= u_{1} =(1,2,5,4)^{\mathrm{T}}$

Table 6 Example 4.2: Numerical study of Algorithm 1 and $u_{0}= u_{1} =(-3,-4,1,-5)^{\mathrm{T}}$

Example 4.3

Let ${\mathcal {X}} = l_{2}$ be a real Hilbert space with the sequences of real numbers satisfying the following condition

$$\begin{aligned} \Vert u_{1}\Vert ^{2} + \Vert u_{2}\Vert ^{2} + \cdots + \Vert u_{n}\Vert ^{2} + \cdots < + \infty . \end{aligned}$$

(57)

Assume that a mapping ${\mathcal {S}}: {\mathcal {D}} \rightarrow {\mathcal {D}}$ is defined by

$$\begin{aligned} G(u) = (5 - \Vert u\Vert ) u,\quad \forall \, u \in {\mathcal {X}}, \end{aligned}$$

where ${\mathcal {D}} = \{ u \in {\mathcal {X}} : \Vert u\Vert \le 3 \}.$ We can easily see that ${\mathcal {S}}$ is weakly sequentially continuous on ${\mathcal {X}}$ and the solution set is $VI({\mathcal {D}}, {\mathcal {S}}) = \{0\}.$ Moreover, ${\mathcal {S}}$ is L-Lipschitz continuous with $L=11.$ The mapping ${\mathcal {S}}$ is pseudomonotone on ${\mathcal {D}}$ but not monotone (see for more details [33]). Let considered the following projection formula:

$$\begin{aligned} P_{{\mathcal {D}}} (u) = \left\{ \begin{array}{ll} u &{}\quad \text {if}\ \Vert u\Vert \le 3, \\ \frac{3 u}{\Vert u\Vert }, &{}\quad \text {otherwise}. \\ \end{array} \right. \end{aligned}$$

The numerical consequences of these methods are seen in Figs. 5, 6, 7 and 8 and Table 7. The control requirement shall be taken as follows:

Fig. 5

Numerical illustration of Algorithm 1 with Algorithm 1 in [16] and Algorithm 3.1 in [1] and Algorithm 3.1 in [27] while $u_{0}=u_{1}=(1,1,\ldots , 1_{5000}, 0, 0, \ldots )$

Fig. 6

Numerical illustration of Algorithm 1 with Algorithm 1 in [16] and Algorithm 3.1 in [1] and Algorithm 3.1 in [27] while $u_{0}=u_{1}=(1,1,\ldots , 1_{5000}, 0, 0, \ldots )$

Fig. 7

Numerical illustration of Algorithm 1 with Algorithm 1 in [16] and Algorithm 3.1 in [1] and Algorithm 3.1 in [27] while $u_{0}=u_{1}=(1,2,\ldots , 5000, 0, 0, \ldots )$

Fig. 8

Numerical illustration of Algorithm 1 with Algorithm 1 in [16] and Algorithm 3.1 in [1] and Algorithm 3.1 in [27] while $u_{0}=u_{1}=(1,2,\ldots , 5000, 0, 0, \ldots )$

(1) Algorithm 1 in [16] (shortly, Algorithm A): $\tau = \frac{0.8}{L}, D_{n} = \Vert u_{n} - y_{n}\Vert \le 10^{-4};$

(2) Algorithm 3.1 in [1] (shortly, Algorithm B): $\alpha = 0.70, \tau = \frac{0.8}{L}, \epsilon _{n} = \frac{1}{(n + 1)^{2}}, \psi _{n} = \frac{1}{(n+2)}, \theta _{n} = \frac{5}{10}(1 - \psi _{n}), D_{n} = \Vert t_{n} - y_{n}\Vert \le 10^{-4};$

(3) Algorithm 3.1 in [27] (shortly, Algorithm C): $\alpha = 0.70, \tau = \frac{0.8}{L}, \psi _{n} = \frac{1}{(n+2)}, \epsilon _{n} = \frac{1}{(n + 1)^{2}}, f(u) = \frac{u}{3}, D_{n} = \Vert t_{n} - y_{n}\Vert \le 10^{-4};$

(4) Algorithm 1 (shortly, Algorithm D): $\tau = \frac{0.8}{L}, \alpha = 0.70, \epsilon _{n} = \frac{1}{(n + 1)^{2}}, \psi _{n} = \frac{1}{(n + 2)}, D_{n} = \Vert t_{n} - y_{n}\Vert \le 10^{-4}$ (Table 8).

Table 7 Numerical values for Figs. 5, 6, 7 and 8

Table 8 Numerical values for Figs. 5, 6, 7 and 8