An eco-epidemic model with seasonal variability: a non-autonomous model

Abstract

Seasonal variability strongly affects the animal population in wildlife. It becomes essential to model seasonality in eco-epidemic dynamics to know the effect of system parameters in a periodic environment. This article presents a set of non-autonomous differential equations with time-varying disease transmission rates among prey and predators, the mortality rate of a diseased predator, the predation rate of healthy prey, and an additional food supply. The positiveness, boundedness, and presence of solution are derived. We have proved that the infection-free state is stable if periodic basic reproduction number $R_C(t)<1$. The stability of the coexistence state is shown at $R_C(t)>1$ using the Poincare map and comparison theory. The significance of the parameters related to disease transmission and prevalence is described using sensitivity analysis. Numerical simulation verified our analytical findings and proved that the predator control strategies in the periodic environment via controlling predation rate, disease transmission rate among predators, and death rate of diseased prey lead the system towards an infection-free environment.

1 Introduction

The population dynamic of different species is strongly affected by the seasonal variations [19]. The reproduction rate of the pathogen, the birth of species, emigration of birds, sunlight density, and dynamics of some diseases are the factors highly influenced by seasonal temperature deviation [17, 18]. Anthrax, avian influenza, ebola, Escherichia coli are some zoonotic diseases with seasonality reported in wildlife and livestock [25]. The above facts reveal that periodic fluctuations significantly affect the system’s dynamics. So, it becomes essential to examine the effect of seasonality on the behavior of population communities and model these diseases as periodically forced non-linear systems.

Eco-epidemic dynamics have been broadly introduced in population biology and achieved significant progress. Periodicity can be introduced to eco-epidemic systems via ordinary differential equations with time-varying parameters. The autonomous system with time-varying parameters becomes non-autonomous, showing a more complicated and natural phenomenon than the autonomous system [7, 16]. More precisely, the permanent behavior of an eco-epidemic model can be studied through a non-autonomous model. Thus, the non-autonomous eco-epidemiological system is required to be studied [17, 19]. In the last few years, many scientists have made broad studies on the effect of seasonality on the different dynamics [17,18,19]. They have analyzed various seasonality sources like varying transmission rate, fluctuation in birthrates, vaccination rate, predation rate, death rate and, supply of additional food [17, 19, 26].

Disease control is a vital tool for the population balance of both prey and predator. Chemical control and biological control are two strategies that have been practiced for many years. Chemical control like pesticides (fungicides, bactericides, soil fumigants) are relatively fast-acting and reduce the damage done to crops. Nevertheless, these chemicals are not beneficial for the environment in the long term. They are toxic to target organisms and other organisms; the chemicals can pass through the food chain to the top predators or humans and harm them. Infected individual infects the surrounding; further, they get absorbed and remain as residue in the biomass of coexisting healthy species in the ecosystem [28]. Therefore, various researchers pay keen attention to later approaches for controlling infectious diseases.

The control strategies of infection rate, predation rate, and death rate (Culling or Hunting rate) play an essential part in the pray–predator dynamics. Some mathematicians discussed that the dynamics could be infection-free via appropriate management of predation rate and infection rate [17, 21, 22, 36]. The disease can also be controlled via culling or hunting strategies in diseased prey or predator compartment [20].

The disease progression in ecosystems is a relevant area of research for its massive impact on the population. Research has shown that infected prey harvesting affects infection prevalence. Therefore, it is beneficial to consider disease progression while formulating a model for real-world ecosystems [1, 13, 24, 29, 34]. Some of the authors also developed model with both prey–predator are suffering from an infection [3, 6, 9, 14, 22]. It is discussed in [4, 30] that healthy prey is more active than the infected one. Some articles [2, 11] discussed models with the infection in the predator, where the diseased predator is incapable of predating on healthy prey [2]. Some researchers discussed the horizontal transmission of disease among predators [6, 31]. The supply of additional food (non-prey food resources) to a predator is one of the biological control methods used in horticultural areas to intensify biological control levels. Some authors also consider this in their articles [10, 27, 28].

Based on these pieces of information, we are inclined to examine the outcome of predator regulation methods on diseased predator–prey dynamics with periodically varying additional food to predator, disease transmission rate, predation rate, and death rate. We have formulated a four-compartment non-autonomous model with infection in prey and predator to show the effect of these time-varying parameters.

The following Sect. 2 contains a set of four non-autonomous differential equations taking time-varying disease transmission rates, predation rate, and death rate representing diseased prey–predator dynamics. In Sect. 3, we study that all solutions are positive, and these solutions start and always remain in a bounded region $\Omega$ for any initial conditions. Section 4 describes the classification and existence of steady states. We have done basic reproduction number and stability analysis in Sect. 5. Section 6 performs the sensitivity analysis to determine the impact of system parameters on reproduction number. Section 7 presents a numerical simulation to support our analytical findings. We have discussed and concluded the quantitative results in Sect. 8. This section also contains the biological interpretation of our results.

2 The systematic development of the model

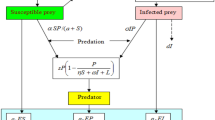
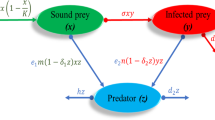
The proposed system has two types of species; the prey and predator. We assumed an infectious disease in prey, and the disease of prey spreads in predators through predation. When there is no infection, prey and predator are denoted by X(t) and W(t), respectively. The present dynamics is developed based on the following assumptions:

• 1 When infection and predator are absent, the growth of prey follows the logistic differential equation $\frac{\mathrm{{d}}X}{\mathrm{{d}}t}=rX(1-\frac{X}{K})$, where r and K are given in Table 1.

• 2 The presence of infection decomposes the prey population X(t) into two categories: susceptible prey S(t) and infective prey I(t). We have considered that the disease is incurable, i.e., once a prey gets an infection, it will either die with disease-induced death rate $\delta _1$ or be removed before having the possibility of reproducing. For this reason, we have not considered birth terms in infective class [24]. Thus, the logistic equation takes the form; $\frac{\mathrm{{d}}S}{\mathrm{{d}}t}=rS(1-\frac{S}{K})$.

• 3 In the absence of a predator, the infection spreads among healthy prey with a bilinear incidence rate $\gamma S I$, i.e., where $\gamma$ is disease contact rate.

• 4 The infectious disease is transmitted in predators via predation of infected prey; the predator population W(t) can also be partitioned into two categories: Healthy predator P(t) and infected predator Y(t). The disease is also communicable among predators through direct transmission with Holling type-II functional response with the disease transmission rate $\sigma$. Here, we considered the disease transmission process identical to predation. We assumed that when a healthy predator comes in contact with an infected one, it could not be easily infected (encountered) due to its self-immunity. The time required to infect a healthy individual is considered handling time. For this reason, we used Holling type-II functional response as its used when a predator needs handling time to encounter the prey.

• 5 The healthy predator predates on both healthy and diseased prey with predation rates $\alpha$ and $\beta$ respectively. Here, the predation rate for infected prey is different from that of healthy prey because infected prey has restricted movement due to infection and can easily be encountered. Again, the conversion rates of healthy and infected prey to a healthy predator are $\epsilon _1$ and $\epsilon _2$. The healthy predator dies with a natural death rate $\delta _2$. We assumed that infected predator predates only on infected prey [2, 8] with predation rate $\rho$ because the infected predator is weakened due to infection and cannot harvest the healthy prey. The conversion coefficient of the infected prey to the infected predator is $\epsilon _3$. All these interactions are with Holling type-I functional response. We further assumed that an infected predator never recovers and dies out with a disease death rate $\delta _3$.

• 6 The healthy predator also grows due to alternative food resources with a rate of b.

We have formulated the following non-autonomous model based upon the above assumption:

$$\begin{aligned} \left. \begin{array}{l} \displaystyle \frac{\mathrm {{d}}S}{\mathrm {{d}}t} = r \left( 1-\frac{S}{K}\right) S-\alpha (t) P S-\gamma (t) S I,\\ \displaystyle \frac{\mathrm {{d}}I}{\mathrm {{d}}t} = \gamma (t) S I-\beta I P- \rho I Y- \delta _1 I,\\ \displaystyle \frac{\mathrm {{d}}P}{\mathrm {{d}}t} =b(t) P +\epsilon _1 \alpha (t) P S + \epsilon _2 \beta I P- \frac{\sigma (t) P Y}{a+P}-\delta _2(t) P,\\ \displaystyle \frac{\mathrm {{d}}Y}{\mathrm {{d}}t} = \epsilon _3 \rho I Y+ \frac{\sigma (t) P Y}{a+P}- \delta _3(t) Y.\\ \end{array} \right\} \end{aligned}$$

(1)

The initial condition of model are $S(0)=S_0 >0$, $I(0)=I_0 >0$, $P(0)=P_0>0$, $Y(0)=Y_0>0$. All the parameters of the system are positive. The description of parameters and their range of values are shown in Table 1. We studied the parameter values of [4, 23, 24, 29, 30, 33] and set parameter values of the model in such a way that all the value lies between the observed range except the value where we did not get the model solutions.

Table 1 Model parameter values, their biological interpretation and range.

In the present model, disease transmission parameters $\gamma (t)$ and $\sigma (t)$, predation rate of healthy prey $\alpha (t)$, mortality rate of healthy and diseased predator $\delta _2(t)$ and $\delta _3(t)$ and rate of supplying additional food b(t) are considered as time-dependent parameters varying with one year period. We can write these parameters for all $t\ge 0$ in the following way:

$$\begin{aligned}&\gamma \left( t\right) =\gamma _0\left[ 1+\omega _1\sin \left( \frac{2\pi t}{365}\right) \right] ,\ \sigma \left( t\right) =\sigma _0\left[ 1+\omega _2\sin \left( \frac{2\pi t}{365}\right) \right] ,\\&\alpha \left( t\right) =\alpha _0\left[ 1+\omega _3\sin \left( \frac{2\pi t}{365}\right) \right] ,\delta _2\left( t\right) =\left( \delta _2\right) _0\left[ 1+\omega _4\sin \left( \frac{2\pi t}{365}\right) \right] , \\&b\left( t\right) =b_0\left[ 1+\omega _5\sin \left( \frac{2\pi t}{365}\right) \right] , \ \delta _3\left( t\right) =\left( \delta _3\right) _0\left[ 1+\omega _6\sin \left( \frac{2\pi t}{365}\right) \right] . \end{aligned}$$

Here, $\gamma _0$ and $\sigma _0$ are the average disease transmission rates between prey and predator respectively, $\alpha _0$ is average predation rate, $b_0$ is the average rate of food supply to the predator and, $(\delta _2)_0$ and $(\delta _3)_0$ are the average death rate of healthy and diseased predator respectively. Further, $\omega _1$, $\omega _2$, $\omega _3$, $\omega _4$, $\omega _5$ and $\omega _6$ are relative amplitude of seasonal variation. The above-described parameter simulates the periodic fluctuations in the suggested system.

The subsequent Sect. 3 examined whether the solutions of the system (1) are positive and time-bounded with the initial conditions. The above means that the population of interacting species is always positive and grows logistically for a long time interval as resources in a particular patch are limited.

3 Positivity and boundedness

We consider that the initial conditions of model (1) are, $S\left( \kappa \right) =\varphi _1\left( \kappa \right) >0$, $I\left( \kappa \right) =\varphi _2\left( \kappa \right) >0$, $P\left( \kappa \right) =\varphi _3\left( \kappa \right) >0$ and $Y\left( \kappa \right) =\varphi _4\left( \kappa \right) >0$, $\forall \kappa \in \left[ -\infty ,0\right]$ and $\varphi _i \in \mathcal {C}{\left( \left[ -\infty ,0\right] ,R^4\right) }$. Where, $\mathcal {C}{\left( \left[ -\infty ,0\right] ,R^4\right) }$ is the Banach space of continuous function of $\left[ -\infty ,0\right]$ towards $R^4$. Also, it is realistic to assume that $\varphi _i\left( 0\right) >0$, $\forall \ i=1,2,3,4$.

Theorem 3.1

If the initial conditions for model (1) are $S\left( \kappa \right) =\varphi _1\left( \kappa \right) >0$,

$I\left( \kappa \right) =\varphi _2\left( \kappa \right) >0$, $P\left( \kappa \right) =\varphi _3\left( \kappa \right) >0$ and $Y\left( \kappa \right) =\varphi _4\left( \kappa \right) >0$, $\forall \kappa \in \left[ -\infty ,0\right]$ with $\varphi _i\left( 0\right) >0$ $\left( i=1,2,3,4\right)$, then its solutions are positive, $\forall \ t>0$.

Proof

Consider T is a number defined as $T= \sup \{t>0: S\left( t\right)>0,I\left( t\right)>0,P\left( t\right)>0,Y\left( t\right) >0\}$. Clearly $T>0$. Now, either $t=T=\infty$ or $T<\infty$. In earlier case, all solutions are obviously positive. In later case, all solutions are also positive. To prove this, we take the contradiction that at least one of $S\left( T\right)$, $I\left( T\right)$, $P\left( T\right)$ and $Y\left( T\right)$ is zero. Let us suppose that $S\left( T\right) =0$.

Now, we write the equations one of the system (1) in the following form:

$$\begin{aligned}&\frac{\mathrm{{d}}S}{\mathrm{{d}}t}\ge -\frac{r S^2}{K}-\alpha (t) P S- \gamma (t) S I,\nonumber \end{aligned}$$

this leads to,

$$\begin{aligned}&S\left( T\right) \ge \frac{S_0\exp \left\{ -\int _{0}^{T}\left( \alpha \left( u\right) P\left( u\right) +\gamma \left( u\right) I\left( u\right) \right) \mathrm{{d}}u\right\} }{S_0\int _{0}^{T}\left\{ \frac{r}{K}\exp \left\{ -\int _{0}^{T}\left( \alpha \left( u\right) P\left( u\right) +\gamma \left( u\right) I\left( u\right) \right) \mathrm{{d}}u\right\} \mathrm{{d}}v\right\} +1}>0.\nonumber \end{aligned}$$

Thus $S\left( T\right)>0 \Rightarrow S\left( t\right) >0$ for any value of $t>0$. Which contradict our assumption that $S\left( T\right) =0$, hence $S\left( t\right) >0$, $\forall t>0$.

Now, consider $I\left( T\right) =0$, $P\left( T\right) =0$ and $Y\left( T\right) =0$ simultaneously.

Again, the rest of equations of system (1) can be written as:

$$\begin{aligned}&\frac{\mathrm{{d}}I}{\mathrm{{d}}t}\ge -\beta P I-\rho Y I-\delta _1I,\\&\frac{\mathrm{{d}}P}{\mathrm{{d}}t}\ge -\frac{\sigma \left( t\right) P Y}{a+P}-\delta _2(t) P,\\&\frac{\mathrm{{d}}Y}{\mathrm{{d}}t}\ge -\delta _3\left( t\right) Y. \end{aligned}$$

this leads to following solutions,

$$\begin{aligned} I\left( T\right)&\ge I_0\exp \left\{ -\int _{0}^{T}\left( \beta P\left( u\right) + \rho Y\left( u\right) +\delta _1\right) \mathrm{{d}}u\right\}>0,\\ P\left( T\right)&\ge P_0\exp \left\{ -\int _{0}^{T}\left( \frac{\sigma \left( u\right) Y\left( u\right) }{a+P\left( u\right) }+\delta _2\left( u\right) \right) \mathrm{{d}}u\right\}>0,\\ Y\left( T\right)&\ge Y_0\exp \{-\int _{0}^{T}\delta _3\left( u\right) \mathrm{{d}}u\}>0. \end{aligned}$$

The solutions $I\left( T\right) >0$, $P\left( T\right) >0$, $Y\left( T\right) >0$ contradict the assumption, $I\left( T\right) =0$, $P\left( T\right) =0$ and $Y\left( T\right) =0$. Thus $I\left( t\right) >0$, $P\left( t\right) >0$, $Y\left( t\right) >0$ for any value of $t>0$. Thus, $I\left( t\right) >0$, $P\left( t\right) >0$ and $Y\left( t\right) >0$, $\forall t>0$. This concludes that all the solutions of the system (1) are positive. $\square$

Theorem 3.2

The solutions of the system (1) are uniformly bounded for any initial value in $R_+^4$.

Proof

We represent the total population of the system (1) as $V\left( t\right) =S\left( t\right) +I\left( t\right) +P\left( t\right) +Y\left( t\right)$. The total derivative of this expression with respect to time t is,

$$\begin{aligned} \frac{\mathrm{{d}}V}{\mathrm{{d}}t}= \frac{\mathrm{{d}}S}{\mathrm{{d}}t} + \frac{\mathrm{{d}}I}{\mathrm{{d}}t} + \frac{\mathrm{{dP}}}{\mathrm{{d}}t} + \frac{\mathrm{{d}}Y}{\mathrm{{dt}}}= & {} r\left( 1-\frac{S}{K}\right) S + \left( \epsilon _1-1\right) \alpha \left( t\right) S P+\left( \epsilon _2-1\right) \beta I P\nonumber \\&+b\left( t\right) P+ (\epsilon _3-1)\rho Y I-\delta _1 I-\delta _2(t) P-\delta _3\left( t\right) Y. \end{aligned}$$

Since, $\epsilon _1,\epsilon _2, \epsilon _3 \le 1$, therefore we get,

$$\begin{aligned} \frac{\mathrm{{d}}V}{\mathrm{{d}}t} \le r\left( 1-\frac{S}{K}\right) S-\delta _1 I -\left( \delta _2\left( t\right) -b\left( t\right) \right) P - \delta _3\left( t\right) Y .\end{aligned}$$

Now, let $\omega = \min \left\{ r,\delta _1,\min \delta _3\left( t\right) ,\min \left( \delta _2\left( t\right) -b\left( t\right) \right) \right\}$. Thus, we have obtained that,

$$\begin{aligned} \frac{\mathrm{{dV}}}{\mathrm{{d}}t} +\omega V\le & {} -\frac{r S^2}{K}+2rS. \end{aligned}$$

Now, consider $f\left( S\right) =2rS-\frac{r S^2}{K}\Rightarrow \max f\left( S\right) = rK$ and $f(S)\le \max f(S)$. Thus,

$$\begin{aligned} \frac{\mathrm {{dV}}}{\mathrm {{dt}}} +\omega V\le&-\frac{r S^2}{K}+2rS\le rK \Rightarrow V\left( t\right) \le \frac{rK}{\omega } + \left( V\left( 0\right) -\frac{rK}{\omega }\right) e^{-\omega t}. \end{aligned}$$

The above expression indicates that as $t \rightarrow \infty$, $e^{-\omega t}\rightarrow 0$ which implies that,

$$\begin{aligned} \mathrm{{lim}}_{t \rightarrow \infty }\sup V(t)\le \frac{rK}{\omega }. \end{aligned}$$

Thus, $V\left( t\right) = S\left( t\right) + I\left( t\right) + P\left( t\right) + Y\left( t\right) \le \frac{rK}{\omega }$. Hence, all populations of the model (1) starts and remain in bounded domain $\Omega = \{\left( S,I,P,Y\right) \in R^4_+ : S+I+P+Y\le \frac{r K}{\omega }, \delta _3(t)>\sigma (t), \delta _2(t)>b(t)\}$ for any initial value. $\square$

The subsequent Sect. 4 reveals the steady-states and their existing conditions for biological relevance.

4 The classification and existence of periodic equilibrium

The equilibriums of non-autonomous system are time-varying equilibria determined by pullback attraction [15, 18]. The model (1) has following periodic steady states:

• (a) The trivial steady state $E_0\left( 0,0,0,0\right)$ always exists.

• (b) The axial steady state $E_1\left( K,0,0,0\right)$ always exists.

• (c) The periodic infection-free steady state $E_2\left( \tilde{S},0, \tilde{P},0\right)$ where, $\tilde{S}=\frac{-b(t)+\delta _2(t)}{\alpha (t)\epsilon _1}$, $\tilde{P}=\frac{r \left( b(t)-\delta _2(t)+K \alpha (t)\epsilon _1\right) }{K \alpha ^2(t)\epsilon _1}$ exists when $\delta _2(t)>b(t)$, $b(t)-\delta _2(t)+K \alpha (t)\epsilon _1>0$ holds.

• (d) The periodic predator-free steady state $E_3\left( \hat{S},\hat{I},0,0\right)$ where, $\hat{S}=\frac{\delta _1}{\gamma }, \hat{X}=\frac{r \left( K \gamma (t) -\delta _1\right) }{K \gamma ^2(t)}$ exists when $K \gamma (t) >\delta _1$.

• (e) The periodic healthy predator-free steady state $E_4\left( \dot{S},\dot{I}, 0, \dot{Y}\right)$ where, $\dot{S}=K\left( \frac{ r\epsilon _3\rho -\gamma (t) \delta _3(t)}{r\epsilon _3 \rho }\right) , \dot{X}=\frac{\delta _3(t)}{\epsilon _3\rho }, \dot{Y}=\frac{-r\delta _1\epsilon _3 \rho +K \gamma (t) \left( -\gamma (t) \delta _3(t)+r\epsilon _3 \rho \right) }{r\epsilon _3 \rho ^2}$ exists when following condition holds:

  $$\begin{aligned}K \gamma (t) r \epsilon _3\rho > K \gamma ^2(t) \delta _3(t)+r \epsilon _3 \delta _1\rho .\end{aligned}$$

• (f) The periodic infected predator-free steady state $E_5\left( \mathbf{S} ,\mathbf{I} ,\mathbf{P} ,0\right)$ where,

  $$\begin{aligned} \mathbf{S}&= \frac{K \left( \gamma (t)\left( -b(t)+\delta _2(t)\right) -\alpha (t)\delta _1\epsilon _2-r\beta \epsilon _2\right) }{K\alpha (t) \gamma (t) \left( \epsilon _1-\epsilon _2\right) -r \beta \epsilon _2},\\ \mathbf{I}&=\frac{ K \alpha (t) \gamma (t)\left( b(t)-\delta _2(t)\right) +\beta r \left( \left( b(t)-\delta _2(t)\right) +\alpha (t) K\epsilon _1\right) +\alpha ^2(t)\delta _1K\epsilon _1}{\beta \left( K\alpha (t) \gamma (t) \left( \epsilon _1-\epsilon _2\right) -r \beta \epsilon _2\right) },\\ \mathbf{P}&= \frac{ K \gamma (t)\left( \gamma (t)\left( -b(t)+\delta _2(t)\right) -\alpha (t)\delta _1\epsilon _2-r\beta \epsilon _2\right) +r\beta \delta _1\epsilon _2}{\beta \left( K\alpha (t)\gamma (t)\left( \epsilon _1-\epsilon _2\right) -r \beta \epsilon _2\right) }, \end{aligned}$$

  exists when following conditions hold:

  • 1 $r\beta \epsilon _2< \min \{\left( \gamma (t)\left( -b(t)+\delta _2(t)\right) -\alpha (t)\delta _1\epsilon _2\right) ,K \alpha (t) \gamma (t) \left( \epsilon _1-\epsilon _2\right) \},$

  • 2 $K\alpha (t)\gamma (t)\left( b(t)-\delta _2(t)\right) +r\beta \left( \left( b(t)-\delta _2(t)\right) +K\alpha (t)\epsilon _1\right) +K\alpha ^2(t)\delta _1\epsilon _1>0.$

• (g) The periodic coexistence steady state $E_6\left( \ddot{S},\ddot{I},\ddot{P},\ddot{Y}\right)$.

Theorem 4.1

The periodic coexistence state $E_6\left( \ddot{S}, \ddot{I}, \ddot{P}, \ddot{Y}\right)$ of the model (1) exists under the following conditions:

• 1 $\rho <\frac{\beta \gamma (t)\delta _3(t)}{\alpha (t)\epsilon _1(K\gamma (t)-\delta _1)}$.

• 2 $G_0>1.$

Proof

At the periodic endemic equilibrium $E_6\left( \ddot{S}, \ddot{I}, \ddot{P}, \ddot{Y}\right)$ the model (1) can be express in the following form:

$$\begin{aligned}&f_1(S,I,P,Y)= r \left( 1-\frac{S}{K}\right) -\alpha (t) P-\gamma (t) I=0, \end{aligned}$$

(2)

$$\begin{aligned}&f_2(S,I,P,Y)= \gamma (t)S-\beta P- \rho Y- \delta _1=0, \end{aligned}$$

(3)

$$\begin{aligned}&f_3(S,I,P,Y)= b(t) +\epsilon _1\alpha (t) S +\epsilon _2 \beta I -\frac{\sigma (t) Y}{a+P}-\delta _2(t)=0 , \end{aligned}$$

(4)

$$\begin{aligned}&f_4(S,I,P,Y)= \epsilon _3\rho I + \frac{\sigma (t) P}{a+P}- \delta _3(t) = 0 . \end{aligned}$$

(5)

On solving (2), (3) and (5), we obtain following values:

$$\begin{aligned} S= & {} \frac{\beta P+\rho Y+\delta _1}{\gamma (t)},\ I=\frac{\delta _3(t)\left( a+P\right) -P \sigma (t) }{\epsilon _3 \rho \left( a +P\right) },\nonumber \\&Y=\frac{A_1 P^2 +A_2 P+ A_3 }{\left( a+P\right) r \epsilon _3 \rho ^2} \end{aligned}$$

(6)

$$\begin{aligned}&A_1=-r \beta \rho \epsilon _3-K\alpha (t)\gamma (t)\rho \epsilon _3, \\&A_2=-a K\alpha (t)\gamma (t)\rho \epsilon _3-a r \beta \rho \epsilon _3- K\gamma ^2(t)\delta _3(t)+K\gamma ^2(t) \sigma (t) +r K\gamma (t) \rho \epsilon _3-r\delta _1\rho \epsilon _3, \\&A_3=-a ( K \gamma ^2(t) \delta _3(t)- K r\gamma (t)\rho \epsilon _3+r \delta _1\rho \epsilon _3). \end{aligned}$$

Now, on substituting all these values in (4), we get the following nonlinear algebraic polynomial in P,

$$\begin{aligned} F_3 P^3+F_2 P^2+F_1 P+F_0 P=0. \end{aligned}$$

(7)

Where,

$$\begin{aligned} F_3= & {} K \alpha ^2(t) \epsilon _1\epsilon _3^2 \rho ^2,\\ F_2= & {} \frac{1}{a^2}F_0 +\frac{1}{a}(a\sigma (t)( K\gamma ^2(t)\delta _3(t) - r K\gamma (t)\rho \epsilon _3+r\delta _1\rho \epsilon _3)-a K\alpha (t)\gamma (t)\rho \sigma (t) (\epsilon _1+\epsilon _3)\\\nonumber&-a \beta \rho r \sigma (t) (-\epsilon _2+\epsilon _3)+2 a^2K \alpha ^2(t)\rho ^2\epsilon _1\epsilon _3),\\ F_1= & {} \frac{1}{a}F_0+aF_2+K\gamma ^2(t)\sigma ^2(t)-a^2 K\alpha ^2(t)\rho ^2\epsilon _1\epsilon _3,\\ F_0= & {} (1-G_0) \left( a^2 K\alpha (t)\gamma (t)\delta _3(t)\rho \epsilon _1+a^2 r\delta _2(t)\rho ^2\epsilon _3+a r K\gamma (t)\rho \sigma (t)\epsilon _3\right) , \end{aligned}$$

and

$$\begin{aligned} G_0=\frac{ra^2b \rho ^2\epsilon _3+a^2 r K \alpha (t)\rho ^2\epsilon _1\epsilon _3+a^2 r \beta \delta _3(t) \rho \epsilon _2+a K \gamma ^2(t)\delta _3(t) \sigma (t) +a r \delta _1 \rho \sigma (t)\epsilon _3}{ a^2 K \alpha (t)\gamma (t)\delta _3(t)\rho \epsilon _1+ r a^2\delta _2(t)\rho ^2\epsilon _3+a r K\gamma (t)\rho \sigma (t)\epsilon _3}. \end{aligned}$$

We clearly see that $F_3$ is always positive. $F_0$ is a negative if condition (2) holds. Again, $F_2$ is negative when $F_0<0$ and the condition (1) holds. Finally, $F_1$ is negative, when $F_0$ and $F_2$ is negative and the condition (1) holds. Thus, there is only one sign change in the equation (7) if condition (1) and (2) holds. Hence, Eq. (7) has only one positive real solution $\ddot{P}$. After having value of $\ddot{P}$, we can easily find the value of $\ddot{S}$, $\ddot{I}$ and $\ddot{Y}$ from expressions (6). Thus, the system (1) has a unique periodic coexistence equilibrium if conditions (1) and (2) holds. $\square$

5 Basic reproduction number and stability

This section investigates the periodic basic reproduction number $R_C(t)$ and stability of the periodic disease-free state $E_2(\tilde{S},0,\tilde{P},0)$ and coexistence state $E_6(\ddot{S},\ddot{I},\ddot{P},\ddot{Y})$.

The basic reproduction $R_0$ number is the measurement of severity of any disease. This number provides the total infective cases; one primary infective has, over its infectious period in an uninfected population. We determined the periodic basic reproduction number $R_C(t)$ through the next generation method [12].

The following two compartments of (1) are responsible for infection:

$$\begin{aligned} \frac{\mathrm{{d}}I}{\mathrm{{dt}}} = \gamma (t) S I-\beta I P- \rho I Y- \delta _1 I, \end{aligned}$$

(8)

$$\begin{aligned} \frac{\mathrm{{d}}Y}{\mathrm{{d}}t} = \epsilon _3 \rho I Y+ \frac{\sigma (t) P Y}{a+P}- \delta _3(t) Y. \end{aligned}$$

(9)

Now, we define the matrices for new infections, i.e, F(t) and transfer terms, i.e., V(t) at disease-free equilibrium $E_2\left( \tilde{S},0, \tilde{P},0\right)$ as follows:

$$\begin{aligned} F(t)= & {} \left( \begin{array}{cc} \gamma (t)\tilde{S} &{} 0 \\ 0 &{} \frac{\tilde{P} \sigma (t) }{a+\tilde{P}} \\ \end{array} \right) =\left( \begin{array}{cc} \frac{\gamma (t)(\delta _2(t)-b(t))}{\alpha (t)\epsilon _1} &{} 0 \\ 0 &{} \frac{r\sigma (t)(b(t)-\delta _2(t)+K\alpha (t)\epsilon _1)}{K\alpha ^2(t)\epsilon _1\left( a+\frac{r (b(t)-\delta _2(t)+K\alpha (t) \epsilon _1)}{\alpha ^2(t)K\epsilon _1}\right) } \\ \end{array} \right) \end{aligned}$$

(10)

and,

$$\begin{aligned} V(t)= & {} \left( \begin{array}{cc} \delta _1+\beta \tilde{P} &{} 0 \\ 0 &{} \delta _3(t)\\ \end{array} \right) =\left( \begin{array}{cc} \frac{r\beta (b(t)-\delta _2(t)+K\alpha (t)\epsilon _1)}{K\alpha ^2(t)\epsilon _1}+\delta _1&{} 0 \\ 0 &{} \delta _3(t)\\ \end{array} \right) . \end{aligned}$$

(11)

So that,

$$\begin{aligned} FV^{-1}=\left( \begin{array}{cc} \frac{\gamma (t)(\delta _2(t)-b(t))}{\alpha (t)\epsilon _1\left( \frac{r\beta \left( b(t)-\delta _2(t)+K\alpha (t)\epsilon _1\right) }{K\alpha ^2(t)\epsilon _1(t)}+\delta _1\right) } &{} 0 \\ 0 &{} \frac{r \sigma (t)(b(t)-\delta _2(t)+K\alpha (t)\epsilon _1)}{K\alpha ^2(t)\delta _3(t)\epsilon _1\left( a+\frac{r(b(t)-\delta _2(t)+K\alpha (t) \epsilon _1)}{K\alpha ^2(t)\epsilon _1}\right) } \\ \end{array} \right) . \end{aligned}$$

(12)

The reproduction number $\hat{R_0}$ is the largest positive root of the following characteristic polynomial G(x) of matrix (12),

$$\begin{aligned} G(x):=x^2- (R_{0\gamma }+R_{0\sigma }) x +R_{0\gamma }R_{0\sigma }=0. \end{aligned}$$

(13)

Where,

$$\begin{aligned} R_{0\gamma }= & {} \frac{K\alpha (t)\gamma (t)(-b(t)+\delta _2(t))}{r\beta b(t)+K\alpha ^2(t)\delta _1\epsilon _1+rK\alpha (t)\beta \epsilon _1-r\beta \delta _2(t)},\\ R_{0\eta }= & {} \frac{r \sigma (t)(b(t)-\delta _2(t)+K\alpha (t)\epsilon _1)}{\delta _3(t)\left( a K\alpha ^(t)\epsilon _1+r b(t)+rK\alpha (t)\epsilon _1-r\delta _2(t)\right) }. \end{aligned}$$

Here, $R_{0\gamma }$ and $R_{0\sigma }$ are the infections caused by prey and predators, respectively in the environment. Equation (13) always has at least one positive root as $(R_{0\gamma }+R_{0\sigma })>0$. Now, when $\hat{R_0}=1$, the largest root of Eq. (13) will be 1. Thus, we see from Eq. (13) that,

$$\begin{aligned} G(1) = 1 - (R_{0\gamma }+R_{0\sigma })+R_{0\gamma }R_{0\sigma }, \end{aligned}$$

(14)

The above equation shows that $R_{0\gamma }+R_{0\sigma }=1 + R_{0\gamma }R_{0\sigma }$ which is true for $R_{0\gamma }=1$ and $R_{0\sigma }=0$. Thus, $R_{0\gamma }+R_{0\sigma }=1$ if and only if $\hat{R_0}=1$. Hence, $\hat{R_{0}}$ and $R_{0\sigma }+R_{0\gamma }$ show identical behavior. Moreover, $\hat{R_{0}}<1\Rightarrow R_{0\sigma }+R_{0\gamma }<1$ and $\hat{R_{0}}>1\Rightarrow R_{0\sigma }+R_{0\gamma }>1$. Hence, the periodic basic reproduction number $R_0$ of the system (1) can be considered as:

$$\begin{aligned} R_0= & {} R_{0\sigma }+R_{0\gamma }=\frac{\gamma (t)S}{\delta _1+\beta P}+\frac{P \sigma (t) }{(a +P)\delta _3(t)}. \end{aligned}$$

(15)

Or,

$$\begin{aligned} R_0= & {} \frac{K\alpha (t)\gamma (t)a(-b(t)+\delta _2(t))}{r\beta b(t) +K\alpha ^2(t)\delta _1\epsilon _1+Kr\alpha (t)\beta \epsilon _1-r\beta \delta _2(t)}\nonumber \\&+ \frac{r \sigma (t)(b(t)-\delta _2(t)+K\alpha (t)\epsilon _1)}{\delta _3(t)\left( a K\alpha ^2(t)\epsilon _1+r\left( b(t)+K\alpha (t)\epsilon _1-\delta _2(t)\right) \right) }. \end{aligned}$$

(16)

Again, we defined the matrix M(t) related to the healthy compartment of model (1) at disease-free equilibrium $E_2(\tilde{S},0,\tilde{P},0)$ with the help of lemma [35]:

$$\begin{aligned}M(t)=\left( \begin{array}{cc} \frac{r(b(t)-\delta _2(t))}{K \alpha (t)\epsilon _1}&{} \frac{b(t)-\delta _2(t)}{\epsilon _1}\\ \frac{r(b(t)-\delta _2(t)+K \alpha (t)\epsilon _1)}{K \alpha (t) } &{} 0\\ \end{array}\right) .\end{aligned}$$

The monodromy matrix $\phi _M(T)$ of the T-periodic linear system, $\frac{\mathrm{{d}}Z}{\mathrm{{d}}t}=M(t)Z$, is given as,

$$\begin{aligned} \phi _{M}(T)=\frac{1}{\frac{1}{2}\left( A-\sqrt{\Delta }\right) -\frac{1}{2}\left( A+\sqrt{\Delta }\right) } \left( \begin{array}{cc} \Pi _1 &{} \Pi _2 \\ \Pi _3 &{} \Pi _4\\ \end{array}\right) . \end{aligned}$$

Where,

$$\begin{aligned} \Pi _1= & {} \Pi _4=\frac{1}{2}\left( e^{\frac{1}{2}\left( C+\sqrt{\Delta }\right) }\left( C-\sqrt{\Delta }\right) -e^{\frac{1}{2}\left( C-\sqrt{\Delta }\right) }\left( C+\sqrt{\Delta }\right) \right) ,\nonumber \\ \Pi _2= & {} D \left( e^{\frac{1}{2}\left( C+\sqrt{\Delta }\right) }-e^{\frac{1}{2}\left( C-\sqrt{\Delta }\right) }\right) ,\nonumber \\ \Pi _3= & {} \frac{1}{4D}\left( e^{\frac{1}{2}\left( C-\sqrt{\Delta }\right) }-e^{\frac{1}{2}\left( C+\sqrt{\Delta }\right) }\right) \left( C-\sqrt{\Delta }\right) \left( C+\sqrt{\Delta }\right) ,\nonumber \\ C= & {} \frac{-r (-b(T)+\delta _2(T))}{K\alpha (T)\epsilon _1}, D=\frac{b(T)-\delta _2(T)}{\epsilon _1},\nonumber \\ \Delta= & {} \frac{r^2(-b(T)+\delta _2(T))^2}{4 K^2\alpha ^2(T)\epsilon _1^2}-\frac{r (-b(T)+\delta _2(T))(b(T)-\delta _2(T)+ K\alpha (T)\epsilon _1)}{K \alpha (T)\epsilon _1}. \end{aligned}$$

The spectrum of $\phi _M(T)$ is given as, $Sp(\phi _M(T))=\{e^{\frac{1}{2}\left( C+\sqrt{\Delta }\right) },e^{\frac{1}{2}\left( C-\sqrt{\Delta }\right) }\}$ and the spectral radius of $\phi _M(T)$ is, $\rho (\phi _M(T))=e^{\frac{1}{2}\left( C+\sqrt{\Delta }\right) }.$ Which always lesser than one for the existence of a disease-free equilibrium. Hence, disease-free equilibrium $E_2(t)$ is linearly asymptotically stable in space $\Omega$.

Now, we consider the linear system (17) and used the approach [35] to analyzed the threshold dynamics of the eco-epidemiological system (1) periodically:

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{dt}}}Y(t,s)=-V(t)Y(t,s), \ \forall t\ge s, Y(s,s)=I. \end{aligned}$$

(17)

Where Y(t, s) and I represent the $2\times 2$ square matrix and identity matrix respectively. The monodromy matrix of linear system (17) $\forall t\ge 0$ is,

$$\begin{aligned} \phi _{-V}(T)=Y(T,0)=\left( \begin{array}{cc} e^{-\left( \delta _1+\frac{r \beta (b(T)-\delta _2(T)+K\alpha (T)\epsilon _1)}{K \alpha ^2(T)\epsilon _1}\right) T} &{} 0 \\ 0 &{} e^{-\delta _3T}\\ \end{array}\right) . \end{aligned}$$

(18)

$$\begin{aligned} \lambda _1=e^{-\left( \delta _1+\frac{r \beta (b(T)-\delta _2(T)+K \alpha (T)\epsilon _1)}{K \alpha ^2(T)\epsilon _1}\right) T}, \ \lambda _2= e^{-\delta _3T}.\end{aligned}$$

Now, we see from the expression that $\lambda _1$ and $\lambda _2$ are always lesser than one for the existence of disease-free equilibrium. Hence, both the eigenvalues of the monodromy matrix (18) are lesser than one if $R_C(t)<1$. So that, $\rho (\phi _{-V}(T))<1$ for the disease-free state.

Let us consider $\Phi (s)$ as the initial distribution of infected individuals, which is T-periodic in s. Then $F(s)\Phi (s)$ represents the distribution of new infection produced by a infected individual at the time s. If $t\ge s$, then $Y(t,s)F(s)\Phi (s)$ is the distribution of totally infected individual at time s and remaining in infected compartment at time t. It follows from [35] that,

$$\begin{aligned} \psi (t)=\int _{-\infty }^{t} {Y(t,s)F(s)\Phi (s)}\mathrm {{d}}s=\int _{0}^{+\infty } {Y(t,t-a)F(t-a)\Phi (t-a)}\mathrm {{d}}a \end{aligned}$$

is the distribution of the new infections cumulated at time t produced by all infected individual $\Phi (s)$ introduced with previous time t. let $C_{T}$ be the ordered Banach space of all T-periodic function of R to $R^2$ with the norm $\Vert \cdot \Vert _{\infty }$ on the positive cone,

$$\begin{aligned} C_{T}^{+}=\{\Phi \in C_{T} : \Phi (t)\ge 0\}, \forall \in \text {R}. \end{aligned}$$

Then, we can define the linear operator $\mathbf{L}$ of $C_{T}\rightarrow C_{T}$ by,

$$\begin{aligned} (\mathbf{L} \Phi )(t)=\int _{0}^{+\infty }Y(t,t-a)F(t-a)\Phi (t-a)\mathrm{{d}}a, \forall \in \text {R}, \ \mathrm{{with}} \ \Phi \in C_{T}. \end{aligned}$$

Definition 5.1

$\texttt {L}$ denotes the operator of new infection and $R_C(t)=\rho (\texttt {L})$ is the basic reproduction number of model (1).

Now, the global asymptotic stability of disease-free equilibrium $E_2(t)$ will be examined through the following fundamental theorem of Wang and Zhao [35].

Lemma 5.2

(See [35], Theorem 2.2) The following proposition is true where $\rho (\phi _{F-V}(T))$ indicates the spectral ray of the monodromy matrix of the system,

$$\begin{aligned} \frac{\mathrm{{d}}Z}{\mathrm{{d}}t}=(F(t)-V(t))\mathrm{{d}}Z; \end{aligned}$$

(19)

• 1 $R_0=1$ if and only if $\rho (\phi _{F-V}(T))=1$.

• 2 $R_0>1$ if and only if $\rho (\phi _{F-V}(T))>1$.

• 3 $R_0<1$ if and only if $\rho (\phi _{F-V}(T))<1$.

Theorem 5.3

The basic reproduction number $R_C(t)<1$ assures the asymptotic stability of T-periodic infection-free state $E_2$ of (1) while this state become locally unstable if $R_C(t)>1$, $\forall t\ge 0$. Where $R_C(t)$ is defined by (15).

Proof

The following expression shows the monodromy matrix of the (),

$$\begin{aligned} \phi _{(F-V)}(T)=\left( \begin{array}{cc} \Upsilon _1 &{} 0 \\ 0 &{}\Upsilon _2\\ \end{array}\right) , t\ge 0. \end{aligned}$$

(20)

Here, $\Upsilon _1=e^{\left( \gamma (T) \tilde{S}-\beta \tilde{P}-\delta _1\right) }=e^{\left( \gamma (T)\left( \frac{-b(T)+\delta _2(T)}{\alpha (T) \epsilon _1}\right) -\beta \left( \frac{r\left( b(T)-\delta _2(T)+K\alpha (T)\epsilon _1\right) }{K\alpha ^2(T)\epsilon _1}\right) -\delta _1\right) }$,

$\Upsilon _2=e^{\left( \frac{\sigma (T) \tilde{P}}{(a+\tilde{P})}-\delta _3(T)\right) }=e^{\left( \frac{\frac{r\sigma (T)\left( b(T)-\delta _2(T)+K\alpha (T)\epsilon _1\right) }{K\alpha ^2(T)\epsilon _1}}{a+\left( \frac{r\left( b(T)-\delta _2(T)+K\alpha (T)\epsilon _1\right) }{K\alpha ^2(T)\epsilon _1}\right) }-\delta _3(T)\right) }.$

Now,

$$\begin{aligned}Sp(\phi _{(F-V)}(T))=\{e^{\left( \gamma (T) \tilde{S}-\beta \tilde{P}-\delta _1\right) T},e^{\left( \frac{\sigma (T) \tilde{P}}{(a+\tilde{P})}-\delta _3(T)\right) T}\}.\end{aligned}$$

It is clear from (15) that to make $R_C(t)<1$, both $\left( \gamma (T) \tilde{S}-\beta \tilde{P}-\delta _1\right)$ and $\left( \frac{\sigma (T) \tilde{P}}{(a+\tilde{P})}-\delta _3(T)\right)$ must be lesser than zero. Thus, both eigenvalues of matrix (20) are lesser than one when $R_C(t)<1$. This concludes that $\rho (\phi _{(F-V)}(T))<1$, when $R_C(t)<1$. Which enable us to conclude the local asymptotic stability of T-periodic infection-free state $E_2$. Again, when $R_C(t)>1$, either of $\lambda _1$ and $\lambda _2$ must be positive. Thus one eigenvalue of monodromy matrix (20) is greater than one when $R_C(t)>1$. Hence, $\rho (\phi _{(F-V)}(T))>1$, when $R_C(t)>1$. This results the instability of the steady state $E_2$. $\square$

Theorem 5.4

For any solution of (1), $R_C(t)<1$, guarantees the global asymptotic stability of periodic steady state $E_2(\tilde{S},0,\tilde{P},0)$ in the bounded region $\Omega$ while $R_C(t)>1$ guarantees the instability of $E_2$.

Proof

Theorem 5.3 already described the stability of infection-free state $E_2$ when $R_C(t)<1$. So, it is only remains to that show that $E_2(t)$ is globally attractive for $R_C(t)<1$.

Let us suppose that $R_C(t)<1$. We know that the set $\Omega = \{(S,I,P,Y) \in R^4_+ : S+I+P+Y\le \frac{rk}{\omega }, \delta _3(t)>\sigma (t), \delta _2(t)>b(t)\}$ of system (1) is positively invariant, then for all $\epsilon >0$, $\exists \ T_1>0$ such as $S(t)\le \left( \frac{-b(t)+\delta _2(t)}{\alpha (t) \epsilon _1}+\epsilon \right) , \forall t>T_1.$ Now, we have following equations from the system (1) for $t>T_1$:

$$\begin{aligned}&\frac{\mathrm{{d}}I}{\mathrm{{d}}t} \le \gamma (t)I\left( \frac{-b(t)+\delta _2(t)}{\alpha (t) \epsilon _1}+\epsilon \right) - \beta P I-\rho I Y -\delta _1 I, \end{aligned}$$

(21)

$$\begin{aligned}&\frac{\mathrm{{d}}Y}{\mathrm{{dt}}} = \epsilon _3 \rho Y I + \frac{\sigma (t) P Y}{a+P}-\delta _3(t) Y. \end{aligned}$$

(22)

Subsequently, we assume the complementary system:

$$\begin{aligned}&\frac{\mathrm{{d}}\tilde{I}}{\mathrm{{d}}t} = \gamma (t)\tilde{I}\left( \frac{-b(t)+\delta _2(t)}{\alpha (t) \epsilon _1}+\epsilon \right) - \beta \tilde{P}\tilde{I}-\rho \tilde{I}\tilde{ Y} -\delta _1\tilde{I}, \end{aligned}$$

(23)

$$\begin{aligned}&\frac{\mathrm{{d}}\tilde{Y}}{\mathrm{{d}}t} = \epsilon _3 \rho \tilde{Y}\tilde{I} + \frac{\sigma (t) \tilde{P} \tilde{Y}}{a+\tilde{P}} -\delta _3(t) \tilde{Y}. \end{aligned}$$

(24)

We write this system in the form $\tilde{W'}(t)=M_\epsilon (t)\tilde{W}(t)$. Where $\tilde{W}(t)=(\tilde{I'}(t),\tilde{Y'}(t))$ and,

$$\begin{aligned} M_\epsilon (t)=\left( \begin{array}{cc} \Psi _1 &{}{} 0 \\ 0 &{}{} \Psi _2\\ \end{array}\right) . \end{aligned}$$

(25)

Where, $\Psi _1=\gamma (t)\left( \! \frac{-b(t)+\delta _2(t)}{\alpha (t) \epsilon _1}+\epsilon \!\right) - \beta \left( \frac{r\left( \! b(t)-\delta _2(t)+K\alpha (t)\epsilon _1\!\right) }{K\alpha ^2(t)\epsilon _1}\!\right) -\delta _1,$ $\Psi _2=\left( \!\frac{\frac{r\sigma (t)\left( \! b(t)-\delta _2(t)+K\alpha (t)\epsilon _1\!\right) }{K\alpha ^2(t)\epsilon _1}}{a+\left( \!\frac{r\left( \!b(t)-\delta _2(t)+K\alpha (t)\epsilon _1\!\right) }{K\alpha ^2(t)\epsilon _1}\right) }-\delta _3(t)\!\right)$.

It is clear that,

$$\begin{aligned}{\lim _{{\epsilon }\rightarrow 0^{+}}\phi _{M_{\epsilon }}(T)} =\phi _{F-V}(T).\end{aligned}$$

We know that the spectral radius is continuous and lemma 5.2 states that $R_C(t)<1\Rightarrow \rho (\phi _{F-V}(T))<1$. Therefore,

$$\begin{aligned}\lim _{\epsilon \rightarrow 0^{+}}\rho (\phi _{M_{\epsilon }}(T))=\rho (\phi _{F-V}(T))<1.\end{aligned}$$

Further, there exist $\epsilon ^*>0$ such that $\rho (\phi _{M_{\epsilon }}(T))<1 \ \ \forall \epsilon \in [0,\epsilon ^*[$. Then according to Zhang and Zhao [37], there exist a T-periodic positive function x(t) such that $\tilde{W}(t)=x(t)e^{\xi t}$ is solution of complementary model (24). Since, $\rho (\phi _{M_{\epsilon }}(T))<1\Rightarrow \xi <0$, shows that $\lim _{t\rightarrow \infty }\tilde{W}(t)=0$, as the T-periodic function x(t) is bounded. Applying comparison theorem on (22) one has $\lim _{t\rightarrow \infty }(I(t),Y(t))=(0,0)$. Using theory of asymptotically periodic semiflow we have,

$$\begin{aligned} \lim _{t\rightarrow +\infty }S(t)= \tilde{S},\lim _{t\rightarrow +\infty }P(t)= \tilde{P}. \end{aligned}$$

Hence, the infection-free periodic state $E_2(t)$ is globally attractive of from the above results. $\square$

Theorem 5.5

If $R_C(t)>1$, the periodic coexistence state $E_6(\ddot{S}, \ddot{I}, \ddot{P}, \ddot{Y})$ of system (1) exist and there exist $\theta ^*>0$ in such a way that any solution $\left( \ddot{S}(t),\ddot{P}(t),\ddot{I}(t),\ddot{Y}(t) \right)$ with initial condition $(S_0,P_0,I_0,Y_0)\in R_{+}^2\times in R_{+}^2$ satisfies $\liminf I(t)_{t\rightarrow +\infty }\ge \theta ^*$

and $\liminf Y(t)_{t\rightarrow +\infty }\ge \theta ^*$. Where $\ddot{S}$, $\ddot{I}$ , $\ddot{P}$ and $\ddot{Y}$ are defined in Sect. 4.

Proof

Clearly, the coexistence state $E_6(\ddot{S}, \ddot{I}, \ddot{P}, \ddot{Y})$ of system (1) defined in theorem (4.1) is periodic and positive for $R_C(t)>1$. For clarity, the arrangement of the compartments is done such that the last two compartments corresponds to diseased compartments (i.e., $(\ddot{S},\ddot{P},\ddot{I},\ddot{Y}))$. Now, it is remains to show that $\exists \ \theta ^*>0$ such as any solution $(\ddot{S}, \ddot{P},\ddot{I},\ddot{Y})$ of (1) with initial condition $(S_0,P_0,I_0,Y_0)\in R_{+}^2\times intR_{+}^2$ satisfies $\liminf I(t)_{t\rightarrow +\infty }\ge \theta ^*$ and $\liminf Y(t)_{t\rightarrow +\infty }\ge \theta ^*$.

Suppose that:

$$\begin{aligned} X=\{(S(t),P(t),I(t),Y(t))\in R_+^4\}; \ X_0 = \{(S,P,I,Y)\in R_{+}^2\times intR_{+}^2\}; \end{aligned}$$

$$\begin{aligned} \partial X_0 = X/X_0. \end{aligned}$$

Let Poincare map $P:X\rightarrow X$ related to the system (1), such that

$$\begin{aligned} P(x^0)=\mu (T,x^0), \forall x^0\in X, \end{aligned}$$

where, $\mu (t,x^0)$ is unique solution of system (1) such as $\mu (0,x^0)=x^0$.

It is clear from the definition of Poincare map that:

$$\begin{aligned}P^m(S_0,P_0,I_0,Y_0)= \mu (mT, (S_0,P_0,I_0, Y_0)), \ \forall m\ge 0.\end{aligned}$$

Again, we have from lemma (5.2) that $\rho (\phi _{F-V}(T))>1$ for $R_C>1$. Thus, $\exists$ sufficiently small $\varepsilon >0$, such as $\rho (\phi _{F-V-M_{\varepsilon }(T)})>1.$ Where, the matrix $M_\varepsilon (t)$ is given by:

$$\begin{aligned} M_\varepsilon (t)=\left( \begin{array}{cc} \Lambda _1 &{} 0 \\ 0 &{} \Lambda _2\\ \end{array}\right) . \end{aligned}$$

Where, $\Lambda _1=\gamma (t)\left( \frac{-b(t)+\delta _2(t)}{\alpha (t) \epsilon _1}-\varepsilon \right) - \beta \left( \frac{r\left( b(t)-\delta _2(t)+K\alpha (t)\epsilon _1\right) }{K\alpha ^2(t)\epsilon _1}\right) -\delta _1,$

$\Lambda _2=\left( \frac{\frac{r\sigma (t)\left( b(t)-\delta _2(t)+K\alpha (t)\epsilon _1\right) }{K\alpha ^2(t)\epsilon _1}}{a+\left( \frac{r\left( b(t)-\delta _2(t)+K\alpha (t)\epsilon _1\right) }{K\alpha ^2(t)\epsilon _1}\right) }-\delta _3(t)\right) .$

Now, for $\tilde{H}=\frac{1}{\tilde{S}}$, the first equation of the model (1) takes the following form,

$$\begin{aligned} \frac{\mathrm{{d}}\tilde{H}}{\mathrm{{d}}t}=-r \tilde{H}+\frac{r}{K}+\alpha P \tilde{H} + \gamma (t)I \tilde{H}. \end{aligned}$$

(26)

Now, with help of the value of S, I and Y in (6), we will change the Eq. (26) in the following form,

$$\begin{aligned} \frac{\mathrm{{d}}\tilde{H}}{\mathrm{{d}}t}= \mathbf {A}\tilde{H} + \mathbf {B}P\tilde{H}. \end{aligned}$$

(27)

Where, $\mathbf {A}=-r+\frac{r\delta _1}{K\gamma (t)}+\frac{\gamma (t)\delta _3(t)}{\epsilon \rho }+\frac{r\delta _1\epsilon _3\rho +K\gamma ^2(t)\delta _3(t)-rK\gamma (t)\epsilon _3\rho }{K\epsilon _3\gamma (t)\rho },$

$\mathbf {B}=\alpha (t)+\frac{r\beta }{K\gamma (t)}-\frac{r\beta +K\gamma (t)\alpha (t)}{K\gamma (t)}$.

We consider following perturbation equation for Eq. (27),

$$\begin{aligned} \frac{\mathrm{{d}}\tilde{H}}{\mathrm{{d}}t}= \mathbf {A}\tilde{H} + \mathbf {B}\pi . \end{aligned}$$

(28)

Equation (28) lead to the following solution,

$$\begin{aligned} \tilde{S}(t,\pi )= \frac{\mathbf {A}\tilde{S}(0,\pi )}{\tilde{S}(0,\pi )\mathbf {B}\pi (1-e^{-\mathbf {A}t})+\mathbf {A}e^{-\mathbf {A}t}}, \end{aligned}$$

with arbitrary initial condition $\tilde{S}(0,\pi )$. This system also have a single periodic solution,

$$\begin{aligned} \tilde{S}^*(t,\pi )= \frac{\mathbf {A}\tilde{S}^*(0,\pi )}{\tilde{S}^*(0,\pi )\mathbf {B}\pi (1-e^{-\mathbf {A}t})+\mathbf {A}e^{-\mathbf {A}t}}.\end{aligned}$$

Where, $\tilde{S}^*(0,\pi )$ is given by,

$$\begin{aligned} \tilde{S}^*(0,\pi )= \frac{-\mathbf {A}e^{-\mathbf {A}t}}{\mathbf {B}\pi (1-e^{-\mathbf {A}t})}. \end{aligned}$$

The above equation clarifies that $|\tilde{S}(t,\pi )-\tilde{S}^*(t,\pi )|\rightarrow 0$, when $t\rightarrow \infty$ and consequently $\tilde{S}^*(t,\pi )$ is global on $R_+$. We can easily conclude from $\tilde{S}^*(0,\pi )$ that it is continuous in $\pi$. Further, from the continuity of $\tilde{S}^*(t,\pi )$ with initial condition and value of parameter involves, we can conclude that $\tilde{S}^*(t,\pi )>S_*-\varepsilon$ for sufficiently small $\pi$ and $t\in [0,T]$. In addition to this, we deduced from the periodicity of $\tilde{S}^*(t,\pi )$ and constant $S_*-\varepsilon$ that $\tilde{S}^*(t,\pi )>S_*-\varepsilon$ for sufficiently small $\pi$ and $\forall t\ge 0$.

Let us consider a fixed point $M_0\in \partial X_0$ Now, according to continuity of solution with initial condition, for any $\pi >0$, $\exists \pi ^*>0$ such as $\forall \ (S_0,P_0,I_0,Y_0)\in X_0$, verifying $\Vert (S_0,P_0,I_0,Y_0)- M_0\Vert \le \pi ^*$. Thus, we have:

$$\begin{aligned}\Vert \mu (t,(S_0,P_0,I_0,Y_0))-\mu (t,E_2)\Vert \le \pi , \forall t\in [0,T].\end{aligned}$$

Now, we will show that

$$\begin{aligned} \lim _{m\rightarrow \infty } \sup d(P^m(S_0,I_0,P_0,Y_0),M_0)\ge \pi ^*, \ \forall (S_0,I_0,P_0,Y_0)\in X_0. \end{aligned}$$

(29)

Let us suppose that (29) does not hold good. Then $\exists$ at least one $(S_0,I_0,P_0,Y_0)\in X_0$ such as

$$\begin{aligned} \lim _{m\rightarrow \infty } \sup d(P^m(S_0,I_0,P_0,Y_0),M_0)<\pi ^*. \end{aligned}$$

we will follow the process given in [18] and conclude that the periodic solution $\tilde{S}^*(t,\pi )$ of (28) is global attractive on $R_+$ and $\tilde{S}^*(t,\pi )>S_*-\varepsilon$. Thus we have $S(t) > S_*-\varepsilon$ for sufficiently large t. The differential equations for diseased compartment of system (1) can be written in the following form for amply large t.

$$\begin{aligned}&\frac{\mathrm{{d}}I}{\mathrm{{d}}t} \ge \gamma (t) (S_*-\varepsilon ) I-\beta I P- \rho I Y- \delta _1 I, \end{aligned}$$

(30)

$$\begin{aligned}&\frac{\mathrm{{d}}Y}{\mathrm{{d}}t} = \epsilon _3 \rho I Y+ \frac{\sigma (t) P Y}{a+P}- \delta _3(t) Y. \end{aligned}$$

(31)

Let us consider the system,

$$\begin{aligned}&\frac{\mathrm{{d}}\tilde{I}}{\mathrm{{d}}t} = \gamma (t) (S_*-\eta ) \tilde{I}-\beta \tilde{I}\tilde{ P}- \rho \tilde{I}\tilde{Y}- \delta _1 \tilde{I}, \end{aligned}$$

(33)

$$\begin{aligned}&\frac{\mathrm{{d}}\tilde{Y}}{\mathrm{{d}}t} = \epsilon _3 \rho \tilde{I}\tilde{Y}+ \frac{\sigma (t) \tilde{P}\tilde{ Y}}{a+\tilde{P}}- \delta _3(t) \tilde{Y}. \end{aligned}$$

(34)

Thus according to [37] , from lemma (5.2) $\exists$ a positive T-periodic function such as is solution of (33). Where

$$\begin{aligned}\nu = \frac{1}{T}\ln \rho (\phi _{F-V-M_{\varepsilon }(T)}).\end{aligned}$$

Since, $\rho (\phi _{F-V-M_{\varepsilon }(T)})>1$ therefore $\nu$ is a positive constant. Considering $t=nT$, where n is a nonnegative integer , we have:

if $n\rightarrow \infty$. Since, $\nu T >0$ and . For any nonnegative condition $(I(0),B(0))'$ of (30), $\exists$ $m^*>0$ sufficiently small such as $(I(0),B(0))'\ge m^*(\tilde{I}(0),\tilde{Y}(0))'$. Thus, from comparison principle we deduced that $(I(0),Y(0))'\ge m^*(\tilde{I}(0),\tilde{Y}(0))'$, $\forall t>0$. This allow us to have $I(nT)\rightarrow \infty$, $Y(nT)\rightarrow \infty$ as $n\rightarrow \infty$ which is a contradiction. Hence, according to Theorem 5.5 disease will persist in the population whenever $R_C(t)>1$, $\forall t\ge 0$. $\square$

In the next Sect. 6, we will perform the sensitivity analysis to know how the parameters of the system (1) affects the reproduction number $R_C(t)$.

6 Sensitivity Analysis

Here, we performs the sensitivity analysis of the reproduction number $R_C$ using normalized forward sensitivity index method [5]. This is used to find out the impact of system parameter on reproduction number. For this analysis, we have taken parameter values shown in Table 2. When there is no seasonality i.e., $\omega _1=\omega _2=\omega _3=\omega _4=\omega _5=\omega _6=0$, we have $\sigma (t)=\sigma _0$, $\alpha (t)=\alpha _0$, $\delta _3(t)=(\delta _3)_0$, $\delta _2(t)=(\delta _2)_0$, $b(t)=b_0$, and $\gamma (t)=\gamma _0$ in this situation $R_C(t)$ becomes,

$$\begin{aligned} R_C= & {} \frac{K\alpha _0\gamma _0(-b_0+(\delta _2)_0)}{r\beta b_0 +K\alpha ^2_0\delta _1\epsilon _1+Kr\alpha _0\beta \epsilon _1-r\beta (\delta _2)_0}+ \nonumber \\&\frac{r \sigma _0 (b_0-(\delta _2)_0+K\alpha _0\epsilon _1)}{(\delta _3)_0\left( a K\alpha _0^2\epsilon _1+r b_0+rK\alpha _0\epsilon _1-r(\delta _2)_0\right) }, \end{aligned}$$

(36)

Table 2 The sensitivity indices $\gamma _{y_j}^{R_C}=\frac{\partial R_C}{\partial y_j}\times \frac{y_j}{R_C}$ of the reproduction number for the system (1) to the parameters $y_j$ for the parametric values: $r=6$, $K=100$, $\rho =0.4$, $\alpha _0=0.01$, $\beta =0.9$, $\delta _1=0.1$, $(\delta _2)_0 =0.8$, $(\delta _3)_0=0.65$, $\epsilon _1=0.9$, $\epsilon _2 =0.85$, $\epsilon _3 =0.3$, $a=25$, $b_0 =0.1$, $\gamma _0=1.05$, $\sigma _0=1.55$.

Table 2 shows that for this set of parameter values, parameters r, K,$\beta$, $\epsilon _1$, $\alpha _0$,$b_0$ and a are indirectly proportional to $R_C$ and have negative impact on it while $\sigma _0$, $(\delta _2)_0$ and $\gamma _0$ are directly proportional to $R_C$ and have positive impact on it and, rest of all the parameters do not affect $R_C$.

The incoming section 7 consists of the numerical simulation of the system (1), which is extremely important to verify our theoretical findings.

7 Numerical simulation

It is important to execute any system numerically to verify its theoretical results. We can find out how the parameters of any system affect the system with the help of numerical simulation. We have used hypothetical values based on a real scenario such as the predation rate of healthy prey S is less than that of infected prey I since diseased prey is weak and predator can easily catch them compared to one healthy prey [32]. Hence, $\rho$ and $\beta$ must be greater than $\alpha$. Similarly, the conversion coefficient of healthy prey is assumed to be greater than the infected one. Moreover, we took the conversion coefficient of healthy predator is also greater than infected one.

Fig. 1

Population density distribution with respect to time during the coexistence of population with the following set of parameter: $r=6$, $K=100$, $\omega _1=0.1$, $\omega _2=0.4$, $\omega _3=0.1$,$\omega _4=0.1$, $\omega _5=0.1$, $\omega _6=0.1$,$\alpha _0 =0.01$, $\beta =0.9$, $\rho =0.4$, $\sigma _0=1.55$, $\gamma _0=1.05$, $\delta _1=0.1$,$(\delta _2)_0=0.8$, $(\delta _3)_0=0.65$, $a=25$, $e_1=0.9$, $e_2 =0.85$, $e_3=0.3$, $b_0=0.1$, with the initial condition [$S_0$ $I_0$ $P_0$ $Y_0$]=[19 4 3 50], $R_C=2.0081.$

Fig. 2

Population density distribution with respect to time when infected populations extinct for $\alpha _0 =0.4$ rest of parameter are same as in Fig. 1, $R_C=0.883284.$

Fig. 3

Periodic oscillation to extinction of infected population [(a) infected prey, (b) infected predator] with respect to the predation rate of healthy prey $\alpha$ against time using the parameters set of Fig 1

The numerical simulation of proposed system reveals that for the default parameter set $r=6$, $K=100$, $\rho =0.4$, $\alpha _0=0.01$, $\beta =0.9$, $\delta _1=0.1$, $(\delta _2)_0 =0.8$, $(\delta _3)_0=0.65$, $\epsilon _1=0.9$, $\epsilon _2 =0.85$, $\epsilon _3 =0.3$, $a=25$, $b_0 =0.1$, $\gamma _0=1.05$,$\sigma _0=1.55$ the system (1) shows periodic oscillation around interior equilibrium which is shown in Fig. 1. If we increase the average predation rate of healthy prey $\alpha _0$ to 0.4, keeping the rest of the parameter value the same as in Fig. 1, the diseased prey and predator die out, and we will get a disease-free environment as shown in Fig. 2. To know the effect of $\alpha$ on infected populations, we keep other parameters the same as in Fig. 1 and variate average predation rates of healthy prey $\alpha _0$. Figure 3 clearly shows this situation that increasing predation of healthy prey, periodic oscillation occurs and later the infected prey and predation extinct from the environment at $\alpha _0=0.33$. Again, we see the effect of the death rate of diseased prey $\delta _3$ on the infected population by variation in the average death rate of diseased prey $(\delta _3)_0$ and keeping the rest of the parameters are the same as in Fig. 1. We can see in Fig. 4 that increment in $\delta _3$ leads to periodic oscillation first, then the diseased population to die out at $(\delta _3)_0=1.4$.

Fig. 4

Periodic oscillation to extinction of infected population [(a) infected prey, (b) infected predator] with respect to the death rate of infected predator $\delta _3$ against time using the parameters set of Fig. 1

Finally, the effect of disease transmission coefficient $\sigma$ on infected population can be seen if we variate average disease transmission rate $\sigma _0$ and keep the rest of the parameter set same as in Fig. 1. Figure 5 shows that a decrement in the disease transmission rate leads the infected community to die out at $\sigma _0=0.7$. In Fig. 6, we have shown the graphical representation of sensitivity analysis.

Fig. 5

Periodic oscillation to extinction of infected population [(a) infected prey, (b) infected predator] with respect to the disease transmission coefficient between predator $\sigma$ against time using the parameters set of Fig. 1

Fig. 6

Figure showing the effect of system parameters on reproduction number $R_C$ for the parameter set of Fig. 1

Incoming Sect. 8; we will discuss and conclude our theoretical and numerical findings and their conclusions. We also explain the ecological perception of our results.

8 Conclusion

We have investigated a diseased prey–predator non-autonomous model with infection in prey and predator. We have considered that disease transmission parameters $\sigma$ and $\gamma$, the death rate of healthy and diseased prey $\delta _2$ and $\delta _3$, rate of alternative food b, predation rate of healthy prey $\alpha$ are time-dependent parameters that vary seasonally with one year period. The non-autonomous system is analyzed to understand these parameter’s effect on present prey–predator dynamics in a periodic environment. This article contains an onerous analysis applying the comparison theory and Poincare map theory.

We have analyzed the system (1) and found that a periodic disease-free and coexistence state is locally and globally stable in the domain $R_+^4$. Moreover, the periodic basic reproduction number $R_C(t)$ lesser than one shows the local stability of the disease-free equilibrium, and $R_C(t)$ greater than one shows the instability of the same. Further, the periodic coexistence state is stable when $R_C(t)>1$. In the real world, the present analysis reveals that the predator’s preference to predate on infected prey may lead the system to an endemic situation. Further, increasing predation of healthy prey leads the system toward a disease-free situation with many predators.

Consequently, predation of healthy prey helps healthy predator population grow, and predator chooses most contagious prey so that contagious prey is removed from the population, and only healthy prey remains, thereby preventing spreading disease [21, 28]. Decrement of disease contact rate between predators also results in an infection-free environment as it helps to grow healthy predator who prefers to predate on infected prey resulting a diseased-free environment. We get similar conditions by increasing diseased predator’s death rate, which again helps to grow healthy predator population resulting in the disease-free condition.