Abstract
Dynamics of test particles in the space-time of a quintessential black hole (BH) in a novel four-dimensional Einstein–Gauss–Bonnet (EGB) theory is studied. First, we analyse the properties of the space-time of the BH and possible values of the coupling \(\alpha \) and quintessential parameters q that allows the existence of the event horizon. The scalar invariants of the space-time and effects of the parameters on innermost stable circular orbits (ISCOs) radius are also studied. Moreover, fundamental frequencies such as Keplerian and harmonic oscillations are investigated together with applications to quasi-periodic oscillations (QPOs) where the powerful way to test gravity theories using astrophysical observations of twin-peak QPOs is discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Over the last years, we got several observational tests of general relativity [1, 2, 11, 12]. The theory is overall well tested in both weak and strong regimes, and it meets several fundamental problems. Among other issues, it is incompatible with quantum theory, it requires the inclusion of additional concepts (such as dark matter and dark energy) and solutions of its field equations have non-removable singularities. However, theory allows for modifications and alterations to fix those issues and such modified theories do exist in numbers and studying them is important to be able to compare them against observation data and constrain and estimates parameters of the theories.
One of such modifications is Einstein–Gauss–Bonnet (EGB) theory that is defined in higher dimensional space-time (\(D>4\)). According to Lovelock theorem [26] the only theory of gravity in four-dimensional space-time is the general relativity with non-zero cosmological constant. But recently [13] proposed a new four-dimensional Einstein–Gauss–Bonnet solution obtained using a new approach to the Lovelock theorem. To achieve that, the authors rescaled the Gauss–Bonnet term by the factor \(1/(D-4)\) and took the four-dimensional limit. The solution can be used to study the particle motion in this new model. Background space-time in this case represents a non-standard black hole. based on the study, new tests can be devised which will be used to obtain constraints on EGB parameters.
In Ref.[20], gravitational stability was studied by means of photon motion and quasi-normal modes. It was shown that there is a limiting value for coupling constant \(\alpha \) (\(0<\alpha <0.15\)) appearing in the solutions, above which the black hole (BH) becomes gravitationally unstable.
In Ref.[21], authors obtained electrically charged 4D EGB BH solution. Quantum effects of 4D EGB BH have been explored in Ref.[23], while the solution in 3D EGB has been studied in Ref.[22]. Analysing the gravitational collapse of spherical homogeneous dust in 4D EGB gravity authors of [27] had shown its qualitative similarity to the case of Einstein’s gravity. Quasi-normal modes and superradiant process in 4D EGB gravity have been explored in Ref.[41]. The stability of the solution in 4D EGB gravity through the odd parity perturbation method has been studied in Authors of Ref.[5] investigated the stability of 4D EGB solution using odd parity perturbation method. Exploring the spinning particle motion around 4D EGB BH Authors of [40] studied motion of spinning particles around 4D EGB BH and had shown the existence of two separate orbits for each value pair of spin and orbital angular momentum. The geodesic motion of test particles has been explored in Ref.[14].
There are studies on horizon structure of 4D EGB rotating analogue of the static BH [25], cosmic censorship in 4D EGB gravity [29], stability issues [6, 9], optical [3, 17, 18, 39] and thermodynamic [16, 28, 38] properties of 4D EGB BHs. Authors of [4, 30] studied energetic processes and particle acceleration mechanisms near 4D EGB BHs, while Ref. [24] presents Bardeen BH solution in 4D EGB gravity.
Meanwhile, there are objections to the validity of aforementioned new approach and solutions produced by it. Authors of the original research [13] claimed that 4D solution is not well defined in the comments to the paper. There are arguments, that it is only possible to get solutions for \(D>4\) when Gauss–Bonnet term is present [15]. Other arguments against the solution of 4D EGB gravity and corresponding approach are presented in Refs.[7, 8, 37].
2 Quintessence in 4D Einstein–Gauss–Bonnet black holes
The action for the EGB gravitational theory is described by the following expression:
where R is the Ricci scalar, \(\alpha \) is the GB constant, \(L_m\) is the quintessential (anisotropic) matter field whose non-vanishing stress-energy tensor components, \(L_{GB}\) is Lagrangian of the EGB theory given as
where \(R_{\mu \nu \gamma \sigma }\) is Riemann tensor and \(R_{\mu \nu }\) is Ricci tensor.
The field equation in EGB gravity has the following form:
where the Einstein tensor,
and the Lanczos tensor,
\(T_{\mu \nu }\) defines the stress tensor of the quintessential field which has the following components in the Kiselev black hole solution [19]:
The solution for the space-time around the quintessential black holes in 4D EGB gravitational field theory have been found in Ref.[34] and in spherical coordinates (\(x^{\alpha }=\{t,r,\theta ,\phi \}\)) it has the following form:
with the radial metric function
where q and \(\omega _q\) are parameters of quintessential field, M is the total mass of the BH.
In general, the event horizon of the space-time around a black hole can be found by the condition \(g_{tt}(r_h) =g^{rr}(r_h) = 0\). Due to the complicated form of the solution of the equation for the event horizon, we only provide graphics for the different values of the GB and \(\omega _q\) parameters.
Figure 1 presents the behaviour of event horizon radii of quintessential black holes in 4D EGB gravity, with respect to the variation of the quintessential parameter q for different values of parameters \(\alpha \) and \(\omega _q\). It is seen that as \(q=\alpha =0\) the black lines cross \(r_h/M=2\) and for the positive values of q the even horizon increases, it increases faster for the values of \(\omega _q\) near \(-1\). Moreover, there is a minimum value of event horizon radius at a corresponding critical value of the quintessential parameter, and the critical value increases as the \(\alpha \) parameter is increased as well as the minimum of the event horizon radius.
Next we are interested to determine values of the parameters \(\omega _q\) and q for which the metric (6) can be a black hole solution. One can get the set values of these parameters solving a system of equations \(f(r)=f'(r)=0\). However, it is impossible to have analytical solutions for the q and \(\alpha \) parameters, due to the complexity of the equation, so, one may analyse this problem graphically and numerically.
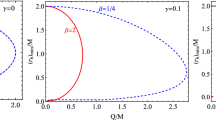
The set of values of the BG parameters \(\alpha \) and quintessential parameter to provide a BH solution given in Eq.(6)
Our detailed analysis in Fig.2 show that the maximum values of both \(\alpha \) and q parameters and their configurations increase as \(\omega _q\) increases. It is interesting to study conditions on the parameters q and \(\alpha \) that allow the black hole solution (6) to have event horizon \(r_h=2M\), in other words, the solution that reflects the Schwarzschild black hole one and does not allow distinguishing the quintessential black hole solution from the Schwarzschild one. Moreover, we have found out that the limit of the metric function given in Eq.(6) at the large values of radial coordinate turns to one for the Schwarzschild case in 4D EGB gravitational theory. It does mean that there are no quintessential field effects at large distances.
The same relation as shown in Fig.2, but for the event horizon radius, the same as Schwarzschild black hole \(r_h=2M\)
In Fig.3, we show similar analysis on the relations provided in Fig.3 for the value of event horizon radius \(r_h=2M\), the same as Schwarzschild black hole event horizon. One can see from the figure that the relation is linear, i.e. as the \(\alpha \) parameter increases the quintessential field parameter increases linearly, and the slope is larger at higher values of \(\omega _q\) parameter.
2.1 Scalar invariants
In this subsection, we show detailed analysis of the space-time properties around the quintessential black holes. We aimed to study the scalar invariants: Ricci scalar, square of Ricci tensor and Kretschmann scalar.
Ricci scalar
Ricci scalar \(R=g^{\mu \nu }R_{\mu \nu }\) of the space-time around the quintessential black hole has the form
where
In the GR limit, the pure quintessential black hole’s Ricci tensor takes the form
Above limit shows that in the absence of the quintessence space-time becomes Ricci flat \(R=0\).
The square of Ricci tensor
Next we study the square of Ricci tensor \({\mathcal {R}}=R_{ab}R^{ab}\) of the space-time around the black hole, and it takes the form
The GR limit has the form,
in Schwarzschild limit it tends to zero, \({\mathcal {R}}=0\).
Kretschmann scalar
Finally, we calculate the Kretschmann scalar of the space-time around the black hole, and it has the following form:
The GR limit (\(\alpha =0\)) of the Kretschmann scalar of the space-time around the black hole,
It has the form \(K=48M^2/r^6\) in the Schwarzschild case.
3 Particle motion
In this section, we study the dynamics of neutral test particles in the space-time of quintessential black hole in 4D EGB theory. The Lagrangian for a neutral particle with mass m
The conserved quantities in the dynamics of the particles read
where \({\mathcal {L}}\) and \({\mathcal {E}}\) are the special angular momentum and energy of test particles, respectively. Equations of motion for a test particle are governed by the normalization condition
where \(\epsilon \) is 0 and \(-1\) for massless and massive particles, respectively.
The equation of motion of the test particles can be governed by timelike geodesics of the space-time around the black hole, and it can be found using Eq.(15). The equation for the radial motion of test particles in the equatorial plane where \(\theta =\pi /2, \dot{\theta }=0\) reads as,
where the effective potential
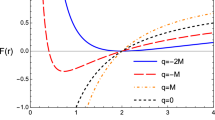
Figure 4 demonstrates the radial dependence of the effective potential for radial motion of test particles in the equatorial plane of the space-time around the quintessential black hole in 4D EGB theory for different values of the GB and quintessential field parameters. It is seen from the figure that the presence of quintessential field decreases the maximum in the values of effective potential, while positive (negative) values of the \(\alpha \) parameter cause to increase (decrease) it and the position where the effective potential takes maximum value slightly shifts to the black hole. Moreover, the increase of \(\omega _q\) parameter also decreases the effective potential and the particles can have orbits closer to the central black hole.
The circular motion of test particles around a black hole can be described by the conditions:
Conditions given in Eq.(18) help to find the expression for angular momentum of the particles at circular orbits, as well as corresponding to specific energy.
The radial profiles of the specific energy (in the left panel) and angular momentum (in the right panel) are shown in Fig. 5 for different values of the parameters \(\alpha \), q and \(\omega _q\). It is seen that the presence of quintessential field decreases both the energy and angular momentum, and the effect of the GB space is essential near the compact object. Moreover, the asymptotic values of the energy and angular momentum decrease as \(\omega =-0.5\) compared to their values at \(\omega _q=-0.35\).
3.1 Innermost stable circular orbits
The circular orbits of test particles around compact gravitational objects can be described in standard way using the condition \(V''_{\mathrm{eff}} \ge 0\). In fact, the innermost stable circular orbit (ISCO) radius is a solution of equation \(V''_{\mathrm{eff}}= 0\) or
It is also hard, and sometimes even impossible, to solve Eq.(20) with respect to the radial coordinate. So, we can solve it numerically and analyse graphically. Below, we will show dependence of ISCO radius of test particles on the quintessential parameter q, by varying the GB and \(\omega _q\) parameters.
According to Fig.6, ISCO expands under the effects of quintessential field. The expansion is linear at \(\omega _q=-0.35\), while at \(\omega _q=-0.5\) we have two possible orbits for the same values of parameters and there is an upper limit for parameter q where two solutions of Eq.(20) coincide. Moreover, negative (positive) values of the GB parameter cause weak increase (decrease) of the ISCO radius.
We are also interested in the possibility of a quintessential black hole producing the same gravitational field the as the Schwarzschild black hole. We will analyse relations between q and \(\alpha \) parameters providing \(r_{\mathrm{ISCO}}=6M\).
The same relations shown in Fig.2, but for the ISCO radius being the same as for the Schwarzschild black hole
In Fig.7, we have shown relations between the GB and quintessential parameters providing the radius of ISCO equal to 6M, mimicking the Schwarzschild black hole case. It is seen that the relations have linear character, which is similar to the results obtained in Fig.3.
3.2 Keplerian frequency
The angular momentum of Keplerian orbits is described by so-called Keplerian frequency, which has the form
and in the space-time around a static black hole, it has the following form
Now we calculate the Keplerian frequency in space-time around the quintessential black hole in 4D EGB theory using expression (22) and we get
Furthermore, for the qualitative analysis to understand the values for frequencies, we will convert the geometrized unit of the frequency to Hz using the following relation:
One can see from Fig. 8 that the presence of quintessential field and positive values of the GB parameter cause the Keplerian frequency near the photonsphere to be slightly lower, while negatives of \(\alpha \) and values of \(\omega _q\) near \(-1\) increase it. This can be useful to propose new tests of the proposed gravity and solution using the QPO data.
3.3 Harmonic oscillations
Here we will investigate the fundamental frequencies of the radial and vertical oscillations of test particles around the BH which are useful to explain the origin mechanisms of QPOs. The frequencies can be calculated, assuming there are radial \(r\rightarrow r_0+\delta r\) and vertical \(\theta \rightarrow \theta _0+\delta \theta \) perturbations to the circular orbits. Using the expansion of the effective potential given in Eq.(17) over r and \(\theta \) we can have the harmonic oscillator equations in the following form:
where radial and vertical angular frequencies are noted \(\varOmega _r\) and \(\varOmega _\theta \), respectively, and it is assumed that they are measured by a distant observer. The expressions for these frequencies have the form,
After a little algebra we can have the following analytic form of the radial and the vertical frequencies in space-time around the quintessential black hole in 4D EGB gravity:
where
Now, we analyse the effects of parameters q, \(\omega _q\) and \(\alpha \) on the radial oscillations graphically.
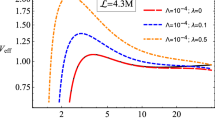
Radial dependencies of radial frequencies are plotted on Fig.9 for the values of \(q=0.01\), \(\omega _q=-0.35\) and \(-0.6\), and \(\alpha \pm 0.5\). By comparing the curves, one can easily see that at \(q=0.01, \omega _q=-0.35\) in GB frame, the frequency is less than in Schwarzschild case. In 4D EGB gravity, when \(\alpha =0.5\) at the same values of the quintessential parameters, the frequency is more than in GR. Frequency decreases at negative values of \(\alpha \) as \(\omega _q\) decreases.
4 QPO models in 4D quintessential field
In this section we study the values of upper and lower frequencies of twin peak QPOs around the quintessential black holes in 4D gravity comparing results with the Schwarzschild and Kerr black hole cases [31, 33, 36]. In this way, according to QPO models, we obtain radial dependencies of the frequencies, as well as the GB and quintessential parameters. Then we will provide the values of the frequencies by fixing the black hole parameters, and plot all possible values of the lower and upper frequencies at the distances from the corresponding ISCO radius to larger distances. In this work, as a simple example, we use the following well-known model called relativistic precession (RP) model [10, 32, 35]. According to this model, the upper and lower frequencies are defined by the radial and orbital frequencies in the form \(\nu _U=\nu _\phi \) and \(\nu _L=\nu _\phi -\nu _r\), respectively. But in modified RP1 and RP2 models they are \(\nu _U=\nu _\theta \), \(\nu _L=\nu _\phi -\nu _r\) and \(\nu _U=\nu _\phi \), \(\nu _L=\nu _\theta -\nu _r\), respectively.
Possible values of upper and lower frequencies of twin-peak QPOs around the 4D quintessential black holes shown in the \(\nu _U-\nu _L\) diagram, comparing rotating Kerr and Schwarzschild black holes, in the frame of RP model. Inclined light blue, orange and green lines correspond to the QPOs with the ratio of upper and lower frequencies 3:2, 4:3 and 5:4, respectively. The brown line is for the ratio 1:1, which is graveyard for the twin peak QPOs. The mass of the BH is taken as \(5M_\odot \)
In Fig.10, we have shown the set of possible relations (values) of upper and lower frequencies of twin peaked QPOs in the RP model. Here we compare the values in the frames of GR (around the Schwarzschild and Kerr black holes) and 4D EGB gravity in the presence of quintessential field effects. In analysis of a twin peak QPO object, we can find the position of the object on the diagram and if it lies on the black line, then we can say the central black hole of the QPO is the pure Schwarzschild black hole. In the case when it’s positioned over the black line (corresponding to the Schwarzschild black hole case) then the central black hole can not exactly be the Schwarzschild one. It can be a rotating Kerr black hole, or it is a 4D quintessential black hole with corresponding spin and quintessential parameters. In this case, there is a problem (not possible) to distinguish the nature of central black hole: it can be either Kerr or quintessential black hole in 4D EGB theory. Let us see another scenario where the position of another twin peak QPO lying under the black line, the source can only be a black hole in 4D EGB gravity.
5 Conclusions
In this work, we have analysed the properties of the space-time of the quintessential BH in 4D EGB gravitational theory and possible values for the coupling \(\alpha \) and quintessential parameters q that provide the existence of event horizon. The case when the quintessential black hole event horizon lies at 2M, the same as the Schwarzschild black hole horizon radius with corresponding parameters, is also discussed. The scalar invariants of the space-time have also been studied and their GR limits are shown. We also have studied a test particle dynamics in the space-time of a quintessential black hole in a novel 4D Einstein–Gauss–Bonnet theory. The effects of the quintessential and GB parameters on the effective potential for radial motion, specific energy and angular momentum of the particles corresponding to their circular orbits have been investigated. The effects of the parameters on ISCO radius have also been studied, and the relations between the quintessential and GB parameters providing 6M ISCO radius are shown, reflecting the same gravitational field effects on ISCO as the Schwarzschild black hole. Moreover, fundamental frequencies such as Keplerian and harmonic oscillations are also studied together with applications to quasi-periodic oscillations (QPOs) where we discussed the way to test gravity theories through astrophysical observations of twin-peak QPOs.
References
Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al.: Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 116(6), 061102 (2016). https://doi.org/10.1103/PhysRevLett.116.061102
Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al.: Tests of General Relativity with GW150914. Phys. Rev. Lett. 116(22), 221101 (2016). https://doi.org/10.1103/PhysRevLett.116.221101
Abdujabbarov, A.; Atamurotov, F.; Dadhich, N.; Ahmedov, B.; Stuchlík, Z.: Energetics and optical properties of 6-dimensional rotating black hole in pure Gauss–Bonnet gravity. Eur. Phys. J. C 75, 399 (2015). https://doi.org/10.1140/epjc/s10052-015-3604-5
Abdujabbarov, A.; Rayimbaev, J.; Turimov, B.; Atamurotov, F.: Dynamics of magnetized particles around 4-D Einstein Gauss-Bonnet black hole. Phys. Dark Univ. 30, 100715 (2020). https://doi.org/10.1016/j.dark.2020.100715
Aguilar-Pérez, G.; Cruz, M.; Lepe, S.; Moran-Rivera, I.: Hairy black hole stability under odd parity perturbations in the Einstein–Gauss–Bonnet model. arXiv e-prints, arXiv:1907.06168 (2019)
Aragón, A.; Bécar, R.; González, P.A.; Vásquez, Y.: Perturbative and nonperturbative quasinormal modes of 4D Einstein-Gauss-Bonnet black holes. Eur. Phys. J. C 80(8), 773 (2020). https://doi.org/10.1140/epjc/s10052-020-8298-7
Arrechea, J.; Delhom, A.; Jiménez-Cano, A.R.: Comment on Einstein-Gauss-Bonnet Gravity in Four-Dimensional Spacetime. Phys. Rev. Lett. 125(14), 149002 (2020). https://doi.org/10.1103/PhysRevLett.125.149002
Bonifacio, J.; Hinterbichler, K.; Johnson, L.A.: Amplitudes and 4D Gauss-Bonnet theory. Phys. Rev. D 102(2), 024029 (2020). https://doi.org/10.1103/PhysRevD.102.024029
Churilova, M.S.: Quasinormal modes of the Dirac field in the novel 4D Einstein–Gauss–Bonnet gravity. arXiv e-prints, arXiv:2004.00513 (2020)
Demyanova; Aleksandra, R.J.; Abdujabbarov, A.; Wen-Biao, H.: Distinguishing regular and singular black holes in modified gravity. Arab. J. Math. 8(10), 2193–5351 (2021). https://doi.org/10.1007/s40065-021-00348-8
Event Horizon Telescope Collaboration; et al., A.: First M87 Event Horizon Telescope Results. II. Array and Instrumentation. Astrophys. J. Lett, 875(1), L2 (2019). https://doi.org/10.3847/2041-8213/ab0c96
Event Horizon Telescope Collaboration; et. al., A.: First M87 Event Horizon Telescope Results. III. Data Processing and Calibration. Astrophys. J. Lett, 875(1), L3 (2019). https://doi.org/10.3847/2041-8213/ab0c57
Glavan, D.; Lin, C.: Einstein-Gauss-Bonnet Gravity in Four-Dimensional Spacetime. Phys. Rev. Lett. 124(8), 081301 (2020). https://doi.org/10.1103/PhysRevLett.124.081301
Guo, M.; Li, P.C.: Innermost stable circular orbit and shadow of the 4D Einstein-Gauss-Bonnet black hole. Eur. Phys. J. C 80(6), 588 (2020). https://doi.org/10.1140/epjc/s10052-020-8164-7
Gürses, M.; Şişman, T.Ç.; Tekin, B.: Is there a novel Einstein-Gauss-Bonnet theory in four dimensions? Eur. Phys. J. C 80(7), 647 (2020). https://doi.org/10.1140/epjc/s10052-020-8200-7
Hegde, K.; Naveena Kumara, A.; Rizwan, C.L.A.; Ajith K., M.; Sabir Ali, M.: Thermodynamics, Phase Transition and Joule Thomson Expansion of novel 4-D Gauss Bonnet AdS Black Hole. arXiv e-prints, arXiv:2003.08778 (2020)
Heydari-Fard, M.; Heydari-Fard, M.; Sepangi, H.R.: Bending of light in novel 4\(D\) Gauss-Bonnet-de Sitter black holes by Rindler-Ishak method. arXiv e-prints, arXiv:2004.02140 (2020)
Islam, S.U.; Kumar, R.; Ghosh, S.G.: Gravitational lensing by black holes in the 4D Einstein-Gauss-Bonnet gravity. J. Cosmol. Astropart. Phys. 2020(9), 030 (2020). https://doi.org/10.1088/1475-7516/2020/09/030
Kiselev, V.V.: Quintessence and black holes. Class. Quantum Gravity 20, 1187–1197 (2003)
Konoplya, R.A.; Zinhailo, A.F.: Quasinormal modes, stability and shadows of a black hole in the novel 4D Einstein–Gauss–Bonnet gravity. arXiv e-prints, arXiv:2003.01188 (2020)
Konoplya, R.A.; Zhidenko, A.: Black holes in the four-dimensional Einstein-Lovelock gravity. Phys. Rev. D 101(8), 084038 (2020). https://doi.org/10.1103/PhysRevD.101.084038
Konoplya, R.A.; Zhidenko, A.: BTZ black holes with higher curvature corrections in the 3D Einstein-Lovelock gravity. Phys. Rev. D 102(6), 064004 (2020). https://doi.org/10.1103/PhysRevD.102.064004
Konoplya, R.A.; Zinhailo, A.F.: Grey-body factors and Hawking radiation of black holes in 4D Einstein-Gauss-Bonnet gravity. Phys. Lett. B 810, 135793 (2020). https://doi.org/10.1016/j.physletb.2020.135793
Kumar, A.; Kumar, R.: Bardeen black holes in the novel \(4D\) Einstein–Gauss–Bonnet gravity. arXiv e-prints, arXiv:2003.13104 (2020)
Kumar, R.; Ghosh, S.G.: Rotating black holes in 4D Einstein–Gauss–Bonnet gravity and its shadow. JCAP 2020(7), 053 (2020). https://doi.org/10.1088/1475-7516/2020/07/053
Lovelock, D.: The Einstein Tensor and Its Generalizations. J. Math. Phys. 12(3), 498–501 (1971). https://doi.org/10.1063/1.1665613
Malafarina, D.; Toshmatov, B.; Dadhich, N.: Dust collapse in 4D Einstein–Gauss–Bonnet gravity. Phys. Dark Univ. 30, 100598 (2020). https://doi.org/10.1016/j.dark.2020.100598
Mansoori, S.A.H.: Thermodynamic geometry of the novel 4-D Gauss Bonnet AdS Black Hole. arXiv e-prints, arXiv:2003.13382 (2020)
Mishra, A.K.: Quasinormal modes and strong cosmic censorship in the regularised 4D Einstein–Gauss–Bonnet gravity. Gen. Relativ. Gravit. 52(11), 106 (2020). https://doi.org/10.1007/s10714-020-02763-2
Naveena Kumara, A.; Rizwan, C.L.A.; Hegde, K.; Ali, M.S.; Ajith, K.M.: Rotating 4D Gauss–Bonnet black hole as a particle accelerator. Ann. Phys. 434, 168599 (2021). https://doi.org/10.1016/j.aop.2021.168599
Rayimbaev, J.; Abdujabbarov, A.; Wen-Biao, H.: Regular nonminimal magnetic black hole as a source of quasiperiodic oscillations. Phys. Rev. D 103(10), 104070 (2021). https://doi.org/10.1103/PhysRevD.103.104070
Rayimbaev, J.; Shaymatov, S.; Jamil, M.: Dynamics and epicyclic motions of particles around the Schwarzschild-de Sitter black hole in perfect fluid dark matter. Eur. Phys. J. C 81(8), 699 (2021). https://doi.org/10.1140/epjc/s10052-021-09488-9
Rayimbaev, J.; Tadjimuratov, P.; Abdujabbarov, A.; Ahmedov, B.; Khudoyberdieva, M.: Dynamics of Test Particles and Twin Peaks QPOs around Regular Black Holes in Modified Gravity. Galaxies 9(4), 75 (2021). https://doi.org/10.3390/galaxies9040075
Shah, H.; Ahmad, Z.; Shah, H.H.: Quintessence background for 4d einstein-gauss-bonnet black holes. Phys. Lett. B 818, 136383 (2021). https://doi.org/10.1016/j.physletb.2021.136383. ISSN 0370-2693
Stella, L.; Vietri, M.; Morsink, S.M.: Correlations in the Quasi-periodic Oscillation Frequencies of Low-Mass X-Ray Binaries and the Relativistic Precession Model. Astrophys. J. 524(1), L63–L66 (1999). https://doi.org/10.1086/312291
Stuchlík, Z.; Kološ, M.: Models of quasi-periodic oscillations related to mass and spin of the GRO J1655–40 black hole. Astron. Astrophys. 586, A130 (2016). https://doi.org/10.1051/0004-6361/201526095
Tian, S.X.; Zhu, Z.H.: Comment on “Einstein-Gauss-Bonnet Gravity in Four-Dimensional Spacetime”. arXiv e-prints, arXiv:2004.09954 (2020)
Wei, S.W.; Liu, Y.X.: Extended thermodynamics and microstructures of four-dimensional charged Gauss-Bonnet black hole in AdS space. Phys. Rev. D 101(10), 104018 (2020). https://doi.org/10.1103/PhysRevD.101.104018
Wei, S.W.; Liu, Y.X.: Testing the nature of Gauss-Bonnet gravity by four-dimensional rotating black hole shadow. Eur. Phys. J. Plus 136(4), 436 (2021). https://doi.org/10.1140/epjp/s13360-021-01398-9
Zhang, Y.P.; Wei, S.W.; Liu, Y.X.: Spinning test particle in four-dimensional Einstein–Gauss–Bonnet Black Hole. arXiv e-prints, arXiv:2003.10960 (2020)
Zhang, C.Y.; Zhang, S.J.; Li, P.C.; Guo, M.: Superradiance and stability of the regularized 4D charged Einstein-Gauss-Bonnet black hole. J. High Energy Phys. 2020(8), 105 (2020). https://doi.org/10.1007/JHEP08(2020)105
Acknowledgements
This research is partly supported by Grant F3-2020092957 of the Uzbekistan Ministry for Innovative Development and by the Abdus Salam International Centre for Theoretical Physics under the Grant No. OEA-NT-01. J.R. acknowledges to the ERASMUS+ project 608715-EPP-1-2019-1-UZ-EPPKA2-JP (SPACECOM).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rayimbaev, J., Tadjimuratov, P., Ahmedov, B. et al. Quintessential effects on quasiperiodic oscillations in 4D Einstein–Gauss–Bonnet gravity. Arab. J. Math. 11, 119–131 (2022). https://doi.org/10.1007/s40065-022-00369-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40065-022-00369-x